Keywords

1 Introduction

Many real-life problems are enmeshed with uncertainties hence making decision-making a herculean task. To address such common challenges, Zadeh [64] introduced fuzzy sets to resolve/curb the embedded uncertainties in decision-making. Some decision-making problems could not be controlled with a fuzzy approach because fuzzy set only considered membership grade whereas, many real-life problems have the component of both membership grade and non-membership grade with the possibility of hesitation. Such cases can best be addressed by IFSs [1, 2]. IFS is described with membership grade \(\mu \), non-membership grade \(\nu \) and hesitation margin \(\pi \) in such a way that their sum is one and \(\mu +\nu \) is less than or equal to one. Due to the usefulness of IFS, it has been applied to tackle pattern recognition problems [43, 57], career determination/appointment processes [7, 18, 19, 23] and other MCDM problems discussed in [3,4,5, 21, 22, 24, 46, 51, 52]. Some improved similarity and distance measures based on the set pair analysis theory with applications have been studied [39, 40].

The idea of IFS though vital, cannot be suitable in a condition where a decision-maker wants to take decision in a multi-criteria problem when \(\mu +\nu \) is greater than one. Suppose \(\mu =\frac{1}{2}\) and \(\nu =\frac{3}{5}\), clearly IFS cannot model such a situation. This provoked Atanassov [2] to propose intuitionistic fuzzy set of second type or Pythagorean fuzzy sets (PFSs) [58, 61] to generalize IFSs such that \(\mu +\nu \) is also greater than one and \(\mu ^2+\nu ^2+\pi ^2=1\). PFS is a special case of IFS with additional conditions and thus has more ability to restraint hesitations more appropriate with higher degree of accuracy. The concept of PFSs have been sufficiently explored by different authors so far [8, 13, 60]. Some new generalized Pythagorean fuzzy information and aggregation operators using Einstein operations have been studied in [26, 31] with application to decision-making. Garg [32] studied some methods for strategic decision-making with immediate probabilities in Pythagorean fuzzy environment, and the idea of linguistic PFSs has been studied with application to multi-attribute decision-making problems [34]. The notion of interval-valued PFSs has been explicated with regards to score function and exponential operational laws with applications [28, 29, 33]. Many applications of PFSs have been discussed in pattern recognitions [10, 12, 15], TOPSIS method applications [27, 66], MCDM problems using different approaches [9, 11, 35, 58, 59, 61, 62, 67] and other applicative areas [6, 20, 29, 36, 65]. Several measuring tools have been employed to measure the similarity and dissimilarity indexes between PFSs with applications to MCDM problems as discussed in [8, 11, 12, 15, 20].

The concept of correlation coefficient which is a vital tool for measuring interdependency, similarity, and interrelationship between two variables was first studied in statistics by Karl Pearson in 1895 to measure the interrelation between two variables or data. By way of extension, numerous professions like engineering and sciences among others have applied the tool to address their peculiar challenges. To equip correlation coefficient to better handle fuzzy data, the idea was encapsulated into intuitionistic fuzzy context and applied to many MCDM problems. The first work on the correlation coefficient between IFSs (CCIFSs) was carried out by Gerstenkorn and Manko [42]. Hung [44] used a statistical approach to develop CCIFSs by capturing only the membership and non-membership functions of IFSs, and CCIFSs was proposed based on centroid method in [45]. Mitchell [48] studied a new CCIFSs based on integral function. Park et al. [49] and Szmidt and Kacprzyk [53] extended the method in [44] by incorporating the hesitation margin of IFS. Liu et al. [47] introduced a new CCIFSs with the application. Garg and Kumar [38] proposed novel CCIFSs based on set pair analysis and applied the approach to solve some MCDM problems. The concept of correlation coefficient and its applications have been extended to complex intuitionistic fuzzy and intuitionistic multiplicative environments, respectively [30, 41]. TOPSIS method based on correlation coefficient was proposed in [37] to solve decision-making problems with intuitionistic fuzzy soft set information. Several other methods of CCIFSs have been studied and applied to decision-making problems [14, 54, 56, 62, 63].

Garg [25] initiated the study of correlation coefficient between Pythagorean fuzzy sets (CCPFSs) by proposing two novel correlation coefficient techniques to determine the interdependency between PFSs, and applied the techniques to MCDM problems. Thao [55] extended the work on CCIFSs in [54] to CCPFSs and applied the approach to solve some MCDM problems. Singh and Ganie [50] proposed some CCPFSs procedures with applications, but the procedures do not incorporate all the orthodox parameters of PFSs. Ejegwa [16] proposed a triparametric CCPFSs method which generalized one of the CCPFSs techniques studied in [25], and applied the method to decision-making problems. Though one cannot doubt the important of distance and similarity measures as viable soft computing tools, the preference for correlation coefficient measure in information measure theory is because of its considerations of both similarity (which is the dual of distance) and interrelationship/interdependence indexes between PFSs.

In the computation of CCPFSs, the idea of weights of the elements of sets upon which PFSs are built are often ignored, which many times lead to misleading results. Thus, Garg [25] proposed some weighted correlation coefficients between PFSs (WCCPFSs). From the work of Garg [25], we are enthused to provide improved methods of computing WCCPFSs for the enhancement of efficient application. In this chapter, some new WCCPFSs methods are proposed which are provable to be more reliable with better performance indexes than the existing ones. The objectives of the work are to

  1. (i)

    explore the WCCPFSs methods studied in [25] and propose some new WCCPFSs methods to enhance accuracy and reliability in measuring CCPFSs.

  2. (ii)

    mathematically corroborate the proposed WCCPFSs methods with the axiomatic conditions for CCPFSs, and numerically verify the authenticity of the proposed methods over the existing ones.

  3. (iii)

    establish the applications of the proposed methods in some MCDM problems.

The rest of the chapter is delineated as follow; Sect. 2 briefly revises some basic notions of PFSs and Sect. 3 discusses some CCPFSs methods studied in [16, 25] with numerical verifications. Section 4 discusses existing WCCPFSs methods, introduces new WCCPFSs methods and numerically verifies their authenticity. Section 5 demonstrates the application of the new WCCPFSs methods in pattern recognition and medical diagnosis problems, all represented in Pythagorean fuzzy values. Section 6 concludes the chapter and gives some areas for future research.

2 Basic Notions of Pythagorean Fuzzy Sets

Definition 2.1

[1] An intuitionistic fuzzy set of X denoted by \(\mathsf {A}\) (where X is a non-empty set) is an object having the form

$$\begin{aligned} \mathsf {A}=\lbrace \langle \dfrac{\mu _\mathsf {A}(x), \nu _\mathsf {A}(x)}{x} \rangle \mid x\in X\rbrace , \end{aligned}$$
(1)

where the functions \(\mu _\mathsf {A}(x),\; \nu _\mathsf {A}(x): X\rightarrow [0,1]\) define the degrees of membership and non-membership of the element \(x\in X\) such that

$$\begin{aligned} 0\le \mu _\mathsf {A}(x)+ \nu _\mathsf {A}(x)\le 1. \end{aligned}$$

For any intuitionistic fuzzy set \(\mathsf {A}\) of X, \(\pi _\mathsf {A}(x)= 1-\mu _\mathsf {A}(x)-\nu _\mathsf {A}(x)\) is the intuitionistic fuzzy set index or hesitation margin of \(\mathsf {A}\).

Definition 2.2

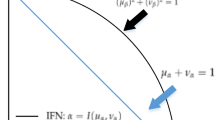
[58] A Pythagorean fuzzy set of X denoted by \(\mathsf {A}\) (where X is a non-empty set) is the set of ordered pairs defined by

$$\begin{aligned} \mathsf {A}=\lbrace \langle \dfrac{\mu _{\mathsf {A}}(x), \nu _{\mathsf {A}}(x)}{x} \rangle \mid x\in X\rbrace , \end{aligned}$$
(2)

where the functions \(\mu _{\mathsf {A}}(x),\; \nu _{\mathsf {A}}(x):X\rightarrow [0,1]\) define the degrees of membership and non-membership of the element \(x\in X\) to \(\mathsf {A}\) such that \(0\le (\mu _{\mathsf {A}}(x))^2 + (\nu _{\mathsf {A}}(x))^2 \le 1\). Assuming \((\mu _{\mathsf {A}}(x))^2 + (\nu _{\mathsf {A}}(x))^2 \le 1\), then there is a degree of indeterminacy of \(x\in X\) to \(\mathsf {A}\) defined by \(\pi _{\mathsf {A}}(x)=\sqrt{1-[(\mu _{\mathsf {A}}(x))^2 + (\nu _{\mathsf {A}}(x))^2]}\) and \(\pi _{\mathsf {A}}(x)\in [0,1]\).

Definition 2.3

[61] Suppose \(\mathsf {A}\) and \(\mathsf {B}\) are PFSs of X, then

  1. (i)

    \(\overline{\mathsf {A}}=\lbrace \langle \dfrac{\nu _{\mathsf {A}}(x), \mu _{\mathsf {A}}(x)}{x} \rangle |x\in X \rbrace \).

  2. (ii)

    \(\mathsf {A}\cup \mathsf {B}=\lbrace \langle \max (\dfrac{\mu _{\mathsf {A}}(x),\mu _{\mathsf {B}}(x)}{x}), \min (\dfrac{\nu _{\mathsf {A}}(x),\nu _{\mathsf {B}}(x)}{x}) \rangle |x\in X \rbrace \).

  3. (iii)

    \(\mathsf {A}\cap \mathsf {B}=\lbrace \langle \min (\dfrac{\mu _{\mathsf {A}}(x),\mu _{\mathsf {B}}(x)}{x}), \max (\dfrac{\nu _{\mathsf {A}}(x),\nu _{\mathsf {B}}(x)}{x}) \rangle |x\in X \rbrace \).

It follows that, \(\mathsf {A}=\mathsf {B}\) iff \(\mu _{\mathsf {A}}(x)=\mu _{\mathsf {B}}(x)\), \(\nu _{\mathsf {A}}(x)=\nu _{\mathsf {B}}(x)\, \forall x\in X\), and \(\mathsf {A}\subseteq \mathsf {B} \) iff \(\mu _{\mathsf {A}}(x)\le \mu _{\mathsf {B}}(x)\), \(\nu _{\mathsf {A}}(x)\ge \nu _{\mathsf {B}}(x)\) \(\forall x\in X\). We say \(\mathsf {A}\subset \mathsf {B}\) iff \(\mathsf {A}\subseteq \mathsf {B}\) and \(\mathsf {A}\ne \mathsf {B}\).

Remark 2.4

Suppose \(\mathsf {A}\), \(\mathsf {B}\) and \(\mathsf {C}\) are PFSs of X. By Definition 2.3, the following properties hold:

  1. (i)
    $$\begin{aligned} \overline{\overline{\mathsf {A}}}=\mathsf {A} \end{aligned}$$
  2. (ii)
    $$\begin{aligned} \mathsf {A}\cap \mathsf {A}=\mathsf {A}\end{aligned}$$
    $$\begin{aligned}\mathsf {A}\cup \mathsf {A}=\mathsf {A}\end{aligned}$$
  3. (iii)
    $$\begin{aligned} \mathsf {A}\cap \mathsf {B}=\mathsf {B}\cap \mathsf {A}\end{aligned}$$
    $$\begin{aligned} \mathsf {A}\cup \mathsf {B}=\mathsf {B}\cup \mathsf {A}\end{aligned}$$
  4. (iv)
    $$\begin{aligned} \mathsf {A}\cap (\mathsf {B}\cap \mathsf {C})=(\mathsf {A}\cap \mathsf {B})\cap \mathsf {C}\end{aligned}$$
    $$\begin{aligned} \mathsf {A}\cup (\mathsf {B}\cup \mathsf {C})=(\mathsf {A}\cup \mathsf {B})\cup \mathsf {C}\end{aligned}$$
  5. (v)
    $$\begin{aligned} \mathsf {A}\cap (\mathsf {B}\cup \mathsf {C})= (\mathsf {A}\cap \mathsf {B})\cup (\mathsf {A}\cap \mathsf {C})\end{aligned}$$
    $$\begin{aligned} \mathsf {A}\cup (\mathsf {B}\cap \mathsf {C})= (\mathsf {A}\cup \mathsf {B})\cap (\mathsf {A}\cup \mathsf {C})\end{aligned}$$
  6. (vi)
    $$\begin{aligned} \overline{(\mathsf {A}\cap \mathsf {B})} =\overline{\mathsf {A}}\cup \overline{\mathsf {B}}\end{aligned}$$
    $$\begin{aligned}\overline{(\mathsf {A}\cup \mathsf {B})}=\overline{\mathsf {A}}\cap \overline{\mathsf {B}}.\end{aligned}$$

Definition 2.5

[12] Pythagorean fuzzy pairs (PFPs) or Pythagorean fuzzy values (PFVs) is characterized by the form \(\langle a,b\rangle \) such that \(a^2+b^2\le 1\) where \(a,b\in [0,1]\). PFPs are used for the assessment of objects for which the components (a and b) are interpreted as membership degree and non-membership degree or degree of validity and degree of non-validity, respectively.

3 Correlation Coefficients Between PFSs

Correlation coefficient in the Pythagorean fuzzy environment was pioneered by the work of Garg [25]. The concept of CCPFSs is very valuable in solving MCDM problems. What follows is the axiomatic definition of CCPFSs.

Definition 3.1

[16] Suppose \(\mathsf {A}\) and \(\mathsf {B}\) are PFSs of X. Then, the CCPFSs for \(\mathsf {A}\) and \(\mathsf {B}\) denoted by \(\mathcal {K}(\mathsf {A}, \mathsf {B})\) is a measuring function \(\mathcal {K}:PFS\times PFS\rightarrow [0,1]\) which satisfies the following conditions;

  1. (i)

    \(\mathcal {K}(\mathsf {A}, \mathsf {B})\in [0,1]\),

  2. (ii)

    \(\mathcal {K}(\mathsf {A}, \mathsf {B})=\mathcal {K}(\mathsf {B}, \mathsf {A})\),

  3. (iii)

    \(\mathcal {K}(\mathsf {A}, \mathsf {B})=1\) if and only if \(\mathsf {A}=\mathsf {B}\).

Now, we recall the existing CCPFSs methods in [16, 25] as follows:

3.1 Some Existing/New CCPFSs Methods

Assume \(\mathsf {A}\) and \(\mathsf {B}\) are PFSs of \(X=\lbrace x_i\rbrace \) for \(i=1,\ldots , n\). Then, the CCPFSs for \(\mathsf {A}\) and \(\mathsf {B}\) as in [25] are as follows:

$$\begin{aligned} \mathcal {K}_1(\mathsf {A}, \mathsf {B})=\dfrac{C(\mathsf {A}, \mathsf {B})}{\max [C(\mathsf {A}, \mathsf {A}),C(\mathsf {B}, \mathsf {B})]} \end{aligned}$$
(3)

and

$$\begin{aligned} \mathcal {K}_2(\mathsf {A}, \mathsf {B})=\dfrac{C(\mathsf {A}, \mathsf {B})}{\sqrt{C(\mathsf {A}, \mathsf {A})C(\mathsf {B}, \mathsf {B})}}, \end{aligned}$$
(4)

where

$$\begin{aligned} \left. \begin{aligned} C(\mathsf {A}, \mathsf {A})=\sum ^n_{i=1}[\mu ^4_\mathsf {A}(x_i)+ \nu ^4_\mathsf {A}(x_i)+ \pi ^4_\mathsf {A}(x_i)]\\ C(\mathsf {B}, \mathsf {B})=\sum ^n_{i=1}[\mu ^4_\mathsf {B}(x_i)+ \nu ^4_\mathsf {B}(x_i)+ \pi ^4_\mathsf {B}(x_i)] \end{aligned} \right\} , \end{aligned}$$
(5)
$$\begin{aligned} C(\mathsf {A}, \mathsf {B})=\sum ^n_{i=1}[\mu ^2_\mathsf {A}(x_i)\mu ^2_\mathsf {B}(x_i)+\nu ^2_\mathsf {A}(x_i)\nu ^2_\mathsf {B}(x_i)+ \pi ^2_\mathsf {A}(x_i)\pi ^2_\mathsf {B}(x_i)]. \end{aligned}$$
(6)

Ejegwa [16] generalized Eq. (3) as follows:

$$\begin{aligned} \mathcal {K}(\mathsf {A}, \mathsf {B})=\dfrac{C(\mathsf {A}, \mathsf {B})}{\max [C(\mathsf {A}, \mathsf {A}),C(\mathsf {B}, \mathsf {B})]}, \end{aligned}$$
(7)

where

$$\begin{aligned} \left. \begin{aligned} C(\mathsf {A}, \mathsf {A})=\sum ^n_{i=1}[\mu ^k_\mathsf {A}(x_i)+ \nu ^k_\mathsf {A}(x_i)+ \pi ^k_\mathsf {A}(x_i)]\\ C(\mathsf {B}, \mathsf {B})=\sum ^n_{i=1}[\mu ^k_\mathsf {B}(x_i)+ \nu ^k_\mathsf {B}(x_i)+ \pi ^k_\mathsf {B}(x_i)] \end{aligned} \right\} , \end{aligned}$$
(8)

and

$$\begin{aligned} C(\mathsf {A}, \mathsf {B})=\sum ^n_{i=1}[\mu ^{\frac{k}{2}}_\mathsf {A}(x_i)\mu ^{\frac{k}{2}}_\mathsf {B}(x_i)+\nu ^{\frac{k}{2}}_\mathsf {A}(x_i)\nu ^{\frac{k}{2}}_\mathsf {B}(x_i)+ \pi ^{\frac{k}{2}}_\mathsf {A}(x_i)\pi ^{\frac{k}{2}}_\mathsf {B}(x_i)], \end{aligned}$$
(9)

for \(k=1,\ldots , 4\).

In particular, for \(k=3\), we have

$$\begin{aligned} \mathcal {K}_3(\mathsf {A}, \mathsf {B})=\dfrac{C(\mathsf {A}, \mathsf {B})}{\max [C(\mathsf {A}, \mathsf {A}),C(\mathsf {B}, \mathsf {B})]}, \end{aligned}$$
(10)

where

$$\begin{aligned} \left. \begin{aligned} C(\mathsf {A}, \mathsf {A})=\sum ^n_{i=1}[\mu ^3_\mathsf {A}(x_i)+ \nu ^3_\mathsf {A}(x_i)+ \pi ^3_\mathsf {A}(x_i)]\\ C(\mathsf {B}, \mathsf {B})=\sum ^n_{i=1}[\mu ^3_\mathsf {B}(x_i)+ \nu ^3_\mathsf {B}(x_i)+ \pi ^3_\mathsf {B}(x_i)] \end{aligned} \right\} , \end{aligned}$$
(11)

and

$$\begin{aligned} C(\mathsf {A}, \mathsf {B})=\sum ^n_{i=1}[\sqrt{(\mu _\mathsf {A}(x_i)\mu _\mathsf {B}(x_i))^3}+\sqrt{(\nu _\mathsf {A}(x_i)\nu _\mathsf {B}(x_i))^3}+ \sqrt{(\pi _\mathsf {A}(x_i)\pi _\mathsf {B}(x_i))^3}]. \end{aligned}$$
(12)

By modifying Eq. (10), we obtain the following new CCPFSs methods as follows:

$$\begin{aligned} \mathcal {K}_4(\mathsf {A}, \mathsf {B})=\dfrac{C(\mathsf {A}, \mathsf {B})}{\text {Aver}[C(\mathsf {A}, \mathsf {A}),C(\mathsf {B}, \mathsf {B})]} \end{aligned}$$
(13)

and

$$\begin{aligned} \mathcal {K}_5(\mathsf {A}, \mathsf {B})=\dfrac{C(\mathsf {A}, \mathsf {B})}{\sqrt{C(\mathsf {A}, \mathsf {A})C(\mathsf {B}, \mathsf {B})}}, \end{aligned}$$
(14)

where \(C(\mathsf {A}, \mathsf {A})\), \(C(\mathsf {B}, \mathsf {B})\) and \(C(\mathsf {A}, \mathsf {B})\) are equivalent to Eqs. (11) and (12). Certainly, \(\mathcal {K}_3(\mathsf {A}, \mathsf {B})\in [0,1]\), \(\mathcal {K}_4(\mathsf {A}, \mathsf {B})\in [0,1]\) and \(\mathcal {K}_5(\mathsf {A}, \mathsf {B})\in [0,1]\), respectively.

Proposition 3.2

The CCPFSs \(\mathcal {K}_4(\mathsf {A}, \mathsf {B})\) and \(\mathcal {K}_5(\mathsf {A}, \mathsf {B})\) are equal if and only if \(C(\mathsf {A}, \mathsf {A})=C(\mathsf {B}, \mathsf {B})\).

Proof

Straightforward.    \(\square \)

Remark 3.3

If \(\mathcal {K}_4(\mathsf {A}, \mathsf {B})=\mathcal {K}_5(\mathsf {A}, \mathsf {B})\) and \(C(\mathsf {A}, \mathsf {A})\ne C(\mathsf {B}, \mathsf {B})\), then it must be as a result of approximation in the computational processes.

3.1.1 Flowchart for the New CCPFSs Methods

figure a

3.2 Numerical Illustrations for Computing CCPFSs

Here, we give examples of PFSs and apply the CCPFSs methods to find the interrelationship between the PFSs. Assume that \(\mathsf {A}\), \(\mathsf {B}\), and \(\mathsf {C}\) are PFSs of \(X=\lbrace a,b,c\rbrace \) such that

$$\mathsf {A}=\lbrace \langle \frac{0.3,0.6,0.7416}{a}\rangle , \langle \frac{0.5,0.3,0.8124}{b}\rangle , \langle \frac{0.4,0.5,0.7681}{a}\rangle \rbrace ,$$
$$\mathsf {B}=\lbrace \langle \frac{0.3,0.6,0.7416}{a}\rangle , \langle \frac{0.5,0.3162,0.8062}{b}\rangle , \langle \frac{0.3873,0.5,0.7746}{a}\rangle \rbrace $$

and

$$\mathsf {C}=\lbrace \langle \frac{0.1,0.1,0.9899}{a}\rangle , \langle \frac{1,0,0}{b}\rangle , \langle \frac{0,1,0}{a}\rangle \rbrace .$$

Now, we find the correlation coefficients between \((\mathsf {A}, \mathsf {C})\), and \((\mathsf {B}, \mathsf {C})\), respectively, using Eqs. (3), (4), (10), (13), and (14).

By using Eqs. (3) and (4), we obtain

$$\begin{aligned} C(\mathsf {A}, \mathsf {C})= & {} \sum _{i=1}^3[(0.3^2\times 0.1^2)+(0.6^2\times 0.1^2)+(0.7416^2\times 0.9899^2)\\+ & {} (0.5^2\times 1^2)+(0.3^2\times 0^2)+(0.8124^2\times 0^2)\\+ & {} (0.3873^2\times 0^2)+(0.5^2\times 1^2)+(0.7746^2\times 0^2)]\\= & {} 1.0434 \end{aligned}$$
$$\begin{aligned} C(\mathsf {B}, \mathsf {C})= & {} \sum _{i=1}^3[(0.3^2\times 0.1^2)+(0.6^2\times 0.1^2)+(0.7416^2\times 0.9899^2)\\+ & {} (0.5^2\times 1^2)+(0.3162^2\times 0^2)+(0.8062^2\times 0^2)\\+ & {} (0.4^2\times 0^2)+(0.5^2\times 1^2)+(0.7681^2\times 0^2)]\\= & {} 1.0434 \end{aligned}$$
$$\begin{aligned} C(\mathsf {A}, \mathsf {A})= & {} \sum _{i=1}^3 [0.3^4+0.6^4+0.7416^4+0.5^4+0.3^4\\+ & {} 0.8124^4+0.4^4+0.5^4+0.7681^4]\\= & {} 1.3825 \end{aligned}$$
$$\begin{aligned} C(\mathsf {B}, \mathsf {B})= & {} \sum _{i=1}^3 [0.3^4+0.6^4+0.7416^4+0.5^4+0.3162^4\\+ & {} 0.8062^4+0.3873^4+0.5^4+0.7746^4]\\= & {} 1.3801 \end{aligned}$$
$$\begin{aligned} C(\mathsf {C}, \mathsf {C})= & {} \sum _{i=1}^3 [0.1^4+0.1^4+0.9899^4+1^4+0^4\\+ & {} 0^4+0^4+1^4+0^4]\\= & {} 2.9604. \end{aligned}$$

Hence,

$$\begin{aligned} \left. \begin{aligned} \mathcal {K}_1(\mathsf {A}, \mathsf {C})=\dfrac{1.0434}{\max [1.3825,2.9604]}=0.3525,\\ \mathcal {K}_1(\mathsf {B}, \mathsf {C})=\dfrac{1.0434}{\max [1.3801,2.9604]}=0.3525, \end{aligned} \right\} \end{aligned}$$
$$\begin{aligned} \left. \begin{aligned} \mathcal {K}_2(\mathsf {A}, \mathsf {C})=\dfrac{1.0434}{\sqrt{1.3825\times 2.9604}}=0.5158,\\ \mathcal {K}_2(\mathsf {B}, \mathsf {C})=\dfrac{1.0434}{\sqrt{1.3801\times 2.9604}}=0.5162. \end{aligned} \right\} \end{aligned}$$

By using Eqs. (10), (13), and (14), we have

$$\begin{aligned} C(\mathsf {A}, \mathsf {C})= & {} \sum _{i=1}^3[\sqrt{(0.3\times 0.1)^3 }+\sqrt{(0.6\times 0.1)^3}+\sqrt{(0.7416\times 0.9899)^3}\\+ & {} \sqrt{(0.5\times 1)^3}+\sqrt{(0.3\times 0)^3}+\sqrt{(0.8124\times 0)^3}\\+ & {} \sqrt{(0.3873\times 0)^3}+\sqrt{(0.5\times 1)^3}+\sqrt{(0.7746\times 0)^3}]\\= & {} 1.3560 \end{aligned}$$
$$\begin{aligned} C(\mathsf {B}, \mathsf {C})= & {} \sum _{i=1}^3[\sqrt{(0.3\times 0.1)^3}+\sqrt{(0.6\times 0.1)^3}+\sqrt{(0.7416\times 0.9899)^3}\\+ & {} \sqrt{(0.5\times 1)^3}+\sqrt{(0.3162\times 0)^3}+\sqrt{(0.8062\times 0)^3}\\+ & {} \sqrt{(0.4\times 0)^3}+\sqrt{(0.5\times 1)^3}+\sqrt{(0.7681\times 0)^3}]\\= & {} 1.3560 \end{aligned}$$
$$\begin{aligned} C(\mathsf {A}, \mathsf {A})= & {} \sum _{i=1}^3 [0.3^3+0.6^3+0.7416^3+0.5^3+0.3^3\\+ & {} 0.8124^3+0.4^3+0.5^3+0.7681^3]\\= & {} 1.9812 \end{aligned}$$
$$\begin{aligned} C(\mathsf {B}, \mathsf {B})= & {} \sum _{i=1}^3 [0.3^3+0.6^3+0.7416^3+0.5^3+0.3162^3\\+ & {} 0.8062^3+0.3873^3+0.5^3+0.7746^3]\\= & {} 1.9793 \end{aligned}$$
$$\begin{aligned} C(\mathsf {C}, \mathsf {C})= & {} \sum _{i=1}^3 [0.1^3+0.1^3+0.9899^3+1^3+0^3\\+ & {} 0^3+0^3+1^3+0^3]\\= & {} 2.9720. \end{aligned}$$

Hence,

$$\begin{aligned} \left. \begin{aligned} \mathcal {K}_3(\mathsf {A}, \mathsf {C})=\dfrac{1.3560}{\max [1.9812,2.9720]}=0.4563,\\ \mathcal {K}_3(\mathsf {B}, \mathsf {C})=\dfrac{1.3560}{\max [1.9793,2.9720]}=0.4563, \end{aligned} \right\} \end{aligned}$$
$$\begin{aligned} \left. \begin{aligned} \mathcal {K}_4(\mathsf {A}, \mathsf {C})=\dfrac{1.3560}{\text {Aver}[1.9812,2.9720]}=0.5475,\\ \mathcal {K}_4(\mathsf {B}, \mathsf {C})=\dfrac{1.3560}{\text {Aver}[1.9793,2.9720]}=0.5477, \end{aligned} \right\} \end{aligned}$$
$$\begin{aligned} \left. \begin{aligned} \mathcal {K}_5(\mathsf {A}, \mathsf {C})=\dfrac{1.3560}{\sqrt{1.9812\times 2.9720}}=0.5588,\\ \mathcal {K}_5(\mathsf {B}, \mathsf {C})=\dfrac{1.3560}{\sqrt{1.9793\times 2.9720}}=0.5591. \end{aligned} \right\} \end{aligned}$$

3.2.1 Comparison of the New Methods of Computing CCPFSs with the Existing Methods

Table 1 contains the computational results for easy analysis.

Table 1 CCPFSs outputs
Full size table

From Table 1, we infer that the (i) CCPFSs methods via maximum approach in [16, 25] cannot determine the interrelationship between almost two equal PFSs with respect to an unrelated PFS, (ii) new CCPFSs methods are very reliable and can determine the interrelationship between almost two equal PFSs with respect to an unrelated PFS. Again, the new CCPFSs methods have better performance indexes when compare to the ones in [16, 25]. From the computations,we conclude that \((\mathsf {B},\mathsf {C})\) are more related to each other than \((\mathsf {A},\mathsf {C})\) because

$$\mathcal {K}_i(\mathsf {B},\mathsf {C})> \mathcal {K}_i(\mathsf {A},\mathsf {C}) \; \forall i=1,2,3,4,5.$$

4 Some Existing/New WCCPFSs Methods

In many applicative areas, different elements of sets have different weights. In order to have a reliable interdependence index between PFSs, the impact of the weights must be put into consideration. Suppose \(\mathsf {A}\) and \(\mathsf {B}\) are PFSs of \(X=\lbrace x_i\rbrace \) for \(i=1,\ldots ,n\) such that the weights of the elements of X is a set \(\alpha =\lbrace \alpha _1, \alpha _2,\ldots , \alpha _n\rbrace \) with \(\alpha _i\ge 0\) and \(\sum ^n_{i=1} \alpha _i=1\).

4.1 Some Existing WCCPFSs Methods

We recall some WCCPFSs methods proposed by Garg [25] as follows:

$$\begin{aligned} \mathcal {\tilde{K}}_1(\mathsf {A}, \mathsf {B})=\dfrac{C_{\alpha }(\mathsf {A}, \mathsf {B})}{\max [C_{\alpha }(\mathsf {A}, \mathsf {A}),C_{\alpha }(\mathsf {B}, \mathsf {B})]} \end{aligned}$$
(15)

and

$$\begin{aligned} \mathcal {\tilde{K}}_2(\mathsf {A}, \mathsf {B})=\dfrac{C_{\alpha }(\mathsf {A}, \mathsf {B})}{\sqrt{C_{\alpha }(\mathsf {A}, \mathsf {A})C_{\alpha }(\mathsf {B}, \mathsf {B})}}, \end{aligned}$$
(16)

where

$$\begin{aligned} \left. \begin{aligned} C_{\alpha }(\mathsf {A}, \mathsf {A})=\sum ^n_{i=1}\alpha _i[\mu ^4_\mathsf {A}(x_i)+ \nu ^4_\mathsf {A}(x_i)+ \pi ^4_\mathsf {A}(x_i)]\\ C_{\alpha }(\mathsf {B}, \mathsf {B})=\sum ^n_{i=1}\alpha _i[\mu ^4_\mathsf {B}(x_i)+ \nu ^4_\mathsf {B}(x_i)+ \pi ^4_\mathsf {B}(x_i)] \end{aligned} \right\} , \end{aligned}$$
(17)

, and

$$\begin{aligned} C_{\alpha }(\mathsf {A}, \mathsf {B})=\sum ^n_{i=1}\alpha _i[\mu ^2_\mathsf {A}(x_i)\mu ^2_\mathsf {B}(x_i)+\nu ^2_\mathsf {A}(x_i)\nu ^2_\mathsf {B}(x_i)+ \pi ^2_\mathsf {A}(x_i)\pi ^2_\mathsf {B}(x_i)]. \end{aligned}$$
(18)

4.2 New Methods of Computing WCCPFSs

By modifying Eqs. (10), (13) and (14), we have the following new WCCPFSs \(\mathsf {A}\) and \(\mathsf {B}\):

$$\begin{aligned} \mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})=\dfrac{C_\alpha (\mathsf {A}, \mathsf {B})}{\max [C_\alpha (\mathsf {A}, \mathsf {A}),C_\alpha (\mathsf {B}, \mathsf {B})]}, \end{aligned}$$
(19)
$$\begin{aligned} \mathcal {\tilde{K}}_4(\mathsf {A}, \mathsf {B})=\dfrac{C_\alpha (\mathsf {A}, \mathsf {B})}{\text {Aver}[C_\alpha (\mathsf {A}, \mathsf {A}),C_\alpha (\mathsf {B}, \mathsf {B})]} \end{aligned}$$
(20)

and

$$\begin{aligned} \mathcal {\tilde{K}}_5(\mathsf {A}, \mathsf {B})=\dfrac{C_\alpha (\mathsf {A}, \mathsf {B})}{\sqrt{C_\alpha (\mathsf {A}, \mathsf {A})C_\alpha (\mathsf {B}, \mathsf {B})}}, \end{aligned}$$
(21)

where

$$\begin{aligned} \left. \begin{aligned} C_\alpha (\mathsf {A}, \mathsf {A})=\sum ^n_{i=1}\alpha _i[\mu ^3_\mathsf {A}(x_i)+ \nu ^3_\mathsf {A}(x_i)+ \pi ^3_\mathsf {A}(x_i)]\\ C_\alpha (\mathsf {B}, \mathsf {B})=\sum ^n_{i=1}\alpha _i[\mu ^3_\mathsf {B}(x_i)+ \nu ^3_\mathsf {B}(x_i)+ \pi ^3_\mathsf {B}(x_i)] \end{aligned} \right\} , \end{aligned}$$
(22)

and

$$\begin{aligned} C_\alpha (\mathsf {A}, \mathsf {B})=\sum ^n_{i=1}\alpha _i[\sqrt{(\mu _\mathsf {A}(x_i)\mu _\mathsf {B}(x_i))^3}+\sqrt{(\nu _\mathsf {A}(x_i)\nu _\mathsf {B}(x_i))^3}+ \sqrt{(\pi _\mathsf {A}(x_i)\pi _\mathsf {B}(x_i))^3}]. \end{aligned}$$
(23)

Proposition 4.1

The WCCPFSs \(\mathcal {\tilde{K}}_4(\mathsf {A}, \mathsf {B})\) and \(\mathcal {\tilde{K}}_5(\mathsf {A}, \mathsf {B})\) are equal if and only if \(C_\alpha (\mathsf {A}, \mathsf {A})=C_\alpha (\mathsf {B}, \mathsf {B})\).

Proof

Straightforward.    \(\square \)

Proposition 4.2

The WCCPFSs \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\), \(\mathcal {\tilde{K}}_4(\mathsf {A}, \mathsf {B})\) and \(\mathcal {\tilde{K}}_5(\mathsf {A}, \mathsf {B})\) are CCPFSs.

Proof

We are to prove that \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\), \(\mathcal {\tilde{K}}_4(\mathsf {A}, \mathsf {B})\) and \(\mathcal {\tilde{K}}_5(\mathsf {A}, \mathsf {B})\) are CCPFSs. First, we show that \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\) is a CCPFS. Thus, we verify that \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\) satisfies the conditions in Definition 3.1.

Clearly, \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\in [0,1]\) implies \(0\le \mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\le 1\). Certainly, \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\ge 0\) since \(C_{\alpha }(\mathsf {A}, \mathsf {B})\ge 0\) and \([C_{\alpha }(\mathsf {A}, \mathsf {A}),C_{\alpha }(\mathsf {B}, \mathsf {B})]\ge 0\). Now, we prove that \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\le 1\). Assume we have the following:

$$\begin{aligned} \sum ^n_{i=1}\mu ^3_\mathsf {A}(x_i)=\omega _1, \quad \sum ^n_{i=1} \mu ^3_\mathsf {B}(x_i)=\omega _2, \end{aligned}$$
$$\begin{aligned} \sum ^n_{i=1}\nu ^3_\mathsf {A}(x_i)=\omega _3, \quad \sum ^n_{i=1} \nu ^3_\mathsf {B}(x_i)=\omega _4, \end{aligned}$$
$$\begin{aligned} \sum ^n_{i=1}\pi ^3_\mathsf {A}(x_i)=\omega _5, \quad \sum ^n_{i=1}\pi ^3_\mathsf {B}(x_i)=\omega _6. \end{aligned}$$

But, \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})=\dfrac{C_\alpha (\mathsf {A}, \mathsf {B})}{\max [C_\alpha (\mathsf {A}, \mathsf {A}),C_\alpha (\mathsf {B}, \mathsf {B})]}\). By Cauchy–Schwarz’s inequality, we get

$$\begin{aligned} \mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})= & {} \dfrac{\sum ^n_{i=1}\alpha _i[\mu ^{\frac{3}{2}}_\mathsf {A}(x_i)\mu ^{\frac{3}{2}}_\mathsf {B}(x_i)+\nu ^{\frac{3}{2}}_\mathsf {A}(x_i)\nu ^{\frac{3}{2}}_\mathsf {B}(x_i)+ \pi ^{\frac{3}{2}}_\mathsf {A}(x_i)\pi ^{\frac{3}{2}}_\mathsf {B}(x_i)]}{\max [\sum ^n_{i=1}\alpha _i(\mu ^3_\mathsf {A}(x_i)+ \nu ^3_\mathsf {A}(x_i)+ \pi ^3_\mathsf {A}(x_i)),\sum ^n_{i=1}\alpha _i(\mu ^3_\mathsf {B}(x_i)+ \nu ^3_\mathsf {B}(x_i)+\pi ^3_\mathsf {B}(x_i))]}\\= & {} \dfrac{\sum ^n_{i=1}\alpha _i [\mu ^{\frac{3}{2}}_\mathsf {A}(x_i)\mu ^{\frac{3}{2}}_\mathsf {B}(x_i)]+ \sum ^n_{i=1}\alpha _i[\nu ^{\frac{3}{2}}_\mathsf {A}(x_i)\nu ^{\frac{3}{2}}_\mathsf {B}(x_i)]+ \sum ^n_{i=1}\alpha _i[ \pi ^{\frac{3}{2}}_\mathsf {A}(x_i)\pi ^{\frac{3}{2}}_\mathsf {B}(x_i)]}{\max [\alpha _i(\sum ^n_{i=1} \mu ^3_\mathsf {A}(x_i)+ \sum ^n_{i=1}\nu ^3_\mathsf {A}(x_i)+ \sum ^n_{i=1}\pi ^3_\mathsf {A}(x_i)),\alpha _i(\sum ^n_{i=1}\mu ^3_\mathsf {B}(x_i)+ \sum ^n_{i=1}\nu ^3_\mathsf {B}(x_i)+ \sum ^n_{i=1}\pi ^3_\mathsf {B}(x_i))]}\\\le & {} \dfrac{\alpha _i[\sum ^n_{i=1} \mu ^{3}_\mathsf {A}(x_i)\sum ^n_{i=1}\mu ^{3}_\mathsf {B}(x_i)]^{\frac{1}{2}}+ \alpha _i[\sum ^n_{i=1}\nu ^{3}_\mathsf {A}(x_i)\sum ^n_{i=1}\nu ^{3}_\mathsf {B}(x_i)]^{\frac{1}{2}}+ \alpha _i[\sum ^n_{i=1} \pi ^{3}_\mathsf {A}(x_i)\sum ^n_{i=1}\pi ^{3}_\mathsf {B}(x_i)]^{\frac{1}{2}}}{\max [\alpha _i(\sum ^n_{i=1}\mu ^3_\mathsf {A}(x_i)+ \sum ^n_{i=1}\nu ^3_\mathsf {A}(x_i)+ \sum ^n_{i=1}\pi ^3_\mathsf {A}(x_i)),\alpha _i(\sum ^n_{i=1}\mu ^3_\mathsf {B}(x_i)+ \sum ^n_{i=1}\nu ^3_\mathsf {B}(x_i)+ \sum ^n_{i=1} \pi ^3_\mathsf {B}(x_i))}\\= & {} \dfrac{\alpha _i[(\omega _1\omega _2)^{\frac{1}{2}}+(\omega _3\omega _4)^{\frac{1}{2}}+(\omega _5\omega _6)^{\frac{1}{2}}]}{\max [\alpha _i(\omega _1+\omega _3+\omega _5),\alpha _i(\omega _2+\omega _4+\omega _6)]}. \end{aligned}$$

Thus,

$$\begin{aligned} \mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})-1\le & {} \dfrac{\alpha _i[(\omega _1\omega _2)^{\frac{1}{2}}+(\omega _3\omega _4)^{\frac{1}{2}}+(\omega _5\omega _6)^{\frac{1}{2}}]}{\max [\alpha _i(\omega _1+\omega _3+\omega _5),\alpha _i(\omega _2+\omega _4+\omega _6)]}-1 \\= & {} \dfrac{\alpha _i[(\omega _1\omega _2)^{\frac{1}{2}}+(\omega _3\omega _4)^{\frac{1}{2}}+(\omega _5\omega _6)^{\frac{1}{2}}]-\max [\alpha _i(\omega _1+\omega _3+\omega _5),\alpha _i(\omega _2+\omega _4+\omega _6)]}{\max [\alpha _i(\omega _1+\omega _3+\omega _5),\alpha _i(\omega _2+\omega _4+\omega _6)]}\\= & {} - \dfrac{\lbrace \max [\alpha _i(\omega _1+\omega _3+\omega _5),\alpha _i(\omega _2+\omega _4+\omega _6)]-\alpha _i[(\omega _1\omega _2)^{\frac{1}{2}}+(\omega _3\omega _4)^{\frac{1}{2}}+(\omega _5\omega _6)^{\frac{1}{2}}]\rbrace }{\max [\alpha _i(\omega _1+\omega _3+\omega _5),\alpha _i(\omega _2+\omega _4+\omega _6)]}\\\le & {} 0. \end{aligned}$$

So \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\le 1\). Hence, \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\in [0,1]\).

Certainly, \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})=\mathcal {\tilde{K}}_3(\mathsf {B}, \mathsf {A})\), so we omit details. Also, we show that \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})=1\) \(\Leftrightarrow \) \(\mathsf {A}=\mathsf {B}\). Suppose \(\mathsf {A}=\mathsf {B}\), then we obtain

$$\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B}) = \dfrac{C_{\alpha }(\mathsf {A},\mathsf {A})}{\max [C_{\alpha }(\mathsf {A},\mathsf {A}),C_{\alpha }(\mathsf {A},\mathsf {A})]} = \dfrac{C_{\alpha }(\mathsf {A},\mathsf {A})}{C_{\alpha }(\mathsf {A},\mathsf {A})} = 1.$$

The converse is straightforward. Therefore, \(\mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {B})\) is a CCPFS. The proofs for \(\mathcal {\tilde{K}}_4(\mathsf {A}, \mathsf {B})\) and \(\mathcal {\tilde{K}}_5(\mathsf {A}, \mathsf {B})\) are similar.

   \(\square \)

4.2.1 Flowchart for the New WCCPFSs Methods

figure b

4.3 Numerical Verifications of the WCCPFSs Methods

By using the information in Subsection 3.2, and putting into consideration the effect of the weights of the elements of \(X=\lbrace a,b,c\rbrace \), we compute the interdependence indexes of \(\mathsf {A}\) and \(\mathsf {B}\). Assume \(\alpha =\lbrace 0.4, 0.32, 0.28\rbrace \), and using Eqs. (15) and (16), we obtain

$$\begin{aligned} C_\alpha (\mathsf {A}, \mathsf {C})= & {} \sum _{i=1}^3[0.4((0.3^2\times 0.1^2)+(0.6^2\times 0.1^2)+(0.7416^2\times 0.9899^2))\\+ & {} 0.32((0.5^2\times 1^2)+(0.3^2\times 0^2)+(0.8124^2\times 0^2))\\+ & {} 0.28((0.3873^2\times 0^2)+(0.5^2\times 1^2)+(0.7746^2\times 0^2))]\\= & {} 0.3674 \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {B}, \mathsf {C})= & {} \sum _{i=1}^3[0.4((0.3^2\times 0.1^2)+(0.6^2\times 0.1^2)+(0.7416^2\times 0.9899^2))\\+ & {} 0.32((0.5^2\times 1^2)+(0.3162^2\times 0^2)+(0.8062^2\times 0^2))\\+ & {} 0.28((0.4^2\times 0^2)+(0.5^2\times 1^2)+(0.7681^2\times 0^2))]\\= & {} 0.3674 \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {A}, \mathsf {A})= & {} \sum _{i=1}^3 [0.4(0.3^4+0.6^4+0.7416^4)+0.32(0.5^4+0.3^4+0.8124^4)\\+ & {} 0.28(+0.4^4+0.5^4+0.7681^4)]\\= & {} 0.4602 \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {B}, \mathsf {B})= & {} \sum _{i=1}^3 [0.4(0.3^4+0.6^4+0.7416^4)+0.32(+0.5^4+0.3162^4+0.8062^4)\\+ & {} 0.28(0.3873^4+0.5^4+0.7746^4)]\\= & {} 0.4591 \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {C}, \mathsf {C})= & {} \sum _{i=1}^3 [0.4(0.1^4+0.1^4+0.9899^4)+0.32(1^4+0^4+0^4)\\+ & {} 0.28(0^4+1^4+0^4)]\\= & {} 0.9841. \end{aligned}$$

Hence,

$$\begin{aligned} \left. \begin{aligned} \mathcal {\tilde{K}}_1(\mathsf {A}, \mathsf {C})=\dfrac{0.3674}{\max [0.4602,0.9841]}=0.3733,\\ \mathcal {\tilde{K}}_1(\mathsf {B}, \mathsf {C})=\dfrac{0.3674}{\max [0.4591,0.9841]}=0.3733, \end{aligned} \right\} \end{aligned}$$
$$\begin{aligned} \left. \begin{aligned} \mathcal {\tilde{K}}_2(\mathsf {A}, \mathsf {C})=\dfrac{0.3674}{\sqrt{0.4602\times 0.9841}}=0.5459,\\ \mathcal {\tilde{K}}_2(\mathsf {B}, \mathsf {C})=\dfrac{0.3674}{\sqrt{0.4591\times 0.9841}}=0.5466. \end{aligned} \right\} \end{aligned}$$

By using Eqs. (19), (20) and (21), we have

$$\begin{aligned} C_\alpha (\mathsf {A}, \mathsf {C})= & {} \sum _{i=1}^3[0.4(\sqrt{(0.3\times 0.1)^3 }+\sqrt{(0.6\times 0.1)^3}+\sqrt{(0.7416\times 0.9899)^3})\\+ & {} 0.32(\sqrt{(0.5\times 1)^3}+\sqrt{(0.3\times 0)^3}+\sqrt{(0.8124\times 0)^3})\\+ & {} 0.28(\sqrt{(0.3873\times 0)^3}+\sqrt{(0.5\times 1)^3}+\sqrt{(0.7746\times 0)^3})]\\= & {} 0.4717 \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {B}, \mathsf {C})= & {} \sum _{i=1}^3[0.4(\sqrt{(0.3\times 0.1)^3}+\sqrt{(0.6\times 0.1)^3}+\sqrt{(0.7416\times 0.9899)^3})\\+ & {} 0.32(\sqrt{(0.5\times 1)^3}+\sqrt{(0.3162\times 0)^3}+\sqrt{(0.8062\times 0)^3})\\+ & {} 0.28(\sqrt{(0.4\times 0)^3}+\sqrt{(0.5\times 1)^3}+\sqrt{(0.7681\times 0)^3})]\\= & {} 0.4717 \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {A}, \mathsf {A})= & {} \sum _{i=1}^3 [0.4(0.3^3+0.6^3+0.7416^3)+0.32(0.5^3+0.3^3+0.8124^3)\\+ & {} 0.28(+0.4^3+0.5^3+0.7681^3)]\\= & {} 0.6604 \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {B}, \mathsf {B})= & {} \sum _{i=1}^3 [0.4(0.3^3+0.6^3+0.7416^3)+0.32(+0.5^3+0.3162^3+0.8062^3)\\+ & {} 0.28(0.3873^3+0.5^3+0.7746^3)]\\= & {} 0.6595 \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {C}, \mathsf {C})= & {} \sum _{i=1}^3 [0.4(0.1^3+0.1^3+0.9899^3)+0.32(1^3+0^4+0^3)\\+ & {} 0.28(0^3+1^3+0^3)]\\= & {} 0.9888. \end{aligned}$$

Hence,

$$\begin{aligned} \left. \begin{aligned} \mathcal {\tilde{K}}_3(\mathsf {A}, \mathsf {C})=\dfrac{0.4717}{\max [0.6604,0.9888]}=0.4770,\\ \mathcal {\tilde{K}}_3(\mathsf {B}, \mathsf {C})=\dfrac{0.4717}{\max [0.6595,0.9888]}=0.4770, \end{aligned} \right\} \end{aligned}$$
$$\begin{aligned} \left. \begin{aligned} \mathcal {\tilde{K}}_4(\mathsf {A}, \mathsf {C})=\dfrac{0.4717}{\text {Aver}[0.6604,0.9888]}=0.5720,\\ \mathcal {\tilde{K}}_4(\mathsf {B}, \mathsf {C})=\dfrac{0.4717}{\text {Aver}[0.6595,0.9888]}=0.5723, \end{aligned} \right\} \end{aligned}$$
$$\begin{aligned} \left. \begin{aligned} \mathcal {K}_5(\mathsf {A}, \mathsf {C})=\dfrac{0.4717}{\sqrt{0.6604\times 0.9888}}=0.5837,\\ \mathcal {K}_5(\mathsf {B}, \mathsf {C})=\dfrac{0.4717}{\sqrt{0.6595\times 0.9888}}=0.5841. \end{aligned} \right\} \end{aligned}$$

4.3.1 Comparison of the New Methods of Computing WCCPFSs with the Existing Methods

Table 2 contains the computational results for easy analysis.

Table 2 WCCPFSs outputs
Full size table

By comparing Tables 1 and 2, it is not superfluous to say that WCCPFSs give a better measure of interrelationship. This bespeaks the impact of weights on measuring correlation coefficient. From Table 2, we surmise that the (i) WCCPFSs techniques via maximum method in [25] and \(\mathcal {\tilde{K}}_3\) cannot determine the interrelationship between almost two equal PFSs with respect to an unrelated PFS, (ii) new WCCPFSs techniques are more reasonable and accurate and can determine the interrelationship between almost two equal PFSs with respect to an unrelated PFS. Again, the new WCCPFSs techniques have better performance indexes in contrast to the ones in [25]. From the computations, we conclude that \((\mathsf {B},\mathsf {C})\) are more related to each other than \((\mathsf {A},\mathsf {C})\).

5 Determination of Pattern Recognition and Medical Diagnostic Problem via WCCPFSs

In this section, we apply the WCCPFSs methods discussed so far to problems of pattern recognition and medical diagnosis to ascertain the more efficient approach and agreement of decision via the WCCPFSs techniques.

5.1 Applicative Example in Pattern Recognition

Pattern recognition is the process of identifying patterns by using machine learning procedure. Pattern recognition has a lot to do with artificial intelligence and machine learning. The idea of pattern recognition is important because of its application potential in neural networks, software engineering, computer vision, etc. Assume there are three pattern \(\mathsf {C}_i\), represented in Pythagorean fuzzy values in \(X=\lbrace x_i\rbrace \), for \(i=1,\ldots ,3\) and \(\alpha =\lbrace 0.4,0.3,0.3\rbrace \). If there is an unknown pattern \(\mathsf {P}\) represented in Pythagorean fuzzy values in \(X=\lbrace x_i\rbrace \). The Pythagorean fuzzy representations of these patterns are in Table 3.

Table 3 Pythagorean fuzzy representations of patterns
Full size table

To enable us to classify \(\mathsf {P}\) into any of \(\mathsf {C}_i\),\(i=1,2,3\), we deploy the WCCPFSs in [25] and the proposed WCCPFSs as follows:

Using Eqs. (15) and (16), we obtain

$$\begin{aligned} C_\alpha (\mathsf {C}_1,\mathsf {P})=0.3805,\, C_\alpha (\mathsf {C}_2,\mathsf {P})=0.4392,\, C_\alpha (\mathsf {C}_3,\mathsf {P})=0.5218, \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {C}_1,\mathsf {C}_1)=0.7088,\, C_\alpha (\mathsf {C}_2,\mathsf {C}_2)=0.7195,\, C_\alpha (\mathsf {C}_3,\mathsf {C}_3)=0.6582,\, C_\alpha (\mathsf {P},\mathsf {P})=0.5095. \end{aligned}$$

Hence,

$$\begin{aligned} \tilde{\mathcal {K}}_1(\mathsf {C}_1,\mathsf {P})=0.5368,\, \tilde{\mathcal {K}}_1(\mathsf {C}_2,\mathsf {P})=0.6104,\, \tilde{\mathcal {K}}_1(\mathsf {C}_3,\mathsf {P})=0.7928. \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_2(\mathsf {C}_1,\mathsf {P})=0.6332,\, \tilde{\mathcal {K}}_2(\mathsf {C}_2,\mathsf {P})=0.7254,\, \tilde{\mathcal {K}}_2(\mathsf {C}_3,\mathsf {P})=0.9011. \end{aligned}$$

Using Eqs. (19), (20) and (21), we have

$$\begin{aligned} C_\alpha (\mathsf {C}_1,\mathsf {P})=0.5434,\, C_\alpha (\mathsf {C}_2,\mathsf {P})=0.5973,\, C_\alpha (\mathsf {C}_3,\mathsf {P})=0.6808, \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {C}_1,\mathsf {C}_1)=0.8277,\, C_\alpha (\mathsf {C}_2,\mathsf {C}_2)=0.8299,\, C_\alpha (\mathsf {C}_3,\mathsf {C}_3)=0.7939,\, C_\alpha (\mathsf {P},\mathsf {P})=0.6312. \end{aligned}$$

Hence,

$$\begin{aligned} \tilde{\mathcal {K}}_3(\mathsf {C}_1,\mathsf {P})=0.6565,\, \tilde{\mathcal {K}}_3(\mathsf {C}_2,\mathsf {P})=0.7197,\, \tilde{\mathcal {K}}_3(\mathsf {C}_3,\mathsf {P})=0.8575. \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_4(\mathsf {C}_1,\mathsf {P})=0.7449,\, \tilde{\mathcal {K}}_4(\mathsf {C}_2,\mathsf {P})=0.8175,\, \tilde{\mathcal {K}}_4(\mathsf {C}_3,\mathsf {P})=0.9554. \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_5(\mathsf {C}_1,\mathsf {P})=0.7518,\, \tilde{\mathcal {K}}_5(\mathsf {C}_2,\mathsf {P})=0.8253,\, \tilde{\mathcal {K}}_5(\mathsf {C}_3,\mathsf {P})=0.9617. \end{aligned}$$

Table 4 presents the results for glance analysis.

Table 4 WCCPFSs outputs
Full size table

From Table 4, \(\mathsf {P}\) is suitable to be classified with \(\mathsf {C}_3\) because \(\mathcal {\tilde{K}}_i(\mathsf {C}_3,\mathsf {P})>\mathcal {\tilde{K}}_i(\mathsf {C}_2,\mathsf {P})>\mathcal {\tilde{K}}_i(\mathsf {C}_1,\mathsf {P})\) \(\forall \) \(i=1,\ldots ,5\).

5.2 Applicative Example in Medical Diagnosis

Medical diagnosis is a delicate exercise because failure to make the right decision may lead to the death of the patient. Diagnosis of diseases is challenging due to embedded fuzziness in the processes. Here, we present a scenario of a mathematical approach of diagnosing a patient medical status via WCCPFSs methods, where the symptoms or clinical manifestations of the diseases are represented in Pythagorean fuzzy values by using hypothetical cases.

Suppose we have a set of diseases \(\mathsf {D}=\lbrace \mathsf {D}_1, \mathsf {D}_2, \mathsf {D}_3, \mathsf {D}_4, \mathsf {D}_5\rbrace \) represented in Pythagorean fuzzy values, where \(\mathsf {D}_1=\) viral fever, \(\mathsf {D}_2=\) malaria, \(\mathsf {D}_3=\) typhoid fever, \(\mathsf {D}_4=\) peptic ulcer, \(\mathsf {D}_5=\) chest problem, and a set of symptoms

$$\mathsf {S}=\lbrace \mathsf {s}_1, \mathsf {s}_2, \mathsf {s}_3, \mathsf {s}_4, \mathsf {s}_5\rbrace $$

for \(\mathsf {s}_1{=}\) temperature, \(\mathsf {s}_2=\) headache, \(\mathsf {s}_3=\) stomach pain, \(\mathsf {s}_4{=}\) cough, \(\mathsf {s}_5=\) chest pain, which are the clinical manifestations of \(\mathsf {D}_i\), \(i=1,\ldots ,5\). From the knowledge of the clinical manifestations, the weight of the symptoms as \(\alpha =\lbrace 0.3,0.25,0.1,0.25,0.1\rbrace \).

Assume a patient \(\mathsf {P}\) with a manifest symptoms \(\mathsf {S}\) is also capture in Pythagorean fuzzy values. Table 5 contains Pythagorean fuzzy information of \(\mathsf {D}_i\), \(i=1,\ldots ,5\) and \(\mathsf {P}\) with respect to \(\mathsf {S}\).

Table 5 Pythagorean fuzzy representations of diagnostic process
Full size table

Now, we find which of the diseases \(\mathsf {D}_i\) has the greatest interrelationship with the patient \(\mathsf {P}\) with respect to the clinical manifestations \(\mathsf {S}\) by deploying Eqs. (15), (16), (19), (20), and (21).

By using Eqs. (15) and (16), we have

$$\begin{aligned} C_\alpha (\mathsf {D}_1,\mathsf {P})=0.4609,\, C_\alpha (\mathsf {D}_2,\mathsf {P})=0.4740,\, C_\alpha (\mathsf {D}_3,\mathsf {P})=0.4213, \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {D}_4,\mathsf {P})=0.3252,\, C_\alpha (\mathsf {D}_5,\mathsf {P})=0.2289,\, C_\alpha (\mathsf {D}_1,\mathsf {D}_1)=0.5930,\, \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {D}_2,\mathsf {D}_2)=0.5203,\, C_\alpha (\mathsf {D}_3,\mathsf {D}_3)=0.5761,\, C_\alpha (\mathsf {D}_4,\mathsf {D}_4)=0.5297,\, \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {D}_5,\mathsf {D}_5)=0.5274,\, C_\alpha (\mathsf {P},\mathsf {P})=0.4859. \end{aligned}$$

Hence,

$$\begin{aligned} \tilde{\mathcal {K}}_1(\mathsf {D}_1,\mathsf {P})=0.7772,\, \tilde{\mathcal {K}}_1(\mathsf {D}_2,\mathsf {P})=0.9110,\, \tilde{\mathcal {K}}_1(\mathsf {D}_3,\mathsf {P})=0.7313, \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_1(\mathsf {D}_4,\mathsf {P})=0.6139,\, \tilde{\mathcal {K}}_1(\mathsf {D}_5,\mathsf {P})=0.4340. \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_2(\mathsf {D}_1,\mathsf {P})=0.8586,\, \tilde{\mathcal {K}}_2(\mathsf {D}_2,\mathsf {P})=0.9427,\, \tilde{\mathcal {K}}_2(\mathsf {D}_3,\mathsf {P})=0.7963, \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_2(\mathsf {D}_4,\mathsf {P})=0.6410,\, \tilde{\mathcal {K}}_2(\mathsf {D}_5,\mathsf {P})=0.4522. \end{aligned}$$

Using Eqs. (19), (20) and (21), we obtain

$$\begin{aligned} C_\alpha (\mathsf {D}_1,\mathsf {P})=0.6354,\, C_\alpha (\mathsf {D}_2,\mathsf {P})=0.6840,\, C_\alpha (\mathsf {D}_3,\mathsf {P})=0.5945, \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {D}_4,\mathsf {P})=0.4646,\, C_\alpha (\mathsf {D}_5,\mathsf {P})=0.3608,\, C_\alpha (\mathsf {D}_1,\mathsf {D}_1)=0.7468,\, \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {D}_2,\mathsf {D}_2)=0.7143,\, C_\alpha (\mathsf {D}_3,\mathsf {D}_3)=0.7383,\, C_\alpha (\mathsf {D}_4,\mathsf {D}_4)=0.7146,\, \end{aligned}$$
$$\begin{aligned} C_\alpha (\mathsf {D}_5,\mathsf {D}_5)=0.7154,\, C_\alpha (\mathsf {P},\mathsf {P})=0.7163. \end{aligned}$$

Hence,

$$\begin{aligned} \tilde{\mathcal {K}}_3(\mathsf {D}_1,\mathsf {P})=0.8508,\, \tilde{\mathcal {K}}_3(\mathsf {D}_2,\mathsf {P})=0.9549,\, \tilde{\mathcal {K}}_3(\mathsf {D}_3,\mathsf {P})=0.8052, \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_3(\mathsf {D}_4,\mathsf {P})=0.6486,\, \tilde{\mathcal {K}}_3(\mathsf {D}_5,\mathsf {P})=0.5037. \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_4(\mathsf {D}_1,\mathsf {P})=0.8685,\, \tilde{\mathcal {K}}_4(\mathsf {D}_2,\mathsf {P})=0.9562,\, \tilde{\mathcal {K}}_4(\mathsf {D}_3,\mathsf {P})=0.8174, \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_4(\mathsf {D}_4,\mathsf {P})=0.6493,\, \tilde{\mathcal {K}}_4(\mathsf {D}_5,\mathsf {P})=0.5040. \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_5(\mathsf {D}_1,\mathsf {P})=0.8688,\, \tilde{\mathcal {K}}_5(\mathsf {D}_2,\mathsf {P})=0.9562,\, \tilde{\mathcal {K}}_5(\mathsf {D}_3,\mathsf {P})=0.8175, \end{aligned}$$
$$\begin{aligned} \tilde{\mathcal {K}}_5(\mathsf {D}_4,\mathsf {P})=0.6494,\, \tilde{\mathcal {K}}_5(\mathsf {D}_5,\mathsf {P})=0.5040. \end{aligned}$$

Table 6 presents the results for glance analysis.

Table 6 WCCPFSs outputs
Full size table

From Table 6, it is inferred that the patient is suffering from malaria since

$$\mathcal {\tilde{K}}_i(\mathsf {D}_2,\mathsf {P})>\mathcal {\tilde{K}}_i(\mathsf {D}_1,\mathsf {P})>\mathcal {\tilde{K}}_i(\mathsf {D}_3,\mathsf {P})>\mathcal {\tilde{K}}_i(\mathsf {D}_4,\mathsf {P})>\mathcal {\tilde{K}}_i(\mathsf {D}_5,\mathsf {P})$$

for \(i=1,\ldots ,5\).

6 Conclusion

In this chapter, we have studied some techniques of calculating CCPFSs and WCCPFSs, respectively. It is found that the approach of WCCPFSs is more reliable than CCPFSs. By juxtaposing the existing methods of computing WCCPFSs and the novel ones, it is proven that the novel methods of calculating WCCPFSs are more accurate and efficient. Some MCDM problems were considered via the existing and the novel WCCPFSs methods to demonstrate applicability. The novel methods of computing WCCPFSs could be applied to more MCDM problems via object-oriented approach in cases of larger population. Extending the concept of weights on elements of PFSs to other existing correlation coefficients in Pythagorean fuzzy domain [16, 50] could be of great interest in other different applicative areas through clustering algorithm.