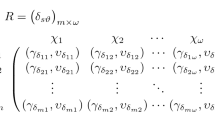Schweizer–Sklar Muirhead Mean Aggregation Operators Based on Pythagorean Fuzzy Sets and Their Application in Multi-criteria Decision-Making

Abstract

Schweizer–Sklar (SS) operations are more flexible to aggregate the information, and the Muirhead mean (MM) operator can examine the interrelationships among the family of attributes. MM operator is more proficient and more generalized than many aggregation operators to cope with awkward and inconsistence information in realistic decision issues. The objectives of this manuscript are to explore the SS operators based on Pythagorean fuzzy set (PFS) and studied their score function, accuracy function, and their relationships. Further, based on these operators, the MM operators based on PFS, called Pythagorean fuzzy MM (PFMM) operator, Pythagorean fuzzy weighted MM (PFWMM) operator, and their special cases are presented. Additionally, the multi-attribute decision-making (MADM) problem is solved by using the explored operators based on PFS to observe the consistency and efficiency of the discovered approach. Finally, the advantages, comparative analysis, and their geometrical representations are also discussed.

1 Introduction

MADM is a proficient technique that can provide the ranking results for the finite alternatives according to the attribute values of different alternatives and it is the important aspect of decision sciences. In recent years, the development of enterprises and social decision‐making in all aspects are related to the issue of MADM. In real decision process, an important problem is how to express the attribute value more efficiently and accurately. In the real world, because of the complexity of decision‐making problems and the fuzziness of decision‐making environments, it is not enough to express attribute values of alternatives by exact values. For this the notion of fuzzy set (FS) was explored by Zadeh [1]. FS composes of the grade of supporting belonging to the unit interval, as a proficient technique to cope with unreliable and awkward information in realistic decision issues. At the point when a decision-maker gives the data as pair (0.5, 0.4) for truth and falsity grades, the notion of FS is not able to resolve it. For coping with such kind of issues, Atanassove [2] introduced the notion of intuitionistic FS (IFS) with the condition that the total of supporting and supporting against grades isn't surpassed from unit interval. IFS has gotten more consideration from researchers and a huge number of researchers have investigated their speculations [3,4,5].

There are some practical cases if the decision-maker gives 0.9 for positive grade and 0.3 for negative so their sum must be greater than 1, unlike the problem captured in IFS. Therefore, the work of Yager [6] called Pythagorean FS (PFS) can be successfully applied in different awkward fields because the sum of the square of positive grade and square of negative grade is restricted to [0,1]. Due to its constraint, PFS becomes an essential tool to cope with awkward and difficult fuzzy information. Since it was established, it has received the attention of many researchers and it is utilized in the environment of aggregation operators, similarity measures, hybrid aggregation operators, and so on. The various existing works based on PFS are elaborated as follow as:

• 1. Operators-based Approaches: Based on the aggregation operators, many scholars have successfully utilized in the environment of PFS. For instance, Mohagheghi et al. [7] explored the new last aggregation evaluation based on PFSs, Ma and Xu [8] presented weighted averaging/geometric aggregation operators based on PFSs, Wei [9] discovered interaction aggregation operators based on PFSs, Garg [10] introduced information aggregation using Einstein operations based on PFSs, Garg [11] examined the confidential levels based on Pythagorean fuzzy aggregation operators, new logarithmic and aggregation operators based on PFSs were presented by Garg [12, 13] discovered the novel neutrality operation based on PFSs and their aggregation operators.

• 2. Measures-based Approaches: Similarity measure (SM) is a proficient technique to accurately examine the degree between any two objects. Many scholars have applied SM in different notions. For example, Wei and Wei [14] explored similarity measures based on PFSs, Garg [15] presented correlation coefficient based on PFSs, Biswas and Sarkar [16] discovered the similarity measures based on point operators by using PFSs, Li and Zeng [17] introduced distance measures based on PFSs and Zhang [18] examined similarity measures based on PFSs.

• 3. Hybrid Operators-based Approaches: To find the interrelationships between two objects, the hybrid aggregation operators play an essential role in the environment of realistic decision theory. Various scholars using the PFSs, explored different hybrid aggregation operators. For example, Liang et al. [19] discovered geometric Bonferroni mean operators based on PFSs, Prioritized aggregation operators [20], Bonferroni mean aggregation operators [21], Dombi aggregation operators [22], power aggregation operators [23], etc. [24,25,26].

After that, a more generalized operator was presented, that is, the Muirhead mean [26], which was added an alterable parametric vector P on the basis of considering interrelationships among multiple input parameters, and some existing operators are its special cases, for instance, arithmetic and geometric mean (GM) operators (not considering the correlations), Bonferroni mean (BM) operator, and Maclaurin symmetric mean (MSM). When dealing with MCDM problems, some aggregation operators cannot consider the relationship between any input parameters, while Muirhead mean (MM) operator can take into account the correlation between inputs by a variable parameter. Therefore, the MM operator is more superior when dealing with MCDM problems.

Multi-criteria decision-making refers to the use of existing decision information, in the case of multi-criteria that are in conflict with each other and cannot coexist, and in which the limited alternatives are ranked or selected in a certain way. Schweizer–Sklar operation uses a variable parameter to make their operations more effective and flexible. MCDM alludes to the utilization of existing choice data, for the situation of multi-models that are in strife with one another and can't exist together, and in which the constrained options are positioned or chosen with a specific goal in mind. SS activity utilizes a variable boundary to make their tasks increasingly successful and adaptable. What's more, PFS can deal with inadequate, uncertain, and conflicting data under fuzzy conditions. Subsequently, we directed further examination on SS tasks for PFS and applied SS activities to MCDM issues. Besides, in light of the fact that the MM operator thinks about interrelationships among different info boundaries by the alterable parametric vector, subsequently consolidating the MM operator with the SS activity gives some collection operators, and it was progressively significant to build up some new way to comprehend the MCDM issues in the Pythagorean fuzzy environment. As indicated by this, the reason furthermore, noteworthiness of this article are.

• 1. To build up various new MM operators by consolidating MM operators, SS activities, and PFS.

• 2. To talk about some significant properties and various instances of these operators set forward.

• 3. To manage a MCDM strategy for PFS data more adequately dependent on the operators set forward.

• 4. To show the feasibility and prevalence of the recently evolved strategy.

The aims of this manuscript are summarized as follow: In Sect. 2, we briefly state the fundamental conceptions of PFS, SS T-norm (SSTN), SS T-conorm (SSCTN), and MM operators. In Sect. 3, we explore the SS operators based on PFS and studied their score function, accuracy function, and their relationships. Further, based on these operators, the MM operators based on PFS are called Pythagorean fuzzy MM (PFMM) operator, Pythagorean fuzzy weighted MM (PFWMM) operator, and their special cases are presented. In Sect. 4, multi-attribute decision-making (MADM) problem is solved by using the explored operators based on PFS to observe the consistency and efficiency of the produced approach. Finally, the advantages, comparative analysis, and their geometrical representation are also discussed. The conclusion of this manuscript is discussed in Sect. 5.

2 Preliminaries

In this study we review some basic notions of PFSs and their fundamental laws. Throughout this manuscript, the universal set is expressed by .

2.1 Pythagorean Fuzzy Sets

Definition 1:

[6] A PFS ${\mathcal{R}}_{P}$ is initiated by

$$ {\mathcal{R}}_{P} = \left\{ {\left( {\mu_{{{\mathcal{R}}_{P} }} (x),\eta_{{{\mathcal{R}}_{P} }} (x)} \right):x \in {\mathcal{X}}} \right\} $$

(1)

where $\mu_{{_{P} }}$ and $\eta_{{_{P} }}$ are the grades of supporting and supporting against, with a condition such that $0 \le \mu _{{Rp}}^{2} \left( x \right) + \eta _{{Rp}}^{2} \left( x \right) \le 1$. The refusal grade is of the form $\xi _{{Rp}} \left( x \right) = 1 - \left( {\mu _{{Rp}}^{2} \left( x \right) + \eta _{{Rp}}^{2} \left( x \right)} \right)^{{\frac{1}{2}}}$. The Pythagorean fuzzy number (PFN) is denoted by ${\mathcal{R}}_{{P - {{i}}}} = \left( {\mu_{{{\mathcal{R}}_{{P - {{i}}}} }} ,\eta_{{{\mathcal{R}}_{{P - {{i}}}} }} } \right)$. Further, the score function and accuracy function for PFS ${\mathcal{R}}_{P - 1} = \left( {\mu_{{{\mathcal{R}}_{P - 1} }} ,\eta_{{{\mathcal{R}}_{P - 1} }} } \right)$ are initiated by

$$ {\mathcal{S}}_{SF} \left( {{\mathcal{R}}_{P - 1} } \right) = \mu_{{{\mathcal{R}}_{P - 1} }}^{2} - \eta_{{{\mathcal{R}}_{P - 1} }}^{2} $$

(2)

$$ {\mathcal{H}}_{AF} \left( {{\mathcal{R}}_{P - 1} } \right) = \mu_{{{\mathcal{R}}_{P - 1} }}^{2} + \eta_{{{\mathcal{R}}_{P - 1} }}^{2} $$

(3)

where ${\mathcal{S}}_{SF} \left( {{\mathcal{R}}_{P - 1} } \right) \in \left[ { - 1,1} \right]$ and ${\mathcal{H}}_{AF} \left( {{\mathcal{R}}_{P - 1} } \right) \in \left[ {0,1} \right]$.

To examine the interrelationships between any two PFSs ${\mathcal{R}}_{P - 1} = \left( {\mu_{{{\mathcal{R}}_{P - 1} }} ,\eta_{{{\mathcal{R}}_{P - 1} }} } \right)$ and ${\mathcal{R}}_{P - 2} = \left( {\mu_{{{\mathcal{R}}_{P - 2} }} ,\eta_{{{\mathcal{R}}_{P - 2} }} } \right)$, then

$$ {\text{If}}\;{\mathcal{S}}_{SF} \left( {{\mathcal{R}}_{P - 1} } \right) > {\mathcal{S}}_{SF} \left( {{\mathcal{R}}_{P - 2} } \right) \Rightarrow {\mathcal{R}}_{P - 1} > {\mathcal{R}}_{P - 2} ; $$

(4)

$$ {\text{If}}\;{\mathcal{S}}_{SF} \left( {{\mathcal{R}}_{P - 1} } \right) = {\mathcal{S}}_{SF} \left( {{\mathcal{R}}_{P - 2} } \right) \Rightarrow , $$

(5)

$$ {\text{If}}\;{\mathcal{H}}_{AF} \left( {{\mathcal{R}}_{P - 1} } \right) > {\mathcal{H}}_{AF} \left( {{\mathcal{R}}_{P - 2} } \right) \Rightarrow {\mathcal{R}}_{P - 1} > {\mathcal{R}}_{P - 2} ; $$

(6)

$$ {\text{If}}\;{\mathcal{H}}_{AF} \left( {{\mathcal{R}}_{P - 1} } \right) = {\mathcal{H}}_{AF} \left( {{\mathcal{R}}_{P - 2} } \right) \Rightarrow {\mathcal{R}}_{P - 1} = {\mathcal{R}}_{P - 2} . $$

(7)

Further, we discussed the existing operator based on PFSs, which is discussed below. For any two PFSs ${\mathcal{R}}_{P - 1} = \left( {\mu_{{{\mathcal{R}}_{P - 1} }} ,\eta_{{{\mathcal{R}}_{P - 1} }} } \right)$ and ${\mathcal{R}}_{P - 2} = \left( {\mu_{{{\mathcal{R}}_{P - 2} }} ,\eta_{{{\mathcal{R}}_{P - 2} }} } \right)$, then.

• 1. ${\mathcal{R}}_{P - 1} \oplus {\mathcal{R}}_{P - 2} = \left( {\left( {\mu_{{{\mathcal{R}}_{P - 1} }}^{2} + \mu_{{{\mathcal{R}}_{P - 2} }}^{2} - \mu_{{{\mathcal{R}}_{P - 1} }}^{2} \mu_{{{\mathcal{R}}_{P - 2} }}^{2} } \right)^{\frac{1}{2}} ,\eta_{{{\mathcal{R}}_{P - 1} }} \eta_{{{\mathcal{R}}_{P - 2} }} } \right)$;

• 2. ${\mathcal{R}}_{P - 1} \otimes {\mathcal{R}}_{P - 2} = \left( {\mu_{{{\mathcal{R}}_{P - 1} }} \mu_{{{\mathcal{R}}_{P - 2} }} ,\left( {\eta_{{{\mathcal{R}}_{P - 1} }}^{2} + \eta_{{{\mathcal{R}}_{P - 2} }}^{2} - \eta_{{{\mathcal{R}}_{P - 1} }}^{2} \eta_{{{\mathcal{R}}_{P - 2} }}^{2} } \right)^{\frac{1}{2}} } \right)$;

• 3. $\delta {\mathcal{R}}_{P - 1} = \left( {\left( {1 - \left( {1 - \mu_{{{\mathcal{R}}_{P - 1} }}^{2} } \right)^{\delta } } \right)^{\frac{1}{2}} ,\eta_{{{\mathcal{R}}_{P - 1} }}^{\delta } } \right)$;

• 4. $\delta {\mathcal{R}}_{P - 1} = \left( {\mu_{{{\mathcal{R}}_{P - 1} }}^{\delta } ,\left( {1 - \left( {1 - \eta_{{{\mathcal{R}}_{P - 1} }}^{2} } \right)^{\delta } } \right)^{\frac{1}{2}} } \right)$.

2.2 Muirhead Mean Operator

Definition 2:

[26] For any positive real numbers ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, the MM operator is initiated by

$$ MM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \left( {\frac{1}{\xi !}\mathop \sum \nolimits_{{\sigma \in S_{\xi } }} \mathop \prod \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{{\mathcal{P}}_{{{i}}} }} } \right)^{{\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}}} $$

(8)

where $\sigma \left( {{i}} \right),\left( {{{i}} = 1,2,..,\xi } \right)$ expressed any permutations of $\left( {{{i}} = 1,2,..,\xi } \right)$ and $S_{\xi }$ expressed the family of permutations $\left( {{{i}} = 1,2,..,\xi } \right)$. Additionally, Eq. (8), holds the following axioms.

• 1. If ${\mathcal{P}} = \left( {1,0,0, \ldots ,0} \right)$, then the MM convert to $MM^{{\left( {1,0,0, \ldots ,0} \right)}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \frac{1}{\xi }\sum\nolimits_{{{{i}} = 1}}^{\xi } {{\mathcal{R}}_{{P - {{i}}}} }$, which is expressed the arithmetic averaging operator.

• 2. If ${\mathcal{P}} = \left( {\frac{1}{\xi },\frac{1}{\xi }, \ldots .,\frac{1}{\xi }} \right)$, then the MM convert to $MM^{{\left( {\frac{1}{\xi },\frac{1}{\xi }, \ldots .,\frac{1}{\xi }} \right)}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \prod\nolimits_{{{{i}} = 1}}^{\xi } {{\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{\frac{1}{\xi }}} }$, which is expressed the geometric mean operator.

• 3. If ${\mathcal{P}} = \left( {1,1,0, \ldots ,0} \right)$, then the MM convert to $MM^{{\left( {1,1,0, \ldots ,0} \right)}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) =$ $\left( {\frac{1}{{\xi \left( {\xi - 1} \right)}}\sum\nolimits_{{{{i}} \ne j = 1}}^{\xi } {{\mathcal{R}}_{{P - {{i}}}} } {\mathcal{R}}_{P - j} } \right)^{\frac{1}{2}}$, which is expressed the Bonferroni mean operator.

• 4. If ${\mathcal{P}} = \left( {\overbrace {1,1, \ldots ,1,1}^{k}\overbrace {0,0,0,0, \ldots ,0}^{\xi - k}} \right)$, then the MM convert to $MM^{{\left( {\overbrace {1,1, \ldots ,1,1}^{k}\overbrace {0,0,0,0, \ldots ,0}^{\xi - k}} \right)}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) =$ $\left( {\frac{{ \oplus_{{1 \le {{i}}_{1} \le \ldots . \le {{i}}_{k} \le \xi }} \otimes_{j = 1}^{k} {\mathcal{R}}_{{P - {{i}}j}} }}{{C_{\xi }^{k} }}} \right)^{\frac{1}{k}}$, which is expressed the Maclaurin symmetric mean operator.

From Def. (2) and the exceptional instances of the MM operator referenced above, we realize that the favorable position of the MM operator is that it can catch the general interrelationships among the numerous input boundaries and it is a speculation of some current total operators.

2.3 Schweizer–Sklar Operations

In this study, we review the basic notions of SS operations, which contain the SS sum and product based on T-norm and T-conorm.

Definition 3:

[27] For any two PFSs ${\mathcal{R}}_{P - 1} = \left( {\mu_{{{\mathcal{R}}_{P - 1} }} ,\eta_{{{\mathcal{R}}_{P - 1} }} } \right)$ and ${\mathcal{R}}_{P - 2} = \left( {\mu_{{{\mathcal{R}}_{P - 2} }} ,\eta_{{{\mathcal{R}}_{P - 2} }} } \right)$, then.

$$ {\mathcal{R}}_{P - 1} \cap_{{{\mathcal{T}},{\mathcal{T}}^{*} }} {\mathcal{R}}_{P - 2} = \left( {{\mathcal{T}}\left( {\mu_{{{\mathcal{R}}_{P - 1} }} ,\mu_{{{\mathcal{R}}_{P - 2} }} } \right),{\mathcal{T}}^{*} \left( {\eta_{{{\mathcal{R}}_{P - 1} }} ,\eta_{{{\mathcal{R}}_{P - 2} }} } \right)} \right) $$

(9)

$$ {\mathcal{R}}_{P - 1} \cup_{{{\mathcal{T}},{\mathcal{T}}^{*} }} {\mathcal{R}}_{P - 2} = \left( {{\mathcal{T}}^{*} \left( {\mu_{{{\mathcal{R}}_{P - 1} }} ,\mu_{{{\mathcal{R}}_{P - 2} }} } \right),{\mathcal{T}}\left( {\eta_{{{\mathcal{R}}_{P - 1} }} ,\eta_{{{\mathcal{R}}_{P - 2} }} } \right)} \right) $$

(10)

where ${\mathcal{T}}$ and ${\mathcal{T}}^{*}$ are expressed the T-norm (TN) and T-conorm (TCN). Additionally, the SSTN and SSTCN are discussed below:

$$ {\mathcal{T}}_{SS,\gamma } \left( {x,y} \right) = \left( {x^{\gamma } + y^{\gamma } - 1} \right)^{{\frac{1}{\gamma }}} $$

(11)

$$ {\mathcal{T}}_{SS,\gamma }^{*} \left( {x,y} \right) = 1 - \left( {\left( {1 - x} \right)^{\gamma } + \left( {1 - y} \right)^{\gamma } - 1} \right)^{{\frac{1}{\gamma }}} $$

(12)

where $\gamma < 0, x, y$ , $\in \left[ {0,1} \right]$. If $\gamma = 0$, then ${\mathcal{T}}_{\gamma }$ ( x, y ) =  and ${\mathcal{T}}_{\gamma }^{*}$ (x, y ) =   x + y − xy, which are expressed the algebraic TN and TCN. Further, we have defined the SSTN and SSTCN for PFS, which are stated below:

Definition 4:

For any two PFSs ${\mathcal{R}}_{P - 1} = \left( {\mu_{{{\mathcal{R}}_{P - 1} }} ,\eta_{{{\mathcal{R}}_{P - 1} }} } \right)$ and ${\mathcal{R}}_{P - 2} = \left( {\mu_{{{\mathcal{R}}_{P - 2} }} ,\eta_{{{\mathcal{R}}_{P - 2} }} } \right)$, then the generalized union and intersection using SS operational laws, such that

$$ {\mathcal{R}}_{P - 1} \otimes_{{{\mathcal{T}},{\mathcal{T}}^{*} }} {\mathcal{R}}_{P - 2} = \left( {{\mathcal{T}}\left( {\mu_{{{\mathcal{R}}_{P - 1} }}^{2} ,\mu_{{{\mathcal{R}}_{P - 2} }}^{2} } \right),{\mathcal{T}}^{*} \left( {\eta_{{{\mathcal{R}}_{P - 1} }}^{2} ,\eta_{{{\mathcal{R}}_{P - 2} }}^{2} } \right)} \right) $$

(13)

$$ {\mathcal{R}}_{P - 1} \oplus_{{{\mathcal{T}},{\mathcal{T}}^{*} }} {\mathcal{R}}_{P - 2} = \left( {{\mathcal{T}}^{*} \left( {\mu_{{{\mathcal{R}}_{P - 1} }}^{2} ,\mu_{{{\mathcal{R}}_{P - 2} }}^{2} } \right),{\mathcal{T}}\left( {\eta_{{{\mathcal{R}}_{P - 1} }}^{2} ,\eta_{{{\mathcal{R}}_{P - 2} }}^{2} } \right)} \right) . $$

(14)

Based on Eqs. (11) and (12), we present SS operations based on PFSs, such that

$$ {\mathcal{R}}_{P - 1} \otimes_{SS} {\mathcal{R}}_{P - 2} = \left( {\begin{array}{*{20}c} {\left( {\mu_{{{\mathcal{R}}_{P - 1} }}^{2\gamma } + \mu_{{{\mathcal{R}}_{P - 2} }}^{2\gamma } - 1} \right)^{{\frac{1}{2\gamma }}} ,} \\ {\left( {1 - \left( {\left( {1 - \eta_{{{\mathcal{R}}_{P - 1} }}^{2} } \right)^{\gamma } + \left( {1 - \eta_{{{\mathcal{R}}_{P - 2} }}^{2} } \right)^{\gamma } - 1} \right)^{{\frac{1}{\gamma }}} } \right)^{\frac{1}{2}} } \\ \end{array} } \right) $$

(15)

$$ {\mathcal{R}}_{P - 1} \oplus_{SS} {\mathcal{R}}_{P - 2} = \left( {\begin{array}{*{20}c} {\left( {1 - \left( {\left( {1 - \mu_{{{\mathcal{R}}_{P - 1} }}^{2} } \right)^{\gamma } + \left( {1 - \mu_{{{\mathcal{R}}_{P - 2} }}^{2} } \right)^{\gamma } - 1} \right)^{{\frac{1}{\gamma }}} } \right)^{\frac{1}{2}} ,} \\ {\left( {\eta_{{{\mathcal{R}}_{P - 1} }}^{2\gamma } + \eta_{{{\mathcal{R}}_{P - 2} }}^{2\gamma } - 1} \right)^{{\frac{1}{2\gamma }}} } \\ \end{array} } \right) $$

(16)

$$ {\Delta }{\mathcal{R}}_{P - 1} = \left( {\begin{array}{*{20}c} {\left( {1 - \left( {{\Delta }\left( {1 - \mu_{{{\mathcal{R}}_{P - 1} }}^{2} } \right)^{\gamma } - \left( {{\Delta } - 1} \right)} \right)^{{\frac{1}{\gamma }}} } \right)^{\frac{1}{2}} ,} \\ {\left( {{\Delta }\eta_{{{\mathcal{R}}_{P - 1} }}^{2\gamma } - \left( {{\Delta } - 1} \right)} \right)^{{\frac{1}{2\gamma }}} } \\ \end{array} } \right) $$

(17)

$$ {\mathcal{R}}_{P - 1}^{{\Delta }} = \left( {\begin{array}{*{20}c} {\left( {{\Delta }\mu_{{{\mathcal{R}}_{P - 1} }}^{2\gamma } - \left( {{\Delta } - 1} \right)} \right)^{{\frac{1}{2\gamma }}} ,} \\ {\left( {1 - \left( {{\Delta }\left( {1 - \eta_{{{\mathcal{R}}_{P - 1} }}^{2} } \right)^{\gamma } - \left( {{\Delta } - 1} \right)} \right)^{{\frac{1}{\gamma }}} } \right)^{\frac{1}{2}} } \\ \end{array} } \right). $$

(18)

Theorem 1:

For any two PFSs ${\mathcal{R}}_{P - 1} = \left( {\mu_{{{\mathcal{R}}_{P - 1} }} ,\eta_{{{\mathcal{R}}_{P - 1} }} } \right)$ and ${\mathcal{R}}_{P - 2} = \left( {\mu_{{{\mathcal{R}}_{P - 2} }} ,\eta_{{{\mathcal{R}}_{P - 2} }} } \right)$, then

• 1. ${\mathcal{R}}_{P - 1} \oplus_{SS} {\mathcal{R}}_{P - 2} = {\mathcal{R}}_{P - 2} \oplus_{SS} {\mathcal{R}}_{P - 1}$;

• 2. ${\mathcal{R}}_{P - 1} \otimes_{SS} {\mathcal{R}}_{P - 2} = {\mathcal{R}}_{P - 2} \otimes_{SS} {\mathcal{R}}_{P - 1}$;

• 3. ${\Delta }\left( {{\mathcal{R}}_{P - 1} \oplus_{SS} {\mathcal{R}}_{P - 2} } \right) = {\Delta }{\mathcal{R}}_{P - 1} \oplus_{SS} {\Delta }{\mathcal{R}}_{P - 2}$;

• 4. ${\mathcal{R}}_{P - 1}^{{{\Delta }_{1} + {\Delta }_{2} }} = {\Delta }_{1} {\mathcal{R}}_{P - 1} \otimes_{SS} {\Delta }_{2} {\mathcal{R}}_{P - 1}$

Proof:

Straightforward.

3 Pythagorean Fuzzy Schweizer–Sklar Muirhead Mean Aggregation Operations

The aim of this study is to present the MM operators based on PFS are called Pythagorean fuzzy MM (PFMM) operator, Pythagorean fuzzy weighted MM (PFWMM) operator, and their special cases are presented.

After that, a more generalized operator was presented, that is, the Muirhead mean [26], which was added an alterable parametric vector P on the basis of considering interrelationships among multiple input parameters, and some existing operators are its special cases, for instance, arithmetic and geometric mean (GM) operators (not considering the correlations), Bonferroni mean (BM) operator, and Maclaurin symmetric mean (MSM). When dealing with MCDM problems, some aggregation operators cannot consider the relationship between any input parameters, while Muirhead mean (MM) operator can take into account the correlation between inputs by a variable parameter. Therefore, the MM operator is more superior when dealing with MCDM problems.

Multi-criteria decision-making refers to the use of existing decision information, in the case of multi-criteria that are in conflict with each other and cannot coexist, and in which the limited alternatives are ranked or selected in a certain way. Schweizer–Sklar operation uses a variable parameter to make their operations more effective and flexible. MCDM alludes to the utilization of existing choice data, for the situation of multi-models that are in strife with one another and can't exist together, and in which the constrained options are positioned or chosen with a specific goal in mind. SS activity utilizes a variable boundary to make their tasks increasingly successful and adaptable. What's more, PFS can deal with inadequate, uncertain, and conflicting data under fuzzy conditions.

3.1 Pythagorean Fuzzy Schweizer–Sklar Muirhead Mean Operator

The aims of this study are to explore the idea of PFSSMM operator and their results to improve the quality of the explored work. The special cases of the explored work are also explored in this sub-section.

Definition 5:

For any family of PFSs ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, the PFSSMM operator is initiated by

$$ PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \left( {\frac{1}{\xi !}\mathop \sum \nolimits_{{\sigma \in S_{\xi } }} \mathop \prod \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{{\mathcal{P}}_{{{i}}} }} } \right)^{{\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}}}, $$

(19)

where $\sigma \left( {{i}} \right),\left( {{{i}} = 1,2,..,\xi } \right)$ expressed any permutations of $\left( {{{i}} = 1,2,..,\xi } \right)$ and $S_{\xi }$ expressed the family of permutations $\left( {{{i}} = 1,2,..,\xi } \right)$.

By using Eq. (19) and the novel operational laws of SS, which are stated in the form of Def. (4), we get Theorem 2.

Theorem 2:

For any family of PFSs ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, then by using Eq. (19) and Def. (4), we get Pythagorean fuzzy Schweizer–Sklar MM operator, such that

$$ \begin{array}{*{20}c} {\quad \quad \quad PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = } \\ {\left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\sum\nolimits_{{\sigma \in S_{\xi } }} {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\sum\nolimits_{{{{i}} = 1}}^{\xi } {{\mathcal{P}}_{{{i}}} } \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} ,} \\ {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\sum\nolimits_{{\sigma \in S_{\xi } }} {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\sum\nolimits_{{{{i}} = 1}}^{\xi } {{\mathcal{P}}_{{{i}}} } \left( {\left( {\begin{array}{*{20}c} {1 - } \\ {\eta_{{P - \sigma \left( {{i}} \right)}}^{2} } \\ \end{array} } \right)^{\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\frac{1}{2}} } \\ \end{array} } \right)} \\ \end{array} $$

(20)

Proof:

By using the Def. (4), we get

$$ {\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{{\mathcal{P}}_{{{i}}} }} = \left( {\begin{array}{*{20}c} {\left( {{\mathcal{P}}_{{{i}}} \mu_{{{\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}} }}^{2\gamma } - \left( {{\mathcal{P}}_{{{i}}} - 1} \right)} \right)^{{\frac{1}{\gamma }}} ,} \\ {\left( {1 - \left( {{\mathcal{P}}_{{{i}}} \left( {1 - \eta_{{{\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}} }}^{2} } \right)^{\gamma } - \left( {{\mathcal{P}}_{{{i}}} - 1} \right)} \right)^{{\frac{1}{\gamma }}} } \right)} \\ \end{array} } \right) $$

$$ \mathop \prod \limits_{{{{i}} = 1}}^{\xi } {\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{{\mathcal{P}}_{{{i}}} }} = \left( {\begin{array}{*{20}c} {\left( {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \mu_{{{\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}} }}^{2\gamma } - \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} + 1} \right)^{{\frac{1}{\gamma }}} ,} \\ {\left( {1 - \left( {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {1 - \eta_{{{\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}} }}^{2} } \right)^{\gamma } - \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} + 1} \right)^{{\frac{1}{\gamma }}} } \right)} \\ \end{array} } \right) $$

$$ \mathop \sum \limits_{{\sigma \in S_{\xi } }} \mathop \prod \limits_{{{{i}} = 1}}^{\xi } {\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{{\mathcal{P}}_{{{i}}} }} = \left( {\begin{array}{*{20}c} {1 - \left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {1 - \left( {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \mu_{{{\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}} }}^{2\gamma } - \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} + 1} \right)^{{\frac{1}{\gamma }}} } \right)^{\gamma } - 1} \right)^{{\frac{1}{\gamma }}} ,} \\ {\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {1 - \left( {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {1 - \eta_{{{\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}} }}^{2} } \right)^{\gamma } - \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} + 1} \right)^{{\frac{1}{\gamma }}} } \right)^{\gamma } - 1} \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right) $$

$$ \begin{aligned} & PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \left( {\frac{1}{\xi !}\mathop \sum \limits_{{\sigma \in S_{\xi } }} \mathop \prod \limits_{{{{i}} = 1}}^{\xi } {\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{{\mathcal{P}}_{{{i}}} }} } \right)^{{\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}}} = \\ & \quad \quad \quad \quad \quad \left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} ,} \\ {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\left( {\begin{array}{*{20}c} {1 - } \\ {\eta_{{P - \sigma \left( {{i}} \right)}}^{2} } \\ \end{array} } \right)^{\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\frac{1}{2}} } \\ \end{array} } \right) \\ \end{aligned} $$

Hence complete the proof.

Additionally, we have proved some properties like Monotonicity, Commutativity, and some special cases of the explored operators.

Theorem 3:

For any two families of PFSs ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$ and ${\mathcal{R}}_{{P - {{i}}}}^{\prime }$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, if $\mu_{{{\mathcal{R}}_{{P - {{i}}}} }} \ge \mu_{{{\mathcal{R}}_{{P - {{i}}}} }}^{\prime }$ and $\eta_{{{\mathcal{R}}_{{P - {{i}}}} }} \le \eta_{{{\mathcal{R}}_{{P - {{i}}}} }}^{\prime }$, then

$$ PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) \ge PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1}^{\prime } ,{\mathcal{R}}_{P - 2}^{\prime } , \ldots ,{\mathcal{R}}_{P - \xi }^{\prime } } \right). $$

(21)

Proof:

Let $PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \left( {T,I} \right)$ and $PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1}^{\prime } ,{\mathcal{R}}_{P - 2}^{\prime } , \ldots ,{\mathcal{R}}_{P - \xi }^{\prime } } \right) = \left( {T^{\prime } ,I^{\prime } } \right)$, where

$$ T = \left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} 1 \\ { + \frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} $$

$$ T^{\prime} = \left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu^{\prime}\,_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} $$

and

$$ I = \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\left( {\begin{array}{*{20}c} {1 - } \\ {\eta_{{P - \sigma \left( {{i}} \right)}}^{2} } \\ \end{array} } \right)^{\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\frac{1}{2}} $$

$$ I^{\prime} = \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\left( {\begin{array}{*{20}c} {1 - } \\ {\eta^{\prime}\,_{{P - \sigma \left( {{i}} \right)}}^{2} } \\ \end{array} } \right)^{\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\frac{1}{2}}. $$

By hypothesis it’s given that $\mu_{{{\mathcal{R}}_{{P - {{i}}}} }} \ge \mu_{{{\mathcal{R}}_{{P - {{i}}}} }}^{\prime }$ and $\eta_{{{\mathcal{R}}_{{P - {{i}}}} }} \le \eta_{{{\mathcal{R}}_{{P - {{i}}}} }}^{\prime }$, then

$$ \left( {1 + \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \right)^{{\frac{1}{\gamma }}} \ge \left( {1 + \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu^{\prime}\,_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \right)^{{\frac{1}{\gamma }}} $$

$$ \Rightarrow 1 - \left( {1 + \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \right)^{{\frac{1}{\gamma }}} \le 1 - \left( {1 + \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu^{\prime}\,_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \right)^{{\frac{1}{\gamma }}} $$

$$ \Rightarrow \left( {1 - \left( {1 + \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \right)^{{\frac{1}{\gamma }}} } \right)^{\gamma } \ge \left( {1 - \left( {1 + \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu^{\prime}\,_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \right)^{{\frac{1}{\gamma }}} } \right)^{\gamma } $$

$$ \Rightarrow \left( {1 + \frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {1 - \left( {1 + \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \right)^{{\frac{1}{\gamma }}} } \right)^{\gamma } - 2} \right)} \right)^{{\frac{1}{\gamma }}} \le \left( {1 + \frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {1 - \left( {1 + \mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu^{\prime}\,_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \right)^{{\frac{1}{\gamma }}} } \right)^{\gamma } - 2} \right)} \right)^{{\frac{1}{\gamma }}} $$

$$ \begin{aligned} & \Rightarrow \left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} \\ & \quad \quad \quad \quad \ge \left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\mathop \sum \limits_{{\sigma \in S_{\xi } }} \left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} \left( {\mu^{\prime}\,_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} \\ \end{aligned}. $$

Similarly, we examine the $\eta_{{{\mathcal{R}}_{{P - {{i}}}} }} \le \eta_{{{\mathcal{R}}_{{P - {{i}}}} }}^{\prime }$, then by combining the above both, we get

$$ PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) \ge PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1}^{\prime } ,{\mathcal{R}}_{P - 2}^{\prime } , \ldots ,{\mathcal{R}}_{P - \xi }^{\prime } } \right). $$

Theorem 4:

For any two families of PFSs ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$ and ${\mathcal{R}}_{{P - {{i}}}}^{\prime }$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, if ${\mathcal{R}}_{{P - {{i}}}}^{\prime }$ is a permutations of ${\mathcal{R}}_{{P - {{i}}}}$, then

$$ PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1}^{\prime } ,{\mathcal{R}}_{P - 2}^{\prime } , \ldots ,{\mathcal{R}}_{P - \xi }^{\prime } } \right). $$

(22)

Proof:

Omitted.

Additionally, we will examine the special cases of the explored operators based on PFSs.

• 1. If ${\mathcal{P}} = \left( {1,0,0, \ldots ,0} \right)$, then the MM convert to Pythagorean fuzzy Schweizer–Sklar arithmetic averaging operator

  $$ \begin{aligned} & PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \frac{1}{\xi }\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{R}}_{{P - {{i}}}} \\ & \quad \quad = \left( {\left( {1 - \left( {1 + \frac{1}{\xi }\left( {\sum\nolimits_{{{{i}} = 1}}^{\xi } {\left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2} - 1} \right)^{\gamma } } - 2} \right)} \right)} \right)^{{\frac{1}{2\gamma }}} ,\left( {1 + \frac{1}{\xi }\left( {\sum\nolimits_{{\sigma \in S_{\xi } }} {\eta_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } } - 2} \right)^{{\frac{1}{\gamma }}} } \right)^{\frac{1}{2}} } \right) \\ \end{aligned}. $$

  (23)

• 2. If ${\mathcal{P}} = \left( {\delta ,0,0, \ldots ,0} \right)$, then the MM convert to Pythagorean fuzzy Schweizer–Sklar generalized arithmetic averaging operator

  $$ \begin{aligned} & PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \left( {\frac{1}{\xi }\mathop \sum \limits_{{{{i}} = 1}}^{\xi } {\mathcal{R}}_{{P - {{i}}}}^{\delta } } \right)^{{\frac{1}{\delta }}} \\ & = \left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\delta }\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi }\left( {\sum\nolimits_{{{{i}} = 1}}^{\xi } {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\delta \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 1} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} ,} \\ {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\delta }\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi }\left( {\sum\nolimits_{{{{i}} = 1}}^{\xi } {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\delta \left( {\left( {\begin{array}{*{20}c} {1 - } \\ {\eta_{{P - \sigma \left( {{i}} \right)}}^{2} } \\ \end{array} } \right)^{\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 1} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\frac{1}{2}} } \\ \end{array} } \right) \\ \end{aligned}. $$

  (24)

• 3. If ${\mathcal{P}} = \left( {1,1,0, \ldots ,0} \right)$, then the MM convert to Pythagorean fuzzy Schweizer–Sklar Bonferroni mean operator

  $$ \begin{aligned} & PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \left( {\frac{1}{{\xi \left( {\xi - 1} \right)}}\mathop \sum \limits_{{{{i}} \ne j = 1}}^{\xi } {\mathcal{R}}_{{P - {{i}}}} {\mathcal{R}}_{P - j} } \right)^{\frac{1}{2}} \\ & \quad \quad = \left( {\begin{array}{*{20}c} {\left( {\frac{1}{2}\left( {\begin{array}{*{20}c} {1 + } \\ {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\xi \left( {\xi - 1} \right)}}\left( {\sum\nolimits_{{{{i}} \ne j = 1}}^{\xi } {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } + } \\ {\mu_{P - \sigma \left( j \right)}^{2\gamma } - 1} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } \\ \end{array} } \right)} \right)^{{\frac{1}{2\gamma }}} ,} \\ {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\frac{1}{2}\left( {\begin{array}{*{20}c} {1 + } \\ {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\xi \left( {\xi - 1} \right)}}\left( {\sum\nolimits_{{{{i}} \ne j = 1}}^{\xi } {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } + } \\ {\mu_{P - \sigma \left( j \right)}^{2\gamma } - 1} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } \\ \end{array} } \right)} \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\frac{1}{2}} } \\ \end{array} } \right) \\ \end{aligned}. $$

  (25)

• 4. If ${\mathcal{P}} = \left( {\overbrace {1,1, \ldots ,1,1}^{k}\overbrace {0,0,0,0, \ldots ,0}^{\xi - k}} \right)$, then the MM convert to Pythagorean fuzzy Schweizer–Sklar Maclaurin symmetric mean operator

  $$ \begin{aligned} & PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \left( {\frac{{ \oplus_{{1 \le {{i}}_{1} \le \ldots . \le {{i}}_{k} \le \xi }} \otimes_{j = 1}^{k} {\mathcal{R}}_{{P - {{i}}j}} }}{{C_{\xi }^{k} }}} \right)^{\frac{1}{k}} \\ & \quad \quad = \left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{k}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{C_{\xi }^{k} }}\left( {\sum\nolimits_{{1 \le {{i}}_{1} \le \ldots . \le {{i}}_{k} \le \xi }} {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\sum\nolimits_{j = 1}^{k} {\left( {\mu_{{P - \sigma \left( {{{i}}_{j} } \right)}}^{2\gamma } - 1} \right)} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 1} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} ,} \\ {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{k}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{C_{\xi }^{k} }}\left( {\sum\nolimits_{{1 \le {{i}}_{1} \le \ldots . \le {{i}}_{k} \le \xi }} {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\sum\nolimits_{j = 1}^{k} {\left( {\left( {\begin{array}{*{20}c} {1 - } \\ {\eta_{{P - \sigma \left( {{{i}}_{j} } \right)}}^{2} } \\ \end{array} } \right)^{\gamma } - 1} \right)} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - 1} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\frac{1}{2}} } \\ \end{array} } \right) \\ \end{aligned}. $$

  (26)

• 5. If ${\mathcal{P}} = \left( {\frac{1}{\xi },\frac{1}{\xi }, \ldots .,\frac{1}{\xi }} \right)$, then the MM convert to Pythagorean fuzzy Schweizer–Sklar geometric mean operator

  $$ \begin{aligned} & PFSSMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \mathop \prod \limits_{{{{i}} = 1}}^{\xi } {\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{\frac{1}{\xi }}} \\ & \quad \quad = \left( {\left( {1 + \frac{1}{\xi }\left( {\sum\nolimits_{{\sigma \in S_{\xi } }} {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } } - 2} \right)^{{\frac{1}{\gamma }}} } \right)^{\frac{1}{2}} ,\left( {1 - \left( {1 + \frac{1}{\xi }\left( {\sum\nolimits_{{{{i}} = 1}}^{\xi } {\left( {\eta_{{P - \sigma \left( {{i}} \right)}}^{2} - 1} \right)^{\gamma } } - 2} \right)} \right)} \right)^{{\frac{1}{2\gamma }}} } \right) \\ \end{aligned}. $$

  (27)

3.2 Pythagorean Fuzzy Schweizer–Sklar Weighted Muirhead Mean Operator

The aim of this study is to explore the idea of PFSSWMM operator and their results to improve the quality of the explored work. The special cases of the explored work are also explored in this sub-section.

Definition 6:

For any family of PFSs ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, the WMM operator is initiated by

$$ PFSSWMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \left( {\frac{1}{\xi !}\sum\nolimits_{{\sigma \in S_{\xi } }} {\prod\nolimits_{{{{i}} = 1}}^{\xi } {{\mathcal{R}}_{{P - \sigma \left( {{i}} \right)}}^{{{\mathcal{P}}_{{{i}}} \omega_{{W - {{i}}}} }} } } } \right)^{{\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}}}, $$

(28)

where $\sigma \left( {{i}} \right),\left( {{{i}} = 1,2,..,\xi } \right)$ expressed any permutations of $\left( {{{i}} = 1,2,..,\xi } \right)$ and $S_{\xi }$ expressed the family of permutations $\left( {{{i}} = 1,2,..,\xi } \right)$. The weight vector is denoted and defined by: $\omega_{W} = \left( {\omega_{W - 1} ,\omega_{W - 2} ,..,\omega_{W - \xi } } \right)^{T}$ with a condition that is $\sum\nolimits_{{{{i}} = 1}}^{\xi } {\omega_{{W - {{i}}}} } = 1$, $\omega_{{W - {{i}}}} \in \left[ {0,1} \right],{{i}} = 1,2,3, \ldots ,\xi$.

By using Eq. (28) and the novel operational laws of SS, which are stated in the form of Def. (4), we get Theorem 5.

Theorem 5:

For any family of PFSs ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, then by using Eq. (28) and Def. (4), we get Pythagorean fuzzy Schweizer–Sklar MM operator, such that

$$ \begin{aligned} & PFSSWMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = \\ & \left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\sum\nolimits_{{\sigma \in S_{\xi } }} {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\sum\nolimits_{{{{i}} = 1}}^{\xi } {{\mathcal{P}}_{{{i}}} } \omega_{{W - {{i}}}} \left( {\mu_{{P - \sigma \left( {{i}} \right)}}^{2\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{2\gamma }}} ,} \\ {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\frac{1}{\xi !}\left( {\sum\nolimits_{{\sigma \in S_{\xi } }} {\left( {\begin{array}{*{20}c} {1 - } \\ {\left( {\begin{array}{*{20}c} {1 + } \\ {\sum\nolimits_{{{{i}} = 1}}^{\xi } {{\mathcal{P}}_{{{i}}} } \omega_{{W - {{i}}}} \left( {\left( {1 - \eta_{{P - \sigma \left( {{i}} \right)}}^{2} } \right)^{\gamma } - 1} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } } - 2} \right)} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\gamma } - \frac{1}{{\mathop \sum \nolimits_{{{{i}} = 1}}^{\xi } {\mathcal{P}}_{{{i}}} }}} \\ \end{array} } \right)^{{\frac{1}{\gamma }}} } \\ \end{array} } \right)^{\frac{1}{2}} } \\ \end{array} } \right) \\ \end{aligned}. $$

(29)

Proof:

Straightforward. (The proof of this theorem id similar to the proof of Theorem 2).

Theorem 6:

For any two families of PFSs ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$ and ${\mathcal{R}}_{{P - {{i}}}}^{\prime }$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, if $\mu_{{{\mathcal{R}}_{{P - {{i}}}} }} \ge \mu_{{{\mathcal{R}}_{{P - {{i}}}} }}^{\prime }$ and $\eta_{{{\mathcal{R}}_{{P - {{i}}}} }} \le \eta_{{{\mathcal{R}}_{{P - {{i}}}} }}^{\prime }$, then

$$ PFSSWMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) \ge PFSSWMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1}^{\prime } ,{\mathcal{R}}_{P - 2}^{\prime } , \ldots ,{\mathcal{R}}_{P - \xi }^{\prime } } \right). $$

(30)

Proof:

Straightforward. (The proof of this theorem id similar to the proof of Theorem 3).

Theorem 7:

For any two families of PFSs ${\mathcal{R}}_{{P - {{i}}}} \left( {{{i}} = 1,2,3, \ldots ,\xi } \right)$ and ${\mathcal{R}}_{{P - {{i}}}}^{\prime }$, with their parameter vectors ${\mathcal{P}} = \left( {{\mathcal{P}}_{1} ,{\mathcal{P}}_{2} , \ldots ,{\mathcal{P}}_{l} } \right) \in R^{l}$, if ${\mathcal{R}}_{{P - {{i}}}}^{\prime }$ is a permutations of ${\mathcal{R}}_{{P - {{i}}}}$, then

$$ PFSSWMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1} ,{\mathcal{R}}_{P - 2} , \ldots ,{\mathcal{R}}_{P - \xi } } \right) = PFSSWMM^{{\mathcal{P}}} \left( {{\mathcal{R}}_{P - 1}^{\prime } ,{\mathcal{R}}_{P - 2}^{\prime } , \ldots ,{\mathcal{R}}_{P - \xi }^{\prime } } \right) $$

(31)

Proof:

Straightforward. (The proof of this theorem id similar to the proof of Theorem 4).

4 Multi-criteria Decision-Making Problems Based on Pythagorean Fuzzy Schweizer–Sklar Muirhead Mean Aggregation Operations

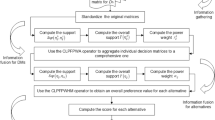
To examine the proficiency of the explored operators in this manuscript, we presented the MCDM technique based on weighted MM operators by using Pythagorean fuzzy information’s. To addressed effectively such kind of issues, we choose the family of alternatives and their criteria with weight vectors, whose expressions are summarized in the following ways: ${\mathcal{A}}_{AL} = \left\{ {{\mathcal{A}}_{AL - 1} ,{\mathcal{A}}_{AL - 2} , \ldots ,{\mathcal{A}}_{AL - m} } \right\}$ and ${\mathcal{C}}_{CR} = \left\{ {{\mathcal{C}}_{CR - 1} ,{\mathcal{C}}_{CR - 2} , \ldots ,{\mathcal{C}}_{CR - \xi } } \right\}$ with their weight vector $\omega_{W} = \left( {\omega_{W - 1} ,\omega_{W - 2} , \ldots ,\omega_{W - \xi } } \right)^{T}$ with a condition that is $\sum\nolimits_{{{{i}} = 1}}^{\xi } {\omega_{{W - {{i}}}} } = 1,\omega_{{W - {{i}}}} \in \left[ {0,1} \right]$. For resolving such kind of issues, we construct the decision matrix, whose representation is of the form $R = \left( {{\mathcal{R}}_{{P - {{i}}j}} } \right)_{m \times \xi }$, whose every entries in the form of Pythagorean fuzzy numbers that are ${\mathcal{R}}_{{P - {{i}}j}} = \left( {\mu_{{{\mathcal{R}}_{{P - {{i}}j}} }} ,\eta_{{{\mathcal{R}}_{{P - {{i}}j}} }} } \right)$. Then the steps of the decision-making technique is summarized in the following ways:

• Step 1: By using Eq. (32), we normalized the decision matrix, if needed.

  $$ R = \left\{ {\begin{array}{*{20}c} {\left( {\mu_{{{\mathcal{R}}_{{P - {{i}}j}} }} ,\eta_{{{\mathcal{R}}_{{P - {{i}}j}} }} } \right)} & {for\;be\xi ef{{i}}t} \\ {\left( {\eta_{{{\mathcal{R}}_{{P - {{i}}j}} }} ,\mu_{{{\mathcal{R}}_{{P - {{i}}j}} }} } \right)} & {for\;cost} \\ \end{array} } \right. $$

  (32)

• Step 2: By using Eq. (29), we aggregated the normalized decision matrix.

• Step 3: By using Eq. (2), examine the score values of the aggregated values.

• Step 4: Rank to all alternatives, and examine the best one.

• Step 5: The end.

Example 1:

We allude to a case of MCDM to demonstrate the plausibility and legitimacy of the introduced technique. We allude to the decision-making issue in Ref. [28]. There is a speculation organization, which plans to pick the most ideal interest in the other options. There are four potential alternatives for the speculation organization to browse: (1) a vehicle organization ${\mathcal{A}}_{AL - 1}$; (2) a food organization ${\mathcal{A}}_{AL - 2}$; (3) a PC organization ${\mathcal{A}}_{AL - 3}$; (4) an arms organization ${\mathcal{A}}_{AL - 4}$. The venture organization will think about the accompanying three assessment records to settle on decisions: (1) the hazard investigation ${\mathcal{C}}_{CR - 1}$; (2) the development examination ${\mathcal{C}}_{CR - 2}$; and (3) the natural impact investigation. Among ${\mathcal{C}}_{CR - 1}$ and ${\mathcal{C}}_{CR - 2}$ are the advantage standards and ${\mathcal{C}}_{CR - 3}$ is the cost basis. The weight vector of the standards is w = (0.5, 0.3, 0.2)T. The four potential options are assessed regarding the over three rules by the type of SVNSs, and single-esteemed neutrosophic choice network $R$ is developed as recorded in Table 1.

Table 1 Original decision matrix

Then the steps of the decision-making technique are summarized in the following ways:

• Step 1: By using Eq. (32), we normalized the decision matrix, if needed, but it’s not needed, see Table 2.

  Table 2 Normalized decision matrix

• Step 2: By using Eq. (29), we aggregated the normalized decision matrix for ${\mathcal{P}} = \left( {1,1,1} \right), \gamma = - 1$.

  $$ {\mathcal{A}}_{AL - 1} = \left( {0.5547,0.4462} \right),{\mathcal{A}}_{AL - 2} = \left( {0.4492,0.4308} \right),{\mathcal{A}}_{AL - 3} = \left( {0.5455,0.4382} \right),{\mathcal{A}}_{AL - 4} = \left( {0.4559,0.4258} \right) $$

• Step 3: By using Eq. (2), examine the score values of the aggregated values.

  $$ {\mathcal{S}}_{SF} \left( {{\mathcal{A}}_{AL - 1} } \right) = 0.1086,{\mathcal{S}}_{SF} \left( {{\mathcal{A}}_{AL - 2} } \right) = 0.01613,{\mathcal{S}}_{SF} \left( {{\mathcal{A}}_{AL - 3} } \right) = 0.1056,{\mathcal{S}}_{SF} \left( {{\mathcal{A}}_{AL - 4} } \right) = 0.0265 $$

• Step 4: Rank to all alternatives, and examine the best one.

  $$ {\mathcal{A}}_{AL - 1} \ge {\mathcal{A}}_{AL - 3} \ge {\mathcal{A}}_{AL - 4} \ge {\mathcal{A}}_{AL - 2} $$

The best alternative is ${\mathcal{A}}_{AL - 1}$.

• Step 5: The end.

To check the effect of the boundaries vectors ${\mathcal{P}}$ and $\gamma$ on the decision-making of the case, we select assorted boundaries vectors ${\mathcal{P}}$ and $\gamma$ and give the arranging aftereffects of the other options. We can see the outcomes in Tables 3.

Table 3 Examine the fluency of the parameter for $\gamma = - 0.1$

From the above analysis it is clear that for the different values of parameter the same ranking results are given, the best option is ${\mathcal{A}}_{AL - 1}$.

4.1 Advantages of the Explored Operators

Additionally, to examine the reliability and proficiency of the explored operators, we choose the Pythagorean fuzzy kind of information’s to find the accuracy and superiority of the explored operators.

Example 2:

We allude to a case of MCDM to demonstrate the plausibility and legitimacy of the introduced technique. We allude to the decision-making issue in Ref. [28]. There is a speculation organization, which plans to pick the most ideal interest in the other options. There are four potential alternatives for the speculation organization to browse: (1) a vehicle organization ${\mathcal{A}}_{AL - 1}$; (2) a food organization ${\mathcal{A}}_{AL - 2}$; (3) a PC organization ${\mathcal{A}}_{AL - 3}$; (4) an arms organization ${\mathcal{A}}_{AL - 4}$. The venture organization will think about the accompanying three assessment records to settle on decisions: (1) the hazard investigation ${\mathcal{C}}_{CR - 1}$; (2) the development examination ${\mathcal{C}}_{CR - 2}$; and (3) the natural impact investigation. Among ${\mathcal{C}}_{CR - 1}$ and ${\mathcal{C}}_{CR - 2}$ are the advantage standards and ${\mathcal{C}}_{CR - 3}$ is the cost basis. The weight vector of the standards is w = (0.5, 0.3, 0.2)T. The four potential options are assessed regarding the over three rules by the type of SVNSs, and single-esteemed neutrosophic choice network $R$ is developed as recorded in Table 4.

Table 4 Original decision matrix

Then the steps of the decision-making technique are summarized in the following ways:

• Step 1: By using Eq. (32), we normalized the decision matrix, if needed, but it’s not needed, see Table 5.

  Table 5 Normalized decision matrix

• Step 2: By using Eq. (29), we aggregated the normalized decision matrix for ${\mathcal{P}} = \left( {1,1,1} \right), \gamma = - 0.1$.

  $$ {\mathcal{A}}_{AL - 1} = \left( {0.9458,0.0402} \right),{\mathcal{A}}_{AL - 2} = \left( {0.9225,0.0408} \right),{\mathcal{A}}_{AL - 3} = \left( {0.9555,0.0416} \right),{\mathcal{A}}_{AL - 4} = \left( {0.9499,0.0405} \right) $$

• Step 3: By using Eq. (2), examine the score values of the aggregated values.

  $$ {\mathcal{S}}_{SF} \left( {{\mathcal{A}}_{AL - 1} } \right) = 0.8930,{\mathcal{S}}_{SF} \left( {{\mathcal{A}}_{AL - 2} } \right) = 0.9056,{\mathcal{S}}_{SF} \left( {{\mathcal{A}}_{AL - 3} } \right) = 0.9112,{\mathcal{S}}_{SF} \left( {{\mathcal{A}}_{AL - 4} } \right) = 0.9008 $$

• Step 4: Rank to all alternatives, and examine the best one.

  $$ {\mathcal{A}}_{AL - 3} \ge {\mathcal{A}}_{AL - 2} \ge {\mathcal{A}}_{AL - 4} \ge {\mathcal{A}}_{AL - 1} $$

The best alternative is ${\mathcal{A}}_{AL - 3}$.

• Step 5: The end.

To check the effect of the boundaries vectors ${\mathcal{P}}$ and $\gamma$ on the decision-making of the case, we select assorted boundaries vectors ${\mathcal{P}}$ and $\gamma$ and give the arranging aftereffects of the other options. We can see the outcomes in Tables 6.

Table 6 Examine the fluency of the parameter for γ = –0.1

From the above analysis it is clear that for the different values of parameter the same ranking results are given, the best option is ${\mathcal{A}}_{AL - 3}$.

4.2 Comparative Analysis of the Explored Operators

The comparison of the explored approach with some existing approaches evaluates the reliability and effectiveness of the explored operators. The information of the existing operators are discussed below, for instance, Pythagorean fuzzy Schweizer–Sklar arithmetic averaging (PFSSAA) operator, Pythagorean fuzzy Schweizer–Sklar Bonferroni mean (PFSSBM) operator, Pythagorean fuzzy Schweizer–Sklar Maclaurin symmetric mean (PFSSMSM) operator, intuitionistic fuzzy Schweizer–Sklar arithmetic averaging (IFSSAA) operator, intuitionistic fuzzy Schweizer–Sklar Bonferroni mean (IFSSBM) operator, and intuitionistic fuzzy Schweizer–Sklar Maclaurin symmetric mean (IFSSMSM) operator. The comparative analysis of the explored work with some existing works is discussed in the form of Table 7, for Example 1.

Table 7 Comparative analysis for the information of Example 1

From the above analysis it is clear that the explored operator and existing operators give the different ranking values, and the best one is ${\mathcal{A}}_{AL - 2}$ and ${\mathcal{A}}_{AL - 1}$.

The comparative analysis of the explored work with some existing works is discussed in the form of Table 8, for Example 2.

Table 8 Comparative analysis for the information’s of Example 2

From the above analysis it is clear that the explored operator and existing operators give the same ranking values, and the best one is ${\mathcal{A}}_{AL - 3}$.

4.3 Graphical Representations of the Explored Operators

The graphical interpretation of the explored work with some existing approaches is discussed in the form of figures, to improve the quality of the research work, to examine the reliability and effectiveness of the explored work. The comparative analysis of the explored work with some existing works, which are discussed in the form of Table 7, is summarized with the help of Fig. 1.

Fig. 1

Geometrical interpretation of the explored work for Table 5

From the above figure, it is clear that Fig. 1 contains five series which show different colors representing by the family of alternatives. There are many places which show the values are called the score function. By using these values we examine the best alternative from the family of alternatives.

The comparative analysis of the explored work with some existing works, which are discussed in the form of Table 8, is summarized with the help of Fig. 2.

Fig. 2

Geometrical interpretation of the explored work for Table 6

From the above figure, it is clear that Fig. 2 contains five series which show different colors representing by the family of alternatives. There are many places which show the values are called the score function. By using these values we examine the best alternative from the family of alternatives.

From the above analysis, it is clear that the explored operators based on PFSs are more proficient and more valuable than existing methods.

5 Conclusion

SS activity can make data conglomeration progressively adaptable, and the MM operator can consider the relationship among contributions by a variable parameter. Since customary MM is just accessible for genuine numbers and PFS can all the more likely express deficient and dubious data in choice frameworks. The objectives of this manuscript, first we explore the SS operators based on PFS and studied their score function, accuracy function, and their relationships. The limitation of the SS operators is discussed below:

• 1. Multi-criteria decision-making refers to the use of existing decision information, in the case of multi-criteria that are in conflict with each other and cannot coexist, and in which the limited alternatives are ranked or selected in a certain way. Schweizer–Sklar operation uses a variable parameter to make their operations more effective and flexible. In addition, PFS can handle incomplete, indeterminate, and inconsistent information under fuzzy environments. Therefore, we conducted further research on SS operations for PFS and applied SS operations to MCDM problems. Furthermore, because the MM operator considers interrelationships among multiple input parameters by the alterable parametric vector, hence combining the MM operator with the SS operation gives some aggregation operators, and it was more meaningful to develop some new means to solve the MCDM problems in the Pythagorean fuzzy environment. According to this, the purpose and significance of this article are

• 2. To develop a number of new MM operators by combining MM operators, SS operations, and PFS;

• 3. To discuss some meaningful properties and a number of cases of these operators put forward;

• 4. To deal with an MCDM method for PFS information more effectively based on the operators put forward;

• 5. To demonstrate the viability and superiority of the newly developed method.

Further, based on these operators, the MM operators based on PFS are called PFMM operator, PFWMM operator, and their special cases are presented. Additionally, MADM problem is solved by using the explored operators based on PFS to observe the consistency and efficiency of the produced approach. Finally, the advantages, comparative analysis, and their geometrical representation are also discussed.

In future, we will extend these ideas into complex fuzzy sets [29], picture hesitant fuzzy sets [30, 31], complex q-rung orthopair fuzzy sets [32,33,34], etc. [35–40]. By considering the superiority of new PFS, we can also extend them to some other aggregation operators, such as power mean aggregation operators, Bonferroni mean operators, Heronian mean operators, and so on.