Hypergraph Topology

Abstract

Consider a hypergraph H with vertex set $V=\{v_1,v_2,\ldots v_n\}$ and hyperedge set $E=\{e_1,e_2,\ldots e_m\}$. Two edges are adjacent if their intersection is non-empty. A neighbourhood of a vertex $v_i$, denoted by $N(v_i)$ is defined as the collection of vertices in adjacent edges of $v_i$. Hence, every edge is contained in a neighbourhood. A hypergraph topology is a family T of neighbourhood of vertices in V which satisfies the following conditions

• $\phi$ ,V $\epsilon$ T

• If $N(v_i),N(v_j)$ $\epsilon$ T then $N(v_i)\cap N(v_j)$ $\epsilon$ T

• If $N(v_i)$ $\epsilon$ T for each i $\epsilon$ I then $\cup _{i \epsilon I}N(v_i)$ $\epsilon$ T

The elements of T are called open sets. Thus, a topology T defined on a hypergraph H is called hypergraph topological space, denoted by (H, T). Also for a subhypergraph, similarly a subhypergraph induced topology is defined. The concept of closed sets, continuity, connectedness, metric and homeomorphism are also discussed

1 Introduction

The hypergraph topology is not concerned with the physical layout of the hypergraph, but shows what connections exist between the vertices and hyperedges. Thus, for the same hypergraph we can define different topologies. Hypergraph H is a pair (V, E) where V is the set of vertices and E is the set of edges called hyperedges which is a continuous closed curve containing the vertices. Each hyperedge consists of any finite number of vertices. Topological Hyper-Graphs were defined in a paper Topological Hyper-Graphs by Sarit Buzaglo, Rom Pinchasi and Gunter Rote in 4 December 2007. They defined topological hypergraphs as vertices enclosed by Jordan Curves. A family of simple closed curves in the plane is a family of pseudo-circles, if every two curves in the family are either disjoint or properly cross at precisely two points. They discussed more on graphical properties in topological hypergraphs. In this paper, also hyperedge is defined as pseudo-circles. But here we concentrated only on topological properties. Instead of topological hypergraph, we defined it as hypergraph topological space by defining hypergraph topology. The paper also discusses the concept of closed sets, continuity and connectedness, and their properties. This is further extended to homeomorphism.

2 Preliminaries

Hypergraph H is a pair (V, E) where V is the set of vertices and E is the set of edges called hyperedges which is a continuous closed curve containing the vertices. Each hyperedge consists of any finite number of vertices. Consider a hypergraph H with vertex set $V=\{v_1,v_2, \ldots v_n\}$ and hyperedge set $E=\{e_1,e_2,\ldots e_m\}$. Two edges are adjacent if their intersection is non-empty. To every hypergraph, we define a subhypergraph as follows. A subhypergraph is a hypergraph with some vertices or edges removed. Subhypergraph $H_A$ induced by a subset A of V is defined as $H_A=(A,\{e_i\cap A ;e_i\cap A \ne \emptyset \})$ where $e_i \epsilon E$.

For example, consider the above hypergraph H. Define $A \subset V$ as $A=\{v_1,v_3,v_6\}$. Then $H_A=(A,e_i\cap A \ne \emptyset ;i=1,2,3)$ $=(A,E_A),where E_A=\{e_{1_A},e_{3_A}\}$ The subhypergraph $H_A$ is shown below (Fig. 1).

Fig. 1

Subhypergraph

As our interest is on connected hypergraphs, hyperpaths is defined. A hyperpath between vertices $v_1$ and $v_k$ is defined as an alternative sequence of distinct vertices and hyperedges $v_1, e_1, v_2, e_2, \ldots , e_{k-1}, v_k$ such that $\{v_i, v_{i+1}\} \subseteq e_i$ for $1\le i \le k-1$.

A hypergraph is connected if there is a hyperpath between every pair of vertices. Otherwise, it is disconnected.

A metric is a function $d:X \times X \rightarrow R$ which satisfies the following conditions

• $d(v_i,v_j)\ge 0$

• $d(v_i,v_j)=0 \iff v_i=v_j$

• $d(v_i,v_j)=d(v_j,v_i)$

• $d(v_i,v_k) \le d(v_i,v_j)+d(v_j,v_k)$

3 Hypergraph Topological Space

A neighbourhood of a vertex $v_i$ denoted by $N(v_i)$ is defined as the collection of vertices in adjacent edges of $v_i$. Hence, every edge is contained in a neighbourhood. A hypergraph topology is a family T of neighbourhood of vertices in V which satisfies the following conditions

• $\phi$ ,V $\epsilon$ T

• If $N(v_i),N(v_j)$ $\epsilon$ T then $N(v_i)\cap N(v_j)$ $\epsilon$ T

• If $N(v_i)$ $\epsilon$ T for each i $\epsilon$ I then $\cup _{i \epsilon I}N(v_i)$ $\epsilon$ T

The elements of T are called open sets. Thus, a topology T defined on a hypergraph H is called hypergraph topological space, denoted by (H, T). Since neighbourhood of a vertex is an open set, the closed set is the complement of a neighbourhood.

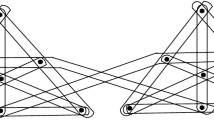
For example, a hypergraph H is shown below (Fig. 2).

Fig. 2

Hypergraph

Here $V=\{v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_8\}$ and $E=\{e_1,e_2,e_3\}$ where $e_1=\{v_1,v_2,v_3,v_4\}$, $e_2=\{v_4,v_5\}$ $e_3=\{v_5,v_6,v_7,v_8\}$

$N(v_1)=\{v_1,v_2,v_3,v_4,v_5\}=N(v_2)=N(v_3)$,

$N(v_4)=\{v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_8\}=V=N(v_5)$,

$N(v_6)=\{v_4,v_5,v_6,v_7,v_8\}=N(v_7)=N(v_8)$

The hypergraph topology that can be defined are

• $T=\{\phi ,V,N(v_1)\}$

• $T=\{\phi ,V,N(v_5)\}$

• $T=\{\phi ,V,N(v_8)\}$

• $T=\{\phi ,V,N(v_3)\}$, etc.

(H, T) is the hypergraph topological space. $H=(V,E)$ with $A\subset V$. $H_A$ is the subhypergraph of H.

The subhypergraph topology on $H_A$ is defined by $T_A=\{A\cap N(v_i);N(v_i)\epsilon T\}$.

$N(v_1)=N(v_2)=N(v_3)=\{v_1,v_2,v_3,v_4,v_5\}$,$N(v_4)=N(v_5)=V$,$N(v_6)=N(v_7)=N(v_8)=\{v_4,v_5,v_6,v_7,v_8\}$

$T=\{\phi ,V,N(v_1)\}$.

Using the above hypergraph $A=\{v_1,v_3,v_6\}$.$A\cap \phi =\phi$,$A\cap V=A \cap N(v_4)=A$,

$A \cap N(v_1)=\{v_1,v_3\}$.

$T_A=\{\phi , A,\{v_1,v_3\}\}$ is not a topology induced by A. This is because the subhypergraph has disjoint hyperedges. So we shall redefine A using hyperpaths .

In the context of hypergraph topology, a hyperpath between vertices $v_1$ and $v_k$ is a sequence of vertices $v_1,v_2, \dots ,v_k$ such that $\cap _{i=1}^{k}N(v_i)\ne \phi$. By this, we can define connectedness in hypergraph topological space. Thus, the connectedness in hypergraph theory and topological theory is similar with respect to neighbourhood of vertices. Now we shall come back to see what is subhypergraph topological space.

Consider an example (Fig. 1) as let A be the vertices in the hyperpath $v_1,e_1,v_4,e_2,v_5$. That is $A=\{v_1,v_4,v_5\}$.

The subhypergraph induced by A is shown below (Fig. 3).

Fig. 3

Subhypergraph induced by A

Let $T=\{\phi ,V,N(v_8)\}$ Then $A \cap \phi =\phi$, $A \cap V =A$, $A \cap N(v_8)=\{v_4,v_5\}$. Thus, $T_A=\{\phi , A,\{v_4,v_5\}\}$ is the induced subhypergraph topology.

As we defined the open set, we can think of closed sets.

4 Closed Set

A set other than V is closed if its complement is a neighbourhood of a vertex. Thus, a set is closed if its complement is open. Thus, $\phi$ and V are both closed and open.

In the previous example by Fig. 1, $\phi ^{c}=V$,

$V^{c}=\phi$, $N(v_1)^{c}=\{v_6,v_7,v_8\}=N(v_2)^{c}=N(v_3)^{c}$,

$N(v_4)^{c}=\phi =N(v_5)^{c}$

$N(v_6)^{c}=\{v_1,v_2,v_3\}=N(v_7)^{c}=N(v_8)^{c}$ are not neighbourhoods.

The closed set in this topology is $\phi ,V,\{v_6,v_7,v_8\},\{v_1,v_2,v_3\}$

Hence, complement of every set in a hypergraph topology is a closed set.

So similar to simple theorems in general topology, we have these in hypergraph topology also.

Theorem 1

The union of any collection of open set is open.The intersection of a finite number of open set is open.

Proof

Every neighbourhood is an open set. By the definition of hypergraph topology, any union of elements in a topology, T, is contained in T, and the union of open sets is open in T.

Similarly, by the definition of hypergraph topology, intersection of elements of T is in T. That is, intersection of open sets is open.    $\square$

Theorem 2

The intersection of a collection of closed set is closed. The union of a finite number of closed set is closed.

Proof

The complement of the intersection of closed sets is the union of the complement of closed sets. That is, it is the union of open sets . Since union of open set is open, the complement of intersection of closed set is open. Hence, the intersection of closed set is closed. Again by De Morgan’s law, complement of union of closed set is the intersection of open set, which is open. Hence, union of closed set is closed.    $\square$

5 Continuity in Hypergraph Topology

Let us define the continuity in hypergraph topological space.

Let $(H_1,T_1)$ and $(H_2,T_2)$ be hypergraph topological spaces. A function $f:H_1 \rightarrow H_2$ is said to be continuous if for each neighbourhood $N(v_i)$ of $H_2$, the set $f^{-1}(N(v_i))$ is a neighbourhood of $H_1$. By this definition, we derive the following theorem using closed sets.

Theorem 3

Let $(H_1,T_1)$ and $(H_2,T_2)$ be hypergraph topological spaces. Then $f:H_1 \rightarrow H_2$ is continuous if and only if for every closed set W in $H_2$, the set $f^{-1}(W)$ is closed in $H_1$.

Proof

Assume that f is continuous. By definition, for each neighbourhood $N(v_i)$ in $H_2$, the set $f^{-1}N(v_i)$ is a neighbourhood of $H_1$. Let W be a closed set in $H_2$. Then by definition of closed set $W^c$ is a neighbourhood in $H_2$. By continuity,$f^{-1}(W^c)$ is a neighbourhood in $H_1$. $f^{-1}(W^c)=(f^{-1}(W))^c$

Let $v_i \in f^{-1}(W^c)$

$\iff f(v_i)\in W^c$

$\iff f(v_i)\notin W$

$\iff v_i \notin f^{-1}(W)$ ,since f is continuous

$\iff v_i\in (f^{-1}(W^))^c$.

Therefore $f^{-1}(W^c)=(f^{-1}(W^))^c$

$(f^{-1}(W^{)})^c$ is a neighbourhood in $H_1$ . This implies that $f^{-1}(W)$ is closed in $H_1$.

Conversely assume that for every closed set W in $H_2$,$f^{-1}(W)$ is closed in $H_1$.

W is closed in $H_2$ $\implies$ $W^c$ is open in $H_2$

$\implies$ $W^c$ is a neighbourhood in $H_2$

$f^{-1}(W)$ is closed in $H_1$ $\implies$ $(f^{-1}(W))^c$ is a neighbourhood in $H_1$

$\implies$ $f^{-1}(W^c)$ is a neighbourhood in $H_1$. Thus, for every neighbourhood $W^c$ in $H_2$ there exist $f^{-1}(W^c)$, neighbourhood in $H_1$ $\implies$ f is continuous.    $\square$

Using continuous mapping the connectedness can be proved by the next theorem.

Theorem 4

Let $(H_1,T_1)$ and $(H_2,T_2)$ be two hypergraph topological spaces. If $f:H_1 \rightarrow H_2$ is continuous and $H_1$ is a connected, then $f(H_1)$ is a connected hypergraph topological space.

Proof

Since $H_1$ is connected, there exists a hyperpath between every pair of vertices.

$\implies$ $\cap _{i=1}^{n} N(v_i)\ne \phi$ for every i

claim: $f(\cap _{i=1}^{n} N(v_i))= \cap _{i=1}^{n} f(N(v_i))$

$w \epsilon f(\cap _{i=1}^{n} N(v_i))\iff f^{-1}(w)\epsilon \cap _{i=1}^{n} N(v_i))$

$\iff f^{-1}(w)\epsilon N(v_i))$ for every i

$\iff w \epsilon f(N(v_i))$ for every i

$\iff w \epsilon \cap _{i=1}^{n} f(N(v_i))$

Hence, $f(\cap _{i=1}^{n} N(v_i))= \cap _{i=1}^{n} f(N(v_i))\ne \cap _{i=1}^{n}f(\phi )\ne \phi$

Thus, there is a hyperpath between every pair of vertices in $f(H_1)$

Thus, $f(H_1)$ is connected.    $\square$

6 Metric in Hypergraph Topology

The function $d(v_i,v_j)=k$, where k is the length of shortest hyperpath in a hypergraph topology, follows all the axioms of the metric. So with this metric defined by $d(v_i,v_j)=k$, where k is the length of shortest hyperpath in a hypergraph topology is a function $d:V \times V \rightarrow R$ , which satisfies the following conditions

• $d(v_i,v_j)\ge 0$

• $d(v_i,v_j)=0 \iff v_i=v_j$

• $d(v_i,v_j)=d(v_j,v_i)$

• $d(v_i,v_k) \le d(v_i,v_j)+d(v_j,v_k)$

This hypergraph topology induced by this metric is called metric hypergraph topology. For example, by Fig. 1, $d(v_1,v_1)=0$, $d(v_1,v_4)=1$, $d(v_1,v_5)=2$, $d(v_1,v_7)=3$. That is the first three conditions are satisfied. Also $d(v_1,v_7)=3$ and $d(v_1,v_4)+d(v_4,v_7)=1+2=3$. From Fig. 4, $d(v_1,v_8)=4$ and $d(v_1,v_3)+d(v_3,v_8)=2+3=5$. Thus, $d(v_i,v_k) \le d(v_i,v_j)+d(v_j,v_k)$. Hence, the fourth condition is also satisfied. With this metric (H, d) is a metric hypergraph space.

7 Homeomorphism in Hypergraphs

Homeomorphism is a bijective correspondence that preserves the topological structure, it gives the connection between the neighbourhoods of $H_1$ and $H_2$. Two hypergraphs $H_1$ and $H_2$ are homeomorphic if one of the hypergraph is obtained from the other by subdivision or smoothing out of the vertices.

7.1 Subdivision

In subdivision, edges are subdivided into edges by introducing suitable number of vertices. Using Fig. 1,consider the edge $e_1=\{v_1,v_2,v_3,v_4\}$

Add two new vertices as common.Let the new vertex be $w_1$ and $w_2$.Hence by subdivision, the new edges are $\{v_1,v_2,w_1,w_2\}$ and $\{w_1,w_2,v_3,v_4\}$ (Fig. 4).

Fig. 4

Hypergraph obtained by subdivision

7.2 Smoothing Out

In smoothing out the edge is smoothed out to an edge by deleting suitable number of vertices in common. For example, in Fig. 4 consider the edges $\{v_1,v_2,w_1,w_2\}$ and $\{w_1,w_2,v_3,v_4\}$ . They have the intersection $\{w_1,w_2\}$. By smoothing out $w_1$ and $w_2$, the edge $\{v_1,v_2,v_3,v_4\}$ is obtained .

8 Conclusion

By defining hypergraph topological space with hypergraph topology using neighbourhood of a vertex a new branch of topology is evolved. Thus, hypergraph is a topological space in which vertices are points, and each edge is a region in a plane. The concept of closed set, continuity, connectedness in hypergrah topological space are discussed. Using hyperpath metric is defined by giving metric hypergraph space. The homeomorphism in hypergraph is defined. Further, investigation is being done on the homeomorphism and to homology of hypergraph topological space.