1 Introduction

As one of the classical parameters that indicate how reliable a graph G is, the edge-connectivity \(\lambda (G)\), defined as the minimum number of edges whose removal renders G disconnected, has attracted much attention in recent years. In 1932, Whitney [18] established one of the basic foundations of edge-connectivity for graphs: the edge-connectivity \(\lambda (G)\) of a connected graph G is bounded above by the minimum degree \(\delta (G)\). Thus, in order to study reliability and fault tolerance of graphs, sufficient conditions for graphs satisfying \(\lambda (G) = \delta (G)\) (so called maximally edge-connected) are of great interest. For other results the reader is referred to, for example, [5] and the survey [12].

Hypergraphs are a natural generalization of graphs in which “edges” may consist of more than 2 vertices. More precisely, a hypergraph \(H = (V, E)\) consists of a set V and a collection E of non-empty subsets of V. The elements of V are called vertices and the elements of E are called hyperedges, or simply edges. We define the order and size of H by \(n = |V(H)|\) and \(m = |E(H)|\), respectively. Unless specified otherwise, we consider only simple hypergraphs, i.e., hypergraphs whose edges are distinct. An r-uniform hypergraph H is a hypergraph such that all edges of H have cardinality r. We use \(K_n^{r}\) to denote the complete r-uniform hypergraph of order n, i.e., the hypergraph on n vertices whose edge set consists of all possible r-subsets of the vertex set. A hypergraph is called linear if any two edges of the hypergraph share at most one vertex. Obviously, every (simple) graph is a (linear) 2-uniform hypergraph.

For \(v, w \in V\), v and w are said to be adjacent, if there exists an edge \(e \in E\) such that \(\{v, w\} \subseteq e\). A vertex v and an edge e are said to be incident if \(v \in e\). The degree of a vertex v, denoted by \(d_H(v)\), is the number of edges which are incident to v. The minimum degree and maximum degree among the vertices of H are denoted by \(\delta (H)\) and \(\Delta (H)\), respectively. The neighborhood of a vertex v, denoted by \(N_H(v)\), is the set of all vertices different from v that are adjacent to v. If H is clear from the contest, we denote \(d_H(v)\) and \(N_H(v)\) by d(v) and N(v), respectively. For \(X \subseteq V\), use H[X] to denote the subgraph of H induced by X.

A walk in a hypergraph H is a finite alternating sequence \(W = (v_{0}, e_{1}, v_{1}, e_{2}, ... , e_{k}, v_{k})\), where \(v_{i} \in V\) for \(i \in \{0, 1, ... , k\}\) and \(e_{j} \in E\) such that \(\{v_{j - 1}, v_{j}\} \in e_{j}\) for \(j \in \{1, 2, ... , k\}\). A walk W is a path if all the vertices \(v_{i}\) for \(i \in \{0, 1, ..., k\}\) and all the edges \(e_{j}\) for \(j \in \{1, 2, ... , k\}\) in W are distinct. The length of a path, is the number of edges that it contains. We define the distance between two vertices u and v, denoted by \(d_H(u, v)\), as the length of a shortest path between u and v. A hypergraph is connected, if there is a walk between any pair of its vertices, otherwise it is disconnected. The diameter D(H) of a connected hypergraph H is defined by \(D(H) = max_{u, v \in V(H)}d_H(u, v)\).

We can extend the concept of edge-connectivity from graph theory to hypergraphs in a natural way in which the concept can be generalized. For a subset \(S \subseteq E(H)\), we define \(H - S\) to be the hypergraph obtained from H by deleting the edges in S without affecting the rest of the hypergraph. When \(H - S\) is disconnected, we say that S is an edge-cut. The minimum cardinality of an edge-cut in a connected hypergraph H is called its edge-connectivity, denoted by \(\lambda (H).\)

There has been several papers investigating the connectivity of the hypergraphs. In [19], Zykov presented a Menger-type theorem for hypergraphs. Edge augmentation of hypergraphs are studied in the literature (see e.g. [1, 2, 4]). Gu and Lai [10] gave necessary and sufficient conditions for an r-uniform hypergraphic sequence to have a k-edge-connected relazation. Jami et al. [13] provided a generalization of a result on edge-connectivity of permutation graphs for hypergraphs. In [6], Dankelmann and Meierling observed that \(\lambda (H) \le \delta (H)\) for general hypergraphs, and generalized some well-known sufficient conditions for graphs G satisfying \(\lambda (G) = \delta (G)\) to hypergraphs. In [7], the authors investigated vertex-connectivity of hypergraphs. For a subset \(X \subset V(H)\), \(H - X\) denotes the hypergraph obtained by removing the vertices X from H and removing all the edges that intersect X. The vertex-connectivity \(\kappa (H)\), is defined as the minimum cardinality of such X whose removal makes G disconnected. In [7], they also defined another vertex-connectivity for hypergraphs, and considered the complexity of the two kinds of vertex-connectivity for hypergraphs. The following result in [7] provided a generalization of a result of Whitney [18] on connectivity of graphs to hypergraphs.

Theorem 1.1

([7]). Let H be a hypergraph with at least two vertices. Then \(\kappa (H) \le \lambda (H) \le \delta (H)\).

Thus, we call a hypergraph H satisfying \(\lambda (H) = \delta (H)\) (resp. \(\kappa (H) = \delta (H)\)) maximally edge-connected (resp. maximally vertex-connected). If, furthermore, every minimum edge-cut consists of edges incident with one vertex, then H is said to be super edge-connected, or simply, super-\(\lambda\). Our main work is to investigate how some sufficient conditions for graphs to be maximally edge-connected or super-\(\lambda\) can be generalized to uniform and/or linear hypergraphs. In Section 2, we present results that will be useful in our arguments. In Section 3, two kinds of degree conditions for equality of edge-connectivity and minimum degree for graphs are generalized to uniform linear hypergraphs. In Section 4, we generalize a sufficient condition for maximally edge-connected graphs depending on the order, the maximum degree and the minimum degree as well as on the diameter, to uniform linear hypergraphs. In Section 5, we generalize a sufficient condition for maximally edge-connected graphs and super-\(\lambda\) graphs depending on the size, the order, the minimum degree and a parameter (as defined in Section 5) to uniform hypergraphs.

2 Preliminary lemmas

In this section, we will list or prove some lemmas which will be used in our later proofs.

In a connected hypergraph \(H = (V, E)\), let \(S \subseteq E\) be a minimum edge-cut of H and \(H_{1}\) be a component of \(H - S\). A vertex v of \(H_{1}\) is internal if v is not incident with any edge of S; otherwise, v will be external. In 1981, Goldsmith confirmed a very useful lemma in [9] when he studied the n-th order edge-connectivity of graphs. Now we present the special case of his lemma as follows.

Lemma 2.1

([9]). Let S be a minimum edge-cut of a graph G. If \(\lambda (G) < \delta (G)\), then each component of \(G - S\) contains at least two internal vertices.

And we will give a similar result with Lemma 2.1 for uniform linear hypergraphs.

Lemma 2.2

Let H be an r-uniform linear hypergraph and S be a minimum edge-cut of H. If \(\lambda (H) < \delta (H)\), then each component of \(H - S\) contains at least one internal vertex.

Proof

Let \(H_{1}\) be a component of \(H - S\) and x be an external vertex of \(H_{1}\). Set \(E_{1} = \{ e \in E \mid x \in e\) and \(e \in E(H_{1})\}\), and \(E_{2} = \{ e \in E \mid x \in e\) and \(e \in S\}\). Obviously, \(E_{2} \ne \varnothing\). If \(E_{1} = \varnothing\), then \(\delta (H) > \lambda (H) = |S| \ge |E_{2}| = d(x) \ge \delta (H)\), a contradiction. Thus, \(E_{1} \ne \varnothing\). It follows that \(|E_{1}| + |E_{2}| = d(x) \ge \delta (H) > \lambda (H) = |S| = |E_{2}| + |S - E_{2}|\), which implies that \(|E_{1}| > |S - E_{2}|\). Since H is linear and each edge of \(S - E_{2}\) is incident with at most \(r - 1\) vertices in \(V(H_{1})\), we have

$$\begin{aligned} |(\bigcup \limits _{e \in S - E_{2}} e) \cap V(H_{1})| \le (r - 1)|S - E_{2}| < (r - 1)|E_{1}| = |\bigcup \limits _{e \in E_{1}} (e - \{x\})|, \end{aligned}$$

and \((\bigcup \limits _{e \in E_{1}} (e - \{x\})) \cap (\bigcup \limits _{e \in E_{2}} (e - \{x\})) = \varnothing\), which implies that there exists at least one vertex \(w \in N(x) \cap (\bigcup \limits _{e \in E_{1}} e)\) that is not covered by any edge of S, i.e., w is an internal vertex of \(H_{1}\). \(\square\)

Our lemma implies the following two results of [6] for linear r-uniform hypergraphs to be maximally edge-connected.

Theorem 2.3

([6]). Let H be an r-uniform linear hypergraph with \(D(H) \le 2\). Then \(\lambda (H) = \delta (H)\).

Proof

Let S be a minimum edge-cut of H. The distance condition implies that there exists at least one component of \(H - S\) that contains no internal vertex. Then by Lemma 2.2, we have \(\lambda (H) \ge \delta (H)\) and the result holds. \(\square\)

If \(\lambda (H) < \delta (H)\), then by Lemma 2.2, each component of \(H - S\) contains at least one internal vertex w. It follows that each component of \(H - S\) contains at least \(1 + (r - 1)\delta (H)\) vertices (\(N(w) \cup \{w\} \subseteq V(H_{1})\) and thus \(|V(H_{1})| \ge 1 + (r - 1)d(w) \ge 1 + (r - 1)\delta (H)\)). Hence, \(|V(H)| \ge 2 + 2(r - 1)\delta (H)\), and we obtain the following condition for linear uniform hypergraphs to be maximally edge-connected.

Theorem 2.4

([6]). Let H be an r-uniform linear hypergraph of order n. If \(n \le 1 + 2(r - 1)\delta (H)\), then \(\lambda (H) = \delta (H)\).

The special case \(r = 2\) is the classical result as the following.

Corollary 2.5

Let G be a connected graph of order n. Then \(\lambda (G) = \delta (G)\), if

  1. (1)

    \(n \le 2\delta (G) + 1\); Chartrand [3]

  2. (2)

    \(D(G) \le 2\); Plesník [15].

3 Degree conditions

We now work towards a generalization of some degree conditions for equality of edge-connectivity and minimum degree for graphs to linear uniform hypergraphs. We point out here that we present the same generalizations as that of [16], but use a different method from [16]. For the sake of completeness, we also give the complete proof in our paper. In 1974, Lesniak [14] proved the following strengthening result of Corollary 2.5 (1) for graphs.

Theorem 3.1

([14]). If G is a graph of order n with \(d(u) + d(v) \ge n - 1\) for all distinct non-adjacent vertices u and v, then \(\lambda (G) = \delta (G)\).

Below we present a generalization of the above result for r-uniform linear hypergraphs.

Theorem 3.2

Let H be an r-uniform linear hypergraph of order n. If \(d(u) + d(v) \ge \lceil \frac{n - 1}{r - 1}\rceil\) for all distinct non-adjacent vertices u and v, then \(\lambda (H) = \delta (H)\).

Proof

Let \(H = (V, E)\) and let \(S \subseteq E\) be a minimum edge-cut of H. Then \(H - S\) consists of two parts \(H_{1}\) and \(H_{2}\) such that there are no edges between \(H_{1}\) and \(H_{2}\). Denote the vertex set of \(H_{i}\) by \(V_{i}\) for \(i = 1, 2\). We claim that there exists no internal vertex in \(H_{1}\) or \(H_{2}\). Suppose, on the contrary, that there exist internal vertices \(x_{i} \in V_{i}\) for \(i = 1, 2\). Then \(x_{1}\) and \(x_{2}\) are non-adjacent and \(d(x_{1}) + d(x_{2}) \le \lfloor \frac{|V_{1}| - 1}{r - 1}\rfloor + \lfloor \frac{|V_{2}| - 1}{r - 1}\rfloor \le \frac{n - 2}{r - 1} < \frac{n - 1}{r - 1}\), contradict to the hypothesis. Thus, by Lemma 2.2, we have that \(\lambda (H) = \delta (H)\). \(\square\)

Fig. 1
figure 1

A 3-uniform linear hypergraph \(H_1\)

Full size image

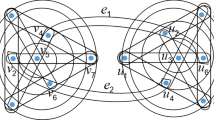
Note that Theorem 3.1 is a special case of Theorem 3.2 when \(r = 2\). Fig. 1 shows that Theorem 3.2 is in a sense a best possible result, since \(d(u) + d(v) \ge \lceil \frac{n - 1}{r - 1}\rceil - 1\) for all pairs of non-adjacent vertices of \(H_1\) and \(H_1\) is not maximally edge-connected.

Theorem 3.3

Let H be an r-uniform linear hypergraph of order n. If for each edge e there exist at least \(r - 1\) vertices incident with e such that each degree is at least \(\lceil \frac{\lfloor \frac{n}{2} \rfloor }{r - 1}\rceil\), then \(\lambda (H) = \delta (H)\).

Proof

Let S be a minimum edge-cut of H and let \(H_{1}\) be a component of \(H - S\) with the minimum cardinality. Then \(|V(H_{1})| \le \lfloor \frac{n}{2} \rfloor\). If \(|V(H_{1})| = 1\), then the result follows. In the following, we assume that \(|V(H_{1})| \ge 2\). Let \(v \in V(H_{1})\) such that \(d(v) = min \{d(x) \mid x \in V(H_{1})\}\). Set \(E_{1} = \{ e \in E \mid v \in e\) and \(e \in E(H_{1})\}\), and \(E_{2} = \{ e \in E \mid v \in e\) and \(e \in S\}\). We consider the following two cases.

Case 1::

\(d(v) \ge \lceil \frac{\lfloor \frac{n}{2} \rfloor }{r - 1}\rceil\) It follows that \(d(x) \ge \lceil \frac{\lfloor \frac{n}{2} \rfloor }{r - 1}\rceil\) for all \(x \in V(H_{1})\). Since \(d_{H_{1}}(x) \le \lfloor \frac{|V(H_{1})| - 1}{r - 1}\rfloor \le \lfloor \frac{\lfloor \frac{n}{2} \rfloor - 1}{r - 1}\rfloor\), we see that \(H_{1}\) contains no internal vertices. And by Lemma 2.2, we have \(\lambda (H) = \delta (H)\).

Case 2::

\(d(v) < \lceil \frac{\lfloor \frac{n}{2} \rfloor }{r - 1}\rceil\)

If \(E_{1} = \varnothing\), then \(\delta (H) \le d(v) = |E_{2}| \le |S| = \lambda (H)\), and the result follows. Now, we assume that \(E_{1} \ne \varnothing\). In this condition, by our hypothesis, we have \(d(x) \ge \lceil \frac{\lfloor \frac{n}{2} \rfloor }{r - 1}\rceil\) for any \(x \in X\), where \(X = \bigcup \limits _{e \in E_{1}} (e - \{v\})\), which implies that each vertex x in X is an external vertex. Set \(Y = \{e_{u} \in E \ | \ u \in e_{u} \in S\) and \(u \in X\}\), then \(Y \cap E_{2} = \varnothing\) since H is linear. It follows that \((r -1)|E_{1}| = |X| = |(\bigcup \limits _{e \in Y} e) \cap X| \le (r - 1)|Y|\) and we have \(|E_{1}| \le |Y|\). Thus, \(\delta (H) \le d(v) = |E_{1}| + |E_{2}| \le |Y| + |E_{2}| \le |S| = \lambda (H) \le \delta (H)\), and the proof is complete. \(\square\)

Fig. 2
figure 2

A 3-uniform linear hypergraph \(H_2\)

Full size image

It is easy to check that \(H_1\) in Fig. 1 is a regular hypergraph and Fig. 1 can also show that Theorem 3.3 is a best possible result in a sense. Now, we give an irregular hypergraph \(H_2\) (see Fig. 2), which is not maximally edge-connected, and there exist at least \(r - 1\) vertices incident with each edge such that each degree is at least \(\lceil \frac{\lfloor \frac{n}{2} \rfloor }{r - 1}\rceil - 1\).

When \(r = 2\), as a special case of Theorem 3.3, we can get the following degree condition for maximally edge-connected graphs.

Theorem 3.4

([11]). Let G be a connected graph. If for each edge e there exists at least one vertex v incident with e such that \(d(v) \ge \lfloor \frac{n}{2}\rfloor\), then \(\lambda (G) = \delta (G)\).

4 A sufficient condition about order

In this section, we present a generalization of the following result by Esfahanian.

Theorem 4.1

([8]). Let G be a graph with maximum degree \(\Delta \ge 3\), minimum degree \(\delta\), diameter D and order n. Then \(\lambda (G) = \delta (G)\), when

$$\begin{aligned} n \ge (\delta - 1)[\frac{(\Delta - 1)^{D - 1} + \Delta (\Delta - 2) - 1}{\Delta - 2}] + 1. \end{aligned}$$

Now, consider an r-uniform linear hypergraph \(H = (V, E)\) with maximum degree \(\Delta (H) = \Delta\) and let \(X_{0} \subset V\) with \(X_{0} = \{x_1, x_2, ..., x_p\}\), where \(|X_{0}| = p\). Denote by \(\overline{X_{0}} = V \backslash X_0\). For each \(x_{i} \in X_{0}\), let \(X_{i} = N(x_{i}) \cap \overline{X_{0}}\), where \(i \in \{1, 2, ..., p\}\). For a vertex \(x \in \overline{X_{0}}\), \(d(x, X_{0})\) denotes min\(\{d(x, u) \mid u \in X_{0}\}\). Define \(k = max\{d(x, X_{0}) \mid x \in \overline{X_{0}}\}\). We claim that n, the order of H, is bounded by:

$$\begin{aligned}&n \le |X_{0}| + |X_{1}|[1 + (\Delta - 1)(r - 1) + (\Delta - 1)^{2}(r - 1)^{2} + \cdots + (\Delta - 1)^{k - 1}(r - 1)^{k - 1}]\\&\qquad + \;|X_{2}|[1 + (\Delta - 1)(r - 1) + (\Delta - 1)^{2}(r - 1)^{2} + \cdots + (\Delta - 1)^{k - 1}(r - 1)^{k - 1}]\\&\qquad +\; \cdots + |X_{p}|[1 + (\Delta - 1)(r - 1) + (\Delta - 1)^{2}(r - 1)^{2} + \cdots + (\Delta - 1)^{k - 1}(r - 1)^{k - 1}] \end{aligned}$$

which is equivalent to

$$\begin{aligned} n \le |X_{0}| + [\sum \limits _{i = 1}^{p}|X_{i}|][\sum \limits _{i = 0}^{k - 1}(\Delta - 1)^{i}(r - 1)^{i}]. \end{aligned}$$
(1)

To see the validity of the above claim, observe that for each vertex \(u \in \overline{X_{0}}\), there exists a vertex \(x_{j} \in X_{0}\) such that \(d(u, x_j) \le k\). And, in the right-hand side of the inequality (1), for each \(x_i \in X_{0}\), the maximum number of vertices in \(\overline{X_{0}}\), which are at distance less than or equal to k from \(x_{i}\), is computed.

Using the discussion above we now compute the upper-bound on n, as a function of other hypergraph parameters.

Theorem 4.2

Let n, \(\lambda\), \(\delta\), \(\Delta\) and D respectively be the order, the edge-connectivity, the minimum degree, the maximun degree and the diameter of an r-uniform linear hypergraph \(H = (V, E)\). If \(\lambda < \delta\) and \(\Delta > 2\), then

$$\begin{aligned} n \le (\delta - 1)[\frac{(\Delta - 1)^{D - 1}(r - 1)^{D} + (\Delta - 1)^{2}(r - 1)^{2} - r}{(\Delta - 1)(r - 1) - 1}]. \end{aligned}$$

Proof

Let \(S \subseteq E\) be a minimum edge-cut of H. We can partition V into two disjoint non-empty sets Y and \({\overline{Y}}\) such that \(H - S\) contains no edges between Y and \({\overline{Y}}\). Let \(Y_{0}\) and \(\overline{Y_{0}}\) be the sets of external vertices respectively in Y and \({\overline{Y}}\). Let \(D_{Y} = max\{d(y, Y_{0}) \mid y \in Y\}\), and \(D_{{\overline{Y}}} = max\{d(y^{'}, \overline{Y_{0}}) \mid y^{'} \in {\overline{Y}}\}\). Since \(\lambda < \delta\), then \(D_{Y} \ge 1\) and \(D_{{\overline{Y}}} \ge 1\) by Lemma 2.2. And it is easy to see that \(D_{Y} + D_{{\overline{Y}}} + 1 \le D\).

Set \(Y_{0} = \{x_1, x_2, ..., x_p \}\), and \(\overline{Y_0} = \{x_1^{'}, x_2^{'}, ..., x_q^{'}\}\) where \(p = |Y_{0}|\) and \(q = |\overline{Y_0}|\). Let \(X_{i} = N(x_{i}) \cap (Y - Y_0)\) and \(X_{i}^{'} = N(x_{i}^{'}) \cap ({\overline{Y}} - \overline{Y_0})\), where \(x_i \in Y_0\) and \(x_i^{'} \in \overline{Y_0}\). Combining with the above claim of n, we have

$$\begin{aligned} \begin{aligned} n =&|Y| + |{\overline{Y}}| \le |Y_0| + [\sum \limits _{i = 1}^{|Y_0|}|X_{i}|][\sum \limits _{i = 0}^{D_Y - 1}(\Delta - 1)^{i}(r - 1)^{i}]\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + |\overline{Y_0}| + [\sum \limits _{i = 1}^{|\overline{Y_0}|}|X_{i}^{'}|][\sum \limits _{i = 0}^{D_{{\overline{Y}}} - 1}(\Delta - 1)^{i}(r - 1)^{i}]. \end{aligned} \end{aligned}$$

Without loss of generality, we assume that \(D_{{\overline{Y}}} \le D_{Y}\). Thus, we have:

$$\begin{aligned} \begin{aligned} n \le&|Y_0| + |\overline{Y_0}| + [\sum \limits _{i = 1}^{|Y_0|}|X_{i}|][\sum \limits _{i = 0}^{D_{{\overline{Y}}} - 1}(\Delta - 1)^{i}(r - 1)^{i} + \sum \limits _{i = D_{{\overline{Y}}}}^{D_{Y} - 1}(\Delta - 1)^{i}(r - 1)^{i}]\\&+ [\sum \limits _{i = 1}^{|\overline{Y_0}|}|X_{i}^{'}|][\sum \limits _{i = 0}^{D_{{\overline{Y}}} - 1}(\Delta - 1)^{i}(r - 1)^{i}]\\ =&|Y_0| + |\overline{Y_0}| + (\sum \limits _{i = 1}^{|Y_0|}|X_{i}| + \sum \limits _{i = 1}^{|\overline{Y_0}|}|X_{i}^{'}|)[\sum \limits _{i = 0}^{D_{{\overline{Y}}} - 1}(\Delta - 1)^{i}(r - 1)^{i}]\\&+ [\sum \limits _{i = 1}^{|Y_0|}|X_{i}|][\sum \limits _{i = D_{{\overline{Y}}}}^{D_Y - 1}(\Delta - 1)^{i}(r - 1)^{i}] \end{aligned} \end{aligned}$$

Since each edge of S is incident with at most \((r - 1)\) vertices of \(Y_0\), we have \(|Y_0| \le (r - 1)\lambda\). And it is easy to see that \(|Y_0| + |\overline{Y_0}| \le \lambda r\), \(|X_i| \le (d(x_i) - 1)(r - 1) \le (\Delta - 1)(r - 1)\) and \(|X_i^{'}| \le (\Delta - 1)(r - 1)\). It follows that

$$\begin{aligned}&\begin{aligned} n \le&|Y_0| + |\overline{Y_0}| + (|Y_0| + |\overline{Y_0}|)(\Delta - 1)(r - 1)[\sum \limits _{i = 0}^{D_{{\overline{Y}}} - 1}(\Delta - 1)^{i}(r - 1)^{i}]\\&+ |Y_0|(\Delta - 1)(r - 1)[\sum \limits _{i = D_{{\overline{Y}}}}^{D_Y - 1}(\Delta - 1)^{i}(r - 1)^{i}] \end{aligned} \\&\quad \le \lambda r + \lambda r(\Delta - 1)(r - 1)[\sum \limits _{i = 0}^{D_{{\overline{Y}}} - 1}(\Delta - 1)^{i}(r - 1)^{i}] + (r - 1)\lambda (\Delta - 1)(r - 1)[\sum \limits _{i = D_{{\overline{Y}}}}^{D_Y - 1}(\Delta - 1)^{i}(r - 1)^{i}] \\&\quad = \lambda r + (r - 1)\lambda (\Delta - 1)(r - 1)[\sum \limits _{i = 0}^{D_Y - 1}(\Delta - 1)^{i}(r - 1)^{i}] + \lambda (\Delta - 1)(r - 1)[\sum \limits _{i = 0}^{D_{{\overline{Y}}} - 1}(\Delta - 1)^{i}(r - 1)^{i}] \\&\quad = \lambda r + \lambda (\Delta - 1)(r - 1)^{2}\frac{1 - (\Delta - 1)^{D_Y}(r - 1)^{D_Y}}{1 - (\Delta - 1)(r - 1)} + \lambda (\Delta - 1)(r - 1)\frac{1 - (\Delta - 1)^{D_{{\overline{Y}}}}(r - 1)^{D_{{\overline{Y}}}}}{1 - (\Delta - 1)(r - 1)} \end{aligned}$$

Let \(a = (\Delta - 1)(r - 1)\), one has

$$\begin{aligned} \begin{aligned} n \le&\lambda r + \lambda (r - 1)a\frac{1 - a^{D_Y}}{1 - a} + \lambda a\frac{1 - a^{D_{{\overline{Y}}}}}{1 - a}\\ =&\lambda \big \{r + \frac{a}{a - 1}[(r - 1)a^{D_Y} - r + a^{D_{{\overline{Y}}}}]\big \} \end{aligned} \end{aligned}$$

Using the fact that \(D_{Y} \ge 1\), \(D_{{\overline{Y}}} \ge 1\) and \(D_{Y} + D_{{\overline{Y}}} + 1 \le D\), one can show that

$$\begin{aligned} \begin{aligned} n \le&\lambda \big \{r + \frac{a}{a - 1}[(r - 1)a^{D - 2} + a - r]\big \}\\ =&\lambda \frac{(r - 1)a^{D - 1} + a^{2} - r}{a - 1} \end{aligned} \end{aligned}$$

We remind that the above relation has been computed with the assumption that \(\lambda < \delta\). Thus, we have

$$\begin{aligned} n \le (\delta - 1)\frac{(\Delta - 1)^{D - 1}(r - 1)^{D} + (\Delta - 1)^{2}(r - 1)^{2} - r}{(\Delta - 1)(r - 1) - 1}. \end{aligned}$$

This completes the proof. \(\square\)

See Fig. 3, we give an r-uniform linear hypergraph \(H_3\) which is not maximally edge-connected and reaches the upper bound presented in Theorem 4.2. \(H_3\) is constructed by r copies of \(H_0\) and adding a new edge consisting of all the vertices of degree r, where \(H_0\) is also an r-uniform linear hypergraph. Theorem 4.2 yields the following result whose special case \(r = 2\) is Theorem 4.1.

Fig. 3
figure 3

(a) \(H_0\); (b) \(H_3\)

Full size image

Theorem 4.3

Let H be an r-uniform linear hypergraph with maximum degree \(\Delta \ge 3\), minimum degree \(\delta\) and diameter D. Then \(\lambda (H) = \delta (H)\) when

$$\begin{aligned} |V(H)| \ge (\delta - 1)[\frac{(\Delta - 1)^{D - 1}(r - 1)^{D} + (\Delta - 1)^{2}(r - 1)^{2} - r}{(\Delta - 1)(r - 1) - 1}] + 1. \end{aligned}$$

5 A sufficient condition about size

In this section, we will work towards a sufficient condition for maximally edge-connected and super-\(\lambda\) r-uniform hypergraphs. And, we need the following definition. For two integers n and k, we define \(\left( {\begin{array}{c}n\\ k\end{array}}\right) = \frac{n!}{k!(n-k)!}\) when \(k \le n\) and \(\left( {\begin{array}{c}n\\ k\end{array}}\right) = 0\) when \(k > n\).

Definition 5.1

For two integers \(\delta\) and r with \(r \ge 2\), define \(t = t(\delta , r)\) to be the largest integer such that \(\left( {\begin{array}{c}t-1\\ r-1\end{array}}\right) \le \delta\). That is, t is the integer satisfying \(\left( {\begin{array}{c}t-1\\ r-1\end{array}}\right) \le \delta < \left( {\begin{array}{c}t\\ r-1\end{array}}\right)\).

Lemma 5.2

Let H be a connected r-uniform hypergraph of order n, size m, minimum degree \(\delta\) and edge-connectivity \(\lambda\). If \(\lambda < \delta\), then

$$\begin{aligned} m \le \left( {\begin{array}{c}n-t\\ r\end{array}}\right) + \left( {\begin{array}{c}t\\ r\end{array}}\right) + \delta - 1, \end{aligned}$$

where \(t = t(\delta , r)\).

Proof

Let S be an arbitrary minimum edge-cut and let X denote the vertex set of the component of \(H - S\) with minimum number of vertices, and \(Y = V(H) - X\). We first show that \(|Y| \ge |X| \ge t\). Suppose \(|X| \le t - 1\). Then we obtain

$$\begin{aligned} \begin{aligned} |X|\delta \le \sum \limits _{x \in X}d(x) \le&|X|\left( {\begin{array}{c}|X| - 1\\ r - 1\end{array}}\right) + (r - 1)\lambda \\ \le&|X|\left( {\begin{array}{c}|X| - 1\\ r - 1\end{array}}\right) + (r - 1)(\delta - 1), \end{aligned} \end{aligned}$$

and thus,

$$\begin{aligned} \begin{aligned} \left( {\begin{array}{c}t - 1\\ r - 1\end{array}}\right) \le \delta \le&\left( {\begin{array}{c}|X|\\ r - 1\end{array}}\right) - \frac{r - 1}{|X| - r + 1}\\ \le&\left( {\begin{array}{c}t - 1\\ r - 1\end{array}}\right) - \frac{r - 1}{|X| - r + 1}. \end{aligned} \end{aligned}$$
(2)

If \(|X| = 1\), then \(\lambda = \delta\), contradicting \(\lambda < \delta\). So, \(|X| \ge r\), by the fact that H[X] is connected, and the inequality (2) is impossible. Therefore, we have \(t \le |X| \le |Y| \le n - t\), and

$$\begin{aligned} \begin{aligned} m - |S| \le&\left( {\begin{array}{c}n\\ r\end{array}}\right) - \sum \limits _{i = 1}^{r - 1}\left( {\begin{array}{c}|X|\\ i\end{array}}\right) \left( {\begin{array}{c}|Y|\\ r - i\end{array}}\right) \\ =&\left( {\begin{array}{c}n\\ r\end{array}}\right) - \big [\left( {\begin{array}{c}n\\ r\end{array}}\right) - \left( {\begin{array}{c}|X|\\ r\end{array}}\right) - \left( {\begin{array}{c}|Y|\\ r\end{array}}\right) \big ]\\ =&\left( {\begin{array}{c}|X|\\ r\end{array}}\right) + \left( {\begin{array}{c}n - |X|\\ r\end{array}}\right) . \end{aligned} \end{aligned}$$

This bound leads to

$$\begin{aligned} \begin{aligned} m \le&\left( {\begin{array}{c}|X|\\ r\end{array}}\right) + \left( {\begin{array}{c}n - |X|\\ r\end{array}}\right) + (\delta - 1). \end{aligned} \end{aligned}$$

Since \(f(x) = \left( {\begin{array}{c}x\\ r\end{array}}\right) + \left( {\begin{array}{c}n - x\\ r\end{array}}\right)\) is a decreasing function when \(1 \le x \le \frac{n}{2}\) and a increasing function when \(\frac{n}{2} \le x \le n\), we obtain

$$\begin{aligned} \begin{aligned} m \le&\left( {\begin{array}{c}t\\ r\end{array}}\right) + \left( {\begin{array}{c}n - t\\ r\end{array}}\right) + (\delta - 1). \end{aligned} \end{aligned}$$

\(\square\)

Theorem 5.3

Let H be a connected r-uniform hypergraph of order n, size m, minimum degree \(\delta\) and edge-connectivity \(\lambda\). If

$$\begin{aligned} m \ge \left( {\begin{array}{c}n-t\\ r\end{array}}\right) + \left( {\begin{array}{c}t\\ r\end{array}}\right) + \delta - 1, \end{aligned}$$

then \(\lambda = \delta\), unless that H is a hypergraph obtained from \(K_t^{r} \cup K_{n-t}^{r}\) by adding \(\delta - 1\) edges, where \(t = t(\delta , r)\).

Proof

If \(m > \left( {\begin{array}{c}n-t\\ r\end{array}}\right) + \left( {\begin{array}{c}t\\ r\end{array}}\right) + \delta - 1\), then by Lemma 5.2, we have \(\lambda = \delta\). If \(m = \left( {\begin{array}{c}n-t\\ r\end{array}}\right) + \left( {\begin{array}{c}t\\ r\end{array}}\right) + \delta - 1\), then by the proof of Lemma 5.2, we have that the inequalities in the proof of Lemma 5.2 must by equalities, which implies that \(\lambda = \delta - 1\), \(|X| = t\), \(|Y| = n - t\), \(H[X] \cong K_t^{r}\) and \(H[Y] \cong K_{n-t}^{r}\). This completes the proof. \(\square\)

Corollary 5.4

([17]). Let G be a connected graph of order n, size m, minimum degree \(\delta\) and edge-connectivity \(\lambda\). If

$$\begin{aligned} m \ge \left( {\begin{array}{c}n - \delta - 1\\ 2\end{array}}\right) + \left( {\begin{array}{c}\delta + 1\\ 2\end{array}}\right) + \delta - 1, \end{aligned}$$

then \(\lambda = \delta\), unless that G is a graph obtained from \(K_{\delta +1} \cup K_{n-\delta -1}\) by adding \(\delta - 1\) edges.

Proof

When \(r = 2\), then \(t = \delta + 1\) by the Definition 5.1. Thus, the result follows from Theorem 5.3. \(\square\)

Lemma 5.5

Let H be a connected r-uniform hypergraph of order n, size m, minimum degree \(\delta\) and edge-connectivity \(\lambda\). If H is not super-\(\lambda\), then

$$\begin{aligned} m \le \left( {\begin{array}{c}n-t+1\\ r\end{array}}\right) + \left( {\begin{array}{c}t-1\\ r\end{array}}\right) + \delta , \end{aligned}$$

where \(t = t(\delta , r)\).

Proof

Let S be an arbitrary minimum edge-cut such that every component of \(H - S\) has at least two vertices. Let X denote the vertex set of the component of \(H - S\) with minimum number of vertices, and \(Y = V(H) - X\). Clearly, \(|Y| \ge |X| \ge 2\). We first show that \(|Y| \ge |X| \ge t - 1\). Suppose \(|X| \le t - 2\). Then we obtain

$$\begin{aligned} \begin{aligned} |X|\delta \le \sum \limits _{x \in X}d(x) \le&|X|\left( {\begin{array}{c}|X| - 1\\ r - 1\end{array}}\right) + (r - 1)\lambda \\ \le&|X|\left( {\begin{array}{c}|X| - 1\\ r - 1\end{array}}\right) + (r - 1)\delta , \end{aligned} \end{aligned}$$

and thus,

$$\begin{aligned} \begin{aligned} \left( {\begin{array}{c}t - 1\\ r - 1\end{array}}\right) \le \delta \le&\left( {\begin{array}{c}|X|\\ r - 1\end{array}}\right) \le \left( {\begin{array}{c}t - 2\\ r - 1\end{array}}\right) , \end{aligned} \end{aligned}$$
(3)

a contradiction. Therefore, we have \(t - 1 \le |X| \le |Y| \le n - t + 1\), and

$$\begin{aligned} \begin{aligned} m - |S| \le \left( {\begin{array}{c}|X|\\ r\end{array}}\right) + \left( {\begin{array}{c}n - |X|\\ r\end{array}}\right) , \end{aligned} \end{aligned}$$

and so

$$\begin{aligned} \begin{aligned} m \le&\left( {\begin{array}{c}|X|\\ r\end{array}}\right) + \left( {\begin{array}{c}n - |X|\\ r\end{array}}\right) + \delta \\ \le&\left( {\begin{array}{c}n - t + 1\\ r\end{array}}\right) + \left( {\begin{array}{c}t - 1\\ r\end{array}}\right) + \delta . \end{aligned} \end{aligned}$$

\(\square\)

By the same argument as that of Theorem 5.3 and Corollary 5.4, the following results follows.

Theorem 5.6

Let H be a connected r-uniform hypergraph of order n, size m, minimum degree \(\delta\) and edge-connectivity \(\lambda\). If

$$\begin{aligned} m \ge \left( {\begin{array}{c}n-t+1\\ r\end{array}}\right) + \left( {\begin{array}{c}t-1\\ r\end{array}}\right) + \delta , \end{aligned}$$

then H is super-\(\lambda\), unless \(t \ge 3\) and H is a hypergraph obtained from \(K_{t-1}^{r} \cup K_{n-t+1}^{r}\) by adding \(\delta\) edges between \(K_{t-1}^{r}\) and \(K_{n-t+1}^{r}\) such that \(\delta (H) = \delta\), where \(t = t(\delta , r)\).

Corollary 5.7

([17]). Let G be a connected graph of order n, size m, minimum degree \(\delta\) and edge-connectivity \(\lambda\). If

$$\begin{aligned} m \geq \left( {\begin{array}{c}n-\delta \\ 2\end{array}}\right) + \left( {\begin{array}{c}\delta \\ 2\end{array}}\right) + \delta , \end{aligned}$$

then G is super-\(\lambda\), unless \(\delta \ge 2\) and G is a graph obtained from \(K_{\delta } \cup K_{n-\delta }\) by adding \(\delta\) edges between \(K_{\delta }\) and \(K_{n-\delta }\) such that \(\delta (G) = \delta\).