Analysis of Rotor Supported in Double-Layer Porous Journal Bearing with Gyroscopic Effects

Abstract

In this paper, a numerical analysis on the dynamics of a multi-degree of freedom shaft–rotor, supported on bearings, is presented. The system is a shaft with multiple rotor discs attached to it and supported on double-layer porous journal bearings. The system is modelled using finite element methods. Euler-Bernoulli beam element theory is used for modelling the shaft. The discs are considered as rigid. The support bearings are modelled based on linear spring elements for stiffness and linear damping elements for viscous damping coefficients. The rotor dynamic model of the system is analysed by incorporating the gyroscopic effects due to the precession of the offset discs and the bearing stiffness and damping anisotropy. The fluid flow in double-layer porous film is analysed using Brinkman equations to consider lubricant additives influences. The pressure gradients with respect to linearized perturbation of displacements and velocities under dynamic conditions are derived using Reynolds modified equation for Ocvirk (short) bearing. The dynamic linear and cross-coupled coefficients (stiffness and damping) dependent on speed are calculated using dynamic pressure gradients for the double-layer porous journal bearings. The system is represented in reduced order state-space form, and eigen value problem is solved to calculate its whirl frequencies. The rotor system critical speeds are obtained by plotting the Campbell diagram. This paper provides the basis for rotor system design with support bearings, representative of a multi-stage centrifugal pump. The design helps to identify and prevent rotor vibrations.

1 Introduction

Turbomachinery system often consists of several offset mounted rotors on a shaft, which in turn is supported on bearings. During run-up and run-down, the system has to cross through critical speeds. Hence, rotor dynamic analysis of such systems becomes a preliminary design requirement.

Ruhl and Booker [1] developed a finite element analysis of a turbo rotor system. The system has distributed mass and stiffness parameters. Consistent matrices are employed for the finite element model. Free and forced vibration rotor system responses are obtained. A shaft supported on hydrodynamic bearings is investigated by Kim and Lee [2]. The finite element model consists of five elements of equal length. Rao et al. [3] performed rotor dynamic analysis of a synchronous generator consisting of flywheels, armature, core, fan and a rotor shaft using ANSYS environment. The bearing oil film is modelled with spring as well as damping coefficients. The mass unbalance of the rotor system is modelled in accordance with ISO1940 standards. Modal analysis and rotor unbalance calculations are performed. Rotor orbit whirl plots and Campbell diagram for the rotor system are presented. Shravankumar and Tiwari [4] presented a comparative analysis of the effects of gyroscopic moments on a cantilever rotor system, using different numerical methods. The gyroscopic effect on simple rotor systems is discussed. Hsu [5] performed experimental and numerical studies on a turbomolecular rotor pump. The system is a flexible rotor-bearing system with discrete discs and bearings. The mass and stiffness properties are distributed. Gyroscopic moments due to disc precession are considered. He et al. [6] analysed the natural frequencies, critical speeds and unbalance responses for a multi-stage centrifugal pump. It is observed that the support stiffness has a large influence on the critical speed of rigid modes, while having less influence on the critical speeds of the flexible modes.

Lund and Thomsen [7] and Rao [8] presented calculation methodology of stiffness and damping coefficients using linearized perturbation method. Lin and Hwang [9] evaluated porous bearings stability. The hydrodynamic journal bearings performance considering the lubricant additive effects is studied using porous and couple stress media models [10, 11], respectively. Rao et al. [12] evaluated improvement in static characteristics of a double-layer porous bearing. Rao et al. [13] presented static and stability coefficients of double-layer porous (or layers of surface film topped with porous film) to the conventional journal bearing. Stability characteristics of porous layered journal bearings are enhanced by lubricant additives properties.

2 Finite Element Modelling

A flexible shaft-bearing system (multi-degree of freedom) with rigid discs modelled using finite element method is presented. A schematic diagram of the shaft–rotor-bearing system, along with finite element discretization is shown in Fig. 1.

Fig. 1

Rotor system model and discretization into finite elements in yz transverse plane

The primary assumptions for modelling include a flexible shaft, rigid discs and flexible bearing supports. The shaft–rotor geometry is axisymmetric. The properties considered for the shaft include distributed mass and stiffness. The disc properties are concentrated mass, diametric moment of inertia and polar moment of inertia. Four degrees of freedom (DoFs) are considered for the model, two translational DoFs along the two transverse directions and two rotational DoFs about the same. Gyroscopic effects due to shaft and disc mass are considered. No effects of unbalance mass or misalignment between shaft and bearings are considered. Four rigid discs are mounted along the length of the shaft, and it is assumed for simplicity that centres of gravity of the rigid discs coincide with that of the elastic shaft. Figure 2a shows the beam element. The shaft element is a two-node beam element with four degrees of freedom at each node.

Fig. 2

Conventions (positive) for nodal displacements, rotations, forces and moments. a beam element and b rigid disc element

There are two linear displacements u_x and u_y (along the X and Y axes) and two rotational displacements θ_y and θ_x (about the X and Y axes). The elements have isotropy, and they are also symmetric about the Z axis. Because of the symmetry of the shaft elements, the same mass matrices and same stiffness matrices result in the two transverse planes XZ and YZ. The rigid disc element is shown in Fig. 2b.

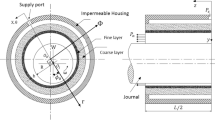
The Brinkman equations are used to model fluid flow in the double porous region. These dynamic coefficients correspond to a double-layer porous hydrodynamic journal bearing (Fig. 3). The stiffness and damping coefficients are represented using linear spring and damping elements in Fig. 3b–c.

Fig. 3

a Double-layer porous journal bearing, b Linear spring element with positive conventions for nodal displacements and forces and c Linear damping element with positive conventions for nodal velocities and forces

2.1 Shaft Model

Euler-Bernoulli theory of bending is used for modelling the shaft finite element. Mass and stiffness properties of the shaft element are considered, and its internal damping is neglected. Also, the gyroscopic moments due to the rotation of elemental shaft masses about the bearing centre lines are considered. The equations of motion for the shaft element are in Eq. (1).

$$\left[ {m_{\text{s}}^{\text{e}} } \right]\left\{ {\ddot{u}_{\text{s}}^{\text{e}} } \right\} + \left[ {g_{\text{s}}^{\text{e}} } \right]\left\{ {\dot{u}_{\text{s}}^{\text{e}} } \right\} + \left[ {k_{\text{s}}^{\text{e}} } \right]\left\{ {u_{\text{s}}^{\text{e}} } \right\} = \left\{ {f_{\text{s}}^{\text{e}} } \right\}.$$

(1)

$\left[ {m_{\text{s}}^{\text{e}} } \right]$ is the elemental mass matrix, obtained as the summation of the mass matrices corresponding to translation as well as rotation motion, $\left[ {g_{\text{s}}^{\text{e}} } \right]$ is the elemental gyroscopic matrix, $\left[ {k_{\text{s}}^{\text{e}} } \right]$ is the elemental stiffness matrix, displacement vector is $\left\{ {u_{\text{s}}^{\text{e}} } \right\} = \left\lfloor {\begin{array}{*{20}c} {x^{i} } & {y^{i} } & {\theta_{y}^{i} } & {\theta_{x}^{i} } & {x^{i + 1} } & {y^{i + 1} } & {\theta_{y}^{i + 1} } & {\theta_{x}^{i + 1} } \\ \end{array} } \right\rfloor$, subscripts i and i + 1 are the position of the two nodes along Z axis, and $\left\{ {f_{\text{s}}^{\text{e}} } \right\}$ is the force vector.

2.2 Rigid Disc Model

The discs are modelled as point masses. Also, gyroscopic moments in two transverse planes exist due to the offset position of these discs on the shaft, which results in a change of angular momentum and therefore gyroscopic moment. Any external forces acting on the discs, such as due to unbalance, are also considered.

$$\left[ {m_{\text{d}}^{\text{e}} } \right]\left\{ {\ddot{u}_{\text{d}}^{\text{e}} } \right\} + \left[ {g_{\text{d}}^{\text{e}} } \right]\left\{ {\dot{u}_{\text{d}}^{\text{e}} } \right\} = \left\{ {f_{\text{d}}^{\text{e}} } \right\}.$$

(2)

$\left[ {m_{\text{d}}^{\text{e}} } \right]$ is the elemental mass matrix, $\left[ {g_{\text{d}}^{\text{e}} } \right]$ is the elemental gyroscopic matrix for the rigid disc, and $\left\{ {f_{\text{d}}^{\text{e}} } \right\}$ is the elemental force vector acting on a disc. Displacement vector is $\left\{ {u_{\text{d}}^{\text{e}} } \right\} = \left\lfloor {\begin{array}{*{20}c} {x^{j} } & {y^{j} } & {\theta_{y}^{j} } & {\theta_{x}^{j} } \\ \end{array} } \right\rfloor^{T}$.

2.3 Double-Layer Porous Journal Bearing Model

The double-layer porous journal bearings are modelled using a total of eight dynamic coefficients which are used at each shaft end to model the fluid film bearings. Using the principle of superposition

$$f_{x} = k_{xx} x + k_{xy} y + c_{xx} \dot{x} + c_{xy} \dot{y},\,\,f_{y} = k_{yx} x + k_{yy} y + c_{yx} \dot{x} + c_{yy} \dot{y}$$

(3)

The load capacity coefficient ratio (C_w) and eight dynamic coefficients for double-layer porous journal bearing [12, 13] are obtained from the stiffness coefficient ratio (C_k) and damping coefficient ratio (C_c) as

$$\begin{aligned} & C_{w} = {{w_{ijl} } \mathord{\left/ {\vphantom {{w_{ijl} } {w_{ijh} }}} \right. \kern-0pt} {w_{ijh} }} = {{\Delta_{\text{s}} } \mathord{\left/ {\vphantom {{\Delta_{\text{s}} } {\Delta_{\text{p}} }}} \right. \kern-0pt} {\Delta_{\text{p}} }},\,\,C_{k} = {{k_{ijl} } \mathord{\left/ {\vphantom {{k_{ijl} } {k_{ijh} }}} \right. \kern-0pt} {k_{ijh} }} = {{\Delta_{\text{s}} } \mathord{\left/ {\vphantom {{\Delta_{\text{s}} } {\Delta_{\text{p}} }}} \right. \kern-0pt} {\Delta_{\text{p}} }}, \\ & \quad C_{c} = {{c_{ijl} } \mathord{\left/ {\vphantom {{c_{ijl} } {c_{ijh} }}} \right. \kern-0pt} {c_{ijh} }} = {1 \mathord{\left/ {\vphantom {1 {\Delta_{\text{p}} }}} \right. \kern-0pt} {\Delta_{\text{p}} }} \\ \end{aligned}$$

(4)

The journal eccentricity ratio is obtained from Newton–Raphson iterative procedure for the given bearing parameters and operating conditions.

2.4 Boundary Conditions and Assembly

The system shown (Fig. 1) is discretized into seven numbers of elements with four degrees of freedom at each node. This gives the size of the assembled matrices are 28 × 28. Then, the fixed boundary conditions are considered at one end of the spring and damper elements which represent the two journal bearings. With the application of these boundary conditions, the size of the assembled matrices reduces to 24 × 24. In matrix form, the assembled system equations of motion are represented as in Eq. (5).

$$\left[ M \right]\left\{ {\ddot{U}} \right\} + \left[ G \right]\left\{ {\dot{U}} \right\} + \left[ C \right]\left\{ {\dot{U}} \right\} + \left[ K \right]\left\{ U \right\} = \left\{ F \right\}. .$$

(5)

$\left[ M \right]$, $\left[ G \right]$, $\left[ C \right]$ and $\left[ K \right]$ are the assembled mass, gyroscopic, damping and stiffness matrices of the rotor-bearing system.

2.5 Rotor Dynamic Analysis

Equation (5) is solved as an eigen value problem to obtain the whirl frequencies. The homogenous equation of Eq. (5) is reduced into first-order differential equations of size 2n times. This is called as state-space reduction and is given in Eq. (6). The eigen values and eigen vectors of Eq. (6) are calculated using QZ algorithm or Cholesky factorization in MATLAB environment.

$$\left\{ {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{v}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} & {\left[ I \right]} \\ { - \left[ {\left[ {M^{ - 1} } \right]\left[ K \right]} \right]} & { - \left[ {\left[ {M^{ - 1} } \right]\left[ {\left( {C + \omega G} \right)} \right]} \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right\}.$$

(6)

The eigen values obtained are complex quantities, because of the viscous damping. These eigen values can be used to identify the damped critical speeds of the rotor system.

3 Results and Discussion

In this section, numerical simulation is carried out to obtain the following: the dynamic coefficients of the bearing as a function of the rotor spin frequency; whirl frequencies of the system. Table 1 gives the various geometric and material properties of the shaft–discs–bearings, required to carry out the numerical analysis.

Table 1 Geometric and material properties of the rotor system with double porous layer bearing

The bearing stiffness and damping with spin speed of the rotor are shown in Fig. 4a–b. It can be observed from Fig. 4b, the stiffness coefficient k_yx (cross-coupled) is negative for the entire speed range.

Fig. 4

a Bearing stiffness coefficients versus spin speed and b Bearing damping coefficients versus spin speed

Figure 5 shows the Campbell diagram for the rotor-bearing system under study. The natural frequencies in the Campbell diagram are split into two: a slow one where the whirl is opposed to the spin, and a fast one where their directions are the same. The split in the natural frequencies indicates the forward whirl and reverse whirl. In this system, this split is due to the gyroscopic effect as well the asymmetric nature of the bearing stiffness coefficients in the two transverse directions. Each rotor mode consists of forward precession and reverse precession. The 1× straight line in Fig. 6 represents the synchronous frequency, which is representative of any mass unbalance exciting the rotor.

Fig. 5

Campbell diagram in the operating speed range of 10–300 rad/s

Fig. 6

Intersection of forward and reverse precession modes with order lines ranging from 1× to 10 × for calculation of critical speeds

The critical speeds of the rotor system for synchronous whirl condition are given by υ = ω. These critical speeds can be used in the design of the rotor to decide the operating speed range as well as the vibration prone spin speeds. Figure 7 shows variation of system damping with spin frequency for rotors supported on double-layer porous journal bearings. The negative real part of the lowest eigenvalues is plotted versus spin frequency. The rotor system on double porous bearings (Fig. 7a–b) is stable over the entire spin frequency range.

Fig. 7

Variation of system damping with spin frequency. a γ₁ = 0.08, γ₂ = 0.02. b γ₁ = 0.2, γ₂ = 0.02

4 Conclusions

This study presents finite element method modelling of dynamics of a shaft–rotor system, with multiple rotor discs and supported on double-layer porous journal bearings. The whirl frequencies and system damping are evaluated for a lubricant film double porous layer with porous layer II (low permeability) over porous layer I (bearing surface adsorbent high permeability layer). The whirl frequencies obtained for various spin speeds using speed dependent eight dynamic coefficients of double porous layer journal bearing are plotted as a Campbell diagram. The design of a rotor system of a multi-stage centrifugal pump with support bearings helps to identify the operating speed range as well as prevent the rotor vibration spin speeds.