1 Introduction

Porous gas bearings, on account of their superior performance, have attained widespread acceptance in precision equipment. Supply of working fluid pressurized externally through porous bushing ensures better pressure dissemination at film region which is difficult to achieve with orifices and grooves even though positioned strategically. Working fluid characteristics like low viscosity and compressibility nature tends the bearing to run at higher speed and eccentricity ratio even at lesser loads. Because of the porosity, conventional aerostatic porous bearings possess inferior load-carrying capacity [1] and are prone to pneumatic hammer instability [2]. Since the working fluid can easily seep through the porous bushing, addition of another layer consisting of super fine powder of materials having relatively low permeability can be advantageous. This double-layer porous bushing configuration can enhance the bearing performance and can curtail the existing instability issues. An improvement in bearing performance using double-layered porous bearing configuration was observed by several researchers [3, 4]. Since the performance of precision equipment depends directly on the dynamic behavior of rotor-bearing pair, it is essential to investigate its stability characteristics during the design stage itself.

Over the past few decades, majority of the published investigations related to porous journal bearings are focused primarily on identifying its static and dynamic characteristics. Saha and Majumdar [1] presented a theoretical investigation to attain the static characteristics of gas journal bearings equipped with a two-layered porous bushing configuration. The authors reported that porous bearings with two-layered bushing configuration possess better load-carrying capacity when compared to a bearing with single porous bushing. Majumdar and Kumar [5] studied steady-state, stiffness and damping behavior of hybrid gas journal bearing with a double-layered porous bushing. The studies were conducted by taking into account of radial flow in porous region and two-dimensional flow in the film region. Their analysis advocates that the bearing with double porous layer had better stability in comparison to a single porous layer. Rao et al. [6] considered a long journal bearing approximation to investigate the performance characteristics of journal bearings with twofold porous bushing. The study was focused on the impact of using couple stress fluid on the bearing performance. Their analysis states that the use of a low permeable porous layer adjacent to the film region assisted by a high permeable porous layer aids in enhancing the load-carrying capability along with reducing the frictional losses. Yoshimoto et al. [7] carried out numerical and experimental studies using porous restrictors to evaluate the static behavior of aerostatic journal bearings. The authors conducted the experiments to evaluate the extent of influence of a low permeable restricted porous layer fabricated on bulk porous bushing. They reported an increased bearing performance using a restricted porous layer. Majumdar and Majumder [8] presented a numerical investigation to ascertain the stability characteristics of a porous journal bearings with gas as the working fluid. The authors presented the journal center trajectories under different operating conditions using nonlinear transient method. It is evident from all the afore discussed reports on gas lubricated journal bearings with double-layered porous bushing it has been observed that all the investigations assume adherence (no-slip) of fluid in the film at the porous bearing surface and this has been the regular practise. Since the viscous shear in the clearance region results in tangential velocity component in the film at the porous and film region interface [9], it becomes essential to consider a nonzero velocity of fluid at the interface between film and porous region.

An analysis to predict the consequence of velocity slip on static performance characteristics of hybrid gas bearings with porous bushing was presented by Singh et al. [10]. The dynamic characteristics of conventional porous bearing with velocity slip effect were studied theoretically by Chattopadhyay and Majumdar [11]. In the solution process, they have eliminated the time dependent terms using the first-order perturbation technique. The resulting linear differential equations are discretized using finite difference method. Approximate solution was obtained using Gauss–Seidel iterative method with successive over relaxation scheme. They observed a minor effect on bearing dynamic characteristics by considering velocity slip effects. Sakim et al. [12] inspected the influence of non-Newtonian fluid along with velocity slip in the film on the static performance characteristics of porous bearings. In their analysis, they have considered the elastic deformation of bushing. They reported that bushing deformation diminishes the static performance. Although most of the analysis on porous bearings was carried out by neglecting the elastic deformation of porous bushing, the importance of accounting elastic deformations was emphasized by Elsharkawy [13]. Jing Liu [14] presented the influence of structure elastic deformation on bearing dynamics by considering Winkler’s model. Lee et al. [15] considered slip flow effects to assess load-carrying capability, stiffness and damping characteristics of an air lubricated journal bearings for microelectromechanical system applications. They reported that slip flow effects are prominent at low bearing speeds and at higher environment temperatures. It is observed that in-spite of the importance to consider nonzero velocity condition at the vicinity of film and porous region interface, very few studies are reported in the open literature for a hybrid gas journal bearing with double-layered porous bushing. One such study using the velocity slip boundary condition proposed by Beavers–Joseph at porous-film interface was presented by Kumar et al. [16]. Analysis for the steady-state performance characteristics was carried out for a two-layered porous gas journal bearing. Further, stability characteristics were obtained by first-order linear perturbation method. It is well known that linear perturbation theory can be used to determine the mass parameter, from which one can have an idea on the stable operating region. However, once the instability sets in, information on journal center motion cannot be obtained by using this theory. On the flip side, nonlinear transient analysis can be used to track the journal center locus. It is also customary to use Newton–Raphson iterative scheme to solve the nonlinear governing equations. However, this method fails to converge at higher bearing number values [16, 17]. Hence, it is proposed to use third-order total variation diminishing (TVD) Runge–Kutta scheme to solve the governing equation at porous and film regions.

Accordingly, in the current article, nonlinear transient analysis of a rigid rotor supported on a hybrid, finite gas lubricated journal bearings with double-layered porous bushing is presented. Velocity slip in the film at the interface between film and porous region is considered using the Beavers–Joseph boundary condition. Modified Reynolds equation at film region, governing equations at porous region and equations of journal motion are solved using third-order TVD Runge–Kutta Method. From analysis, journal center trajectories are obtained from which the system steadiness can be identified. The impact of velocity slip and various system parameters on the values of critical mass parameter is studied.

2 Numerical analysis

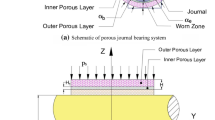
Figure 1 illustrates the configuration of gas lubricated journal bearing with double-layered porous bushing together with the reference coordinate system. In order to support the loads, fluid-film pressure generated due to the hydrodynamic action is supported with external pressurization.

Fig. 1
figure 1

Schematic diagram of externally pressurized double-layered porous gas journal bearing

Full size image

For the porous layers with anisotropic permeability, assuming the flow to be laminar, viscous and isothermal, governing equations are obtained using Darcy’s law. Equations governing the flow of fluid through porous layers in non-dimensional form are presented as:

For coarse layer

$$\bar{K}_{x2} \frac{{\partial^{2} \bar{p}_{2}^{{'^{2} }} }}{{\partial \theta^{2} }} + \left( {\frac{R}{H}} \right)^{2} \frac{{\partial^{2} \bar{p}_{2}^{{'^{2} }} }}{{\partial \bar{y}^{2} }} + \bar{K}_{z2} \left( {\frac{D}{L}} \right)^{2} \frac{{\partial^{2} \bar{p}_{2}^{{'^{2} }} }}{{\partial \bar{z}^{2} }} - 2\Lambda \gamma_{{p_{2} }} \left( {\frac{R}{H}} \right)^{2} \frac{{\partial \bar{p}_{2}^{'} }}{\partial \tau } = 0$$
(1)

For fine layer

$$\bar{K}_{x1} \frac{{\partial^{2} \bar{p}_{1}^{{'^{2} }} }}{{\partial \theta^{2} }} + \left( {\frac{R}{H}} \right)^{2} \frac{{\partial^{2} \bar{p}_{1}^{{'^{2} }} }}{{\partial \bar{y}^{2} }} + \bar{K}_{z1} \left( {\frac{D}{L}} \right)^{2} \frac{{\partial^{2} \bar{p}_{1}^{{'^{2} }} }}{{\partial \bar{z}^{2} }} - 2\Lambda \gamma_{{p_{1} }} \left( {\frac{R}{H}} \right)^{2} \frac{{\partial \bar{p}_{1}^{'} }}{\partial \tau } = 0$$
(2)

To consider velocity slip in the film at the porous bearing surface, Reynolds equation which governs the fluid flow at the clearance space is modified. The generalized governing equation at bearing clearance region in non-dimensional form is presented as:

$$\frac{\partial }{{\partial \theta^{*} }}\left( {\bar{h}^{3} \left( {1 + \xi_{x} } \right)\frac{{\partial \bar{p}^{2} }}{{\partial \theta^{*} }}} \right) + \left( {\frac{D}{L}} \right)^{2} \frac{\partial }{{\partial \bar{z}}}\left( {\bar{h}^{3} \left( {1 + \xi_{z} } \right)\frac{{\partial \bar{p}^{2} }}{{\partial \bar{z}}}} \right) = 2\Lambda \frac{\partial }{{\partial \theta^{*} }}\left( {\bar{h}\bar{p}\left( {1 + \xi_{ox} } \right)} \right) + 4\Lambda \frac{\partial }{\partial \tau }\left( {\bar{p}\bar{h}} \right) + \beta \left. {\frac{{\partial \bar{p}_{1}^{' 2} }}{{\partial \bar{y}}}} \right|_{{\bar{y} = 1}}$$
(3)

The detailed procedure for deriving these equations was mentioned in Singh [18] and Kumar [19]. In Eq. (3) the functions \(\xi_{x,z}\) and \(\xi_{ox}\) consider the influence of velocity slip which are dependent on film thickness \(\left( {\bar{h}} \right)\), slip coefficient (α) and permeability factors (σ).

Now using the rotating coordinate system

$$\left( {\frac{\partial }{{\partial \theta^{*} }}} \right)_{\text{fixed}} = \left( {\frac{\partial }{\partial \theta }} \right)_{\text{rotating}}$$
$$\left( {\frac{\partial }{\partial \tau }} \right)_{\text{fixed}} = \left( {\frac{\partial }{\partial \tau }} \right)_{\text{rotating}} - \frac{\partial \phi }{\partial \tau }\frac{\partial }{\partial \theta }$$
(4)

A detailed description in deriving the above mentioned relations was mentioned in [20]. Using Eq. (4) Eq. (3) can be written as

$$\frac{\partial }{\partial \theta }\left( {\bar{h}^{3} \left( {1 + \xi_{x} } \right)\frac{{\partial \bar{p}^{2} }}{\partial \theta }} \right) + \left( {\frac{D}{L}} \right)^{2} \frac{\partial }{{\partial \bar{z}}}\left( {\bar{h}^{3} \left( {1 + \xi_{z} } \right)\frac{{\partial \bar{p}^{2} }}{{\partial \bar{z}}}} \right) = 2\Lambda \frac{\partial }{\partial \theta }\left( {\bar{h}\bar{p}\left( {1 + \xi_{ox} } \right)} \right) + 4\Lambda \frac{\partial }{\partial \tau }\left( {\bar{p}\bar{h}} \right) - 4\Lambda \dot{\phi }\frac{\partial }{\partial \theta }\left( {\bar{p}\bar{h}} \right) + \beta \left. {\frac{{\partial \bar{p}_{1}^{' 2} }}{{\partial \bar{y}}}} \right|_{{\bar{y} = 1}}$$
(5)

Equations (1), (2) and (5) are solved for the pressure values at coarse, fine and film regions, respectively. Appropriate boundary conditions associated during the solution process are as follows:

At coarse porous region

$$\bar{p}_{2}^{'} \left( {\theta ,0,\bar{z}} \right) = \bar{p}_{{\rm s}} \; {\text{at}}\; 0 \le \theta \le 2\pi , - 1 \le \bar{z} \le + 1\quad \left( {\text{supply pressure condition}} \right)$$
$$\bar{p}_{2}^{'} \left( {\theta ,\bar{y},\bar{z}} \right) = \bar{p}_{2}^{'} \left( {\theta + 2\pi ,\bar{y},\bar{z}} \right) \;{\text{at}}\; 0 \le \bar{y} \le \chi , - 1 \le \bar{z} \le 1 \quad ( {\text{continuity condition)}}$$
$$\bar{p}_{2}^{'} \left( {\theta ,\bar{y}, \pm 1} \right) = 1.0 \;{\text{at}}\; 0 \le \theta \le 2\pi , 0 \le \bar{y} \le \chi \quad ( {\text{ambient condition)}}$$
$$\frac{{\partial \bar{p}_{2}^{'} }}{{\partial \bar{z}}}\left( {\theta ,\bar{y},0} \right) = 0 \;{\text{at}}\; 0 \le \theta \le 2\pi , 0 \le \bar{y} \le \chi \quad ( {\text{symmetry condition) }}$$

At fine porous region

$$\bar{p}_{1}^{'} \left( {\theta ,\bar{y},\bar{z}} \right) = \bar{p}_{1}^{'} \left( {\theta + 2\pi ,\bar{y},\bar{z}} \right) \;{\text{at}}\; \chi \le \bar{y} \le 1, - 1 \le \bar{z} \le 1\quad ( {\text{continuity condition)}}$$
$$\bar{p}_{1}^{'} \left( {\theta ,\bar{y}, \pm 1} \right) = 1.0 \;{\text{at}}\; 0 \le \theta \le 2\pi , \chi \le \bar{y} \le 1 \quad ( {\text{ambient condition)}}$$
$$\frac{{\partial \bar{p}_{1}^{'} }}{{\partial \bar{z}}}\left( {\theta ,\bar{y},0} \right) = 0\; {\text{at}}\; 0 \le \theta \le 2\pi , \chi \le \bar{y} \le 1 \quad ( {\text{symmetry condition)}}$$

At porous layers interface

$$\bar{p}_{1}^{'} \left( {\theta ,\bar{z}} \right) = \bar{p}_{2}^{'} \left( {\theta ,\bar{z}} \right) \; {\text{at}}\; 0 \le \theta \le 2\pi , - 1 \le \bar{z} \le + 1 \quad \left( {\text{matching condition}} \right)$$
$$\frac{{\partial \bar{p}_{1}^{{'^{2} }} }}{{\partial \bar{y}}}\left( {\theta ,\bar{z}} \right) = \bar{K}_{y2} \frac{{\partial \bar{p}_{2}^{{'^{2} }} }}{{\partial \bar{y}}}\left( {\theta ,\bar{z}} \right) \;{\text{at}}\; 0 \le \theta \le 2\pi , - 1 \le \bar{z} \le + 1\quad \left( {\text{flow continuity condition}} \right)$$

At film region

$$\frac{{\partial \bar{p}}}{{\partial \bar{z}}} \left( {\theta ,0} \right) = 0 \;{\text{at }}\; 0 \le \theta \le 2\pi \quad ( {\text{symmetry condition)}}$$
$$\bar{p}\left( {\theta ,\bar{z}} \right) = \bar{p}\left( {\theta + 2\pi ,\bar{z}} \right) \; {\text{at }}\; - 1 \le \bar{z} \le 1\quad ( {\text{continuity condition)}}$$
$$\bar{p}\left( {\theta , \pm 1} \right) = 1.0 \;{\text{at }} \; 0 \le \theta \le 2\pi \quad( {\text{ambient condition)}}$$

At porous-film interface

$$\bar{p}_{1}^{'} \left( {\theta ,1,\bar{z}} \right) = \bar{p}_{0} \left( {\theta ,\bar{z}} \right)\; {\text{at}}\; 0 \le \theta \le 2\pi , - 1 \le \bar{z} \le + 1\quad \left( {\text{matching condition}} \right)$$

Due to the nonlinearity of Eq. (5) obtaining an analytical solution is very difficult. Therefore, a third-order TVD Runge–Kutta scheme is used to obtain the numerical solution for in-hand problem.

The governing equation of flow at the clearance zone, i.e., modified Reynolds equation is discretized with finite volume discretization

$$\frac{\partial }{\partial \,\theta }\left( {\bar{h}^{3} \left( {1 + \zeta_{x} } \right)\frac{{\partial \,\bar{p}^{2} }}{\partial \,\theta }} \right)\,\, = \frac{{\,\left( {\bar{h}_{{i + \frac{1}{2}}}^{3} \left( {1 + \zeta_{x} } \right)_{{i + \frac{1}{2}}} \left( {\frac{{\partial \,\bar{p}^{2} }}{\partial \,\theta }} \right)_{{i + \frac{1}{2}}} \, - \,\,\bar{h}_{{i - \frac{1}{2}}}^{3} \left( {1 + \zeta_{x} } \right)_{{i - \frac{1}{2}}} \left( {\frac{{\partial \,\bar{p}^{2} }}{\partial \,\theta }} \right)_{{i - \frac{1}{2}}} } \right)}}{\Delta \theta }$$

where,

$$\,\,\,\,\,\bar{h}_{{i \pm \frac{1}{2}}}^{3} \,\,\,\, = \,\,\,\frac{1}{2}\left[ {\,\bar{h}_{i}^{3} \, + \bar{h}_{i \pm 1}^{3} \,} \right]$$
$$\,\,\,\,\,(1\, + \,\zeta_{x} \,)_{{i \pm \frac{1}{2}}}^{{}} \,\,\,\, = \,\,\,\frac{1}{2}\left[ {\,\,(1\, + \,\zeta_{x} \,)_{i}^{{}} \, + \,(1\, + \,\zeta_{x} \,)_{i \pm 1}^{{}} \,} \right]$$
$$\,\,\,\,\,\,\,\left( {\frac{{\partial \,\bar{p}^{2} }}{\partial \,\theta }} \right)_{{i + \frac{1}{2}}} \,\, = \,\,\,\frac{{\left( {\bar{p}_{i + 1}^{2} \, - \,\bar{p}_{i}^{2} } \right)}}{\Delta \theta }$$

Non-dimensional pressure (\(\bar{p}\)) value at cell-face center is approximated using an upwind interpolation expression mentioned in [21].

$$\bar{p}_{{i + \frac{1}{2 },R}} = {\raise0.7ex\hbox{${\left( {2\bar{p}_{i + 1} + 5\bar{p}_{i} - \bar{p}_{i - 1} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {2\bar{p}_{i + 1} + 5\bar{p}_{i} - \bar{p}_{i - 1} } \right)} 6}}\right.\kern-0pt} \!\lower0.7ex\hbox{$6$}},\bar{p}_{{i + \frac{1}{2 }, L}} = {\raise0.7ex\hbox{${\left( {2\bar{p}_{i} + 5\bar{p}_{i + 1} - \bar{p}_{i + 2} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {2\bar{p}_{i} + 5\bar{p}_{i + 1} - \bar{p}_{i + 2} } \right)} 6}}\right.\kern-0pt} \!\lower0.7ex\hbox{$6$}}$$

Discretized governing equations at clearance and porous regions are solved by using a third-order TVD Runge–Kutta method. Optimal coefficients of the scheme and a comprehensive description of the method are mentioned elsewhere [22]. The domain has been initialized and residual values are obtained at gird points. These residual values are used to update the pressure values at grid points for the next time step using the relation shown in Eq. (6)

$$\,\,\,\,p_{{\left( {i,j} \right)}}^{(1)} \,\,\,\, = \,\,p_{{\left( {i,j} \right)}}^{n} \, + \,\Delta t.{\text{residual}}_{(i,j)}^{n}$$
$$\,\,\,\,p_{{\left( {i,j} \right)}}^{(2)} \,\,\,\, = \,\,\frac{3}{4}p_{{\left( {i,j} \right)}}^{n} \, + \frac{1}{4}p_{{\left( {i,j} \right)}}^{(1)} + \,\frac{1}{4}\Delta t.{\text{residual}}_{(i,j)}^{(1)}$$
(6)
$$\,\,\,\,p_{{\left( {i,j} \right)}}^{n + 1} \,\,\,\, = \,\,\frac{1}{3}p_{{\left( {i,j} \right)}}^{n} \, + \frac{2}{3}p_{{\left( {i,j} \right)}}^{(2)} + \,\frac{2}{3}\Delta t.{\text{residual}}\,_{(i,j)}^{(2)}$$

A uniform grid size with three-dimensional pattern is adopted. The computational grid consists of 36 node points in circumferential direction, 10 and 13 node points in axial and radial directions, respectively. In order to take the advantage of symmetry, one half of the bearing is taken into account. Initially, i.e., at \(\tau = 0\) with \(\dot{\varepsilon } = \dot{\phi } = 0\) Eqs. (1, 2, 5) are solved using appropriate boundary conditions. The process is continued with a time increment (\(\Delta t\)) of 1e−4 until the maximum residual values in the clearance region reduces to 1e−8. Once the set convergence criteria are achieved, dimensionless fluid film response along radial and tangential directions is obtained from the converged pressure values.

$$\bar{F}_{{\rm r}} = \frac{1}{2}\mathop \int \limits_{0}^{1} \mathop \int \limits_{0}^{2\pi } \bar{p}_{o} \cos \theta {\text{d}}\theta {\text{d}}\bar{z}$$
$$\bar{F}_{\Phi } = \frac{1}{2}\mathop \int \limits_{0}^{1} \mathop \int \limits_{0}^{2\pi } \bar{p}_{o} \sin \theta {\text{d}}\theta {\text{d}}\bar{z}$$
(7)

\(\bar{F}_{\text{r}}\) and \(\bar{F}_{\Phi }\) obtained at \(\tau = 0\) are used to estimate the steady-state characteristics using the following expressions.

$$\bar{W}_{0} = \frac{{W_{0} }}{{LDP_{{\rm a}} }} = \left\{ {\bar{F}_{r0}^{2} + \bar{F}_{{\Phi 0}}^{2} } \right\}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$
$$\phi_{0} = - { \tan }^{ - 1} \left( {\bar{F}_{{\Phi 0}} / \bar{F}_{{{\text{r}}0}} } \right)$$
(8)

where \(\bar{F}_{{{\text{r}}0}}\) and \(\bar{F}_{{\Phi 0}}\) represents the non-dimensional film force response along \(r\) and \(\Phi\) direction, respectively, at \(\tau = 0\).

Referring to Fig. 1, assuming rigid rotor, governing equations of journal motion along the center line and its perpendicular direction in dimensionless form can be presented as:

$$\ddot{\varepsilon } = \varepsilon \dot{\phi }^{2} + A\bar{F}_{\text{r}} + B { \cos }\phi$$
(9)
$$\ddot{\phi } = \frac{{ - 2\dot{\varepsilon }\dot{\phi }}}{\varepsilon } + \frac{{A\bar{F}_{\Phi } }}{\varepsilon } - \frac{{B { \sin }\phi }}{\varepsilon }$$
(10)

where \(\bar{M} = \frac{{MC\omega^{2} }}{{LDp_{{\rm s}} }} , A = \frac{1}{{\bar{M}}}, B = \frac{{\bar{W}}}{{\bar{M}}}\)

Governing differential equations in eccentricity ratio (\(\varepsilon\)), attitude angle (\(\phi\)) as presented in Eqs. (9) and (10) which are of second order can be solved using initial position and velocity. If the initial conditions coincide with the steady-state conditions, the system will always remain at the steady-state equilibrium position. Therefore, a minor disturbance is given by providing the attitude angle as zero instead of steady-state attitude angle value. With these inputs, for a time step of \(\Delta \tau\), governing equations of journal motion are solved using third-order TVD Runge–Kutta method to obtain new \(\varepsilon ,\phi ,\dot{\varepsilon } \;{\text{and}}\; \dot{\phi }\). Further, these values are used to identify fresh \(\bar{F}_{\text{r}}\) and \(\bar{F}_{\Phi }\). This process is reiterated for the subsequent time steps until a certain locus of journal center (stable or unstable) is attained. A flowchart illustrating the solution procedure is presented in Fig. 2.

Fig. 2
figure 2

Flowchart of the solution procedure

Full size image

By observing the trajectory of the journal center locus, stability of the system can be anticipated. If the journal center tries to reach its steady-state position when disturbed, results in a journal center locus that doesn’t develop over time. In such a situation the bearing is considered as operating under stable condition. Whereas if the journal center, when disturbed, deviates from its steady-state equilibrium operating location and toward the clearance circle, the bearing is considered unstable. To authenticate the present numerical method, steady-state characteristics (load capacity and attitude angle) are attained for a gas lubricated journal bearing with double-layered porous bushing. Table 1 presents the comparison of steady-state characteristic values obtained from the present method with published results.

Table 1 Comparison of steady-state characteristics of double-layered porous bearing with the available data from Ref. [16]
Full size table
$$L/D = 1.0, H/R = 0.2, \varepsilon_{0} = 0.2, \beta = 1.0, \alpha = 0.1, \sigma = 100, \gamma_{p1} = 200, \gamma_{p2} = 1.0,\bar{K} _{y2} = 200.0$$

3 Results and discussion

In the current study nonlinear transient analysis was carried out to identify journal center trajectories, thereon critical mass parameter \(\left( {\bar{M}_{{\rm c}} } \right)\) values for a rigid rotor mounted on a hybrid, finite gas lubricated journal bearings with double-layered porous bushing. Tangential velocity slip in the film at the interface between film and porous region was taken into account. The analysis was carried out assuming isotropic permeability, i.e., \(\overline{K}_{x1} \, = \,\overline{K}_{x2} \, = \,\overline{K}_{z1} \, = \,\overline{K}_{z2} \, = \,1.0\) and \(\sigma_{x} \, = \,\sigma_{z} \, = \,\,\sigma\). In order to incorporate nonzero fluid velocity in film at the porous bearing surface, two independent parameters α and σ are considered. Instances of journal orbit approaching equilibrium position, limit cycle (marginally stable) and unstable journal center trajectories are presented in Fig. 3a–c. The trajectories are obtained for a parameters of L/D = 1.0, H/R = 0.2,\(\bar{P}_{{\rm s}} = 3.0,\) ε0 = 0.6, β = 1.0, α = 0.1, σ = 100 and ˄ = 10.0. Respective mass parameter \(\left( {\bar{M}} \right)\) value is notified in the figure. At a prescribed mass parameter value if the rotor center navigates in a specific orbit, it is considered as a critical mass parameter \(\left( {\bar{M}_{{\rm c}} } \right)\) value.

Fig. 3
figure 3

a Journal center trajectory (Point stable), b journal center trajectory (limit cycle), c journal center trajectory (unstable)

Full size image

Figure 3b shows the journal center trajectory for a critical mass parameter value of 1.198. One can obtain a point stable journal center trajectories for a mass parameter values below the values of critical mass parameter and this is depicted in Fig. 3a. For the values beyond the critical mass parameter, journal center trajectory grows continuously as presented in Fig. 3c. One can obtain critical whirl ratio \(\left( {\lambda_{{\rm c}} } \right)\) using the limit cycle trajectory and the procedure is as follows:

Figure 4a depicts one such limit cycle trajectory with parameters of length to diameter ratio of 1.0, H/R = 0.2, \(\bar{P}_{{\rm s}} = 5.0,\) ε0 = 0.6, β = 1.0, α = 0.1, σ = 100, ˄ = 35.0. The value of critical mass parameter \(\left( {\bar{M}_{{\rm c}} } \right)\) is 2.9035. Corresponding to the limit cycle trajectory, Fig. 4b presents the dimensionless amplitude (both vertical and horizontal) against dimensionless time.

Fig. 4
figure 4

a Limit cycle trajectory of journal center, b non-dimensional vertical and horizontal displacement of journal center verses time. Whirl ratio obtained is 0.712

Full size image

From Fig. 4b, non-dimensional whirling time period is attained as \(\left( {\tau_{P} = \omega t_{P} = 8.82} \right)\). We know that the frequency of whirling can be obtained using \(\omega_{P} = \left( {{\raise0.7ex\hbox{${2\Pi }$} \!\mathord{\left/ {\vphantom {{2\Pi } {t_{P} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t_{P} }$}}} \right)\) and accordingly whirl ratio is obtained as \({\raise0.7ex\hbox{${\omega_{P} }$} \!\mathord{\left/ {\vphantom {{\omega_{P} } \omega }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\omega $}} = \left( {{\raise0.7ex\hbox{${2\Pi }$} \!\mathord{\left/ {\vphantom {{2\Pi } {\tau_{P} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\tau_{P} }$}}} \right) = 0.712.\) Readers are requested to refer Laha et al. [23] for detailed description of the followed procedure.

Form the governing differential Eqs. (1, 2, 5), it is observed that the stability characteristics of the hybrid, finite gas journal bearings with double porous layered bushing can be influenced by several bearing design parameters as well as the slip parameters. Since these bearings are designed to operate at higher speeds, a systematic study was conducted by considering the bearing number \(\left( \Lambda \right)\) as independent variable. The influence of slip parameters, eccentricity ratio, supply pressure and anisotropic permeability on critical mass parameter values is investigated.

3.1 Effect of eccentricity ratio

Because of low viscous and compressible fluid, gas bearings tends to function at high eccentricity ratio even for lesser loads. Figure 5 presents the deviation of critical mass parameter values with speed and eccentricity ratio. The figure indicates that increasing eccentricity ratio increases the critical mass parameter value, from this observation it seems that the bearings operating with higher eccentricity ratio will have better stability. It is also noticed that with increase in speed critical mass parameter value increases for all eccentricity ratio \(\left( \varepsilon \right)\) values.

Fig. 5
figure 5

Effects of eccentricity ratio and speed parameter on critical mass parameter

Full size image

3.2 Effect of slip coefficient (α)

Figure 6 shows the comparison of critical mass parameter values for various values of slip coefficient for a double-layered journal bearing of isotropic permeability. Comparison with no-slip case discloses that slip in the velocity of fluid deteriorates bearing stability. At lower values of slip coefficient, the influence of velocity slip is more prominent and the same can be observed with decreased critical mass parameter values. No significant variation in the values of the critical mass parameter has observed at slip coefficient values (> 0.5) and converges to the no-slip condition values.

Fig. 6
figure 6

Effects of slip coefficient and bearing number (\(\Lambda\)) on critical mass parameter

Full size image

3.3 Effect of σ

Figure 7 presents a comparison plot of critical mass parameter values obtained for an isotropic two-layered porous gas journal bearing for different permeability factor (σ) values. It is ascertained from the figure that for a particular value of σ, the critical mass parameter value increases with an increase in bearing number. At values of σ above 500, the difference in the critical mass parameter values is not significant and approaches to no-slip condition at higher values. Form Figs. 6 and 7, it is observed that both the slip parameters α and σ have similar effect on the bearing stability characteristics.

Fig. 7
figure 7

Variation of critical mass parameter values with bearing number (\(\Lambda\)) for various values of σ

Full size image

Figure 8 demonstrates the pressure distribution of the double-layered porous gas journal bearings at different slip parameter values for the same operating conditions mentioned in Figs. 6 and 7. It is observed that in both the cases, slip in the velocity of fluid reduces the film pressure and it is more prominent for lower values of α and σ.

Fig. 8
figure 8

Pressure distribution along circumferential direction at symmetry plane of bearings with a Sigma variation, b alpha variations

Full size image

3.4 Effect of supply pressure

The effect of higher supply to ambient pressure ratio on the critical mass parameter values is presented in Fig. 9. From the figure, it is seen that for bearing number values (< 6) higher pressure ratio substantially diminishes the critical mass parameter values. However, it is interesting to observe that for bearing number values (> 6) the critical mass parameter values rises with the surge in supply pressure values. At small \(\Lambda\) values, the effect of external pressurization is significant than hydrodynamic pressure and higher pressure ratio in such cases can cause pneumatic hammer [24]. At high bearing number, it seems that the hydrodynamic forces dominate over external pressure and diminish the pneumatic hammer effect which in turn increases the critical mass parameter value.

Fig. 9
figure 9

Variation of critical mass parameter with supply pressure

Full size image

3.5 Effect of anisotropy

Effect of anisotropic permeable porous bushing (\(\overline{K}_{x1} \, = \,\overline{K}_{x2} \, = \,1.0,\,\,\overline{K}_{z1} \, = \,\overline{K}_{z2} \, = \,0.8\)) on the bearing stability is investigated. Figure 10 depicts the comparison of critical mass values obtained for bearing with isotropic and anisotropic permeability conditions. It can be seen that anisotropic permeability condition slightly diminishes the bearing stability. It is also noted that at lower bearing numbers the difference in the values of critical mass parameter is significant and this difference diminishes at higher bearing number values.

Fig. 10
figure 10

Effect of bearing anisotropy on critical mass parameter values

Full size image

Furthermore, the critical mass parameter values obtained based on nonlinear transient were compared with the values realized using linear perturbation analysis [16]. Figure 11 presents the compassion of the critical mass parameter values for the same operating conditions using both the methods. In the linear perturbation analysis, the critical mass parameter values are predicted using the eight linearized fluid film coefficients, whereas in the nonlinear transient analysis the fluid film nonlinearity is considered. Although discrepancy is observed between the two methods of solution, results obtained using nonlinear transient analysis are considered to be more accurate.

Fig. 11
figure 11

Comparison of critical mass parameter values obtained using linear perturbation analysis and nonlinear transient analysis

Full size image

4 Conclusions

Nonlinear transient analyses were performed in order to attain the knowledge on the stability characteristics of a rigid rotor mounted on a hybrid, finite gas lubricated journal bearings with double-layered porous bushing. Reynolds equation is modified to consider velocity slip in the film at the porous bearing surface using Beavers–Joseph boundary condition. Third-order TVD Runge–Kutta scheme was used to solve the governing differential equations at film, porous regions as well as equations of motion. The onset of instability is represented by critical mass parameter \(\left( {\bar{M}_{{\rm c}} } \right)\). Deviation of \(\bar{M}_{{\rm c}}\) with respect to the bearing number (\(\Lambda\)) for various values of eccentricity ratio, slip parameter values and anisotropy has been studied and the following inferences are drawn from the results obtained.

  1. 1.

    Critical mass parameter value increases with increases in eccentricity ratio (\(\varepsilon\)) for any bearing number value (\(\Lambda\)), which shows that the bearing operating at higher values of \(\varepsilon\) have better stability.

  2. 2.

    Slip parameters, permeability factor (σ) and slip coefficient (α) deteriorate the bearing stability. From the results, it is observed that under the influence of slip parameters (σ and α) the critical mass parameter value decreases. The effect of slip parameters on the critical mass parameter is more significant at their lower values.

  3. 3.

    Velocity slip in the film at the interface between film and porous region decreases the film pressure.

  4. 4.

    For porous gas bearings operating at high supply to ambient pressure ratio and bearing number, it seems that dominance of hydrodynamic pressure over external supply pressure results in higher critical mass parameter values.

  5. 5.

    Anisotropic permeability reduces the bearing stability and it is significant at lower bearing numbers (\(\Lambda\)).