Keywords

1 Introduction

Merkin et al. in [26] investigated the reaction-diffusion traveling waves that occur in isothermal auto-catalysis chemical system. The researchers proposed that the reactions take place in two regions. These regions are separated and parallel. The quadratic auto-catalysis represents the reaction in region I and is presented by

$$\begin{aligned} A+B \rightarrow 2 B (rate~k_{1} a b), \end{aligned}$$
(1.1)

with the step of the linear decay

$$\begin{aligned} B \rightarrow C (rate~k_{2} b), \end{aligned}$$
(1.2)

where a and b are indicating the concentrations of reactant A and auto-catalyst B, the \(k_{i}(i=1,2)\) are the rate constants and C is some inert product of reaction. The reaction in region II was the quadratic auto-catalytic step (1.1) only. The two regions were considered to be coupled through a linear diffusive interchange of the auto-catalytic species B. In this study we assume a similar kind of system as I, but having cubic auto-catalysis

$$\begin{aligned} A+2B \rightarrow 3 B (rate~k_{3} a b^{2}) \end{aligned}$$
(1.3)

together with a linear decay step

$$\begin{aligned} B \rightarrow C (rate~k_{4} b). \end{aligned}$$
(1.4)

This gives to the system of equations below.

The subsequent nonlinear problem on \(\varsigma >0\) and \(\tau >0\) for the dimensionless concentrations \((\alpha _{1}, \beta _{1})\) in region I and \((\alpha _{2}, \beta _{2})\) in region II of species A and B is considered

$$\begin{aligned} \frac{\partial \alpha _{1}}{\partial \tau } =\frac{\partial ^{2}\alpha _{1}}{\partial \varsigma ^{2}}-\alpha _{1} \beta _{1}^{2}, \end{aligned}$$
(1.5)
$$\begin{aligned} \frac{\partial \beta _{1}}{\partial \tau } = \frac{\partial ^{2}\beta _{1}}{\partial \varsigma ^{2}}+\alpha _{1} \beta _{1}^{2}-k \beta _{1}+ \gamma (\beta _{2}-\beta _{1}), \end{aligned}$$
(1.6)
$$\begin{aligned} \frac{\partial \alpha _{2}}{\partial \tau } = \frac{\partial ^{2}\alpha _{2}}{\partial \varsigma ^{2}}-\alpha _{2} \beta _{2}^{2}, \end{aligned}$$
(1.7)
$$\begin{aligned} \frac{\partial \beta _{2}}{\partial \tau } = \frac{\partial ^{2}\beta _{2}}{\partial \varsigma ^{2}}+\alpha _{2} \beta _{2}^{2}+ \gamma (\beta _{1}-\beta _{2}), \end{aligned}$$
(1.8)

with the boundary conditions

$$\begin{aligned} \alpha _{i}(0, \tau )=\alpha _{i}(L, \tau )=1,~~\beta _{i}(0,\tau )=\beta _{i}(L, \tau )=0. \end{aligned}$$
(1.9)

The dimensionless constants k and \(\gamma \) indicates the strength of the auto-catalyst decay and the coupling between the two regions respectively.

The system of Eqs. (1.5)–(1.8) also studied by [30] for space-fractional derivative. The fractional extension of CIACS is similarly useful and gives very interesting consequences, in this regards one can refer the work on fractional calculus [5, 18, 34, 37, 40]. The main idea of this work is to apply the q-HATM [19] on the CIACS and study the effectiveness and accuracy of this method. The q-HATM is a combination of q-HAM [19] and Laplace transform. Also we modified the work [31, 32] to q-HATM [19]. The convergence of q-HAM and applications of this method on models are studied in details [7, 14,15,16,17, 27].

The present article is organized as follows. The second section describes the basic idea of the standard q-HATM. The third section is devoted to the application of q-HATM to CIACS. The forth section is devoted to the numerical results. In the last section, we summarize the results in the conclusion.

2 Basic Ideas of the q-HATM

Definition 2.1

If \(D^{r}_{\tau }\) is linear differential operator of order r, then the Laplace transform for the fractional derivative \(D^{r}_{\tau }f(\tau )\) is given as

$$\begin{aligned} \mathcal {L}(D^{r}_{\tau }f(\tau )) = s^{r}F(s) - \sum _{k=0}^{r-1}f^{(k)}(0^{+}) s^{r-k-1}, \quad \tau >0, \end{aligned}$$
(2.1)
$$ F(s)=\int _{0}^{\infty } f(\tau ) e^{-s \tau } d\tau . $$

In order to illustrate the basic concepts and the treatment of this method we let \(\mathcal {N}[\alpha (\varsigma ,\tau )] = g(\varsigma ,\tau )\), where \(\mathcal {N}\) represents the nonlinear partial differential operator in general. The Linear operator can be divided into two parts. The first part represents the linear operator of the highest order and indicates by L. The second part represents the reminder parts of the linear operator and indicates by R. So, it can be illustrated as

$$\begin{aligned} L\alpha (\varsigma ,\tau ) + R\alpha (\varsigma ,\tau ) + N\alpha (\varsigma ,\tau ) = g(\varsigma ,\tau ), \end{aligned}$$
(2.2)

where \(N\alpha (\varsigma ,\tau )\) denotes the nonlinear terms. Now, if we let \(L = D^{r}_{\tau }\) and apply the Laplace transform to Eq. (2.2) we obtain

$$\begin{aligned} \mathcal {L}[D^{r}_{\tau }\alpha (\varsigma ,\tau )] + \mathcal {L}[R\alpha (\varsigma ,\tau )] + \mathcal {L}[N\alpha (\varsigma ,\tau )] = \mathcal {L}[g(\varsigma ,\tau )]. \end{aligned}$$
(2.3)

Making use of (2.1) we then have

$$\begin{aligned} \mathcal {L}[\alpha (\varsigma ,\tau )] - \frac{1}{s} \sum _{i=0}^{r-1}\alpha ^{(i)}(\varsigma ,0) s^{-i-1} + \frac{1}{s}\mathcal {L}[R\alpha (\varsigma ,\tau ) + N\alpha (\varsigma ,\tau ) - g(\varsigma ,\tau )] = 0. \end{aligned}$$
(2.4)

We express a nonlinear operator as

$$\begin{aligned} \begin{aligned} \mathcal {N}[\phi (\varsigma ,\tau ,q)]&=\mathcal {L}[\phi (\varsigma ,\tau ;q)] - \frac{1}{s} \sum _{i=0}^{r-1}\phi ^{(i)}(\varsigma ,0) s^{-i-1} \\&\quad + \frac{1}{s}\mathcal {L}[R(\phi (\varsigma ,\tau ;q)) + N\phi ((\varsigma ,\tau ;q)) - g(\varsigma ,\tau ))], \end{aligned} \end{aligned}$$
(2.5)

In the above expression \(q\in [0,1/n]\) is denoting an embedding parameter and \(\phi (\varsigma ,\tau ;q)\) is a real function of \(\varsigma \), \(\tau \) and q. By modifying the well known concept of homotopy methods Liao [20,21,22,23] constructed the deformation equation of zero order written as

$$\begin{aligned} (1 - n q)\mathcal {L} [\phi (\varsigma ,\tau ;q) - \alpha _{0}(\varsigma ,\tau )] = q h H(\varsigma ,\tau ) \mathcal {N}[\phi (\varsigma ,\tau ;q)], \end{aligned}$$
(2.6)

Here \(h \ne 0\) is an auxiliary parameter, \(H(\varsigma ,\tau ) \ne 0\) is an auxiliary function, \(\alpha _{0}(\varsigma ,\tau )\) is an initial approximation for \(\alpha (\varsigma ,\tau )\) and \(\phi (\varsigma ,\tau ;q)\) is an unknown function. It is obvious that, when \( q = 0\) and \(q = 1/n\), we have

$$\begin{aligned} \phi (\varsigma ,\tau ;0) = \alpha _{0}(\varsigma ,\tau ), \quad \phi (\varsigma ,\tau ;1) = \alpha (\varsigma ,\tau ), \end{aligned}$$
(2.7)

respectively. Therefore, as q increases from 0 to 1/n, then there is a variation in solution \(\phi (\varsigma ,\tau ;q)\) from the initial approximation \(\alpha _{0}(\varsigma ,\tau )\) to the solution \(\alpha (\varsigma ,\tau )\). Writing \(\phi (\varsigma ,\tau ;q)\) in series form by using Taylor theorem about q we get the following result

$$\begin{aligned} \phi (\varsigma ,\tau ;q) = \alpha _{0}(\varsigma ,\tau ) + \sum _{m=1}^{\infty } \alpha _{m}(\varsigma ,\tau )q^{m}, \end{aligned}$$
(2.8)

where

$$\begin{aligned} \alpha _{m}(\varsigma ,\tau ) = \frac{1}{m!}\frac{\partial ^{m}\phi (\varsigma ,\tau ;q)}{\partial q^{m}}\mid _{q=0}. \end{aligned}$$
(2.9)

If various parameters, operators and the initial approximation are properly selected, the series (2.8) converges at \(q=\frac{1}{n}\) and we get

$$\begin{aligned} \alpha (\varsigma ,\tau ) = \alpha _{0}(\varsigma ,\tau ) + \sum _{m=1}^{\infty }\varsigma _{m}(\varsigma ,\tau ) \left( \frac{1}{n}\right) ^{m}. \end{aligned}$$
(2.10)

Let us now define the vectors

$$\begin{aligned} \vec {\alpha }_{m}(\varsigma ,\tau ) = \left\{ {{{\alpha _{0}(\varsigma ,\tau ),\alpha _{1}(\varsigma ,\tau ),\alpha _{2}(\varsigma ,\tau ),\ldots ,\alpha _{m}(\varsigma ,\tau )}}}\right\} . \end{aligned}$$
(2.11)

Now we differentiate the Eq. (2.6) m times with respect to q, then set \(q = 0\) and finally divide them by m!, and we get

$$\begin{aligned} \mathcal {L}[\alpha _{m}(\varsigma ,\tau ) - \mathcal {X}_{m} \alpha _{m-1}(\varsigma ,\tau )] = h H(\varsigma ,\tau ) \mathcal {R}_{m}(\vec {\alpha }_{m-1}(\varsigma ,\tau )). \end{aligned}$$
(2.12)

Here

$$\begin{aligned} \mathcal {R}_{m}(\vec {\alpha }_{m-1}) = \frac{1}{(m-1)!} \frac{\partial ^{m-1} (\mathcal {N}[\phi (\varsigma ,\tau ;q)] ) }{\partial q^{m-1}}|_{q=0} \end{aligned}$$
(2.13)

and

$$ \mathcal {X}_{m} = \left\{ \begin{array}{c l} 0 &{} \text {if}~m\le 1,\\ n &{} \text {if}~m > 1. \end{array} \right. $$

On finding the inverse of Laplace transform of (2.12) we get a power series solution \( \alpha (\varsigma ,\tau ) = \sum _{m=0}^{\infty }\alpha _{m}(\varsigma ,\tau ) (\frac{1}{n})^{m} \) of the original Eq. (2.2).

To determine the interval of convergence of the q-HATM solutions, we use the h-curves. We can obtain the h-curves by plotting the derivative of the q-HATM solutions with respect to \(\tau \) against h and then setting \(\tau =0\). Finally, the horizontal line in the h curve which parallels the \(\varsigma \) axis gives the interval of convergence [21]. However, this procedure cannot determine the optimal value of h. Hence, we use the procedure which has been discussed by [3, 10, 24, 31, 32, 39]. Let

$$\begin{aligned} \triangle (h) = \int _{\Omega } \left( \mathcal {N} (\alpha _{n}(\varsigma ,\tau ) )\right) ^{2} \mathrm {d}\Omega , \end{aligned}$$
(2.14)

which denotes the exact square residual error for Eq. (2.2) integrated over the whole physical region. As \(\triangle (h)\rightarrow 0\), the rate of convergence of the q-HATM solution increases. To obtain the optimal values of the convergence control parameter h, we minimize \(\triangle (h)\) associated with the nonlinear algebraic equation

$$\begin{aligned} \frac{\mathrm {d}\triangle (h)}{\mathrm {d}h}=0. \end{aligned}$$
(2.15)

2.1 Convergence Analysis

To establish the convergence of the solution, we first need to give some conditions needed to prove the convergence of the series (2.10). These have been given by Odibat [29] and Elbeleze et al. [8] and Huseen and El-Tawil [14] via the following theorem:

Theorem 2.1.1

Let the solution components \(\alpha _0, \alpha _1, \alpha _2, \ldots \) be expressed as given in (2.12). The series solution \(\sum _{m=0}^{\infty }\alpha _m (\frac{1}{n})^{m}\) written in (2.10) converges if \(\exists \) \(0< r < n\) s.t. \(||\alpha _{m+1} ||\le (\frac{r}{n})||\alpha _m ||\) for all \(m\ge m_0\), for some \(m_0 \in N\).

Moreover, the estimated error is given by

$$\begin{aligned} ||\alpha -\sum _{m=0}^k \alpha _m (\frac{1}{n})^{m}||\le & {} \frac{1}{1-(\frac{r}{n})}(\frac{r}{n})^{k+1}||\alpha _0||. \end{aligned}$$
(2.16)

3 q-HATM solution of CIACS

In this portion, we apply the q-HATM on CIACS. We take the initial conditions to satisfy the boundary conditions, namely

$$\begin{aligned} \alpha _{i}(\varsigma ,0)=1-\sum _{n=1}^{\infty } a_{ni} \cos (0.5 (L - 2 \varsigma ) \lambda ) \sin (\lambda L/2), (i=1,2), \end{aligned}$$
(3.1)
$$\begin{aligned} \beta _{i}(\varsigma ,0)=\sum _{n=1}^{\infty } b_{ni} \cos (0.5 (L - 2 \varsigma ) \lambda ) \sin (\lambda L/2), (i=1,2), \end{aligned}$$
(3.2)

where \(\lambda =\frac{n \pi }{L}.\) As we know that HAM is based on a particular type of continuous mapping

$$\begin{aligned} \alpha _{i}(\varsigma ,\tau )\rightarrow \phi _{i}(\varsigma ,\tau ;q),\quad \beta _{i}(\varsigma ,\tau )\rightarrow \psi _{i}(\varsigma ,\tau ;q) \end{aligned}$$

such that, as the embedding parameter q increases from 0 to 1/n, \(\phi _{i}(\varsigma ,\tau ;q)\), \(\psi _{i}(\varsigma ,\tau ;q)\) and \(i =1, 2\) varies from the initial iteration to the exact solution.

We now present the nonlinear operators

$$\begin{aligned} {\begin{aligned} \mathcal {N}_{i}(\phi _{i}(\varsigma ,\tau ;q))&= \mathcal {L}_{i}\left( \phi _{i}(\varsigma ,\tau ;q)\right) -\frac{1}{s} \alpha _{i}(\varsigma ,0) \\&\quad +\,\frac{1}{s}\mathcal {L}_{i}\left( -\phi _{i,\varsigma \varsigma }(\varsigma ,\tau ;q)+ \phi _{i}(\varsigma ,\tau ;q) \psi _{i}^{2}(\varsigma ,\tau ;q)\right) ,\\ \mathcal {M}_{i}(\psi _{i}(\varsigma ,\tau ;q))&= \mathcal {L}_{i}\left( \psi _{i}(\varsigma ,\tau ;q)\right) -\frac{1}{s} \beta _{i}(\varsigma ,0) \\&\quad +\,\frac{1}{s}\mathcal {L}_{i}\left( -\psi _{i,\varsigma \varsigma }(\varsigma ,\tau ;q)+(-2(i-1)k+ik) \psi _{i}(\varsigma ,\tau ;q)\right. \\&\quad \left. +\, (-1)^{i}\gamma (\psi _{1}(\varsigma ,\tau ;q)-\psi _{2}(\varsigma ,\tau ;q))-\phi _{i}(\varsigma ,\tau ;q) \psi _{i}^{2}(\varsigma ,\tau ;q)\right) . \end{aligned}} \end{aligned}$$

Now, we develop a set of equations, using the embedding parameter q

$$\begin{aligned} (1-n q) \mathcal {L}_{i} (\phi _{i}(\varsigma ,\tau ;q)-\alpha _{i0}(\varsigma ,\tau ))= q h H(\varsigma ,\tau ) \mathcal {N}_{i}(\phi _{i}(\varsigma ,\tau ;q)), \end{aligned}$$
$$\begin{aligned} (1-n q) \mathcal {L}_{i} (\psi _{i}(\varsigma ,\tau ;q)-\beta _{i0}(\varsigma ,\tau ))= q h H(\varsigma ,\tau ) \mathcal {M}_{i}(\psi _{i}(\varsigma ,\tau ;q)), \end{aligned}$$

with the initial conditions

$$ \phi _{i}(\varsigma ,0;q)= \alpha _{i0}(\varsigma ,0),\quad \psi _{i}(\varsigma ,0;q)= \beta _{i0}(\varsigma ,0), (i=1,2) $$

where \(h\ne 0\) and \(H(\varsigma ,\tau ) \ne 0\) are the auxiliary parameter and the auxiliary function, respectively. We expand \(\phi _{i}(\varsigma ,\tau ;q)\) and \(\psi _{i}(\varsigma ,\tau ;q)\) in series form by employing the Taylor theorem with respect to q, and get

$$\begin{aligned} \phi _{i}(\varsigma ,\tau ;q)=\alpha _{i0}(\varsigma ,\tau )+\sum _{m=1}^{\infty } \alpha _{im}(\varsigma ,\tau ) q^{m}, \end{aligned}$$
(3.3)
$$\begin{aligned} \psi _{i}(\varsigma ,\tau ;q)=\beta _{i0}(\varsigma ,\tau )+\sum _{m=1}^{\infty } \beta _{im}(\varsigma ,\tau ) q^{m}, \end{aligned}$$
(3.4)

where

$$\begin{aligned} \alpha _{im}(\varsigma ,\tau )=\frac{1}{m!}\frac{\partial ^{m}\phi _{i}(\varsigma ,\tau ;q)}{\partial q^{m}}|_{q=0}, \end{aligned}$$
$$\begin{aligned} \beta _{im}(\varsigma ,\tau )=\frac{1}{m!}\frac{\partial ^{m}\psi _{i}(\varsigma ,\tau ;q)}{\partial q^{m}}|_{q=0}. \end{aligned}$$

If we let \(q=\frac{1}{n}\) into (3.3)–(3.4), the series become

$$\begin{aligned} \alpha _{i}(\varsigma ,\tau )=\alpha _{i0}(\varsigma ,\tau )+\sum _{m=1}^{\infty } \alpha _{im}(\varsigma ,\tau )\left( \frac{1}{n}\right) ^{m}, \end{aligned}$$
$$\begin{aligned} \beta _{i}(\varsigma ,\tau )=\beta _{i0}(\varsigma ,\tau )+\sum _{m=1}^{\infty } \beta _{im}(\varsigma ,\tau )\left( \frac{1}{n}\right) ^{m}. \end{aligned}$$

Now, we construct the mth-order deformation equation from (2.12)–(2.13) as follows:

$$\begin{aligned} \mathcal {L}_{i} (\alpha _{im}(\varsigma ,\tau )-\mathcal {X}_{m} \alpha _{i(m-1)}(\varsigma ,\tau ))= h H(\varsigma ,\tau ) R_{1}((\vec {\alpha }_{i(m-1)},\vec {\beta }_{i(m-1)})), \end{aligned}$$
$$\begin{aligned} \mathcal {L}_{i} (\beta _{im}(\varsigma ,\tau )-\mathcal {X}_{m} \beta _{i(m-1)}(\varsigma ,\tau ))= h H(\varsigma ,\tau ) R_{2}((\vec {\alpha }_{i(m-1)},\vec {\beta }_{i(m-1)})), \end{aligned}$$

with initial conditions \(\alpha _{im}(\varsigma ,0)=0,\quad \beta _{im}(\varsigma ,0)=0, m>1\) where

$$\begin{aligned} \begin{aligned} R_{1}((\vec {\alpha }_{i(m-1)},\vec {\beta }_{i(m-1)}))&=\mathcal {L}_{i}\left( \alpha _{i(m-1)}(\varsigma ,\tau )\right) -\frac{1}{s} \alpha _{i}(\varsigma ,0) (1-\frac{\mathcal {X}_{m}}{n}) \\&\quad +\,\frac{1}{s}\mathcal {L}_{i}\left( -\alpha _{i(m-1),\varsigma \varsigma }(\varsigma ,t)+ \alpha _{i (m-1)}(\varsigma ,\tau ) \beta _{i (m-1)}^{2}(\varsigma ,\tau )\right) , \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} R_{2}((\vec {\alpha }_{i(m-1)},\vec {\beta }_{i(m-1)}))&= \mathcal {L}_{i (m-1)}\left( \beta _{i (m-1)}(\varsigma ,\tau )\right) -\frac{1}{s} \beta _{i}(\varsigma ,0) \left( 1-\frac{\mathcal {X}_{m}}{n}\right) \\&\quad +\, \frac{1}{s}\mathcal {L}_{i}\left( -\beta _{i(m-1),\varsigma \varsigma }(\varsigma ,\tau )+(-2(i-1)k+ik) \beta _{i(m-1)}(\varsigma ,\tau )\right. \\&\quad +\, (-1)^{i}\gamma (\beta _{1(m-1)}(\varsigma ,\tau )-\beta _{2(m-1)}(\varsigma ,\tau )) \\&\quad -\,\left. \alpha _{i(m-1)}(\varsigma ,\tau ) \beta _{i(m-1)}^{2}(\varsigma ,\tau ;q)\right) . \end{aligned} \end{aligned}$$

If we take \(\mathcal {L}_{i}=\) Laplace transform (\(i=1,2\)) then the right inverse of \(\mathcal {L}_{i}=\) inverse Laplace transform will be \(\mathcal {L}_{i}^{-1}\)

$$\begin{aligned} \alpha _{im}=\mathcal {X}_{m} \alpha _{i(m-1)}+h \mathcal {L}_{i}^{-1} R_{1}((\vec {\alpha }_{i(m-1)},\vec {\beta }_{i(m-1)})), \end{aligned}$$
(3.5)
$$\begin{aligned} \begin{aligned} \beta _{im}=&\mathcal {X}_{m}\beta _{i(m-1)}+h \mathcal {L}_{i}^{-1} R_{2}((\vec {\alpha }_{i(m-1)},\vec {\beta }_{i(m-1)})). \end{aligned} \end{aligned}$$
(3.6)

4 Numerical Results

In this part, we compute the first approximations. We show the behavior of the solution graphically and investigate the intervals of convergence by the h-curves. Also, we will compute the average residual error. Finally, we will check the accuracy of the q-HATM solutions by comparing with another numerical method using the command NDSolve by Mathematica. We take the initial approximation

$$\begin{aligned} \alpha _{i0}(\varsigma ,\tau )= \alpha _{i0}(\varsigma ,0), \quad \beta _{i0}(\varsigma ,\tau )= \beta _{i0}(\varsigma ,0). \end{aligned}$$
(4.1)

For \(m=1\), we obtain the first approximation as following:

$$\begin{aligned} \alpha _{i1}= & {} h \mathcal {L}_{i}^{-1}\left( \mathcal {L}_{i}\left( \alpha _{i0}(\varsigma ,\tau )\right) -\frac{1}{s} \alpha _{i}(\varsigma ,0)(1-\frac{\mathcal {X}_{m}}{n})\right. \end{aligned}$$
(4.2)
$$\begin{aligned}&\left. +\frac{1}{s}\mathcal {L}_{i}\left( -\alpha _{i0,\varsigma \varsigma }(\varsigma ,\tau )+ \alpha _{i0}(\varsigma ,\tau ) \beta _{i0}^{2}(\varsigma ,\tau )\right) \right) , \end{aligned}$$
(4.3)
$$\begin{aligned} \beta _{i1}= & {} h \mathcal {L}_{i}^{-1}\left( \mathcal {L}_{i}\left( \beta _{i0}(\varsigma ,\tau )\right) -\frac{1}{s} \beta _{i}(\varsigma ,0) (1-\frac{\mathcal {X}_{m}}{n}) \right. \end{aligned}$$
(4.4)
$$\begin{aligned}&+\,\frac{1}{s}\mathcal {L}_{i}\left( -\beta _{i0,\varsigma \varsigma }(\varsigma ,\tau )+(-2(i-1)k+ik) \beta _{i0}(\varsigma ,\tau )\right. \end{aligned}$$
(4.5)
$$\begin{aligned}&\left. \left. +\, (-1)^{i}\gamma (\beta _{10}(\varsigma ,\tau )-\beta _{20}(\varsigma ,\tau ))-\alpha _{i0}(\varsigma ,\tau ) \beta _{i0}^{2}(\varsigma ,\tau ;q)\right) \right) . \end{aligned}$$
(4.6)

And by the similar procedure we can evaluate the rest of the approximation.

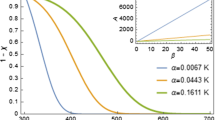
First we show the q-HATM solutions for CIACS for different values of \(\tau \). In Fig. 1 the q-HATM solutions are displayed against \(\varsigma \) for \(n=5\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.08\), \(a_{n_{2}}=0.07\), \(b_{n_{1}}=0.0054\), \(b_{n_{2}}=0.0055\) with \(\tau =0.5, 15, 50.\) From this figure we find that the oscillation produced by the reaction in the system of finite size. And also, we find that, beside the boundaries, the q-HATM solutions are more significant compared the q-HATM solutions far away from the boundaries. The amplitude of the oscillation decays with increasing the distance from the boundaries. These behaviors agree with [4, 6, 9]. It is clear that the symmetric pattern for CIACS with respect to \(\varsigma =L/2\). The two dominant modes generated from the boundaries are travelling towards the center. Thus permanent travelling waves solution exists in systems of finite size with periodic initial conditions and these behaviors agree with [25]. For more details for the effects of other parameters on the behaviors of CIACS see [26, 33].

Fig. 1
figure 1

The q-HATM solutions are displayed against \(\varsigma \) for \(n=5\), \(k=0.01\), \(\gamma =0.4\), \(L=100\), \(a_{n_{1}}=0.08\), \(a_{n_{2}}=0.07\), \(b_{n_{1}}=0.0054\), \(b_{n_{2}}=0.0055.\) Solid line: \(\tau =0.5\), Dash line: \(\tau =15\), and Dot line: \(\tau =50\)

Full size image
Fig. 2
figure 2

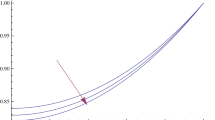
The h-curve of the 5-terms of q-HATM solutions at \(n=1\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(\varsigma =20\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). Solid line \(= \alpha _{1\tau }(\varsigma ,0), \beta _{1\tau }(\varsigma ,0)\), Dash line \(= \alpha _{2\tau }(\varsigma ,0), \beta _{2\tau }(\varsigma ,0)\)

Full size image

4.1 h-Curves

To observe the intervals of convergence of the q-HATM solutions, we draw the h-curves of 5 terms of q-HATM solutions in Figs. 2, 3 and 4 for \(n=1, 5\) and \(n=20\) respectively. In Fig. 2a, we draw \(\alpha _{1\tau }(\varsigma ,0)\), \(\alpha _{2\tau }(\varsigma ,0)\) and in Fig. 2b we draw \(\beta _{1\tau }(\varsigma ,0)\), \(\beta _{2\tau }(\varsigma ,0)\) against h respectively at \(k=0.01\), \(\gamma =0.4\), \(L=100\), \(\varsigma =20\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). From these figures, we note that the straight line that parallels the h-axis provides the valid region of the convergence [21].

Fig. 3
figure 3

The h-curve of the 5-terms of q-HATM solutions at \(n=5\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(\varsigma =20\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002.\) Solid line \(= \alpha _{1\tau }(\varsigma ,0), \beta _{1\tau }(\varsigma ,0)\), Dash line \(= \alpha _{2\tau }(\varsigma ,0), \beta _{2\tau }(\varsigma ,0)\)

Full size image
Fig. 4
figure 4

The h-curve of the 5-terms of q-HATM solutions at \(n=20\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(\varsigma =20\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). Solid line \(= \beta _{1\tau }(\varsigma ,0), \alpha _{1\tau }(\varsigma ,0)\), Dash line \(= \alpha _{2\tau }(\varsigma ,0), \beta _{2\tau }(\varsigma ,0)\)

Full size image

4.2 Average Residual Errors

We notice, however, that h-curve does not give the best value of the parameter h. So, we evaluate the optimal values of the convergence-control parameters by the minimum of the averaged residual errors [1,2,3, 11, 13, 24, 31, 32, 35, 36, 38, 39]

$$\begin{aligned} E_{\alpha _{i}}(h)=\frac{1}{N M} \sum _{s=0}^{N} \sum _{j=0}^{M} \left[ \mathcal {N} \left( \sum _{k=0}^{m}\alpha _{ik}\left( \frac{100 s}{N}, \frac{30 j}{M}\right) \right) \right] ^{2}, \end{aligned}$$
(4.7)
$$\begin{aligned} E_{\beta _{i}}(h)=\frac{1}{N M} \sum _{s=0}^{N} \sum _{j=0}^{M} \left[ \mathcal {M} \left( \sum _{k=0}^{m}\beta _{ik}\left( \frac{100 s}{N}, \frac{30 j}{M}\right) \right) \right] ^{2}, \end{aligned}$$
(4.8)

corresponding to a nonlinear algebraic equations

$$\begin{aligned} \frac{d E_{\alpha _{i}}(h)}{d h}= & {} 0,\end{aligned}$$
(4.9)
$$\begin{aligned} \frac{d E_{\beta _{i}}(h)}{d h}= & {} 0. \end{aligned}$$
(4.10)

We show \( E_{\alpha _{i}}(h)\) and \(E_{\beta _{i}}(h)\) in Figs. 5, 6, 7 and 8 and in Table 1 for different values of n. Figures 3–8 and Table 2 show that the \(E_{\alpha _{i}}(h)\) and \(E_{\beta _{i}}(h)\) for 5 terms q-HATM solutions. We set into (4.9)–(4.10) \(N=100\) and \(M=30\) with \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). We use the command Find Minimum and Minimize of Mathematica and the plotting of residual error against h to get the optimal values h.

Fig. 5
figure 5

The averaged residual errors at the 5-terms of the q-HATM solutions for \(\alpha _{1}(\varsigma ,\tau )\) with \(0\le \varsigma \le 100, 0 \le \tau \le 30\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002.\) a \(n=1\), b \(n=5\), c \(n=20\)

Full size image
Fig. 6
figure 6

The averaged residual errors at the 5-terms of the q-HATM solutions for \(\beta _{1}(\varsigma ,\tau )\) with \(0\le \varsigma \le 100, 0 \le \tau \le 30\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). a \(n=1\), b \(n=5\), c \(n=20\)

Full size image
Fig. 7
figure 7

The averaged residual errors at the 5-terms of the q-HATM solutions for \(\alpha _{2}(\varsigma ,\tau )\) with \(0\le \varsigma \le 100, 0 \le \tau \le 30\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). a \(n=1\), b \(n=5\), c \(n=20\)

Full size image
Fig. 8
figure 8

The averaged residual errors at the 5-terms of the q-HATM solutions for \(\beta _{2}(\varsigma ,\tau )\) with \(0\le \varsigma \le 100, 0 \le \tau \le 30\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). a \(n=1\), b \(n=5\), c \(n=20\)

Full size image
Table 1 Optimal values of h for q-HATM solutions of \(\alpha _{i}(\varsigma ,\tau )\) at \( 0\le \varsigma \le 100, 0\le \tau \le 30\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\)
Full size table
Table 2 Optimal values of h for q-HATM solutions of \(\beta _{i}(\varsigma ,\tau )\) at \( 0\le \varsigma \le 100\), \(0\le \tau \le 30\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\)
Full size table
Fig. 9
figure 9

The comparison of the 5-terms of the q-HATM solutions with numerical method in Mathematica for \(n=5\), \(h_{\alpha _{1}}=-0.30\), \(h_{\beta _{1}}=-0.18\), \(h_{\alpha _{2}}=-0.30\), \(h_{\beta _{2}}=-0.21\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\)

Full size image

4.3 Comparison Analysis

Now, we compare 5-terms of q-HATM solutions obtained with a numerical method using the commands with Mathematica 9 for solving CIACS numerically. We draw the 5-terms of HATM solutions in Fig. 9. Figure 9 shows the comparison of q-HATM solutions with numerical method for \(n=5\), \(k=0.1\), \(\gamma =0.2\), \(L=100\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). We observed from this figure that the QHATM solutions have a good agreement with the results by Mathematica.

Fig. 10
figure 10

The absolute error between the 6-terms of the q-HATM solutions with numerical solutions by (4.11)–(4.14) scheme for a \(\alpha _{1}\), b \(\beta _{1}\), c \(\alpha _{2}\), and d \(\beta _{2}\) with \(h=-1.95\), \(k=0.1\), \(\gamma =0.2\), \(L=1\), \(T=1\), \(\Delta \varsigma =\frac{1}{50}\), \(\Delta \tau =\frac{1}{9000}\), \(a_{n_{1}}=0.001\), \(a_{n_{2}}=0.002\), \(b_{n_{1}}=0.001\), \(b_{n_{2}}=0.002\). Solid line \((n=1)\), Dashed line \((n=5)\)

Full size image

We also compare our results also with finite differences method. We descretise with time step: \(\Delta \tau =\frac{T}{N_{\tau }}\) and in space with grid spacing \(\Delta \varsigma =\frac{L}{N_{\varsigma }}\), and let \(\tau _{j}=j \Delta \tau ,\) where \(0\le j \le N_{\tau }\) and \(\varsigma _{n}=n \Delta \varsigma , 0\le n \le N_{\varsigma }.\) We put \(\alpha _{1, n}^{j}=\alpha _{1}(\varsigma , \tau )\), \(\beta _{1, n}^{j}=\beta _{1}(\varsigma , \tau )\), \(\alpha _{2, n}^{j}=\alpha _{2}(\varsigma , \tau )\) and \(\alpha _{2,n}^{j}=\alpha _{2}(\varsigma , \tau )\). Then the finite differences approximations for (1.5)–(1.8) are given by

$$\begin{aligned} \alpha _{1, n}^{j+1}=(1-2 r)\alpha _{1, n}^{j}+r (\alpha _{1, n+1}^{j}+\alpha _{1, n-1}^{j})-\Delta \tau (\alpha _{1, n}^{j}(\beta _{1, n}^{j})^{2}), \end{aligned}$$
(4.11)
$$\begin{aligned} \begin{aligned} \beta _{1, n}^{j+1}&=(1-2 r)\beta _{1, n}^{j}+r (\beta _{1, n+1}^{j}+\beta _{1, n-1}^{j}) \\&\quad +\,\Delta \tau \left( -k \beta _{1, n}^{j}+\gamma (\beta _{2, n}^{j}-\beta _{1, n}^{j})- (\alpha _{1, n}^{j}(\beta _{1, n}^{j})^{2})\right) , \end{aligned} \end{aligned}$$
(4.12)
$$\begin{aligned} \alpha _{2, n}^{j+1}=(1-2 r)\alpha _{2, n}^{j}+r (\alpha _{2, n+1}^{j}+\alpha _{2, n-1}^{j})-\Delta \tau (\alpha _{2, n}^{j}(\beta _{2, n}^{j})^{2}), \end{aligned}$$
(4.13)
$$\begin{aligned} \begin{aligned} \beta _{1, n}^{j+1}&=(1-2 r)\beta _{1, n}^{j}+r (\beta _{1, n+1}^{j}+\beta _{1, n-1}^{j})-\beta _{1, n}^{j})\\&\quad +\,\gamma (\beta _{1, n}^{j}-\beta _{2, n}^{j})-\Delta \tau (\alpha _{1, n}^{j}(\beta _{1, n}^{j})^{2}), \end{aligned} \end{aligned}$$
(4.14)

where \(r=\frac{\Delta \tau }{(\Delta \varsigma )^{2}}\). We mention that here we use the central difference scheme for the space derivatives of second order and the forward difference scheme for the time derivative of order one [28]. The initial and boundary conditions become

$$\alpha _{i, n}^{0}=\alpha _{i}(\varsigma (n))=\alpha _{i, n}, \beta _{i, n}^{0}=\beta _{i}(\varsigma (n))=\beta _{i, n}, \quad i=1, 2, \quad n=0,1,2, \ldots , N_{\varsigma },$$
$$\alpha _{i, 0}^{j}=1=\alpha _{i, N}^{j}, \beta _{i, 0}^{j}=0=\beta _{i, N}^{j}, i=1,2, j=1,2,\ldots , N_{\tau }.$$

Stable solutions with the (4.11)–(4.14) scheme are only obtained if \(r<\frac{1}{2}.\) See, e.g., [12, 28] for a proof that this condition gives the stability limit for the (4.11)–(4.14) scheme. In Fig. 10, the absolute error between the q-HATM solutions and the numerical solutions by the (4.11)–(4.14) scheme are plotted. Also, in this figure we show that the effect of the factor \(\frac{1}{n}\) on the accelerate of the convergence. It is clear when n is increasing, the absolute error is decreasing.

5 Conclusion

In this paper, the q-HATM was employed to analytically compute approximate solutions of CIACS. By comparing q-HATM solutions with results by Mathimatica, the averaged residual error the residual error and finite difference method were found an excellent agreement. Also the effected on the accelerating of the convergence by the factor \(\frac{1}{n}\) is shown. Mathematica was used for the computations of this article.