1 Introduction

The theory of fractional derivatives and integral operators has attracted a great attention of scientists due to its wide uses and importance in mathematics, physics, biology, economics and finance. The mathematical models, coupled equations, linear and nonlinear equations having initial and boundary conditions, applied in various fields and technologies, can extend and describe more general through the fractional calculus [1–8]. An excellent literature and hereditary properties involving fractional operators for differential and integral equations concerning fractional calculus were reported by number of researchers [9–16]. The Rosenau–Hyman equation occurs in formation of patterns in liquid drops having compaction solutions was discovered by Rosenau and Hyman [17]. The compactons studies of the Rosenau–Hyman equation play effective role in applied sciences and mathematical physics [18–23]. Recently, the fractional Rosenau–Hyman equation is studied by Molliq and Noorani by using VIM and HPM [24]. These techniques have some shortcomings such as small convergence region, strongly depend on Lagrange’s multiplier, correctional functional, calculating integrals appear in VIM and small/large parameters assumptions mentioned in HPM.

In this work, numerical simulation of the time-fractional Rosenau–Hyman equation is conducted with the application of q-homotopy analysis transform technique (q-HATT) and reduced differential transform technique. The q-HATT is a graceful combination of q-HAM and Laplace transform, which provides multiple approximate solutions. The q-HAM proposed by El-Tavil and Huseen [25, 26] is a generalized form of homotopy analysis scheme firstly discovered by Liao [27, 28] and homotopy perturbation approach firstly given by He [29–31]. In recent years, semi-analytical techniques have also been coupled with Laplace transform algorithm such as Laplace decomposition technique [32], homotopy perturbation transform technique [33–35] and homotopy analysis transform technique [36–38] to analyze integer and fractional differential equations describing real-word problems arising in scientific and technological areas.

The q-HATT gives us with a straightforward way to insure the convergence of series solution with the help of the auxiliary parameter ħ, the embedding parameter \(q \in \left[ {0,\frac{1}{n}} \right]\,\,\,(n \ge 1),\) asymptotic parameter n, auxiliary function H(x, t) and the initial guess u 0(x, t) to find the series solution in more general form. On the other hand, we illustrate the reduced differential transform technique (RDTT) [39–41] to examine the time-fractional Rosenau–Hyman equation with small size computational work and provide rapidly convergent series solution. The proposed schemes can be performed very easily (free from any assumption or calculating integrals), uniformly valid in nonlinear equations for small/large parameters. The outline of the present article is as follows: In Sect. 2, the definition of Caputo fractional derivative and its Laplace transform formula are discussed. In Sect. 3, the basic idea of q-HATT is presented. Section 4 contains the basic idea of RDTT. In Sect. 5, implementation of q-HATT on time-fractional Rosenau–Hyman equation is discussed. In Sect. 6, RDTT is applied on time-fractional Rosenau–Hyman equation. Numerical results and discussion for time-fractional Rosenau–Hyman equation are presented in Sect. 7. Finally, Sect. 8 is dedicated to conclusions.

2 Preliminaries

Here, we present the basic definition and properties of fractional ordered derivatives.

Definition 2.1

If f (t) be a function of t, then the fractional ordered derivative in terms of Caputo [42] is defined and expressed as:

$$D_{t}^{\alpha } f(t) = J^{n - \alpha } D_{t}^{n} f(t) = \frac{1}{\varGamma (n - \alpha )}\int\limits_{0}^{t} {(t - \tau )^{n - \alpha - 1} } f^{n} (\tau ){\text{d}}\tau ,$$
(1)

for \(n - 1 < \alpha \le n,\,\,n \in N,\,\,t > 0.\)

Definition 2.2

If \(D_{t}^{\alpha } f(t)\) is the Caputo derivative of the function f(t), then its Laplace transform is presented as [42, 43]

$$L\left[ {D_{t}^{\alpha } f(t)} \right] = s^{\alpha } L\left[ {f(t)} \right] - \sum\limits_{r = 0}^{n - 1} {s^{\alpha - r - 1} } f^{\left( r \right)} (0^{ + } ),\quad \,n - 1 < \alpha \le n.$$
(2)

3 Basic idea of q-HATT

To demonstrate the basic plan and solution procedure of this approach, we take a fractional nonlinear differential equation written as:

$$D_{t}^{\alpha } {\kern 1pt} {\kern 1pt} u(x,t) + R{\kern 1pt} {\kern 1pt} u(x,t) + N{\kern 1pt} u(x,t) = g(x,t),\quad \,n - 1 < \alpha \le n.$$
(3)

In the fractional Eq. (3), \(D_{t}^{\alpha } u(x,t)\) is indicating the fractional derivative of the function u(x, t) defined by Caputo, R is denoting the linear differential operator, N is representing the general nonlinear differential operator and g(x, t) is representing a function arising from the source.

By putting up the application of Laplace transform on fractional Eq. (3), we have

$$L{\kern 1pt} \left[ {D_{t}^{\alpha } u} \right] + L[Ru] + L{\kern 1pt} [N{\kern 1pt} u] = L[g(x,t)].$$
(4)

By employing the differentiation formula of the Laplace transform, it gives

$$s^{\alpha } L[u] - \sum\limits_{k = 0}^{n - 1} {s^{\alpha - k - 1} u^{(k)} (x,0)} + L{\kern 1pt} [R{\kern 1pt} u] + L[Nu] = L[g(x,t)].$$
(5)

On simplifying, we get the following result:

$$L[u] - \frac{1}{{s^{\alpha } }}\sum\limits_{k = 0}^{n - 1} {s^{\alpha - k - 1} u^{(k)} (x,0)} + \frac{1}{{s^{\alpha } }}\left[ {L[Ru] + {\kern 1pt} L[Nu] - L[g(x,t)]} \right] = 0.$$
(6)

According to HAM, the nonlinear operator is presented as:

$$\begin{aligned} N[\phi (x,t;q)] & = L[\phi (x,t;q)] - \frac{1}{{s^{\alpha } }}\sum\limits_{k = 0}^{n - 1} {s^{\alpha - k - 1} \phi^{(k)} (x,t;q)(0^{ + } )} \\ & \quad + \frac{1}{{s^{\alpha } }}\left[ {L{\kern 1pt} [R\phi (x,t;q)] + L[N\phi (x,t;q)] - L[g(x,t)]} \right]. \\ \end{aligned}$$
(7)

In Eq. (7) \(q \in [0,\,1/n]\), and \(\phi (x,\,t{\kern 1pt} {\kern 1pt} ;q)\) is indicating a real function of x, t and q. In view of well-known HAM, the homotopy is constructed in the following manner:

$$(1 - nq)L[\phi (x,t{\kern 1pt} ;q) - u_{0} (x,t)] = \hbar qH(x,t)N[u(x,t)].$$
(8)

In Eq. (8), L is denoting the Laplace transform operator, \(n \ge 1,\,q \in \left[ {0,\frac{1}{n}} \right]\) is known as the embedding parameter, H(x, t) indicates a nonzero auxiliary function, ħ ≠ 0 is an auxiliary parameter and u 0(x, t) is an initial guess of u(x, t). It is clear that, when the embedding parameter q = 0 and \(q = \frac{1}{n},\) it gives

$$\phi (x,t;0) = u_{0} (x,t),\quad \phi \left( {x,t;\frac{1}{n}} \right) = u(x,t),$$
(9)

respectively. Hence, as q increases from 0 to \(\frac{1}{n}\), the solution \(\phi (x,t{\kern 1pt} {\kern 1pt} ;q)\) varies from the initial guess u 0(x, t) to the solution u(x, t) of the nonlinear fractional differential equation. On expanding the function \(\phi (x,t{\kern 1pt} {\kern 1pt} ;q)\) in series form by using Taylor’s formula about q, we have

$$\phi (x,t{\kern 1pt} ;q) = u_{0} (x,t) + \sum\limits_{m = 1}^{\infty } {u_{m} (x,t)q^{m} } ,$$
(10)

where

$$u_{m} (x,t) = \frac{1}{m!}\frac{{\partial^{m} \phi (x,t;q)}}{{\partial q^{m} }}\left| {_{q = 0} .} \right.$$
(11)

If the values of u 0(x, t), n, ħ and H(x, t) are selected in a proper manner, the series (10) converges at \(q = \frac{1}{n}\), and then, we get

$$u(x,t) = u_{0} (x,t) + \sum\limits_{m = 1}^{\infty } {u_{m} (x,t)\left( {\frac{1}{n}} \right)}^{m} .$$
(12)

Equation (12) must be one of the solutions of the nonlinear Eq. (3). Using definition (12), the governing equation can be derived from the deformation equation of zero order (8).

Now, we define the vectors as

$$\vec{u}_{m} = \{ u_{0} (x,t),u_{1} (x,t), \ldots ,u_{m} (x,t)\} .$$
(13)

Next on differentiating the zeroth-order deformation Eq. (8) m-times with respect to q and then dividing them by m! and finally putting q = 0, we arrive at the following mth-order deformation equation:

$$L[u_{m} (x,t) - k_{m} u_{m - 1} (x,t)] = \hbar H(x,t)\Re_{m} (\vec{u}_{m - 1} ).$$
(14)

Using the inverse Laplace transform in Eq. (14), it gives

$$u_{m} (x,t) = k_{m} u_{m - 1} (x,t) + \hbar L^{ - 1} [H(x,t)\Re_{m} (\vec{u}_{m - 1} )].$$
(15)

In the above Eq. (15), the values of \(\Re_{m} (\vec{u}_{m - 1} )\) and k m are presented as:

$$\Re_{m} (\vec{u}_{m - 1} ) = \frac{1}{(m - 1)!}\frac{{\partial^{m - 1} N[\phi (x,t;q)]}}{{\partial q^{m - 1} }}\left| {_{q = 0} ,} \right.$$
(16)

and

$$k_{m} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {m \le 1} \hfill \\ {n,} \hfill & {m > 1} \hfill \\ \end{array} ,} \right.$$
(17)

respectively.

4 Reduced differential transform technique (RDTT)

To demonstrate the basic solution procedure of RDTT, we take a function p(x, t) and consider that it can be expressed as a product of two single variable functions, i.e., \(p(x,t) = \delta (i)\eta (j)\). On the basis of the properties of the one-dimensional differential transform, the function p(x, t) can be defined as:

$$p(x,t) = \sum\limits_{i = 0}^{\infty } {\delta (i)} x^{i} \sum\limits_{j = 0}^{\infty } {\eta (j)} t^{j} = \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {P(i,j)x^{i} t^{j} } } ,$$
(18)

where \(P(i,j) = \delta (i)\eta (j)\) is the spectrum of p(x, t).

Let R D indicates the reduced differential transform operator and \(R_{D}^{ - 1}\) the inverse reduced differential transform operator [39]. The basic definitions and operations of the reduced differential transform are as follows.

Definition 4.1

If p(x, t) is analytical and continuously differentiable about the space variable x and time variable t in the domain of interest, then the t-dimensional spectrum function

$$P_{k} (x) = \frac{1}{\varGamma (k\alpha + 1)}\left[ {\frac{{\partial^{k} }}{{\partial t^{k} }}p(x,t)} \right]_{{t = t_{0} }} ,$$
(19)

is the fractional reduced transformed function of p(x, t), where α is a parameter which describes the order of time-fractional derivatives. The differential inverse transform of P k (x) is demonstrated in the following way

$$p(x,t) = \sum\limits_{k = 0}^{\infty } {W_{k} (x)(t - t_{0} )^{k\alpha } } .$$
(20)

On comparing Eqs. (19) and (20), it can be observed that

$$p(x,t) = \sum\limits_{k = 0}^{\infty } {\frac{1}{\varGamma (k\alpha + 1)}} \left[ {\frac{{\partial^{k} }}{{\partial t^{k} }}p(x,t)} \right]_{{t = t_{0} }} (t - t_{0} )^{k\alpha } .$$
(21)

If we set t = 0, Eq. (13) is reduced to

$$p(x,t) = \sum\limits_{k = 0}^{\infty } {\frac{1}{\varGamma (k\alpha + 1)}} \left[ {\frac{{\partial^{k} }}{{\partial t^{k} }}p(x,t)} \right]_{{t = t_{0} }} t^{k\alpha } .$$
(22)

From the above definition, it can be observed that the idea of the fractional reduced differential transform is obtained from the power series expansion of a function.

Definition 4.2

If \(u(x,t) = R_{D}^{ - 1} [U_{k} (x)],v(x,t) = R_{D}^{ - 1} [V_{k} (x)]\) and the convolution Θ indicates the fractional reduced differential transform version of the multiplication, then the fundamental operations of the fractional reduced differential transform are expressed in Table 1.

Table 1 Fundamental operations of the fractional reduced differential transform technique
Full size table

5 Implementation of q-HATT

Here we show the efficiency and applicability of q-HATT for examining the time-fractional Rosenau–Hyman equation which is characterized as

$$\frac{{\partial^{\alpha } u}}{{\partial t^{\alpha } }} = u\frac{{\partial^{3} u}}{{\partial x^{3} }} + u\frac{\partial u}{\partial x} + 3\frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }},\quad \,t > 0,\quad 0 < \alpha \le 1.$$
(23)

with the initial condition

$$u(x,0) = - \frac{8}{3}c\cos^{2} \left( {\frac{x}{4}} \right).$$
(24)

Here, u = u(x, t) is the function of space coordinate x and time t, c is arbitrary constant. The time-fractional Rosenau–Hyman equation occurs in the investigation of nonlinear dispersion in the formation of patterns in liquid drops [17].

To solve Eqs. (23) and (24), we apply the Laplace transform along with the initial condition, and it gives

$$L\left[ {u(x,t)} \right] - \frac{1}{s}\left( { - \frac{8}{3}c\cos^{2} \left( {\frac{x}{4}} \right)} \right) - \frac{1}{{s^{\alpha } }}L\left[ {u\frac{{\partial^{3} u}}{{\partial x^{3} }} + u\frac{\partial u}{\partial x} + 3\frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right] = 0.$$
(25)

The nonlinear operator is

$$\begin{aligned} N\left[ {\phi (x,t;q)} \right] & = L\left[ {\phi (x,t;q)} \right] - \frac{1}{s}\left( { - \frac{8}{3}c\cos^{2} \left( {\frac{x}{4}} \right)} \right) - \frac{1}{{s^{\alpha } }}L\left[ {\phi (x,t;q)\frac{{\partial^{3} \phi (x,t;q)}}{{\partial x^{3} }}} \right. \\ & \left. {\quad + \,\phi (x,t;q)\frac{\partial \phi (x,t;q)}{\partial x} + 3\frac{\partial \phi (x,t;q)}{\partial x}\frac{{\partial^{2} \phi (x,t;q)}}{{\partial x^{2} }}} \right], \\ \end{aligned}$$
(26)

and thus

$$\begin{aligned} \Re_{m} (\vec{u}_{m - 1} ) & = L(u_{m - 1} ) + \frac{1}{s}\left( {1 - \frac{{k_{m} }}{n}} \right)\frac{8}{3}c\cos^{2} \left( {\frac{x}{4}} \right) - \frac{1}{{s^{\alpha } }}L\left[ {\sum\limits_{r = 0}^{m - 1} {u_{r} \frac{{\partial^{3} u_{m - 1 - r} }}{{\partial x^{3} }}} } \right. \\ & \quad \left. { + \sum\limits_{r = 0}^{m - 1} {u_{r} \frac{{\partial u_{m - 1 - r} }}{\partial x}} + 3\sum\limits_{r = 0}^{m - 1} {\frac{{\partial u_{r} }}{\partial x}\frac{{\partial^{2} u_{m - 1 - r} }}{{\partial x^{2} }}} } \right] \\ \end{aligned}$$
(27)

The deformation equation of mth-order is given by:

$$L\left[ {u_{m} (x,t) - k_{m} u_{m - 1} (x,t)} \right] = \hbar \Re_{m} (\vec{u}_{m - 1} ).$$
(28)

Using the inverse of Laplace transform operator on above equation, we get the following result

$$u_{m} (x,t) = k_{m} u_{m - 1} (x,t) + \hbar L^{ - 1} \left[ {\Re_{m} (\vec{u}_{m - 1} )} \right].$$
(29)

On solving Eq. (29), it yields

$$\begin{aligned} u_{0} (x,t) & = - \frac{8}{3}c\cos^{2} \left( {\frac{x}{4}} \right) \\ u_{1} (x,t) & = \frac{2}{3}\hbar c^{2} \sin \left( {\frac{x}{2}} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}, \\ u_{2} (x,t) & = \frac{2}{3}\hbar \left( {\hbar + n} \right)c^{2} \sin \left( {\frac{x}{2}} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \frac{1}{3}\hbar^{2} c^{3} \cos \left( {\frac{x}{2}} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}}, \\ u_{3} (x,t) & = \frac{2}{3}\hbar \left( {\hbar + n} \right)^{2} c^{2} \sin \left( {\frac{x}{2}} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \frac{2}{3}\hbar^{2} (\hbar + n)c^{3} \cos \left( {\frac{x}{2}} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} \\ & \quad - \frac{1}{6}\hbar^{3} c^{4} \sin \left( {\frac{x}{2}} \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}}, \\ u_{4} (x,t) & = \left( {\hbar + n} \right)u_{3} (x,t) + \hbar^{2} (\hbar + n)^{2} c^{3} \cos \left( {\frac{x}{2}} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} - \frac{1}{3}\hbar^{3} (\hbar + n)c^{4} \sin \left( {\frac{x}{2}} \right)\frac{{t^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} \\ & \quad - \frac{1}{12}\hbar^{4} c^{5} \cos \left( {\frac{x}{2}} \right)\frac{{t^{4\alpha } }}{{\varGamma \left( {4\alpha + 1} \right)}}, \\ \end{aligned}$$
(30)

Using the same way, the remaining of the components u m (x, t) for m > 4 can be obtained, and the series expansion is given as:

$$u(x,t) = u_{0} (x,t) + \sum\limits_{m = 1}^{\infty } {u_{m} (x,t)} \left( {\frac{1}{n}} \right)^{m} ,$$
(31)

Equation (31) represents the family of q-HATT series solutions for Eq. (23). The expansion of q-HATT series solution (31) directly converges to HAM when n = 1 and RDTT, HPM, VIM solution series by putting n = 1 and ħ = −1. If we set ħ = −1, n = 1 and α = 1 in \(\sum\nolimits_{m = 0}^{N} {u_{m} (x,t)} \left( {\frac{1}{n}} \right)^{m}\) when N → ∞, it converges to the standard exact solution given as [44]

$$u(x,t) = - \frac{8}{3}c\cos^{2} \left( {\frac{1}{4}(x - ct)} \right),\quad \left| {x - ct} \right| \le 2\pi ,$$
(32)

where c indicates the arbitrary constant [17].

6 Implementation of RDTT

Here, we illustrate RDTT for examining the time-fractional Rosenau–Hyman equation (23) with initial condition (24)

By the application of RDTT to Eq. (23), we get the following recurrence relation:

$$\frac{\varGamma (m\alpha + \alpha + 1)}{\varGamma (m\alpha + 1)}U_{m + 1} (x) = \sum\limits_{r = 0}^{m} {U_{r} \frac{{\partial^{3} U_{m - r} }}{{\partial x^{3} }}} + \sum\limits_{r = 0}^{m} {U_{r} \frac{{\partial U_{m - r} }}{\partial x}} + 3\sum\limits_{r = 0}^{m} {\frac{{\partial U_{r} }}{\partial x}\frac{{\partial^{2} U_{m - r} }}{{\partial x^{2} }}} .$$
(33)

Using the RDTT to the initial condition (24), we get

$$U_{0} (x) = - \frac{8}{3}c\cos^{2} \left( {\frac{x}{4}} \right).$$
(34)

Using Eq. (34) in Eq. (33), we obtain the following values of U m (x), for m = 1, 2, 3, …, as

$$\begin{aligned} U_{1} (x) & = - \frac{2}{3}c^{2} \sin \left( {\frac{x}{2}} \right)\frac{1}{{\varGamma \left( {\alpha + 1} \right)}},\quad U_{2} (x) = \frac{1}{3}c^{3} \cos \left( {\frac{x}{2}} \right)\frac{1}{{\varGamma \left( {2\alpha + 1} \right)}}, \\ U_{3} (x) & = \frac{1}{6}c^{4} \sin \left( {\frac{x}{2}} \right)\frac{1}{{\varGamma \left( {3\alpha + 1} \right)}},\quad U_{4} (x) = - \frac{1}{12}c^{5} \cos \left( {\frac{x}{2}} \right)\frac{1}{{\varGamma \left( {4\alpha + 1} \right)}}, \\ & \,\,\,\,\,\, \vdots \\ \end{aligned}$$
(35)

Using the above way, the rest of the components can be found, and using the differential inverse reduced transform of U m (x), m = 1, 2, 3, …, we get

$$u(x,t) = \sum\limits_{m = 0}^{\infty } {U_{m} (x)t^{m\alpha } } = U_{0} (x) + U_{1} (x)t^{\alpha } + U_{2} (x)t^{2\alpha } + U_{3} (x)t^{3\alpha } + \cdots ,$$
(36)

which converges to the standard exact solution given as below [44]:

$$u(x,t) = - \frac{8}{3}c\cos^{2} \left( {\frac{1}{4}(x - ct)} \right),\quad \left| {x - ct} \right| \le 2\pi ,$$
(37)

where c represents the arbitrary constant [17].

This is the same solution series obtained by q-HATT, at ħ = −1, n = 1. We observe that the reduced differential transform technique is very easier to implement and requires less computational work for convergent solution series. The maple package is used for graphical representation of q-HATT solution series and RDTT (q-HATT, ħ = −1, n = 1) solution series of time-fractional Rosenau–Hyman equation.

7 Results and discussion

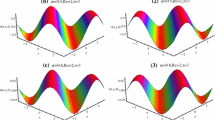
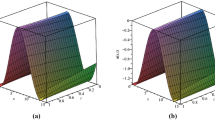
In this part of the article, we enumerate the results found by using q-HATT and RDTT. The multiple graphical surface solutions of Eq. (23) are depicted in Fig. 1. In Fig. 1a–c, we can observe that the results obtained with aid of q-HATT and RDTT are in an excellent agreement with the exact solution. Figure 2 depicts the relation between approximate solution u(x, t) and time t for distinct values of α. In Fig. 2, it is to be noted that the value of α significantly affects the displacement. Figure 3a–d represents ħ- and n-curves. The value of ħ is selected, corresponding to arbitrary n(n ≥ 1) from the convergence range. From Fig. 3a–d, we can notice from ħ- and asymptotic n-curves that q-HATT have great efficiency and accuracy and gives convergent solution series at large admissible domain. We can observe from ħ-curves that the convergence range is directly proportional to n

Fig. 1
figure 1

Fourth-order family of approximate q-HATT (for ħ = −1 and n = 1) and RDTT solution u(x, t) of Eq. (23) versus x and time t at c = 0.5 and α = 1: a exact solution; b approximate solution; c absolute error E 4(u) = |u ex − u app|

Full size image
Fig. 2
figure 2

Fourth-order approximate q-HATT (for ħ = −1 and n = 1) and RDTT solution u(x, t) versus time t for Eq. (23) at x = 20 and c = 0.5 for various values of α

Full size image
Fig. 3
figure 3

ħ- and asymptotic n-curves show the comparative study at x = 20 and c = 0.5 for fourth-order approximation q-HATT solutions of Eq. (23): a ħ-curve at n = 1 and t = 0.05 for different values of α; b ħ-curve at n = 10 and t = 0.05 for different order approximation; c ħ-curve at n = 200 and t = 0.05 for different order approximation; d asymptotic n-curves, at (ħ, t) = (−1, 0.05) for distinct values of α

Full size image

8 Conclusions

In this paper, q-HATT is used for numerical simulation of the time-fractional Rosenau–Hyman equation at large admissible domain compared to VIM, HPM [24] and RDTT. The ħ- and asymptotic n-curves show the validity of q-HATT for infinitely many acceptable q-HATT solutions and the middle point of ħ-curve interval, i.e., ħ = −n is a suitable choice, at this point the numerical solution converges to the exact solution. The application of RDTT tool to solve time-fractional Rosenau–Hyman equation in efficient way is demonstrated. Moreover, the computational work contained in RDTT tool is very small, simple and attractive. Thus, it can be concluded that the both q-HATT and RDTT are highly efficient and user friendly to investigate nonlinear fractional differential equations.