Analytical Approach to Fractional Navier–Stokes Equations by Iterative Laplace Transform Method

Abstract

In this paper, we have presented iterative Laplace transform scheme to examine fractional Navier–Stokes equations in cylindrical coordinates with initial conditions. The arbitrary ordered derivatives are described in terms of Caputo. By utilizing only the initial conditions, the analytical expressions are derived in the closed form. The results achieved with the aid of the proposed technique are graphically presented.

1 Introduction

The fractional calculus has become a strong mechanism for finding the solutions of many problems pertaining to control engineering, physics, signal processing, mathematical biology, viscoelasticity, electromagnetism, and mathematical physics and other areas of sciences as well as technology. Several methods can be found in the literature to derive the solution of fractional order differential equation such as ADM [12], HAM [14], HPM [5], Homotopy perturbation transform method (HPTM) [9, 10, 19] and fractional Laplace Adomian decomposition method (FLADM) [7], LPM [20], LHAM [21]  and so on. The above mentioned techniques provide immediate and easily seen symbolic terms of numerical approximate solutions as well as of analytical solutions to both linear and nonlinear fractional differential equations.

In 2006, Daftardar-Gejji and Jafari introduced the iterative technique for examining numerically to non-linear functional equations [4, 6, 7]. Since then the iterative approach is being used to find the solution of several non-linear differential equations of arbitrary order [1] and viewing fractional BVP [3]. Recently, Jafari et al. has made elegant use of Laplace transform in this iterative method and it became a popular method known as iterative Laplace transform method (ILTM) [8] to examine a system of partial differential equations of fractional order, Fokker–Plank equation [18] as well. In recent, time-fractional Schrödinger equations [15], fractional heat and wave-like equation [16] and fractional Telegraph equations [17] are solved successfully by the use of ILTM.

In the present study, we consider the time-fractional Navier–Stokes equation having initial condition in cylindrical coordinate and are expressed in operator form as

$$ D_{t}^{\alpha } u(r,t) = P + v\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right),u(r,o) = f(r),\quad 0 < \alpha \le 1 $$

(1.1)

where $D_{t}^{\alpha } u(r,t)$ indicates the Caputo fractional derivative of order $\alpha \,,$ $P = - \frac{\partial p}{\rho \partial z},\,u$ indicates the velocity, $\rho$ is the pressure, $v$ is the kinematics viscosity, t is the time and $\alpha$ is a parameter representing the order of the time–fractional derivatives. In particular for $\alpha = 1,$ the fractional Navier–Stokes Eq. (1.1) reduces to the standard Navier–Stokes equation.

The main object of this paper, we shall extend the application of Iterative Laplace transform algorithm to derive the solution of the time-fractional Navier–Stokes equations.

2 Some Basic Definitions

In this portion, we list certain basic definitions of fractional calculus along with elegant properties of Laplace transform.

Definition 1

The Caputo derivative of arbitrary order [2] of function $u(r,t)\,$ is presented as

$$ \begin{aligned} D_{t}^{\alpha } u(r,t) & = \frac{1}{{\Gamma (m - \alpha )}}\;\int\limits_{0}^{t} {(t - \eta )^{m - \alpha - 1} } u^{(m)} (r,\eta )d\eta ,\quad m - 1 < \alpha \le m,m \in N, \\ & = J_{t}^{m - \alpha } D^{m} u\left( {r,t} \right). \\ \end{aligned} $$

(2.1)

Here $D^{m} \equiv \frac{{d^{m} }}{{dt^{m} }}$ and $J_{t}^{\alpha }$ indicates the Riemann-Liouville integral operator of fractional order $\alpha > 0$, presented as [11]

$$ J_{t}^{\alpha } u\left( {r,t} \right) = \frac{1}{{\Gamma \left( \alpha \right)}}\int\limits_{0}^{t} {\left( {t - \eta } \right)^{\alpha - 1} u\left( {r,\eta } \right)d\eta } ,\;\eta > 0,\left( {m - 1 < \alpha \le m} \right),m \in N. $$

(2.2)

Definition 2

The Laplace transform of $f(t)\,,\,\,t > 0$ is expressed as [11, 13]

$$ L[f(t)] = F(t) = \int\limits_{0}^{\infty } {e^{ - st} } f(t)dt. $$

(2.3)

Definition 3

The Laplace transform of $D_{t}^{\alpha } u(r,t)$ is presented in following manner [11, 13]

$$ L[D_{t}^{\alpha } u\;(r,t)] = L[u(r,t)] - \sum\limits_{k = o}^{m - 1} {u^{k} (r,0)} \,s^{\alpha - k - 1} ,\,m - 1 < \alpha \le m,m \in N, $$

(2.4)

3 Basic Idea of ILTM

To explain the basic idea of iterative Laplace transform approach [8], we take the subsequent fractional non-linear partial differential equation having the prescribed initial conditions can be expressed in the form of an operator as

$$ D_{t}^{\alpha } {\kern 1pt} {\kern 1pt} u(r,t) + R{\kern 1pt} {\kern 1pt} u(r,t) + N{\kern 1pt} {\kern 1pt} u(r,t) = g(r,t),\quad m - 1 < \alpha \le m,\quad m \in N, $$

(3.1)

$$ u^{\left( k \right)} (r,0) = h_{k} (r),\quad k = 0,1,2, \ldots ,m - 1, $$

(3.2)

where $D_{t}^{\alpha } u(r,t)$ is the Caputo derivative of arbitrary order $\alpha ,\,\,\;m - 1 < \alpha \le m$, presented by Eq. (2.1), R is a linear operator and may contain rest of fractional derivatives of order less than $\alpha$, $N$ indicates a non-linear operator which may contain other derivatives of fractional order less than $\alpha \;$ and $g\left( {r,t} \right)$ is a known analytic function.

Applying the Laplace transform on Eq. (3.1), we have

$$ L{\kern 1pt} [D_{t}^{\alpha } {\kern 1pt} {\kern 1pt} u(r,t)] + L{\kern 1pt} [R\,u\;(r,t) + Nu(r,t)] = L[g(r,t)]. $$

(3.3)

Making use of the differentiation property of the Laplace transform, we find

$$ L\,[u(r,t)] = \frac{1}{{s^{\alpha } }}\sum\limits_{k = 0}^{m - 1} {s^{\alpha - 1 - k} } u^{k} (r,0) + \frac{1}{{s^{\alpha } }}L{\kern 1pt} {\kern 1pt} [g(r,t)] - \frac{1}{{s^{\alpha } }}L{\kern 1pt} {\kern 1pt} [R{\kern 1pt} {\kern 1pt} u(r,t) + N{\kern 1pt} {\kern 1pt} u(r,t)]. $$

(3.4)

On taking inverse Laplace transform on Eq. (3.4), we have

$$ \begin{aligned} u(r,t) & = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}\left( {\sum\limits_{k = 0}^{m - 1} {s^{\alpha - 1 - k} } u^{k} (r,0) + L[g(r,t)]} \right)} \right] \\ & - L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L[R{\kern 1pt} u(r,t) + Nu(r,t)]} \right]. \\ \end{aligned} $$

(3.5)

Now, applying the iterative method,

$$ u(r,t) = \sum\limits_{i = 0}^{\infty } {u_{i} (r,t)}. $$

(3.6)

As $R$ is a linear operator, so we have

$$ R\left( {\sum\limits_{i = 0}^{\infty } {u_{i} (r,t)} } \right) = \sum\limits_{i = 0}^{\infty } {R\left[ {u_{i} (r,t)} \right]}, $$

(3.7)

whereas the non-linear operator N is splitted as

$$ \begin{aligned} N\left( {\sum\limits_{i = 0}^{\infty } {u_{i} (r,t)} } \right) & = N\left[ {u_{0} (r,t)} \right] \\ & + \sum\limits_{i = 1}^{\infty } {\left\{ {N\left( {\sum\limits_{k = 0}^{i} {u_{k} (r,t)} } \right) - N\left( {\sum\limits_{k = 0}^{i - 1} {u_{k} (r,t)} } \right)} \right\}} . \\ \end{aligned} $$

(3.8)

Putting the results given by Eqs. from (3.6) to (3.8) in the Eq. (3.5), we obtain

$$ \begin{aligned} \sum\limits_{i = 0}^{\infty } {u_{i} (r,t)} & = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}\left( {\sum\limits_{k = 0}^{m - 1} {s^{\alpha - 1 - k} } u^{k} (r,0) + L{\kern 1pt} {\kern 1pt} [g(r,t)]} \right)} \right] \\ & - L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left[ {\sum\limits_{i = 0}^{\infty } {R\left[ {u_{i} (r,t)} \right]} } \right.} \right. + N{\kern 1pt} \left[ {u_{0} (r,t)} \right] \\ & + \sum\limits_{i = 1}^{\infty } {\left. {\left. {\left\{ {N\left( {\sum\limits_{k = 0}^{i} {u_{k} (r,t)} } \right) - N\left( {\sum\limits_{k = 0}^{i - 1} {u_{k} (r,t)} } \right)} \right\}} \right]} \right]} . \\ \end{aligned} $$

(3.9)

We have defined the recurrence formulae as

$$ u_{0} (r,t) = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}\left( {\sum\limits_{k = 0}^{m - 1} {s^{\alpha - 1 - k} } u^{k} (r,0) + L{\kern 1pt} {\kern 1pt} \left( {g(r,t)} \right)} \right)} \right] $$

(3.10)

$$ u_{1} (r,t) = - L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L{\kern 1pt} {\kern 1pt} \left[ {R{\kern 1pt} {\kern 1pt} \left( {u_{0} (r,t)} \right) + N\left( {u_{0} (r,t)} \right)} \right]} \right],\, $$

(3.11)

$$ \begin{aligned} u_{{m + 1}} (r,t) = & - L^{{ - 1}} \left[ {\frac{1}{{s^{\alpha } }}L\left[ {R{\kern 1pt} {\kern 1pt} \left( {u_{m} (r,t)} \right) - \left\{ {N\left( {\sum\limits_{{k = 0}}^{m} {u_{k} (r,t)} } \right)} \right.} \right.} \right. \\ & - N\left. {\left. {\left. {\left( {\sum\limits_{{k = 0}}^{{m - 1}} {u_{k} (r,t} )} \right)} \right\}} \right]} \right],m \ge 1 \\ \end{aligned} $$

(3.12)

Therefore the $m$-term approximate solution of Eqs. (3.1) and (3.2) in series form is given by

$$ u(r,t) \cong u_{0} (r,t) + u_{1} (r,t) + u_{2} (r,t) + , \ldots , + u_{m} (r,t),\quad m = 1,2, \ldots . $$

(3.13)

4 Solutions of the Time-Fractional Navier–Stokes Equations

In this part, we have made an attempt to solve the time-fractional Navier–Stokes equations by the application of iterative Laplace transform scheme.

Example 1

Consider the subsequent Navier–Stokes equation involving time–fractional derivative written by

$$ D_{t}^{\alpha } u = P + \frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r},0 < \alpha \le 1, $$

(4.1)

Surrounding the initial condition

$$ \,u(r,t) = 1 - r^{2} $$

(4.2)

Taking the Laplace transform of the Eq. (4.1), and making use of the result given by (4.2), we get,

$$ L\,[u(r,t)] = \frac{1}{s}\left( {1 - r^{2} } \right) + \frac{P}{{s^{\alpha + 1} }} + \frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right). $$

(4.4)

Applying inverse Laplace transform to the Eq. (4.4), we arrive at the subsequent result

$$ u(r,t) = (1 - r^{2} ) + P\frac{{t^{\alpha } }}{{\Gamma (\alpha + 1)}} + L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right)} \right]. $$

(4.5)

Now, making use of the iterative method, substituting the results of the Eqs. from (3.6) to (3.8) in the Eq. (4.5) and making use of the results given by the Eqs. (3.10) to (3.12), we determine the components of the ILTM solution as follows

$$ u_{0} (r,t) = (1 - r^{2} ) + P\frac{{t^{\alpha } }}{{\Gamma (\alpha + 1)}}, $$

(4.6)

$$ \begin{aligned} u_{1} (r,t) & = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left[ {\frac{{\partial^{2} u_{0} }}{{\partial {\text{r}}^{ 2} }} + \frac{1}{\text{r}}\frac{{\partial u_{0} }}{{\partial {\text{r}}}}} \right]} \right] \\ & = - \frac{{4t^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}}, \\ \end{aligned} $$

(4.7)

$$ u_{n + 1} (r,t) = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u_{n} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{n} }}{\partial r}} \right)} \right] = 0.\quad \forall \;n \ge 1. $$

(4.8)

The other components may be obtained accordingly.

Thus, the closed form solution in the series form is can be obtained as

$$ \begin{aligned} u\left( {r,\,t} \right) & = u_{0} (r,t) + u_{1} (r,t) + u_{2} (r,t) + u_{3} (r,t) + , \ldots , \\ & = \left( {1 - r^{2} } \right) + \left( {P - 4} \right)\frac{{t^{\alpha } }}{{\Gamma (\alpha + 1)}}\;. \\ \end{aligned} $$

(4.9)

Special Cases

• (i) The result in (4.9) was derived by Momani and Odibat [12] with the aid of the different scheme that is ADM.

• (ii) The result in (4.9) deduced by Ragab et al. [14] by the application of HAM.

• (iii) A result in (4.9) has an analogy with the result of Ganji et al. [5] has been obtained by using HPM.

• (iv) For $\alpha = 1\,,$ the result in (4.9) reduces to the following simple form

$$ u(r,t) = \left( {1 - r^{2} } \right) + \left( {P - 4} \right)t. $$

(4.10)

This result was obtained earlier by Kumar et al. [10] by using the method of HPTM.

Example 2

Next, consider the subsequent Navier–Stokes equation concerning to time–fractional derivative given by

$$ D_{t}^{\alpha } u = \frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r},\quad 0 < \alpha \le 1, $$

(4.11)

with the initial condition

$$ u(r,0) = r\,, $$

(4.12)

Taking the Laplace transform of the Eq. (4.11), and making use of the result given by (4.12), we have,

$$ L\,[u(r,t)] = \frac{r}{s} + \frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right). $$

(4.14)

Applying inverse Laplace transform to the Eq. (4.14), we get

$$ u(r,t) = r + L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right)} \right]. $$

(4.15)

Now, making use of the iterative method, substituting the results of the Eqs. from (3.6) to (3.8) in the Eq. (4.15) and making use of the results given by the Eqs. (3.10) to (3.12), we determine the components of the ILTM solution as follows

$$ u_{0} (r,t) = \,\;r\,, $$

(4.16)

$$ \begin{aligned} u_{1} (r,t) & = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u_{0} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{0} }}{\partial r}} \right)} \right] \\ & = \frac{1}{r}\frac{{t^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}}, \\ \end{aligned} $$

(4.17)

$$ \begin{aligned} u_{2} (r,t) & = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u_{1} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{1} }}{\partial r}} \right)} \right] \\ & = \frac{1}{{r^{3} }}\frac{{t^{2\alpha } }}{{\Gamma \left( {2\alpha + 1} \right)}}, \\ \end{aligned} $$

(4.18)

$$ \begin{aligned} u_{3} (r,t) & = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u_{2} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{2} }}{\partial r}} \right)} \right] \\ & = \frac{9}{{r^{5} }}\frac{{t^{3\alpha } }}{{\Gamma \left( {3\alpha + 1} \right)}}, \\ \end{aligned} $$

(4.19)

and

$$ \begin{aligned} u_{n} (r,t) & = L^{ - 1} \left[ {\frac{1}{{s^{\alpha } }}L\left( {\frac{{\partial^{2} u_{n - 1} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{n - 1} }}{\partial r}} \right)} \right] \\ & = \frac{{1^{2} \times 3^{2} \cdots \left( {2n - 1} \right)^{2} }}{{r^{2n - 1} }}\frac{{t^{n\alpha } }}{{\Gamma \left( {n\alpha + 1} \right)}}, \\ \end{aligned} $$

(4.20)

and so on. The other components may be obtained accordingly.

Thus, the closed form solution in the series form is can be obtained as

$$ \begin{aligned} u\left( {r,\,t} \right) & = u_{0} (r,t) + u_{1} (r,t) + u_{2} (r,t) + u_{3} (r,t) + , \ldots , \\ & = r + \sum\limits_{n = 1}^{\infty } {\frac{{1^{2} \times 3^{2} \cdots \left( {2n - 1} \right)^{2} }}{{r^{2n - 1} }}} \frac{{t^{n\alpha } }}{{\Gamma \left( {n\alpha + 1} \right)}}. \\ \end{aligned} $$

(4.21)

Special Cases

• (i) The result in (4.21) was obtained by Ragab et al. [14] using the different method known as HAM.

• (ii) The result in (4.21) was given by Ganji et al. [5] using the different technique known as HPM technique.

• (iii) The result in (4.21) deduced by Momani and Odibat [12] by the application of ADM.

• (iv) For $\alpha = 1\,\,,$ the result in (4.21) reduces to the following simple form

$$ u(r,t) = r + \sum\limits_{n = 1}^{\infty } {\frac{{1^{2} \times 3^{2} \cdots \left( {2n - 1} \right)^{2} }}{{r^{2n - 1} }}} \frac{{t^{n} }}{n!}. $$

(4.22)

This result was obtained earlier by Kumar et al. [10] by using the method of HTPM.

5 Numerical Results and Discussions

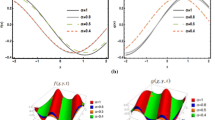
In this part, we present some numerical results for Navier–Stokes equation concerning to time–fractional derivative. Figures 1 and 2 present the ILTM solution of Navier–Stokes equation concerning to time–fractional derivative for α = 1 and 2 respectively. Figure 3 presents the ILTM solution of Navier–Stokes equation concerning to time–fractional derivative with respect to r for distinct values of α.

Fig. 1

The surface of solution $u(r,t),$ when $\alpha = 1\,,P = 1$ for Eq. (4.9)

Fig. 2

The surface of solution $u(r,t),$ when $\alpha = 0.5\,,P = 1$ for Eq. (4.9)

Fig. 3

The nature of the solution $u(r,t)$ w.r.t. $r,$ when $P = 1$ for diverse values of $\alpha \;$ for Eq. (4.9)