A New Stable Algorithm for Fractional Navier–Stokes Equation in Polar Coordinate

Abstract

This paper presents a new approximate method based on operational matrices of fractional integrations and differentiations for fractional Navier–Stokes equation in polar coordinate system using Legendre scaling functions as a basis. Convergence analysis as well as error analysis of the proposed methods is given. Numerical stability of the method is shown. Numerical examples are given to show the effectiveness of the proposed method. Results are compared with existing analytical methods to show the accuracy of the proposed method.

Introduction

The Navier–Stokes equation (NSE) is fundamental equation of the computational fluid dynamics. It relates pressure and external forces acting on a fluid to the response of the fluid flow. The NSE and continuity equations are given by

$$\begin{aligned}&\frac{\partial u}{\partial t}+\left( {\underline{u} \cdot \nabla } \right) \underline{u} =-\frac{1}{\rho }\nabla p+v\nabla ^{2}\underline{u} , \end{aligned}$$

(1a)

$$\begin{aligned}&\nabla \underline{u} =0, \end{aligned}$$

(1b)

where $\underline{u}$ is the velocity, $\nu$ is the kinematics viscosity, p is the pressure, $\rho$ is density and t is the time variable.

We transfer all motion in polar coordinates $(r,\theta ,z)$ where z axis coincides with the axis of cylinder. Taking $u_r =u_\theta =0$ and $u_z =u(r,t)$, the NSE in polar coordinate reduces to following form

$$\begin{aligned} \frac{\partial u}{\partial t}=-\frac{\partial p}{\rho \partial z}+\nu \left( {\frac{\partial ^{2}u}{\partial r^{2}}+\frac{1}{r}\frac{\partial u}{\partial r}} \right) , \end{aligned}$$

(2)

Recently El-Shahed and Salem [6] and Odibat and Momani [21] have generalised the classical NSE by replacing first order time derivative to fractional order time derivative $\alpha$, where $0<\alpha \le 1$. In the present paper we shall consider the unsteady flow of a viscous fluid in a tube in which the velocity field is a function of only one space coordinate and time as one of the dependent variable. So our aim is to study numerically the following generalised form of FNSE [6, 21], namely

$$\begin{aligned} \frac{\partial ^{\alpha }u(r,t)}{\partial t^{\alpha }}=P+\nu \left( {\frac{\partial ^{2}u(r,t)}{\partial r^{2}}+\frac{1}{r}\frac{\partial u(r,t)}{\partial r}} \right) ,\quad 0<\alpha \le 1, \end{aligned}$$

(3)

subject to the initial and boundary conditions:

$$\begin{aligned} u(r,0)=g(r),\quad u(0, t)=g_1 (t),\quad u(1, t)=g_2 (t)\quad \hbox {for}\,\, 0\le r,t \le 1, \end{aligned}$$

where $P=-\frac{\partial p}{\rho \partial z}$, r is spatial domain.

There exist several analytical methods to solve fractional Navier–Stokes equations. In [21], Odibat and Momani solve Eq. (3) using Adomian decomposition method (ADM). Some other analytical approaches are modified Laplace decomposition method [15], homotopy analysis method [25], homotopy perturbation method [9], homotopy perturbation transform method [2]. In [16], Chaurasia and Kumar used Mittag–Leffler and Bessel functions to obtain analytical solution of FNSE in circular cylinder.

In this paper we are using numerical approach based on operational matrices of fractional integration and differentiation. There exist a vast literature for theory and applications of fractional differential equations in areas such as hydrology [1, 13, 18, 27, 28], physics [7, 8, 12, 19, 23, 32, 35] and finance [10, 24, 26]. For construction of operational matrices and their applications to solve fraction differential equations see [14, 17, 31, 33, 34]. In this method we first get finite dimensional approximate solution taking finite dimensional basis in r–t plane, which in turn leads to a system of linear algebraic equations whose solution is obtained using Sylvester’s approach. This in turn gives us the approximate solution of the FNSE.

In general for the existence and uniqueness of the solution for the fractional Navier–Stokes equation (FNSE) there does not exist any analytical methods. Stability and convergence are not shown for the methods given above. In this paper we give a new stable numerical approach along with error and convergence analysis for FNSE. Due to the complexity and non-local nature of the fractional order derivatives, it is not encouraged to search for a strong solution. In this paper, we solve this issue by giving solution in the sense of association in the same lines as developed by Colombeau, see [3, 4, 22]. This gives satisfactory concept of solution. With some additional condition on approximating sequence, we obtain the strong solution.

The present paper is organised as follows. In second section, we describe basic preliminaries. In third section, we construct operational matrices of fractional differentiation and integration using Legendre scaling functions as basis. In fourth section, we describe the algorithm for the construction of approximate solutions. In fifth section, we give the error analysis of the proposed method. In sixth section, we describe the convergence of the method. In seventh section, we discuss the stability of our method based on maximum absolute error and root mean square error. In eighth section, we present numerical experiments and discussions to show the effectiveness of the proposed method.

Preliminaries

There are several definitions of fractional order derivatives and integrals. These are not necessarily equivalent. In this paper, the fractional order differentiations and integrations are in well-known Caputo and Riemann–Liouville sense respectively [5, 20].

The Legendre scaling functions $\left\{ {\phi _i (t)} \right\}$ in one dimension are defined by

$$\begin{aligned} \phi _i (t)=\left\{ {\begin{array}{l@{\quad }l} \sqrt{(2i+1)}P_i (2t-1), &{}\hbox {for }0\le t<1. \\ 0,&{} otherwise, \\ \end{array}} \right. \end{aligned}$$

where $P_i (t)$ is Legendre polynomials of order i on the interval $[-1,1]$, given explicitly by the following formula;

$$\begin{aligned} P_i (t)=\sum _{k=0}^i {(-1)^{i+k}\frac{(i+k)!}{(i-k)!} \frac{t^{k}}{(k!)^{2}}} . \end{aligned}$$

(4)

Using one dimensional Legendre scaling functions, we construct two dimensional Legendre scaling function $\phi _{i_1 ,i_2 }$,

$$\begin{aligned} \phi _{i_1 ,i_2 } (x,t)=\phi _{i_1 } (x)\phi _{i_2 } (t),\quad i_1 ,i_2 \in N_0 , \quad \mathrm{N}_0 =\left\{ {0,1,2,\ldots } \right\} . \end{aligned}$$

An explicit expression of two dimensional Legendre scaling functions are given as

$$\begin{aligned} \phi _{i_1 ,i_2 } (x,t)=\left\{ {\begin{array}{l@{\quad }l} \sqrt{(2i_1 +1)}\sqrt{(2i_2 +1)}P_{i_1 } (2x-1)P_{i_2 } (2t-1), &{}\hbox {for }0\le x<1, \; 0\le t<1. \\ 0,&{} otherwise. \\ \end{array}} \right. \end{aligned}$$

From the above formula it is clear that two dimensional Legendre scaling functions are orthogonal;

$$\begin{aligned} \int \limits _0^1 {\int \limits _0^1 {\phi _{i_1 ,i_2 } (x,t)\phi _{j_1 ,j_2 } (x,t)} } dxdt=\left\{ {\begin{array}{l@{\quad }l} 1, &{} i_1 = j_1~and~i_2 = j_2 , \\ 0 , &{} otherwise. \\ \end{array}} \right. \end{aligned}$$

and $\left( {\phi _{i_1 ,i_2 } } \right)$ form a complete orthonormal basis.

So, a function $f(x,t)\in L^{2}([0,1]\times [0,1])$, can be approximated as

$$\begin{aligned} f(x,t)\cong \sum _{i_1 =0}^{n_1 } {\sum _{i_2 =0}^{n_2 } {c_{i_1 ,i_2 } } } \varphi _{i_1 ,i_2 } (x,t)=C^{T}\phi (x,t), \end{aligned}$$

(5)

where $C=[c_{0,0} ,\ldots ,c_{0,n_2 } ,\ldots ,c_{n_1 ,1} ,\ldots ,c_{n_1 ,n_2 } ]^{T}$;

$$\begin{aligned} \phi (x,t)=[\phi _{0,0} (x,t),\ldots ,\phi _{0,n_2 } (x,t),\ldots ,\phi _{n_1 ,1} (x,t),\ldots ,\phi _{n_1 ,n_2 } (x,t)]^{T}. \end{aligned}$$

The coefficients $c_{i_1 ,i_2 }$ in the Fourier expansions of f(x, t) are given by the formula,

$$\begin{aligned} c_{i_1 ,i_2 } =\int \limits _0^1 {\int \limits _0^1 {f(x,t)} \phi _{i_1 ,i_2 } (x,t)dxdt} . \end{aligned}$$

(6)

Using matrix notation Eq. (5) can be written as,

$$\begin{aligned} f(x,t)\cong \phi ^{T}(x)C\phi (t), \end{aligned}$$

(7)

where $\phi (x)=[\phi _0 (x),\ldots ,\phi _{n1} (x)]^{T}$, $\phi (t)=[\phi _0 (t),\ldots ,\phi _{n2} (t)]^{T}$ and $C=\left( {c_{i_1 ,i_2 } } \right) _{(n_1 +1)\times (n_2 +1)}$.

Operational Matrices

Theorem 3.1

Let $\phi (x)=[\phi _0 (x),\phi _1 (x),\ldots ,\phi _n (x)]^{T}$, be Legendre scaling vector and consider $\alpha >0$, then

$$\begin{aligned} I^{\alpha }\phi _i (x)=I^{(\alpha )}\phi (x), \end{aligned}$$

(8)

where $I^{(\alpha )}=\left( {\left. {\omega (i,j)} \right) } \right.$, is $(n+1)\times (n+1)$ operational matrix of fractional integral of order $\alpha$ and its (i, j)th entry is given by

$$\begin{aligned} \omega (i,j)= & {} (2i+1)^{1/2}(2j+1)^{1/2}\\&\times \,\sum _{k=0}^i \sum _{l=0}^j {(-1)^{i+j+k+l}}\frac{(i+k)!(j+l)!}{(i-k)!(j-l)!(k)!(l!)^{2}(\alpha +k+l+1)\Gamma (\alpha +k+1)}\\ 0\le & {} i,j\le n. \end{aligned}$$

Proof

Pl. see [29]. $\square$

Theorem 3.2

Let $\phi (x)=[\phi _0 (x),\phi _1 (x),\ldots ,\phi _n (x)]^{T}$, be Legendre scaling vector and consider $\beta >0$, then

$$\begin{aligned} D^{\beta }\phi _i (x)=D^{(\beta )}\phi (x), \end{aligned}$$

(9)

where $D^{(\beta )}=\left( {\eta (i,j)} \right)$, is $(n+1)\times (n+1)$ operational matrix of Caputo fractional derivative of order $\beta$ and its (i, j)th entry is given by

$$\begin{aligned} \eta (i,j)= & {} (2i+1)^{1/2}(2j+1)^{1/2}\sum _{k=\left\lceil \beta \right\rceil }^i \sum _{l=0}^j {(-1)^{i+j+k+l}}\\&\times \frac{(i+k)!(j+l)!}{(i-k)!(j-l)!(k)!(l!)^{2}(k+l+1-\beta )\Gamma (k+1-\beta )}. \end{aligned}$$

Proof

Pl. see [30]. $\square$

Method of Solution

In this section for any approximation we take $n_1 =n_2 =n$, and describe the algorithm for the construction of approximate solution of the Eq. (3). If $D_t^\alpha u=w$, then

$$\begin{aligned} u=I_t^\alpha (w)+u_0 (r). \end{aligned}$$

(10)

From Eqs. (3) and (10) we get

$$\begin{aligned} w=P+\nu \left( {D_r^2 \left( I_t^\alpha (w)+u_0 (r)\right) +\frac{1}{r}D_r \left( I_t^\alpha (w)+u_0 (r)\right) } \right) , \end{aligned}$$

(11)

Eqs. (3) and (11) are equivalent. Equation (11) can be written as

$$\begin{aligned} rw=rP+\nu \left( {rD_r^2 \left( I_t^\alpha (w)+u_0 (r)\right) +D_r^1 \left( I_t^\alpha (w)+u_0 (r)\right) } \right) , \end{aligned}$$

(12)

Let

$$\begin{aligned} G(r)=\nu \left( rD_r^2 +D_r^1 \right) (u_0 (r)). \end{aligned}$$

(13)

From Eqs. (12) and (13) we can write,

$$\begin{aligned} rw=rP+\nu \left( {rD_r^2 \left( I_t^\alpha (w)\right) +D_r^1 \left( I_t^\alpha (w)\right) } \right) +G(r), \end{aligned}$$

(14)

Approximating

$$\begin{aligned} w(r,t)\cong w_n (r,t)=\phi ^{T}(r)C \phi (t), \end{aligned}$$

(15)

where C is a square matrix to be found.

Using Eq. (15) and operational matrices for the operators $D_r^2 I_t^\alpha$ and $D_r^1 I_t^\alpha$ in Eq. (14), we obtain,

$$\begin{aligned} r\phi ^{T}(r)C\phi (t)=rP+\nu \left( {r\phi ^{T}(r)\left( D_r^{(2)} \right) ^{T}CI_t^{(\alpha )} \phi (t)+\phi ^{T}(r)\left( D_r^{(1)} \right) ^{T}CI_t^{(\alpha )} \phi (t)} \right) +G(r), \end{aligned}$$

(16)

where $I_t^{(\alpha )}$ is an operational matrix of fractional integration of order $\alpha$ and $D_r^{(1)}$, $D_r^{(2)}$ are an operational matrix of fractional differentiation of order 1 and 2 respectively.

Further approximating the following approximations

$$\begin{aligned} G(r)\cong & {} G_n (r)=\phi ^{T}(r)A\phi (t), \end{aligned}$$

(17)

$$\begin{aligned} h(r)= & {} rP\cong h_n (r)=\phi ^{T}(r)B\phi (t), \end{aligned}$$

(18)

$$\begin{aligned} r\phi ^{T}(r)= & {} \phi ^{T}(r)E, \end{aligned}$$

(19)

where the matrix A, B and E are known matrices and can be calculated using Eq. (6).

From Eqs. (16)–(19) we get,

$$\begin{aligned} \phi ^{T}(r)EC\phi (t)= & {} \phi ^{T}(r)B\phi (t)+\nu \phi ^{T}(r)E(D_r^{(2)} )^{T}CI_t^{(\alpha )} \phi (t) \nonumber \\&+\,\phi ^{T}(r)(D_r^{(1)} )^{T}CI_t^{(\alpha )} \phi (t)+\phi ^{T}(r)A\phi (t), \end{aligned}$$

(20)

Now Eq. (20) can be written as,

$$\begin{aligned} LC+CM+N=0, \end{aligned}$$

(21)

where $L=\nu ((D_r^{(2)} )^{T})+inverse (E) (D_r^{(1)} )^{T}$, $M=-inverse (I_t^{(\alpha )} )$ and $N=inverse (E)(A+B)inverse (I_t^{(\alpha )} ).$

Equation (21) is a Sylvester equation which can be solved easily to get the matrix C.

Using the value of C in Eq. (15), we can find w and further using value of w in Eq. (10) we can obtain an approximate solution for time fractional Navier–Stokes equation.

Error Analysis

Theorem 5.1

Let $\frac{\partial ^{\alpha }f(x,t)}{\partial t^{\alpha }}\in L^{2}([0,1]\times [0,1])$, and $\frac{\partial ^{\alpha }f_n (x,t)}{\partial t^{\alpha }}$ be its approximation obtained by using $(n+1)^{2}$, 2-dimensional Legendre scaling vectors. Assuming $\left| {\frac{\partial ^{\alpha +4}f(x,t)}{\partial x^{2}\partial t^{\alpha +2}}} \right| \le K$, we have the following upper bound for error

$$\begin{aligned} \left\| {\frac{\partial ^{\alpha }f(x,t)}{\partial t^{\alpha }}-\left( {\frac{\partial ^{\alpha }f_n (x,t)}{\partial t^{\alpha }}} \right) } \right\| ^{2}_{L^{2}} < \left( {\frac{K^{2}}{65536}} \right) \left( {F_3 \left( -\frac{1}{2}+n\right) } \right) ^{2} \end{aligned}$$

where,

$$\begin{aligned} \left\| {f(x,t)} \right\| _{L^{2}} =\left( {\int \limits _0^1 {\int \limits _0^1 {\left| {f(x,t)} \right| ^{2}dx} dt} } \right) ^{\frac{1}{2}} \end{aligned}$$

and $F_n (z)$ is the Poly Gamma function defined by,

(22)

Proof

Let $\frac{\partial ^{\alpha }f(x,t)}{\partial t^{\alpha }}=\sum _{i_1 =0}^\infty {\sum _{i_2 =0}^\infty {c_{i_1 ,i_2 } \phi _{_{i_1 ,i_2 } } } } (x,t)$. Truncating it to level n, we get $\left( {\frac{\partial ^{\alpha }f_n (x,t)}{\partial t^{\alpha }}} \right) =\sum _{i_1 =0}^n {\sum _{i_2 =0}^n {c_{i_1 ,i_2 } \phi _{_{i_1 ,i_2 } } } } (x,t)$, thus,

$$\begin{aligned} \frac{\partial ^{\alpha }f(x,t)}{\partial t^{\alpha }}-\left( {\frac{\partial ^{\alpha }f_n (x,t)}{\partial t^{\alpha }}} \right)= & {} \sum _{i_1 =n+1}^\infty {\sum _{i_2 =n+1}^\infty {c_{i_1 ,i_2 } \phi _{_{i_1 ,i_2 } } } } (x,t), \end{aligned}$$

(23)

$$\begin{aligned} \left\| {\frac{\partial ^{\alpha }f(x,t)}{\partial t^{\alpha }}-\left( {\frac{\partial ^{\alpha }f_n (x,t)}{\partial t^{\alpha }}} \right) } \right\| ^{2}_{L^{2}}= & {} \int \limits _0^1 {\int \limits _0^1 {\left( {\frac{\partial ^{\alpha }f(x,t)}{\partial t^{\alpha }}-\left( {\frac{\partial ^{\alpha }f_n (x,t)}{\partial t^{\alpha }}} \right) } \right) ^{2}dx} dt} \nonumber \\= & {} \sum _{i_1 =n+1}^\infty {\sum _{i_2 =n+1}^\infty {c_{_{i_1 ,i_2 } }^2 } } , \end{aligned}$$

(24)

Similar process as in [11] and using our condition, we get,

$$\begin{aligned} \left| {c_{i_1 ,i_2 } } \right| ^{2} < \frac{9K^{2}}{64(2i_1 -3)^{4}(2i_2 -3)^{4}}. \end{aligned}$$

(25)

so from Eqs. (24) and (25),

$$\begin{aligned} \left\| {\frac{\partial ^{\alpha }f(x,t)}{\partial t^{\alpha }}-\left( {\frac{\partial ^{\alpha }f_n (x,t)}{\partial t^{\alpha }}} \right) } \right\| ^{2}_{L^{2}} < \left( {\frac{K^{2}}{65536}} \right) \left( {F_3 \left( -\frac{1}{2}+n\right) } \right) ^{2}. \end{aligned}$$

(26)

$\square$

Convergence Analysis

Definition 6.1

A sequence of functions $u_n$ is said to be a solution in the sense of association of $L(u)=f$, $u(0,x)=u_0 (x)$, where L is a linear fractional differential operator involving fractional derivatives and integrations with respect to x and t; if $\mathop {\lim }\nolimits _{n\rightarrow \infty } \left\langle {L(u_n )-f_n ,\left. \phi \right\rangle } \right. =0$, for all $C^{\infty }$ function $\phi$ having compact support in $(0,1)\times (0,1)$.

Theorem 6.1

If the constructed approximations $\{w_n \}$, where $w_n (r,t)=\phi ^{T}(r)C\phi (t)$, satisfy $\left\| {\bar{{L}}(w_n )-h_n -G_n } \right\| _{L^{2}} <K,\forall n;$ then, $w_n$ is a solution in the sense of association, where $\bar{{L}}(w)=rw-\nu \left( {rD_r^2 (I_t^\alpha (w))+D_r^1 (I_t^\alpha (w))} \right)$.

Proof

Observe that $w_n (r,t)=\phi ^{T}(r)C\phi (t)$ satisfy

$$\begin{aligned} \left\langle {\bar{{L}}(w_n )-h_n -G_n ,\left. {\phi _{ij} } \right\rangle } \right. =0,\quad \hbox {for }0\le i,\; j\le n. \end{aligned}$$

(27)

Let $V_n =$ span $\{\phi _i (r)\phi _j (t): i=0,1,\ldots ,n. j=0,1,\ldots ,n\}$.

Then by linearity,

$$\begin{aligned} \left\langle \bar{{L}}(w_n )-h_n -G_n , \psi \right\rangle =0,\quad \hbox {for all }\psi \in V_n . \end{aligned}$$

(28)

Since $\left( {\phi _{i_1 ,i_2 } } \right)$ form a complete orthonormal basis for the Hilbert space $L^{2}\left( {[0,1]\times [0,1]} \right)$, we can get $\psi _n \in V_n$, such that

$$\begin{aligned} \left\| {\psi _n (r,t)-\psi (r,t)} \right\| _{L^{2}} \rightarrow 0. \end{aligned}$$

(29)

Our assumption,

$$\begin{aligned} \left\| {\bar{{L}}(w_n )-h_n -G_n } \right\| _{L^{2}} <K, \end{aligned}$$

(30)

in Eq. (28), We can write

$$\begin{aligned} \left\langle \bar{{L}}(w_n )-h_n -G_n, {\psi (r,t)} \right\rangle= & {} \left\langle {\bar{{L}}(w_n )-h_n -G_n ,\left. {(\psi (r,t)-\psi _n (r,t)+\psi _n (r,t))} \right\rangle } ,\right. \nonumber \\= & {} \left\langle \bar{{L}}(w_n )-h_n -G_n , {\psi _n (r,t)} \right\rangle \nonumber \\&+\,\left\langle \bar{{L}}(w_n )-h_n -G_n , {(\psi (r,t)-\psi _n (r,t))} \right\rangle . \end{aligned}$$

(31)

Now using Eq. (28), in (31), we get

$$\begin{aligned} \left| {\left\langle \bar{{L}}(w_n )-h_n -G_n , {\psi (r,t)} \right\rangle } \right| \le \left\| {\bar{{L}}(w_n )-h_n -G_n } \right\| _{L^{2}} \left\| {\psi (r,t)-\psi _n (r,t)} \right\| _{L^{2}} , \end{aligned}$$

(32)

from Eqs. (29), (30) and (32), it follows that $\mathop {\lim }\nolimits _{n\rightarrow \infty } \left\langle \bar{{L}}(w_n )-h_n -G_n , {\psi (r,t)} \right\rangle =0$.

So $w_n$ is a solution in the sense of association. $\square$

Corollary 6.1

In addition to statement of the Theorem 6.1, if $\bar{{L}}(w_n )$ converges to $\bar{{L}}(w)$ in $L^{2}$ norm then w forms a strong solution.

Proof

By the Theorem 6.1, $w_n$ forms a solution in the sense of association so

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } \int {\bar{{L}}(w_n )\varphi =0, } \Rightarrow \int {\bar{{L}}(w)\varphi =0, } \Rightarrow \int {\bar{{L}}(w)\bar{{L}}(w)=0,} \forall \varphi \in L^{2}, \end{aligned}$$

$\Rightarrow \bar{{L}}(w)=0$. So w forms a strong solution. $\square$

Numerical Stability

The accuracy of proposed method is demonstrated by calculating absolute error, average deviation $\sigma$ also known as root mean square error (RMS). They are calculated using the following equations

$$\begin{aligned} \Delta u(r_i ,t_j )=\left| {u_e (r_i ,t_j )-u_a (r_i ,t_j )} \right| , \end{aligned}$$

(33)

and

$$\begin{aligned} \sigma _{(N+1)^{2}} =\left\{ {\left. {\frac{1}{(N+1)^{2}}\sum _{i=0}^N {\sum _{j=0}^N {[u_e (r_i ,t_j )-u_a (r_i ,t_j )]^{2}} } } \right\} ^{1/2}} \right. , \end{aligned}$$

(34)

where $u_e (r_i ,t_j )$ is the exact value of output function at point $(r_i ,t_j )$ and $u_a (r_i ,t_j )$ is the approximate value of output function at the same point.

From now wards, considering h(r) as input function. Adding random noise term in input function we demonstrate the stability of the proposed method.

In all examples, the exact and input function with noise are denoted by h(r) and $h^{\delta }(r)$, respectively, where $h^{\delta }(r)$ is obtained by adding a noise $\delta$ to h(r) such that $h^{\delta }(r_i )=h(r_i )+\delta \theta _i$, where $r_i =ih, i=1,2,\ldots ,N, Nh=1$; and $\theta _i$ is the uniform random variable with values in [$-$1, 1] such that

$$\begin{aligned} \mathop {\max }\limits _{1\le i\le N} \left| {h^{\delta }(r_i )-h(r_i )} \right| \le \delta . \end{aligned}$$

(35)

Reconstructed output function $u_a^\delta (r,t)$(with $\delta$ noise) and $u_a^0 (r,t)$ (without noise) are obtained with and without noise term in the input function h(r) and using Eqs. (10) and (15) these are given by

$$\begin{aligned} u_a^\delta (r,t)\cong & {} \phi ^{T}(r)C^{\delta }I^{(\alpha )}\phi (t)+g(r), \end{aligned}$$

(36)

$$\begin{aligned} u_a^0 (r,t)\cong & {} \phi ^{T}(r)CI^{(\alpha )}\phi (t)+g(r), \end{aligned}$$

(37)

where $C^{\delta }$ and C are known matrices and they are obtained from the following equations:

Table 1 Noise reduction H(r, t) for $N=10$ at different values of $\delta$

Fig. 1

Noise reduction H(r, t) for $N=10$ and $\delta =0.0001$

Fig. 2

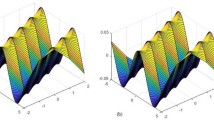
Approximate solution for $\alpha =0.5$, Example 1

Fig. 3

Approximate solution for $\alpha =1$, Example 1

Fig. 4

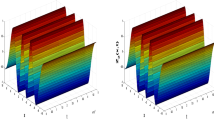
Absolute error for $\alpha =1$, Example 1

Fig. 5

Absolute error for $\alpha =0.9$, Example 1

$LC^{\delta }+C^{\delta }M+N^{\delta }=0$ and $LC+CM+N=0$, where L, M, N are same as in Eq. (21) and

$$\begin{aligned} N^{\delta }=inverse (E)(A+B^{\delta })inverse (I^{(\alpha )}), \end{aligned}$$

(38)

we approximate $h^{\delta }(r)$ as

$$\begin{aligned} h^{\delta }(r)=h(r)+\delta \theta _i \cong \phi ^{T}(r)B^{\delta }\phi (t). \end{aligned}$$

(39)

From Eqs. (36) and (37)

$$\begin{aligned} u_a^\delta (r,t)-u_a^0 (r,t)\cong \phi ^{T}(r)\left( {C^{\delta }-C} \right) I^{(\alpha )}\phi (t). \end{aligned}$$

(40)

Let

$$\begin{aligned} H(r,t)=u_a^\delta (r,t)-u_a^0 (r,t)\cong \phi ^{T}(r)\left( {C^{\delta }-C} \right) I^{(\alpha )}\phi (t), \end{aligned}$$

(41)

then H(r, t) reflects the noise reduction capability of the method. Its values at various points and its graph are shown in Table 1 and Fig. 1.

Fig. 6

The behaviour of solution for different values of $\alpha$ at $\hbox {t}=1$, Example 1

Fig. 7

The behaviour of solution for different values of $\alpha$ at $\hbox {r}=1$, Example 1

Fig. 8

Difference of absolute errors with and without noise, Example 1

In Table 1, we list the noise reduction.

In eighth section, two examples are solved with and without noise to illustrate the stability of the proposed method. In all the two examples, we add the noise $\delta =\sigma _{(N+1)^{2}}$, for two different values of $N=10,20$. For different values of N we calculate maximum absolute error and root mean square errors denoted by $E_1$ and $E_2$ respectively for input functions without noise term and these respective errors are denoted by $E_1^{*}$ and $E_2^{*}$ for input function with noise respectively. In Table 3, we have listed the different values of $E_1 ,E_2 ,E_1^*$ and $E_2^{*}$ for $N=10,20$. From the table it is clear that the there is a very small change in errors when we add noise term in input function showing the stability of our method.

In Figs. 8 and 14 the difference of absolute errors with and without noise are plotted for Examples 1 and 2 respectively and it is observed that it is very small so our method is stable.

Numerical Results and Discussion

Example 1

Consider the following time-fractional Navier–Stokes equation [9, 15, 16, 21, 25];

$$\begin{aligned} \frac{\partial ^{\alpha }u(r,t)}{\partial t^{\alpha }}=P+\frac{\partial ^{2}u(r,t)}{\partial r^{2}}+\frac{1}{r}\frac{\partial u(r,t)}{\partial r},\quad 0<\alpha \le 1, \end{aligned}$$

(42)

with initial-boundary conditions $u(r,0)=1-r^{2},$

and exact solution . For simplicity taking $P=1$. Figures 2 and 3, show the approximate solution of Eq. (42),for different values of $\alpha =0.5$ and 1 respectively. Figures 4 and 5 show the absolute error graph of Eq. (42), for $\alpha = 1$ and 0.9 respectively.

Figures 6 and 7 show the behaviour of approximate solution of Eq. (42), for different values of $\alpha =0.7,0.8,0.9$ and 1 for fix value of $t=1$ and $r=1$ respectively. From Figs. 6 and 7, it is clear that solution varies continuously for different values of $\alpha$ and approaches monotonically to integer order NSE continuously as $\alpha \rightarrow 1$ (Fig. 8).

In Table 2, we compare results obtain by our numerical algorithm and existing analytical methods [9, 16, 25].

Table 2 Comparison of results for example 1 for different values of $\alpha$

Example 2

Consider the following time-fractional Navier–Stokes equation;

$$\begin{aligned} \frac{\partial ^{\alpha }u(r,t)}{\partial t^{\alpha }}=\frac{\partial ^{2}u(r,t)}{\partial r^{2}}+\frac{1}{r}\frac{\partial u(r,t)}{\partial r},\quad 0<\alpha \le 1, \end{aligned}$$

(43)

with initial-boundary conditions as $u(r,0)=r^{2}$, $u(0,t)=4t, u(1,t)=1+4t$ and exact solution $u(r,t)=r^{2}+4t$, for $\alpha =1$.

Figures 9 and 10 show the approximate solution of Eq. (43) for different values of $\alpha =0.5$ and 1 respectively. Figure 11 shows the absolute error graph of Eq. (43), for $\alpha =1$.

Fig. 9

Approximate solution for $\alpha =0.5$, Example 2

Fig. 10

Approximate solution for $\alpha =1$, Example 2

Fig. 11

Absolute error for $\alpha =1$, Example 2

Figures 12 and 13 show the behaviour of approximate solution of Eq. (43), for different values of $\alpha =0.7,0.8,0.9$ and 1 for fix value of $t=1$ and $r=1$ respectively. From Figs. 12 and 13, it is clear that solution varies continuously for different values of $\alpha$ and approaches monotonically to integer order NSE continuously as $\alpha \rightarrow 1$ (Fig. 14).

Fig. 12

The behaviour of solution for different values of $\alpha$ at $\hbox {t}=1$, Example 2

Fig. 13

The behaviour of solution for different values of $\alpha$ at $\hbox {r}=1$, Example 2

Fig. 14

Difference of absolute errors with and without noise, Example 2

In Table 3, we list the errors $E_1 ,E_2 ,E_1^*$ and $E_2^{*}$ to show the stability of our method.

Table 3 Absolute and RMS errors with and without noise

Conclusions and Future Work

The approximate solutions can be obtained by solving some algebraic equations, so it is very handy for computational purposes. There are few numerical methods to solve FNSE but none of them show the stability and convergence of method. In our method stability with respect to the data is restored and accuracy is good even for high noise levels in the data. Convergence and error analysis are also given. From numerical examples we show that solution varies continuously for different values of $\alpha$. For $\alpha =1$ solution for standard NSE is obtained. For future work we can use different orthonormal polynomials to achieve better accuracy.