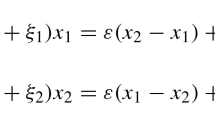Keywords

12.1 Introduction

Oscillatory processes are widely used in various fields of both fundamental and applied science. The theory of oscillations, which studies oscillations occurring in various systems, is an intensively developing field of modern mathematics and physics [11, 20, 22, 26]. The main models of the theory of oscillations are the linear and nonlinear oscillators, rotators, RLC circuit, etc. These are used in modeling of physical processes in various real-life systems. New features of oscillatory processes appear in the cases when there is a large number of interacting subsystems. The standard model of wave processes is a finite and infinite chain of coupled (interacting) oscillators. Such chains are often used in radio engineering as filters that allocate or suppress signals with frequencies lying in a certain band. From the fundamental point of view, chains of oscillators are used as models of solid media with oscillations and waves with various properties [3, 16, 27]. The oscillatory processes of a large number of such elements are called waves. Wave phenomena are widespread in nature: waves on the surface of a fluid, sound waves in a gas, compression-expansion waves in a solid, vibrations of a string and membrane, electromagnetic waves, etc.

Note that, in addition to nonlinear oscillations, there are also nonlinear waves described by nonlinear partial differential equations. Within the framework of the theory of nonlinear waves there exist the standard models, similar to the reference models in the theory of oscillations, namely, simple waves, shock waves, as well as the solitary waves (solitons), that play significant roles in the theory of nonlinear processes. One of the basic models for studying the nonlinear processes is the sine-Gordon model (a chain of nonlinear oscillators connected by coil springs) [17].

Another example of a strong nonlinear system playing a significant role in modern research is hysteresis (see [4, 9, 14, 18, 19, 28] and related references). Hysteretic behavior is typical both for the characteristics of substances (ferroelectrics, ferromagnetics, piezoelectrics, etc.), and for the dynamics of many mechanical systems (backlash, stop, etc.). In the mechanical systems hysteretic nonlinearities arise due to an aging of the material and must be taken into account at the modeling level for the corresponding mechanical systems. The hysteresis in such systems leads to the problem of investigation of nonlinear operator-differential equations, which is an extremely complex problem.

Such an interest to hysteretic phenomena is caused by high incidence of these phenomena in a various technical systems (such as robotic, mechanical, electro-mechanical systems, management systems for tracking of aircrafts, etc.) Also, these phenomena determine some unusual elasto-plastic properties of modern nanomaterials (such a properties are served as a base for construction of modern self-healing materials) on the basis of fullerene films. Moreover, the hysteretic phenomena are widely known in biology, chemistry, economics, etc. It should be noted that the hysteretic behavior of such systems is caused by either their internal structure, or the presence of separate blocks with hysteretic characteristics. Of course, when modeling the dynamics of such systems, it is necessary to use an adequate mathematical apparatus.

Currently used models of hysteretic phenomena both constructive (such as non-ideal relay, Preisach and Ishlinskii-Prandtl models, etc. [21]), and phenomenological (Bouc-Wen model, Duhem model, etc. [6]) assume a priori the stability of the parameters that identify the hysteretic properties of the corresponding operators. However, the stability of parameters in real-life engineering systems (e.g., in the systems modelled by the coupled inverted pendula [20]) does not always take place. In this way, such operators are the natural model in the situation when the parameters of hysteresis carrier are under influence of stochastic, uncontrollable affections. For example, it is difficult to control the switching numbers of non-ideal relay, which is a part of control systems of the corresponding devices, when the various external factors take place (in this case the switching numbers may be subjected to random changes). These circumstances make it necessary to develop the extended models of hysteretic effects, taking into account the stochastic changes in the parameters of the corresponding hysteretic operators. We note that the equations with random parameters (principally such equations are linear) were considered in [13, 30, 31]. The strongly nonlinear differential equations containing the operator nonlinearity with random properties have not been considered in the literature. Thus, construction and investigation of the properties of hysteretic operators with random parameters seems novel and promising problem.

An important problem is the study of resonance phenomena in systems with hysteresis [9]. In this way we note a well-known fact: in the presence of viscous friction the harmonic resonance is not realized (for details see, e.g., [8]). In particular, in [8] it is considered the dynamics of the oscillator with strong nonlinearity (authors studied its phase portrait and the trajectory). It is proved that the form of periodic solutions depends on the “origin” of strong nonlinearity. The main result of [8] is that for a class of equations, which describe the harmonic oscillations with resonance external force and hysteretic operator in the right part of equation, the presence or absence of unbounded solutions depend on the amplitude of the external excitation.

In this chapter we study the resonance properties of systems in which the energy pumping is realized due to the presence of external source with hysteretic nature. Examples of such systems are the oscillations of the ferromagnetic ball in a magnetic field, oscillations of the system of coupled oscillators when the “connection force” has a hysteretic nature [18], etc. Moreover, we introduce the new class of hysteretic operators with random parameters. We consider the definition of these operators in terms of the “input-output” relations. The properties of such operators are also considered and discussed for the example of a non-ideal relay with random parameters. Application of hysteretic operator with stochastic parameters is demonstrated for the example of simple oscillating system and the results of numerical simulations are presented. Also, the dynamics of nonlinear oscillatory system (discrete mechanical sine-Gordon system) is investigated taking into account the hysteretic coupling conditions between individual links of such a system. We consider the sine-Gordon model in the case when the links between pendulums contain hysteresis nonlinearities (modified sine-Gordon model). On the basis of numerical modeling, the dynamics of soliton-like solutions in such a system is studied and filtering properties of hysteretic links are established.

12.2 Oscillator Under Hysteretic Force

12.2.1 Unbounded Solutions to Autonomous Systems with Hysteretic Blocks with Negative Spin

Let us consider a system whose dynamics is described by the following equation with the corresponding initial conditions:

$$\begin{aligned} \begin{array}{c} \ddot{x}+ \omega ^{2}x=R[\alpha ,\beta ,\omega _{0}]x,\\ \\ x(0)=x_{0},\,\,\dot{x}(0)=x_{1}. \end{array} \end{aligned}$$
(12.1)

where \(R[\alpha ,\beta ,\omega _{r}]\) is a non-ideal relay operator with the negative spin, and \(\omega _{0}\) is an initial state of this operator. A more detailed description of the properties of such an operator can be found in [9].

Theorem. Let the initial value satisfies the condition \(x_{0}\notin [\alpha ,\beta ]\). Then, the corresponding solutions are unbounded.

Proof: For simplicity we consider the case where \(\alpha =-1\), \(\beta =1\). Let us assume that the initial conditions obey the following inequality \(x_{0}<-1\), then at a certain initial period of time (\(t\ge 0)\) the solution to (12.1) will have the form \(x_{0}=A_{1}\cos (t+\varphi _{0})+1\), \(0\le t\le t_{0}\), where \(t_{1}\) is the time at which the equality \(x(t_{1})=1\) is satisfied. It is clear that this moment exists. The solution to (12.1) at interval \([t_{1},t_{2}]\) will be determined by the relation \(x_{1}(t)=A_{1}\cos (t+\varphi _{1})\). Here \(t_{2}\) is the moment at which the equality \(x_{1}(t_{2})=-1\) is satisfied. It is also clearly that such a moment exists (\(A_{1}\ge 1\) because \(x_{1}(t_{1})=1\)), etc.

Thus, in the absence of switching the solution to (12.1) is composed of the functions defined by following relations for even n:

$$ x_{n}(t)=A_{n}\cos (t+\varphi _{n})+1, $$

and for odd n:

$$ x_{n+1}(t)=A_{n+1}\cos (t+\varphi _{n+1}). $$

Using the continuity conditions for solution and its derivative at the point \(t_{n}\) (the moment when the right switching number is achieved) we obtain the following equality:

$$\begin{aligned} \left\{ \begin{array}{rcl} A_{n}\cos (\varphi _{n})+1&{}=&{}A_{n+1}\cos (\varphi _{n+1}),\\ -A_{n}\sin (\varphi _{n})&{}=&{}-A_{n+1}\sin (\varphi _{n+1}),\\ A_{n}\cos (\varphi _{n})+1&{}=&{}1. \end{array} \right. \end{aligned}$$
(12.2)

Squaring and summing the first two equalities in (12.2) we obtain:

$$\begin{aligned} \left\{ \begin{array}{rcl} A_{n}^2\cos ^2(\varphi _{n})+2A_{n}\cos (\varphi _{n})+1&{}=&{}A_{n+1}^2\cos ^2(\varphi _{n+1}),\\ A_{n}^2\sin ^2(\varphi _{n})&{}=&{}A_{n+1}^2\sin ^2(\varphi _{n+1}),\\ A_{n}\cos (\varphi _{n})&{}=&{}0, \end{array} \right. \end{aligned}$$
(12.3)

or

$$\begin{aligned} \left\{ \begin{array}{rcl} A_{n}^2+2A_{n}\cos (\varphi _{n})+1&{}=&{}A_{n+1}^2,\\ A_{n}\cos (\varphi _{n})&{}=&{}0. \end{array} \right. \end{aligned}$$
(12.4)

Finally we obtain:

$$\begin{aligned} A_{n}^2+1=A_{n+1}^2 \end{aligned}$$
(12.5)

Similarly, for the next interval, at the point at which the solution has the value −1, we have:

$$\begin{aligned} \left\{ \begin{array}{rcl} A_{n+1}\cos (\varphi _{n+2})&{}=&{}A_{n+2}\cos (\varphi _{n+3})+1,\\ -A_{n+1}\sin (\varphi _{n+2})&{}=&{}-A_{n+2}\sin (\varphi _{n+3}),\\ A_{n+1}\cos (\varphi _{n+2})&{}=&{}-1. \end{array} \right. \end{aligned}$$
(12.6)

Squaring the first two equalities:

$$\begin{aligned} \left\{ \begin{array}{rcl} A_{n+1}^2\cos ^2(\varphi _{n+2})-2A_{n+1}\cos (\varphi _{n+2})+1&{}=&{}A_{n+2}^2\cos ^2(\varphi _{n+3}),\\ A_{n+1}^2\sin ^2(\varphi _{n+2})&{}=&{}A_{n+2}^2\sin ^2(\varphi _{n+3}),\\ A_{n+1}\cos (\varphi _{n+2})&{}=&{}-1. \end{array} \right. \end{aligned}$$
(12.7)

Then, summation of them leads to

$$\begin{aligned} \left\{ \begin{array}{rcl} A_{n+1}^2-2A_{n+1}\cos (\varphi _{n+2})+1&{}=&{}A_{n+2}^2,\\ A_{n}\cos (\varphi _{n})&{}=&{}-1. \end{array} \right. \end{aligned}$$
(12.8)

Finally we get:

$$\begin{aligned} A_{n+2}^2=A_{n+1}^2+3 \end{aligned}$$
(12.9)

Then, from (12.8) and (12.9) it follows:

$$ A_{n+2}^2=A_{n}^2+4 $$

In other words, if the initial value is such that the hysteretic element “works”, then the corresponding solution is unbounded. Results of numerical simulations are presented in Fig. 12.1.

Fig. 12.1
figure 1

Solution (left panel) and phase portrait (right panel) to (12.1) with given initial conditions

Full size image

Note 1. Let us note that the solution oscillates and the rate of growth of amplitude is proportional to \(\sqrt{t}\).

Note 2. The theorem remains valid for other types of hysteretic nonlinearities. The main requirement is the positiveness of the loop’s area.

12.2.2 Systems with Coulomb and Viscous Friction

“Natural” generalization of the system under consideration is the system with various types of friction (namely, the Coulomb and viscous friction). The dynamics of oscillator with a viscous friction can be described by the equation:

$$\begin{aligned} \begin{array}{c} \ddot{x}+ 2b\dot{x}+\omega ^{2}x=R[\alpha ,\beta ,\omega _{0}]x,\\ x(0)=x_{0},\,\, \dot{x}(0)=x_{1}. \end{array} \end{aligned}$$
(12.10)

In the following consideration we assume that switching numbers of a non-ideal relay are symmetric relative to the origin. Considering the dynamics of the solution, it should be noted that once the amplitude of the solution becomes high enough, the work of the friction force balances the energy obtained by the oscillator from the hysteretic element. Let us consider two cases related to the different kind of the roots of characteristic equation of the linear part of the (12.10).

Let us consider (12.10) with a given initial conditions for these two cases:

$$\begin{aligned} \ddot{x}^{+}+ 2b\dot{x}^{+}+\omega ^{2}x^{+}=1, \end{aligned}$$
(12.11)
$$\begin{aligned} \ddot{x}^{-}+ 2b\dot{x}^{-}+\omega ^{2}x^{-}=-1. \end{aligned}$$
(12.12)

For the first case a solution to equation has the following form:

$$\begin{aligned} x^{+}(t)=\frac{1}{\omega ^{2}}+C_{1}\exp {\left[ t\left( -b-\sqrt{b^2-\omega ^2}\right) \right] }+C_{2}\exp {\left[ t\left( -b+\sqrt{b^2-\omega ^2}\right) \right] } \end{aligned}$$
(12.13)

Obviously, the term \(\frac{1}{\omega ^{2}}\) is an asymptotic limit for this solution, and therefore, if the inequalities \(\alpha <\frac{1}{\omega ^{2}}\), \(\beta >-\frac{1}{\omega ^{2}}\) are satisfied for some T, then the inequality \(x^{+}=-\alpha \) is obeyed too. Further dynamics will be determined by an equation with a value of a non-ideal relay converter equal \(-\alpha =-1\). Reasoning in a similar way, it is easy to establish that for some \(T_{1}\) the solution will take the value \(\alpha \). Taking into account the fact that the equations are autonomous, the solutions obtained in this way will be periodic. A period can be found using the following relations:

$$\begin{aligned} x^{+}(t)=C_{1}\exp {(t\lambda _{1})}+C_{2}\exp {(t\lambda _{2})},\end{aligned}$$
(12.14)
$$\begin{aligned} x^{-}(t)=C_{3}\exp {(t\lambda _{3})}+C_{4}\exp {(t\lambda _{4}}), \end{aligned}$$
(12.15)

where

$$\begin{aligned} \begin{array}{c} \displaystyle C_{1}=\frac{\left( 1+\omega ^2\right) \left( -b+\sqrt{b^2-\omega ^2}\right) }{2\omega ^2\sqrt{b^2-\omega ^2}},\\ \\ \displaystyle C_{2}=\frac{\left( 1+\omega ^2\right) \left( b+\sqrt{b^2-\omega ^2}\right) }{2\omega ^2\sqrt{b^2-\omega ^2}},\\ \\ \displaystyle C_{3}=-\frac{\left( -1+\omega ^2\right) \left( -b+\sqrt{b^2-\omega ^2}\right) }{2\omega ^2\sqrt{b^2-\omega ^2}},\\ \\ \displaystyle C_{4}=-\frac{\left( 1+\omega ^2\right) \left( b+\sqrt{b^2-\omega ^2}\right) }{2\omega ^2\sqrt{b^2-\omega ^2}},\\ \\ \lambda _{1}=\lambda _{3}=-b-\sqrt{b^2-\omega ^2},\\ \lambda _{2}=\lambda _{4}=-b+\sqrt{b^2-\omega ^2},\\ \end{array} \end{aligned}$$
(12.16)

and the period of oscillations is determined by

$$\begin{aligned} T=\frac{\pi }{\sqrt{b^2-\omega ^2}}. \end{aligned}$$
(12.17)

Let us consider the second case when the roots of the characteristic equation to the linear part of (12.10) are complex conjugate. Then, the solution to the equation with initial conditions can be written as follows:

$$\begin{aligned} x(t)=\exp {(-bt)}\left[ B\cos (\omega t)+C\sin (\omega t)\right] -\frac{1}{\omega _{0}^2}, \end{aligned}$$
(12.18)

where \(\omega =\sqrt{b^2-\omega _{0}^2}\).

Taking into account the initial conditions, we get:

$$\begin{aligned} -\frac{1}{\omega _{0}^2}+\frac{1+\omega _{0}^2}{\omega _{0}^2}\sqrt{1+\left( \frac{b}{\omega }\right) ^2}\exp {(-bt)}\sin \left[ \omega t+\arcsin \left( \frac{1}{\sqrt{1+\left( \frac{b}{t}\right) ^2}}\right) \right] =1. \end{aligned}$$
(12.19)

A half period can be defined as a solution to a transcendental equation (12.19). A solution and phase portrait are shown in the following Fig. 12.2.

Fig. 12.2
figure 2

Solution (left panel) and phase portrait (right panel) to (12.10) with given initial conditions

Full size image

Note that for a given value of the parameter \(b=1\), a bifurcation occurs. Such a bifurcation corresponds to a change in the period (see Fig. 12.3).

Fig. 12.3
figure 3

Oscillations in the system (12.10) at \(b=0.9\) (left panel) and \(b=1.1\) (right panel)

Full size image

The dynamics of the oscillator with the Coulomb friction under external hysteretic affection is described by the equation:

$$\begin{aligned} \ddot{x}+\eta \mathrm {sign}(\dot{x})+x=R[\alpha ,\beta ,\omega _{0}]x \end{aligned}$$
(12.20)

Multiplying both sides of (12.21) by \(\dot{x}\), and integrating over the period T we obtain:

$$\begin{aligned} \int \limits _{0}^{T}\frac{1}{2}\frac{d}{dt}(\dot{x}^2+x^2)\mathrm {d}t=-\int \limits _{0}^{T}\eta \mathrm {sign}(\dot{x})\dot{x}\mathrm {d}t+\int \limits _{0}^{T}\dot{x}R[\alpha ,\beta ,\omega _{0}]x\mathrm {d}t, \end{aligned}$$
(12.21)
$$\begin{aligned} \varDelta E=-\eta \int \limits _{0}^{T}|\dot{x}|\mathrm {d}t+S_{p}. \end{aligned}$$
(12.22)

From the (12.22) it follows that the energy gain \(\varDelta E\) will be positive if the work of friction forces will be smaller than the loop’s area \(S_{p}\) (otherwise it will be negative). Thus, the considered system can be treated as a system with the negative feedback. Let us note that at steady-state regime the condition \(2(x_{\max }-x_{\min })\eta =S_{p}\) is satisfied. This means that the amplitude of the oscillation is such that the work of frictional forces on the period is equal to the loop’s area. These results are illustrated in Fig. 12.4.

Fig. 12.4
figure 4

Solution (left panel) and phase portrait (right panel) to the system (12.20) at \(\eta =0.5\)

Full size image

As it can be seen from the presented results, a harmonic oscillator with Coulomb and viscous friction under hysteretic external force significantly differs from the “classical” model of a harmonic oscillator, where, regardless to initial conditions, the damped oscillations in the vicinity of equilibrium point take place.

12.2.3 Frequency “trapping” in the System with Relay Nonlinearity: The Small Parameter Method

Synchronization of periodic self-oscillations by a harmonic external force has been a long-studied phenomenon, which can be formulated as follows. As soon as the frequency of the external excitation becomes close to the frequency of free self-oscillations, synchronization (“trapping”) of the frequency occurs. Let us consider a self-oscillating system with one degree of freedom, which is under periodic external force with a frequency \(\omega \) (we consider the case where this frequency is close to the frequency of free self-oscillations).

$$\begin{aligned} \ddot{x}+ 2b\dot{x}+\omega _{0}^{2}x=R[\alpha ,\beta ,\omega _{r}]x+B_{1}\sin {\omega t}. \end{aligned}$$
(12.23)

To analyze the dynamic features of such a system, the small parameter method is used [10], which allows to make an identification of the process of frequency “trapping” (the frequency of external harmonic force) by an autonomous system with hysteresis. To do this, we rewrite the original (12.23) in the form:

$$\begin{aligned} \ddot{x}+\omega _{0}^{2}x=\varepsilon \left( -2b\dot{x}+R[\alpha ,\beta ,\omega _{r}]x+B_{1}\sin {\omega t}\right) , \end{aligned}$$
(12.24)

where \(\varepsilon \) is a small parameter. The solution to this equation can be written in the following standard form:

$$\begin{aligned} x=A\cos {\psi }+\varepsilon u_{1}\left( A,\psi \right) +\cdots , \end{aligned}$$
(12.25)

where \(\psi =\omega t+\varphi (t)\), and \(u_{1}\left( A,\psi \right) \) are unknown functions which do not contain resonance frequencies; A and \(\varphi \) are the amplitude and phase, respectively, which satisfy the following equations:

$$\begin{aligned} \dot{A}=\varepsilon f_{1}\left( A,\varphi \right) +\ldots ;\,\dot{\varphi }=-\varDelta +\varepsilon F_{1}\left( A,\varphi \right) +\cdots , \end{aligned}$$
(12.26)

and \(\varDelta =\omega -\omega _{0}\) is the frequency difference. \(F_{1},f_{1}\) are unknown functions that are to be determined from the condition of the absence of resonant terms in the function \(u_{1}\). Substituting the general form of the solution into the original equation, taking into account the equations for the amplitude and phase and using the described definitions we obtain for \(\dot{x}\) and \(\ddot{x}\):

$$\begin{aligned} \dot{x}=\dot{A}\cos {\psi }-A\sin {\psi }\dot{\psi }+\varepsilon \dot{u}_{1}\omega ; \end{aligned}$$
(12.27)
$$\begin{aligned} \ddot{x}=\ddot{A}\cos {\psi }-2\dot{A}\sin {\psi }\dot{\psi }-A\cos {\psi }\dot{\psi }^{2}-A\sin {\psi }\ddot{\psi }+\varepsilon \ddot{u}_{1}\omega ^{2}. \end{aligned}$$
(12.28)

Substituting the obtained expressions in the left side of the (12.24), and using (12.25) and (12.26) we get:

$$\begin{aligned} \begin{array}{l} \ddot{x}+\omega _{0}^{2}x =\ddot{A}\cos {\psi }-2\dot{A}\sin {\psi }\dot{\psi }-A\cos {\psi }\dot{\psi }^{2}-A\sin {\psi }\ddot{\psi }+\varepsilon \ddot{u}_{1}\omega ^{2}+\\ \\ +\,\omega _{0}^{2}A\cos {\psi }+\omega _{0}^{2}\varepsilon u_{1}=\varepsilon \ddot{u}_{1}\omega ^{2}+\omega _{0}^{2}\varepsilon u_{1}-\left( 2\dot{A}\dot{\psi }+A\ddot{\psi }\right) \sin {\psi }+\\ \\ +\,\left( \ddot{A}-A\dot{\psi }^{2}+\omega _{0}^{2}A\right) \cos {\psi }=\\ \\ =\varepsilon \ddot{u}_{1}\omega ^{2}+\omega _{0}^{2}\varepsilon u_{1}-\left( 2\varepsilon f_{1}\left( -\varDelta +\varepsilon F_{1}\right) +A\varepsilon \dot{F}_{1}\right) \sin {\psi }+\\ \\ +\,\left( \varepsilon \dot{f}_{1}-A(-\varDelta +\varepsilon F_{1})^{2}+\omega _{0}^{2}A\right) \cos {\psi }. \end{array} \end{aligned}$$
(12.29)

For the right side of the (12.24) we obtain in the same manner:

$$\begin{aligned} \begin{array}{l} \varepsilon \left( -2b\dot{x}+R[\alpha ,\beta ,\omega _{r}]x+f(t)\right) =\\ \\ =\varepsilon \left( R[\alpha ,\beta ,\omega _{r}]x-2b\left( \dot{A}\cos {\psi }-A\sin {\psi }\dot{\psi }+\varepsilon u_{1}\omega )\right) +f(t)\right) =\\ \\ =\varepsilon \left( R[\alpha ,\beta ,\omega _{r}]x-2b\varepsilon f_{1}\cos {\psi }+2b A\left( -\varDelta +\varepsilon F_{1}\right) \sin {\psi }+\varepsilon u_{1}\omega +f(t)\right) . \end{array} \end{aligned}$$
(12.30)

Equating the terms of the same order of smallness in the right and left parts, we obtain the equation for determining the unknown function \(u_{1}\):

$$\begin{aligned} \begin{array}{l} \displaystyle \omega ^{2}\frac{\partial ^{2}u_{1}}{\partial \psi ^{2}}+\omega _{0}^{2}u_{1}=\left( 2\omega _{0}f_{1}-A\frac{\partial F_{1}}{\partial \varphi }\varDelta \right) \sin {\psi }+\left( 2\omega _{0}AF_{1}-A\frac{\partial f_{1}}{\partial \varphi }\varDelta \right) \cos {\psi }-\\ \\ -\,AR[\alpha ,\beta ,\omega _{r}]x\cos {\psi }+f(t). \end{array} \end{aligned}$$
(12.31)

From the condition of the absence of resonant terms in the function \(u_{1}(A,\psi )\) (factors at harmonic functions are equal to zero) we obtain the following equations for the unknown functions \(F_{1}\) and \(f_{1}\):

$$\begin{aligned} 2f_{1}-A\frac{\varDelta }{\omega _{0}}\frac{\partial F_{1}}{\partial \varphi }=-2b A -\frac{B_{1}}{\omega }\sin {\varphi };\,\,2AF_{1}+\frac{\varDelta }{\omega _{0}}\frac{\partial f_{1}}{\partial \varphi }= AR[\alpha ,\beta ,\omega _{r}]x -\frac{B_{1}}{\omega }\cos {\varphi }. \end{aligned}$$
(12.32)

The particular solution to this system is:

$$\begin{aligned} f_{1}=-b A -\frac{B_{1}\sin {\varphi }}{\omega +\omega _{0}};\,\, F_{1}=\frac{R[\alpha ,\beta ,\omega _{r}]x}{2} -\frac{B_{1}\cos {\varphi }}{A(\omega +\omega _{0})}. \end{aligned}$$
(12.33)

In the first approximation in \(\varepsilon \) from (12.33) and (12.26), taking into account the condition \(u_ {1}(A,\psi )=0\) we get:

$$\begin{aligned} \dot{A}=-b A -\frac{B_{1}\sin {\varphi }}{\omega +\omega _{0}}, \dot{\varphi }=-\varDelta +\frac{R[\alpha ,\beta ,\omega _{r}]x}{2} -\frac{B_{1}\cos {\varphi }}{A(\omega +\omega _{0})}. \end{aligned}$$
(12.34)

The numerical values of the amplitude and phase are presented in Fig. 12.5. In Fig. 12.6 we present the amplitude-phase portrait as well. The amplitude-phase portrait of the system (12.34) is characterized by complex behavior, with many self-intersections.

Fig. 12.5
figure 5

Aplitude (left panel) and phase (right panel) versus time for the following parameters: \(b=0.5\), \(B_{1}=1\), \(\omega _{0}=1\), \(\omega =1.2\), \(\alpha =-\beta =1\), \(\omega _{r}=1\)

Full size image
Fig. 12.6
figure 6

Aplitude-phase portrait for the system under consideration with the parameters as in Fig. 12.5

Full size image

In Fig. 12.7 we present the numerical solution to the system (12.23) together with the time dependence of the disturbing force, as well as the behavior of the system without external excitation.

Fig. 12.7
figure 7

Left panel: numerical solution to the system (12.23); Middle panel: time dependence of the disturbing force; Right panel: system behavior without external force

Full size image

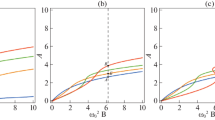
As follows from the presented numerical results, the solution to the system becomes not-smooth while switching of a non-ideal relay takes place function. Analyzing the obtained solution, it can be noted that it contains harmonics of a smaller amplitude in addition to the main harmonics. Note that the synchronization of the frequency of free self-oscillations with the frequency of external force also takes place for systems containing hysteretic nonlinearity. As the amplitude of the external force increases, the frequency interval (\(\varDelta \)) increases too (at this interval the frequency “trapping” takes place). Figure 12.8 presents the dependence of the amplitude of the external force on the frequency of the periodic force, at which the frequency “trapping” occurs.

Fig. 12.8
figure 8

The frequency “trapping” domain

Full size image

12.3 Oscillator Under Hysteretic Force with Random Parameters

12.3.1 Non-ideal Relay with Random Parameters

Consider a non-ideal relay (a detailed description of this and other hysteretic converters, as well as their properties in the case of deterministic parameters, are given in the classical book of Krasnosel’skii and Pokrovskii [9]), in which the switching numbers are not fixed, but are treated as random variables with absolutely continuous distribution function. Concerning these random variables, we make the following assumption: the probability density of each of the switching numbers will be assumed to be finite with non-intersecting supports. We denote these switching numbers as \(\varphi _{\alpha }(u)\) and \(\varphi _{\beta }(u)\). We will consider the case when the supports of the function \(\varphi _{\alpha }(u)\) and \(\varphi _{\beta }(u)\) are contained in the intervals \([u_{\alpha }^{-},u_{\alpha }^{+}]\) and \([u_{\beta }^{-},u_{\beta }^{+}]\), respectively.

Following the basic ideas presented in [9] (as well as, following the terminology presented in this book), the dynamics of the input-output relations for the operator of a non-ideal relay with random switching numbers is determined by two relations, namely: “input-state” and “state-output”. We assume that all permissible continuous inputs are given on the non-negative semi-axis \((t>0)\) (the input-output relation for this converter R has the form \(x(t)=R\left[ t_{0}, x_{0}, \alpha , \beta \right] u(t),\,(t\ge t_{0})\)). The space of possible states of such an operator is defined as \(\varOmega =\varOmega (\omega , p, u)\), \(\left( \omega ={0,1}, 0\le p \le 1, -\infty< u < +\infty \right) \).

The variable state of the converter \(R\left[ {(1; p_{0});x_{0}}; \varphi _{\alpha }(u);\varphi _{\beta }(u)\right] u(t)\) is a random value that takes the value 0 with probability \((1-p(t))\) and a value of 1 with probability p(t). In other words, it can be presented as a pair \(\{1; p(t)\}\) (here the second output component corresponds to the probability that at the time t the first component is 1). The output of this converter is a random function x(t) (Markovian process) taking a value of 1 with probability p(t). The rule that determines the value of probability p(t) will be given below.

12.3.1.1 Definition of Input-Output Relation for a Non-ideal Relay with Random Switching Numbers

Following the classical scheme proposed in [9], we give the definition of the input-output relation by means of a three-step construction:

  • At the first step we define the input-output relation on the monotonic inputs only;

  • At the second step, using the semi-group identity, the input-output relation is defined for all piece-wise monotonic inputs;

  • At the third step, using the special limit construction, the corresponding converter will be defined for all monotonic inputs.

We define the operator R on the monotonic inputs. Let us assume that at the initial time point \(t_{0}\) (to simplify the calculations, we assume that \(t_{0}=0\)) the operator R is in the state \({1; p_{0}; u_{0}}\in \varOmega , \left( u(0)=u_{0}\right) \). Let the input u(t) be a monotonic increase, then for the time \(t>0\) the output is \(x(t)=\{1; p(t)\}\) where

$$\begin{aligned} p(t)=\max \left\{ p_{0}; \int \limits _{-\infty }^{u(t)}\varphi _{\beta }(u)\mathrm {d}u\right\} . \end{aligned}$$
(12.35)

The semi-group identity for the operator R immediately follows from the definition. Let \(t_{1}\) be an arbitrary moment of time satisfying the inequality \(0<t_{1}<t\), then the semi-group identity for the operator of a non-ideal relay has the form:

$$\begin{aligned} R\left[ t_{0}; p_{0}; u_{0}; \varphi _{\alpha }; \varphi _{\beta }\right] u(t)=R\left[ t_{1};R\left[ t_{0}; p_{0}; u_{0}; \varphi _{\alpha }; \varphi _{\beta }\right] u(t_{1});u(t_{1}); \varphi _{\alpha }; \varphi _{\beta } \right] u(t). \end{aligned}$$
(12.36)

To define an operator on the piece-wise monotonic inputs (in the case of a finite interval [0, T]), we break this interval by points \(t_{1}, t_{2},\ldots , t_{n}\) into intervals of monotonicity. On each of them we define the corresponding operator as an operator on a strictly monotonic input whose initial state will be defined as the state at the instant corresponding to the “last” change in the behavior of the input.

To determine the operator R on continuous inputs, we use the following limit construction. Let \(u(t) (t\in [0,T])\) be an arbitrary continuous input. Let us consider an arbitrary sequence of piece-wise monotonic inputs \({u_{n}(t)},\,(n=1,2,...)\) that converges uniformly to each element of this sequence u(t). A single-variable state \(p_{n}(t),\,(n=1,2,...)\) will form a sequence of state variables \({p_{n}(t)},\,(n=1,2,...)\). Let us prove that the sequence \({p_{n}(t)},\,(n=1,2,...)\) converges uniformly. We estimate the absolute value of the difference:

$$\begin{aligned} \left| p_{n}(t)-p_{m}(t)\right| \le \max \limits _{t} \left| \int \limits _{-\infty }^{u_{n}(t)}\varphi _{\alpha }(u)\mathrm {d}u-\int \limits _{-\infty }^{u_{m}(t)}\varphi _{\alpha }(u)\mathrm {d}u\right| =\max \limits _{t} \left| \int \limits _{u_{n}(t}^{u_{m}(t)}\varphi _{\alpha }(u)\mathrm {d}u\right| . \end{aligned}$$
(12.37)

Since the function \(\varphi _{\alpha }(u)\) is continuous, and because of uniform convergence also

$$ \lim \limits _{n,m\rightarrow \infty }\max \limits _{t} \left| u_{n}(t)- u_{m}(t)\right| =0, $$

as well as, using the mean value theorem:

$$\begin{aligned} \max \limits _{t} \left| \int \limits _{u_{n}(t}^{u_{m}(t)}\varphi _{\alpha }(u)\mathrm {d}u\right| \le \max \limits _{t} \varphi _{\alpha }(t)\left[ u_{n}(t)- u_{m}(t)\right] \nonumber \end{aligned}$$

the right-hand side of the inequality (12.37) tends to zero. Thus, the sequence of probabilities \(p_{n}(t)\) is fundamental (the continuity is obvious), then there is \(\lim \limits _{n\rightarrow \infty } p_{n}(t)=p(t)\), which is comparable to an arbitrary continuous input u(t).

12.3.1.2 Monotonicity of a Non-ideal Relay with Random Parameters

Let us consider the monotonicity property for the constructed converter. We determine the monotonicity with respect to the initial state of the non-ideal relay: if \(\{u(t_{0}, x_{0}\},\,\{v(t_{0}, y_{0}\}\in \varOmega (\alpha ,\beta ),\,x_{0}\le y_{0}\) and \(u(t)\le v(t)\,\,(t\ge t_{0})\), then we have:

$$R\left[ t_{0},x_{0},\alpha ,\beta \right] u(t)\le R\left[ t_{0},x_{0},\alpha ,\beta \right] v(t)\,\,(t\ge t_{0}).$$

This property can be used as the definition of a non-ideal relay. In order to use it, we define the outputs corresponding to monotonic inputs. Applying a semi-group identity, we define the outputs for piece-wise monotonic inputs. Further, this relation is extended by means of the special limit construction to all monotonic inputs. In this case, this relation will be the exclusive. We can also note a natural monotonicity in the switching numbers. With respect to the modified operator of a non-ideal relay with random parameters, the analogue of monotonicity can be presented in the form of the following theorem.

Theorem 12.1

Let \(p\{x_{01}=1\}\ge p\{x_{02}=1\}\) and \(x_{1}(t)\ge x_{2}(t)\). Then for any t: \(p\{x_{1}=1\}\ge p\{x_{2}=1\}\).

12.3.2 Dynamics of a System Under Non-ideal Relay with Random Parameters

In order to show the action of the developed operator on the real physical system let us consider the simple oscillating system under hysteretic force with random parameters. Such a simple system is considered in [23, 24] and the external force has the form of a non-ideal relay with inversion of the switching numbers. One of the main results of these studies is the existence of unlimited solutions, namely, if the initial conditions are such that the hysteretic operator is triggered at the first cycle of oscillations, then the corresponding solution is unlimited, while the growth rate of the amplitude is proportional to the square root of time. Let us consider an analogous system with a non-ideal relay with switching numbers distributed according to an even-dimensional law. The equation of motion together with the corresponding initial conditions has the following form:

$$\begin{aligned} \begin{array}{c} \ddot{x}(t)+ \omega ^{2}x(t)=R[t_{0};p_{0};u_{0};\varphi _{\alpha };\varphi _{\beta }]x(t),\\ \\ x(0)=x_{0},\,\dot{x}(0)=x_{1}. \end{array} \end{aligned}$$
(12.38)

To implement the numerical solution of the system (12.38), it is necessary to generate a set of random values corresponding to the switching numbers. Let us consider the case when \(\varphi _{\alpha }(u)\) and \(\varphi _{\beta }(u)\) corresponds to the uniform distribution law for \(\alpha \) and \(\beta \). For definiteness, we will assume that these functions correspond to uniform distributions in the intervals \([-1.5,-0.5]\) and [0.5, 1.5], respectively. The solution of the system (12.38) can be obtained by specifying the initial conditions and the values of the switching numbers corresponding to the non-ideal relay. At each period, the switching numbers are selected from the corresponding distributions with the initial conditions for the next realization corresponding to the values of the phase coordinates obtained at the previous step. Using the described algorithm, a solution to the system (12.38) is obtained and the corresponding law of motion together with the phase portrait are shown in Fig. 12.9. Let us note, that non-smooth character of the phase portrait is caused by the hysteretic nature of the external excitation, as well as the random nature of the parameters of a non-ideal relay.

Fig. 12.9
figure 9

Solution (top panel) and phase portrait (bottom panel) for the system (12.38)

Full size image

The following theorem characterizes the dynamics of the system (12.38).

Theorem 12.2

Let us suppose that the supports of the function \(\varphi _{\alpha }\) and \(\varphi _{\beta }\) do not intersect. Then \(\overline{\lim \limits _{t\rightarrow \infty }x(t)}=\infty \), that is the amplitude tends to infinity with probability equals to 1.

The proof of this theorem follows from the fact that the area of the minimal hysteretic loop is positive \(S_{\min }>0\), as a consequence, the amplitude value at each cycle satisfies the inequality:

$$A_{n}^{2}(t)\ge n S_{\min }.$$

We also note that under the conditions of the theorem, the rate of growth of the amplitude with probability 1 is proportional to the square root of time.

12.4 Hysteresis in Discrete Sine-Gordon Model

12.4.1 Bouc-Wen Model

Dependencies of hysteretic type are determined by input-output correspondences, when the output depends not only on the instantaneous value of the input, but also on its behavior in the preceding moments of time (memory effect). Mathematical models of mechanical properties of many building materials, such as reinforced concrete, steel, wood, as well as the damping materials, usually include a nonlinear hysteresis mechanism that takes into account the restoring properties of these structures.

Mathematical models of hysteresis-type phenomena are rather diverse and include both design models (backlash, stop, non-ideal relay, as well as their continuous analogues, namely the Ishlinskii and Preisach models [9]), and phenomenological models (S-converter, Duhem model, Bouc-Wen model, etc. [1, 5, 7, 14, 29]). In this paper, we focus on the phenomenological approach based on the Bouc-Wen model for describing the hysteresis nonlinearity [2, 7, 23].

Fig. 12.10
figure 10

Visualization of the Bouc-Wen model

Full size image

Let us consider the equation of motion of a single-degree-of-freedom (Fig. 12.10) system:

$$\begin{aligned} \mu \ddot{u}(t) + F(u,z) = f(t), \end{aligned}$$
(12.39)

where \(\mu \) is the mass, u(t) is the displacement, F(u, z) is the restoring force and f(t) is the excitation force (hereafter the overdot indicates the derivative with respect to time). Following the Bouc-Wen approach the restoring force is presented as (the corresponding function depends on the input and output states)

$$\begin{aligned} F(u,z) = \alpha k u(t) + (1-\alpha ) k z(t). \end{aligned}$$
(12.40)

From (12.40) it follows that the restoring force F(u, z) can be divided into elastic and hysteretic parts, where k is the yielding stiffness, \(\alpha \) is the ratio of post-yield to pre-yield (elastic) stiffnesses and z(t) is the non-dimensional hysteretic parameter that satisfies the following nonlinear differential equation with zero initial condition \((z(0) = 0)\):

$$\begin{aligned} \dot{z}(t) = \left[ A - |z(t)|^n(\beta +\mathrm {sign}\left( z(t)\dot{u}(t)\right) \gamma ) \right] \dot{u}(t), \end{aligned}$$
(12.41)

where, A, \(\beta \), \(\gamma \) and n are non-dimensional parameters controlling the behavior of the model and \(\mathrm {sign(\cdot )}\) is the standard signum-function. For small values of the positive exponential parameter n the transition from elastic to post-elastic branch is smooth, whereas for large values of this parameter the transition becomes abrupt, approaching that of a bilinear model. Parameters \(\beta \) and \(\gamma \) control the size and shape of the hysteretic loop. Thus, such a multi-parameter model describes wide class of hysteretic systems [2, 7, 23].

12.4.2 Discrete Sine-Gordon Model with Hysteretic Nonlinearity

The most well-known and well-studied equations in mathematical physics are equations describing the propagation of waves in a linear medium. For a nonlinear medium with hysteresis properties, there are no ready-made methods for solution of such equations.

One of the interesting results of the analysis of wave propagation processes in nonlinear media is the existence of soliton solutions—solitary waves behaving like particles. One of the models that has a soliton solution is the sine-Gordon system. This system can be presented as a chain of nonlinear pendulums with elastic torsion-tied links. This model is widely used both in biology and in physics. This system has many applications, including the propagation of crystal defects and domains in ferromagnetic and ferroelectric materials, the propagation of splay waves on biological (lipid) membranes, one-dimensional model of elementary particles and propagation of magnetic flux quanta in the long Josephson junction [17].

Fig. 12.11
figure 11

Hysteretic sine-Gordon system model

Full size image

In what follows we consider a mechanical system with hysteretic links [12, 25]. The physical model of such a system is shown in Fig. 12.11. It is a chain of identical pendulums strung on a string and connected by springs [15]. Pendulums oscillate transversely to the direction of the chain. The principal feature of the mechanical system under consideration is that the backlash-type hysteretic nonlinearity [24] is included in the connection between two neighboring pendulums. This system is a modification of the classical mechanical sine-Gordon system and can be called hysteretic sine-Gordon system.

Let \( \mu \) be the mass of the pendulum, \( \mu l^2 \) is the moment of inertia, l is the length, and \( \kappa \) is the torsion constant of the spring. When the deviation of the pendulum with number m from the equilibrium point by an angle \( \theta _m \) takes place, the gravitational force moment \( - \mu gl \sin \theta _m \) acts on the pendulum alongside the torsional moment acting on the side of adjacent springs \( - \kappa (\theta _m - \theta _ {m-1}) + \kappa (\theta _ {m + 1} - \theta _ {m}) \). Since the hysteretic nonlinearity is included in the system, the equation of motion can be presented as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu l^2 \ddot{\theta }_m = -\mu gl\sin \theta _m + \omega ^{l}_m + \omega ^{r}_m,\\ \omega ^{l}_m = L[\omega ^{l}_m(t_0);y^{l}_m(t_0)]y^{l}_m(t),\\ y^{l}_m = -\kappa (\theta _m - \theta _{m-1}),\\ \omega ^{r}_m = L[\omega ^{r}_m(t_0);y^{r}_m(t_0)]y^{r}_m(t),\\ y^{r}_m = \kappa (\theta _{m+1} - \theta _{m}), \end{array}\right. } \end{aligned}$$
(12.42)

where the time-dependent outputs \( \omega ^{l}_m, \omega ^{r}_m \) and inputs \( y^{l}_m, y^{r}_m \) (these inputs are the corresponding moments affecting single pendulum from the left and right sides relative to neighbor pendula, respectively) are the corresponding outputs and inputs for the physically realizable converter \(L[\cdot ]\) in the frame of Krasnosel’skii and Pokrovskii approach [9], and \(\omega ^{\ldots }_m(t_0)\), \(y^{\ldots }_m(t_0)\) are the corresponding initial states (output and input, respectively) of the converter.

12.4.3 Numerical Results

It is known that the operator interpretation of the hysteretic nonlinearity implies the non-smoothness of the corresponding operator. Therefore, in our numerical simulation we use the approach to hysteresis based on the Bouc-Wen phenomenological model. In this case, the sine-Gordon system with the hysteretic nonlinearity in the links takes the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{r} \mu l^2 \ddot{\theta }_m = -\mu gl\sin {\theta _m} -\alpha \kappa (\theta _m - \theta _{m-1}) - (1-\alpha )\kappa z_m^{l} +\\ +\,\alpha \kappa (\theta _{m+1} - \theta _m) + (1-\alpha )\kappa z_m^{r},\end{array} \\ \dot{z}_m^{l} = \left( A - |z_m^{l}|^n\left\{ \beta +\mathrm {sign}\left[ z_m^{l}(\dot{\theta }_m - \dot{\theta }_{m-1})\right] \right\} \gamma \right) (\dot{\theta }_m - \dot{\theta }_{m-1}),\\ \dot{z}_m^{r} = \left( A - |z_m^{r}|^n\left\{ \beta +\mathrm {sign}\left[ z_m^{r}(\dot{\theta }_{m+1} - \dot{\theta }_m)\right] \right\} \gamma \right) (\dot{\theta }_{m+1}- \dot{\theta }_m). \end{array}\right. } \end{aligned}$$
(12.43)

We performed the numerical simulation of the dynamics of the mechanical system described by (12.43). Namely, we obtained the numerical solutions to the Cauchy’s problem for  (12.43) using the 4-th order Runge-Kutta method (our numerical results obtained using MATLAB\(^\circledR \) system). For example, for results presented in Fig. 12.12 (right panel) the model time is \(t = 200\) and the corresponding time-step is \(h = 0.1\). In such a system appearance of soliton-like solutions is expected (in the same manner as for the classical sine-Gordon system). The solitary wave, which is the solution to (12.43), is treated as a dynamical object that retains energy for a long time. The chain has a finite length \( m = 100 \) (we recall that we consider a discrete system), and its ends are fixed. The initial conditions for pendulums

$$ {\theta _1(t_0),\dot{\theta }_1(t_0),\theta _2(t_0),\dot{\theta }_2(t_0),\ldots ,\theta _{m-1}(t_0),\dot{\theta }_{m-1}(t_0),\theta _m(t_0),\dot{\theta }_m(t_0)} $$

generate a family of solitonic solutions moving with different velocities along the (m, t)-plane with reflection at the ends of the chain (\( m = 1, m = 100 \)). For the parameters of the hysterestic blocks formalized by means of the Bouc-Wen model, \( z_{m}^{l}(t_{0}) \), \( z_{m}^{r}(t_ {0}) \), the initial conditions are zero by default.

Fig. 12.12
figure 12

Simulation of the collision of two soliton-like solutions without hysteresis (left panel) and with hysteresis (right panel) in the links

Full size image

Let us have a look on the dynamics of two solitonic solutions launched from opposite ends of the chain, as shown in Fig. 12.12. The corresponding initial conditions

$$ {\theta _1(t_0) = 2 \pi ,\dot{\theta }_1(t_0) = 1,\theta _2(t_0) = 0 ,\ldots ,\dot{\theta }_{m-1}(t_0) = 0,\theta _m(t_0) = 2 \pi ,\dot{\theta }_m(t_0) = 1} $$

generate two pulses, moving towards each other. During the simulation, two solitary waves collide in situations without (\( \alpha = 1 \), left panel) and with (\( \alpha = 0.75, \beta = 0.1, \gamma = 0.9 \), right panel) hysteresis in the links. The interaction of two pulses can demonstrate the nature of the colliding formations, since solitons interacting with each other, show special properties (similar to particle behavior). As follows from the numerical results presented in Fig. 12.12 (left panel), the dynamics of solutions demonstrates all the properties of soliton-like objects (they do not change their shape and speed). In the case when there are hysteretic connections between the pendulums (right panel in Fig. 12.12), soliton-like solution changes the speed (as can be seen by breaking the symmetry of the reflection process at the ends of the chain), retaining its shape, as well as the nature of interaction.

In order to study the influence of hysteresis bonds in the system, we consider the case in which the vibrations of 25th (\( \theta _{25}(t_0) = 2 \pi , \dot{\theta }_{25}(t_0) = 0 \)) and 75th (\(\theta _{75}(t_0) = \pi , \dot{\theta }_{75}(t_0) = 0 \)) pendulums are excited with the corresponding initial conditions. Under these initial conditions, the oscillations of the corresponding components are excited in the chain (Fig. 12.13 (left panel)). In the case when the hysteresis in the links is taken into account (Fig. 12.13 (right panel)), spatial localization of oscillations is observed.

Let us consider in more detail the evolution of the states of the components of the chain \( (\theta (t), \dot{\theta }(t)) \) in the neighborhood of 25th and 75th pendulums. Figures 12.14 and 12.15 show the phase portraits for 24th, 25th, 26s, 74th, 75th, 76s pendulums, respectively together with corresponding hysteretical loops (such loops are obtained as a numerical solution to (12.41) of the Bouc-Wen model). As follows from these figures, in the absence of hysteretic bonds \( (\alpha = 1) \) the dynamics of pendulums demonstrates a complex oscillatory structure. However, in the presence of hysteresis in the bonds \( (\alpha = 0.5, \beta = 0.1, \gamma = 0.9) \), the dynamics in the neighborhood of the 25th pendulum is regularized and the stable limit cycle can be seen. Note a similar behavior for the 75th pendulum (Fig. 12.15).

Fig. 12.13
figure 13

Simulation of the dynamics of localized oscillations of pendulums in a chain without hysteresis (left panel) and with hysteresis (right panel) in the links

Full size image
Fig. 12.14
figure 14

Phase portraits of 24th, 25th, 26s pendulums without hysteresis (left panel) and with hysteresis (right panel) in the links. The input (right panel) shows the corresponding hysteretic loop obtained as a solution to (12.41)

Full size image
Fig. 12.15
figure 15

Phase portraits of 74th, 75th, 76s pendulums without hysteresis (left panel) and with hysteresis (right panel) in the links. The input (right panel) shows the corresponding hysteretic loop obtained as a solution to (12.41)

Full size image

Also, we investigated the influence of the hysteretic blocks in the connections between pendulums by using the methods of spectral analysis. We performed the Fourier transform for the 25th pendulum in the presence of hysteretic block \( (\alpha = 0.5, \beta = 0.1, \gamma = 0.9) \) and without \( (\alpha = 1) \) it. The corresponding results are shown in Fig. 12.16. As it follows from the results presented in this figure, the oscillation spectrum changes after inclusion of hysteretic bonds. Thus we can conclude that the hysteresis in such a system plays a role of a “filter” that quenches frequencies corresponding to small-amplitude oscillations and releases the main frequency.

Fig. 12.16
figure 16

The oscillation spectrum of the 25th pendulum without hysteresis (left panel) and with hysteresis (right panel) in the link

Full size image

12.5 Conclusions

In this chapter we study the resonant properties of autonomous system in which the energy “pumping” takes place due to the presence of a part with hysteretic properties. Unlimited solutions to differential equation corresponding to autonomous system containing hysteretic part with inversion of switching numbers are investigated. The cases of Coulomb and viscous friction for the system being considered and the occurrence of self-oscillatory regimes is established. We applied also the small parameter approach to the problem of the frequency “trapping” in the system under consideration. It is shown that the “trapping” band is uniquely dependent on the amplitude of the external force.

Also we present a generalization of the classical hysteretic converter in the form of non-ideal relay to the case when its switching numbers are randomly distributed according to a corresponding law. The properties of this converter are established (namely, the definition, together with the monotonicity), as well as the dynamics of the simple mechanical system in the form of oscillator under hysteretic force determined by a non-ideal relay with random parameters is considered.

Special attention was paid to the dynamics of an oscillatory system with many degrees of freedom under conditions of hysteretic blocks in the coupling between the individual parts of the system. This system can be classified as a modified mechanical model of the sine-Gordon system in the case when the connections between the pendulums contain a hysteretic nonlinearity. The hysteretic nonlinearity was formalized by means of the Bouc-Wen model which allows a fairly simple numerical realization. On the basis of numerical simulations, the dynamics of the solitonic solution for this system was studied taking into account the hysteretic nature of the coupling. It was demonstrated that the presence of hysteretic coupling leads to a change in the speed of propagation of the solitary solution while maintaining the character of interaction between various solitary solutions. Also, the results of numerical simulation demonstrate the regularizing role of hysteresis bonds in the character of oscillatory motions. The filtering properties of hysteretic bonds are inferred from the spectral analysis of the oscillatory motions of individual components of the system under consideration.