Keywords

1 Introduction

The problem of the laminar incompressible three-dimensional (3D) mixed convection lid-driven cubical cavity has a large number of applications in engineering and science such as crystal growth, electronic device cooling, food processing, metal casting and phase change as the freezing of water for latent thermal storage systems, solar power collector, glass production, etc. A number of numerical experiments for a free convection dominated heat transfer has been conducted for the past few decades, few of such numerical experiments are called as the benchmark solutions, which are used in investigating the performance of numerical methodologies and solving the incompressible laminar Navier–Stokes equations for complicated problems. From the literature, it is found that majority of numerical work has been confined to 2D flow. Kosef and Street [1, 2] stressed the necessity to study the 3D nature of the flows arising in the lid-driven cavity due to the presence of no-slip boundary conditions along with the sparse characteristics of incompressible flows. A similar problem was numerically analyzed by Iwatsu and Hyun [3] with the moving top wall kept at higher temperature than at the bottom wall for the possibility of air temperature distribution for a wide range of control parameters such as 102 ≤ Re ≤ 2000, and 0 ≤ Ri ≤ 10. Both 2D and 3D lid-driven cavity problems are analyzed by Mohammad and Viskanta [4]. They established that this movement of the lid in a cavity can get rid of all convective cells due to bottom heating. For a 2D lid-driven cavity, the effect of buoyancy on the flow and heat transfer for higher values of Pr was analyzed by Moallemi and Jang [5] with 102 ≤ Re ≤ 2000 for different levels of the Ri. They showed that free convection contribution always assists the forced convection magnitude. The mixed convection in a top wall moving lid-driven 2D cavity was examined by Prasad et al. [6]. They showed that when the negative Grashof number (Gr) is more and aspect ratio (AR) is equal to 0.5 and 1.0, a strong convection is exhibited, and when AR is 2, a Hopf bifurcation is observed. Sharif [7] analyzed a supplementary flow visualization of a laminar incompressible combined free and forced convective heat transfer in 2D rectangular driven cavities with AR of 10. They observed that the local Nusselt number (Nu) at the heated moving wall initiates with a higher value and decreases rapidly to a lower value towards the right side. However, the Nu at the cold wall shows the fluctuations close to the right wall. This is due to the presence of a vortex at the cold wall. In an inclined cavity with Ri = 0.1, Benkacem et al. [8] remarked that the average Nu augments slowly with the inclination while for Ri = 10, it increases rapidly in the case of natural convection. Aydin et al. [9] analyzed the mixed convection in a shear and buoyancy-driven cavity with lower wall heated and moving cold sidewalls. With the motivation of the above work, in the present article, the mixed convective flow of air in 3D cubical lid-driven cavity flows are carried out numerically. Numerical results are obtained for 100 < Re < 400 and 0.001 < Ri < 10. The fluid flow and heat transfer characteristics are visualized using the contours of streamlines, isotherms, vortex corelines with respect to different Ri and Re.

2 Physical System

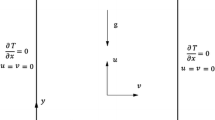
The lid-driven 3D cavity filled with air is considered as shown in Fig. 1.

Fig. 1
figure 1

3D cubical-driven cavity of length L

Full size image

The top wall, Y = L(m), is moving in its own plane with a constant velocity U0 (m/s), and the other boundary walls are at rest. The top and bottom walls are kept at the isothermal temperature in which the bottom wall has the higher temperature (TH) than the top wall (TC) with ΔT  =  TH − TC > 0. Also, the remaining four walls are assumed as adiabatic.

Steady laminar 3D nondimensional form for the conservation of mass, momentum, and energy equations with an inclusion of the buoyant Boussinesq approximations for the density variation is written as

$$ {\text{div}} \,\varvec{V} = 0 $$
(1)
$$ \left( {\varvec{V}\,.\,{\text{grad}}} \right)\varvec{V} = - {\text{grad}}\,p + \frac{1}{{Re}}\,.\,{\nabla }^{2} \varvec{V} + {{Ri}}\,.\,{T}^*\varvec{e} $$
(2)
$$ \left( {\varvec{V}\,.\,{\text{grad}}} \right)T^* = \frac{1}{{{{Re}}\,.\,{ \Pr }}}.{\nabla }^{2} {T}^* $$
(3)

where V = (U, V, W), e = (0, 1, 0), p, t, and T* = \( \frac{{T - T_{C} }}{{\Delta T}} \) represents dimensionless velocity vector along (X, Y, Z) directions, the unit vector in the vertical direction, pressure, time, and temperature, respectively. The reference scales for nondimensionalization are U0, ρU 20 , and L/U0 for velocity, pressure, and time, respectively, Re = \( U_{0} L/\upnu \), Rayleigh number Ra = \( \frac{{g\beta \left( {\Delta T} \right)L^{3} }}{\nu \alpha } \), where \( \beta \) is the thermal expansion coefficient, \( \nu \) is the kinematic viscosity; Grashof number Gr = \( \frac{{g\beta \left( {\Delta T} \right)L^{3} }}{{\nu^{2} }} \), and g is the gravity; Prandtl number Pr = \( \nu \)/α; and the mixed convection parameter, Ri = \( \frac{\text{Gr}}{{{{Re}}^{2} }} \).

For the above mathematical problems (1)–(3), the boundary conditions are

V = (1, 0, 0) at Y = 1 and V = 0 at Y  =  0, X = 0, 1, and Z = 0, 1

T* = 1 at Y = 0, and T* = 0 at Y = 1 and \( \frac{{\partial {T^{*}}}}{\partial X} = 0, \) at X = 0, 1 and

\( \frac{{\partial {T^{*}}}}{\partial Z} = 0, \) Z = 0, 1.

The nondimensional heat transfer rate at the hot wall is calculated by the Nusselt number, whose local value along the hot wall is given by \( Nu = \left( {\frac{{\partial T^{*}}}{\partial Y}} \right)_{Y = 0} \). The average Nusselt number is obtained by integrating the local Nusselt number along the hot wall and is calculated as \( \overline{\text{Nu}} \) = \( - \int_{X = 0}^{X = 1} {\int_{Z = 0}^{Z = 1} {\left( {\frac{{\partial T^{*} }}{\partial Y}} \right)_{Y = 0} {\text{d}}X\,{\text{d}}Z} } \).

3 Numerical Method

The flow model, geometry, the initial and boundary conditions for this problem were set in the buoyant Boussinesq SimpleFoam of the computational fluid dynamics solver, namely, OpenFOAM. It is a steady-state solver for the buoyant flow of incompressible fluids including Boussinesq approximation. To calculate the spatial derivatives, the second-order upwind finite volume numerical method was used. For acceleration means, conjugate gradient squared method was used. Divergent and Laplacian terms are discretized by the QUICK and Gauss linear schemes respectively.

Table 1 shows the comparison between the present laminar solution and numerical results found in the literature [3, 10] in terms of \( \overline{\text{Nu}} \) along the hot wall. There is an excellent agreement between the present results and the results available in the literature.

Table 1 Validation of present simulations with respect to \( \overline{Nu} \) at the hot wall for Re = 400 and Ri = 1
Full size table

4 Results and Discussion

The simulated results are presented in terms of isotherms and streamlines in terms of the control parameters arising in the system.

Figure 2 depicts the isotherms for different Re and Ri. The patterns of isotherms show that for the small Ri (=0.001), the mechanically driven forced convection controls the buoyancy-driven convection. Figure 2a, d, show the forced convection induced by the movement of lid. While as Ri augmented to the value 1, the buoyant convection deforms the isotherms and these 3D structures become stronger further when Re moved to the value of 400 (Fig. 2c, f). The deformation of the isotherm field increases with Ri. Especially, the flow is dominated by the buoyancy and the heat transfer is controlled due to the natural convection, assigning that the forced convection due to the movement of the lid is almost absent. For Ri = 1, an agreement between the these free and forced convections, is clearly seen in Fig. 2b.

Fig. 2
figure 2

Isotherms for different Ri and Re

Full size image

Figure 3 illustrates the streamlines and the vorticity in the cubical cavity for different Re and Ri. There are two similar vortices in the cavity and interact with each other at the middle of the cavity. The swirling nature of the streamlines around the vortex line in each case is clearly seen. The vortex corelines have their origin/end at the bounding walls and surrounded by the streamlines. The strength of the vorticity increases as Re or Ri increases. The energy exchange between the two closed vortices occurs at the middle of the cavity.

Fig. 3
figure 3

Visualizing vortex corelines and streamtraces for different Re and Ri

Full size image

5 Conclusion

The present investigation directed the 3D mixed convection in a cubical lid-driven cavity for suitable collaboration of three different Re and Ri values and their effects are explored with respect to behaviors of the fluid flow and thermal fields. With lower Re values, the isotherm maintains a two dimensionality but when Re is large, the thermal field shows vigorous three dimensionalities for small Ri values. On the other hand, the stabilizing buoyancy effects become dominant at large Ri. In the considered problem the heat transfer rate is mostly convective and the three dimensionality of the thermal field is weak.

The implications of Ri play a key role in \( \overline{\text{Nu}} \) at the vicinity of the walls. When Ri is large, overall heat transfer is vanquished, and the conductive heat transfer model prevails. For very small values of Ri with the combination of large Re, complex 3D structures are noticeable. It can be concluded that the present results show that the overall heat is enhanced by vigorous forced convection.