1 Introduction

Many engineering problems, where mixed convection flow and heat transfer occurs, can be predicted with the use of a simple model known as lid-driven cavity flow. This model can be used for the description of heat transfer phenomenon in the following applications: electronic devices cooling, geothermal systems, lubrication technologies, chemical processes, solar energy systems, etc. Detailed application of this model was presented in [1]. Additionally heat and fluid flow in a square cavity are a standard test case for code validation. This is well-known in the field of applied mathematics and numerical methods [2, 3].

Mixed convection heat transfer and fluid flow in a square cavity were studied by many scientists and it is well described in the literature. Modelling of this problem can be classified into two categories, based on applied boundary conditions, influencing buoyancy forces. The first group is related to Dirichlet boundary conditions i.e. constant temperature on the surface of the wall. The second group is related to Neumann boundary conditions i.e. constant heat flux on the surface of the wall. Most studies described in the literature are dedicated to the first group [4–9]. However this study is related to modelling heat and fluid flow in a square cavity, in which, constant heat flux boundary condition is employed on the bottom horizontal wall.

Studies related to mixed convection heat and fluid flow where the Neumann boundary conditions are applied, are rarely described in the literature. Mixed convection heat transfer in a cavity, in the presence of thermal sources, were studied in series of papers by Papanicolaou and Jaluria [10–13]. Authors examined numerically mixed convection heat transfer from an isolated thermal source with uniform surface heat flux located in a rectangular cavity with a fluid outlet [10]. Analysed Richardson and Reynolds number were in the range 0–10 and 50–2000 respectively. The working fluid was air. Authors found that average Nusselt number increased with increasing Richardson number at fixed Reynolds number. More intensive increase in heat transfer rate with increasing Richardson number was also observed. Additionally influence of different configurations resulting from various locations of heat source and outlet was investigated. In [11] authors presented numerical study on transition from steady, laminar regime to a periodic regime in a cavity filled with air subjected to heating via a heat source. The heating source was located on one of the vertical walls. Influence of Grashof and Reynolds numbers on resulting heat transfer and fluid flow were investigated. It was found that flow became unstable beyond a critical value of Richardson number. Small fluid elements at the centre of the cavity were cooled and heated periodically. Consequently this resulted in circulation of bulk mass of the fluid which was caused by density change. In [12] authors numerically studied conjugate heat transfer in the case of an isolated, constant source of heat flux, located on one of the walls. The configuration of the cavity included an external flow which flowed into cavity through an inlet located on the left vertical wall and flowed out via outlet located on the right vertical wall. Influence of the following parameters on a heat transfer in the cavity were tested: Reynolds number, Richardson number, ratio of the wall material thermal conductivity to fluid thermal conductivity (air) and location of the heat source. Results showed that with increasing heat flux applied on heat sources surfaces, heat transfer rate from these surfaces also increased. Moreover it was observed that circulation of the fluid in the cavity was stronger and temperatures of heat sources were higher. Different locations of the heat source strongly influenced heat transfer rate. Authors concluded that heat source location led to buoyancy-assisting mixed convection flows, resulted in lower temperatures on the surfaces and higher heat transfer rates. In [13] authors performed a numerical study of combined forced and natural convective cooling of heat-dissipating electronic components. Those components were located in a rectangular cavity and cooled by an external through-flow of air. Richardson number was varied from 0.01 to 10. Influence of heat sources number and location on heat transfer rate and fluid flow in the cavity was analysed. As it was shown location of the heat source on the right vertical wall is the most beneficial case in terms of cooling.

Hsu and Wang [14] carried out a numerical study on mixed convection in a cavity. Discrete heat sources were embedded on a vertical board located on the bottom wall of the cavity. Air flow was directed into the cavity through an inlet located on the left vertical wall and flowed out through an outlet located on the opposite wall. Hsu and Wang studied influence of the same parameters as Papanicolaou and Jaluria [12] on heat transfer and fluid flow. It was shown that at fixed Reynolds number decrease of Richardson number resulted in decrease of average Nusselt number. Highest temperature gradients were located near heat sources. Also it was observed that with increasing Reynolds number heat transfer rate also increased. Guo and Sharif [15] numerically analysed mixed convection heat transfer in a rectangular cavity with constant heat flux located on the centre part of the bottom wall. The side walls were isothermal and moved in the vertical direction. Heat source length was changed in a range 0.2–0.8 L. Computations were done for Richardson number range 0.1–10. Authors studied impact of Richardson number, heat source length and location, and aspect ratio of the cavity on maximum temperature and Nusselt number. It was found that low Ri values influenced temperature in such a way that it was more uniformly distributed within the cavity. Also it was found relatively large region of the cavity is affected by the heat source. It was also noticed that the region affected by the heat source became larger with increasing heat source length. Ogut [16] examined mixed convection in an inclined lid-driven cavity filled with air. Two vertical walls were adiabatic, while the bottom wall was heated-up via constant heat flux. The moving lid was isothermal. Richardson number was in a range 0.1–100 and inclination angle varied from 0° to 180°. Author found that inclination angle did not have significant effect on heat transfer and fluid flow for Ri = 0.1. Richardson number significantly influenced heat transfer rate and with increasing Richardson number the average Nusselt number increased as well. Shahi et al. [17] numerically investigated mixed convection nano-fluid flows in a square cavity with inlet and outlet ports. Constant heat source was symmetrically located at the bottom wall. Richardson number was changed in the range of 0 ≤ Ri ≤ 10. It was found that increase in solid volume fraction, resulted in increase in average Nusselt number at the heat source surface and in decrease of average bulk temperature. Mansour et al. [18] examined mixed convection in a square cavity partially heated from below and filled with water-base nano-fluid. Authors considered impact of Reynolds number, solid volume fraction, different heat source lengths and locations on local and average Nusselt number along the heat source. The heat source length was varied by 0.2 ≤ L ≤ 0.8. It was found that for high Reynolds numbers (Re = 100) the lid-driven effect was dominant. For small values of Reynolds number (Re = 10) an increase in effect of heat source presence on heat and fluid flow was observed. Cho et al. [19] numerically investigated heat transfer in water-based nano-fluids confined within a lid-driven cavity with wavy left and right walls. On the left wall constant heat flux was applied and the right wall was maintained at a lower temperature. Both the upper and lower walls were thermally insulated and moved in the horizontal direction. Results showed that for studied range of Richardson number, mean Nusselt number increased, when volume fraction of nano-particles and Grashof number increased.

Above described literature review shows that studies dedicated to mixed convection heat transfer in a lid-driven cavity with Neuman boundary conditions are limited. Additionally none of the researchers, except Ogut [16], did not examine the case, where heat flux was applied on the whole surface of the wall. However the main aim of his work was to analyse effect of an inclination angle on heat transfer rate. Thus, Prandtl number was kept constant.

In present study mixed convection heat transfer in lid-driven cavity is investigated. Fluid in the cavity is heated through the surface of the bottom wall via a constant heat flux and cooled via the moving lid, which is kept at constant, low temperature. Two vertical walls are thermally insulated. This simple configuration was not considered in the literature. Nevertheless, in our opinion, it is an important problem since the constant heat flux boundary condition is more physically realistic. Mathematical treatment of a heat transfer with use of constant temperature boundary condition is easier. However, most engineering issues do not fulfil isothermal conditions at boundaries. Modelling of heat transfer phenomena using constant heat flux boundary condition better reflects actual situation. As previously shown, literature on this topic is rare, and thorough study is needed. Furthermore all of the papers were aimed at calculating local and mean Nusselt number along the surface where the heat flux was employed. In such situations the method of Nusselt number calculation is well known from e.g. [15, 16, 18]. Thus, no results for Nusselt number on other surfaces are available in the literature. In the present study the main goal is to investigate variation of local Nusselt number on the moving lid which is maintained at a constant temperature. In order to calculate local and mean Nusselt number at this surface, approach similar to this presented in [20] is used.

In this work we decided to focus on following problems: the first is to examine influence of a wide range of Prandtl number and Richardson number on heat transfer and fluid flow in the cavity. The second objective is to explain mechanisms of scraping of the boundary layer phenomenon in the cavity. The third goal is to provide a benchmark solution for this simple configuration with use very fine resolution grid (1024 × 1024).

2 The problem description

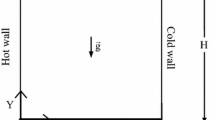
The scheme of the model and the boundary conditions are depicted in Fig. 1 in form of a two-dimensional square cavity of length side L. The top lid surface moves with constant velocity UT from left side of the cavity to the right, while the other walls are stationary. The top lid surface is maintained at constant temperature TT. A working fluid is heated through the bottom wall via a constant heat flux \(q^{{\prime \prime }}\). Vertical walls are adiabatic. Acceleration of gravity acts in the negative vertical direction.

Fig. 1
figure 1

Numerical domain and the boundary conditions

Full size image

In order to examine influence of Prandtl number on heat transfer, following working fluids were chosen for simulation: air, water and industrial aniline. Prandtl numbers of these fluids are 0.71, 9.54 and 56.00 respectively. Grashof number was fixed at 104.

3 Mathematical model

Two-dimensional, steady state, laminar fluid flow and heat transfer in a square cavity are modelled. Fluid is treated as Newtonian and incompressible. Thermophysical properties at reference temperature TT are assumed to be constant, except density in the buoyancy term which follows the Boussinesq approximation [21]. It is also assumed that radiation heat transfer is negligible compared to convective and conductive mechanisms of heat exchange in the fluid. Additionally viscous dissipation is also neglected.

The governing equations for the problem are the continuity, momentum and energy equation. After applying these assumptions, these equations in non-dimensional form can be written as follows

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$
(1)
$$U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + \frac{1}{Re}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right)$$
(2)
$$U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial P}{\partial Y} + \frac{1}{Re}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) + \frac{Gr}{{Re^{2} }}\theta$$
(3)
$$U\frac{\partial \varTheta }{\partial X} + V\frac{\partial \varTheta }{\partial Y} = \frac{1}{PrRe}\left( {\frac{{\partial^{2} \varTheta }}{{\partial X^{2} }} + \frac{{\partial^{2} \varTheta }}{{\partial Y^{2} }}} \right)$$
(4)

where U and V are dimensionless components of the velocity vector in the X and Y direction respectively, P is dimensionless pressure and Θ is dimensionless temperature. Non-dimensional parameters are Reynolds Re, Grashof Gr and Prandtl Pr numbers. Non-dimensional variables and non-dimensional parameters are defined as follows:

$$X = \frac{x}{L},Y = \frac{y}{L},U = \frac{u}{{U_{T} }},V = \frac{v}{{U_{T} }},P = \frac{p}{{\rho U_{T}^{2} }},\varTheta = \frac{{T - T_{T} }}{{\Delta T}}$$
(5)
$$Re = \frac{{U_{T} L}}{\nu },Gr = \frac{{g\beta L^{3}\Delta T}}{{\nu^{2} }},Pr = \frac{\nu }{\alpha },Ri = \frac{Gr}{{Re^{2} }}$$
(6)

All distances are normalized by L, all velocities are normalized by U T , and pressure is normalized by ρU 2 T , where ρ is fluid density. Temperature is normalized as (T − T T )/ΔT, where ΔT is a temperature difference defined as follows:

$$\Delta T = \frac{{q^{{\prime \prime }} L}}{k}$$
(7)

where \(q^{{\prime \prime }}\) is a heat flux applied on the bottom cavity wall. Thermophysical properties of the fluid appearing in Eq. 6 are kinematic viscosity (ν), thermal expansion coefficient (β), thermal conductivity (k) and thermal diffusivity (α). Non-dimensional ratio Gr/Re 2 in Eq. 3 is Richardson number. It represents the magnitude of natural convection relative to the forced convection. Ri number is commonly used parameter for assessment the convection flow regime. If Ri ≫ 1 than natural convection regime occurs, whereas forced convection is dominant for Ri ≪ 1. In the range of Ri = 0.1–1.0 both natural and forced convection play significant role in heat transfer and neither can be neglected.

Boundary conditions are depicted in Fig. 1 and are specified as follows:

$$\left. {\begin{array}{*{20}l} {Y = 0,} \hfill & {0 < X < 1,} \hfill & {U = 0,} \hfill & {V = 0} \hfill & {\partial \varTheta /\partial Y = - 1} \hfill \\ {Y = 1,} \hfill & {0 < X < 1,} \hfill & {U = 1,} \hfill & {V = 0} \hfill & {\varTheta = 0} \hfill \\ {X = 0,} \hfill & {0 < Y < 1,} \hfill & {U = 0,} \hfill & {V = 0} \hfill & {\partial \varTheta /\partial X = 0} \hfill \\ {X = 1,} \hfill & {0 < Y < 1,} \hfill & {U = 0,} \hfill & {V = 0} \hfill & {\partial \varTheta /\partial X = 0} \hfill \\ \end{array} } \right\}$$
(8)

For each wall of the cavity the no-slip and the no-permeable wall boundary conditions were applied.

Once velocity and temperature distributions in the cavity are obtained, local and area-averaged Nusselt numbers are calculated as follows:

$$Nu = \frac{hL}{k} = - \frac{{\left( {\frac{\partial T}{\partial y}} \right)_{Y = 1} L}}{{\overline{{T_{B} }} - T_{T} }},\quad \overline{Nu} = \frac{1}{L}\int_{0}^{L} N udX$$
(9)

where \(\bar{T}_{B}\) is an average temperature at the bottom surface wall (A B ) and is defined as:

$$\bar{T}_{B} = \frac{{\int_{{A_{B} }} {T_{B} } dA}}{{A_{B} }}$$
(10)

4 Numerical details

The set of governing equations was discretized and solved with the use of ANSYS-CFX software [22]. The discretization method is an element-based finite volume approach [23] using non-staggered grid layout such that the control volumes are the same for all transport equations. In order to avoid a checkerboard pressure field, the Rhie-Chow algorithm is used [24]. ANSYS-CFX is a fully implicit coupled solver, which solves continuity equation Eq. 1 and momentum equations Eqs. 2 and 3 as a single system. Thus the pressure–velocity coupling is inherent in the solution procedure (pressure correction equation is not needed as opposed to the segregated solvers).

In the simulations very fine meshes with resolution of 1024 × 1024 are used in order to accurately resolve boundary layers near the cavity walls. Two mesh-laws for nodes distribution are applied: uniform and geometric. For the geometric mesh type the arrangement of the nodes in the mesh is given by [25]:

$$s_{i + 1} = s_{i} + r\Delta$$
(11)

where si is the spatial location of the node, Δ is the step size and r is the rate of grid stretching. The uniform mesh is used when the working fluid is air. In other cases geometric mesh is used. Use of different meshes was caused by convergence problems. For fluids with higher Prandtl numbers (compared to air), it was impossible to obtain convergent solution on the uniform mesh. Additionally to facilitate convergence of the solution each simulation was calculated twice, first on the coarse mesh and then on the 1024 × 1024 mesh. Solution from the coarse mesh was mapped on the dense mesh and then used as initial conditions.

Convergence criteria used for each set of parameters were similar as those adopted in [4]

$$\frac{{\left| {\varPsi^{n + 1} \left( {i,j} \right) - \varPsi^{n} \left( {i,j} \right)} \right|}}{{{\text{Max}}\left| {\varPsi^{n + 1} \left( {i,j} \right)} \right|}} < 10^{ - 6} \quad {\text{and}}\quad \left| {1.0 - \frac{{\overline{Nu}_{T} }}{{\overline{Nu}_{B} }}} \right| < 0.05$$
(12)

where i and j denote coordinates of the nodes in the numerical mesh, n is the iteration loop counter, Ψ is a dependent variable (u, v or T) and \(\overline{Nu}_{T}\) and \(\overline{Nu}_{B}\) are area-averaged Nusselt numbers on the top and bottom walls respectively. Calculations were performed in a parallel mode on Supernova supercomputer of Wroclaw Centre for Networking and Supercomputing, being a part of Wroclaw University of Technology. Computational time was lengthened with increasing Prandtl number and decreasing Richardson number. For example to fulfil convergence criteria Eq. 12 in the case of Ri = 1 and Pr = 0.71 calculations lasted few hours. In the case of Ri = 0.001 and Pr = 56.0 calculations lasted 10 days.

To validate described earlier study, two different test-cases were considered. The first was standard flow without heat transfer in a lid-driven cavity of length side L. Calculations were carried out on the uniform mesh of resolution 1024 × 1024 for Reynolds number Re = 1000 and compared with the very accurate results presented in [2]. Excellent agreement was obtained and the comparison of plots for streamlines, vorticity and pressure are presented in Fig. 2. In Tables 1 and 2 numerical values of non-dimensional velocity, pressure and vorticity are presented.

Fig. 2
figure 2

Comparison of the steady state results for Re = 1000 (mesh size 1024 × 1024). From left to right stream function, vorticity and pressure. First row results presented in [2], second row present results

Full size image
Table 1 Horizontal nondimensional velocity, pressure and vorticity through the vertical centerline of the cavity at Re = 1000 on grid 1024 × 1024
Full size table
Table 2 Vertical nondimensional velocity, pressure and vorticity through the vertical centerline of the cavity at Re = 1000 on grid 1024 × 1024
Full size table

The second test-case was the same as this treated by Ogut [16]. Validation was performed on uniform mesh with resolution 1024 × 1024 for Richardson number Ri = 0.1 and Prandtl number Pr = 0.71. Comparison of plots for streamlines and isotherms is depicted in Fig. 3. Additionally difference between area-averaged Nusselt number from this study and Ogut results was <2 %.

Fig. 3
figure 3

Comparison of the steady state results for Ri = 0.01 (Re = 1000; mesh size 1024 × 1024). Left column stream function, right column isotherms of non-dimensional temperature Θ. First row results presented in [16], second row present results

Full size image

5 Results and discussion

In this study the fluid flow and heat transfer phenomena are investigated for a wide range of Richardson numbers and Prandtl numbers. Sixteen numerical simulations were performed. Prandtl numbers were Pr = 0.71, 9.47 and 56.00 respectively. Ri values range was 0.001–1.0. Grashoff number was fixed at 104. Correspondingly the range of Reynolds numbers was from Re = 100 to Re = 3162. The set of parameters used during simulations is presented in Table 3.

The calculated streamlines and isotherms fields for Ri = 1.0 (Re = 100) and for three different values of Pr are shown in Fig. 4. Movement of the fluid is driven by the shear induced by the moving lid. This results in fluid circulation in the clockwise direction. In the lower right cavity corner secondary counter-clockwise vortex appears. It can be seen that Pr does not have an influence on the pattern of the flow field. On the other hand Pr strongly affects temperature distribution. It is clear that with increase of Pr number temperature gradient also increases. The temperature field is formed due to combined effects of natural convection caused by heat flux on the bottom wall and forced convection caused by the driving lid moving in the right direction. Cold fluid particles localized near the driving lid are moved to the right vertical wall due to shear forces. Then they are heated on the bottom wall. At the same time hot fluid particles localized at the bottom cavity part move towards left vertical wall. This is caused by buoyancy forces. After reaching the top of cavity area fluid particles are cooled by the low temperature fixed at the lid. These two phenomena result in circulating fluid flow. Due to fluid movement isotherms also rotate in the clockwise direction. In the limit for the highest values of Pr, isotherms are moved to the left and to the bottom walls. Thus temperature boundary layer thickness decreases. It results in increase of temperature gradient near the walls. Consequently for fluids with large Pr, higher values of Nu are expected (Table 4).

Fig. 4
figure 4

Distribution of streamlines (left) and isotherms (right) in the cavity for Ri = 1.0 (Re = 100) and different Prandtl numbers. From top to the bottom Pr = 0.71, 9.47 and 56.00 respectively

Full size image
Table 3 The set of parameters used in the simulations
Full size table

Figure 5 shows distribution of streamlines and isotherms in the cavity for Ri = 0.1 (Re = 316) and for three different values of Pr. Due to higher velocity of the moving lid circulation increases, and secondary counter-clockwise vortex in the right cavity corner enlarges. Moreover the core of the primary vortex is shifted slightly to the left and to the bottom. Curvature of the streamlines is more deformed near the left top cavity corner compared to previous case (with Ri = 1.0). This is primarily due to shearing effect of the driving lid. With increasing Pr one can see that it does not influence the pattern of the flow field. Regarding temperature field the situation is contrary. Circulation of isotherms is more visible compared to Ri = 1.0. In the case of Pr = 0.71, in the centre and in the right cavity part the zone with uniform fluid temperature expands. An increasing Pr causes that zone expands and for Pr = 56.00 it occupies about 85 % of the cavity. Thickness of temperature boundary layer decreases with increasing Pr and layer is shifted to the left and bottom wall. The highest temperature gradients exist in thin regions on the left and bottom wall where the thinnest temperature boundary layer is localized. In the lower right corner, where the secondary counter-clockwise vortex appears, temperature boundary layer is thicker. Strong vorticity field in this corner results in increasing temperature gradient, but only in the thin layer. Overall thickness of the boundary layer in this zone is large compared to the middle zone of bottom wall and it constitutes thermal resistance. However with increasing Pr isotherms are moved towards the corner and temperature gradients increase.

Fig. 5
figure 5

Distribution of streamlines (left) and isotherms (right) in the cavity for Ri = 0.1 (Re = 316) and different Prandtl numbers. From top to the bottom Pr = 0.71, 9.47 and 56.00 respectively

Full size image

Streamlines and isotherms for Ri = 0.01 and for three different Pr values are presented in Fig. 6. In this case Re = 1000 and fluid circulation is strong. The third vortex occurs in the bottom left cavity corner. This vortex also rotates counter-clockwise direction, same as secondary vortex in the bottom right corner. The vortex-occupied area in the right corner slightly extends. The primary vortex core displacement is significant. Its position is close to the cavity centre, this results from increasing inertia forces. For each Pr value the flow field is almost the same, this shows that it does not affect streamlines. In contrast Pr influences on heat transfer. It is evident that with increasing Pr the zone with uniform temperature distribution also increases. The temperature boundary layer becomes thinner. This results in enhancement of heat transfer (due to higher temperature gradients, which exist predominantly on the left and bottom wall and in areas occupied by secondary vortices). For Pr = 56.00 one can see that secondary vortices contribute to thicken the temperature boundary layer. Consequently the width of the temperature boundary layer in these places is almost constant, despite temperature gradient increases.

Fig. 6
figure 6

Distribution of streamlines (left) and isotherms (right) in the cavity for Ri = 0.01 (Re = 1000) and different Prandtl numbers. From top to the bottom Pr = 0.71, 9.47 and 56.00 respectively

Full size image

Fully developed vortex flow in the cavity for Ri = 0.001 (Re = 3162) is depicted in Fig. 7. In this case degeneration of the streamlines in the left top corner (caused by the shearing effect), is so strong that the fourth counter-clockwise vortex appears. Circulation of the fluid is very strong. This results in increase of the zones occupied by the left and right bottom secondary vortex. Additionally the centre of the primary vortex core almost coincides with the cavity centre. Similarly to previous cases (with lower values of Ri) also in this case Pr does not influence streamlines in the cavity. The resulting streamlines caused by shearing forces driven by the moving lid and viscosity of the fluid. On the contrary impact of Pr on temperature distribution is apparent, in terms of isotherms distribution. Even for low Prandtl number (Pr = 0.71), zone with uniform temperature field is very large and it covers about 75 % of the cavity. With increasing Pr the thickness of temperature boundary layer is very thin. However in the bottom corners, where secondary vortices occur, the temperature boundary layer width remains unchanged. Nevertheless temperature gradients increase in these areas with increasing Pr. The opposite effect occurs on the top wall, near the left top corner. Highest temperature gradients exist here due to the thinnest temperature boundary layer. In the vicinity of the left top corner highest values for local Nu are expected. This is confirmed by simulation results, treated in the following.

Fig. 7
figure 7

Distribution of streamlines (left) and isotherms (right) in the cavity for Ri = 0.001 (Re = 3162) and different Prandtl numbers. From top to the bottom Pr = 0.71, 9.47 and 56.00 respectively

Full size image

Distributions of the local Nusselt number along the moving wall for Pr = 0.71 and four different values of Ri are depicted in Fig. 8. The expectation that the highest values of Nu will be located in the left top cavity corner is clearly confirmed for each value of Ri. The maximum Nu occurs for X = 0 and decreases with increasing X. This phenomenon can be explained as follows. Let it be assumed that the lid is stationary and infinitely long, and vertical walls are blades which move from right to left direction (opposite to the direction of lid motion in the actual case). This manipulation is fully allowable and does not influence the solution, due to governing equations for actual and imaginary problem are identical. Movement of the blades causes scraping of the temperature boundary layer. Just behind the blade temperature boundary layer is very thin and grows along the lid. Thinner temperature boundary layer results in smaller thermal resistance. Theoretically with increasing Re (decreasing Ri) in the left top cavity corner thickness of the temperature boundary layer tends to zero and Nu tends to infinity. This can be observed in the presented Nu plots (Figs. 8, 9, 10). Effect of temperature boundary layer scraping by the walls (blades) is larger with decreasing Ri i.e. increasing Re. However developing of the temperature boundary layer is fast and Nu decreases abruptly only in a range of X = 0–0.1. With decrease of Ri local Nu curve flattens and curve slope near the left vertical wall increases. One can observe that scraping effect occurs and increases 10 times the Nu maximum (for Ri = 0.001) in comparison with the case where Ri = 1.0.

Fig. 8
figure 8

Distribution of the Nusselt number along the lid for Prandtl number Pr = 0.71 and different Richardson numbers. From left to right and from top to the bottom Ri = 1, 0.1, 0.01 and 0.001 respectively

Full size image
Fig. 9
figure 9

Distribution of the Nusselt number along the lid for Prandtl number Pr = 9.47 and different Richardson numbers. From left to right and from top to the bottom Ri = 1, 0.1, 0.01 and 0.001 respectively

Full size image
Fig. 10
figure 10

Distribution of the Nusselt number along the lid for Prandtl number Pr = 56 and different Richardson numbers. From left to right and from top to the bottom Ri = 1, 0.1, 0.01 and 0.001 respectively

Full size image

Figure 9 shows local variations of Nu along the top wall for Pr = 9.47 and Ri ranges from 1.0 to 0.001. It is clear that Nu increases with increasing Pr. The curves of local Nu distribution are very similar in shape. In comparison with case of Pr = 0.71, local Nu plots are more flattened and Nu values are higher. Sharp peak of Nu near the left top cavity corner is much more visible compared to case of Pr = 0.71. This is caused by superposition of the scraping effect and fluid impingement on the top wall near the left top corner. The second phenomena is triggered out by buoyancy forces and fluid circulation. In the cases where Pr is higher, buoyancy forces are stronger and superimposing of mentioned effects results in significant increase of local Nu maximum. For Ri values smaller than 0.01 fluid circulation is very strong and forced convection dominates (even for Pr = 56.00). With decreasing Ri local Nu values increase. Irrespective of decreasing Ri abrupt increasing of Nu always occurs in the range of X = 0–0.1. After reaching X = 0.1 the curve slope monotonically decreases. This means that the area size, where the highest Nu values occur, does not depend on Ri. The same conclusions can be adopted in case of Pr = 56.00. The results for this case are depicted in Fig. 10. Consequently the area size, where the highest Nu values occur, does not depend on Pr as well. This is very important conclusion because it shows that mechanism of temperature boundary layer developing is similar in each studied cases and this is governed by the universal law. Additionally increasing Pr does not change the character of local Nu. The only result is substantial increase of Nu and area averaged Nusselt number \(\overline{Nu}\).

In Table 4 average values of Nusselt numbers over the surface of the top lid are presented. With increasing Pr and decreasing Ri rate of the heat transfer increases. This is confirmed by increasing \(\overline{Nu}\). For the smallest values of Ri heat transfer rate is almost 5 times larger for Pr = 56.00 case compared to Pr = 0.71 case. With increasing Pr and decreasing Ri time needed for simulation performing also lengthened. Furthermore problems with fulfilment of the condition defined by Eq. 12 in terms of Nu appeared, and error began to rise. For the limiting case in this study, i.e. for Pr = 56.00 and Ri = 0.001 the error was maximal but <5 %. In Fig. 11 the calculated values of \(\overline{Nu}\) at the top wall, in terms of Ri, are depicted. With decreasing Ri heat transfer rate increases and the curve slope increases with increasing Pr.

Fig. 11
figure 11

Variation of the average Nusselt number with respect to Richardson number calculated at the lid

Full size image
Table 4 Average Nusselt numbers \(\overline{Nu}\) on the top and bottom wall
Full size table

6 Conclusions

In this study numerical modelling of mixed convection heat transfer and fluid flow in a lid-driven cavity with constant heat flux applied on the bottom wall was performed. Despite the simplicity of this case it was not considered in the literature. Calculations involved a wide range of Richardson number and Prandtl number, while the Grashof number was fixed. The main goal was to identify the effects of Richardson number and Prandtl number on the area averaged Nusselt number. Numerical simulations were carried out on very fine meshes (resolution 1024 × 1024) to provide benchmark solution. Based on the obtained results the following findings can be summarized:

  1. 1.

    In the studied range of Richardson number, Prandtl number does not have an impact on flow field pattern but strongly influences temperature field and heat transfer phenomena.

  2. 2.

    In the case of constant Grashof number heat transfer rate increases with increasing Prandtl number and decreasing Richardson number.

  3. 3.

    For Richardson number values smaller than 0.01 forced convection dominates.

  4. 4.

    The highest values of Nusselt number are observed in the left top cavity corner. This is caused by combined effect of two mechanisms: scraping of temperature boundary layer phenomenon and fluid impingement with the top wall triggered out by circulation fluid movement and buoyancy forces.

  5. 5.

    The size of the area where the highest values of Nusselt numbers occurs does not depend on Richardson number and Prandtl number, which implies a universal law of rebuilding of the temperature boundary layer.

  6. 6.

    Increasing Prandtl number results in increase of temperature gradient and in reducing the thickness of the temperature boundary layer.

  7. 7.

    For low Ri values the temperature in the cavity centre is uniformly distributed. The same effect was noticed by Guo and Sharif [15].