Keywords

1 Introduction

The fractional derivative has been widely applied in many research areas which have been perceived an enormous growth in the last four decades. For examples, the models approaching the backgrounds of economics, physics, circuits, heat transfer, diffusion, electro-chemistry, and even biology are always apprehensive with fractional derivative [1,2,3,4,5]. In fact, fractional derivative based approaches establish more advanced and updated models of engineering systems than the ordinary derivative based approaches do in many applications. The theories of fractional derivatives generalize the idea of ordinary derivatives to some extent. The literature shows that there is no field that has remained untouched by fractional derivatives. However, development still needs to be achieved before the ordinary derivatives could be truly interpreted as a subset of the fractional derivatives [6,7,8].

In 2012, Safiel et al. [9] examines the effect of screening and treatment on the transmission of HIV/AIDS infection in a population and shows the screening of HIV infectives and treatment of screened HIV infectives has the effect of reducing the transmission of the disease. Kaur et al. [10] studied the transmission of infectives and counselling on the spread of HIV infection. In 2009, Ding and Ye [11] introduce a fractional-order HIV infection of CD4\(^+\) T-cells model, which determined the non-negative solutions, and carry out a detailed analysis on the stability of equilibrium. Gkdogan et al. [12] have applied the multi-step differential transform method to present an analytical solution of nonlinear fractional order HIV model for infection of CD4\(^+\) T cells. Recently, Arafa et al. [13] describes the fractional-order model for HIV infection of CD4\(^+\) T cells with therapy effect, and they employed Generalized Euler Method to find the numerical solution of such problem.

More precisely, we reflect on a HIV/AIDS virus dynamic model describing the interaction between the host susceptible CD4\(^+\) T cells (H), infected CD4\(^+\) T cells (I) and virus (V), and it is formulated by the following non-linear system of fractional differential equations in Caputo sense

$$\begin{aligned} D^\alpha _0 H = \mu - (\delta + \gamma ) HV - d_1 H + \sigma I \end{aligned}$$
(1a)
$$\begin{aligned} D^\alpha _0 I = \delta HV - (d_2 + \sigma ) I \end{aligned}$$
(1b)
$$\begin{aligned} D^\alpha _0 V = \beta I - \gamma HV - d_3V \end{aligned}$$
(1c)

and the initial conditions are

$$\begin{aligned} H(0)=H_0 , I(0)=I_0, V(0)=V_0, \end{aligned}$$
(2)

where the formation rate of susceptible host cells is \(\mu \), die at a rate \( d_1 H\) and turn into infected \( \delta H V \) by virus, recovered or cured at a rate \( \sigma I \) and destroy at a rate \( \gamma H V \) due to fusion. Infected cells might be killed because of virion in their nucleus. The loss rate of infected cells is given by \( (d_2 + \sigma ) I \), where \( d_2 I \) is the death rate of infected cells and \( \sigma I \) is the cure rate into the susceptible cells. Finally, virions are produced by infected cells at a rate \( \beta I \), decays at a rate \( d_3 V \), and destroy at a rate \( \gamma H V \) due to fusion.

In this study, we analysed a HIV/AIDS dynamical model with effect of fusion. One more vital feature of the model is the fact that we incorporate also a cure rate of the infected cells to the susceptible cells.

2 Analysis of the Model

2.1 Positivity and Boundedness

Denote and let \( x(t)=[ H(t), I(t), V(t) ]^{T}\). To prove the main theorem, we need the following generalized mean value theorem and corollary [9, 12].

Lemma 1

([11]). Suppose that \(f(x) \in C[a,b]\) and Caputo derivative \(D^\alpha _a f(x) \in C[a,b] \) for \(0<\alpha \le 1\), then we have

$$\begin{aligned} f(x)=f(a)+ \frac{1}{\Gamma (\alpha )}(D^\alpha _a f)(\tau )(x-a)^\alpha \end{aligned}$$
(3)

with \(a \le \tau \le x\), \(\forall x \in ( a, b]\).

Corollary 2

Let \(f(x) \in C[a,b]\) and Caputo derivative \(D^\alpha _a f(x) \in C[a,b]\) for \(0<\alpha \le 1\).

  • If \(D^\alpha _a f(x) \ge 0\), \(\forall x \in (a, b)\), then f(x) is non-decreasing function for each \(x \in [a, b]\).

  • If \(D^\alpha _a f(x) \le 0\), \(\forall x \in (a, b)\), then f(x) is non-increasing function for each \(x \in [a, b]\).

Theorem 3

There is a unique solution \(x(t)=[ H(t), I(t), V(t) ]^T \) to the system (1) and initial condition (2) on \(t \ge 0\) and the solution will remain in . Furthermore, H(t) and I(t) are all bounded.

Proof

According to Lin [14], we can determine the solution on \((0, +\infty )\), by solving the model (1) and initial conditions (2), which is not only existent but also unique. Subsequently, we have to explain the non-negative octant is a positively invariant region. From Eq. (1), we find

$$\begin{aligned} D^\alpha _0 H = \mu > 0, \ D^\alpha _0 I = \delta HV \ge 0, \ D^\alpha _0 V = \beta I \ge 0. \end{aligned}$$
(4)

By Corollary 2, the solution of model (1) will be remain in . Furthermore, from equation (1) we make out that

$$\begin{aligned} D^\alpha _0 T_{total} = \mu -\gamma HV - d_1 H - d_2 I, \end{aligned}$$

where, \(T_{total} = H+I\).

Death by infected CD4+ T cells occurs faster than death by natural means; that is, \(d_2 > d_1\). Therefore,

$$\begin{aligned} D^\alpha _0 T_{total} + d_1 T_{total} < \mu . \end{aligned}$$
(5)

Thus, by Corollary 2, in the case of HIV infection, the total T-cell population, \(T_{total}\), i.e., the sub populations H(t) and I(t), are bounded.

2.2 Equilibrium Points, Reproduction Number and Local Stability

Equilibrium Points. To evaluate the equilibrium points of model (1), let

$$\begin{aligned} D^\alpha _0 H = 0, \ D^\alpha _0 I = 0, \ D^\alpha _0 V = 0. \end{aligned}$$
(6)

Then \(E_0=(\frac{\mu }{d_1}, 0, 0)\) and \(E^*=(H^*, I^*, V^*)\) are the infection-free and endemic equilibrium points, respectively, where

$$\begin{aligned} H^* = \frac{d_3(d_2 + \sigma )}{\beta \delta - \gamma (d_2 + \sigma )}, \end{aligned}$$
$$\begin{aligned} I^* = \frac{\delta (d_1d_3(d_2 + \sigma )+\mu (\gamma (d_2 + \sigma )-\beta \delta )}{(\gamma (d_2 + \sigma )-\beta \delta )(d_2(\gamma +\delta )+\gamma \sigma )}, \end{aligned}$$
$$\begin{aligned} V^* = \frac{\mu (\beta \delta - \gamma (d_2 + \sigma ))-d_1d_3(d_2 + \sigma )}{d_2 d_3 (\gamma +\delta )+d_3 \gamma \sigma }. \end{aligned}$$

Reproduction Number. Now, we compute the reproduction number (\(\mathfrak {R}_0\)) for the model (1). \(\mathfrak {R}_0\) is defined as the number of secondary infections due to a single infection in a completely susceptible population, and it is

$$\begin{aligned} \mathfrak {R}_0 = \frac{\beta \delta \mu }{(d_1 d_3 + \gamma \mu ) (d_2 + \sigma )}. \end{aligned}$$
(7)

Local Stability of Equilibria. The Jacobian matrix of model (1) at a general point is given by

$$\begin{aligned} J= \begin{pmatrix} -d_1-(\gamma + \delta )V &{} \sigma &{} -(\gamma + \delta )H \\ \delta V &{} -d_2-\sigma &{} \delta H \\ -\gamma V &{} \beta &{} -d_3 - \gamma H\\ \end{pmatrix} \end{aligned}$$
(8)

Based on Jacobian matrix approach by evaluating (8) at infection-free equilibrium point \(E_0\), we can obtain the following results:

Lemma 4

The infection-free equilibrium point \(E_0\) is locally asymptotically stable if all eigenvalues \(\lambda _i\) of the Jacobian matrix \(J(E_0)\) for model (1), satisfy \(|arg(\lambda _i) |> \alpha \frac{\pi }{2}\).

Proof

The Jacobian matrix \(J(E_0)\) for model (1) evaluated at the infection-free equilibrium steady state \(E_0\), is given by

$$\begin{aligned} J(E_0)= \begin{pmatrix} -d_1 &{} \sigma &{} -(\gamma + \delta )\frac{\mu }{d_1} \\ 0 &{} -d_2-\sigma &{} \delta \frac{\mu }{d_1} \\ 0 &{} \beta &{} -d_3 - \gamma \frac{\mu }{d_1}\\ \end{pmatrix} \end{aligned}$$
(9)

The characteristic equation of the Jacobian matrix \(J(E_0)\) is

$$\begin{aligned} (\lambda + d_1)(\lambda ^2 +a_1 \lambda +a_2)=0, \end{aligned}$$

where, \(a_1 = (\sigma + d_2 + d_3 + \gamma \frac{\mu }{d_1}) > 0,\) and,

$$\begin{aligned} a_2 = \frac{(d_1d_3+\mu \gamma )(d_2+\sigma )-\beta \delta \mu }{d_1} = \frac{1-\mathfrak {R}_0}{d_1 (d_1d_3+\mu \gamma )(d_2+\sigma )}. \end{aligned}$$
(10)

Many researchers studied the Routh-Hurwitz stability conditions for fractional order systems [12,13,14,15], and describe the necessary and sufficient condition \(|arg(\lambda _i) |> \alpha \frac{\pi }{2}\), for various models. Routh–Hurwitz criteria states that all roots of the characteristic equation \((\lambda + d_1)(\lambda ^2 +a_1 \lambda +a_2)=0\) have negative real parts if and only if \(a_1>0\) and \(a_2>0\). Therefore, Eq. (10) implies that if \(\mathfrak {R}_0<1\) then all roots will be negative and for this condition the necessary and sufficient condition will satisfy. Hence, a sufficient condition for the local asymptotic stability of the equilibrium points is that the eigenvalues \(\lambda _i\) of the Jacobian matrix of \(J(E_0)\) satisfy the condition \(|arg(\lambda _i) |> \alpha \frac{\pi }{2}\). This confirms that fractional-order differential equations are, at least, as stable as their integer order counterpart.

The global existence of the solution of the fractional differential equation always becomes a most important concern, which is carry out in the next section.

2.3 Global Stability of Equilibria

Lemma 5

([14]). Assume that the function satisfies the following conditions in the global space:

  1. (I)

    The function G(t, x(t)) is Lebesgue measurable with respect to t on .

  2. (II)

    The function G(t, x(t)) is continuous with respect to x(t) on .

  3. (III)

    \(\displaystyle \frac{\partial G(t, x(t))}{\partial x}\) is continuous with respect x(t) on .

  4. (IV)

    \(\Vert G(t, x(t)) \Vert \le \omega + \lambda \Vert x \Vert \), for almost every and all .

Here, \(\omega , \lambda \) are two positive constants and \(x(t) = [H(t), I(t), V(t)]^T\).

Then, the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} D^\alpha _t x(t) = G(t, x(t)),\\ x(t_0)=x_0, \end{array}\right. } \end{aligned}$$
(11)

has a unique solution.

Theorem 6

There is a unique solution for system (1) and solution remains in .

Proof

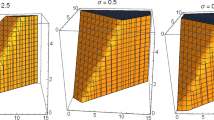
From Lemma 5, we obtain the unique solution on \((0, \infty )\) by solving the system (1). Firstly, Lin [14] discussed the proof of theorem and shows that the solution is not only exist but also unique. In Theorem 3, we already proof that the solution of model (1) will be remain in . The global stability of the model also verified with the help of Fig. 1, which shows after some time the susceptible population is going to constant while the number of infected population and virions are tends to zero, i.e., we achieve the infection-free stage.

3 Numerical Results and Discussion

In this article, we will solve the system (1) by using Mathematica 9. Consider that \(\mu =10\ mm^{-3} day^{-1}\), \(\beta =160\ day^{-1}\), \( \delta =0.000024\ mm^{3} day^{-1}\), \(\gamma =0.00001\ mm^{3} day^{-1}\), \( \sigma =0.2\ day^{-1}\), \( d_3=3.4\ day^{-1} \) [13]. We choose \( d_1=0.05\ day^{-1} \) and \( d_2=0.6\ day^{-1} \) (since death rate of host infected cells by virions will be slightly higher than those of susceptible cells) with initial conditions \(H(0)=1000\), \(I(0)=10\) and \(V(0)=10\). The recovery rate \( \sigma \) will vary for situation of the patient, such as availability of the drugs, etc.

Fig. 1.
figure 1

The densities of the host susceptible population H(t), infected population I(t) and virions V(t) when \(\alpha =1\), \(\mu =10\), \(\beta =160\), \(\delta =0.000024\), \(\gamma =0.00001\), \(d_1=0.05\), \(d_2=0.06\), \(d_3=3.4\). The solid line (\(\sigma =0.23\)), the dashed line (\(\sigma =0.20\)), and the dotted line (\(\sigma =0.17\)).

Full size image

Figure 1(a) shows that the host susceptible CD4\(^+\) T cell population decreases with increase of time and tends to positive equilibrium point \(\frac{\mu }{d_1}\). Figure 1(b) verify that infected CD4\(^+\) T cell population is increases in the first ten days, after that it decreases drastically with increase of time and it tends to zero. Similarly, Fig. 1(c) exhibit that first ten days the virus population is increases rapidly compare to infected population later on decreased radically and it tends to zero.

4 Conclusion

In this paper, we establish a system of Caputo sense fractional-order HIV/AIDS dynamics model with the help of Srivastava and Hattaf et al. [16, 17]. The author explained the non-negative solutions and boundedness as an essential part of any population dynamics model. The authors have defined the equilibrium points and reproduction number for the proposed model. By using stability analysis on an anticipated fractional order system, we obtained a sufficient condition on the parameters for the stability of the infection-free steady state. The recent appearance of fractional differential equations as models in some fields of applied mathematics makes it necessary to investigate analysis of solution for such equations and we hope that this work is a step in this direction. The numerical solutions have performed for different values of \(\sigma \).