1 Introduction

Stochastic systems are becoming widely used as realistic models of physical phenomena than deterministic systems. Also, the solution of the deterministic system is itself mean of the stochastic solution of the model [1]. Nowadays, stochastic differential equations are drawing a lot of attention because of their evolution in systems of our daily life. Therefore, involving the stochasticity in the formulation of the differential equations provides an attractive study of the phenomena of interest. Stochastic differential equations (SDEs) now describe applications in many disciplines including engineering, finance and economics, physics, population dynamics, biology and medicine. These applications involve some type of complexity, for instance, in epidemiology there is a lack of knowledge in transmission factors of a disease, the unexpected and complicated changes in economy and so on. Therefore, the differential equation cannot be considered in deterministic sense but in probabilistic sense.

The mathematical tools required to solve the stochastic differential equation are different from the corresponding deterministic equation. When the uncertainty is considered through stochastic process (e.g., Wiener process), the outcome is a stochastic differential equation. The existence of the Wiener process in SDE restricts the stochastic process to particular pattern, e.g., the Gaussian distribution. Many applications in many disciplines have been studied by [2,3,4], for example.

The study of stability is an important qualitative property of the dynamics of stochastic and random systems. While the theory of stability for stochastic and random differential equations has been widely studied by [5, 6], for example, there is a lack of study of the global mean square exponential stability. The main objective of this paper is to study the global mean square exponential stability of the steady state of SDE. Accordingly, we move to the stochastic HIV/AIDS model to study the stability of \(E^{0}\).

The epidemic of HIV is one of the most major health problems during the last three decades. HIV/AIDS disease caused millions of deaths. As yet, there is no remedy for HIV. This disease threatens our daily life; therefore, many problems always arise for researchers regarding it [7,8,9]. Theoretically, mathematics plays a vital role in describing the HIV dynamics. It provides mathematical models which can describe the immunological response to the infection with HIV disease; moreover, these models enable us to make predictions about the disease, i.e., identifying the patterns of the AIDS epidemic [10, 11].

Many papers have studied the deterministic version of HIV infection analytically and numerically by defining ordinary differential equations [12, 13], for example. Fractional calculus is a generalization of the classical calculus to an arbitrary order. It can be found in many applications in fluid dynamics, biomathematics, epidemiology, etc. Two of the most important fractional derivatives in applications are Riemann–Liouville fractional derivative and the Caputo fractional derivative. Many mathematical models including HIV/AIDS model in [14,15,16,17,18,19,20,21] have been studied analytically and numerically by defining the derivative in the fractional sense.

The study of stability of steady-state points is a good way to identify the solution behavior without solving the system. Many works have considered the stability of HIV/AIDS models, for instance [11, 22, 23].

Unlike other infectious traditional diseases, HIV can take many features; therefore, there exist sources of uncertainty. This uncertainty motivates the existence of random variables (e.g., coefficients, initial conditions, forcing terms) or stochastic terms in the mathematical model. For modeling rapidly fluctuating phenomena, an extremely useful Gaussian white noise is involved [24]. It is realistic and clear that the stochastic model is more pragmatic compared by the deterministic model, and the work done by [25] clarifies this by studying the Influenza model with constant vaccination. The HIV/AIDS epidemic model under stochastic perturbations was studied by [3, 26, 27]. Authors in [28, 29] have dealt with the stochastic HIV/AIDS epidemic model numerically using Euler–Maruyama (EM) and Runge–Kutta techniques. The fractional stochastic epidemic systems were studied numerically by [14, 30] like SIS and SIRS models.

Lyapunov functions have a pivotal role in the study of stability of deterministic and stochastic systems, and more details can be found in [31, 32]. Introducing a suitable Lyapunov function enables us to obtain different stability conditions. Regardless of initial states of the system, global exponential stability makes any trajectory tends to the attractor of the system [33], and the resulting oscillations will decay in an exponential rate. Few researchers have addressed the stochastic global exponential stability of the disease-free equilibrium point under stochastic perturbations, see [3, 27]. Using Lyapunov approach, we shall investigate the stochastic global exponential stability of \(E^{0}\). This will be shown by investigating the stochastic global exponential stability of the equilibrium point for general Eq. (1) and accordingly for HIV/AIDS stochastic system. Now, consider the general stochastic differential equation

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} &{}{\dot{x}}(t) = \mu (t,x(t)) + \sigma (t,x(t)){\dot{B}}(t) \quad t\ge t_{0}, \, x \in {\mathbb {R}} \\ &{}x(t_{0}) = x_{0} \end{aligned} \end{array}\right. \end{aligned}$$
(1)

The solution of this equation is

$$\begin{aligned} x(t) = x_{0} + \int _{t_{0}}^{t} \mu (s,x(s)) \mathrm{d}s + \int _{t_{0}}^{t} \sigma (s,x(s))\mathrm{d}B(s), \end{aligned}$$
(2)

where the last term is known as an Itô (stochastic) integral. Theorems of existence and uniqueness of solution (2) are considered in [34].

In (1), x(t) is the current state of the system, and B(t) is a one-dimensional Gaussian standard Wiener process \(B(t) \sim N(0,t)\) which is defined on the complete filtered probability space \((\Omega ,{\mathcal {F}},{\mathcal {F}}_{t}^{B},{\mathbb {P}})\), where \({\mathcal {F}}_{t}^{B}\) is the filtration generated by it up to time t. The functions \(\mu (t,x(t)), \, \, \sigma (t,x(t))\) are continuous and differentiable defined on \(\left[ t_{0}, \infty \right) \times {\mathbb {R}} \rightarrow {\mathbb {R}}\). Assume that for every \(x_{0}\), there exists a unique global solution \(x(t,t_{0},x_{0})\). Moreover, assume that \(\mu (t,0) = \sigma (t,0) = 0\), i.e., the system admits the zero solution \(x(t) = 0\). Also, \(\mu , \sigma \) are assumed to satisfy Lipschitz condition, i.e., for \(L > 0, \, \, \, \vert \mu _{1}(t,x(t)) - \mu _{1}(t,x^{*}(t)) \vert \le L \vert x(t) - x^{*}(t) \vert \), i.e., \(\vert \dfrac{\partial \mu (t,x(t))}{\partial x} \vert < L\) and also for \(\sigma (t,x(t))\). Our main results begin by studying the stability of (1). Then, we will obtain the necessary and sufficient conditions for global exponential mean square stability of zero solution of the linear system of HIV/AIDS which are the same conditions of the stability of the disease-free equilibrium point of the corresponding nonlinear system.

The plan of our paper is as follows: Sect. 2 is dedicated to some important preliminaries. In Sect. 3, the proof of the global mean square exponential stability of the trivial equilibrium of (1) is presented. Also, it is devoted to the study of HIV/AIDS model, and we shall investigate the necessary and sufficient conditions for stochastic global exponential stability of the disease-free equilibrium. In Sect. 4, areas of stability are obtained and numerical simulations of the solution are carried out followed by results and discussion section. Conclusions and future works are presented to close the paper in Sect 6.

2 Preliminaries

Definition 1

[35, 36] A stochastic process \(\{X(t),t \ge 0\}\) defined on the probability space \((\Omega ,{\mathcal {F}},{\mathbb {P}})\) is called a second-order stochastic process if X(t) is a 2-r.v \(\forall \, \, t \ge 0\). Then,

$$\begin{aligned} {\mathbb {E}}[X^{2}(t)] < \infty . \end{aligned}$$

\({\mathcal {L}}^{p}\{ [a,b];{\mathbb {R}} \}\) is the family of \({\mathbb {R}}\)-valued \({\mathcal {F}}_{t}\)-adapted stochastic processes \(\{X(t),a \le t \le b\}\) such that \(\int _{a}^{b} \left| X(s)\right| ^{p} \mathrm{d}s < \infty \). Stochastic process \(\{X(t)\}_{a \le t \le b}\) in \({\mathcal {L}}^{p}\{ [a,b];{\mathbb {R}} \}\) such that \( \int _{a}^{b} {\mathbb {E}} \left| X(s)\right| ^{p} \mathrm{d}s < \infty \) is p-integrable process. For \(p=2\), X(t) is a square integrable stochastic process.

Definition 2

[32] The zero solution of (1) is

  1. 1.

    Mean square stable if for each \(\epsilon> 0, \, \, \, \exists \, \, \, \delta > 0\) and \(\vert x_{0} \vert ^{2} < \delta \) such that

    $$\begin{aligned} {\mathbb {E}}\vert x(t,t_{0},x_{0})\vert ^{2} < \epsilon . \end{aligned}$$
  2. 2.

    Exponentially mean square stable if it is mean square stable and \(\exists \, \, \lambda , C > 0\) such that

    $$\begin{aligned} {\mathbb {E}}\vert x(t,t_{0},x_{0})\vert ^{2} \le C \vert x_{0} \vert ^{2} e^{-\lambda (t-t_{0})}. \end{aligned}$$
  3. 3.

    Globally exponentially mean square stable if it is mean square stable and \(\forall \, \, \delta > 0\), \(\exists \, \, \lambda >0\), \(K(\delta ) > 0\) such that

    $$\begin{aligned} {\mathbb {E}}\vert x(t,t_{0},x_{0})\vert ^{2} \le K(\delta ) e^{-\lambda (t-t_{0})}. \end{aligned}$$

Lemma 3

[32] Itô formula is the chain rule in Itô calculus which gives an expression to the differential of \(x(t) := u(t,x(t))\) of (1). Assume that \(u(t,x(t)): [t_{0},\infty ) \times {\mathbb {R}} \rightarrow {\mathbb {R}}\) with continuous partial derivatives \(\frac{\partial }{\partial t}\), \(\frac{\partial }{\partial x}\), \( \frac{\partial ^{2}}{\partial x^{2}}\) and \(\mathrm {L}\) as a generator of (1), then

$$\begin{aligned} \mathrm{d} x(t)&= \mathrm {L} \, u(t,x(t)) \mathrm{d}t + \sigma (t,x(t)) \frac{\partial u(t,x(t))}{\partial x} \mathrm{d}B(t) \nonumber \\&= \left[ \frac{\partial u(t,x(t))}{\partial t} + \mu (t,x(t)) \frac{\partial u(t,x(t))}{\partial x} + \dfrac{1}{2!} \sigma ^{2}(t,x(t)) \frac{\partial ^{2} u(t,x(t))}{\partial x^{2}}\right] \mathrm{d}t \nonumber \\&\quad + \sigma (t,x(t)) \frac{\partial u(t,x(t))}{\partial x} \mathrm{d}B(t). \end{aligned}$$
(3)

Theorem 4

[37] Let \(X(t) \in {\mathcal {M}}^{2}([0,T],{\mathbb {R}})\) where \({\mathcal {M}}^{2}([0,T],{\mathbb {R}})\) is the family of square integrable processes, i.e., \( {\mathbb {E}} \int _{a}^{b} \left| X(s)\right| ^{2} \mathrm{d}s < \infty \). Then, for \(0 \le t_{0} \le t_{1} < T\)

$$\begin{aligned} {\mathbb {E}} \int _{t_{0}}^{t_{1}} X(s) \mathrm{d}B_{s} = 0. \end{aligned}$$

Proof

Let \(\psi _{i}, \, 1 \le i \le k\) are bounded random variables such that \(\psi _{i}\) are \({\mathcal {F}}_{t_{i}}\)-measurable, then

$$\begin{aligned} {\mathbb {E}} \int _{t_{0}}^{t_{1}} X(s) \mathrm{d}B_{s} = \sum _{i=1}^{k} {\mathbb {E}} \left[ \psi _{i} (B_{t_{i+1}} - B_{t_{i}}) \right] = \sum _{i=1}^{k} {\mathbb {E}} \psi _{i} {\mathbb {E}} \left[ B_{t_{i+1}} - B_{t_{i}} \right] = 0, \end{aligned}$$
(4)

where \(B_{t_{i+1}} - B_{t_{i}}\) is independent of \({\mathcal {F}}_{t_{i}}\). \(\square \)

Remark 5

[38] The one-dimensional Wiener process \(B(t) \sim N(0,t)\) is said to be a standard Wiener process if

$$\begin{aligned} \begin{aligned}&B(0) = 0, \\&{\mathbb {E}}\left[ \mathrm{d}B(t)\right] = 0, \\&{\mathbb {E}}\left[ \mathrm{d}B(t) \mathrm{d}t \right] = 0, \\&{\mathbb {E}}\left[ \mathrm{d}B^{2}(t)\right] = \mathrm{d}t. \end{aligned} \end{aligned}$$

Definition 6

[32] The Lyapunov function \({\mathcal {V}}(t,x)\) is positive definite if \({\mathcal {V}}(t,0) \equiv 0\), and \({\mathcal {V}}(t,x) \ge \upsilon (x)\) for \(t \in [0, \infty ), \, \, x \in {\mathbb {R}}\) where \(\upsilon (x)\) is a nondecreasing positive definite function \(\upsilon (0) = 0 , \, \upsilon (x) > 0 \) for \( x \ne 0\). The Lyapunov function \({\mathcal {V}}(t,x)\) is negative-definite if \(-{\mathcal {V}}(t,x)\) is positive-definite.

3 Main results

First, this section focuses on general SDE (1), and we shall prove the global mean square exponential stability of the zero solution. Second, we move to stochastic HIV/AIDS model, and we will study the stochastic global exponential stability of the disease-free equilibrium by considering the linearized system.

Theorem 7

The zero solution of (1) is exponentially mean square stable.

Proof

Let \(c_{i} > 0, \, i = 1,2, \ldots \), choose a Lyapunov positive definite function \({\mathcal {V}}(t,x(t)) \ge c_{1} \vert x(t) \vert ^{2}\) with a negative definite function \(\mathrm {L}{\mathcal {V}}(t,x(t)) \le -c_{2}\vert x(t) \vert ^{2}\), and \({\mathcal {V}}(t_{0},x_{0}) \le c_{3} \vert x_{0} \vert ^{2}\) which guarantees the boundedness of \({\mathcal {V}}(t,x(t))\) at \(t=t_{0}\). The Lyapunov function is monotone nonincreasing, i.e.,

$$\begin{aligned} {\mathbb {E}}\left[ {\mathcal {V}}(t,x(t)) \right] \le {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0})\right] . \end{aligned}$$

Then, the zero solution is mean square stable as

$$\begin{aligned} {\mathbb {E}}\vert x(t) \vert ^{2} \le \dfrac{1}{c_{1}}{\mathbb {E}}\left[ {\mathcal {V}}(t,x(t)) \right] \le \dfrac{1}{c_{1}} {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0})\right] \le c_{4} \vert x_{0}\vert ^{2} < \infty , \end{aligned}$$

and x(t) is a square-integrable stochastic process as

$$\begin{aligned} \int _{t_{0}}^{t}{\mathbb {E}}\vert x(s) \vert ^{2} \mathrm{d}s \le \dfrac{-1}{c_{2}}{\mathbb {E}}\left[ {\mathcal {V}}(t,x(t)) - {\mathcal {V}}(t_{0},x_{0}) \right] \le \dfrac{1}{c_{2}} {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0}) \right] \le c_{5} \vert x_{0}\vert ^{2} < \infty . \end{aligned}$$

For exponentially mean square stability, for \(\lambda > 0\), we have \({\mathcal {V}}(t,x(t)) \ge c_{1} e^{\lambda t} \vert x(t) \vert ^{2}\), so

$$\begin{aligned} {\mathbb {E}}\vert x(t) \vert ^{2} \le \dfrac{1}{c_{1}} e^{-\lambda t} {\mathbb {E}}\left[ {\mathcal {V}}(t,x(t)) \right] \le \dfrac{1}{c_{1}} e^{-\lambda t} {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0}) \right] \le c_{4} \vert x_{0}\vert ^{2}. \end{aligned}$$

\(\square \)

Theorem 8

The zero solution of (1) is globally exponentially mean square stable.

Proof

From Theorem 6, the zero solution is exponentially stable in mean square. For global stability, define the Lyapunov function with \(\mathrm {L}{\mathcal {V}}(t,x(t)) \le 0\), for \(0 \le k < 1, \, \, t \ge t_{0}\)

$$\begin{aligned} {\mathcal {V}}(t,x(t)) = e^{\varepsilon t} \vert x(t) \vert ^{2} + k \int _{t-t_{0}}^{t} e^{\varepsilon s} x^{2}(s) \mathrm{d}s, \end{aligned}$$
(5)

which implies

$$\begin{aligned} {\mathcal {V}}(t_{0},x_{0}) \le e^{\varepsilon t_{0}} \vert x_{0} \vert ^{2} + k t_{0} e^{\varepsilon t_{0}} \vert x_{0} \vert ^{2}. \end{aligned}$$

From Itô formula (3)

$$\begin{aligned} \mathrm{d}{\mathcal {V}}(t,x(t)) = \mathrm {L}{\mathcal {V}}(t,x(t)) \mathrm{d}t + {\mathcal {V}}_{x}(t,x(t)) \sigma (t,x(t)) \mathrm{d}B(t), \end{aligned}$$

implies

$$\begin{aligned} \begin{aligned}&{\mathbb {E}} \left[ {\mathcal {V}}(t,x(t)\right] - {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0})\right] \\&= {\mathbb {E}} \int _{t_{0}}^{t} \mathrm {L}{\mathcal {V}}(\tau ,x(\tau ))d\tau + {\mathbb {E}} \left[ \int _{t_{0}}^{t} {\mathcal {V}}_{x}(\tau ,x(\tau )) \sigma (t,x(\tau )) \mathrm{d}B(\tau )\right] . \end{aligned} \end{aligned}$$

The last term vanishes by the zero-mean property of stochastic integral (Theorem 4). Therefore,

$$\begin{aligned} {\mathbb {E}} \left[ {\mathcal {V}}(t,x(t)\right] - {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0})\right] \le 0. \end{aligned}$$

Then,

$$\begin{aligned} e^{\varepsilon t} {\mathbb {E}}\vert x(t) \vert ^{2} \le {\mathbb {E}}\left[ {\mathcal {V}}(t,x(t)) \right] \le {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0}) \right] \le e^{\varepsilon t_{0}} \vert x_{0}\vert ^{2} + k t_{0} e^{\varepsilon t_{0}}\vert x_{0}\vert ^{2}, \end{aligned}$$

implies,

$$\begin{aligned} {\mathbb {E}}\vert x(t) \vert ^{2} \le \vert x_{0}\vert ^{2} (1 + k t_{0}) e^{-\varepsilon (t-t_{0})}. \end{aligned}$$

Choose \(\varepsilon >0\) and a size of the interval \(t_{0}\) such that

$$\begin{aligned} \begin{aligned}&t_{0} e^{-\varepsilon t_{0}}< 1, \\&k e^{\varepsilon t_{0}} < 1. \end{aligned} \end{aligned}$$
(6)

By the induction, we have to prove the global stability for \(t \ge t_{0}\). Firstly, for \(\left[ t_{0},2t_{0} \right) \), using (6)

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\vert x(t) \vert ^{2}&\le \vert x_{0}\vert ^{2} (1 + k t_{0}) e^{-\varepsilon (t-t_{0})}\\&\le \vert x_{0}\vert ^{2} (1 + k e^{\varepsilon t_{0}}) e^{-\varepsilon (t-t_{0})}\\&\le \dfrac{1}{1-k e^{\varepsilon t_{0}}} \vert x_{0}\vert ^{2}e^{-\varepsilon (t-t_{0})}. \end{aligned} \end{aligned}$$
(7)

For \(\left[ 2t_{0}, 3t_{0} \right) \), using (6), (7)

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\vert x(t) \vert ^{2}&\le \vert x_{0}\vert ^{2} (1 + k t_{0}) e^{-\varepsilon (t-t_{0})}\\&\le \vert x_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } + k e^{\varepsilon t_{0}} e^{-\varepsilon (t-t_{0})} (1 + k e^{\varepsilon t_{0}}) \vert x_{0}\vert ^{2} e^{-\varepsilon (t_{0} - t_{0})}\\&= \vert x_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } + \vert x_{0}\vert ^{2} (k e^{\varepsilon t_{0}} + k^{2} e^{2\varepsilon t_{0}}) e^{-\varepsilon (t-t_{0})}\\&= \vert x_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } \left( 1 + k e^{\varepsilon t_{0}} + k^{2} e^{2\varepsilon t_{0}} \right) \\&\le \dfrac{1}{1 - k e^{\varepsilon t_{0}}} \vert x_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) }. \end{aligned} \end{aligned}$$

For \(\left[ n t_{0}, (n+1) t_{0}\right) , \, \, \, n = 1, 2, \ldots \)

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\vert x(t) \vert ^{2}&\le \vert x_{0}\vert ^{2} (1 + k t_{0}) e^{-\varepsilon (t-t_{0})} \\&\le \vert x_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } \left( 1 + k e^{\varepsilon t_{0}} + k^{2} e^{2\varepsilon t_{0}} + \cdots + k^{n} e^{n\varepsilon t_{0}} \right) \\&\le \dfrac{1}{1 - ke^{\varepsilon t_{0}}} \vert x_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) }. \end{aligned} \end{aligned}$$

So

$$\begin{aligned} {\mathbb {E}}\vert x(t) \vert ^{2} \le \dfrac{1}{1-k e^{\varepsilon t_{0}}} \vert x_{0}\vert ^{2}e^{-\varepsilon (t-t_{0})}. \end{aligned}$$

Therefore, the zero solution of (1) is globally exponentially mean square stable. \(\square \)

3.1 Stochastic HIV/AIDS Model

Here we introduce the important result in this paper, consider the nonlinear deterministic version of HIV/AIDS model

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} &{}{\dot{S}}(t) = \mu - \beta S(t)I(t) - \mu S(t)\\ &{}{\dot{I}}(t) = \beta S(t)I(t) - \mu I(t) - \delta I(t)\\ &{}{\dot{A}}(t) = \delta I(t) - \mu A(t) - d A(t)\\ &{}S(t_{0}) = S_{0}, \, \, \, I(t_{0}) = I_{0}, \, \, \, A(t_{0}) = A_{0}. \, \, \, \\ \end{aligned} \end{array}\right. \end{aligned}$$
(8)

The infected class is I(t), and this class can pass the disease to the susceptibles S(t). The infected individuals can become AIDS and go to the class A(t). The parameter \(\mu \) is the rate of birth and nature death, \(\beta \) is the transmission rate of infection, \(\delta \) is the rate of infected individuals to be AIDS, d is the death rate caused by AIDS disease and all the parameters \( \mu , \beta , \delta , d \in \left[ 0 , \infty \right) \). The basic reproduction ratio denoted by \(R_{0}\) of an infection is the expected number of cases directly generated by one case in a population where all individuals are susceptible to catch the disease, so

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm{d}I(t)}{\mathrm{d}t}&= I(t) \left( \beta S(t) - \mu - \delta \right) \\&\le I(t) \left( \beta S_{0} - \mu - \delta \right) , \end{aligned} \end{aligned}$$

So, the disease is spreading for \(\beta S_{0} > \mu + \delta \). Then, the basic reproduction number is \(R_{0} = \dfrac{\beta }{\delta + \mu }\).

This model admits two equilibria:

  1. 1.

    Disease-free equilibrium \(E^{0} = (1,0,0)\) which is globally stable when \(R_{0} < 1\) for lower transmission \(\beta \) like social distancing, getting tested and treated for sexually transmitted disease (STD) and so on.

  2. 2.

    Endemic equilibrium \(E^{\star } = \left( \dfrac{\delta + \mu }{\beta },\dfrac{(\beta - \delta - \mu )\mu }{\beta (\delta + \mu )},\dfrac{\delta \mu (\beta - \delta - \mu )}{\beta (d+\mu )(\delta + \mu )}\right) \) which is globally stable when \(R_{0} > 1\) and the disease will not disappear.

Lemma 9

The endemic equilibrium \(E^{\star } = (S^{\star },I^{\star },A^{\star })\) of (8) is globally asymptotically stable if \(R_{0} > 1\).

Proof

Define the Lyapunov function as follows

$$\begin{aligned} {\mathcal {V}}(S,I,A) = (S - S^{\star } \log (S)) + (I - I^{\star } \log (I)) + (A - A^{\star } \log (A)). \end{aligned}$$

Then,

$$\begin{aligned} \dfrac{\mathrm{d}{\mathcal {V}}}{\mathrm{d}t} = \left( 1 - \dfrac{S^{\star }}{S} \right) \dfrac{\mathrm{d}S}{\mathrm{d}t} + \left( 1 - \dfrac{I^{\star }}{I} \right) \dfrac{\mathrm{d}I}{\mathrm{d}t} + \left( 1 - \dfrac{A^{\star }}{A} \right) \dfrac{\mathrm{d}A}{\mathrm{d}t}. \end{aligned}$$

At the steady state, using the relations

$$\begin{aligned} \mu = \beta S^{\star } I^{\star } + \mu S^{\star }, \quad \beta S^{\star } I^{\star } = (\mu + \delta ) I^{\star } \quad \text {and} \quad \delta I^{\star } = (\mu + d) A^{\star }. \end{aligned}$$

Then,

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm{d}{\mathcal {V}}}{\mathrm{d}t}&= \left( 1 - \dfrac{S^{\star }}{S} \right) \left( -\mu (S-S^{\star }) + \beta S^{\star } I^{\star } - \beta S I \right) + \left( 1 - \dfrac{I^{\star }}{I} \right) \left( -(\mu + \delta )(I-I^{\star }) \right) \\&\quad +\left( 1 - \dfrac{A^{\star }}{A} \right) \left( -(\mu + d)(A-A^{\star }) \right) \\&= -\mu \dfrac{(S-S^{\star })^{2}}{S} - \beta S I \left( 1 - \dfrac{S^{\star }}{S} \right) \left( 1 - \dfrac{S^{\star } I^{\star }}{S I}\right) - (\mu + \delta )\dfrac{(I-I^{\star })^{2}}{I} \\&\quad - (\mu + d)\dfrac{(A-A^{\star })^{2}}{A}. \end{aligned} \end{aligned}$$

The arithmetic mean is always greater than or equal to the geometrical mean; then, \(\left( 1 - \dfrac{S^{\star }}{S} \right) \le 0\) and \(\left( 1 - \dfrac{S^{\star } I^{\star }}{S I}\right) \le 0\). This implies \(\dfrac{\mathrm{d}{\mathcal {V}}}{\mathrm{d}t} \le 0\), and \(\dfrac{\mathrm{d}{\mathcal {V}}}{\mathrm{d}t} = 0\) only when \((S,I,A) = (S^{\star },I^{\star },A^{\star })\). Then, \(E^{\star }\) is globally asymptotically stable by using the principle of LaSalle invariant [39]. \(\square \)

For developing the stochastic model, there are two ways of perturbations. First, we can replace an environmental deterministic parameter by a random parameter [1]. Second, one can add a stochastic driving force (term) to the deterministic model without changing any parameter. Here, we assume a nonparametric stochastic perturbations of Gaussian white noise type. This perturbation has been used by [40]. Then, the stochastic HIV/AIDS model becomes

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} &{}\mathrm{d}S(t) = \left( \mu - \beta S(t)I(t) - \mu S(t) \right) \mathrm{d}t + \sigma S(t) I(t) \mathrm{d}B(t)\\ &{}\mathrm{d}I(t) = \left( \beta S(t)I(t) - \mu I(t) - \delta I(t)\right) \mathrm{d}t + \sigma S(t) I(t) \mathrm{d}B(t)\\ &{}\mathrm{d}A(t) = \left( \delta I(t) - \mu A(t) - \mathrm{d} A(t)\right) \mathrm{d}t + \sigma A(t) \mathrm{d}B(t)\\ \end{aligned} \end{array}\right. \end{aligned}$$
(9)

The real constant \(\sigma \) represents the intensity of the environmental fluctuations. By centering system (9) on the equilibrium \(E^{0}\) using the transformation

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} &{}x(t) = S(t) - 1 \\ &{}y(t) = I(t) \\ &{}z(t) = A(t)\\ \end{aligned} \end{array}\right. \end{aligned}$$

Then,

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} &{}\mathrm{d}x(t) = \left( -\beta (x(t)+1)y(t) - \mu x(t) \right) \mathrm{d}t + \sigma (x(t)+1) y(t) \mathrm{d}B(t)\\ &{}\mathrm{d}y(t) = \left( \beta (x(t)+1)y(t) - \mu y(t) - \delta y(t)\right) \mathrm{d}t + \sigma (x(t)+1) y(t) \mathrm{d}B(t)\\ &{}\mathrm{d}z(t) = \left( \delta y(t) - \mu z(t) - \mathrm{d} z(t)\right) \mathrm{d}t + \sigma z(t) \mathrm{d}B(t)\\ \end{aligned} \end{array}\right. \end{aligned}$$

Then, the corresponding linear system is

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} &{}\mathrm{d}x(t) = \left( -\beta y(t) - \mu x(t) \right) \mathrm{d}t + \sigma y(t) \mathrm{d}B(t)\\ &{}\mathrm{d}y(t) = \left( \beta y(t) - \mu y(t) - \delta y(t)\right) \mathrm{d}t + \sigma y(t) \mathrm{d}B(t)\\ &{}\mathrm{d}z(t) = \left( \delta y(t) - \mu z(t) - \mathrm{d}z(t)\right) \mathrm{d}t + \sigma z(t) \mathrm{d}B(t)\\ \end{aligned} \end{array}\right. \end{aligned}$$
(10)

Following the argument of Theorem 8, the next theorem investigates the necessary and sufficient conditions for stochastic global exponential stability of the disease-free equilibrium of (9) which are the sufficient conditions for global mean square exponential stability of the zero equilibrium point of linear system (10).

Theorem 10

The disease-free equilibrium of (9) is stochastically globally exponentially stable if for \(\varepsilon > 0, \, \, 0 \le k < 1\)

$$\begin{aligned} \begin{aligned}&\beta \le \min \{ \delta + \mu , 2\mu - \varepsilon -k, \dfrac{1}{3} \left[ 2\mu + \delta -2\sigma ^{2} - \varepsilon -k \right] \}, \\&2\mu \le \varepsilon + \delta - 2d + \sigma ^{2} + k. \end{aligned} \end{aligned}$$
(11)

Proof

Consider the Lyapunov function

$$\begin{aligned} {\mathcal {V}}(t,x(t),y(t),z(t)) = e^{\varepsilon t} \left[ x^{2}(t) + y^{2}(t) + z^{2}(t)\right] + k \int _{t-t_{0}}^{t} e^{\varepsilon s}\left[ x^{2}(s)+y^{2}(s)+z^{2}(s)\right] \mathrm{d}s. \end{aligned}$$

Then,

$$\begin{aligned} \begin{aligned} \mathrm{d}{\mathcal {V}}(t,x(t),y(t),z(t))&= \mathrm {L}{\mathcal {V}}(t,x(t),y(t),z(t)) \mathrm{d}t\\&\quad + \sigma y(t) {\mathcal {V}}_{x}(t,x(t),y(t),z(t)) \mathrm{d}B(t)\\&\quad + \sigma y(t) {\mathcal {V}}_{y}(t,x(t),y(t),z(t)) \mathrm{d}B(t)\\&\quad + \sigma z(t) {\mathcal {V}}_{z}(t,x(t),y(t),z(t)) \mathrm{d}B(t), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \mathrm {L}{\mathcal {V}}(t,x(t),y(t),z(t))&= 2 e^{\varepsilon t} x(t) (-\beta y(t) - \mu x(t)) + 2 e^{\varepsilon t} y(t) (\beta y(t) - \mu y(t) - \delta y(t)) \\&\quad + 2 e^{\varepsilon t} z(t) (\delta y(t) - \mu z(t) - \mathrm{d} z(t)) + 2 e^{\varepsilon t} \sigma ^{2} y^{2}(t) + e^{\varepsilon t} \sigma ^{2} z^{2}(t) \\&\quad + \varepsilon e^{\varepsilon t} (x^{2}(t) + y^{2}(t) + z^{2}(t)) + k e^{\varepsilon t} \left[ x^{2}(t) + y^{2}(t) + z^{2}(t)\right] \\&\quad - k e^{\varepsilon (t-t_{0})} \left[ x^{2}(t-t_{0}) + y^{2}(t-t_{0}) + z^{2}(t-t_{0}) \right] \\&\le e^{\varepsilon t} \lbrace \left. \beta (x^{2}(t) + y^{2}(t)) - 2\mu x^{2}(t) + 2\beta y^{2}(t) - 2\delta y^{2}(t) - 2\mu y^{2}(t) \right. \\&\left. +\delta (z^{2}(t) + y^{2}(t)) - 2\mu z^{2}(t) - 2d z^{2}(t) + \sigma ^{2}z^{2}(t) + 2 \sigma ^{2} y^{2}(t) \right. \\&\quad + \varepsilon \left[ x^{2}(t) + y^{2}(t) + z^{2}(t) \right] + k \left[ x^{2}(t) + y^{2}(t) + z^{2}(t)\right] \rbrace \\&\quad - k e^{\varepsilon (t-t_{0})} \left[ x^{2}(t-t_{0}) + y^{2}(t-t_{0}) + z^{2}(t-t_{0}) \right] . \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} \begin{aligned} \mathrm{d}{\mathcal {V}}(t,x(t),y(t),z(t))&\le e^{\varepsilon t} \left[ \left( \varepsilon + \beta -2\mu + k \right) x^{2}(t) \right. \\&\quad + \left. e^{\varepsilon t} \left( \varepsilon + 3\beta -2\mu - \delta +2\sigma ^{2} + k \right) y^{2}(t) \right. \\&\quad + \left. e^{\varepsilon t} \left( \varepsilon + \delta -2\mu - 2d + \sigma ^{2} + k \right) z^{2}(t) \right] \mathrm{d}t\\&\quad - k e^{\varepsilon (t-t_{0})} \left[ x^{2}(t-t_{0}) + y^{2}(t-t_{0}) + z^{2}(t-t_{0}) \right] \mathrm{d}t\\&\quad + \sigma \left[ y(t) {\mathcal {V}}_{x} + y(t) {\mathcal {V}}_{y} + z(t) {\mathcal {V}}_{z} \right] \mathrm{d}B(t). \end{aligned} \end{aligned}$$

Taking the expectation

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\left[ \mathrm{d}{\mathcal {V}}(t,x(t),y(t),z(t))\right]&\le e^{\varepsilon t} \left[ \left( \varepsilon + \beta -2\mu + k \right) {\mathbb {E}} \vert x(t) \vert ^{2} \right. \\&\quad + \left. e^{\varepsilon t} \left( \varepsilon + 3\beta -2\mu - \delta +2\sigma ^{2} + k \right) {\mathbb {E}} \vert y(t) \vert ^{2} \right. \\&\quad + \left. e^{\varepsilon t} \left( \varepsilon + \delta -2\mu - 2d + \sigma ^{2} + k \right) {\mathbb {E}} \vert z(t) \vert ^{2} \right. \\&\quad - \left. k e^{\varepsilon (t -t_{0})} {\mathbb {E}} \left[ x^{2}(s-s_{0}) + y^{2}(s-s_{0}) + z^{2}(s-s_{0}) \right] \right] \mathrm{d}t\\&\quad + \sigma {\mathbb {E}} \left[ \left( y(t) {\mathcal {V}}_{x} + y(t) {\mathcal {V}}_{y} + z(t) {\mathcal {V}}_{z} \right) \mathrm{d}B(t)\right] . \end{aligned} \end{aligned}$$

By Remark 5, the last term vanishes. Then \({\mathbb {E}}\left[ \dfrac{\mathrm{d}{\mathcal {V}}}{\mathrm{d}t}\right] \le 0\) if

$$\begin{aligned} \begin{aligned}&R_{0} \le 1 \quad \text {i.e.,} \quad \beta < \delta + \mu , \quad \varepsilon + \beta -2\mu + k \le 0 \\&\varepsilon + 3\beta -2\mu - \delta +2\sigma ^{2} + k \le 0 \quad \text {and} \quad \varepsilon + \delta -2\mu - 2d + \sigma ^{2} + k \le 0. \end{aligned} \end{aligned}$$

The first three conditions imply \(\beta \le \min \lbrace \delta + \mu , 2\mu - \varepsilon -k, \dfrac{1}{3} \left[ 2\mu + \delta -2\sigma ^{2} - \varepsilon -k \right] \rbrace \).

For global stability, it is known that \({\mathcal {V}}\) is monotone nonincreasing, then

$$\begin{aligned} {\mathbb {E}}\left[ {\mathcal {V}}(t,x(t),y(t),z(t))\right] \le {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0},y_{0},z_{0})\right] \end{aligned}$$

Then,

$$\begin{aligned} \begin{aligned} e^{\varepsilon t}{\mathbb {E}}\left[ x^{2}(t) + y^{2}(t) + z^{2}(t)\right]&\le {\mathbb {E}}\left[ {\mathcal {V}}(t,x(t),y(t),z(t))\right] \\&\le {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},x_{0},y_{0},z_{0}) \right] \\&\le e^{\varepsilon t_{0}}\left( x^{2}_{0} + y^{2}_{0} + z^{2}_{0}\right) + k t_{0} e^{\varepsilon t_{0}} (x^{2}_{0} + y^{2}_{0} + z^{2}_{0}). \end{aligned} \end{aligned}$$

Assume

$$\begin{aligned} \begin{aligned}&x^{2}(t) + y^{2}(t) + z^{2}(t) = N^{2}(t),\\&x^{2}_{0} + y^{2}_{0} + z^{2}_{0} = N^{2}_{0}. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} e^{\varepsilon t} {\mathbb {E}}\vert N(t) \vert ^{2} \le {\mathbb {E}}\left[ {\mathcal {V}}(t,N(t)) \right] \le {\mathbb {E}}\left[ {\mathcal {V}}(t_{0},N_{0}) \right] \le e^{\varepsilon t_{0}} \vert N_{0}\vert ^{2} + k t_{0} e^{\varepsilon t_{0}}\vert N_{0}\vert ^{2}, \end{aligned}$$

implies

$$\begin{aligned} {\mathbb {E}}\vert N(t) \vert ^{2} \le \vert N_{0}\vert ^{2} (1 + k t_{0}) e^{-\varepsilon (t-t_{0})}. \end{aligned}$$

By (6) and the induction, we can show

$$\begin{aligned} {\mathbb {E}}\vert N(t) \vert ^{2} \le \dfrac{1}{1 - k e^{\varepsilon t_{0}}} \vert N_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } \quad t \ge t_{0}. \end{aligned}$$
(12)

Firstly, for \(\left[ t_{0},2t_{0} \right) \), using (6),

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\vert N(t) \vert ^{2}&\le \vert N_{0}\vert ^{2} (1 + k t_{0}) e^{-\varepsilon (t-t_{0})}\\&\le \vert N_{0}\vert ^{2} (1 + k e^{\varepsilon t_{0}}) e^{-\varepsilon (t-t_{0})}\\&\le \dfrac{1}{1-k e^{\varepsilon t_{0}}} \vert N_{0}\vert ^{2}e^{-\varepsilon (t-t_{0})}. \end{aligned} \end{aligned}$$
(13)

For \(\left[ 2t_{0}, 3t_{0} \right) \), using (6), (13)

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\vert N(t) \vert ^{2}&\le \vert N_{0}\vert ^{2} (1 + k t_{0}) e^{-\varepsilon (t-t_{0})}\\&\le \vert N_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } + k e^{\varepsilon t_{0}} e^{-\varepsilon (t-t_{0})} (1 + k e^{\varepsilon t_{0}}) \vert N_{0}\vert ^{2} e^{-\varepsilon (t_{0} - t_{0})}\\&= \vert N_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } + \vert N_{0}\vert ^{2} (k e^{\varepsilon t_{0}} + k^{2} e^{2\varepsilon t_{0}}) e^{-\varepsilon (t-t_{0})}\\&= \vert N_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } \left( 1 + k e^{\varepsilon t_{0}} + k^{2} e^{2\varepsilon t_{0}} \right) \\&\le \dfrac{1}{1 - k e^{\varepsilon t_{0}}} \vert N_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) }. \end{aligned} \end{aligned}$$

For \(\left[ n t_{0}, (n+1) t_{0}\right) , \, \, \, n = 1, 2, \ldots \)

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\vert N(t) \vert ^{2}&\le \vert N_{0}\vert ^{2} (1 + k t_{0}) e^{-\varepsilon (t-t_{0})} \\&\le \vert N_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) } \left( 1 + k e^{\varepsilon t_{0}} + k^{2} e^{2\varepsilon t_{0}} + \cdots + k^{n} e^{n\varepsilon t_{0}} \right) \\&\le \dfrac{1}{1 - ke^{\varepsilon t_{0}}} \vert N_{0}\vert ^{2} e^{-\varepsilon \left( t - t_{0}\right) }. \end{aligned} \end{aligned}$$

So if conditions (11) hold as well as inequality (12), then the zero solution of (10) is globally exponentially mean square stable. Consequently, the disease-free equilibrium point of (9) is stochastically globally exponentially stable. \(\square \)

4 Numerical example

Consider the stochastic HIV/AIDS model

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} &{}\mathrm{d}S(t) = \left( 1.5 - 2 S(t)I(t) - 1.5 S(t) \right) \mathrm{d}t + 0.5 S(t) I(t) \mathrm{d}B(t)\\ &{}\mathrm{d}I(t) = \left( 2 S(t)I(t) - 1.5 I(t) - 4 I(t)\right) \mathrm{d}t + 0.5 S(t) I(t) \mathrm{d}B(t)\\ &{}\mathrm{d}A(t) = \left( 4 I(t) - 1.5 A(t) - A(t)\right) \mathrm{d}t + 0.5 A(t) \mathrm{d}B(t)\\ &{}S_{0} = 0.5, \, \, I_{0} = 3, \, \, \, A_{0} = 1.5.\\ \end{aligned} \end{array}\right. \end{aligned}$$
(14)

4.1 Stochastic Euler–Maruyama Scheme

For numerical approximation, Brownian motion is discretized by dividing [0, T] into \(N>0\) subintervals; then, \(\Delta t = \dfrac{T}{N}\). Further, \(\Delta B_{n} = B_{t_{n+1}} - B_{t_{n}}\) where \(\Delta B_{n} \sim N(0,\Delta t)\). The stochastic integral \(\int _{0}^{T} \sigma (s,x) \mathrm{d}B(s) \approx \sum _{n=0}^{N} \sigma (t_{n},x_{n})(B_{t_{n+1}} - B_{t_{n}})\). Therefore, for good approximation of this integral, \(\Delta t\) must be small enough as the mesh of partition of [0, T] goes to zero. From solution (2),

$$\begin{aligned} \int _{t_{n}}^{t_{n+1}} \mu (s,x) \mathrm{d}s \approx \mu (t_{n},x_{n})\Delta t \quad \text {and} \quad \int _{t_{n}}^{t_{n+1}} \sigma (s,x) \mathrm{d}B(s) \approx \sigma (t_{n},x_{n})\Delta B_{n}. \end{aligned}$$

Then, Euler–Maruyama scheme has the form

$$\begin{aligned} x_{n+1} = x_{n} + \mu (t_{n},x_{n}) \Delta t + \sigma (t_{n},x_{n})\Delta B_{n}. \end{aligned}$$
(15)

The data required in the algorithm are the process \(x(t_{n})\) with random sample of normal distribution, and the result is the position of the process \(x(t_{n+1})\) at the time \(t_{n+1}\). Euler–Maruyama is strongly convergent with order 0.5, This means that if we want to reduce the error 10 times, we have to make the step size 100 times smaller. Unfortunately, the step size cannot be too small because of computational errors and time. Rates of convergence of this scheme are given by [41]. More approximation methods can be used like the Milstein scheme (which increases the accuracy of Euler by adding a second-order “correction” term in the scheme) and Runge–Kutta scheme. These methods converge strongly with order 1, i.e., if we want to reduce the error 10 times, we have to make the step size 10 times smaller. Sometimes it is computationally costly to compute the derivatives, so we avoid the Runge–Kutta scheme. Milstein scheme is superior to the Euler–Maruyama. It was shown first by [42].

4.2 Numerical illustrations

Inequalities (11) are the conditions of global mean square exponential stability of the zero solution of (10) and the disease-free equilibrium of (9). Given by these conditions and in space of parameters \((\beta ,\mu ,\delta )\), the stochastic global exponential stability regions of \(E^{0}\) of (9) are shown in Fig. 1 for different values of the parameter \(\sigma \) and in Fig. 2 for different values of the parameter d. The regions of stability are shown in three-dimensional space with \(k=0.01\) and \(\varepsilon = 0.2\).

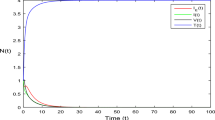
For the numerical simulations, this paper deals with the numerical simulation algorithm of the trajectories of Brownian motion and the scheme of Euler–Maruyama that have been presented by the extant literature [43, 44]. Author in [1] has shown that the scheme of Euler–Maruyama converges to the equilibria of the system for small enough step sizes. As we studied stochastic nonlinear HIV/AIDS model (9) via corresponding linear system (10), we perform a numerical simulation for the zero solution of (10) at first. From the stability region for \(\sigma = 0.5\), choosing the coordinates \((\beta ,\mu ,\delta ) = (1.5,2,4)\), all 50 trajectories for each of the variables S(t), I(t) and A(t) converge to zero and this is shown in Fig. 4.

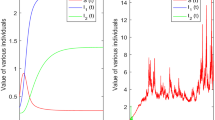
For the numerical simulation of the disease-free equilibrium of (9) and with the same coordinates (1.5, 2, 4), we have obtained 50 trajectories for each process converging to the disease-free equilibrium \(E^{0} = (1,0,0)\) in Fig. 3a. With the coordinates (5, 1.5, 2), Fig. 3b shows an unstable disease-free equilibrium and the solutions converge to the epidemic equilibrium (0.7, 0.1285, 0.1028).

Fig. 1
figure 1

Regions of stability of the disease-free equilibrium of (9) with \(d=1\)

Full size image
Fig. 2
figure 2

Regions of stability of the disease-free equilibrium of (9) with \(\sigma =0.5\)

Full size image

5 Results and discussion

Theorem 10 indicates that the epidemic dies out if condition (11) holds. These conditions are necessary and sufficient for stochastic global exponential stability of \(E^{0}\). Stability regions become better for small values of \(\sigma \). For \(\sigma = 0.5\), when \(d \rightarrow 0\) we still have the same stability region of \(E^{0}\). For larger values of the death rate caused by AIDS, the stability region increases.

With condition (11), all solutions converge to \(E^{0}\) and the disease dies out eventually. All solutions do not converge to \(E^{0}\) if condition (11) is not met. The epidemic will persist, and the number of susceptibles and the infected individuals in the population tend to positive constants. Euler–Maruyama does a better job as we reduce the step size \(\Delta t\), and we lose the convergence for specific values of \(\Delta t\), for instance, if \(\Delta t = 0.5\), trajectories do not converge to the equilibrium point .

Fig. 3
figure 3

Fifty trajectories for each process S(t)(blue), I(t)(red) and A(t)(green)

Full size image
Fig. 4
figure 4

Fifty trajectories for each process S(t)(blue), I(t)(red) and A(t)(green)

Full size image

6 Conclusion and further directions

Our paper has highlighted the stochastic global exponential stability of the disease-free equilibrium point of the stochastic HIV/AIDS model. Necessary and sufficient conditions are obtained. Many numerical simulations are carried out to support the analytical results. For further directions, we can consider the uncertainty in the differential equation by assuming that the coefficients, initial conditions and forcing terms are random variables and/or stochastic processes. In this case, the equation is termed as random differential equation (RDE). Existence of these random variables allows for a wider type of probability distributions (e.g., Poisson, geometrical, binomial, gamma, etc.), and this makes RDE very important for describing the real-life applications rightfully. Moreover, we hope that our work will be applicable to stochastic models influenced by fractional Brownian motion.