Barrier Coverage Lifetime Maximization in a Randomly Deployed Bistatic Radar Network

Abstract

Maximizing the lifetime of barrier coverage is a critical issue in randomly deployment sensor networks. In this paper, we study the barrier coverage lifetime maximization problem in a bistatic radar network, where the radar nodes follow a uniform deployment. We first construct a coverage graph to describe the relationship among different bistatic radar pairs. We then propose a solution to maximize the barrier lifetime: An algorithm is first proposed to find all barriers based on coverage graph and then determines the operation time for each barrier by using linear programming method. We also propose two heuristic algorithms called greedy algorithm and random algorithm for large-scale networks. Simulation results validate the effectiveness of the proposed algorithms.

This paper is supported in part by the National Natural Science Foundation of China (No. 61760929, 61461030, 61371141).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Barrier coverage of wireless sensor network has been widely used as an effective tool in security applications, such as international boundary surveillance and critical infrastructure protection [1]. Wireless sensors usually operate in unattended environments with limited power supply by small-sized batteries. How to ensure network work beyond single sensor lifetime is a critical issue for barrier coverage. Recently, many algorithms that schedule the sensor working states have been proposed for maximizing the barrier coverage lifetime [2,3,4], however, they are based on the disk sensing model or sector sensing model. In the disk sensing model, the covered area of sensor is a disk centered at its location with radius as the sensing range. While in the sector sensing model, the covered area of sensor is a sector region of a disk [5].

For the disk model, Kumar et al. [6] first propose an Randomized Independent Sleeping (RIS) algorithm, where each sensor independently determines whether to be activated with a predefined probability. Chen et al. [7] propose a localized algorithm called Localized Barrier Coverage Protocol (LBCP) for ensuring local barrier coverage and show that the LBCP outperforms RIS by up to six times. Kumar et al. [8] propose an optimal solution to the problem of how to maximize the total barrier coverage lifetime in homogeneous or heterogeneous networks. Kim et al. [9] identify a new security problem of the proposed algorithms in [8] and propose two remedies for the barrier coverage problem. For the sector sensing model, Zhao et al. [4] propose an efficient algorithm to solve the barrier coverage lifetime maximization problem based on sector sensing model.

Recently, coverage problem based on radar sensors has become a new research focus. Radar sensor emits radio and collects echo reflected from target. Radar determines whether the target exists or not by analyzing the difference between the original radio and collected echo [10]. There are two types of radar sensors according to the location of the transmitter and receiver. Transmitter and receiver co-locate in the monostatic radar. Transmitter and receiver are deployed separatively in the bistatic radar [11]. Much unlike the disk coverage model of monostatic radar, the coverage area of bistatic radar pair can be characterized by the Cassini oval with foci at transmitter and receiver location. Previous studies about coverage problem of bistatic radar focus on the nodes deployment for constructing target coverage and barrier coverage [12, 13].

In this paper, we study the barrier coverage lifetime problem for bistatic radar sensor networks. We first construct a coverage graph based on the connected coverage region of bistatic radar pairs. We then propose an algorithm to find barriers in the network and apply the linear programming method to assign operation time slots for each barrier such that the total barrier lifetime can be maximized. We also propose two heuristic algorithms called Greedy Algorithm and Random Algorithm for large-scale networks. As far as we know, the work most similar to ours is [14]. Compared to [14], our work in this paper have several distinct differences: First, the initial energy of radar nodes and the energy consumption rate of transmitter and receiver are considered as different in our work; While there are set the same in [14]. Second, the work [14] does not consider the bistatic radar sensor when their coverage region is disjoint, but our work have considered this issue. Third, each barrier found in this paper satisfies the condition that each receiver only couple with one transmitter while the barrier in [14] does not have such a constraint.

The rest of this paper is organized as follows. We present the network model and problem description in Sect. 2. Section 4 provides our solutions, and simulation results are given in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Network Model and Problem Description

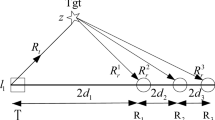
We consider a bistatic radar sensor network consisting of M transmitters and N receivers randomly deployed in a $W\times H$ rectangle region. For a transmitter-receiver pair $T_iR_j$, the Signal-to-Noise Ratio (SNR) of $R_j$ due to a target located at z can be computed by [15]:

$$\begin{aligned} SNR_z(T_i,R_j)=\frac{C}{\Vert T_iz\Vert ^2\Vert R_jz\Vert ^2}, \end{aligned}$$

(1)

where C is a constant reflecting the physical characteristics of the bistatic radar such as the antenna gain of the transmitter and receiver. $\Vert T_iz\Vert$ denotes the Euclidean distance between $T_i$ and z. Given the detection requirement $SNR_{th}$, a target can be detected by the $(T_i, R_j)$ pair, if $SNR_z(T_i, R_j) \ge SNR_{th}$.

We assume that transmitters can use orthogonal frequencies to avoid interference at receivers [16, 17]. Thus a receiver can potentially couple with different transmitters by changing the working frequency at different time slot. However, a receiver can only couple with one transmitter at a time slot since a receiver cannot work with two different frequencies at the same time. For ease of presentation, in this paper, we define the vulnerability of the target located at z as:

$$\begin{aligned} l(z)\doteq \sqrt{\Vert T_iz\Vert \cdot \Vert R_jz\Vert } \end{aligned}$$

(2)

The vulnerability contour can be characterized by Cassini oval with foci at the transmitter and receiver location. Given the SNR threshold $\gamma$, we define the maximum vulnerability as:

$$\begin{aligned} l_{max}=\root 4 \of {\frac{C}{SNR_{th}}}. \end{aligned}$$

(3)

A target located at z can be detected by the $(T_i, R_j)$ pair, if $l(z) \le l^2_{max}$. In this regard, we also say that the point z can be covered by the $(T_i, R_j)$ pair.

Let two virtual nodes s and t denote the left boundary and right boundary, respectively. We say that a bistatic radar pair $(T_i,R_j)$ form a sub-barrier with s and t, if the coverage region of $(T_i, R_j)$ overlaps with the left and right boundary. A barrier consists of a chain of bistatic radar pairs starting at s and ending at t, where the coverage regions of adjacent radar pairs overlap with each other. Since a receiver can only couple with one transmitter at a time, in one barrier a receiver can only appear at most once. On the other hand, a transmitter can couple with different receivers, and in one barrier a transmitter may appear in different bistatic radar pairs.

Let $E_{T_i}$ and $E_{R_j}$ denote the initial energy of the $T_i$ and $R_j$, respectively. We assume that both transmitters and receivers consume the energy at a flat rate in the working state. Let $\alpha _t$ and $\alpha _r$ denote the energy consumption rate of an active transmitter and an active receiver, respectively. We assume $\alpha _t \ge \alpha _r$, since in general signal transmission consumes more energy than signal reception. The lifetime of $T_i$ and $R_j$ can be computed by $\frac{E_{T_i}}{\alpha _t}$ and $\frac{E_{R_j}}{\alpha _r}$, respectively.

3 Constructing a Barrier Coverage Graph

In this section, we construct a barrier coverage graph (BCG) based on the connected coverage areas of bistatic radars. Without loss of generality, we index the transmitters and receivers according to their x-coordinate from the left boundary to the right boundary of the network. For each bistatic transmitter-receiver pair $(T_i, R_j)$, the shape of its coverage region depends on the relation between $l_{max}$ and $d(T_i,R_j)$, and can be divided into two types:

(a1) When $d(T_i,R_j)\le 2 l_{max}$, the coverage region of a $(T_i, R_j)$ pair is a connected region, as shown in Fig. 1 (a); In this case, we denote the connected coverage region of $(T_i,R_j)$ as $A_{ij}$. Note that $A_{ij}$ contains both $T_i$ and $R_j$.

(a2) When $d(T_i,R_j)> 2l_{max}$, the coverage region of a $(T_i, R_j)$ pair contains two disconnected ellipse regions, as shown in Fig. 1 (b). In this case, we let $A_{i(j)}$ and $A_{(i)j}$ to denote the two disconnected coverage regions, respectively. Note that $A_{i(j)}$ contains $T_i$; but does not contain $R_j$. And $A_{(i)j}$ contains $R_j$, but not $T_i$.

It can be shown that when $d(T_i, R_j)$ increases, both the coverage region of $A_{i(j)}$ and $A_{(i)j}$ reduce. When the distance is larger than some threshold, the two coverage regions do not contribute much in barrier construction. So we do not consider a $(T_i, R_j)$ pair when $d(T_i, R_j) > D_{max}$.

Fig. 1.

Coverage region of bistatic radar $T_iR_j$

In this paper, we use the connected coverage regions from all bistatic radar pairs to search potential barriers. For simplicity, we use the coverage region to denote the covered area of a pair of transmitter and receiver, which might be in the form of $A_{ij}$, or $A_{i(j)}$ and $A_{(i)j}$. We construct a barrier coverage graph $G=(V,E)$ as follows. In the graph, V is the set of all coverage regions plus two virtual nodes s and t. There are M transmitters and N receivers in the network. So there are in total MN candidate bistatic transmitter-receiver pairs.

In the first step, we determine the shape of bistatic radar coverage region. If its coverage region is a connected region $A_{ij}$, we use only one vertex $A_{ij}$ in the graph to represent this $(T_i, R_j)$ pair. Otherwise, two vertices $A_{i(j)}$ and $A_{(i)j}$ are used to represent this bistatic radar pair. Therefore, the vertex set V consists of $(2\times M\times N+2)$ elements at most.

The set of edges E is constructed as follows:

(b1) An edge connects the virtual node s and a vertex, if the coverage region of the vertex overlaps with the left boundary.

(b2) An edge connects the virtual node t and a vertex, if the coverage region of the vertex overlaps with the right boundary.

(b3) There exists an edge between two vertices, if the coverage regions of the two vertices who is constructed by different receivers overlap with each other.

Furthermore, an edge does not exist in between two vertices in the following cases:

(c1) Two vertices represent the same bistatic radar pair, which happens when the coverage region of bistatic radar contains two disconnected regions. That is, no edge exists in between the two vertices $A_{i(j)}$ and $A_{(i)j}$.

(c2) Two vertices represent two bistatic radar pairs of using different transmitters but the same receiver. That is, no edge exists in between $A_{ij}$ and $A_{i'j} (A_{(i')j}, A_{i'(j)})$. This due to the constraint that one receiver can only couple with one transmitter at a time.

Fig. 2.

Illustration of coverage regions by $(T_1, R_1)$ and $(T_2, R_2)$.

In the edge construction process, we need to determine whether or not two coverage regions overlap with each other. There are two cases when two coverage regions overlap:

(d1) One of the coverage regions is not totally contained in another coverage region, as illustrated in Fig. 2 (a)−(d) and Fig. 3 (a)−(d). In this case, the two coverage regions can expand the barrier coverage region, and an edge should be added to connect the two respective vertices. Furthermore, the perimeter of two coverage regions have at least one intersection point.

(d2) One of the coverage regions is totally contained in another coverage region, as illustrated in Fig. 2 (e) and Fig. 3 (e) and (f). In this case, the contained coverage region cannot help to expand the barrier coverage. We do not add an edge in between the two respective vertices. Therefore, we can compute the intersection point between the perimeter of two coverage regions to determine whether the coverage regions of two vertices overlap with each other or not.

We next use an example to show how to determine whether two coverage regions overlap with each other. We first consider the case of two bistatic radar pairs consist of different transmitters and receivers, e.g., $(T_1, R_1)$ and $(T_2, R_2)$. All possible relations of their coverage regions are shown in Fig. 2 (a)−(e). Assume there is a point P(x, y) on the perimeter of the coverage region of $(T_1, R_1)$, and P is also covered by the $(T_2, R_2)$ pair. Then its location (x, y) can be computed by:

$$\begin{aligned} \left\{ \begin{array}{ll} [(x-x_{T_1})^2+(y-y_{T_1})^2]\cdot [(x-x_{R_1})^2+(y-y_{R_1})^2]=l_{max}^4\\ ((x-x_{T_2})^2+(y-y_{T_2})^2)\cdot [(x-x_{R_2})^2+(y-y_{R_2})^2]=l_{max}^4 \end{array}\right. \end{aligned}$$

(4)

If Eq. (4) exists at least one real root, we say that their coverage regions overlap with each other. Otherwise, their coverage regions are not overlapped.

For the case that a radar pair $(T_2, R_2)$ contains two disconnected coverage regions, as shown in Fig. 2 (b) and (c), we first use the above method to determine whether there exists an intersection point between the coverage region of $(T_1, R_1)$ and the coverage regions of $(T_2, R_2)$. If at least one intersection point exist and let IP denote the intersection points set. We further determine which coverage region $A_{2(2)}$ or $A_{(2)2}$ of the pair $(T_2, R_2)$ intersects with $A_{11}$ or both two regions intersect with $A_{11}$.

We solve this problem by using following method. Compute the midpoint C of the line $\overline{T_2 R_2}$ connecting $T_2$ and $R_2$. Denote its coordinate as $(\frac{x_{R_2}+x_{T_2}}{2},\frac{y_{T_2}+y_{R_2}}{2})$. We compare the horizontal ordinate of each intersection point in IP with $\frac{x_R+x_T}{2}$. An edge exists between the vertex $A_{11}$ and $A_{2(2)}$ in the coverage graph, if all the horizontal ordinate of intersection points are smaller than $\frac{x_{R_2}+x_{T_2}}{2}$. And an edge exists between $A_{11}$ and $A_{(2)2}$, if all the horizontal ordinate of intersection points are larger than $\frac{x_{R_2}+x_{T_2}}{2}$. Otherwise, there are two edges connect $A_{11}$ with $A_{2(2)}$ and $A_{(2)2}$, respectively.

We next consider the case that two bistatic radar pairs consist of a same transmitter, e.g., $(T_1, R_1)$ and $(T_1, R_2)$. All possible relations of their coverage regions are shown in Fig. 3. According to the above analysis, we know that there exists an edge between the vertices $A_{11}$ and $A_{12}$ in Fig. 3 (a) and (b). For the cases in Fig. 3 (c) and (d), there exist an edge between the vertices between $A_{11}$ and $A_{(1)2}$, $A_{(1)1}$ and $A_{(1)2}$, respectively. There is no edge between the vertices in Fig. 3 (e) and (f).

Fig. 3.

Illustration of coverage regions by $(T_1, R_1)$ and $(T_1, R_2)$.

4 Solution to the Barrier Coverage Lifetime Maximization Problem

4.1 Finding Barriers Algorithm

Based on the constructed coverage graph G, we propose an algorithm to find barriers in the network. First, we label the vertices in the coverage graph G. Recall that we index the transmitters and receivers according to their x-coordinate from the left boundary to the right boundary, thus:

$$\begin{aligned} x_{T_1}\le x_{T_2}\le ...\le x_{T_M}\\ x_{R_1}\le x_{R_2}\le ...\le x_{R_N} \end{aligned}$$

The vertices V in the coverage graph G represent the connected coverage area of each bistatic radar pair. For ease of description, we index the vertices according to the x-coordinate of the transmitter and receiver constructing such vertex. The indexing way is as follows. Assume there are totally $U_1$ vertices constructed by node $T_1$, we index those $U_1$ vertices from $v_1$ to $v_{U_1}$ according to the receiver’s x-coordinate constructing such vertex. If two vertices (such as $A_{1(j)}$ and $A_{(1)j}$) corresponding to the same bistatic radar, we use two successive number to represent those two vertices. We then index the vertices constructed by $T_2$ from $v_{U_1+1}$ by using the same way until all vertices are indexed.

For two vertices in the graph, we say their are neighbour if there exist an edge between them. An algorithm is proposed to find barriers in the network. The main idea of algorithm is that call function findpath to iterate through the neighbours of vertex. The input parameters for the function findpath include: (e1): coverage graph G; (e2): P is the found path in the previous iteration and its structure is like $P=\{s,v_1,v_3,...,v_l\}$. (e3) the set Q whose elements are the receiver number already used by vertices in found path P; (e4) the elements in the set U are the vertices that may be the vertex that can’t reach the destination or is constructed by the same receiver as that vertices in found path P; (e5) we will explain function of set C in the following paragraph.

In each iteration, we first find the final vertex in the found path P and denote it as L, and then find all neighbour vertices set Next of L. Before go to the next step, we filter the vertices in set Next, three types vertices are excluded from the set Next: the vertices whose corresponding bistatic radar pair is constructed by the receivers in the set Q, the reason is that one receiver can’t couple with different transmitters in one barrier; The vertices belong to the set U and the set C. After the filter process, if the set Next is not empty, we first check whether the virtual node t is in the set Next, if it does, one barrier found. The algorithm records the barrier and returns back to the previous (last) iteration to find another path. Otherwise, the algorithm calls the function findpath to lengthen the found path P by visiting each element in the set Next.

The vertex set V consists of $(2\times M\times N+2)$ elements at most and the total number of all possible paths from s to t is in the order of $O((2\times M\times N)!)$.

The structure of found path of Algorithm 1 is $B_k=(s,T_iR_j,...,T_mR_n,t)$. Assume there are K paths in the network, the lifetime of each barrier is determined by the residual energy of radar sensors constructing such barrier. Thus:

$$\begin{aligned} L(B_k) = \mathop {\min }\limits _{\scriptstyle 1 \le i \le m\atop \scriptstyle 1 \le j \le n} \{ \frac{e_{T_i}}{\alpha _T},\frac{e_{R_j}}{\alpha _R}\}, \{T_1,...,T_m, R_1,...,R_n\} \in B_k \end{aligned}$$

(5)

4.2 Linear Programming Method

Recall that a same bistatic radar node can appear in more than one barrier. If a barrier is scheduled to work till one of node dies, some other barriers containing this dead node also cannot work any more. On the other hand, we can schedule the working interval for each of these barriers, such that the total working intervals can be maximized. Suppose there are K barriers in $\mathcal {B}_N$, each working for $t_k, k=1,...,K$ time slots. The problem of maximizing network lifetime for $\mathcal {B}_N$ can be formulated as the following optimization problem.

$$\begin{aligned} \begin{array}{*{20}{l}} \mathrm {maximize\;\;\;{} L(\mathcal {B}_N) = t_1+t_2+...+t_K}\\ {s.t.\;\;\;{} \left\{ \begin{array}{l} \sum \limits _{k = 1}^K {\alpha _{t}}{t_k} \le E_{T_i};\quad \mathrm {for}\;\mathrm {all}\,1 \le i \le M, \\ \sum \limits _{k = 1}^K {\alpha _{r}}{t_k} \le E_{R_j};\quad \mathrm {for}\; \mathrm {all}\, 1 \le j \le N, \end{array} \right. } \end{array} \end{aligned}$$

(6)

where the constraints indicate that the consumed energy of each node in all barriers should not exceed its initial energy. We apply the linear programming method solve the Eq. (6).

4.3 Greedy Algorithm and Random Algorithm

The main idea of these two algorithms are summarized as follows: Firstly, based on the coverage graph G, starting from the virtual s, we choose a neighbour as a sub-node to construct one barrier: In the Greedy algorithm, we choose the neighbour with maximal residual lifetime; While in the random algorithm, we choose a neighbour randomly. Secondly, based on the constructed barrier $B_s$, we activate the barrier $t_{g}$ unit time ($t_g=\epsilon$ if $L(B_s) \ge \epsilon$; $t_g=L(B_s)$ if $L(B_s)< \epsilon$, where $\epsilon$ is called activation granularity). Thirdly, after $t_g$ time, update the residual energy of the bistatic radar nodes. If the energy of a node is exhausted, this node will not be selected in the next iteration. The barrier finding process continues, until not barriers can be found.

5 Simulation Results

We consider a network with M transmitters and N receivers randomly deployed in a rectangle region with size of $40\times 10$. In all simulations. We set the maximum vulnerability of network as $l_{max}=5$, and the detection energy consumption rate of transmitter and receiver are $\alpha _t=1.5$ and $\alpha _r=1$, respectively. We also set the maximum distance threshold between transmitter and receivers as $D_{max}=20$. The initial energies are uniformly distributed in [1, 10]. We use the optimization toolbox in Matlab to solve the linear programming. All results are the average of 100 different deployments.

Figure 4 compares the barrier coverage lifetime achieved by our proposed algorithms (Linear Programming, Greedy Algorithm and Random Algorithm) and the lifetime achieved by activating all bistatic radar nodes until there is no barrier in the network. We can observe that the proposed algorithms can prolong the barrier coverage lifetime and the lifetime increases with the increase of deployed transmitters. It can also be seen that the lifetime by the Greedy Algorithm is close to that by linear programming method. However, we note that the linear programming method cannot be applied to large-scale networks due to its high computation complexity.

Fig. 4.

Comparison of the barrier coverage lifetime.

Figure 5 compares the lifetime for the Greedy Algorithm and Random Algorithm when the transmitters are more than eleven. Note that the linear programming solution could take days for computation, so we do not include them into comparison. The results indicate that the next nodes selection strategy in the barrier finding step has great impact on the total barrier coverage lifetime: The Greedy Algorithm can achieve better results compared to the Random Algorithm, since it achieves local optima by choosing the next node with the maximal residual lifetime.

Fig. 5.

Comparison of the barrier coverage lifetime.

6 Conclusion

We have studied the barrier coverage lifetime maximization problem in a randomly deployed bistatic radar network. We first constructed a coverage graph based on the connected coverage region of bistatic radar pairs. We have also proposed an algorithm to find all barriers based on the coverage graph. The linear programming method as well as two heuristic algorithms have been used to determine the operation time for each barrier whiling maximizing the barrier coverage lifetime.