Keywords

1 Introduction

Due to homogeneity and excellent strength-to-weight ratio, monolithic thin-wall components are widely used in aerospace, marine, electronics, and automobile industry. Airframe structures of modern commercial and military aircraft contain hundreds of unitized monolithic metal structural components, which comprise of thinner ribs and webs. In aero-engine construction, about 90% parts are thin-walled. An impeller blade can be an example of thin-wall asymmetric-open component while engine-casing can be considered as thin-wall axisymmetric-closed components (Geng et al. 2011). Panels or structural parts and heat sinks of processors of electronics products such as laptop computers are also made up of thin-wall parts. Thin-wall machining is essential in the manufacture of dies and molds required to produce thin-wall plastic parts. It is also used in power engineering applications such as turbine blades, housings, and enclosures.

The conventional thin-wall structural components are manufactured in parts and then assembled together using riveting or welding operations. The process involves high part cost, and it is time-consuming and laborious (Campbell 2011). Machining thin-wall parts eliminate the need for different setups and processes; however, it consumes a lot of power because of machining of about 90–95% bulk material. Today’s manufacturing and tool room industry are striving to reduce the component cost and to improve the product quality in terms of surface finish and dimensional accuracy. To fulfill these requirements, it is imperative to focus research attention on improving the product quality and overall productivity during machining of thin-wall components.

In general, machining of parts having thin sections is called as thin-wall machining. Peripheral milling is a commonly used in machining of thin-wall parts. During the machining process, low-rigidity thin sections deflect under the influence of milling force and the heat generated by severe plastic deformation. Various milling parameters, viz., feed per tooth, axial depth of cut, radial depth of cut, tool diameter, spindle speed, and tool angles influence the magnitude of the milling force, which in turn affects the accuracy of the machined component.

According to Kennedy and Earls (2007), a wall of thickness in the range of 1–2.5 mm can be considered as a thin-wall. Yang (1980) defined the thin plates and thick plates for plate bending theory as:

$$ \left. {\begin{array}{*{20}l} {{\text{Thick plate}} = t/p > (1/5)} \hfill \\ {{\text{Thin plate}} = (1/100) \le t/p \le (1/5)} \hfill \\ \end{array} } \right\}, $$
(1)

where p is the shorter length of two edges of the plate and t is the plate thickness.

The main difference between thin-wall machining and normal machining is that in thin-wall machining, there is very less amount of material left to support against the milling force. This leads to lower stiffness of the workpiece and results in vibrations and deformation. Consequently, the effect of the milling parameters on thin-wall machining gets amplified compared to that of a normal machining operation.

2 Challenges in Thin-Wall Machining

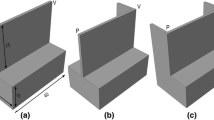
Most of the thin-wall components used in the industry are machined from aluminum and titanium blocks. Aluminum is widely used because of its low yield stress and good machinability rating. Moreover, good fatigue resistance makes it favorable in aerospace and automobile applications. In the field of thin-wall machining, high-speed thin-wall machining is gaining popularity due to its merits such as low milling force, low cutting temperature, reduced machining time, and generation of the better quality surface (Davim et al. 2008). High-speed machining utilizes machine tools having very high spindle power rating and thus it is very expensive. It requires high capital investment, which may not affordable by the small-scale industries. Therefore, it is essential to explore the employment of conventional low to medium duty computer numerical control (CNC) machining centers for manufacturing of quality thin-wall structures. Figure 1 shows a schematic representation of thin-wall machining process.

Fig. 1
figure 1

Wall deflection and form error produced in machining thin-wall feature

Full size image

For the chosen milling parameters, the material to be cut is PQRS, however, under the action of milling force, the wall deflects causing the material P′Q′R′ to remain uncut. As the cutter moves away in the feed direction (Y direction), the wall recovers elastically and the material remains uncut which results in thicker top and thinner base. The thin-wall parts are always machined on computer numerically controlled (CNC) machines. Despite this, the process of thin-wall machining is not devoid of problems. This is because the process control by CNC is based on idealized geometry and does not take into account the deformation of the parts. As a result, there is a significant deviation between the desired part profile and the manufactured one. To reduce the form error generated due to the deflection and to improve the surface finish of work part, it is essential to set the milling parameters at their optimum levels. In view of this, if the deflection is predicted beforehand, effective countermeasures can be undertaken to obtain the desired process performance, that is, manufacturing of a dimensionally accurate finished component with good surface quality.

Another important aspect related to machining of aluminum thin-wall components is the surface roughness. Aluminum alloys possess a comparatively low modulus of elasticity, which causes the workpiece to spring back. This spring back action often results in deflection and chatter. Chatter affects the material removal rate (MRR) and leads to poor surface finish, part rejection and loss of productivity.

As seen in the Fig. 1, thin walls deflect under the action of milling force, which in turn affects the quality and accuracy of the work part. A need was thus identified to develop a realistic numerical model to predict the process responses, which will help for better control of the process parameters during the actual cutting operation.

Literature reports esteemed research articles and reports published by international universities, industry, and research organizations on various aspects of thin-wall machining such as analytical modeling, numerical modeling, experimental investigations into influence of milling parameters, viz., feed, depth of cut, tool geometry parameters, tool path planning strategies and optimization of milling process parameters. From the reported literature, it was concluded that a significant amount of work is reported on 2-D as well as 3-D simulations of the bulk milling operation (Bacaria et al. 2001; Soo et al. 2004; Davim et al. 2008; Özel and Ulutan 2012; Özel et al. 2010, 2011; Maranhão and Davim 2010; Maurel-Pantel et al. 2012; Jiao et al. 2015). Extensive research has been reported on simulation of orthogonal metal cutting process using 2-D FEM methods. Thin-wall milling using a helical end-milling cutter is a complex operation and is difficult to comprehend and analyze in a 2-D domain. Research attempts have been reported on 3-D FEM modeling and simulation of machining of low-rigidity thin-wall parts to study the milling forces, deflection, stresses, cutting temperature, and chip morphology obtained during the process (Ning et al. 2003; Wan et al. 2005; Gang 2009; Rai and Xirouchakis 2008, 2009; Li et al. 2015; Cheng et al. 2015). Most of them carried out 3-D simulation of metal cutting for only one rotation of milling cutter hence lack applicability because in reality, it is essential to simulate the complete pass of the milling cutter over the specified length of the work part to obtain the instantaneous wall deflection.

Keeping this in view, in the present work, a Lagrangian-based 3-D FEM-based numerical model has been developed to simulate the deflection of workpiece wall during thin-wall machining of aluminum 2024-T351 alloy. The developed model was aimed to accurately compute the milling forces, temperature, stress distribution and to study the chip formation in work part for chosen process parameters by considering realistic material behavior, friction consideration, damage model, heat generation and by employing realistic geometry of the milling tool. Subsequently, experimental trials were carried out to validate the developed model. Details of the model development are presented in the sections to follow.

3 Overview of the Process Model Development

To understand and improve the thin-wall machining process, it is important to develop a mathematical model to establish a realistic relationship between input and output process parameters. The primary objective of this work was to analyze the metal cutting phenomenon in thin-wall milling process by carrying out a thermomechanical analysis. The work mainly includes the following steps. These steps are schematically depicted in Fig. 2.

Fig. 2
figure 2

Overall approach and development of 3-D numerical model

Full size image

  • Design of geometric models of helical cutting tool, workpiece and selection of suitable mesh element.

  • Choosing the material models and material failure criteria.

  • Specify governing equation and boundary conditions.

  • Selection and application of required process conditions.

  • Solution of the problem using finite element analysis (FEA) tool in nonlinear mode.

  • Determination of stress–strain, temperature profiles in the workpiece-cutting tool interaction zone, and computation of process performance parameters such as milling force, stress distribution, cutting temperature, part deflection, and chip morphology.

  • Validation of computed responses with the experimental results.

  • Evaluation of computational efficiency of developed 3-D numerical simulation approach.

These steps are discussed at length in the following sections.

4 Thermomechanical Modeling of End-Milling Operation

In the end-milling operation, the material is removed from the workpiece using a rotating tool. The thin-wall sections are deformed due to the influence of forces developed during tool-workpiece interaction and the heat generated during cutting. The milling force developed depends upon various process parameters; therefore, the accuracy of the component depends upon the proper selection of the process parameters during machining. In the machining process, heat is generated due to plastic deformation and frictional contact between the workpiece and the tool. The heat generated directly influences the material properties. Therefore, it is essential to couple the mechanical and thermal responses to obtain the solution for such a problem. In this work, a fully coupled thermomechanical analysis of thin-wall milling operation has been attempted.

4.1 Assumptions

Numerical modeling and simulation of thin-wall machining involve complex interaction between the tool and workpiece, contact modeling, material properties. The following assumptions were made in the present thermomechanical modeling:

  • The helical milling cutter has sharp cutting edges.

  • The milling cutter is stiffer than the workpiece hence it is modeled as a rigid body. It has translation, rotation, and thermal degrees of freedom.

  • Workpiece material is deformable. It is isotropic and homogeneous in nature.

  • The workpiece material is free of residual stresses.

  • Initial temperatures for both workpiece and the tool are set at 25 °C.

  • Workpiece and tool surfaces lose the heat generated during the machining process to the environment by convection. The convection coefficient, h c is assumed as 20 W/m2 °C (Kiliçaslan 2009).

  • The workpiece has uniform thickness along the height and width. There are no deformations present in the workpiece at the commencement of the machining simulation.

  • It is considered as 90% of the total energy generated due to plastic deformation process converts into the heat energy (Li et al. 2002).

  • It is also considered that the entire energy that generates during metal cutting operation transforms into heat energy and half of the heat dissipates into the chip (Li et al. 2002).

4.2 Workpiece, Tool Geometry, and Finite Element Meshing

Initially, the geometric models of cutting tool and workpiece have been developed. The thin-wall workpiece was modeled as an inverted cantilever structure with bottom portion being constrained, while the other three ends were free. The tool geometry influences the surface properties of the machined workpiece, so importance has been given to accurately model the cutting tool. A 3-D model of the end mill with actual tool geometry parameters was designed using a CAE tool and then imported in Abaqus/Explicit as a solid 3-D homogeneous part. Figure 3 shows the workpiece, cutting tool, and relevant geometric parameters.

Fig. 3
figure 3

Workpice geometry and dimensions

Full size image

The influence of vibrations of thin-wall structure that occurs during the machining was not considered in this work. The parameters related to cutting tool geometry are listed in Table 1.

Table 1 Cutting tool geometry parameters
Full size table

Thin-wall machining process involves nonlinear and complex interaction between the tool and workpiece. It also involves large deformations. It is thus essential to employ proper element type for the modeling process. The workpiece is meshed with 3-D solid elements C3D8RT to carry out the thermomechanical analysis. It is a 3-D displacement-temperature coupled 8-noded solid element with reduced integration and hourglass control. As shown in Fig. 4 the entire geometry is discretized into very small finite elements. For this particular case, the tool and the workpiece were discretized into 12,650 and 293,745 elements, respectively. Also, it can be seen that element size on the work material varies at different regions of the workpiece. The mesh density was kept higher at the workpiece-cutter interaction region, which helps in better simulation of chip formation at the cutting region. Remaining regions of the workpiece were coarsely meshed to reduce the number of elements in the non-active areas of the machining process.

Fig. 4
figure 4

Workpiece-tool meshing and boundary conditions

Full size image

Figure 4 also depicts the boundary conditions that applied on workpiece and tool geometries. The workpiece was constrained at the bottom to imitate the clamping action during machining. The end-milling cutter was given two motions, namely linear motion along feed direction and rotational motion about its own axis. The initial temperature of the tool and workpiece was set at room temperature. Heat loss to the environment from the tool and workpiece interface was considered primarily by the convection.

4.3 Material Properties

In this work, numerical simulations have been performed for milling of aluminum 2024-T351 aerospace grade commercial alloy. It possesses high strength and good fatigue resistance and is widely used in aircraft wing and fuselage structures. The workpiece material is considered to be an elastic-plastic type. The end mill is considered to be made of uncoated tungsten carbide (WC).

Tungsten carbide otherwise known as cemented carbide composes of tungsten carbide powder (85–95%) cemented with a binder material namely cobalt or nickel. It has many desirable qualities such as high resistant to abrasion, erosion, wear, compression, and heat (Juneja 2003). The effect of machining process parameters on the cutting tool wear is not considered of the present study; therefore, the tool is to be considered as a rigid body throughout the simulation. Table 2 shows the mechanical and thermal properties of the workpiece as well as the tool material (Mabrouki et al. 2008).

Table 2 Workpiece and cutting tool material properties (Mabrouki et al. 2008)
Full size table

4.4 Material Constitutive Model

During the metal cutting process, the material deforms plastically and is subjected to high strains, strain rates, and temperature conditions. To describe the thermomechanical behavior of a material undergoing deformation at such high strains and strain rate conditions, Johnson and Cook developed a constitutive material model in 1983. As per their model, the equivalent flow stress \( \bar{\sigma }_{jc} \) can be computed as

$$ \bar{\sigma }_{jc} \varvec{ = }\left( {A + B\bar{\varepsilon }^{n} } \right)\left[ {1 - c\ln \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{\varvec{o}} }}} \right)} \right]\left( {1 - \left( {\frac{{T_{\text{c}} - T_{\text{room}} }}{{T_{\text{melt}} - T_{\text{room}} }}} \right)^{m} } \right) $$
(2)

Table 3 lists the J-C material model constants for aluminum 2024-T351 alloy (Mabrouki et al. 2008).

Table 3 J-C material coefficients for A2024-T351 (Mabrouki et al. 2008)
Full size table

4.5 Material Damage Model

In the metal cutting process, chips are formed as a result of excessive (large) material deformation at the cutting tool-work material interface under the action of applied force. The material is said to have failed when it loses its load carrying capacity. In machining processes, the prediction and control of the material failure is a critical issue. In order to investigate the surface finish and integrity of the produced parts, it is essential to simulate the damage and fracture of the material under the action of applied loads.

In this work, the ductile failure of work material was simulated under the high strain, strain rate conditions. Effects of temperature on the deformation were also considered. For this purpose, Johnson and Cook (1985) shear failure criterion was used to model the chip detachment. Deformation occurring in the final stage of chip evolution was computed using the evolution law which is based on fracture energy principle (Liu et al. 2014). Damage in the element is initiated by scalar damage coefficient D. It is a sum of ratios of increments in equivalent plastic strain \( \Delta \bar{\varepsilon } \) to the equivalent strain at fracture initiation \( \varepsilon_{{fi}} \). It is given in Eq. (3). The damage initiates when scalar damage parameter D exceeds unity.

$$ D =\Sigma \frac{{\Delta \bar{\varepsilon }}}{{\varepsilon_{{fi}} }} $$
(3)

The equivalent strain at failure initiation \( \varepsilon_{{fi}} \) is

$$ \varepsilon_{{fi}} \varvec{ = }\left[ {D_{1} + D_{2} \exp \left( {D_{3} \frac{P}{{\bar{\sigma }}}} \right)} \right]\left[ {1 + D_{4} \ln \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{\varvec{o}} }}} \right)} \right]\left( {1 + D_{5} \left( {\frac{{T_{\text{c}} - T_{\text{room}} }}{{T_{\text{melt}} - T_{\text{room}} }}} \right)} \right) $$
(4)

The J-C damage constants (D1-D5) are shown in Table 4. It can be observed that coefficient D5 is zero. This indicates that temperature has no effect on the damage initiation during machining of the aluminum alloy 2024-T351. Stress triaxiality and strain rate effects are considered to be main factors for damage initiation (Mabrouki et al. (2008)).

Table 4 Johnson–Cook failure parameters for A2024-T351 (Mabrouki et al. 2008)
Full size table

When the damage of a ductile material initiates, the stress–strain relationship no longer represents the material behavior during deformation. After the damage initiation, the use of stress–strain relation causes strong mesh dependency which is based on strain localization. This reduces the energy dissipation as the mesh becomes smaller. Influence of mesh dependency on energy dissipation can be reduced using the Hillerborg’s fracture energy principle. According to this principle, the fracture energy can be computed as

$$ G_{f} = \int\limits_{{\bar{\varepsilon }_{0i} }}^{{\bar{\varepsilon }_{\text{f}} }} {L\bar{\sigma }_{Y} } {\text{d}}\bar{\varepsilon } = \int\limits_{0}^{{\bar{u}_{f} }} {\bar{\sigma }_{Y} } {\text{d}}\bar{u} $$
(5)

The damage evolution parameter (ω s ) is given as

$$ \omega_{s} = \frac{{L\bar{\varepsilon }}}{{\bar{u}_{f} }} = \frac{{\bar{u}}}{{\bar{u}_{f} }} $$
(6)

The equivalent plastic displacement at failure can be expressed by

$$ \bar{u}_{f} = \frac{{2G_{f} }}{{\sigma_{y} }}$$
(7)

where G f is the fracture energy dissipation. It can be determined by:

$$ G_{f} = \left( {\frac{{1 - \nu^{2} }}{E}} \right)K_{c}^{2} $$
(8)

where \( K_{c} \) is the fracture toughness of the material.

4.6 Workpiece-Milling Tool Contact Model

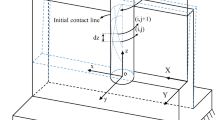
Study of the effect of friction between the end-milling tool and workpiece is important as it affects the cutting forces, temperature at the cutting zone and chip, product quality and tool surface wear. In this work, workpiece and milling tool contact has been considered by employing the modified Coulomb friction model. According to this model, the contact between chip and tool rake surface region is divided into two regions, viz., sliding and sticking region (see Fig. 6).

Fig. 6
figure 5

Distribution of normal and shear stress at chip-tool interface

Full size image

During metal cutting, the friction due to sticking occurs very near to the contact of cutting edge with the workpiece, while the friction due to sliding occurs far away from the contact area. The sliding region follows the Coulomb friction law. At the sticking region, the frictional stress \( \tau_{f} \) is equal to the critical frictional stress \( \tau_{\text{criti}} \). Accordingly the frictional stress can be expressed as

$$ \tau_{f} = k_{\text{chip}} \;\text{when}\;\mu \sigma_{n} \varvec{ > }k_{\text{chip}} \;\;({\text{Sticking region}}) $$
(9)
$$ \tau_{f} = \mu \sigma \;\text{when}\;\mu_{n} \sigma \varvec{ < }k_{\text{chip}} \;\;({\text{Sliding region}}) $$
(10)

In the present work, the coefficient of friction μ is considered as 0.17 (Liu et al. 2014). In what follows, the solution methodology is presented.

4.7 Solution Methodology

After the development of geometric models of workpiece and tool, material properties, material damage law, and friction law were applied and thermomechanical analysis of thin-wall end milling was carried out. The mathematical equations employed in the present work are given below.

4.7.1 Mechanical Analysis

The differential equation of motion that governs the mechanical displacement is given by

$$ \rho \ddot{u} + c\dot{u} + ku = F $$
(11)

Equation (11) is rewritten in matrix form as

$$ \left[ M \right]\ddot{u} + \left[ C \right]\dot{u} + \left[ K \right]u = F $$
(12)

Nodal acceleration at the beginning of time increment can be obtained by rewriting Eq. (12) as

$$ \ddot{u}_{i} = M^{ - 1} \left( {F - C\dot{u}_{i} - Ku_{i} } \right) $$
(13)

In the present work, explicit formulation was employed which uses central difference scheme to discretize the equations. The acceleration equation can be written as

$$ \ddot{u}_{i} = \frac{{\left( {\dot{u}_{i + 1/2 + } - \dot{u}_{i - 1/2} } \right)}}{{(\Delta t_{i + 1} + \Delta t_{i} )/2}} $$
(14)

Velocity change is calculated by integrating acceleration term using central difference method. The velocity at the middle of the current step can be computed as

$$ \dot{u}_{i + 1/2} = \left( {\frac{{\Delta t_{i + 1} + \Delta t_{i} }}{2}} \right)\ddot{u}_{i} + \dot{u}_{i - 1/2} $$
(15)

Displacement is calculated by integrating velocity through time, which is then used to obtain the displacement at the end of a time step. It is given by

$$ u_{i + 1} = u_{i} + \Delta t_{i + 1} \dot{u}_{i + 1/2} $$
(16)

4.7.2 Thermal Analysis

The governing equation for the transient heat conduction during the machining process is written as

$$ \rho C_{p} \frac{\partial T}{\partial t} = \frac{\partial }{\partial x}\left[ {k_{x} \frac{\partial T}{\partial x}} \right] + \frac{\partial }{\partial y}\left[ {k_{y} \frac{\partial T}{\partial y}} \right] + \frac{\partial }{\partial z}\left[ {k_{z} \frac{\partial T}{\partial z}} \right] + \dot{Q} $$
(17)

Equation (17) can be rewritten in matrix form as

$$ \left[ {\bar{C}} \right]\dot{T} + \left[ {\bar{K}} \right]T = \dot{Q} $$
(18)

Solving the nodal temperature rate from the above equation yields

$$ \dot{T}_{i} = C^{ - 1} \left( {\dot{Q} - KT_{i} } \right) $$
(19)

After applying the forward difference integration scheme on Eq. (19), the nodal temperature rate is given by

$$ \dot{T}_{i} = \frac{{T_{i + 1} - T_{i} }}{{\Delta t_{i + 1} }} $$
(20)

Equation (20) can be rewritten as

$$ T_{i + 1} = (\Delta t_{i + 1} )\dot{T}_{i} + T_{i} $$
(21)

The explicit expression for nodal temperature rate can finally be written as

$$ T_{i + 1} = (\Delta t_{i + 1} )C^{ - 1} \left( {\dot{Q} - KT_{i} } \right) + T_{i} $$
(22)

Total volumetric heat generation rate is due to the heat generated during plastic deformation and friction at the work-tool interface. The generation of heat due to plastic deformation is expressed as

$$ \dot{Q}_{\text{pl}} = \eta_{p} \sigma \dot{\varepsilon }_{p} $$
(23)

By considering that most of the energy of plastic deformation converts into heat energy, in this work, \( \eta_{p} \) is taken as 0.9 (Li et al. 2002). During the metal cutting operation, friction at the workpiece-tool contact region generates significant heat. The volumetric heat flux due to friction is given by

$$ \dot{Q}_{f} = f_{f} \cdot \eta_{f} \cdot \tau_{f} \cdot \dot{\gamma }_{s} $$
(24)

During the metal cutting operation, the tool and workpiece surfaces dissipate the heat to the environment. This phenomenon is described by using Newton’s law of convection as

$$ \dot{q}_{\text{conv}} = h_{c} (T_{c} - T_{\text{room}} ) $$
(25)

The milling process involves large deformations and continuously changing contact between cutting and workpiece. With the above-stated Eqs. (11)–(25), Abaqus/Explicit, the FEA solver computed the responses such as milling force, wall deflection, and cutting temperature. In the present analysis, explicit time integration scheme has been used to solve the transient problem. It was originally developed to solve high-speed dynamic problems those were difficult to simulate using the implicit method. This scheme is simple and can handle problems which involve high nonlinearity, large deformation, complex friction contact conditions, thermomechanical coupling and fragmentation. The formulation using explicit solution can be of Eulerian, Lagrangian, or Arbitrary Lagrangian–Eulerian (ALE) type. Figure 7 shows a comparison between Lagrangian, Eulerian, and ALE formulations. In the Lagrangian formulation, the finite element mesh is attached to the material and follows the mesh deformation. The Lagrangian formulation is used to analyze transient problems which undergo large deformations. It is widely used due to its ability to form chips and to determine the chip geometry as a function of cutting parameters, plastic deformation process, and material properties. This enables the evolution of the cut material from its nascent stage to a stable state without any predetermined material geometrical boundary conditions. The development of chip is entirely a function of physical deformation process, machining parameters, and the input material properties.

Fig. 7
figure 6

Comparison of motion of mesh and material with Lagrangian, Eulerian, and ALE formulation

Full size image

In the Eulerian formulation, the finite element mesh is fixed in the space and the material flows through the control volume that eliminates the possibility of element distortion during the process. It reduces the computation time as fewer elements required for the analysis. These models do not need separation criteria for simulating the material failure. The major drawback of the Eulerian formulation is that it needs prior knowledge of the chip geometry, chip-tool contact length, chip thickness, and contact conditions to simulate the chip formation. Thus in this formulation, it is needed to keep the conditions of chip thickness, tool-chip contact length and contact conditions constant. Therefore, the Eulerian formulation is not suitable for simulation of workpiece deformation in metal cutting. To overcome these drawbacks, researchers have developed a new iterative procedure which combines the best features of Lagrangian and Eulerian formulations. It is called Arbitrary Lagrangian–Eulerian (ALE) approach. According to this approach, the mesh follows the flow of material. The displacements are computed in Lagrangian steps. For velocity computation, the mesh is repositioned and the problem is solved in Eulerian step. The combined formulation avoids the severe element deformation which is a typical problem often associated with the Lagrangian approach. However, in view of simplicity and high computational efficiency, most of the 3-D FEM-based simulations of metal cutting operations have used the Lagrangian formulation. Therefore in the present work, the same approach has been used.

In the present work, Abaqus/Explicit, a commercial finite element solver has been used to carry out 3-D numerical simulations of machining of thin walls. A computer system of 3.9 GHz 4 GB RAM processor has been employed. Extensive trials have been carried out to fine tune the FEM solver parameters. In general, a typical simulation of material removal during a complete pass of the milling tool along the wall length of 50 mm took about 340–350 h.

5 Experimental Validation of FEM-Based Simulation of Thin-Wall Machining

After the development of numerical model, experimental validation of the responses predicted by the numerical model was carried out. For this purpose, an experimental setup was developed on a three-axis computer numerically controlled vertical machining center (CNC-VMC). Figure 8 depicts the details of the experimental setup developed. The workpiece was clamped in a workpiece holder, which was fixed firmly on a piezoelectric sensor based three-component dynamometer (make: Kistler 9272B). The dynamometer is capable of measuring three components of milling force (F x , F y and F z ). The dynamometer was mounted firmly onto the base plate of the machine tool. For the data acquisition, the dynamometer was connected to a computer through a force measurement multichannel charge amplifier (type 5070A). The data sampling rate was set to 500 Hz per channel. The component F x is normal to the machined wall surface. The component F y is oriented along the direction of feed movement and the F z component is along the tool’s axis. The workpiece deflection was measured by Solartron linear variable differential transformer (LVDT) sensor. Experiments were repeated thrice for each set of process conditions.

Fig. 8
figure 7

Experimental setup for thin-wall milling

Full size image

By using the developed numerical model, the responses such as milling force and wall deflection were measured during thin-wall machining process. In addition, the efficiency of the developed model in terms of the computational time was also analyzed. Milling conditions used for simulation studies are listed in Table 5. The results obtained during the numerical simulation of machining thin-wall aluminum 2024-T351 alloy part are discussed in the following sections.

Table 5 Milling conditions employed for thin-wall machining simulation
Full size table

5.1 Milling Force

Using the developed experimental setup, force components, namely F x , F y and F z , were recorded for a typical process condition (Test case 1) as mentioned in Table 5. For the same process condition, a numerical simulation using the developed mathematical model was carried out. Figure 9 shows the comparison between the simulation predictions and the experimental results.

Fig. 9
figure 8

Comparison of simulated and measured milling force components F x , F y , and F z

Full size image

The dotted lines represent the moving average values of components of milling force recorded in the stable region during machining experiments, while the solid lines represent the moving average values of simulation results. It can be noted that the forces computed by the numerical model are in good agreement with the experimental results. Average prediction errors were noted to be 13.93, 20.82, and 32.68% in F x , F y and F z directions, respectively. Numerical predictions are found to be lower than that of experimental results. This is attributed to the uncontrollable factors such as material inhomogeneity, errors due to tool and workpiece setting, tool vibration and tool run-out. It can be observed that the prediction error of F z is quite high in comparison with that of F x and F y . It may be due to fact that the magnitude of F z is smaller and it is more sensitive than the other force components. It is also to be noted that the factors such as re-cutting of chips and ploughing of cutting tool edges on the work surface result in the generation of fluctuating force values.

From the plots, it can be seen that the trends of variations of experimental and numerical forces are similar. However the forces are fluctuating, which may be due to the fact that during the cutting process, the material softens due to the rise in temperature which reduces the force values. As the magnitude of force decreases, the heat production also reduces which in turn affects the metal softening effect that further leads to rise in the milling forces.

5.2 Wall Deflection and Form Error

In thin-wall milling operation, the low-rigidity thin-wall part deflects due to the application of milling forces. During the experiments, it was observed that maximum deflection occurs at top portion of the wall in comparison to that its base. It is due to the low rigidity of top portion of the workpiece and the base has sufficient rigidity as it is firmly supported by the bulk material. Figure 10 depicts the variation of deflection along the workpiece length measured perpendicular to the feed direction. It is noted that the deflections at free ends of the workpiece are higher in comparison to that of the middle portion of the wall. The two ends are less stiff and deflect readily under the action of milling force, whereas the center portion has sufficient rigidity as it is supported by the material all around. It can also be observed that experimentally obtained deflection values are slightly on the higher side than those obtained in the simulations. The mean absolute error between the experimental and numerically obtained results was noted to be 11%. The trends of variations of predicted results were matching well with respective experimental measurements. Figure 11 shows the comparison of wall sections obtained in numerical simulation and experimental study.

Fig. 10
figure 9

Comparison of the deflection at top portion of the wall (2 mm below the top edge): numerical and experimental results

Full size image
Fig. 11
figure 10

Wall cross sections obtained during experiment and numerical simulation

Full size image

It can be seen that during the thin-wall machining, machined wall base is thinner than that of the top potion. This is because, due to low rigidity, instantaneous deflection of top end is more, which leads to lower cutting of the top portion in comparison with that of the desired depth of cut. The developed numerical model could successfully simulate this phenomenon.

Similar to test case 1, experiments were conducted for three other test cases. Table 6 summarizes the values of measured and simulated milling force components, wall deflection, and workpiece temperature for all the four test cases.

Table 6 Comparison of the simulated and measured responses for test cases listed in Table 5
Full size table

It can be seen that the milling force component values predicted by the developed model match well with the values that are obtained by experiments for all the test cases. Mean prediction errors for F x , F y , F z , and wall deflection were noted to be 11.61, 16.38, 26.1, and 10.02%. Overall a very good agreement between the simulated and experimentally measured responses has been noted which demonstrates the capability of the developed model to predict the process responses accurately. Thus, the present 3-D FEM-based numerical model has predicted important process performance parameters such as milling force and wall deflection quite accurately and easily. A prior knowledge about these parameters will certainly help the process engineers to tune up the process parameters to achieve the desired process performance. Predicted milling forces can be used to estimate the energy requirement. This model is capable of predicting the instantaneous wall deflection, which will be useful in correcting the tool path to minimize the form error that occurs during the thin-wall milling process. Thus, it can be said that numerical modeling and simulation provides a useful tool to the engineers and scientists to carry out a prior detail study of the machining process. Further, this model can be used to carry out parametric analysis of thin-wall machining, i.e., a study on influence of process parameters, viz., axial depth of cut, radial depth of cut, feed, and cutting speed, tool geometry parameters, viz., tool diameter, and helix angle on the performance parameters such as part accuracy, milling forces, and power consumption. This model can also be employed to study the thin-wall machining operation of important and difficult-to-cut materials, viz., titanium alloys, Inconel, etc.

6 Conclusion

This chapter presented, in details, the development of a numerical (FEM) model for the thin-wall machining process. A realistic three-dimensional thermomechanical finite element based FEM model has been developed to simulate the complex physical interaction of helical cutting tool and workpiece during thin-wall milling of an aerospace grade aluminum alloy. Lagrangian formulation with explicit solution scheme was employed to simulate the interaction between helical milling cutter and the workpiece. The behavior of the material at high strain, strain rate and the temperature was defined by Johnson–Cook material constitutive model. Johnson–Cook damage law and friction law were used to account for chip separation and contact interaction. Experimental work was carried out to validate the results predicted by the mathematical model. The developed model predicted the forces in radial, feed, and axial directions with errors of 11.61, 16.38, and 26.1%, respectively. The prediction error for deflection at the top portion of thin-wall was 10.02%. It was noted that maximum deflections occur at the free ends of the wall as compared to that at the center. It was also observed that due to the deflection of the wall, some material at the top of the wall remained uncut that further leads to geometric form error in the workpiece. The results can be used to set the process parameters to obtain the desired process performance in terms of product accuracy. This model can further be improved by considering the material anisotropy, inhomogeneity, and prestresses in the work part.