A prediction model for the milling of thin-wall parts considering thermal-mechanical coupling and tool wear

Abstract

In thin-wall milling processes, the interactions between cutting loads and the displacement of the thin-wall part lead to varying tool-workpiece engagement boundaries and undesired surface form errors. This unavoidable issue becomes more severe in the machining of titanium alloys due to their poor machinability caused by the low thermal conductivity, high strength and high chemical reactivity. This paper presents a new predictive model to calculate the cutting-induced thermal-mechanical loads and workpiece deflection in milling Ti-6Al-4V thin-wall components. The cutting heat sources and the development of tool flank wear were considered in the modelling process to improve the prediction accuracy. The cutting loads were modelled analytically and calculated using an efficient iterative algorithm, and the deformation of the thin-wall part was simulated through a finite element model. A series of cutting experiments were conducted under various cutting conditions to validate the predicted results. Both the cutting forces and thin-wall displacement were recorded to examine prediction accuracy, and good agreements have been achieved between the measured results and simulated outcomes. The predicted cutting forces in the radial, feed and axial directions are within errors of 14%, 10% and 5%, respectively, concerning the experimental values. Meanwhile, the maximum predicted deformation errors at the initial, middle and end portions of the workpiece are less than 20%.

1 Introduction

Thin-wall components made of titanium alloys are widely used in the automotive, aeronautical and aerospace industries. In the milling process, the low rigidity of thin-wall components and cutting-induced loads may cause deformation of the thin walls, which result in the deviation of tool-part engagement boundaries from the nominal positions and lead to unavoidable surface form errors. Ti-6Al-4V is one typical kind of difficult-to-machine materials due to its poor thermo-mechanical properties. The low thermal conductivity causes the accumulation of large amounts of cutting heat in the cutting region, which results in high cutting temperature [1], whereas the high chemical activity leads to severe adhesion and diffusion wear of the cutting tool. Therefore, the prediction of the cutting loads and deformation of the workpiece in the milling of titanium thin-wall components is of significant importance.

In the last decades, many efforts have been made to solve the deformation, or geometrical deviation, problem in milling thin-wall components. In these studies, the cutting force model is an essential tool for both deformation prediction and process optimization, and the outcomes of the force model can be used as a fundamental database for prediction of tool/workpiece deflection, machining stability, stress distribution and surface integrity. According to published literature, many force models have been proposed for helix end mill [2,3,4,5,6]. Usually, these models were established by mechanical and analytical methods. In most mechanical models, the cutting edges of the tool were discretized into a finite number of elements along the axis direction and the cutting action of each slice was modelled as the oblique cutting process. The cutting force components of each slice were calculated from specific cutting coefficients obtained from experimental results [7]. Thus, the accuracy of the model depended on the calibration and fitting of the specific cutting coefficients obtained from a large number of experiments with various cutting conditions. Meanwhile, this method is only valid for a given tool-workpiece pair. Therefore, many studies devoted to developing analytical models in which the orthogonal cutting theory was extended to oblique cutting through equivalent plane approach, and mathematical relations between force components, tool geometry, material behaviour and cutting conditions were established [4, 8,9,10]. Similarly, each cutting tooth was discretized into a series of infinitesimal slices in these models, and the cutting action of each slice was equivalent to the classical oblique cutting process. Compared with mechanical models, analytical models were more efficient, and these models can be applied to various cutting conditions.

Apart from the calculation of cutting forces, tool wear is another critical issue that needs to be considered, especially in machining of titanium alloys. The poor machinability of titanium alloys usually leads to severe tool damage. Previous studies have shown that under the condition of tool wear, additional cutting loads have a significant influence on the interaction of tool and workpiece [11, 12]. In order to develop worn tool force models that can provide accurate prediction, detailed discussion about the nature of tool flank wear was proposed by Usui et al. [13] and Smithey et al. [14]. In these studies, the linear relation between the width of the plastic flow region and total wear land was studied, and the worn tool force models for both turning and milling process were established. Sun et al. [15] developed a 3D milling force model under the effects of tool flank wear. Hou et al. [16] proposed a wear recognition method of flat end mill for milling of difficult-to-cut materials. Liang and Liu [17] and Liang et al. [18] investigated the effects of tool wear on the plastic deformation; prediction models of the plastic deformation depth induced by additional thermo-mechanical stress considering tool flank wear were proposed. Li et al. [19] investigated the mechanism of flank wear of PCD tools and developed an analytical model by considering the combined effects of tool/workpiece dynamic characteristics and properties.

Concerning cutting loads, cutting heat has also been taken into account in the milling process. During the milling process, cutting heat is generated due to plastic deformation of workpiece material and frictional effect between tool and workpiece. The cutting heat could not be ignored in metal cutting since it seriously affects the integrity of the finished surface, material properties and tool wear conditions. In metal cutting, heat partition ratios and temperature rise on chip and tool were determined analytically through functional analysis, and several analytical cutting temperature modelling approaches have been proposed [20,21,22,23]. Yan et al. [24] presented an analytical model of the effect of tool flank wear on thermal stresses and residual stress. Further, better prediction results of the workpiece temperature distribution were achieved for end mill by the study of Lin et al. [25]. In a more recent study, the temperature predictive model in intermittent milling process with continuously varying chip thickness was proposed by Sun et al. [26].

However, above studies were carried out for normal turning or milling process and they were under the assumption of rigid workpiece without considering workpiece deformation. To solve the issues in thin-wall milling process, Budak and Altintas [27] analysed the variations of workpiece structure and the disengagement of tool-workpiece when predicting the peripheral milling process of flexible structures. Ratchev et al. [28] presented an integrated method for prediction of workpiece deflection during milling of low-rigidity parts. Based on the previous work, it was recognised that the flexible force model and iterative algorithm have a direct impact on the accuracy of prediction results. Thus, several algorithms associated with the flexible model in the peripheral milling of the thin-wall component have been presented. Wan and Zhang [29] developed a general model that considers the contact conditions of tool-workpiece and iterative corrections of radial cutting depths as well as the rigidity of workpiece. Kang and Wang [30] established two new efficient iterative algorithms including the flexible iterative algorithm and a double iterative algorithm. Inspired by these algorithms, an improved flexible iteration strategy was presented by Sun and Jiang [31] to predict the force-induced deformation and varying engagement boundaries.

It can be seen that the majority of previous studies on the thin-wall milling process focused on the force-induced errors, chip temperature rise and 3D-FEA analysis, while few literatures regarding tool wear and multiple cutting loads exist. Therefore, this paper presents a more accurate machining error prediction model that focused on cutting loads induced deformation in milling of thin-wall components. In the proposed model, a theoretical cutting force model of helical milling tool was developed based on the oblique cutting analysis. The influence of tool flank wear was considered to meet the actual cutting conditions, so the basic cutting force model was extended to include the effects of tool flank wear. This model also considered the combined impact of both the primary and tertiary heat sources and predicts the thermal deformation of the workpiece based on the FEA method. The workpiece deflection was predicted using a flexible iterative algorithm considering the feedback effect of deformation and tool-workpiece engagement variation. The calculation of cutting loads and simulation of part deformation were implemented in MATLAB and ABAQUS software. The accuracy of the model was demonstrated by force and displacement measurements in real time during milling of Ti-6Al-4V thin-wall workpiece under various machining conditions.

2 Dynamical cutting loads in thin-wall milling process

In this study, the thin-wall milling process was modelled with the consideration of the dynamic cutting forces, the development of tool wear, the thermal-mechanical coupling effect and the real-time deformation of the thin-wall part.

2.1 Forces in oblique cutting processes

In order to simplify the complex tool geometry and tool-workpiece engagement, the cutting teeth of the helical tool were discretised into a finite number (n) of axial elements with equal thickness along the tool axis and each axial segment has a length of d_z = a_p/n, as shown in Fig. 1. For an infinitesimal element {i, j} of the cutting tooth, the cutting action can be represented with the oblique cutting mechanism, and {i, j} presents the cutter node which is the intersection of ith cutting tooth and jth horizontal mesh line. The index of the tooth i = 1, 2, …N_f, where N_f is the total number of cutter tooth. The index of the axial elements j = 1, 2, …n, where n is the number of axial elements.

Fig. 1

Material removal process in thin-wall milling

In this model, the cutting planes and parameters are defined in the local coordinate of cutting tool. The instantaneous tangential, F_t(ϕ_{i, j}), radial, F_r(ϕ_{i, j}) and axial F_a(ϕ_{i, j}) cutting forces acting on element {i, j} can be presented as functions of cutting edge oblique angle λ_s, shear strength τ_s, uncut chip thickness h(ϕ_{i, j}), oblique shear angles (ϕ_n, ϕ_e), oblique rake angles (γ_n, γ_e), oblique friction angles (β_n, β_a) and resultant force direction (θ_n, θ_e) [3]:

$$ {\displaystyle \begin{array}{c}{F}_{\mathrm{t}}\left({\phi}_{\mathrm{i},\mathrm{j}}\right)=\frac{\uptau_{\mathrm{s}}\mathrm{bh}\left({\upphi}_{\mathrm{i},\mathrm{j}}\right)}{\sin \left({\upphi}_{\mathrm{n}}\right)}\cdotp \frac{\cos \left({\upbeta}_{\mathrm{n}}-{\upgamma}_{\mathrm{n}}\right)+\tan {\upeta}_{\mathrm{c}}\sin {\upbeta}_{\mathrm{n}}\tan {\uplambda}_{\mathrm{s}}}{\sqrt{\cos^2\left({\upphi}_{\mathrm{n}}+{\upbeta}_{\mathrm{n}}-{\upgamma}_{\mathrm{n}}\right)+{\tan}^2{\upeta}_{\mathrm{c}}{\sin}^2{\upbeta}_{\mathrm{n}}}}\\ {}{F}_{\mathrm{r}}\left({\phi}_{\mathrm{i},\mathrm{j}}\right)=\frac{\uptau_{\mathrm{s}}\mathrm{bh}\left({\upphi}_{\mathrm{i},\mathrm{j}}\right)}{\sin \left({\upphi}_{\mathrm{n}}\right)}\cdotp \frac{\sin \left({\upbeta}_{\mathrm{n}}-{\upgamma}_{\mathrm{n}}\right)}{\cos {\uplambda}_{\mathrm{s}}\sqrt{\cos^2\left({\upphi}_{\mathrm{n}}+{\upbeta}_{\mathrm{n}}-{\upgamma}_{\mathrm{n}}\right)+{\tan}^2{\upeta}_{\mathrm{c}}{\sin}^2{\upbeta}_{\mathrm{n}}}}\\ {}{F}_{\mathrm{a}}\left({\phi}_{\mathrm{i},\mathrm{j}}\right)=\frac{\uptau_{\mathrm{s}}\mathrm{bh}\left({\upphi}_{\mathrm{i},\mathrm{j}}\right)}{\sin \left({\upphi}_{\mathrm{n}}\right)}\cdotp \frac{\cos \left({\upbeta}_{\mathrm{n}}-{\upgamma}_{\mathrm{n}}\right)\tan {\uplambda}_{\mathrm{s}}-\tan {\upeta}_{\mathrm{c}}\sin {\upbeta}_{\mathrm{n}}}{\sqrt{\cos^2\left({\upphi}_{\mathrm{n}}+{\upbeta}_{\mathrm{n}}-{\upgamma}_{\mathrm{n}}\right)+{\tan}^2{\upeta}_{\mathrm{c}}{\sin}^2{\upbeta}_{\mathrm{n}}}}\ \end{array}} $$

(1)

where b is the width of cut and h(ϕ_{i, j}) is the varying chip thickness determined by the immersion angle ϕ_{i, j}.

Apart from the calculation of shearing forces, the effect of tool wear has also been taking into account. Tool wear occurs due to the continuous rubbing contact and plough effect between the tool flank surface and workpiece surface, resulting in additional friction force generated in the contact area. Only tool flank wear was considered and discussed in this model because it contributes most significantly to the temperature rise of the workpiece. The contact area of flank wear land and workpiece is shown in Fig. 2.

Fig. 2

Tool flank wear land in oblique cutting

Taking into account the effects of tool flank wear, the cutting forces can be expressed as the superposition of the cutting forces attributed to the shear effect and those attributed to the effect of rubbing contact. The forces under the effect of tool flank wear are analysed in cutting direction and thrust direction. As a result, the instantaneous cutting forces can be modified as:

$$ \left\{\begin{array}{c}{F}_t^{\prime}\left({\phi}_{i,j}\right)={F}_t\left({\phi}_{i,j}\right)+{F}_{tw}\\ {}{F}_r^{\prime}\left({\phi}_{i,j}\right)={F}_r\left({\phi}_{i,j}\right)+{F}_{rw}\\ {}{F}_a^{\prime}\left({\phi}_{i,j}\right)={\mathrm{F}}_{\mathrm{a}}\left({\upphi}_{\mathrm{i},\mathrm{j}}\right)\end{array}\right. $$

(2)

where F_tw and F_rw are the feed component force and rubbing force respectively, which can be calculated by integrating the flow stress along the length of wear land [18]:

$$ {\displaystyle \begin{array}{c}{F}_{rw}=\left\{\begin{array}{cc}\begin{array}{c}{b}^{\prime }{\int}_0^{VB^{\prime }}{\sigma}_0\frac{VB^{\prime }-{x}^2}{VB^{\prime }} dx\ \\ {}\kern5em \end{array}& {VB}^{\prime }<{L}_{VB}^{\ast}\\ {}{b}^{\prime }{\int}_0^{VB^{\prime }-{L}_{VB}^{\ast }}{\sigma}_0 dx+{b}^{\prime }{\int}_{VB^{\prime }-{L}_{VB}^{\ast}}^{VB^{\prime }}{\sigma}_0{\left(\frac{VB^{\prime }-{x}^2}{VB^{\prime }}\right)}^2 dx& {VB}^{\prime}\ge {L}_{VB}^{\ast}\end{array}\right.\\ {}{F}_{tw}=\left\{\begin{array}{cc}{b}^{\prime }{\int}_0^{VB^{\prime}\left(1-\sqrt{\frac{\tau_0}{\sigma_0}}\right)}{\tau}_0 dx+{b}^{\prime }{\int}_{VB^{\prime}\left(1-\sqrt{\frac{\tau_0}{\sigma_0}}\right)}^{VB^{\prime }}{\mu \sigma}_0\frac{VB^{\prime }-{x}^2}{VB^{\prime }} dx& {VB}^{\prime }<{L}_{VB}^{\ast}\\ {}{b}^{\prime }{\int}_0^{VB^{\prime }-{L}_{VB}^{\ast}\sqrt{\frac{\tau_0}{\sigma_0}}}{\tau}_0 dx+{b}^{\prime }{\int}_{VB^{\prime }-{L}_{VB}^{\ast}\sqrt{\frac{\tau_0}{\sigma_0}}}^{VB^{\prime }}\mu {\sigma}_0{\left(\frac{VB^{\prime }-{x}^2}{VB^{\prime }}\right)}^2 dx& {VB}^{\prime}\ge {L}_{VB}^{\ast}\end{array}\right.\end{array}} $$

(3)

where b^′ and VB^′ are the effective contact width and the effective wear band width on the contact area in oblique cutting. σ₀ and τ₀ are the normal and tangential stresses that can be obtained from the modified Oxley’s force model. μ is the friction coefficient at the tool-workpiece contact area. ${L}_{VB}^{\ast }$ is the critical length of flank wear land, and this value for a fixed tool-workpiece material pair can be obtained by experimental observations [14].

With the determination of elemental forces ${F}_t^{\prime}\left({\phi}_{i,j}\right)$, ${F}_r^{\prime}\left({\phi}_{i,j}\right)$ and ${F}_a^{\prime}\left({\phi}_{i,j}\right)$, the component forces within the reference Cartesian-Coordinate can be calculated by the following transformation:

$$ \left\{\begin{array}{c}{F}_x\left({\phi}_{i,j}\right)\\ {}{F}_y\left({\phi}_{i,j}\right)\\ {}{F}_z\left({\phi}_{i,j}\right)\end{array}\right\}=T\left\{\begin{array}{c}{F}_t^{\prime}\left({\phi}_{i,j}\right)\\ {}{F}_r^{\prime}\left({\phi}_{i,j}\right)\\ {}{F}_a^{\prime}\left({\phi}_{i,j}\right)\end{array}\right\} $$

(4)

where F_x(ϕ_{i, j}), F_y(ϕ_{i, j}), F_z(ϕ_{i, j}) are forces in the feed, normal and axial directions. T is the transformation matrix defined as:

$$ T=\left[\begin{array}{ccc}-\mathit{\cos}{\phi}_{i,j}& -\mathit{\sin}{\phi}_{i,j}& 0\\ {}\mathit{\sin}{\phi}_{i,j}& -\mathit{\cos}{\phi}_{i,j}& 0\\ {}0& 0& 1\end{array}\right] $$

(5)

On any infinitesimal segment of the cutting tooth, the differential forces acting on this segment can be expressed as:

$$ \mathrm{d}{F}_d\left(\phi, z\right)={F}_d\left({\phi}_{i,j}(z)\right) dz\kern0.5em \left(d=x,y,z\right) $$

(6)

In order to calculate the total cutting forces on each tooth, the differential cutting forces on the jth segment of ith tooth are integrated along the axial direction as following:

$$ {F}_d\left(i,j\right)={\int}_{z_l}^{z_u}{F}_d\left({\phi}_{i,j}(z)\right) dz\kern0.5em \left(d=x,y,z\right) $$

(7)

where z_u and z_l are the upper and lower limits of z-axis boundaries for element {i, j}.

In the cutting force model of helix end mill cutter, the immersion-dependent upper and lower axial limits of z-axis boundaries can be defined as [27]:

$$ {\displaystyle \begin{array}{c}{z}_u=\frac{1}{\uppsi_{\mathrm{i},\mathrm{j}}}\left[{\phi}_{1,0}-\frac{2\pi \left(i-1\right)}{N_f}-{\phi}_{en}\right]\\ {}{z}_l=\frac{1}{\uppsi_{\mathrm{i},\mathrm{j}}}\left[{\phi}_{1,0}-\frac{2\pi \left(i-1\right)}{N_f}-{\phi}_{ex}\right]\end{array}} $$

(8)

Overall, the instantaneous cutting forces acting on multiple cutting edges can be obtained by integrating the total differential forces along each tooth:

$$ {F}_{\mathrm{x}}\left({\phi}_{\mathrm{i},\mathrm{j}}\right)={\sum}_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{f}}}{\sum}_{\mathrm{j}=1}^n{\mathrm{F}}_x\left(i,j\right),\kern0.5em {\mathrm{F}}_{\mathrm{y}}\left({\upphi}_{\mathrm{i},\mathrm{j}}\right)={\sum}_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{f}}}{\sum}_{\mathrm{j}=1}^n{\mathrm{F}}_y\left(i,j\right),\kern0.5em {\mathrm{F}}_{\mathrm{z}}\left({\upphi}_{\mathrm{i},\mathrm{j}}\right)={\sum}_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{f}}}{\sum}_{\mathrm{j}=1}^n{\mathrm{F}}_z\left(i,j\right) $$

(9)

2.2 Modelling of thermal loads

A huge amount of cutting heat is generated due to the plastic deformation of workpiece material, tool/chip and tool/workpiece friction during the cutting process of metallic materials. Since the cutting heat affects material properties and thermal stress which are crucial to the prediction of thin-wall deflection, the dynamic thermal load has to be calculated in the model.

As shown in Fig. 3, there are three heat sources in the milling process: the primary deformation zone, the secondary deformation zone at the tool/chip interface and the tertiary deformation zone at the tool/workpiece interface. The total heat generated can be expressed as the sum of heat generated in the three deformation zones:

$$ {Q}_{\mathrm{gen}}={Q}_{\mathrm{s}}+{Q}_{\mathrm{f}}+{Q}_{\mathrm{r}} $$

(10)

where Q_s is the amount of heat generated in the primary deformation zone, Q_f is the amount of heat generated in the secondary deformation zone due to the friction effect and Q_r is the amount of heat generated in the tertiary deformation zone due to the rubbing effect.

Fig. 3

Heat generation in the cutting process

However, not all the heat is consumed in the raising of the workpiece temperature. In the milling processes, a proportion of heat generated in the primary deformation zone and tertiary deformation zone is transferred to the chips and cutting tool. And most of the heat generated in the second deformation zone is moved away by the cutter and continuous chip flow due to the extrusion and friction on the tool-chip interface, which has little influence on the temperature rise of workpiece. Therefore, the total thermal energy flows into workpiece during the milling process can be expressed as follows:

$$ {Q}_{\mathrm{gen}}=\left(1-{R}_1\right){Q}_{\mathrm{s}}+\left(1-{R}_3\right){Q}_{\mathrm{r}} $$

(11)

where R₁ and R₃ is the partition coefficient of heat energy conducted into chips and tool in the primary deformation and tertiary zones, respectively.

The heat flux in the primary deformation zone and tertiary deformation zone is expressed with the following equations:

$$ \left\{\begin{array}{c}{q}_{\mathrm{s}}=\frac{{\mathrm{Q}}_{\mathrm{s}}}{J{A}_s}=\frac{{\mathrm{F}}_{\mathrm{s}}{\mathrm{V}}_{\mathrm{s}}}{J{A}_s}=\frac{{\mathrm{F}}_{\mathrm{s}}{\mathrm{V}}_{\mathrm{s}}\ }{J\frac{\mathrm{b}}{\cos {\uplambda}_{\mathrm{s}}}\frac{\mathrm{h}}{\sin {\upphi}_{\mathrm{n}}}}\\ {}{q}_{\mathrm{r}}=\frac{{\mathrm{Q}}_{\mathrm{r}}}{J{A}_r}=\frac{{\mathrm{F}}_{\mathrm{r}}{\mathrm{V}}_{\mathrm{r}}}{J{\mathrm{A}}_{\mathrm{r}}}=\frac{{\mathrm{F}}_{\mathrm{tw}}V}{J\frac{{\mathrm{V}\mathrm{B}}^{\prime }}{\cos {\uplambda}_{\mathrm{s}}}\frac{{\mathrm{b}}^{\prime }}{\cos {\uplambda}_{\mathrm{s}}}}\end{array}\right. $$

(12)

where F_s, F_r, V, V_S and V_r are the shear force, the frictional force, the cutting velocity, the component of cutting velocity along the shear plane and the component of cutting velocity along the flank face, respectively. A_s and A_r are the contact area in the shear plane and tool flank surface and J is the heat equivalent work.

The shear force F_s and shear velocity V_S are calculated with the following equations [25]:

$$ {\displaystyle \begin{array}{c}{F}_{\mathrm{s}}={\left[{\left({\mathrm{F}}_{\mathrm{a}}\cos {\uplambda}_{\mathrm{s}}-{\mathrm{F}}_{\mathrm{t}}\sin {\uplambda}_{\mathrm{s}}\right)}^2+{\left({\mathrm{F}}_{\mathrm{a}}\cos {\uplambda}_{\mathrm{s}}\cos {\upphi}_{\mathrm{n}}-{\mathrm{F}}_{\mathrm{r}}\sin {\upphi}_{\mathrm{n}}+{\mathrm{F}}_{\mathrm{t}}\cos {\uplambda}_{\mathrm{s}}\cos {\upphi}_{\mathrm{n}}\right)}^2\right]}^{\frac{1}{2}}\\ {}{V}_{\mathrm{s}}=\frac{\cos {\uplambda}_{\mathrm{s}}\cos {\upgamma}_{\mathrm{e}}}{\cos {\upeta}_{\mathrm{c}}\cos \left({\upphi}_{\mathrm{e}}-{\upgamma}_{\mathrm{e}}\right)}V\end{array}} $$

(13)

The heat partition coefficients R₁ and R₃ can be estimated using oblique moving rectangular heat source method and stationary plane heat source model [20], and also Blok’s and Venuvino’s approach [32].

2.3 Modelling of flexible cutting forces

In thin-wall milling, the cutting forces are continually influenced by the deflection of workpiece and variation of workpiece rigidity because the geometry of the tool/workpiece engagement is constantly changed. As presented in Fig. 4, cutting parameters of each element such as the instantaneous chip thickness and radial cutting depth deviate from the nominal values and need to be modified with regard to the deformation of thin wall. Therefore, the flexible model was developed with the consideration of workpiece deflection, which could increase the accuracy of the predictive results.

Fig. 4

Illustration of thin-wall deflection behaviour

Based on the results of previous studies, only the correction of the radial cutting depth is considered in this work, namely, the variations of the immersion boundary [33]. At each engaged cutting element, the actual immersion starting angle ${\phi}_{\mathrm{en}}^{\prime }$ in down milling after deflection can be determined by solving the following equation:

$$ {\phi}_{\mathrm{en}}^{\prime }=\uppi -{\cos}^{-1}\left(1-\frac{2{\mathrm{a}}_{\mathrm{em}}^{\prime }}{\mathrm{R}}\right) $$

(14)

and actual radial cutting depth $2{\mathrm{a}}_{\mathrm{em}}^{\prime }$ can be calculated as:

$$ 2{a}_{\mathrm{e}\mathrm{m}}^{\prime }={\mathrm{a}}_{\mathrm{e}}-{\updelta}_{\mathrm{w}} $$

(15)

where δ_w is the normal workpiece deviation due to the action of cutting loads, and a_e is the desired radial cutting width. δ_w can be obtained using thermo-mechanical finite element analysis. The immersion starting angle ϕ_en is then submitted into Eqs. 8 and 9, the varying upper limit and cutting loads is solved by the iterative algorithm.

For the global iteration scheme, the initial calculated cutting loads are applied on each cutting unit, and the real deflection along current cutting location can be obtained from the FEA solver. Then the tool is rotated to the next feed position, and the cutting loads are corrected by revising the radial cutting depth and immersion angle. The updated cutting loads are applied on the new cutting unit to perform the subsequent simulation, so that corrected part deflection can be obtained. This routine will be repeated until the required precision is achieved, and analyses of all cutting locations are obtained. After the deformation results of the main cutting positions are obtained, the interpolation method is employed to find out the complete displacement error of the part.

To improve iteration efficiency and reduce the time to achieve the convergence condition, a more effective iterative algorithm is employed in this study [30]. As shown in Fig. 5, the oblique blue lines represent tool-workpiece engagement boundaries, and red oblique lines represent the in-cutting edge at each iteration step.

Fig. 5

Modelling of tool-workpiece engagement boundaries

At the first axial position, the initial position of the first iteration is $\overline{{\mathrm{D}}_1^0{\mathrm{E}}_1^0}$. Once the iteration begins, the cutting edge will move repeatedly and get closer to its actual position after each iterative step. After kth step, the cutting tooth reach the convergence position $\overline{{\mathrm{D}}_1^{{\mathrm{k}}_1}{\mathrm{F}}_1^{{\mathrm{k}}_1}}$, and the point ${\mathrm{F}}_1^{{\mathrm{k}}_1}$ will be the corrected in-cutting position. After the first iteration convergence,$\overline{C{\mathrm{A}}_1}$ and $\overline{DB}$ becomes the new engagement boundary. Then $\overline{{\mathrm{D}}_2^0{\mathrm{F}}_2^0}$ is taken as initial position for the iteration process instead of $\overline{{\mathrm{D}}_2^0{\mathrm{E}}_2^0}$. Based on this method, the first iteration step of cutting tooth at nth (n ≥ 2) iteration is defined as $\overline{{\mathrm{D}}_{\mathrm{n}}^0{\mathrm{F}}_{\mathrm{n}}^0}$, which satisfied $\overline{{\mathrm{D}}_{\mathrm{n}}^0{\mathrm{F}}_{\mathrm{n}}^0}$=$\overline{{\mathrm{D}}_{\mathrm{n}-1}^{{\mathrm{k}}_{n-1}}{\mathrm{F}}_{\mathrm{n}-1}^{{\mathrm{k}}_{n-1}}}$. This method could improve the algorithm efficiency since the initial position of each iteration is closer to the final convergence position. In Fig. 5, $\overline{{\mathrm{D}}_{\mathrm{n}}^{{\mathrm{k}}_n}{\mathrm{E}}_{\mathrm{n}}^{{\mathrm{k}}_n}}$ represents the in-cutting edge at nth iteration, ${\updelta}_n^{{\mathrm{k}}_n}$ and ${\mathrm{a}}_n^{{\mathrm{k}}_n}$are the deflection of workpiece and actual radial cutting depth at kth iteration step. During the iterative process, the actual radial cutting depth ${\mathrm{a}}_n^{{\mathrm{k}}_n}$ is iteratively updated as:

$$ {\mathrm{a}}_n^{{\mathrm{k}}_n}={\mathrm{a}}_{\mathrm{e}}-{\updelta}_n^{{\mathrm{k}}_n}-\Delta \updelta $$

(16)

where ∆δ can be solved by the geometrical relationship as:

$$ {\displaystyle \begin{array}{c}\Delta \delta =\frac{\left({\mathrm{a}}_{\mathrm{e}}-{\updelta}_n^{{\mathrm{k}}_n}\right)\cos {\uplambda}_{\mathrm{s}}\sin \gamma }{\sin \left(\gamma +{\uplambda}_{\mathrm{s}}\right)}\\ {}\gamma ={\tan}^{-1}\left[\left({\updelta}_n^A-{\updelta}_n^{{\mathrm{k}}_n}\right)/\left({a}_p-{h}_n^D\right)\right]\end{array}} $$

(17)

${\delta}_A^n$ and ${h}_n^D$ are the displacement value of upper point A and distance from ${\mathrm{D}}_{\mathrm{n}}^{\mathrm{k}}$ to ${\mathrm{D}}_1^0$ at nth cutting position, respectively.

Meanwhile, the actual immersion starting angle ${\phi}_n^k$ is corrected as:

$$ {\phi}_n^k=\uppi -{\cos}^{-1}\left(1-\frac{2{\mathrm{a}}_n^k}{\mathrm{R}}\right) $$

(18)

Based on above equations, workpiece deflection ${\delta}_n^k$ and corrected cutting loads can be obtained iteratively using proposed cutting load model and FE model. The iteration of each step would stop when the following condition is achieved, namely, the in-cut edge is close enough to its convergence position,

$$ \left|{\mathrm{a}}_n^{{\mathrm{k}}_n}-{\mathrm{a}}_n^{{\mathrm{k}}_n-1}\right|\le \varepsilon $$

where ε is the tolerance that is applied to control the precision of the calculation.

3 FE modelling of thin-wall machining process

Based on the established theoretical model, the instantaneous cutting loads acting on the workpiece can be obtained, which are then applied as the inputs for the FE model to simulate the deflection of the workpiece. MATLAB programs have been developed to calculate the cutting loads for different cutter geometries and machining conditions. The finite element model of thermal-mechanical coupling can be developed using the finite element solver ABAQUS. For simplification, the thin-wall part is assumed to be a low-rigidity rectangular part with the same geometries and material properties of the real workpiece. The inputs to the FEM model are the material properties, calculated cutting loads, various cutting parameters and boundary conditions. The cutting loads are treated as moving-distributed loads and discretised to the relevant nodes of the machined surface. Consequently, the deflection and dynamic characteristic of the machined part could be obtained.

3.1 Application of cutting loads and material removal

In the FE analysis, the calculated cutting forces and heat sources were applied as input to the current cutting units in each time step, and the cutting loads were unloaded from the previous cutting units when the tool moves to the next cutting position. The thermal-mechanical coupling analysis was performed to obtain the coordinates changes of cutting units in the current step, and then the cutting conditions were modified with the corrected cutting loads for the next step. Figure 6 presents the complex schematic of cutting loads and workpiece deformation.

Fig. 6

Interrelation of cutting loads and part deformation

Due to the continuous removal of workpiece materials in the cutting process, the dynamic characteristics and static stiffness of the part changes simultaneously, which further affects the calculation of thin-walled part deformation. In order to simulate the influences of material removal, a set of elements that equivalent to the cutter swept volume at each feed step was deactivated when cutting tool passes from one discrete cutting position to the next.

The detailed analysis process of the established thermal-mechanical coupling model is shown in Fig. 7:

Fig. 7

Outline of flexible cutting load model and thermal-mechanical coupling

3.2 Workpiece material properties and basic setup of FE model

During the simulation, temperature-dependent thermo-physical properties of Ti-6Al-4V material were implemented in this model and its detailed properties are listed in Table 1 [34, 35].

Table 1 Temperature-dependent properties of Ti-6Al-4V

The workpiece was defined as elastic-plastic model and meshed into 99,889 elements and 108,784 nodes. The element type of workpiece was simplified and set as solid element (C3D8T). The influence of material removal was achieved by the model change interaction. The mesh sizes were calculated based on real cutting parameters. Variable mesh density was implemented for the model, and the mesh elements within the finished part were refined to obtain better simulation results. The mesh strategy is shown in Fig. 8. Structural boundary condition was applied on the bottom portion of the workpiece to model the fixture constrains; the degree-of-freedom of the bottom part was fixed along the feed, axial and radial directions, respectively. Thermal boundary condition was applied on the workpiece surface and the initial temperature of the workpiece was set to be the room temperature. The effect of cutting fluid on the workpiece was equivalent to the forced heat exchange process and modelled by applying the relevant convective film coefficient. Detailed parameters of the FEA model are listed in Table 2.

Fig. 8

Mesh strategy of the FEA mode

Table 2 Parameters of the FEA model

4 Experimental analysis and verification

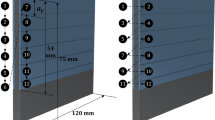
A series of milling experiments were conducted to verify the predictive model of cutting force and workpiece deformation. The experimental setup is presented in Fig. 9. The thin-wall milling tests were carried out using a 3-axis HAAS CNC milling machine. Thin-wall parts with the dimension of 150 mm (length) × 15 mm (height) × 120 mm (width) and 2 mm thickness were clamped on a Kistler 9257B three-component dynamometer. The Lion Precision ECL 130 inductive displacement sensors were employed for on-line measuring of the part deflection, the sensors were placed at three different locations with an equal interval (L1 = 0, L2 = 1/2 L and L3 = L) at the back of the workpiece and mounted on customised brackets. Tungsten Carbide end mill with 4 flutes, 6 mm diameter and 38° helix angle were used to machine the thin-wall components. Moreover, the Kistler 5070A eight-channel charge amplifier was used to amplify and convert the signals from the dynamometer and displacement sensors, then these signals were transferred to the NI DAQ card and the obtained signals were analysed using LabView. The contrast tests were performed when the tools were with different wear conditions, the widths of flank wear (VB) were measured using a Leica Optical microscope before each milling test. In the cutting tests, the collected cutting force signals include high frequency chaotic signals or background noise due to external interferences in the measurement process or internal disturbances of the tool-workpiece system. Therefore, the signal filtering was performed with low-pass filters to remove high frequency noise and undesired dynamic effects, and facilitate the visualization and readability of cutting force waveforms. Different cutting speeds, feed rates and cutting depths were selected orthogonally, as listed in Table 3.

Fig. 9

Experimental setup and the equipment

Table 3 L₉(3⁴) orthogonal array of cutting conditions for milling experiments

5 Results and discussions

In the following section, experimental results and FE model of thin-wall milling are presented and discussed. Tests 1, 7 and 9 were randomly selected as examples to show the experimental results.

5.1 Cutting forces

Figure 10 shows the comparison of cutting forces between the experimental result and calculated outcome. Force component in the normal direction F_y was mainly considered as it plays a dominant role in the workpiece deflection, and the evolution of calculated and measured milling forces of cutting Test 1 in the sample window is given as an example. It can be seen in Fig. 10 that the cutting forces calculated by the flexible force model are in good agreement in magnitude as well in trend with the measured results. The maximum calculated cutting force F_y is 93 N, while the measured data is found to be 91 N. The percentage errors are less than 3%. The differences between the simulated and measured results are attributed to some possible factors including process damping, the changes of workpiece material property and tool run-out.

Fig. 10

Comparison of calculated and measured cutting forces in Test 1

Fresh tools and tools with different degrees of wear were selected to analyse the effects of tool flank wear. Figure 11 presents the variations of measured and calculated forces in Test 7 (VB = 0.035 mm) in a stable state. In this case, it can be observed that the calculated results are well consistent with the experimental results with errors less than 7%, and the trend of evolutions also matches well. It is also shown in Fig. 11 that the maximum calculated force is lower than the measured force. One possible reason leading to the difference is that the length and width of tool flank wear land were not uniform during the milling process, while the tool was considered as to be in an ideal condition in the predictive model. Secondly, other types of tool wear would occur during the milling process, and this led to the increase of cutting forces while only tool flank wear was considered in the proposed model. Additionally, the tool wear rate was treated as a constant in each cutting test, which can also cause prediction errors. All these errors would have uncertain influences on the evolution of cutting forces. It could also be found that the amplitude variation of each force component varies slightly in each rotation period. The main reason is that the cutting forces are affected by different dynamic factors in the milling process, especially in cutting of titanium alloy, factors such as chatter and the wear degree of the tool may affect the cutting forces.

Fig. 11

Comparison of calculated and measured cutting forces in Test 7

5.2 Part deflection and form errors

During the machining process, the thin-wall part deflects due to its low rigidity under the action of cutting loads. Figure 12 shows the displacement of the thin-wall component under cutting conditions of Test 9, which is selected as an example to present the FEA results. Because the thickness and stiffness of the part in the radial direction are smallest compared with those in other directions, and the deformation in the radial direction is much larger, only the deformation in the radial direction is analysed in this paper.

Fig. 12

Modelling of thin-wall deformation

Figure 13 shows the comparison of surface form errors between modelling and experimental results. In the figure, the simulated and measured surface form errors in Test 9 at feed position of L1 = 0, L2 = 1/2 L and L3 = L are presented; the variation of part deformation was measured along the length direction of the workpiece.

Fig. 13

Comparison of measured and predicted surface form errors in Test 9

It can be seen in Fig. 13 that the percentage errors of maximum displacement values at L1, L2 and L3 are 5.6%, 5.4% and 5.9%, respectively; the tendencies are found to match very well. It can be observed that the amplitudes of deformation present an increasing trend towards the free ends of the part due to the lower stiffness of thin-wall part at these areas compared with the middle section of the part. Because of the higher stiffness at the middle of the part, cutting loads and the changes of residual stress have smaller effects on the local deformation. Moreover, the part becomes more flexible in the process due to the unremitting material removal process, which leads to decreasing stiffness and non-uniform residual stress of the part, so the thin-wall part is not symmetrical along the feed direction and relatively larger deformation values were found at the latter half of the part. Due to the influence of part deformation, the actual radial cutting depth decreased and the milling forces were also expected to be lower at the end of the part than those in previous cutting positions. Through FEA results shown in Fig. 12, it can also be found that larger deformation occurred at the top of the part in the axial direction as the stiffness of the upper edge of the part was less than that at the root of the part.

Additionally, through the analysis of results obtained from the orthogonal experiments, the sequence and contribution rate of each experiment factor on target index were determined as radial depth of cut, feed rate, length of flank wear land and spindle speed. Radial cutting depth has a bigger impact on the deformation than other parameters, and with the increase of radial cutting depth, the maximum form error increased significantly. Meanwhile, with the increase of spindle speed, the maximum deformation of the workpiece increased but the gradient tended to be gentle. And it was believed that the workpiece deformation would experience a similar tendency as cutting forces when tool flank wear deteriorated following the typical wear curve because the increased flank wear would lead to softened material and extra thermal-mechanical loads on workpiece. The values and percentage of errors of the measured and predicted results at the middle position L2 are shown in Table 4.

Table 4 Comparison between measured and predicted results for all the milling tests

According to the proposed model, the additional cutting force components and rubbing heat source due to tool flank wear have great effects on the amplitude of part deformation. The deterioration of tool flank wear would lead to increasing cutting force components and extra thermal stress at the tool-workpiece interface, resulting in poor surface quality. Thus, the prediction of thin-wall deformation at the presence of tool flank wear is necessary before actual machining operations.

It should be noted that significant chatter vibration occurred in Test 8, which seriously affects the surface quality of the finished workpiece, and the cutting forces in this case cannot be accurately calculated by the developed model. The chatter marks on the workpiece surface are shown in Fig. 14. At the beginning and end of the cutting process, both the tool and part were inflicted to larger mechanical impact, so the chatter marks were relatively obvious, while the vibration in the middle part was relatively weak. The chatter is mainly due to the relatively large radial cutting depth and low feed rate so that the ploughing force component is dominant while the rigidity of thin-wall part is low, which causes larger force-induced coupling defection of the tool-workpiece system, and resulted in a significant calculation error which is as high as 20.2%. From the aspect of avoiding chatter damage on the machined surface, properly choice of cutting parameters based on the stability lobe diagram (SLD) method is also required [36].

Fig. 14

Machined surface in milling Test 8

To confirm the effects of thermal load, two FEA processes with and without applying cutting heat were carried out based on the established FEM model and the cutting conditions of cutting Test 9. As shown in Fig. 15, it is observed that cutting heat has a great impact on the magnitude of maximal form error as it can change the properties of workpiece material and the distribution of thermal stress. A maximum percentage difference of 19% was found between these two analyses. Therefore, cutting heat cannot be ignored in thin-wall milling, and it is essential for the prediction and control of thin-wall deflection.

Fig. 15

Comparison of surface form errors with and without considering cutting heat

6 Conclusions

In this paper, a new predictive model was developed to analyse the interaction between the cutting loads and part deformation in milling thin-wall parts. The development of tool wear and the thermal effects were taken into account when calculating the flexible milling loads, and an efficient iterative algorithm was employed to improve the accuracy and efficiency of calculation. In the predicting process, the results of the flexible cutting force model and relevant cutting heat sources were applied as the input of the FEA model. Validation experiments of Ti-6Al-4V thin-wall milling were performed to verify the analytical model and simulation results. The main conclusions can be summed up as following:

• 1. It has been demonstrated that the new model was not only reliable but also robust. The deviations between the measured and calculated cutting forces were within the errors of 14%, 10% and 5% in the radial, feed and axial directions, respectively. The errors of cutting cases with a sharp tool were relatively small and within the range of 2 to 7%. Moreover, the maximum predicted deformation errors at the initial, middle and end portions of the workpiece were less than 20%.

• 2. Tool wear effect is critical for predicting cutting loads in milling of difficult-to-machine materials like Ti-6Al-4V. The wear-induced loads and thermal stress could further deteriorate the finished surface and cutting tool. And cutting force components have an increasing trend along with the propagation of tool flank wear.

• 3. By comparing the deformation of thin-wall under the effects of cutting forces and multi-loads, it was found that the deformation caused by multi-loads was about 10–19% larger than that of the deformation caused by milling force. Therefore, it is necessary to study and control the surface form errors caused by thermo-mechanical coupling especially in precision processing of thin-wall parts.

The presented model paves the way for developing new models to estimate surface form errors for machining complex thin-wall parts with the consideration of chatter stability and other cooling strategies.