Application of Total Least Squares Version of ESPRIT Algorithm for Seismic Signal Processing

Abstract

Estimation of frequency with high resolution is a crucial task in signal processing. Raw seismic signals consist of huge noise which can be removed only by using some signal processing methods. In this paper, the ESPRIT algorithm is implemented in order to process the signal. A time series data is taken and the frequency is estimated by total least squares version of ESPRIT algorithm. ESPRIT employs a basic rotational invariance in the subspaces of the signal. The detailed implementation of the algorithm is greatly presented in the following sections.

1 Introduction

Seismology is the study of earthquakes, according to some researches in olden times, the earthquakes are caused by the volcanic explosions that take place under the earth’s crust and the waves travel to the earth’s surface causing the tremors which cause lots of destruction to the mankind and according to some researches, the earthquakes are caused [1] by the drifting of continents which causes the landmass to move and create mass earthquakes. These waves are of two types, one is the transverse waves and the other is the longitudinal waves, the transverse waves travel parallel to the epicenter of the earthquake while the longitudinal waves travel perpendicular to the epicenter of the earthquake. Generally, these earthquakes are detected by a device known as seismograph, it simply records the data of the earthquake like duration, magnitude, etc. [2], this data is further converted, simplified, etc., or simply it is called as processing of seismic signal which is briefly explained below.

1.1 ESPRIT Algorithm

ESPRIT stands for estimation of signal parameters via rotational invariance techniques which is developed on the similar values just like the other subspace procedures but additionally exploits a deterministic connection among subspaces [3]. It is a frequency estimation technique. This method differs from the other subspace methods in that the signal subspace is estimated from the data matrix A rather than the estimated correlation matrix. The essence of ESPRIT lies in the rotational property between staggered subspaces that is invoked to produce the frequency estimates. In the case of a discrete-time signal or time series, this property relies on observations of the signal over two identical intervals staggered in time [4]. This condition arises naturally for discrete-time signals, provided that the sampling is performed uniformly in time. Extensions of the ESPRIT method to a spatial array of sensors, the application for which it was originally proposed, the original, least squares version of the algorithm are described in first place and then the derivation to total least squares ESPRIT was extended [5], which is the preferred method for use, as the derivation of the algorithm requires an extensive amount of formulation and matrix manipulations.

2 Mathematical Modeling

Let us take a complex exponential $S_{0} = e^{j2\pi fn}$ which has a complex amplitude α and a frequency f. The property of the signal which we have taken is shown below [6].

$$S_{0} \left( {n + 1} \right) =\upalpha\,e^{{j2\pi f\left( {n + 1} \right)}} = S_{0} \left( n \right)e^{j2\pi f}$$

(1)

Hence, the phase-shifted version of the present value is the succeeding sample value. The rotation on the unit circle $e^{j2\pi f}$ is a representation of this phase shift.

$$x\left( n \right) = \sum\limits_{p = 1}^{P} {}\upalpha_{p} V\left( {f_{p} } \right)e^{{j2\pi nf_{p} }} + W\left( n \right) = V\emptyset^{n}\upalpha + {\text{W}}\left( {\text{n}} \right) = {\text{S}}\left( {\text{n}} \right) + {\text{W}}\left( {\text{n}} \right),$$

(2)

where the P columns of matrix U are length N interval frequency vectors of the complex exponentials.

$${\text{U}} = [{\text{U}}(f_{1} )\,{\text{U}}\left( {f_{2} } \right) \ldots {\text{U}}\left( {f_{p} } \right)].$$

(3)

The complex exponentials $\upalpha_{p}$ amplitudes are present in the vector α. The diagonal matrix of phase shifts among the adjacent time samples of the individual is the matrix $\emptyset$ complex exponential elements of S(n) [7].

$$\begin{aligned} & \emptyset = {\text{diag}}\{ \emptyset_{1} , \ldots ,\emptyset_{p} \} = \left[ {\begin{array}{*{20}c} {e^{{j2\pi nf_{1} }} } & 0 & \cdots & 0 \\ 0 & {e^{{j2\pi nf_{2} }} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & {e^{{j2\pi nf_{p} }} } \\ \end{array} } \right] \\ & {\text{For}}\,{\text{p}} = 1,2, \ldots ,{\text{P}}, \emptyset_{p} = e^{{j2\pi nf_{p} }} \\ \end{aligned}$$

(4)

This rotation matrix is entirely expressed by the complex exponential frequencies $f_{p}$. If $\emptyset$ can be acquired, then frequency estimates can be acquired. Take two overlaying sub-windows of length N − 1 with the length N time window vector and signal which has the sum of complex exponentials.

$${\text{S}}\left( {\text{n}} \right) = \left[ {\begin{array}{*{20}c} {S_{N - 1} \left( n \right)} \\ {S\left( {n + N - 1} \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {S\left( n \right)} \\ {S_{N - 1} \left( {n + 1} \right)} \\ \end{array} } \right],$$

(5)

where $S_{N - 1} \left( n \right)$ is the length (N − 1) sub-window of S(n), hence $S_{N - 1} \left( n \right) = U_{N - 1} \emptyset^{n}\upalpha$.

Matrix $U_{N - 1}$ is built in the equivalent way as U other than its time window frequency vectors are of length N − 1, represented as $U_{N - 1} \left( f \right)$ [8].

$$U_{N - 1} = \left[ {U_{N - 1} \left( {f_{1} } \right)\,U_{N - 1} \left( {f_{2} } \right) \ldots U_{N - 1} \left( {f_{p} } \right)} \right]$$

(6)

Remember that S(n) is a scalar signal which is shaped up of the sum of complex exponentials at time n.

$$U_{1} = U_{N - 1} \emptyset^{n} \,{\text{and}}\,U_{2} = U_{N - 1} \emptyset^{n + 1}$$

(7)

$U_{1}$ and $U_{2}$ relate to the unstaggered and staggered windows, which is

$${\text{U}}\emptyset = \left[ {\begin{array}{*{20}c} {U_{1} } \\ {*\, * \ldots *} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {*\, * \ldots *} \\ {U_{2} } \\ \end{array} } \right]$$

(8)

The two matrices with vectors having intervals are expressed as

$$U_{2} = U_{1} \emptyset$$

(9)

Observe that both matrices spaces a distinct, however related, (N − 1) dimensional subspace. Assume that we possess a data matrix A with M data records of the length N interval vector signal x(n). By singular value decomposition (SVD), data matrix is

$${\text{A}} = {\text{L}}{\sum }V^{H}$$

(10)

L is a M × M matrix of left singular vectors and v is a N × N matrix of right singular vectors. Each of these matrices is a unit matrix, hence $L^{H} L = I$ and $V^{H} V = I$. Dimensions of the matrix ∑ are M × N which contains singular quantities on the main diagonal which is ordered in a magnitude of decreasing value [9]. The singular valued magnitudes are squared and are equivalent to the eigenvalues of $\hat{R}$ scaled with a M factor and the V’s columns are their related eigenvectors. Hence, v shapes an orthogonal and normalized foundation for the underlying N-dimensional vector space. The signal and noise subspaces are formed by dividing this subspace as V = [V _s /V _n ].

Relating to the p largest magnitudes of the singular values, $V_{s}$ is a matrix of right-hand singular vectors [10]. All of these frequency vectors for ${\text{f}} = f_{1} ,f_{2} , \ldots ,f_{p}$ should lie in the signal subspace since the sum of complex exponentials formed as time window frequency vectors U(f) is contained in the signal portion. Hence, U and $V_{s}$ matrices occupy the identical subspace [11]. Hence, there lies an invertible transformation T that draws $V_{s}$ into U = V _s T.

In this derivation, T transformation is never elucidated, in the other way, it is only constructed just like a mapping inside the subspace of the signal among these two matrices. Divide the subspace of the signal into two tiny subspaces of dimensions (N − 1).

$$V_{s} = \left[ {\begin{array}{*{20}c} {V_{1} } \\ {*\, * \ldots *} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {*\, * \ldots *} \\ {V_{2} } \\ \end{array} } \right],$$

(11)

where $V_{1}$ and $V_{2}$ relate to the staggered and unstaggered subspaces because $U_{1}$ and $U_{2}$ related to the equivalent subspaces.

$$U_{1} = V_{1} T\quad U_{2} = V_{2} T$$

(12)

The rotation Ø subspaces are being corresponded by the matrix U’s staggered and unstaggered elements. A same, though unlike, rotation should be present that associates $V_{1}$ to $V_{2}$ because the matrices $V_{1}$ and $V_{2}$ also spaces these subspaces as $V_{2} = V_{1}\Psi$ [10]. Where $\Psi$ is the matrix of rotation. Remember that the estimation of frequency arrives below for summarizing the rotation matrix Ø subspace. Rotations among the subspaces of staggered signal and the relations altogether combined can be made use of the estimation of Ø [12]. From the data matrix A’s SVD, the matrices $V_{1}$ and $V_{2 }$ are known from the procedure. Primarily solve Ψ by utilizing the technique of least squares.

$$\Psi = \left( {V_{1}^{H} V_{1} } \right)^{ - 1} V_{1}^{H} V_{2}$$

(13)

Substituting $V_{2}^{ } = V_{1} \varPsi$, $U_{2} = V_{2} T = V_{1} \varPsi T$ is acquired. In the same way, solve $U_{2}$, utilizing the relation $U_{2} = U_{1} {\emptyset }$ and substituting $U_{1} = V_{1} T$ and $U_{2} = V_{2} T$ for $U_{1}$, $U_{2} = U_{1} {\emptyset } = V_{1} T{\emptyset }$. Hence, by equating both the right-hand sides of $U_{2} = V_{2} T = V_{1} \varPsi T$ and $U_{2} = U_{1} {\emptyset } = V_{1} T{\emptyset }$. The relation among the two subspaces rotations is

$$\Psi {\text{T}} = {\text{T}}\O \,{\text{or}}$$

Similarly,

$$\Psi = {\text{T}}\O {\text{T}}^{ - 1}$$

(14)

Equations ΨT = TØ and Ψ = TØT⁻¹ [13] must be realized as the association among the matrix Ψ’s eigenvectors and eigenvalues. Hence, elements of the diagonal of Ø, $\emptyset_{p}$ for p = 1, 2, 3, …, P are commonly the Ψ’s eigenvalues. Finally, the frequency estimates are

$$\widehat{{f_{p} }} = \frac{{\angle \emptyset_{p} }}{2\pi },$$

(15)

where the phase of $\emptyset_{p}$ is $\angle \emptyset_{p}$. Even though the utilization of rotational subspaces is the property of the ESPRIT algorithm is very easy. Pay heed that only matrix simple relationships are utilized by us. Primarily, provide an algorithm which has a version of total least squares, a best technique to utilize [10]. Pay heed that $V_{1}$ and $V_{2}$ subspaces are the original subspace’s only estimates that relate to $U_{1}$ and $U_{2}$, naturally acquired through the data matrix A. The subspace rotation’s estimate was acquired by solving $V_{2} = V_{1} \varPsi$ utilizing the least square criterion.

$$\varPsi_{ls} = (V_{1}^{H} V_{1} )^{ - 1} V_{1}^{H} V_{2}$$

(16)

This least square result is acquired by reducing the errors in least square perception from the formulation as given below [10].

$$V_{2} + E_{2} = V_{1} \varPsi$$

(17)

Since $E_{2}$ is a matrix which has errors among $V_{2}$ and the original subspace relating to $U_{2}$. The least square formulation presumes that errors exist especially on $V_{2}$ estimation and on the other side, it presumes that there exist no errors among $V_{1}$ and the original subspace that it is trying to estimate relating to $U_{1}$ [14]. Hence, $V_{1}$ is an estimated subspace too, an extremely accurate formulation is

$$V_{2} + E_{2} = \left( {V_{1} + E_{1} } \right)\varPsi$$

(18)

Errors among $V_{1}$ and the original subspace relating to $U_{1}$ are expressed by the matrix $E_{1}$. Minimizing the Frobenius norm of the two error matrices can acquire the result to this problem, which is known as total least squares (TLS).

$$\left\| {\begin{array}{*{20}c} {E_{1} } & {E_{2} } \\ \end{array} } \right\|{\text{F}}$$

(19)

As the properties of TLS are far away from the expectation, normally lend the process to acquire the TLS solution of Ψ. Primarily, prepare a matrix constructed by the staggered signal subspace matrices $V_{1}$ and $V_{2}$ located adjacent to each other and execute an SVD.

$$\left[ {\begin{array}{*{20}c} {V_{1} } & {V_{2} } \\ \end{array} } \right] = \tilde{L}\widetilde{{\sum }}\tilde{V}^{H}$$

(20)

Later we work on 2P × 2P matrix $\tilde{V}$ of right singular vectors which are divided as P × P quadrants.

$$\tilde{V} = \left[ {\begin{array}{*{20}c} {\tilde{V}_{11} } & {\tilde{V}_{12} } \\ {\tilde{V}_{21} } & {\tilde{V}_{22} } \\ \end{array} } \right]$$

(21)

The subspace rotation matrix Ψ Total least square solution is $\varPsi_{tls} = - \tilde{V}_{12} \tilde{V}_{22}^{ - 1}$. The estimation of frequencies is then acquired by Ψ = TØT⁻¹ and $\tilde{f}_{p} = \frac{{\angle {\emptyset }_{p} }}{2\pi }$ by utilizing $\varPsi_{tls}$ from $\varPsi_{tls} = - \tilde{V}_{12} \tilde{V}_{22}^{ - 1}$ [10].

3 Simulation and Results

• Step 1: The data utilized for the observation is acquired from Book_Seismic_Data.mat of East Texas [3] landmine is the file name. We have taken the source as a dynamite blast which took place at a depth of around 100 ft, one trace has 1501 samples of 0.002 s sampling interval.

• Step 2: The algorithm’s functioning is assessed with known synthetic signal and then ESPRIT algorithm is applied to calculate the seismic signal’s tonal. Synthetic signal’s frequencies are taken as 0.2π, 0.3π, 0.8π, and 1.2π and are shown as complex exponentials.

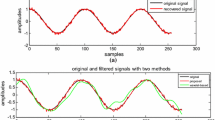
• Step 3: The normalized frequencies are 0.2π and 0.7π. The signal generated is shown in Fig. 1.

  Fig. 1

  

  Synthetic signal with and without noise

• Step 4: In Fig. 2, power spectral density of the synthetic signal is shown. The figure shows peaks are at 0.2 and 0.7 normalized frequencies. That means ESPRIT algorithm is working fine.

  Fig. 2

  

  PSD using ESPIRIT TLS Method for synthetic signal

• Step 5: The raw seismic signal is shown in Fig. 3, which is a single shot taken from [3].

  Fig. 3

  

  Raw seismic signal

• Step 6: The raw seismic signal is detrended which is shown in Fig. 4. Detrending is done in order to remove bias and baseline drift.

  Fig. 4

  

  Detrended raw seismic signal

• Step 7: ESPRIT algorithm is applied on detrended seismic signal and the power spectral density obtained is shown in Fig. 5. The max peak is at 0.958 normalized frequency.

  $$\begin{aligned} w & = \frac{2\pi f}{fs} = 0.0958\uppi \\ & = \frac{2\pi f}{500} \\ & = \frac{2\pi }{fs}f = 0.0958\uppi \\ f & = \frac{500}{2}\,*\,0.0958 \\ & = 250\,*\,0.0958 \\ & = 25\,*\,0.0958 \\ & = 23.950\,{\text{Hz}} \\ \end{aligned}$$

  Fig. 5

  

  FIR band-pass filtered frequency spectrum

• Step 8: In the reference book, it is written that the data is band-pass filtered in the range [15 Hz, 60 Hz]. For ensuring purpose, a BP filter with FIR order 8 is realized. The transfer function of the same is shown in Fig. 6.

  Fig. 6

  

  FFT of band-pass filtered seismic signal

• Step 9: The detrended seismic signal is convolved with FIR BPF and the output is shown in Fig. 6.

• Step 10: The same PSD, as shown in Fig. 7 is obtained. So, the seismic signal tonal is 23.95 Hz.

  Fig. 7

  

  ESPRIT spectrum of BPF detrended seismic signal

  $$\begin{aligned} {\text{Another}}\;{\text{insignificant}}\;{\text{tonal}}\;{\text{is}}\;w_{1} & = \frac{{2\Pi f}}{{f_{s} }} = 0.119\uppi \\ \frac{2\varPi f}{500} & = \, 0.119 \\ f & = \frac{{0.119\uppi\,*\,500}}{{2\uppi}} \\ \therefore \;f & = 250\,*\,0.119 \\ & = 29.75\,{\text{Hz}} \\ \end{aligned}$$

4 Conclusion

In this paper, signal parameter estimation with high resolution is obtained using ESPRIT algorithm. The step-by-step process of the seismic signal analysis has been perfectly presented in the results section, the actual signal strengths in the seismic signal from time series data taken are clearly estimated with peaks of high resolution, and power spectral density for both synthetic and raw seismic signal is obtained. From the results obtained, it is concluded that the ESPRIT algorithm is the best technique for frequency estimation in seismic signal processing which requires less computation.