Processing of Seismic Signal Using Minimum Variance Algorithm

Abstract

Raw seismic signals contain noise which corrupts the real seismic data. To overcome this type of interference in the seismic data, preprocessing is done using the FIR bandpass filter. A new method is proposed in this paper for nonparametric estimation of seismic signals. Minimum variance spectral estimation is an eminent spectrum analysis process that offers a high-frequency resolution in comparison with remaining nonparametric methods. Here, an assured band of frequencies is allowed for processing from supplied data to nullify the unwanted signals. Minimum variance algorithm is used to find out the spectrum of the seismic signal and to improve the resolution of the signals.

1 Introduction

The process of sharing any data of intent among individuals is termed as communication. The transfer of such signals from one place to another may vary in distance through a diverse means of media. The signals that can be construed mathematically are called deterministic signals [1]. Noise, being one such random signal, is ubiquitous and has many forms. Spectral estimation is the process in which frequency of a signal is defined cardinally. On filtering a process with a group of cramped bandpass filters, the power spectrum is resolved.

Spectral estimation essentially converges on assessing noise with great resolution [2]. To accomplish this obligation, there is a necessity of enhancing the signal detection and attaining a consistent measure of the signal with resolution [3]. Seismic waves are used to determine topology of the subsurface layers for better identification of their boundaries [4]. Due to the asymmetry in the layers of the earth, seismic waves are reflected in distinct directions initiating multipath propagation. Earthquake’s origin is determined by the seismic data of that earthquake recorded from at least three diverse receiver positions [5, 6].

1.1 Seismic Signal Processing

Enhancement in the raw seismic source by nullifying the noise improves the authenticity of the seismic signals replicating the seismic event parameters [7]. At the end of any seismic propagation, the seismic waves have minute energy that can be lost at the reception end due to the noise intervention. Considering the random noise as additive white Gaussian noise, it can be attenuated easily through seismic data processing methods. Here, stacking overcomes most of the random noise, thereby improving the SNR by a factor of $\surd {\text{Q}}$, where Q is equivalent to the number of stacked traces.

Coherent noise is mainly caused by ground roll, consistently scattered waves, etc. The seismic data recorded contains ground roll noise. As a part of surface waves, they have high amplitudes. Implementing the bandpass filters in this perspective improves the SNR by reducing this noise [5]. In succeeding section, nonparametric minimum variance spectral estimation process is interpreted.

1.2 Minimum Variance

The minimum variance spectral estimation is the modification of maximum likelihood technique proposed by Capon to interpret two-dimensional power spectral density [8]. Capon’s estimator can be interpreted as a set of filters which are optimized to reduce their response of frequency outside the circle of interest and the width of each filter depends on the information [2, 9]. Thus, the pattern of the filter depends on opted frequency range and information adaptiveness [10].

Here, assumptions are not made unlike the parametric spectral estimation methods [11]. During the propagation of the signal, additive noise dominates the information at low-energy components ensuing into mislaid features. The key concept of minimum variance is to restrict entire output filter’s energy [12]. By calculating the filter bank from its own signal, capon’s method determines the signal power.

Periodogram has high sidelobes rising ambiguity in the amplitude response of the obtained signal [13]. Minimum variance method is used to reduce the sidelobes in turn enlightening resolution and diminishing variance over periodogram. During the signal propagation, there is a chance of system degradation due to several factors intruding the user signal [10].

The minimum variance spectrum estimation technique includes these subsequent steps as follows:

• 1. Create a set of bandpass filters $g_{i} \left( n \right)$, in order to discard the maximal extent of power outside the confined band and thereby achieve distortion less propagation at a given frequency $\omega_{i}$.

• 2. Measure power for every output process $y_{i} \left( n \right)$ by filtering $x\left( n \right)$ with all filters available in the given set.

• 3. Initiate $\widehat{p}_{x} \left( {e^{{j\omega_{i} }} } \right)$ equivalent to the power estimated in the second step divided by filter bandwidth.

The minimum variance spectrum approximation for the given signal is $\widehat{p}_{\text{MV}} = \frac{p + 1}{{e^{H} R_{x}^{ - 1} e}}$, where $R_{x}$ is the $p\, \times \,p$ autocorrelation matrix.

Depending on the filter length (p), the resolution and variance of the minimum variance method vary accordingly. For better resolution, bandwidth of the filter should be small that can be attained only when p is large [3]. In the second section, mathematical modeling of minimum variance algorithm is described. Later in the third section, simulation and results of minimum variance method are explained. In the final section, the paper is concluded by summarizing the minimum variance technique.

2 Mathematical Modeling

Let $x\left( n \right)$ be a wide-sense zero-mean immobile arbitrary mode with $P_{x} \left( {e^{j\omega } } \right)$ as power spectrum and let $g_{i} \left( n \right)$ be a perfect bandpass filter by center frequency $\omega_{i}$ and bandwidth $\Delta$,

$$ \left| {G_{i} \left( {e^{{j\omega }} } \right)} \right| = \left\{ {\begin{array}{*{20}l} {1\quad ;} \hfill & {\left| {\omega - \omega _{i} } \right| < \Delta /2} \hfill \\ {0\quad ;} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(1)

In the output $y_{i} \left( n \right)$ by filtering $x\left( n \right)$ with $g_{i} \left( n \right)$, the power spectrum is determined to be

$$ P_{i} \left( {e^{j\omega } } \right) = P_{x} \left( {e^{j\omega } } \right) \left| {G_{i} \left( {e^{j\omega } } \right)} \right|^{2} $$

(2)

and the power is specified as

$$ \begin{aligned} E\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\} & = \frac{1}{2\pi }\int\limits_{ - \pi }^{\pi } {P_{i} (e^{j\omega } )d\omega } = \frac{1}{2\pi }\int\limits_{ - \pi }^{\pi } {P_{x} \left( {e^{j\omega } } \right)\left| {G_{i} \left( {e^{j\omega } } \right)} \right|^{2} d\omega } \\ & = \frac{1}{2\pi }\mathop \smallint \limits_{{\omega_{i - \Delta /2} }}^{{\omega_{{i +\Delta /2}} }} P_{x} (e^{j\omega } )d\omega \\ \end{aligned} $$

(3)

If $\Delta$ is small enough so that $P_{x} \left( {e^{j\omega } } \right)$ is almost steady throughout the filter’s passband, then power in output process is approximately

$$ E\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\}\, \approx \,P_{x} \left( {e^{{j\omega_{i} }} } \right)\frac{\Delta }{2\pi } $$

(4)

Therefore, it is possible to estimate the power spectral density at the given condition $\omega = \omega_{i}$ from the noise removal scheme by assessing the power in (n) and distributing the spectrum through the controlled frequency limit ranging about $\Delta /2\pi$,

$$ \widehat{p}_{x} \left( {e^{{j\omega_{i} }} } \right) = \frac{{{\text{E}}\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\}}}{\Delta /2\pi } $$

(5)

The periodogram produces an estimate of the power spectrum in a similar fashion. Specifically, $x\left( n \right)$ is made noise resistant through a set of bandpass filters, $h_{i} \left( n \right)$, where

$$ \left| {H_{i} \left( {e^{j\omega } } \right)} \right| = \frac{{{ \sin }\left[ {N\left( {\omega - \omega_{i} } \right)/2} \right]}}{{{\text{N sin}}\left[ {\left( {\omega - \omega_{i} } \right)/2} \right]}} $$

(6)

and the power in every filtered signal is calculated through a single-point model average,

$$ \widehat{E}\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\} = \left| {y_{i} \left( {N - 1} \right)} \right|^{2} $$

(7)

On separating the power approximation with the means of the controlled frequency limit range $\Delta = 2\pi /N$, the periodogram is designed.

In this technique, all the noise-reducing filters available remain identical, altering in terms of the middle frequency. So, they are known for noncontingent nature to the given information. All the random signals have a nonuniform representation all over the path of propagation. So, they are present in the sidelobes of the bandpass filter as well. As the sidelobes are not a desired feature for an efficient technique, their presence is not entertained to overcome the power seepage glitches that occur falsehood in the power approximations. Adaptiveness to the filter removes the sidelobe signals by using the circle of interest for accepting the spectrum of the confined band. This feature makes the complete finest design of the spectral estimation technique.

To estimate the power spectral density of input signal at frequency, $\omega_{i}$, let $g_{i} \left( n \right)$ be a compound p order FIR bandpass filter. To safeguard the changes in the input power at the given frequency $\omega_{i}$, $G_{i} \left( {e^{j\omega } } \right)$ is forced to attain a unity gain at the condition $\omega = \omega_{i}$,

$$ G_{i} (e^{{j\omega_{i} }} ) = \sum\limits_{n = 0}^{p} {g_{i} \left( n \right)e^{{ - jn\omega_{i} }} = 1} $$

(8)

Let $g_{i}$ be the vector of filter coefficients $g_{i} \left( n \right)$,

$$ g_{i} = \left[ {g_{i} \left( 0 \right), g_{i} \left( 1 \right), \ldots , g_{i} \left( p \right)} \right]^{T} $$

(9)

and let $e_{i}$ be the vector of complex exponentials $e^{{jk\omega_{i} }}$,

$$ e_{i} = \left[ {1, e^{{j\omega_{i} }} , \ldots , e^{{jp\omega_{i} }} } \right]^{T} $$

(10)

The constraint on the frequency response given in Eq. (8) may be written in vector form as follows:

$$ g_{i}^{H} e_{i} = e_{i}^{H} g_{i} = 1 $$

(11)

Now, for the power spectrum of $x\left( n \right)$ at frequency $\omega_{i}$ to be measured as accurate as possible, the set of filters must deny the power outside the circle of interest. Therefore, criterion is used for designing the bandpass filter for minimizing the power with respect to the linear constraints of the output process as given in Eq. (11). The power in $y_{i} \left( n \right)$ may be indicated through the autocorrelation matrix $R_{x}$ by

$$ E\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\} = g_{i}^{H} R_{x} g_{i} $$

(12)

The approach for designing the apt filter has got some challenging limitations. To overcome these problems, minimizing Eq. (12) satisfies the condition with respect to the linear constraints given in Eq. (11). The key for this complication is

$$ g_{i} = \frac{{R_{x}^{ - 1} e_{i} }}{{e_{i}^{H} R_{x}^{ - 1} e_{i} }}, $$

(13)

where the smallest amount of $E\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\}$ is equivalent to

$$ \begin{array}{*{20}c} {min} \\ {g_{i} } \\ \end{array} E\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\} = \frac{1}{{e_{i}^{H} R_{x}^{ - 1} e_{i} }} $$

(14)

Thus, Eq. (13) defines the best filter to approximate the input power at frequency $\omega_{i}$, and Eq. (14) gives power in $y_{i} \left( n \right)$, which is used as the estimate, $\widehat{\sigma }_{x}^{2} \left( {\omega_{i} } \right)$, of the input power at frequency $\omega_{i}$. However, the above equations are derived at a fixed frequency $\omega_{i}$, although these equations were derived for a specific frequency $\omega_{i}$; since this frequency was arbitrary, then these equations are valid for all ω [14]. Thus, the desired filter to approximate the input power at frequency ω is

$$ g = \frac{{R_{x}^{ - 1} e}}{{e^{H} R_{x}^{ - 1} e}} $$

(15)

whereas power estimate is given by

$$ \widehat{\sigma }_{x}^{2} \left( \omega \right) = \frac{1}{{e^{H} R_{x}^{ - 1} e}}\,;\,e = \left[ {1,e^{j\omega } , \ldots ,e^{jp\omega } } \right]^{T} $$

(16)

Having designed the bandpass filter bank and estimated the distribution of power in $x\left( n \right)$ as a function of frequency, we may now approximate the power spectrum by separating the power approximate by the confined frequency set. Even if distinct conditions are present to describe a range of frequencies, using the appropriate value for $\Delta$ generates exact white noise power spectral density [14]. Since the minimum variance approximation of power in white noise is $E\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\} = \sigma_{x}^{2} /\left( {p + 1} \right)$, it follows from Eq. (5) that the spectrum estimate is

$$ \widehat{P}_{x} \left( {e^{{j\omega_{i} }} } \right) = \frac{{{\text{E}}\left\{ {\left| {y_{i} \left( n \right)} \right|^{2} } \right\}}}{{\Delta /2\pi }} = \frac{{\sigma_{x}^{2} }}{p + 1}\frac{2\pi }{\Delta } $$

(17)

Therefore, if the bandwidth is given as

$$ \Delta = \frac{2\pi }{p + 1} $$

(18)

the resultant $\widehat{P}_{x} \left( {e^{j\omega } } \right) = \sigma_{x}^{2}$. Using Eq. (18) as the bandwidth of the filter g(n), the power spectrum estimate becomes, in general,

$$ \widehat{P}_{MV} \left( {e^{j\omega } } \right) = \frac{p + 1}{{e^{H} R_{x}^{ - 1} e}} $$

(19)

which is the minimum variance spectrum estimate. Note that $\widehat{P}_{MV} \left( {e^{j\omega } } \right)$ is determined through the autocorrelation matrix $R_{x}$ of the input signal [3].

3 Simulation and Results

Step 1: The seismic signals used in this paper are attained from MATLAB file present in [5], Book_Seismic_Data.mat through a geophone array in Southern United States. This reference data is recorded from the man-made seismic waves to idealistically represent the real-time earthquake scenario. Here, source is observed to be a high-explosive material filled in about 100 feet below the earth surface by making holes. There are 33 traces, each divided individually into 1500 samples with sampling interval of 0.002 s. To analyze this spectrum, one of the traces is considered among the supplied traces.

Step 2: The accuracy of the code written is assessed on comparing with the known synthetic signal. Minimum variance algorithm is then determined to estimate the harmonics of the earthquake recorded seismic data.

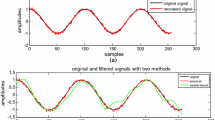
Step 3: Consider the input signal to be a tonal sinusoidal signal $0.98 x e^{ \pm j0.3\pi }$. The produced signal is represented in Fig. 1 with a normalized frequency of 0.4π. The considered signal is corrupted with white noise of variance 1.

Fig. 1

Synthetic signal

Step 4: Power Spectral Density (PSD) of the synthetic signal is shown in Fig. 2. The peak occurs at 0.4 normalized frequency as in Fig. 2. This makes it vivid that the code taken is accurate and functioning well.

Fig. 2

Minimum variance spectrum of synthetic signal

Step 5: In Fig. 3, trace 5 of the seismic signal data is shown.

Fig. 3

Raw seismic signal

Step 6: The bias observed in the given input signal is withdrawn by subtracting the mean of the raw seismic signal to determine the detrended seismic signal as shown in Fig. 4.

Fig. 4

Detrended seismic signal

Step 7: The prescribed minimum variance algorithm is applied on the detrended seismic signal and the PSD achieved out of it is represented in Fig. 5. From this figure, the maximum peak is determined to be at 0.09375π normalized frequency. The sampling frequency is calculated by using the sampling interval 0.002 s as

$$ \begin{aligned} fs = 1/0.002 & = 500 \, \text{Hz} \\ w = \frac{2\pi f}{fs} & = 0.09375\pi \\ & = \frac{2\pi f}{500} \\ & = \frac{2\pi }{fs}f = 0.09375\pi , \\ \end{aligned} $$

where f is the frequency of the signal. It is given by,

$$ \begin{aligned} {\text{Tonal frequency}}\,f = & \frac{{500}}{2}\,*\,0.09375 \\ = & 250\,*\,0.09375 \\ = & 25\,*\,0.9375 = 23.4375\,{\text{Hz}} \\ \end{aligned} $$

Fig. 5

Minimum variance spectrum of detrended synthetic signal

Step 8: The considered seismic data has earthquake signal frequency ranging between 15 and 60 Hz. For realization of bandpass filter, Finite Impulse Response (FIR) order is taken as 8. Its frequency spectrum estimation is shown in Fig. 6.

Fig. 6

FIR bandpass-filtered spectrum

Step 9: The convoluted output of the detrended seismic signal with the FIR bandpass filter is shown in Fig. 7. This eliminates the unwanted signals existing outside the order of the bandpass filter. Fast Fourier transform of bandpass-filtered spectrum is represented in Fig. 8.

Fig. 7

FIR bandpass-filtered detrended synthetic signal

Fig. 8

FFT of bandpass-filtered seismic signal

Step 10: PSD of the bandpass-filtered signal is determined using minimum variance and it is shown in Fig. 9. The maximum peak is obtained at 0.09961π. By repeating the process like step 7, the frequency of the signal is 24.9025 Hz.

Fig. 9

Minimum variance spectrum of the BPF detrended seismic signal

4 Conclusion

Spectral estimation technique offers good resolution and minimum variance. It overcomes sidelobe leakage by making the filters’ data adaptive and avoid the signals out of band. These features make minimum variance method efficient over periodogram. By this technique, SNR is improved by reducing the noises like ground roll noise using FIR bandpass filters and in turn retaining the desired seismic data.