Spiking Neural P Systems with Minimal Parallelism

Abstract

This paper is an attempt to relax the condition of using the rules in a maximally parallel manner in the framework of spiking neural P systems with exhaustive use of rules. To this aim, we consider the minimal parallelism of using rules: if one rule associated with a neuron can be used, then the rule must be used at least once (but we do not care how many times). In this framework, we study the computational power of our systems as number generating devices. Weak as it might look, this minimal parallelism still leads to universality, even when we eliminate the delay between firing and spiking and the forgetting rules at the same time.

1 Introduction

Through millions of years human brain has evolved into a complex and enormous information processing system, where more than a trillion neurons work in a cooperation manner to perform various tasks. Therefore, brain is a rich source of inspiration for informatics. Specifically, it has provided plenty of ideas to construct high performance computing models, as well as to design efficient algorithm. Inspired from the biological phenomenon that neurons cooperate in the brain by exchanging spikes via synapses, various neural-like computing models have been proposed, such as artificial neural networks [1] and spiking neural networks [2]. These neural-like computing models have performed significantly well in solving real life problems.

In the framework of membrane computing, a kind of distributed and parallel neural-like computing model were proposed in 2006 [3], which is called spiking neural P systems (SN P systems for short). Briefly, an SN P system consists of a set of neurons placed in the nodes of a directed graph that are linked by synapses. These neurons send signals (spikes) along synapses (edges of the graph). This is done by means of firing rules, which are of the form $E/a^c \rightarrow a^p;t$: if the number of spikes contained in the neuron is described by the regular expression E (over the alphabet $\{a\}$), then c spikes are consumed and p spikes are produced after a delay of t steps; the produced spikes are sent to all neurons to which there exist synapse leaving the neuron where the rule is applied. The second type of rules are forgetting rules, of the form $a^s \rightarrow \lambda$. The meaning is that $s\ge 1$ spikes are just removed from the neuron, provided that the neuron contains exactly s spikes. The system evolves synchronously: a global clock is assumed and in each time unit each neuron which can use a rule should do it. But the work of the system is sequential locally: only (at most) one rule is used in each neuron. When the computation halts, no further rule can be applied, and a result is obtained, which can be defined in different ways, e.g., in the form of the time elapsed between the first two consecutive spikes sent into the environment.

For the past decade, there have been quite a few research efforts put forward to SN P systems. Many variants of SN P systems have been considered [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Most of the obtained classes of SN P systems are computationally universal, equivalent in power to Turing machines [19,20,21,22,23,24,25,26,27,28]. An interesting topic is to find small universal SN P systems [29,30,31,32,33,34,35]. In certain cases, polynomial solutions to computationally hard problems can also be obtained in this framework [36, 37]. Moreover, SN P systems have been applied to solve real-life problems, for example, to design logic gates, logic circuits [38] and databases [39], to perform basic arithmetic operations [40, 41], to represent knowledge [42], to diagnose fault [43,44,45], to approximately solve combinatorial optimization problems [46].

Besides using the rules of a neuron in the sequential mode introduced above, it is also possible to use the rules in a parallel way. An exhaustive manner of rule application is considered in [47]: whenever a rule is enabled in a neuron, it is used as many times as possible for the number of spikes from that neuron, thus exhausting the spikes it can consume in that neuron. Also in [47], SN P systems with exhaustive use of rules are proved to be universal, both in the accepting and the generative cases.

In this paper we propose a minimal parallelism [48] which, as far as we know, have not yet been considered in the framework of SN P systems: from each set of rules associated with a neuron, if a rule can be used, then the rule must be used at least once (maybe more times, without any restriction). Here we consider SN P systems with minimal parallelism function as generator of numbers, which is encoded in the distance between the first two steps when spikes leave the system. Weak as it might look, we prove the equivalence of our systems with Turing machines in the generative mode, even in the case of eliminating two of its key features – delays and forgetting rules – simultaneously. In the proof of this result, we play a trick (also useful in other similar cases, like [47]) of representing a natural number n (the content of a register) by means of $2n+2$ spikes (in a neuron).

This work is started by the mathematical definition of SN P systems with minimal parallelism, and then the computational power of SN P systems with minimal parallelism is investigated as number generator, in the case of eliminating delays and forgetting rules at the same time. It is proved in a constructive way that SN P systems with minimal parallelism can compute the family of sets of Turing computable natural numbers. At last, the paper is ended with some comments.

2 SN P Systems with Minimal Parallelism

Before introducing SN P systems with minimal parallelism, we recall some prerequisites, including basic elements of formal language theory [49] and basic notions in SN P systems [3, 50].

For a singleton alphabet $\varSigma =\{a\}$, $\varSigma ^*=\{a\}^*$ denotes the set of all finite strings of symbol a; the empty string is denoted by $\lambda$, and the set of all nonempty strings over $\varSigma =\{a\}$ is denoted by $\varSigma ^+$. We can simply write $a^*$ and $a^+$ instead of $\{a\}^*$, $\{a\}^+$. A regular expression over a singleton alphabet $\varSigma$ is defined as follows: (i) $\lambda$ and a is a regular expression, (ii) if $E_1$,$E_2$ are regular expressions over $\varSigma$, then $(E_1)(E_2)$, $(E_1)\cup (E_2)$, and $(E_1)^+$ are regular expressions over $\varSigma$, and (iii) nothing else is a regular expression over $\varSigma$. Each regular expression E is associated with a language L(E), which is defined in the following way: (i) $L(\lambda )=\{\lambda \}$ and $L(a)=\{a\}$, (ii) $L((E_1)\,\cup \,(E_2))=L(E_1)\,\cup \,L(E_2)$, $L((E_1)(E_2))=L(E_1)L(E_2)$, and $L((E_1)^+)=L(E_{1})^+$, for all regular expressions $E_1, E_2$ over $\varSigma$.

In what follows, we give the formal definition of SN P systems with minimal parallelism.

An SN P system with minimal parallelism of degree $m\ge 1$ is a construct of the form

$$\varPi =(O,\sigma _1, \sigma _2, \ldots , \sigma _m, syn, out),$$

where:

• 1. $O=\{a\}$ is a singleton alphabet (a is called spike);

• 2. $\sigma _1, \sigma _2, \ldots , \sigma _m$ are neurons of the form

  $$\sigma _i=(n_i, R_i), 1\le i\le m,$$

  where:

  • (1) $n_i\ge 0$ is the initial number of spikes placed in the neuron $\sigma _i$;

  • (2) $R_i$ is a finite set of rules of the following two forms:

    • Firing rule: $E/a^c \rightarrow a^p;d$, where E is a a regular expression over $\{a\}$, $c\ge 1$, $d\ge 0$, with the restriction $c\ge p$. Specifically, when $d=0$, it can be omitted;

    • Forgetting rule: $a^s \rightarrow \lambda$, for some $s\ge 1$, with the restriction that for each rule $E/a^c \rightarrow a^p;d$ of type (1) from $R_i$, we have $a^s \notin L(E)$;

• 3. $syn\subseteq \{1,2,\ldots ,m\}\times \{1,2,\ldots ,m\}$ is the set of synapses between neurons, with restriction $(i,i)\notin syn$ for $1\le i\le m$ (no self-loop synapse);

• 4. $out\in \{1,2,\ldots ,m\}$ indicates the output neuron, which can emit spikes to the environment.

The firing rule of the form $E/a^c \rightarrow a^p;d$ with $c\ge p\ge 1$ is called an extended rule; if $p=1$, the rule is called a standard rule. If $L(E)=\{a^c\}$, the rule can be simply written as $a^c \rightarrow a^p;d$. Specifically, if $d=0$, it can be omitted and the rule can be simply written as $a^c \rightarrow a^p$.

The firing rule $E/a^c \rightarrow a^p;d\in R_i$ can be applied if the neuron $\sigma _i$ contains k spikes, $a^k\in L(E)$ and $k\ge c$. However, the essential we consider here is not the form of the rules, but the way they are used. Using the rule in a minimal parallel manner, as suggested in the Introduction, means the following. Assume that $k=sc+r$, for some $s\ge 1$ (this means that we must have $k\ge c$) and $0\le r<c$ (the remainder of dividing k by c). Then nc, $1\le n \le s$ spikes are consumed, $k-nc$ spikes remain in the neuron $\sigma _i$, and np spikes are produced after d time units (a global clock is assumed, marking the time for the whole system, hence the functioning of the system is synchronized). If $d=0$, then the produced spikes are emitted immediately, if $d=1$, then the spikes are emitted in the next step, and so on. In the case $d\ge 1$, if the rule is applied at step t, then in steps $t,t+1,\ldots ,t+d-1$ the neuron is closed, and it cannot receive new spikes (if a neuron has a synapse to a closed neuron and sends a spike along it, then the spike is lost). In step $t+d$, the neuron fires and becomes open again, hence it can receive spikes (which can be used in step $t+d+1$). The spikes emitted by a neuron are replicated and are sent to all neurons $\sigma _j$ such that $(i,j)\in syn$.

The forgetting rules are applied as follows: if the neuron contains exactly s spikes, then the rule $a^s \rightarrow \lambda$ can be used, and this means that all s spikes are removed from the neuron.

In each time unit, in each neuron which can use a rule we have to use a rule, either a firing or a forgetting one. Since two firing rules $E_1/a^{c_1} \rightarrow a^p;d_1$ and $E_2/a^{c_2} \rightarrow a^p;d_2$ can have $L(E_1)\cap L(E_2)\ne \emptyset$, it is possible that several rules can be applied in a neuron. This leads to a non-deterministic way of using the rules (but a firing rule cannot be interchanged with a forgetting rule, in the sense that $a^s\notin L(E)$).

The configuration of the system is described both by the numbers of spikes present in each neuron and by the number of steps to wait until it becomes open (if the neuron is already open this number is zero). Thus, the initial configuration is $\langle n_1/0, n_2/0, \dots , n_m/0\rangle$. Using the rules as described above, we can define transitions among configurations. Any sequence of transitions starting from the initial configuration is called a computation. The computation proceeds and a spike train, a sequence of digits 0 and 1, is associated with each computation by marking with 0 for the steps when no spike is emitted by the output neuron and marking with 1 when one or more spikes exit the system. A computation halts if it reaches a configuration where no rule in the neuron can be used.

The result of a computation can be defined in several ways. In this work, we consider SN P systems with minimal parallelism as number generators: assuming the first time and the second time spike(s) emitted from the output neuron is at step $t_1$ and $t_2$, the computation result is defined as the number $t_2-t_1$. For an SN P system $\varPi$, the set of all numbers computed in this way is denoted by $N_2^{min}(\varPi )$, with the subscript 2 reminding that only the distance between the first two spikes of any computation is considered. Then, we denote by $Spik_2N^{min}P_m(rule_k, cons_r, forg_q)$ the family of all sets $N_2^{min}(\varPi )$ computed as above by SN P systems with at most $m\ge 1$ neurons, using at most $k\ge 1$ rules in each neuron, with all spiking rules $E/a^c \rightarrow a^p;d$ having $c\le r$, and all forgetting rules $a^s \rightarrow \lambda$ having $s\le q$. When one of the parameters m, k, r, q is not bounded, then it is replaced with $*$.

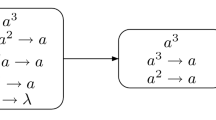
In order to clarify the definitions, we here discuss an example. In this way, we also introduce a standard way to pictorially represent a configuration of an SN P system, in particular, the initial configuration. Specifically, each neuron is represented by a “membrane” (a circle or an oval), marked with a label and having inside both the current number of spikes (written explicitly, in the form $a^n$ for n spikes present in a neuron) and the evolution rules; the synapses linking the neurons are represented by arrows; besides the fact that the output neuron will be identified by its label, $i_0$, it is also suggestive to draw a short arrow which exits from it, pointing to the environment.

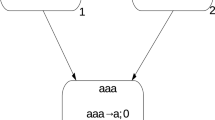
In the system $\varPi _1$ (Fig. 1) we have two neurons, labeled with 1 and 2 (with neuron $\sigma _2$ being the output one), which have 5 and 2 spikes, respectively, in the initial configuration. Both of the two neurons fire at the first step of the computation.

Fig. 1.

A simple example of an SN P system with minimal parallel

In the output neuron $\sigma _2$, the rule $a^2\rightarrow a;0$ is used at the first step, a spike is sent out to the environment and no spike remains in $\sigma _2$. In neuron $\sigma _1$, one can notice that $5=2\times 2+1$, hence we can non-deterministically choose the rule $a^5/a^2\rightarrow a$ to be applied once or twice at the same time. If $\sigma _1$ uses the rule twice at the first step, it sends two spikes to neuron $\sigma _2$ immediately (one for each use of the rule) and neuron $\sigma _2$ spikes again, using the rule $a^2\rightarrow a;0$ at the second step of the computation. Thus, the result of the computation in this case is $2-1=1$.

If the rule $a^5/a^2\rightarrow a$ is used only once at the first step by neuron $\sigma _1$, it sends one spike to neuron $\sigma _2$. At the second step, neuron $\sigma _2$ fires again, using the rule $a\rightarrow a;1$ at the second step. At the third step the spike generated emits the system and the result of the computation is $3-1=2$.

Hence, $\varPi _1$ generates the finite set $\{1, 2\}$.

3 Universality Result

In this section we prove that SN P systems with minimal parallelism are still universal when eliminating both delays and forgetting rules at the same time. Nevertheless, the elimination has a price in terms of the number of neurons in the modules. Our universality proof will use the characterization of NRE by means of register machine.

A register machine is a construct $M=(m, H, l_0, l_h, I)$, where m is the number of registers, H is the set of instruction labels, $l_0$ is the start label (labeling an ADD instruction), $l_h$ is the halt label (assigned to instruction HALT), and I is the set of instructions; each label from H labels only one instruction from I, thus precisely identifying it. The labeled instructions are of the following forms:

• $l_i: (ADD(r), l_j)$ (add 1 to register r and then go to the instruction with label $l_j$),

• $l_i: (SUB(r), l_j, l_k)$ (if register r is non-empty, then subtract 1 from it and go to the instruction with label $l_j$, otherwise go to the instruction with label $l_k$),

• $l_h: HALT$ (the halt instruction).

It is known that the register machine can compute all sets of numbers which are Turing computable, even with only three registers [51]. Hence, it characterizes NRE, i.e., $N(M)=NRE$ (NRE is the family of length sets of recursively enumerable languages – the family of languages recognized by Turing machines). We have the convention that when comparing the power of two number generating devices, number zero is ignored.

In the proof below, we use the characterization of NRE by means of register machine, with an additional care paid to the delay from firing to spiking, and forgetting rules. Because all rules we use have the delay 0, we write them in the simpler form $E/a^c\rightarrow a^p$, hence omitting the indication of the delay. Also a change is made in the notation below: we add $dley_t$ to the list of features mentioned between parentheses, meaning that we use SN P systems whose rules $E/a^c\rightarrow a^p;d$ have $d\le t$ (the delay is at most t).

Theorem 1

$$Spik_2N^{min}P_{*}(rule_3, cons_4, forg_0, dley_0)=NRE.$$

Proof

In view of the Turing-Church thesis, the inclusion in NRE can be proved directly, so we only have to prove the inclusion $NRE\subseteq Spik_2N^{min}P_{*}(rule_3, cons_4, forg_0, dley_0)$. The proof is achieved in a constructive way, that is, an SN P system with minimal parallelism is constructed to simulate the universal register machine.

Let $M=(m, H, l_0, l_h, I)$ be a universal register machine. Without lose of generality, we assume that the result of a computation is the number from register 1 and this register is never decremented during the computation.

We construct an SN P system $\varPi$ as follows, simulating the register machine M and spiking only twice, at an interval of time which corresponds to the number computed by the register machine.

For each register r of M we consider a neuron $\sigma _r$ in $\varPi$ whose contents correspond to the contents of the register. Specifically, if the register r holds the number $n\ge 0$, then the neuron $\sigma _r$ will contain $2n+2$ spikes; therefore, any register with the value 0 will contain two spikes.

Increasing by 1 the contents of a register r which holds the number n means increasing by 2 the number of spikes from the neuron $\sigma _r$; decreasing by 1 the contents of a non-empty register means to decrease by 2 the number of spikes; checking whether the register is empty amounts at checking whether $\sigma _r$ has two spikes inside.

With each label l of an instruction in M we also associate a neuron $\sigma _l$. Initially, all these neurons are empty, except for the neuron $\sigma _{l_0}$ associated with the start label of M, which contains 2 spikes. This means that this neuron is “activated”. During the computation, the neuron $\sigma _l$ which receives 2 spikes will become active. Thus, simulating an instruction $l_i: (op(r), l_j, l_k)$ of M means starting with neuron $\sigma _{l_i}$ activated, operating the register r as requested by op, then introducing 2 spikes in one of the neuron $\sigma _{l_j}$, $\sigma _{l_k}$, which becomes active in this way. When the neuron $\sigma _{l_h}$, associated with the halting label of M, is activated, the computation in M is completely simulated in $\varPi$, and we have to output the result in the form of a spike train with the distance between the first two spikes equals to the number stored in the first register of M. Additional neurons will be associated with the registers and the labels of M, in a way which will be described immediately.

In what follows, the work of system $\varPi$ is described (that is how system $\varPi$ simulates the ADD, SUB instructions of register machine M and outputs the computation result).

Simulating an ADD instruction $l_i:(ADD(r),l_j,l_k)$

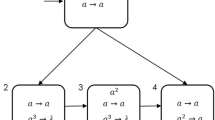
This instruction adds one to the register r and switches non-deterministically to label $l_j$ or $l_k$. As seen in Fig. 2, this module is initiated when two spikes enter neuron $\sigma _{l_i}$. Then the neuron $\sigma _{l_i}$ sends two spikes to neuron $\sigma _{i,1}$, $\sigma _{i,2}$ and $\sigma _r$, adding one to the content of the register. In the next step, the spikes emitted by $\sigma _{i,1}$ arrive in $\sigma _{i,3}$ (which will in turn be sent to $\sigma _{i,6}$ in the following step) and $\sigma _{i,4}$, while the spikes of $\sigma _{i,2}$ reaches $\sigma _{i,4}$ and $\sigma _{i,5}$. Neuron $\sigma _{i,4}$ will allow us to switch non-deterministically to either $\sigma _{l_j}$ or $\sigma _{l_k}$. If $\sigma _{i,4}$ uses the rule $a^4/a^2\rightarrow a$ only once, then two spikes will be blocked in $\sigma _{i,8}$ (those coming from $\sigma _{i,4}$ and $\sigma _{i,5}$), while just one will arrive in neuron $\sigma _{i,7}$, waiting for other spikes to come. In the next step, the neuron $\sigma _{i,4}$ fires again (this time applying the rule $a^2 \rightarrow a^2$), sending two spikes to $\sigma _{i,7}$ and $\sigma _{i,8}$. The two spikes are blocked in $\sigma _{i,8}$ again, while the two spikes from $\sigma _{i,4}$ and the spike from $\sigma _{i,6}$ reaches $\sigma _{i,7}$. Together with the one spike await, the neuron $\sigma _{i,7}$ can get fired, activating neuron $\sigma _{l_j}$ one step later.

Fig. 2.

Module ADD (simulating $l_i:(ADD(r),l_j,l_k)$)

On the other hand, if $\sigma _{i,4}$ uses the rule $a^4/a^2\rightarrow a$ twice, it consumes all of the four spikes inside, and produces two spikes, having no spike left. This means that, in the following step, $\sigma _{i,7}$ receives two spikes and $\sigma _{i,8}$ gets three (two from $\sigma _{i,4}$ and one from $\sigma _{i,5}$). Now $\sigma _{i,8}$ contains three spikes and fires, activating $\sigma _{l_k}$ in the following step. One step later, $\sigma _{i,7}$ receives another spike from $\sigma _{i,6}$ and the three spikes together get blocked here.

It is clear that, after each ADD instruction, neuron $\sigma _{i,7}$ and $\sigma _{i,8}$ will hold three or two spikes, respectively, depending on the times of application of rule $a^4/a^2\rightarrow a$ chosen non-deterministically in the neuron $\sigma _{i,4}$. Thanks to the regular expressions used in the rules of $\sigma _{i,7}$ and $\sigma _{i,8}$, this does not disturb further computations using this instruction.

Simulating a SUB instruction $l_i:(SUB(r),l_j,l_k)$

The SUB module (shown in Fig. 3) is initiated when two spikes are sent to neuron $\sigma _{l_i}$. This neuron fires and its spike reaches neurons $\sigma _{r,1}$, $\sigma _{r,2}$ and $\sigma _r$. The three rules of neuron $\sigma _r$ allow us to differentiate whether the register is empty or not. As we have explained, a register containing the value n means the corresponding neuron holds $2n+2$ spikes. If register r stores number $n>0$, that is to say $\sigma _r$ contains at least 4 spikes, the spike coming from $\sigma _{l_i}$ makes the neuron fire (by the rule $aaa(aa)^{+}/a^3\rightarrow a$) and send a spike to $\sigma _{r,6}$, which makes sure that the rule is used only once. In the next step, $\sigma _{r,6}$ gets fired and send a spike to $\sigma _{r,8}$, and another spike passing from $\sigma _{r,2}$ to $\sigma _{r,4}$ reaches $\sigma _{r,8}$ at the same time. These two spikes make $\sigma _{r,8}$ can not be fired. In parallel, two spikes will arrive in neuron $\sigma _{r,7}$, one along $\sigma _{r,1}$-$\sigma _{r,3}$-$\sigma _{r,5}$-$\sigma _{r,7}$, and the other $\sigma _r$-$\sigma _{r,6}$-$\sigma _{r,7}$. These two spikes make $\sigma _{r,7}$ get fire, then $\sigma _{r,9}$, and as we will explain later, eventually allow us to reach $\sigma _{l_j}$.

Fig. 3.

Module SUB (simulating $l_i:(SUB(r),l_j,l_k)$)

On the other hand, when register r stores number zero ($\sigma _r$ contains 2 spikes), the spike received from $\sigma _{l_i}$ fires the rule $a^3/a^2\rightarrow a$. The neuron $\sigma _r$ spikes, consuming two of the three spikes it contains. This spike is sent to neuron $\sigma _{r,6}$, then to neurons $\sigma _{r,7}$ and $\sigma _{r,8}$. In the following step, $\sigma _r$ fires again (using the rule $a\rightarrow a$), consuming its last spike and sending a new spike to $\sigma _{r,7}$ and $\sigma _{r,8}$ (the value of register r is now degraded and needs to be reconstituted). This spike reaches neuron $\sigma _{r,7}$ at the same time that the one coming from $\sigma _{r,5}$. Then $\sigma _{r,7}$ cannot get fired because it contains now three spikes. Meanwhile, $\sigma _{r,8}$ also contains now three spikes. It gets fired and spikes, allowing $\sigma _{r,10}$ to fire in the following step. It also emits two spikes to $\sigma _r$ which reconstitute the value 0 in the register r before reaching $\sigma _{l_k}$.

The reader can check that two AND modules (the AND module is shown in Fig. 4) are embedded in the SUB module, making sure that further instructions associated with register r will not wrongly switches to $l_i$ and $l_j$ here. In this module, only if $\sigma _{d_1}$ and $\sigma _{d_2}$ get fired simultaneously, neuron $\sigma _{d_6}$ receives three spikes and gets fired. Otherwise, it will receive two spikes and get blocked. Hence, $\sigma _{l_j}$ or $\sigma _{l_k}$ can get fired only if $\sigma _{l_i}$ is activated, and other instructions associated with register r will not activate them wrongly. Also the spikes remained in the neurons $\sigma _{r,7}$ and $\sigma _{r,8}$ do not disturb further computations.

Fig. 4.

Module AND

Because we do not know whether $l_j$ and $l_k$ are labels of ADD, SUB, or halting instructions, hence in both of the ADD and the SUB module the rules in the neurons $\sigma _{l_j}$, $\sigma _{l_k}$ are written in the form $a^2\rightarrow a^{\delta (l_s)}$, where the function $\delta : H\rightarrow \{1,2\}$ is defined as below:

$$\begin{aligned} \delta (l)= \left\{ \begin{array}{ll} 2, &{} \text {if}~{ l}~\text {is the label of an ADD instruction,}\\ 1, &{} \text {otherwise.} \\ \end{array} \right. \end{aligned}$$

Outputting a computation

As shown in Fig. 5, when the computation in M halts, two spikes reach the neuron $\sigma _{l_h}$ of $\varPi _1$. In that moment, register 1 of M stores value n and neuron $\sigma _1$ of $\varPi _1$ contains $2n+2$ spikes. The spike emitted by $l_h$ reaches neuron 1 (hence containing an odd number of spikes). Thanks to the neuron $\sigma _{h,2}$, it leads neuron $\sigma _1$ to fire continuously, consuming two spikes at each step. One step after receiving the spike from $\sigma _{l_h}$, neuron $\sigma _1$ fires and two spikes reach neuron $\sigma _{h,2}$. Next, neuron $\sigma _{h,4}$ simultaneously receives a spike from $\sigma _{h,3}$, gets fired and sends a spike to neuron $\sigma _{out}$, which spikes for the first time one step later. From then on, neuron $\sigma _{h,4}$ receives a couple of spikes from $\sigma _{h,2}$ that do not let it fire again, until two steps after neuron $\sigma _1$ fires for the last time (using the rule $a^3\rightarrow a$). When neuron $\sigma _1$ stops spiking, neuron $\sigma _{h,4}$ will receive one spike, making $\sigma _{out}$ fire again and emitting its second and last spike (exactly n steps after the first one).

Fig. 5.

Module FIN (ending the computation)

From the above description of the work of system $\varPi$, it is clear that the system $\varPi _1$ correctly simulates the register machine M and outputs exactly the value n computed by M, i.e., $N(M)=N_2^{min}(\varPi )$. This concludes the proof.    $\square$

4 Conclusions and Discussions

In this work, we investigated the computational power of SN P systems with minimal parallelism using as number generator. Specifically, an SN P system with minimal parallelism is constructed to compute any set of Turing computable natural numbers. Many issues remain to be investigated for this new class of SN P systems.

It remains to consider the SN P systems with minimal parallelism as language generator. Moreover, it is worth investigating the acceptive case for SN P systems with minimal parallelism.

In the proof of Theorem 1, there are 10 auxiliary neurons in each ADD module, and 27 in each SUB module. So compared to the results in [29,30,31,32,33,34,35], the SN P system with minimal parallelism seems to have no advantage in the aspect of small universal SN P system. It is highly possible that this disadvantage can be made up by constructing the modules differently. This task is left as an open problem to the readers.

Also in the proof of Theorem 1, the feature of delay and forgetting rule are not used. It is of interests to check if the number of neurons in universal SN P systems with minimal parallelism can be reduced with using delay or forgetting rule. Moreover, from a point of view of computation power, the boundary between the universality and non-universality of SN P systems with minimal parallelism is still open.