Keywords

1 Introduction

Rapidly exponential stability of nonlinear systems has the advantage of providing a guarantee on the accelerated time it takes for the nonlinear system to converge to a equilibrium. Actually, under some suitable conditions, the existence of a Lyapunov function with properties is equivalent to stability in the sense of Lyapunov, asymptotic stability, or exponential stability of state equilibrium point [1, 2]. Furthermore, once a Lyapunov function was constructed, a domain of attraction could be estimated. However, the estimate region is very conservative. Recently, Lyapunov methods have been studied a further surge of interest in the nonlinear systems field through powerful tools for obtaining them as sum of squares and here, we will mention the following works, for instance, [3,4,5,6]. In [7,8,9], Sontag and Artestein proposed control Lyapunov function for nonlinear control systems respectively. Without loss of generality, if there exists a control law such that the derivative of Lyapunov function is negative definite, then the state of nonlinear control systems converge to zero. However, when we use the control Lyapunov approach to analyze the stability of nonlinear systems, the controller must be constructed before. In order to satisfy the property of negative definite for control Lyapunov function, the inequalities should holds. Nevertheless, this will lead to a small attractive region. In order to enlarge the domain of attraction, this motivates our present study.

This work deals with design of rapidly exponential stabilizing control techniques for nonlinear mechanical systems with control input. In this paper, a new Lyapunov uniform framework for rapidly exponential stabilization of fully actuated mechanical systems is developed. The Lyapunov function is constructed as a quadratic function with an accelerated parameter. The motivation of this function is that when the value of Lyapunov function is zero vector, the generalized states converge to the desired states in accelerated time. According to the continuous feedback control law for generalized forces, the vectors converge to the zero vectors in accelerated time. Therefore, the states of nonlinear mechanical systems converge to the equilibrium in accelerated time duration.

This paper is organized as follows: Sect. 2 gives the main result on rapidly exponentially stabilization of nonlinear mechanical systems using a continuous Lyapunov function. Section 3 states two numerical simulation results for inverted pendulum on a cart and two link planar manipulator. The results illustrate the stability of this rapidly exponentially continuous feedback stabilization technique in comparison to finite time and asymptotically stabilizing continuous feedback techniques. Finally, Sect. 4 develops a summary of the main conclusions of this paper and future works.

2 Rapidly Exponentially Stabilization of Nonlinear Mechanical Systems

In this paper, we will consider the nonlinear mechanical systems as follows:

$$M\left( q \right)\ddot{q}\text{ + }C\left( {q,\dot{q}} \right)\dot{q} + G\left( q \right) = F\left( {q,\dot{q}} \right)$$

where \(M\left( q \right)\) is a positive definite inertia matrix, and \(C\left( {q,\dot{q}} \right)\) is the time derivative of the inertia matrix, and \(G\left( q \right)\) is a gravity matrix, and \(F\left( {q,\dot{q}} \right)\) is the non-conservative forces.

In this section, a new constructive approach to obtain rapidly exponentially stabilization techniques is developed for nonlinear mechanical systems. There are two steps for this method. First, a novel continuous function of the states is constructed that ensure that when the continuous function converges to zero, the state of nonlinear mechanical systems converges to zero as well. Second, a new continuous Lyapunov function is constructed to guarantee the rapidly exponentially stability of the nonlinear mechanical systems. The two subsections are described as following in details.

2.1 Rapidly Exponentially Stabilization of Nonlinear Mechanical Systems

In the first step of the rapidly exponentially stabilization process, a novel function is developed that ensures the generalized coordinate vectors of nonlinear mechanical systems converge to zero. Furthermore, assume that the desired equilibrium to be stabilized is the origin, namely, the generalized coordinate vector. Now, we will construct a function with some properties as follows.

Proposition 1

Let \(l(q,v):Q \times R^{n} { \to }R^{n}\) be a function that has the following properties:

\(l\left( {q,v} \right)\) is linear in \(v = \dot{q},l\left( {q,v} \right)\) is continuous in q,

\(l\left( {q,v} \right) = \left( {0,0} \right) \Rightarrow q\left( t \right) = 0,\) for \(t \to \infty\).

These properties guarantee that the state of nonlinear mechanical systems \((q,v) \in Q \times R^{n}\) converge to zero in accelerated time when \(l\left( {q,v} \right) = \left( {0,0} \right)\).

According to the nonlinear mechanical systems, we can construct a novel function as follows

$$l\left( {q,v} \right) = v + \frac{\kappa q}{\varepsilon },\kappa > 0,\varepsilon \in \left( {0,1} \right)$$
(1)

Due to the Eq. (1), we have an important Lemma 1 as follows.

Lemma 1

If \(l\left( {q,v} \right)\) is defined by (1) where \(v = \dot{q}\) , then \(l\left( {q,v} \right)\) satisfies the properties in Proposition 1.

Proof

In order to prove the Lemma 1, we will consider the following candidate Lyapunov function \(V\left( q \right) = \frac{1}{2}q^{T} q\).

In order to evaluate on the submanifold \(l\left( {q,v} \right) = \left( {0,0} \right)\), where \(l\left( {q,v} \right)\) is given by Eq. (1), we will adopt the time derivative of candidate Lyapunov function. Therefore, we have

$$\dot{V}\left( q \right) = q^{T} v = - \frac{\kappa }{\varepsilon }q^{T} q = - \frac{2\kappa }{\varepsilon }V \le - CV,$$
(2)

where constant \(C \in \left( {0,\infty } \right)\). From the inequality (2), we can see that \(\dot{V}\left( q \right) = \frac{1}{2}q^{T} q = \frac{1}{2}\left\| q \right\|^{2}\).

The second step of the constructive approach is shown in the following Sect. 2.2. According to a new Lyapunov function, we obtain a rapidly exponentially stabilization technique for nonlinear mechanical systems.

2.2 Rapidly Exponentially Stabilization of Nonlinear Mechanical Systems with Input Forces

In the second step of this rapidly exponentially stabilization approach is considered for nonlinear mechanical systems with input forces. Without loss of generality, a novel vector of generalized input forces is obtained for nonlinear mechanical systems. Furthermore, we will construct a new Lyapunov function with positive definite property. Moreover, the Lyapunov function satisfies the properties listed in Proposition 1. Now, the Lyapunov function is constructed as follows

$$\upsilon \left( {q,v} \right) = \frac{1}{2}l\left( {q,v} \right)^{T} l\left( {q,v} \right)$$
(3)

According to the above candidate Lyapunov function, we can use it to obtain the rapidly exponentially stabilization technique.

Theorem 1

Consider the nonlinear mechanical systems with the following continuous feedback control law given by

$$f\left( {q,v} \right) = - \frac{\gamma }{2}l\left( {q,v} \right) - \frac{\kappa }{\varepsilon }v$$

where \(\gamma > 0,\kappa > 0,\varepsilon \in \left( {0,1} \right)\) , Moreover, \(l\left( {q,v} \right)\) is defined by Eq. (1), then the nonlinear mechanical systems is rapidly exponential stable.

Proof

In order to prove the Theorem 1, we will consider the following candidate Lyapunov function \(\upsilon \left( {q,v} \right) = \frac{1}{2}l\left( {q,v} \right)^{T} l\left( {q,v} \right)\). Due to evaluate on the submanifold \(l\left( {q,v} \right) = \left( {0,0} \right)\), we will take the time derivative of candidate Lyapunov function (3). Thereby, we obtain

$$\dot{\upsilon }\left( {q,v} \right) = l\left( {q,v} \right)^{T} \dot{l}\left( {q,v} \right) = l\left( {q,v} \right)^{T} \left[ {f\left( {q,v} \right) + \frac{\kappa }{\varepsilon }v} \right] = - \gamma V$$

Hence, \(\dot{\upsilon }\left( {q,v} \right) = - \gamma V \le - CV,C \in \left( {0,\infty } \right)\).

3 Numerical Simulation Results

In this section, we will report some numerical results obtained from the inverted pendulum on a cart and two link planar manipulator model [10]. The results show that the continuous feedback controller of this paper is feasible and effective.

3.1 Inverted Pendulum on a Cart

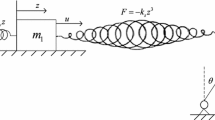
In this subsection, an inverted pendulum on a cart nonlinear mechanical system is considered. In general, this system has two degrees of freedom. The mathematical model is described as follows:

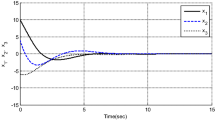
$$\begin{aligned} M\left( q \right) & = \left[ {\begin{array}{*{20}c} {m_{c} + m_{p} } & {m_{p} d\,\cos \theta } \\ {m_{p} d\,\cos \theta } & {I + m_{p} d^{2} } \\ \end{array} } \right]\,,\,C\left( {q,\dot{q}} \right) = \left[ {\begin{array}{*{20}c} 0 & { - m_{p} d\dot{\theta }\,\cos \theta } \\ 0 & 0 \\ \end{array} } \right] \\ G\left( q \right) & = \left[ {\begin{array}{*{20}c} 0 \\ { - m_{p} gd\,\sin \theta } \\ \end{array} } \right]\,,\,F_{c} = \left[ \begin{aligned} f_{c} \left( t \right) \hfill \\ \tau_{c} \left( t \right) \hfill \\ \end{aligned} \right]\,,\,F_{NC} \left( {q,v} \right) = \left[ \begin{aligned} 0 \hfill \\ 0 \hfill \\ \end{aligned} \right], \\ \end{aligned}$$
(4)

where \(m_{c}\) and \(m_{p}\) are the mass of the cart and the pendulum respectively. I represents the center of mass of pendulum inertia, and d is a distance between the center of mass and the pendulum pivot, and g is gravity acceleration. \(f_{c} \left( t \right)\) and \(\tau_{c} \left( t \right)\) are non-conservative forces. The parameters are the same with literature [10], in this paper, we will omit it. In Fig. 1, the horizontal displacement of the cart converges to zero in about 6 s using the finite time stable scheme, whereas it takes the asymptotic stable about 9 s to converge to zero.

Fig. 1
figure 1

Displacement of the cart

Full size image

From Fig. 1, we can see that the rapidly exponentially stable control law is better than the asymptotic stable control law and finite time control law at the beginning. That is to say, the rapidly exponentially stabilization is suit to real time control systems. From Fig. 2, it is easy can be seen that the time for the finite time stable controller shows that the rotational displacement of the pendulum converges to zero after about 6 s. Whereas the rapidly exponentially controller shows that the rotational displacement of the pendulum converges to zero after about 5 s and the asymptotic controller need about 9 s. Figure 3 shows that the velocity of the cart over the time. From the figure, we can see that the rapidly exponentially stable controller is better than the others. Figure 4 shows that the rate of change of the rotational displacement.

Fig. 2
figure 2

Rotational displacement of the pendulum

Full size image
Fig. 3
figure 3

Velocity of the cart

Full size image
Fig. 4
figure 4

Rate of change of the rotational displacement

Full size image

3.2 Two Link Planar Manipulator System

In this subsection, a two-link planar manipulator system of nonlinear mechanical system is considered. The mathematical model is described as follows:

\(M\left( q \right)\ddot{q} + C\left( {q,\dot{q}} \right)\dot{q} + G\left( q \right) = F\left( {q,\dot{q}} \right)\).

The nonlinear model is of the form given by the following equations

$$\begin{aligned} M\left( q \right) & = \left[ {\begin{array}{*{20}l} {\left( {m_{1} + m_{2} } \right)d_{1}^{2} + m_{2} d_{2}^{2} + 2m_{2} d_{1} d_{2} \,\cos \theta_{2} } & {m_{2} \left( {d_{2}^{2} + d_{1} d_{2} \,\cos \theta } \right)} \\ {m_{2} \left( {d_{2}^{2} + d_{1} d_{2} \,\cos \theta } \right)} & {m_{2} d_{2}^{2} } \\ \end{array} } \right], \\ C\left( {q,\dot{q}} \right) & = - m_{2} d_{1} d_{2} \dot{\theta }_{2} \,\sin \theta_{2} \left[ {\begin{array}{*{20}l} 2 & 1 \\ 1 & 0 \\ \end{array} } \right],\;\;F_{c} = \left[ \begin{aligned} \tau_{1} \left( t \right) \hfill \\ \tau_{2} \left( t \right) \hfill \\ \end{aligned} \right],\;\;F_{NC} = \left[ \begin{aligned} 0 \hfill \\ 0 \hfill \\ \end{aligned} \right], \\ G\left( q \right) & = g\left[ {\begin{array}{*{20}l} {\left( {m_{1} + m_{2} } \right)d_{1} \,\cos \theta_{1} + m_{2} d_{2} \,\cos \left( {\theta_{1} + \theta_{2} } \right)} \\ {m_{2} d_{2} \,\cos \left( {\theta_{1} + \theta_{2} } \right)} \\ \end{array} } \right]. \\ \end{aligned}$$

This nonlinear model assumes that the non-conservative forces acting on the system are the control input torques. Figure 5 shows that the link 1 rotation angle versus time. From the Fig. 5, we can see that the rapidly exponentially stable controller is better than the other controllers. It is shows that the continuous feedback controller of this paper is fit to the real time control systems. Figure 6 shows that the link 2 rotation angle versus time. From Fig. 6, we can see that the state of nonlinear mechanical systems converge to equilibrium about 9 s.

Fig. 5
figure 5

Link 1 rotation angle

Full size image
Fig. 6
figure 6

Link 2 rotation angle

Full size image

However, at the beginning, the rapidly exponentially controller is better than the others. Figure 7 represents angular velocity of link 1 and Fig. 8 shows that angular velocity of link 2. From Figs. 7 and 8, we can see that the states of mechanical systems converge to equilibrium at 8 s.

Fig. 7
figure 7

Angular velocity of link 1

Full size image
Fig. 8
figure 8

Angular velocity of link 2

Full size image

4 Conclusion and Future Work

In this paper, a novel approach of continuous feedback control law is developed for nonlinear mechanical systems. According to the vector value function, some properties are satisfied that ensure when this vector value function converges to zero, the state of nonlinear mechanical systems converges to the desired state in accelerated time. Therefore, due to the vector value function, a new Lyapunov function is constructed for nonlinear mechanical systems. Moreover, a continuous feedback control law is used to obtain rapidly exponential stability in accelerated time. Numerical results are illustrated on two classical nonlinear mechanical systems, for instance, an inverted pendulum on a cart and a planar two-link manipulator. Furthermore, comparisons with asymptotic stability and finite time stability for both examples show that the rapidly exponentially stabilization scheme has superior convergence rate while requiring lower control effort. Future work will generalize such rapidly exponentially stabilizing control schemes to multi-body systems.