An Introduction to All-Optical Quantum Controlled-NOT Gates

Abstract

Quantum computer promises to outperform classical computer fundamentally, due to its quantum superposition. Any operations to N qubits can be decomposed into several single-qubit operations and two-qubit controlled-NOT (CNOT) operations in theory. Linear optical quantum computing (LOQC) is one of the most prominent physical quantum systems, which has the advantage of long coherent time and convenience in implementing single qubit operations. However, the realization of two-qubit CNOT gate is the greatest challenge for LOQC, because two photons cannot directly interact with each other by nature. KLM protocol proves the feasibility of LOQC and spurs quantity of research on schematic design and experimental demonstration of CNOT gates by using linear quantum optics system. These researches are very important and nontrivial for LOQC, and this paper gives an overview of different schemes of the proposed CNOT gates and the experimental demonstration.

1 Introduction

Quantum computer promises to outperform classical computer fundamentally, due to its quantum superposition [26]. N qubits in a special superposition quantum state can represent $2^N$ numbers, while N classical bits only represent one of them. Thus, a quantum operation to these N qubits operates all $2^N$ numbers simultaneously. According to this quantum feature, a lot of quantum algorithms have been developed which achieves a speedup, in complexity theory, of classical best algorithms.

Any operations to N qubits can be decomposed into several single-qubit operations and two-qubit CNOT operations in theory. Therefore, how to implement them is crucial to realizing quantum computing for all kinds of physical systems, including photons [16], trapped ions [3], quantum dots [27, 28], superconductors [12] and so on. These systems have their own advantages and disadvantages. Take photon system for example, it has longer coherence time than most other systems. Besides, single-qubit optical gates are easy to implemented using linear optical elements including beam splitters, wave plates, phase shifters, mirrors, etc. [8, 10, 11, 18]. Thus, quantum computation using photons is called LOQC.

However, the realization of two-qubit CNOT gate is the most challenge in LOQC, because two photons cannot directly interact with each other by nature. It was believed that optical nonlinearities, stronger than those available in conventional non-linear media, are essential for LOQC. In 2001, Knill, Laflamme and Milburn proved that it is possible to realize quantum computing by using linear optics, single photons (ancilla), and single photon detectors (also called post-selection), which has been famous as the KLM protocol [8]. The protocol proves the feasibility of LOQC and spurs quantity of research on schematic design and experimental demonstration of CNOT gates by using linear quantum optics system [4, 7, 13, 20–24]. These researches are very important and nontrivial for LOQC.

2 LOQC

2.1 Qubits

A qubit is an elementary unit in quantum computer, which plays the similar role as classical bit. In LOQC, a qubit is usually a single photon with two modes on one certain degree of freedom such as spatial modes and polarization modes [10].

A photon encoded in spatial modes is called a spatial qubit or a dual-rail qubit. The spatial qubit has a choice of two different modes $|0 \rangle _L=|1,0\rangle$ and $|1 \rangle _L=|0,1\rangle$. If a single photon occupies path 0 and a vacuum state in path 1, it is the logical $|0 \rangle _L$. Vice versa, logical $|1 \rangle _L$. Different spatial modes mean different paths.

When the photons internal polarization degree of freedom is used to be the two modes, we call the photon a polarization qubit. In general, a photon horizontally (H-) polarized represents the logical 0, and a photon vertically (V-) polarized represents the logical 1. A polarization qubit and a spatial qubit can interconvert into each other. In quantum computing, a photon can live in the superposition state, so a qubit contains information of both logical 0 and logical 1. While in classical computing, one bit can only be either 0 or 1.

2.2 Optical Components

There are fundamental building blocks in LOQC, such as half-wave plates (HWPs), quarter-wave plates (QWPs), several different beam splitters and so on.

Wave Plates. HWPs and QWPs are common wave plates that can manipulate the polarization encoded photons, and they are made of birefringent crystals that induce a relative phase shift. Its needed that the incident light should be perpendicular to the plain of HWPs and QWPs. The effect of the two wave plates is characterized by the angle $\theta$ rotating from the optical axis to horizontal polarization, which decides how the polarization amplitudes are split. Usually, we mark the HWP with rotating angle $\theta$ as HWP($\theta$). An arbitrary unitary operation U on a single qubit can realized by three wave plates: QWP($\alpha$), HWP($\beta$) and QWP($\gamma$).

Beam Splitters. A Beam Splitter (BS) is a significant component to operate spatial qubits in LOQC [10]. It is a device that can redistribute the amplitudes of two spatial inputs, which is decided by the reflection probability R. In addition, transmission probability T can be deduced by R, since $R+T=1$. The most common one is 1/2BS, which represents $R=1/2$. A matrix describing its effect is $U_{BS}$ as follows:

where $a_i$ and $b_j$ can be comprehended as the amplitude of the input or output in port $a_i$ and $b_j$ respectively, as shown in Fig. 1.

Fig. 1.

Schematic diagrams of several BSs and orientations of the HV and FS bases.

A BS designed to configure parameters with respect to the polarization of the input qubits, called polarizing beam splitter (PBS). It means that PBS can deal with both spatial and polarized information of input photons. The most common PBS transmits H-polarized photons and reflects V-polarized photons totally. Through rotation, PBS can be in different bases, such as HV and FS bases shown in Fig. 1 [23]. In this paper, we mark them as PBS-HV (or PBS) and PBS-FS respectively shown in Fig. 1.

Another important subclass of PBS is the polarization dependent beam splitter (PDBS) [7]. A PDBS is characterized by two parameters, transmission probability for horizontal polarization, $t_H$, and for vertical polarization, $t_V$, in both output modes. A PDBS used latter with parameters of $t_H=1$ and $t_V=1/3$, transmits H-polarized photons totally and V-polarized photon with probability 1/3, while reflects V-polarized photons with probability 2/3.

2.3 Quantum Circuit Model

Analogous to an electrical circuit of a classical computer, a quantum circuit builds a quantum computer, containing wires and several elementary quantum gates [17]. Wires are used to transfer information and quantum gates manipulate it. Classical gates cannot be used to quantum computing, since they cannot deal with the quantum superposition.

Fig. 2.

The equivalence relation of CNOT and CZ gates shown by quantum circuits.

Quantum gates in circuit model can be divided into the single and the multiple qubit gates [14]. A single qubit gate is to convert a single qubit from one form to another. The commons are quantum NOT gate, X gate and Z gate. NOT gates effect is exchanging the state of 0 and 1, and the Z gate is to add negative sign to logical 1.

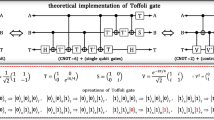
CNOT gate is an important multiple qubit quantum gate. It contains the control qubit and the target qubit. The goal of CNOT gate is to flip the logical state of the target photon if the control photon is logical 1, while do nothing if logical 0. The control qubit remains unchanged. Another multiple qubit gate is the controlled phase gate (CZ gate). The operation of CZ gate is that if the control and target qubits are both logical 1, $\pi$ phase shift is induced. The CNOT gate can be realized by the CZ gate with two Hadamard gates on input and output of target qubit, as Fig. 2 shown.

3 Schemes of CNOT Gates and Experimental Demonstrations

Since the CNOT gate is universal and important, researchers propose a lot of schemes to implement it. Those schemes all require post-selection based on KLM protocol that leads to nonlinearity required by the CNOT gate operation. In this review, we divide those schemes into four classes, that is, the CNOT gate based on bases transformation, the CNOT gate based on path interference, the CNOT gate based on interference of polarized photons and the simplified CNOT gate particular for special cases.

3.1 CNOT Gates Based on Bases Transformation

This subsection introduces one fundamental CNOT gate [22, 23] and two improved CNOT gates based on the fundamental one [4, 21, 24]. They all use polarization encoded qubits and the photon horizontally polarized represents the logical 0, and the photon vertically polarized represents the logical 1.

A Fundamental CNOT Gate. The fundamental CNOT gate is demonstrated by T.B. Pittman et al. Fig. 3(a) shows its schematic graph and two detecting bases. The flip of target qubit is caused by bases transformation on PBS-FS that reflects S-polarized photons and transmits F-polarized photons totally.

Fig. 3.

The CNOT gate based on bases transformation (a) Schematic graph and two detecting bases [23] (b) experimental setup of the CNOT gate [22]

In the device, two single photons are incident on a PBS-FS, respectively formed as control and target input qubits. A polarization-sensitive detector including two single photon detectors and a PBS in path 2 completes the post-selection operation.

Considering the case that the target photon is an arbitrary polarization state, $\mid in\rangle _1 = \alpha H_1+\beta V_1$, and the control photon is V-polarized, $\mid in\rangle _2 = V_2$, the total initial state can be written in FS bases:

$$\begin{aligned} \varPsi _{in}=|in\rangle _1 \otimes |in\rangle _{2}=[\frac{\alpha }{\sqrt{2}}(F_1-S_1)+\frac{\beta }{\sqrt{2}}(F_1+S_1)]\otimes \frac{1}{\sqrt{2}}(F_2+S_2) \end{aligned}$$

The PBS-FS transforms it into:

$$\begin{aligned} \varPsi _{2'1'}=\frac{1}{2}[\alpha (F_{2'}F_{1'}-S_{2'}S_{1'})+\beta (F_{2'}F_{1'}+S_{2'}S_{1'})]+\frac{1}{\sqrt{2}}\varPsi _{II} \end{aligned}$$

Where II includes the amplitudes of the unsuccessful cases that D2 doesn’t receive one or only one photon. Rewriting the amplitudes in mode 2 back in HV bases:

$$\begin{aligned} \varPsi _{2'1'}=\frac{1}{2}[H_d(\alpha V_{1'}+\beta H_{1'})+V_d(\alpha H_{1'}+\beta V_{1'})]+\frac{1}{\sqrt{2}}\varPsi _{II} \end{aligned}$$

If we accept the outputs of first term, $D_{2}$ detects only one H-polarized photon, the output collapses to the state $\alpha V_1+\beta H_1$. This is a flip of the input state when the control state is V-polarized.

The case that control photon state is H-polarized keeps the output of target state unchanged, by using the same device and post-selection operation as above case.

In summary, when the detector receives only one H-polarized photon, the CNOT gate succeeds with a probability of 0.25, which can be increased to 0.5 by using feed-forward control techniques [24].

Figure 3(b) shows experimental setup according to Fig. 3(a), and graphic representation of all components which are used for all following figures. All process be-fore PBS2 are to generate arbitrary input state of control and target qubits. PBS2 realized the PBS-FS in Fig. 3(a). Rather than rotating the PBS through $45^{\circ }$, it is more convenient to rotate the photons polarization and the detector bases by HWPs. Polarization-sensitive detector is realized by a rotatable polarization analyzer $\theta _{2'}$ and a single photon detector, which can only detect one polarized state at any given time. By rotating $\theta _{2'}$, any polarized states can be measured. $\theta _{1'}$ and $D_{1'}$ are used to measure the output states in path $1'$. Experimental results show that the mean error is approximately $8\,\%$ when averaged over all possible input states.

Fig. 4.

The CNOT gate with single ancilla photon [21]. (a) Schematic graph (b) experimental setup.

An Improved CNOT Gate with a Single Ancilla Photon. In order to preserve the information of control qubit in the first device, an improved scheme adopting a single ancilla photon is proposed based on the first CNOT [21], shown in Fig. 4(a). The function of the gate is realized by the fundamental CNOT gate, the lower PBS-FS. The additional upper PBS and the single ancilla photon are used to copy the control photon state, which is called quantum encoder, and output into two ports. One is acted as the output of the control qubit, and the other is to interact with the target qubit to implement CNOT operation. Therefore, a CNOT gate with both target and control output is implemented. When a coincidence of three detectors happens and detector DA receives only one H-polarized photon, the gate succeeds with probability of 1/8, which can be increased to 1/4 by using feed-forward control techniques.

In detail, the single ancilla photon is generated in state $(H_a+V_a)/ \sqrt{2}$, and the control qubit is arbitrary state $\alpha H+\beta V$. When the ancilla photon and control photon are mixed on the upper PBS, the output state is $\alpha H_aH+\beta H_aV+\alpha V_aH+\beta V_aV$. Through post-selection that one and only one photon is detected in both output ports, the state $\alpha H_aH+\beta V_aV$ is chosen, which copies the control state.

The experimental setup is shown Fig. 4(b). The block of initial state preparation is to prepare three photons with required polarized states. Then three photons are incident into A, C and T port, respectively acting as the ancilla, control and target qubits. The lower PBS in Fig. 4(a) rotated $45^{\circ }$ with respect to the upper one is accomplished by a fpc (calibrated fiber polarization controller) between the two PBS. Post-selection and qubit analysis are realized by polarizers and single-photon detectors $D_{A,C,T}$.

An Improved CNOT Gate with Entangled Ancilla Photon Pair. Another improved CNOT gate proposed by Pittman et al. [23] is demonstrated by Gasparoni et al. [4]. The scheme requires an entangled ancillary pair photon and two simpler gates, as Fig. 5(a) shown. The lower fundamental CNOT gate and the upper quantum encoder have been analyzed above. The encoder together with the maximally entangled Bell state copies the control qubit into ports $b_1$ and $a_4$. Port $b_1$ is the output of control qubit, and the photon from $a_4$ is to interact with the target qubit on PBS2 to implement the function of CNOT gate. When detector $D_3$ receive F-polarized state and $D_4$ detects H-polarized state simultaneously, the CNOT gate succeeds with probability 1/16, which can be increased to 1/4 by using feed-forward control techniques.

The experimental setup is shown in Fig. 5(b). Pump laser passes through BBO twice and generates two pairs of entangled photons. One pair entangled photon pair acts as the entangled Bell state, and the other pair is disentangled into two single photons by passing through appropriate polarizers. Two single photons are transformed into any initial state by HWPs, and act as the control and target photons respectively. Photons in path $a_2$ and $a_4$ interfere on PBS2, and photons in $a_1$ and $a_3$ interact on PBS1. Finally, the CNOT gate is realized by post-selection, with the fidelity of about $80\,\%$.

Fig. 5.

The CNOT gate with entangled ancilla photon pair [4] (a) schematic graph (b) experimental setup.

3.2 A CNOT Gate with Path Interferences

This subsection recommends the fourth CNOT gate, a gate with path interferences [6, 25]. The control and the target qubits of this gate are both spatial encoded. For control qubit, if a single photon occupies of path $C_0$ and a vacuum state in path $C_1$, it is the logical 0, and vice versa, logical 1.

Fig. 6.

A CNOT gate with path interference [18]. (a) Schematic graph. (b) A polarization qubit and a spatial qubit converted into each other. (c) The schematic experimental realization.

Under the condition of the coincidence $C_{out}$ and $T_{out}$ photon detection, the gate works as follows shown in Fig. 6(a): if the input of control qubit $C_{in}$ is logical 0, the two target modes, $T_0$ and $T_1$, are interfering classically twice on two 1/2BSs. In this case, there is no change of target state, because there is no interaction between the control and target qubits. However, when $C_{in}$ is logical 1, the control and target photons interfere non-classically at the middle 1/3BS. There are two indistinguishable cases: one is that both $C_{1}$ and $T_+$ reflect on 1/3BS causing $\pi$ phase shift, and the other is that both transmit through the 1/3BS. That two cases interfere with each other leading to the target flipping. The other two 1/3BSs are used to balance the amplitude of the non-interference output. This CNOT gate succeed with probability 1/9.

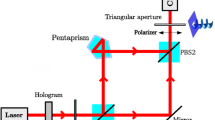
J.L. O’Brien et al. reported the demonstration of that CNOT gate in NATURE [18], as shown in Fig. 6(c). The generated photons are initially polarization encoded, and then are transformed to spatial encoding. To go from polarization encoding to spatial encoding needs a PBS and a HWP in the experiment shown in Fig. 6(b), and vice versa. In the experimental setup, two input polarized qubits pass through the first PBS and are transformed into spatial encoding. Two HWPs($22.5^{\circ }$) implement two 1/2BSs, where the two classical interferences happen, and the middle HWP(OA = $62.5^{\circ }$) implements the three 1/3BSs. The second PBS translates the polarized information after HWP($62.5^{\circ }$) into spatial modes to complete post-selection. Experimental fidelity is 84 %.

3.3 A CNOT Gate with Polarized Photons Interference

This is a CNOT gate with polarized photon interference [7, 13, 20]. Two input qubits are polarization encoded, and H-polarization is logical 0, V-polarization is 1. Implementation of the CNOT gate is shown in Fig. 7. This gate is realized mainly by three PDBSs. PDBS0 with parameters of $t_H=1$ and $t_V=1/3$, and two PDBSa/b have reverse parameters, $t_H=1/3$ and $t_V=1$. Whats more, reflection on PDBS0 once causes a $\pi$/2 phase-shift. The flip of target state when control state is 1, is realized by the process of a $\pi$ phase shift and two HWPs($22.5^{\circ }$) in input and output of target qubit. The phase shift is caused by interference of two indistinguishable cases when two V-polarized photons are mixed on PDBS0. One case is that both of the two photons transmit with probability 1/3, and the other case is that both of them reflect with probability 2/3 leading to a phase shift totally. The other two subsequent PDBSs are used to balance the output amplitudes. HWPs, QWPs and PBSs are to analyze the output state and post-selection. The gate succeeds when two detectors obtain a coincidence in the output with probability of 1/9 and experimental fidelity is 81.8 %.

Fig. 7.

Implementation of the CNOT gate with polarized photons interference [7].

3.4 A Simplified Version of CNOT Gate with a Particular Target Qubit State

Five schemes of CNOT gate described previously are all for the arbitrary control and target states. However, there are some special applications that the target state is bases logic in quantum circuits, for example, target state is the initial state, logical 0 or 1.

Fig. 8.

A simplified version of CNOT gate with bases target qubit state. (a) The input of target qubit is H-polarized state. (b) The input of target qubit is V-polarized state.

The CNOT gate with target state being logical 0 is easy to be realized by only one PBS and one HWP, as Fig. 8(a) shown [2, 15]. The control qubit state is arbitrary, written as $\alpha H+\beta V$, while the target qubit state is H. Target qubit state is transformed to be state $(H+V)/\sqrt{2}$ after HWP($22.5^{\circ }$). Thus $(\alpha HH+\beta VH+\alpha HV+\beta VV)/\sqrt{2}$ is the state of whole system. When passing through the PBS-HV, state $(\alpha HH+\beta VV)/\sqrt{2}$ is obtained under the condition of a coincidence of the two outputs, with success probability 1/2.

We can also realize the special CNOT gate that the target qubit is V-polarized state in the similar way, as Fig. 8(b) shown.

3.5 Comparison and Analysis

In this subsection, we compare and analyze the difficulty of interferences, re-sources consuming and success terms of the six different implements of CNOT gates above.

Interferences. Subwavelength path interferences occur only when the path lengths maintain stable in subwavelength, about the order of 1 $\upmu$m. It is a harsh term in lab, so it requires additional stabilization technology and equipment. However, the stability requirements of second order interference are relaxed to the coherence length of the qubit photons, about 150 $\upmu$m, and can be fulfilled easily without any stability methods. Thus the realization of subwavelength path interference is much more difficult than that of second order interference.

Table 1 shows the comparison of the interference in CNOT gates demonstrated. Only the 4th scheme is spatial encoded, and only it contains subwavelength path interferences. We have discussed that the realization of this gate is very difficult, and such difficulty will restrict its application for scalable LOQC. Compared with the 4th CNOT gate, the other CNOT gates just require at most two second order interferences, thus they all can be implemented more easily.

Resources Consuming. We roughly divide resources required into three parts, the number of required qubits, components and detectors. From the Table 2 we can see that, the 3rd and the 2nd CNOT gates need 4 and 3 single photons and the others are all require 2 photons. For required components and detectors, the first and last one require less and the others are almost similar. The terms in brackets are all response to the case using feed-forward control techniques to increase success probability in Table 3, which requires more resources and are more complex.

Table 1. Comparison of the interferences in CNOT gates demonstrated

Table 2. Resources requirement of the demonstrated CNOT gates

Table 3. Success terms of the CNOT gates

Success Terms. In Table 3, the success indications of the first three CNOT gates are all states. It means that the CNOT gates succeed when detectors receive particular states, which needs one more polarizer or PBS (with one additional detector). While the success indication of the last three is a coincidence detection of two output photons. The success probability indicates that the last scheme provides the highest probability. The 1st one can also reach highest using feed-forward control techniques, while requires more resources and are more complex.

The first scheme realizes a CNOT gate that losses the information of the control qubit, and the last one is limited to the cases that target qubit is logical 0 or 1. The destructive CNOT gates work only when all output ports each detect one photon simultaneously. Without reliable quantum nondestructive measurement (QNM) [9], the detection of the post-selection will destruct the output photons of control and target, so the gates are called destructive gates. Although those CNOT gates preserve the information of control qubit, its destructive property make it difficult to apply to scalable quantum computing. The only one non-destructive CNOT gate is the 3rd one, since its two outputs are not needed to detect by post-selection operation. As Fig. 5 shown, if D3 and D4 detect one particular photon simultaneously, the CNOT gate is successful.

Summary. Generally, the more powerful the CNOT gate is, the more resources it requires. The nondestructive gate is very useful in scalable quantum computing that contains multiple CNOT gates, but it costs more resources than the others. The fifth CNOT gate maybe a promising candidate to implement the scalable quantum computing together with QNM, since it is not resource-consuming and easier to be realized than the others that implement the same function. And from the view of the optical experimental setups, the 5th are simpler.

It may be more efficient to adopt different scheme of CNOT gate according to practical requirements. For example, if the target qubit state is logical 0 or 1, we use the sixth CNOT gate. For the CNOT gate in the middle of circuits, we could adopt the third scheme. Therefore, we combine several schemes to realize a quantum circuit in order to maximize resource efficiency. Until now, the scale of quantum circuits is so small that the scheme of quantum gate is chosen manually. However, in the future, when the scale of quantum circuits grows larger and larger, the choice would have to be made automatically which is similar to the function of compilers in classical computer.

4 Implementation of Quantum Algorithms in the Quantum Circuit Model

The above sections introduce the all-optical quantum CNOT gates, and analyze their properties. This section introduces the application of the CNOT schemes to several important quantum algorithms.

Fig. 9.

Hierarchical structure of quantum computer and classical computer.

Before describing details, we give an overview of the development of linear optical quantum computer, compared with the classical computers [29, 30]. As shown in Fig. 9, the hierarchical structure of classical computer is mainly divided into three levels, software, architecture and hardware. Those three phases would be passed through to implement an algorithm on classical computer. While for quantum computers, there are no software and architecture till now. Thus, a quantum algorithm is directly implemented by the quantum circuits and optical components, just like achieving an algorithm on FPGA.

4.1 Application of CNOT Gates for Shors Quantum Factoring Algorithm

Shors algorithm [26] is the most famous and prominent quantum algorithm. It can factor large numbers in polynomial time on a quantum computer, while the best classical method need exponential time. ChaoYang Lu et al. report an all-optical demonstration of a compiled version of the algorithm [15]. They choose to factorize 15, the simplest instance. This experiment proof-of-principle proves that Shors algorithm can be realized by using photonic qubits.

Fig. 10.

Shors algorithm [15]. (a) The quantum circuit for N = 15. (b) Experimental setup. (c) Two consecutive 6th CNOT gate.

The simplified quantum circuit of Shors algorithm and experimental setup are shown in Fig. 10(a) and (b). Two consecutive CNOT gates are the kernel of the circuit. Considering the target qubits of both CNOTs are logical 0, the 6th CNOT scheme is adopted. Two target qubits are both transformed from H to $(H \pm V) /\sqrt{2}$ by HWPs($22.5^{\circ }$). In Fig. 10(c), three $H \pm V$ polarized photons are incident into two PBSs from three spatial modes. The post-selection operation is a coincidence of three outputs which occurs only when all photons are reflected or transmitted. After that operation, entangled state $HHH \pm VVV$ is outputted, which is the required result of the two CNOT gates.

4.2 Application of CNOT Gates for Solving Systems of Linear Equations

Harrow, Hassidim and Lloyd [5] propose a powerful quantum algorithm to solve systems of linear equations that is a very practical problem. It shows that quantum computers can solve this problem exponentially faster than classical ones in some situations. In 2013, two groups independently demonstrated the algorithm based on different photonic quantum circuits [1, 2]. They both realize the simplest instance of the algorithm for solving $2\times 2$ linear equations on a quantum computer for various input vectors, demonstrating the working principle of the quantum algorithm.

Application of the Simplified CNOT Gate. The simplified quantum circuit designed by X.-D. Cai et al. is shown in Fig. 11 [2]. It uses four qubits. Two CNOTs are contained in the circuit. Because the target qubits of both CNOTs are H-polarized, the 6th scheme is adopted to implement the two consecutive CNOT as 4.1 does.

Fig. 11.

The 1st optimized quantum circuit for solving systems of linear equations.

Application of the Third and Fifth CNOT Gates. Another different implementation is reported by Stefanie Barz et al. [1]. As shown in Fig. 12, optimized quantum circuit contains two separate CNOT gates. Figure 13 shows its experimental implementation, where the two CNOT gates respectively adopt the 3rd and the 5th schemes.

Fig. 12.

The 2nd optimized quantum circuit for solving system of linear equations.

Fig. 13.

Experimental implementation of the optimized circuit.

As previous discussion of the 3rd scheme, the valid outputs of CNOT1 are passed to CNOT2 without measurement. This non-destructive CNOT gate cannot be replaced by destructive one, except that the destructive CNOT gates are combined with QNM. CNOT2 is realized by the 5th scheme and succeeds when the coincidence of two final detectors occurs. They choose this scheme because it is more stable and efficient.

In the scalable quantum computing, the output of the former gate usually pass to the next one. Destructive CNOT gates without QNM are less useful, since they have to measure outputs to judge if it succeeds, leading to destruction. In fact, we have to measure the output of each destructive CNOT gates one by one.

Summary. Comparing the two demonstrations, we observe that the same quantum algorithm can be compiled into different circuits, leading to different realization and resources consuming. The simpler quantum circuits optimize to be, the less resources will consume to implement them. Therefore, optimizing circuits is very important and necessary.

5 Discussion

Despite of great progress made in all-optical CNOT gates, there are still some problems to be solved, such as low success probability and low efficiency [19]. In addition to the technology of controlling photons, the technologies of generating and detecting photons in lab are also significant to optical quantum computing. LOQC based on photonic qubits requires large number of indistinguishable single photons that depend on the generation technology of photon sources. Post-selection is to realize two-qubit quantum gates, therefore, the efficiency and accuracy of single photon detectors is crucial for LOQC.