1 Introduction

The capacity of a photon to carry information can be greatly increased if one accesses its many degrees of freedom: spatial, polarization, frequency and the orbital angular momentum (OAM). In doing so, it is possible to make a single photon encode multiple qubits, whose manipulation can give rise to the implementation of photonic quantum logic gates, which are the building blocks of future technologies such as quantum communication [1,2,3,4] and quantum computation [5,6,7,8]. The great advantage in using light for such purposes is the fact that photons are practically unaffected by detrimental decohering processes [9,10,11,12,13,14]. A celebrated result in quantum information science was the demonstration that single-qubit and controlled-NOT (CNOT) gates together are sufficient for realizing universal quantum computation [15]. In realizing such task with optical schemes, the information is commonly encoded on the polarization degree of freedom, in which the one-qubit logic gates are carried out with birefringent wave plates [16]. However, the implementation of an optical two-qubit CNOT operation for single photons demands necessarily the control of a second degree of freedom [17].

In 2001, Knill, Laflamme and Milburn [5] demonstrated a probabilistic method to realize efficient and scalable quantum computation using only linear optical elements, photodetectors and single-photon sources. After that, a number of works have proposed ways to construct CNOT gates with linear optics. For example, Fiorentino et al. created a linear CNOT logic gate using the polarization and momentum of a single photon [18]. Oliveira et. al. realized a single-photon CNOT gate manipulating the polarization and the transverse spatial modes of the electromagnetic field [19]. Deng et. al. theoretically proposed a CNOT operation involving the polarization and the OAM of a single photon, but the use of computer-generated hologram (CGH) inside the circuit was required [20]. More recently, an experimental realization of a linear optical CNOT gate also involving polarization and OAM was reported, however making use of a nonlinear optical element to generate a pair of entangled photons in the state preparation stage, and with a readout process which works by measuring them in coincidence [21].

In this work, we theoretically study and experimentally verify, in a classical light scenario, an optical implementation of a quantum CNOT logic gate manipulating the polarization and OAM degrees of freedom only with linear optical elements. The polarization orientation and the sign of the OAM state are the control and target qubits, respectively. Contrary to the theoretical proposal by Deng and co-workers [20], our CNOT scheme does not require the usage of CGH to process information, which undoubtedly is a practical advantage toward a scalable construction of quantum information processors. We also show that the same apparatus can generate the family of maximally hyper-entangled Bell states involving polarization and OAM states. The readout process, which usually is not straightforward for OAM states, could be performed through the pragmatic triangular aperture method [22,23,24], therefore preventing faulty measurement outcomes.

2 Theory

It is well known that a light beam with the phase dependence \(\exp (i \ell \phi )\), where \(\phi \) is the azimuthal variable, carries an OAM of \(\ell \hbar \) per photon, with \(\ell \) integer [25, 26]. This property, which takes place when the beam wave front has a helical structure, represents a new photonic degree of freedom that raised the possibility of using its high dimensionality to encode a large amount of information in a single photon [27,28,29]. Furthermore, it is also known that OAM states of light, as well as the polarization states, are excellent to be used for quantum communication purposes since such states can be transmitted over long distances with very low loss [30, 31], without any recognized decoherence effect in free space and the possible protection of OAM states in turbulent environments [32, 33]. These properties are also important to achieve fault-tolerant quantum computation, given that information must be communicated by the photons through the many gates in the quantum circuit with suppression of errors. Particularly, the joint manipulation of polarization and OAM to access a higher-dimensional quantum state space of a unique photon is progressively allowing the realization of novel optical quantum information protocols [26]. With this motivation, in this section we propose an experimental method to use OAM states along with polarization to construct a linear optical CNOT gate.

Our experimental proposal consists of submitting a light beam endowed with an arbitrary nonzero OAM to a modified Mach–Zehnder interferometer (MZI) composed of two polarizing beam splitters \(\hbox {PBS}_{{1}}\) and \(\hbox {PBS}_{{2}}\), in which horizontally and vertically polarized fields are, respectively, transmitted and reflected, a mirror, a pentaprism and a charge-coupled-device (CCD) camera. In the experimental setup, which is sketched in Fig. 1, the light beam will have the horizontally and vertically polarized components separated by the first polarizing beam splitter, \(\hbox {PBS}_{{1}}\). The former will be deflected by 90\(^\circ \) toward the second beam splitter \(\hbox {PBS}_{{2}}\), while the latter will reflect twice inside the pentaprism before being deviated. The net effect of the pentaprism is to deviate the light beam by 90\(^\circ \) with high precision, facilitating the alignment of the interferometer, and invert the image, due to the double reflection, as described in Ref. [34]. This last fact causes an inversion in the OAM sign of the output beam that is also sent toward \(\hbox {PBS}_{{2}}\).

Fig. 1
figure 1

Sketch of the optical circuit used to implement a CNOT gate with the polarization and the OAM states acting, respectively, as the control and target qubits

Full size image

In order to understand the effect of the proposed optical circuit, let us investigate, for example, the transformations obtained in the evolution of an input beam that is horizontally polarized and has an arbitrary OAM quantified by \(\ell \). After being transmitted through \(\hbox {PBS}_{{1}}\), the beam will be deflected in the mirror and sent toward \(\hbox {PBS}_{{2}}\) to be again transmitted and detected by the CCD camera. Note that the states of both polarization and OAM are unchanged in this lower arm of the interferometer. On the other hand, in considering a vertically polarized input beam with an arbitrary OAM, \(\ell \), it will be reflected at \(\hbox {PBS}_{{1}}\) to be later deviated by the pentaprism with an inverted OAM, \(-\ell \). This beam will then suffer a new reflection at \(\hbox {PBS}_{{2}}\) before being detected by the CCD camera.

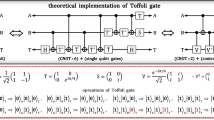
Now, let us translate the overall effect of this optical circuit in terms of quantum logic operations. First, we adopt some basis states for the representation of polarization and OAM. The horizontally and vertically polarized states are \(\left| {0}\right\rangle _{p}\) and \(\left| {1}\right\rangle _{p}\), respectively. In turn, positive and negative OAM states will be represented, respectively, by \(\left| {0}\right\rangle _{o}\) and \(\left| {1}\right\rangle _{o}\). In this form, the basis states that span our four-dimensional space with the polarization and OAM of the photons are \(\{\left| {0_{p}0_{o}}\right\rangle ,\left| {0_{p}1_{o}}\right\rangle ,\left| {1_{p}0_{o}}\right\rangle ,\left| {1_{p}1_{o}}\right\rangle \}\). Observe that if we consider the polarization states as the control and the OAM state as the target, with the experimental proposal above, the four classical CNOT gate transformations are naturally implemented,

$$\begin{aligned}&\left| {0_{p}0_{o}}\right\rangle \rightarrow \left| {0_{p}0_{o}}\right\rangle , \end{aligned}$$
(1)
$$\begin{aligned}&\left| {0_{p}1_{o}}\right\rangle \rightarrow \left| {0_{p}1_{o}}\right\rangle , \end{aligned}$$
(2)
$$\begin{aligned}&\left| {1_{p}0_{o}}\right\rangle \rightarrow \left| {1_{p}1_{o}}\right\rangle , \end{aligned}$$
(3)
$$\begin{aligned}&\left| {1_{p}1_{o}}\right\rangle \rightarrow \left| {1_{p}0_{o}}\right\rangle . \end{aligned}$$
(4)

However, if applied in the single-photon regime, the optical circuit of Fig. 1 also serves as a quantum CNOT logic gate. Indeed, if one considers a general combination of the basis states,

$$\begin{aligned} \left| {\psi }\right\rangle = a\left| {0_{p}0_{o}}\right\rangle +b\left| {0_{p}1_{o}}\right\rangle +c\left| {1_{p}0_{o}}\right\rangle +d\left| {1_{p}1_{o}}\right\rangle , \end{aligned}$$
(5)

the following transformation takes place:

$$\begin{aligned} \left| {\psi }\right\rangle \rightarrow a\left| {0_{p}0_{o}}\right\rangle +b\left| {0_{p}1_{o}}\right\rangle +c\left| {1_{p}1_{o}}\right\rangle +d\left| {1_{p}0_{o}}\right\rangle , \end{aligned}$$
(6)

where the coefficients a, b, c and d are arbitrary complex numbers, satisfying the normalization condition, \(|a|^{2}+|b|^{2}+|c|^{2}+|d|^{2}=1\). Equation 6 is the necessary condition for the implementation of a quantum CNOT gate, i.e., if the control qubit is zero (one), the target qubit is unchanged (changed). We call attention to the fact that the optical devices used in the experimental setup of Fig. 1 can be miniaturized: an important fact if we think about large-scale quantum computation.

Another interesting aspect related to the circuit of Fig. 1 is the possibility of creating hyper-entangled states involving the polarization and the OAM degree of freedom of a single photon. This task can be realized if a Hadamard gate is applied to the control qubit (polarization) prior to the quantum CNOT gate [1]. In fact, with this procedure, we are able to create maximally hyper-entangled Bell states involving the polarization and OAM Hilbert spaces. Therefore, what we need here is an optical element that acts as a Hadamard operation in the polarization state space. A wave plate placed before \(\hbox {PBS}_{{1}}\) that rotates the polarization by 45\(^{\circ }\) would play this role. In this case, in considering both the polarization and OAM states, if the polarization of the incident light is horizontal (vertical), after the wave plate, it is transformed into a diagonal (antidiagonal) polarization, that is,

$$\begin{aligned}&\left| {0_{p}0_{o}}\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left( \left| {0_{p}0_{o}}\right\rangle +\left| {1_{p}0_{o}}\right\rangle \right) , \end{aligned}$$
(7)
$$\begin{aligned}&\left| {0_{p}1_{o}}\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left( \left| {0_{p}1_{o}}\right\rangle +\left| {1_{p}1_{o}}\right\rangle \right) , \end{aligned}$$
(8)
$$\begin{aligned}&\left| {1_{p}0_{o}}\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left( \left| {0_{p}0_{o}}\right\rangle -\left| {1_{p}0_{o}}\right\rangle \right) , \end{aligned}$$
(9)
$$\begin{aligned}&\left| {1_{p}1_{0}}\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left( \left| {0_{p}1_{o}}\right\rangle -\left| {1_{p}1_{o}}\right\rangle \right) . \end{aligned}$$
(10)

Therefore, after these operations, the transformed state will be submitted to the circuit of Fig. 1. The circuit will execute the CNOT operation given by the rules of Eqs. 1–4, producing the complete family of maximally hyper-entangled Bell states

$$\begin{aligned}&\left| {0_{p}0_{o}}\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left( \left| {0_{p}0_{o}}\right\rangle +\left| {1_{p}1_{o}}\right\rangle \right) , \end{aligned}$$
(11)
$$\begin{aligned}&\left| {0_{p}1_{o}}\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left( \left| {0_{p}1_{o}}\right\rangle +\left| {1_{p}0_{o}}\right\rangle \right) , \end{aligned}$$
(12)
$$\begin{aligned}&\left| {1_{p}0_{o}}\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left( \left| {0_{p}0_{o}}\right\rangle -\left| {1_{p}1_{o}}\right\rangle \right) , \end{aligned}$$
(13)
$$\begin{aligned}&\left| {1_{p}1_{o}}\right\rangle \rightarrow \frac{1}{\sqrt{2}}\left( \left| {0_{p}1_{o}}\right\rangle -\left| {1_{p}0_{o}}\right\rangle \right) , \end{aligned}$$
(14)

which demonstrate the entangling properties of the proposed experimental setup.

A fundamental stage in implementing any quantum information protocol is obviously the readout process. In the present case, it is essential that the four basis states of Eqs. 1–4 are distinguishable in an experimental realization. The readout of the polarization basis states, \(\left| {0}\right\rangle _{p}\) and \(\left| {1}\right\rangle _{p}\), is trivial with the usage of linear polarizers oriented along the horizontal and vertical directions. Nevertheless, the readout of the OAM basis states, \(\left| {0}\right\rangle _{o}\) and \(\left| {1}\right\rangle _{o}\), is not so straightforward. Indeed, by direct detection of a light beam endowed with OAM, one can only see the well-known donut-shaped intensity profile, independent of the topological charge of the optical vortex [26].

To circumvent this problem, we propose the observation of the far-field pattern of the output beam after being diffracted by a triangular aperture. This method was proposed in Ref. [22] as a practical and precise procedure to determine the OAM of optical fields. Specifically, it was found that the diffraction pattern is a triangular optical lattice whose number of bright points N on any side of the triangle is related to the topological charge as \(\ell =N-1\). However, the readout process in our protocol does not require the knowledge about \(\ell \), but only its sign. This is where the triangular aperture method is more effective. The sign of \(\ell \), which is related to the handedness of the optical vortex, is found out just by observing the direction to which the triangular optical lattice is pointing. If the triangular lattice points to the same direction of the triangular aperture, we have that the sign of the OAM is positive, which means \(\left| {0}\right\rangle _{o}\). Conversely, if the triangular lattice points to the opposite direction, it signifies that the OAM sign is negative, meaning that the state is \(\left| {1}\right\rangle _{o}\). In this form, for the present setup, the triangular aperture should be placed before the CCD camera for the observation of the handedness of the output optical vortex.

It is worthwhile to point out that, for quantum computation purposes, it is necessary that the degrees of freedom used to process information in the CNOT gates are also conveniently manipulated in the single-qubit gates, as discussed in Introduction. In our context, we should be able to implement such gates for the polarization and OAM states of light. In the first case, this task can be realized by using half-wave plates (HWP) and quarter-wave plates (QWP) [17]. On the other hand, the realization of single-qubit gates with the OAM states for \(\ell = \pm 1\) can be achieved analogously with \(\pi \)- and \(\pi /2\)-converters, respectively, i.e., by appropriate use of cylindrical lenses [16, 25].

3 Experimental methods and results

We realized an experiment following the theoretical proposal sketched in Fig. 1. The light source used was the Gaussian mode of an argon laser operating at 532 nm with a power of 10 mW with vertical polarization. The beam then illuminates a CGH with controllable pixels written in an (Hamamatsu Model X10468-01) spatial light modulator (SLM) for the generation of the helical phase profile, \(\exp (i \ell \phi )\). In our experiment, we created a beam with \(\ell = 1\) before \(\hbox {PBS}_{{1}}\). Next, the reflected beam is deviated by the pentaprism, which also inverts the sign of the OAM, to recombine with the beam transmitted by \(\hbox {PBS}_{{1}}\) at the second polarized beam splitter \(\hbox {PBS}_{{2}}\). After this stage, the output beam passes through an equilateral triangular aperture with side length of 2 mm. Then, a 30-cm-focal-length lens was placed immediately after the aperture to create the far-field diffraction pattern at the focal length of the lens. Finally, the intensity diffraction pattern is registered by the CCD camera.

Fig. 2
figure 2

Experimental intensity profile of the four output states of the setup of Fig. 1, a \(\left| {0_{p}0_{o}}\right\rangle \), b \(\left| {0_{p}1_{o}}\right\rangle \), c \(\left| {1_{p}0_{o}}\right\rangle \), d \(\left| {1_{p}1_{o}}\right\rangle \), by using a linear polarizer and the triangular aperture prior to detection to realize the readout process. The four states could be naturally distinguished. In considering the overlap regions of the photons with opposite sign of the OAM, we estimate the output states of the CNOT gate with approximately 65% of fidelity, limited by the OAM state readout

Full size image
Table 1 Truth table
Full size table

The preparation of the control qubit (polarization) is made by using a half-wave plate (HWP) before \(\hbox {PBS}_{{1}}\), whereas the measurement of it is made with a linear polarizer placed after \(\hbox {PBS}_{{2}}\) oriented either along the vertical or the horizontal direction in order to verify the final control state. The target (OAM) state is measured according to the orientation of the triangular truncated optical lattice observed in the camera [22]. In the absence of the triangular aperture, the intensity patterns of the four output states of Eqs. 1–4 recorded by the camera are the characteristic donut-like intensity profile, without any OAM state information. In a different perspective, Fig. 2 shows the pattern when the aperture is present. We observe that the states with \(\ell = 1\) and \(\ell = -1\) are easily distinguishable. Table 1 shows the truth table of our CNOT gate, whose output state profiles are shown in Fig. 2. The results completely agree with the transformations indicated in Eqs. 1–4.

It is important to mention that despite the light source and readout process employed in our experimental setup being classical, an all quantum-mechanical analog scheme can be achieved by substituting the laser beam by a single-photon source, and, optionally, the triangular aperture by a mode sorter device to determine the photon OAM, as reported in Refs. [35, 36]. However, further investigation of the diffraction pattern obtained with the triangular aperture method shows that it can also be used to distinguish probabilistically the \(\ell =-1\) and \(\ell =1\) OAM states of single photons. This is because the intensity maxima in these two cases have a small overlap region, which means that in the single-photon regime, the detection regions are almost exclusive. Figure 3 shows that in at least 50% of the cases the two OAM states can be perfectly discriminated. Apart from these details regarding the readout process, all optical devices used in our experiment, including the triangular aperture, operate equally in terms of information processing both in the classical and single-photon regimes [16, 17]. Of course, the light source should be replaced by some single-photon source like a quantum dot single-photon source [37], or generated by spontaneous parametric down-conversion [28]. The CCD camera should also be substituted by single-photon detectors which provide the necessary spatial resolution in accordance with Fig. 2.

Fig. 3
figure 3

Illustration of the overlap between the diffraction patterns obtained with the triangular aperture for beams with \(\ell = 1\) (brighter spots) and \(\ell = -1\) (darker spots). In a, we see the two patterns without filter, whereas in b the patterns are shown after the photons have passed through a filter with 0.5 of optical transmittance

Full size image

4 Conclusion

Since the inception of the seminal KLM protocol [5], we have witnessed many advances in the study of linear optical quantum computation. The limitations of this computational approach are well understood today: a fact that raises a number of challenges to be overcome [38, 39]. In this contribution, we theoretically showed and experimentally tested in the limit of classical optical field, without loss of generalization, a linear optical quantum CNOT gate involving the polarization and OAM degrees of freedom, which serve as the control and target qubits, respectively. The experimental setup does not demand the usage of computer-generated holograms to process information: a fact that makes the arrangement suitable for scaling up quantum-computing architectures. The readout process is based only on the use of a linear polarizer and a diffractive triangular aperture. With the present configuration, the experimental results confirmed our theoretical predictions in an unambiguous way. Given the stability of the experimental setup in this classical light regime and the robustness of the polarization and OAM states against environmental noise, we believe that the present proposal brings a promising element to be used in future schemes of linear optical quantum computation.