Keywords

1 Introduction

Quantum computer is an inevitable stage in the development process of computer. Quantum information, especially quantum media information, will have important researching value in the era of quantum computer. Quantum image processing, an area focusing on extending conventional image processing tasks and operations to the quantum computing framework, will be a key issue in quantum information processing field [1].

At present, the quantum image representation methods can be divided into the following categories: lattice method based [2–4], entanglement based [5], vector based [6, 7], FRQI (Flexible Representation of Quantum Images) method [8] and NEQR (Novel Enhanced Quantum Representation) method [9]. The two methods of FRQI and NEQR are widely used in the research of quantum image processing and security. In FRQI, the gray level and the position of the image are expressed as a normalized quantum superposition state. NEQR quantum image indicates an increase in the number of quantum bits required for representing the gray level of image. Therefore, FRQI representation method is taken into consideration to design quantum noise image preparation.

Noise comes mainly from the acquisition, transmission and processing of images. The noise usually used in image processing is Gauss noise (i.e. white noise), uniform noise and impulse noise (i.e. salt and pepper noise). A suitable quantum noise image is helpful to test the effectiveness of the quantum image processing algorithms [10, 11] and/or quantum image security schemes [12–14]. Therefore, producing a quantum noise image whose possibility density function is consistent with a given formulation is a necessary stage to test or verify other quantum image processing methods. Although producing a classical noise image is very simple, its quantum version isn’t so easy because quantum image production need to satisfy the principle of quantum computation. In this paper, a quantum Gauss noise image is prepared using basic quantum transforms based on FRQI quantum image. The research about quantum noise image provides convenience for testing or verifying the effectiveness of the quantum image processing algorithms [15].

The rest of the paper is organized as follows. Section 2 gives the related works on quantum image representations. In Sect. 3, the quantum noise image and its preparation method is proposed. Section 4 is devoted to the simulation results and result analyses. Finally, Sect. 5 concludes the paper.

2 Flexible Representation of Quantum Images

Inspired by the pixel representation for images in classical computers, a flexible representation for quantum images is proposed in [8]. The quantum image corresponding to a classical image sized \(2^{n}\times 2^{n}\) is defined by a quantum encoding state, i.e.,

$$\begin{aligned} \begin{aligned} |I(\theta )\rangle&= \frac{1}{2^{n}}\sum _{i=0}^{2^{2n}-1} (\cos \theta _{i}|0\rangle +\sin \theta _{i}|1\rangle )\otimes |i\rangle , \\ \theta _{i}&\in [0,\frac{\pi }{2}],i=0,1,...,2^{2n}-1, \end{aligned} \end{aligned}$$
(1)

wherein \(\cos \theta _{i}|0\rangle +\sin \theta _{i}|1\rangle \) encodes the color information and \(|i\rangle \) encodes the corresponding position of the quantum image. The position information includes two parts: vertical and horizontal coordinates. Concretely, in a 2n-qubits system,

$$\begin{aligned} \begin{aligned} |i\rangle = |y\rangle |x\rangle&=|y_{n-1}y_{n-2}\cdots y_{0}\rangle |x_{n-1}x_{n-2}\cdot \cdot \cdot x_{0}\rangle , \\ x,y&\in \{ 0,1,\cdots ,2^{n}-1\}, \\ |y_{j}\rangle ,|x_{j}\rangle&\in \{|0\rangle ,|1\rangle \}, j=0,1,\cdots ,n-1, \end{aligned} \end{aligned}$$
(2)

where \(|y\rangle =|y_{n-1}y_{n-2}\cdots y_{0}\rangle \) encodes the first n-qubits along the vertical location and \(|x\rangle =|x_{n-1}x_{n-2}\cdots x_{0}\rangle \) encodes the second n-qubits along the horizontal axis.

3 Quantum Noise Image and its Preparation

The noise of quantum image mainly comes from the transmission and processing of the image, which is mainly based on the additive noise. The noise superimposition process of quantum images can be represented by a degenerate function:

$$\begin{aligned} |G\rangle = |F\rangle +|\eta \rangle \end{aligned}$$
(3)

where \( |F\rangle \) denotes the input quantum image, \(|\eta \rangle \) represents the additive noise and \(|G\rangle \) is the degenerated image after superimposing noise.

Gauss noise and salt and pepper noise are two most common additive noise. Through the degenerate function, it is easy to conclude that the superposition process of variable intensity noises can be equivalent to the quantum noise image preparation process. The feasibility study of quantum preparation of Gauss noise image will be proposed as follows.

Suppose the quantum Gauss noise has the following possibility distribution:

$$\begin{aligned} p(\varphi ) = \frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{(\varphi -\mu )^{2}}{2\sigma ^{2}}} \end{aligned}$$
(4)

wherein, Gauss random variable \(\varphi \) represents gray value coding, \(\mu \) denotes the expectation value and \(\sigma \) expresses the standard deviation. When \(\varphi \) satisfy Eq. (4), ninety-five percent its values fall into the range of \([\mu -2\sigma ,\mu +2\sigma ]\). In many practical situations, noise can be approximated by the Gauss noise. Specially, the preparation process of the FRQI quantum Gauss noise image can be described as follows:

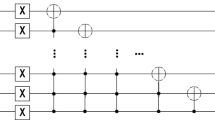
Step 1: Suppose the size of the FRQI image is \(N=2^{n}\times 2^{n}\) and the number of Gauss distribution noise pixels is \(M, M\le N\). The initial quantum image state without noise is:

$$\begin{aligned} |I(\theta )\rangle = \frac{1}{2^{n}}\sum _{i=0}^{2^{2n}-1} (\cos \theta _{i}|0\rangle +\sin \theta _{i}|1\rangle )\otimes |i\rangle \end{aligned}$$
(5)

Step 2: Sampling the range of \([\mu -2\sigma ,\mu +2\sigma ]\) to S bins denoting \(\{\varphi _{1},\varphi _{2},\ldots , \varphi _{S}\}\) which is displayed in Fig. 1.

Fig. 1.
figure 1

Sampling bins of Gauss noise probability density function.

Full size image

It is significant that

$$\begin{aligned} \sum \limits _{i = 1}^S {p({\varphi _i})} \cong 95\,\% \end{aligned}$$

.

Step 3: Selecting \([M \cdot p(\varphi _{1})]\) pixels randomly from the image \(|I(\theta )\rangle \) to construct a set \(P_{1}\), where signal \(``[\cdot ]''\) denotes the rounding operation.

Step 4: Applying unitary transform \(R_{1}\) to quantum image \(|I(\theta )\rangle \), wherein

$$\begin{aligned} {R_1} = I \otimes \sum \limits _{j = 0,j \notin {P_1}}^{{2^{2n}} - 1} {\left| j \right\rangle \left\langle j \right| } + R(2{\varphi _1}) \otimes \sum \limits _{j \in {P_1}} {\left| j \right\rangle \left\langle j \right| } \end{aligned}$$
$$R(2{\varphi _1}) = \left( {\begin{array}{*{20}{c}} {\cos {\varphi _1}} &{} { - \sin {\varphi _1}} \\ {\sin {\varphi _1}} &{} {\cos {\varphi _1}} \\ \end{array}} \right) $$

If denoting the result as

$$\begin{aligned} {R_1}(\left| {I(\theta )} \right\rangle ) \buildrel \varDelta \over = {\left| {I(\theta )} \right\rangle _1} \end{aligned}$$

then this step realize the aim of adding noise whose gray coding is \(\varphi _{1}\) to to the quantum image \(|I(\theta )\rangle \) randomly.

Step 5: For

$$\begin{aligned} k = 2,3, \ldots ,S \end{aligned}$$

selecting randomly \([M \cdot p(\varphi _{k})]\) pixels from the image \(|I(\theta )\rangle _{k-1}\) to construct a set \(P_{k}\), here

$$\begin{aligned} {P_k} \cap {P_{k - 1}} \cap \cdots \cap {P_1} = \varPhi \end{aligned}$$

Then implementing the following operations:

$$\begin{aligned} R({\left| {I(\theta )} \right\rangle _1}) = \left( {\prod \limits _{k = 2}^S {{R_k}} } \right) ({\left| {I(\theta )} \right\rangle _1}) \buildrel \varDelta \over = {\left| {I(\theta )} \right\rangle _n} \end{aligned}$$

where

$$\begin{aligned} {R_k} = I \otimes \sum \limits _{j = 0,j \notin {P_k}}^{{2^{2n}} - 1} {\left| j \right\rangle \left\langle j \right| } + R(2{\varphi _k}) \otimes \sum \limits _{j \in {P_k}} {\left| j \right\rangle \left\langle j \right| } \end{aligned}$$
$$R(2{\varphi _k}) = \left( {\begin{array}{*{20}{c}} {\cos {\varphi _k}} &{} { - \sin {\varphi _k}} \\ {\sin {\varphi _k}} &{} {\cos {\varphi _k}} \\ \end{array}} \right) $$

Thus, the final quantum state \(|I(\theta )\rangle _{n}\) is the quantum Gauss noise image satisfying Eq. (4).

From above steps 1 to 5, the preparation of quantum Gauss noise image is finished.

The whole preparation of quantum noise image costs no more than \(O(2^{4n})\) for a \(2^n \times 2^n\) image. This indicates the efficiency of the preparation process.

4 Experiments

The simulations are based on linear algebra with complex vectors as quantum states and unitary matrices as unitary transforms on the software of Matlab 7.12.0(R2011a). The final step in quantum computation is the measurement, which converts the quantum information into the classical form as probability distributions. Experiments are performed on desktop computer with Intel(R) Xeon(R) CPU E5620 2.40 GHz, 2.39 GHz(4 processors) 8 GB RAM and 64-bit operating system. Figure 2 illustrates the simulation results of quantum original image and quantum Gauss noise image. (a1) is the original image Lena and (a2) is the version after added Gauss noise. (b1) is the original image Cameraman and (b2) is the quantum noise image added Gauss noise. Through simulation, it is verified that preparing a quantum noise image satisfying some probability density is totally feasible.

Fig. 2.
figure 2

Quantum noise image illustration.

Full size image

5 Conclusions

In this paper, a novel quantum noise image preparation scheme based on FRQI image has been proposed. The proposed strategy comprises of five steps which include only elementary unitary transforms. Quantum noise image provides convenience for testing or verifying the effectiveness of the quantum image processing algorithms. Experimental simulation results show the preparation algorithm is effective. Exploring quantum algorithm for other noises methods will be our future work.