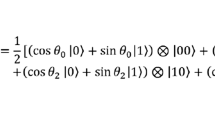1 Introduction

Quantum computation and quantum information is the study of the information processing tasks that can be accomplished using quantum mechanical systems. Like many simple but profound ideas, it was a long time before anybody thought of doing information processing using quantum mechanical systems [1].

Quantum computation is the field that investigates the computational power and other properties of computers based on quantum-mechanical principles. An important objective is to find quantum algorithms that are significantly faster than any classical algorithm solving the same problem. The field started in the early 1980s with suggestions for analog quantum computers by Benioff [2] and Feynman [3, 4], and reached more digital ground when in 1985 Deutsch [5] defined the universal quantum Turing machine. The following years saw only sparse activity, notably the development of the first algorithms by Deutsch and Jozsa [6] and by Simon [7], and the development of quantum complexity theory by Bernstein and Vazirani [8]. However, interest in the field increased tremendously after Peter Shor’s [9] very surprising discovery of efficient quantum algorithms (or simulations on a quantum computer) for the problems of integer factorization and discrete logarithms in 1994.

Since most of current classical cryptography is based on the assumption that these two problems are computationally hard, the ability to actually build and use a quantum computer would allow us to break most current classical cryptographic systems, notably the Rivest, Shamir and Adleman (RSA) system [10, 11]. In contrast, a quantum form of cryptography due to Bennett and Brassard [12] is unbreakable even for quantum computers.

On the other hand, and as well say Hirota et al. [13] inside the introduction of their work:

Quantum computation has appeared in various areas of computer science such as information theory, cryptography, image processing, etc. [1] because there are inefficient tasks on classical computers that can be overcome by exploiting the power of the quantum computation. Processing and analysis of images in particular and visual information in general on classical computers have been studied extensively [14–17]. On quantum computers, the research on images has faced fundamental difficulties because the field is still in its infancy. To start with, what are quantum images or how do we represent images on quantum computers? Secondly, what should we do to prepare and process the quantum images on quantum computers?

Precisely, these two questions represent the essence on which this paper is based, i.e., the correct (and more efficient) internal representation of an image in a quantum context, and its recovery, once processed internally. Thus, we recognize only 3 milestones in the brief history of quantum image processing, namely:

  • All starts with the pioneering work of Prof. Salvador E. Venegas-Andraca [18–21] at Keble College, Oxford University, UK (currently at Tecnológico de Monterrey, Campus Estado de México), where he proposes quantum image representations such as Qubit Lattice [22]; in fact, this is the first doctoral thesis in the specialty,

  • The history continues with the quantum image representation via the Real Ket [23] of Prof. Jose I. Latorre Sentís, at Universitat de Barcelona, Spain, with a special interest in image compression in a quantum context, and

  • Finally, we arrive at the proposal of Prof. Hirota et al. [13] from Tokyo Institute of Technology, for a flexible representation of quantum images to provide a representation for images on quantum computers in the form of a normalized state which captures information about colors and their corresponding positions in the images.

These works marked the path and viability of quantum image processing; however, we believe that a new type of internal representation of images, which enable an easier representation of traditional algorithms of traditional digital image processing in a quantum computer, as well as more easy and efficient recovery of images processed outside the quantum computer is imperative. This is the essence of this work, which is organized as follows:

The new approach for internal image representation is outlined in Sect. 2, where we present the development of quantum Boolean image processing concept. Besides, in this section, we show the proposed new interfaces classical to quantum and quantum to classical, and a new quantum Boolean image denoising called quantum Boolean mean filter (QBMF). In Sect. 3, we discuss the more appropriate metrics for image denoising in a set of experimental results. Finally, Sect. 4 provides a conclusion and future works proposal of the paper.

2 Quantum Boolean image processing (QuBoIP)

QuBoIP is presented as a branch of quantum image processing that is composed of the following steps, namely:

  • Color decomposition and bit slicing

  • Classical-to-quantum interface (C2QI)

  • Quantum Boolean image denoising

  • Quantum-to-classical interface (Q2CI)

  • Bit reassembling and color recomposition

On the other hand, QuBoIP needs a particular type of qubit, being that the fundamental concept of quantum computation and quantum information. In its general shape, the qubit forms linear combinations of states, often called superpositions [24–26]:

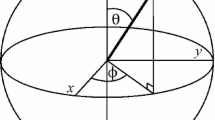
$$\begin{aligned} | \psi \rangle =\alpha | 0 \rangle +\beta \left| 1 \right\rangle , \end{aligned}$$
(1)

where \(\left| \alpha \right| ^{2}+\left| \beta \right| ^{2}=1\), with the states \(\left| \alpha \right\rangle \) and \(\left| \beta \right\rangle \) are understood as different polarization states of light, where \(\upalpha \) and \(\upbeta \) are complex numbers. The special states \(\left| 0 \right\rangle \) and \(\left| 1 \right\rangle \) are known as computational basis states (CBS) and form an orthonormal basis for this vector space, being \(| 0 \rangle =\left[ {{\begin{array}{l} 1 \\ 0 \\ \end{array}}} \right] \) and \(| 1 \rangle =\left[ {{\begin{array}{l} 0 \\ 1 \\ \end{array}}} \right] \). The final and general form of \(| \psi \rangle \) is

$$\begin{aligned} | \psi \rangle = \cos \frac{\theta }{2}| 0 \rangle +\hbox {e}^{i\phi } \sin \frac{\theta }{2}\left| 1 \right\rangle \end{aligned}$$
(2)

where \(0\le \theta \le \pi ,\; 0\le \phi <2\pi \), with \(\alpha = \cos \frac{\theta }{2}\) and \(\beta =\hbox {e}^{i\phi } \sin \frac{\theta }{2}\) [1].

2.1 Color decomposition and bit slicing

We decompose the original noisy image in its color components (i.e., red, green and blue), and in turn, each color component in their corresponding bitplanes thanks to bit slicing, in this case thanks to an own MATLAB\(^{\circledR }\) function [27] called slicer(.), and from which we get many bitplanes as depth in bit has the image to be treated. In Fig. 1, we get 8 bitplanes, where bitplane 7 is called most significant bit (MSB) and it is the most morphologically committed bitplane with the original image [28]. In return, bitplane 0 is the least significant bit (LSB), and it is the least morphologically committed bitplane with the gray image.

Fig. 1
figure 1

Bitplanes of the red component for Angelina obtained by slicing, with special remarks for MSB and LSB (Color figure online)

Full size image

Two important aspects:

  • From here to the end of this paper, we are going to work with MSB, i.e., with we will say “image,” we are saying MSB.

  • The classical version of the slicer(.) function in MATLAB\(^{\circledR }\) code is as follows:

figure a

If we were to highlight the advantage of working in QuBoIP rather than in QuIP [13, 18–23], it would certainly be the fact that as QuBoIP working with CBS exclusively, the measurement is not a problem as in the rest of quantum physics, because when we measured an \(| 1 \rangle \), the result is an unchanged \(| 1 \rangle \), and when we measured an \(| 0 \rangle \), the result is an unchanged \(|0\rangle \).

Figure 2 shows us—in detail—the eight bitplanes of Angelina, from MSB (bitplane 7) to LSB (bitplane 0). Let observe that as we move from MSB to LSB, different bitplanes are increasingly unrecognizable compared with the original image, i.e., Angelina. As we can see, LSB is completely different regarding original Angelina morphology. This is one reason why the LSB is steganography territory [28]. The other reason is that any change in the LSB does not produce visually detectable changes in the original image.

Fig. 2
figure 2

Angelina and her eight bitplanes, including MSB and LSB

Full size image

2.2 Classical-to-quantum interface (C2QI)

In this section, a complete description of the operating principle of this interface is presented. This includes the relationship between external and internal representation of MSB (bitplane 7) for each color.

Figure 3 shows us the relationship between classical 0, \(\alpha \) and \(\hbox {I}_\mathrm{MSB}\). In this case, \(\alpha = 1\) when \(\hbox {I}_\mathrm{MSB} = 0\) and \(| \psi \rangle =| 0 \rangle \), with \(\theta = 0^{\circ }\) and for any \(\phi \).

Fig. 3
figure 3

Relationship between classical 0, \(\alpha \) and \(\hbox {I}_\mathrm{MSB}\)

Full size image

On the other hand, in Fig. 4, we can see the relationship between classical 1, \(\alpha \) and \(\hbox {I}_\mathrm{MSB}\). This case is the opposite of the previous, with \(\alpha = 0\) when \(\hbox {I}_\mathrm{MSB} = 1\) and \(| \psi \rangle =| 1 \rangle \), with \(\theta =\pi \) and for any \(\phi \) too.

Fig. 4
figure 4

Relationship between classical 1, \(\alpha \) and \(\hbox {I}_\mathrm{MSB}\)

Full size image

As we can see, the geometric relationship between Figs. 3 and 4 is inverted. This happens to limiting values on the Bloch’s sphere such as the CBS, that is to say, \(|0\rangle \) and \(|1\rangle \).

We use only the MSB of each color (see Figs. 1, 2), and we introduce the mentioned MSB to the C2QI. The output of such interface will go to the quantum algorithm, directly. See Fig. 5.

Fig. 5
figure 5

Classical-to-quantum interface

Full size image

This interface is automatic and direct because we need the following correspondences, i.e., \(0\rightarrow | 0 \rangle \) and \(1\rightarrow | 1 \rangle \), only. According to this, obviously, \(\alpha =1-\hbox {I}_\mathrm{MSB}\), this task is performed by a classical investor, see Fig. 5. Therefore, we obtain the rest of the wave function component as follows: \(\left| \beta \right| =\sqrt{1-\left| \alpha \right| ^{2}}\), for any \(\phi \) (see Sect. 2). This latter task is performed by an actuator, which builds a wave function \(\psi _\mathrm{in}\) considering that the key factor of its task is the projection on the \(z\) axis (for this reason, it is called \(\hbox {Actuator}_\mathrm{z}\)), i.e., \(\alpha \). As we can see in Figs. 3 and 4, \(\alpha \) is inverted with respect to \(\hbox {I}_\mathrm{MSB}\), i.e., if \(\hbox {I}_\mathrm{MSB}\) = 0, then \(\alpha = 1\), when \(|\psi \rangle =| 0 \rangle \); however, if \(\hbox {I}_\mathrm{MSB} = 1\), then \(\alpha = 0\), when \(| \psi \rangle =| 1 \rangle \). That is to say, it is only necessary to consider the \(z\) axis of Bloch’s sphere when we work with CBS (see Figs. 3, 4), i.e., when we work with one qubit only, which is all that is used in this technology.

Everything mentioned here not only facilitates the construction of future interfaces, but also makes them more simple and robust while maintaining the quality of processing within the quantum computer, for both quantum image processing [18–23] and quantum signal processing [29, 30].

2.3 Quantum Boolean (QuBo) image denoising

In this section, we present a method for quantum Boolean image denoising called QBMF, which works on an internal representation (inside quantum computer) of bitplane 7 (or MSB) for each color component of classical noisy image. Here, we use an algorithm based on a selection mask with a horizontal rafter (see Fig. 6) on that noisy QuBo \(\left| \hbox {I}_\mathrm{MSB} \right\rangle \) to which we must obtain a denoised QuBo \(\left| \hbox {I}_\mathrm{MSB} \right\rangle \) [31–33]. The main idea is to make an interaction between the selection mask and a portion of the QuBo \(\left| \hbox {I}_\mathrm{MSB} \right\rangle \) to be processed (with the same dimension as the mask) and that the result of said interaction to replace central pixel value of the QuBo \(\left| \hbox {I}_\mathrm{MSB} \right\rangle \) portion affected by the selection mask [14–17].

Fig. 6
figure 6

The selection mask on the noisy QuBo \(\left| {\hbox {I}_\mathrm{MSB}} \right\rangle \) in a horizontal rafter produce the denoised QuBo \(\left| {\hbox {I}_\mathrm{MSB}} \right\rangle \)

Full size image

2.3.1 Quantum Boolean mean filter

Based on Fig. 7, we take a selection mask of \(\left| {w\times w} \right\rangle \) (often called kernel, which should be of any size, in this case, \(3 \times 3\), provided it has the same number of rows and columns and the dimension is an odd number) elements, which is applied in a horizontal rafter way.

Fig. 7
figure 7

An example of \(3\times 3\) filter window for selection mask algorithm on a \(\left| \hbox {I}_\mathrm{MSB} \right\rangle \)

Full size image

This algorithm involves four steps based on Fig. 7, namely:

  1. 1.

    Let us calculate the threshold of the algorithm based on the number of elements of the used kernel, i.e., \(\left| t \right\rangle =\left| {\left( {w\times w-1} \right) /2} \right\rangle \)

  2. 2.

    Let us built the selection mask \(\left| {W\left( {rw,cw} \right) } \right\rangle =\left| I_{MSB} \left( r-\left( {1+\left\lfloor {w/2} \right\rfloor } \right) +rw\right. \right. \), \(\left. \left. c-\left( {1+\left\lfloor {w/2} \right\rfloor } \right) +cw \right) \right\rangle \)

    $$\begin{aligned}&\hbox {with}\;r\in \left[ {1+\left\lfloor {w/2} \right\rfloor ,ROW-\left\lfloor {w/2} \right\rfloor } \right] ,\;c\in \left[ {1+\left\lfloor {w/2} \right\rfloor ,COL-\left\lfloor {w/2} \right\rfloor } \right] ,\\&\quad rw\in \left[ {1,w} \right] ,\;\hbox {and}\; cw\in \left[ {1,w} \right] \end{aligned}$$

    being: rw (row index) and cw (column index) inside of the selection mask, respectively; \(\left\lfloor {\bullet } \right\rfloor \) means integer part of a real number; ROW (number of row) and COL (number of column) of the \(\left| \hbox {I}_\mathrm{MSB} \right\rangle \), respectively; \(r\) (row index) and \(c\) (column index) of the \(\left| \hbox {I}_\mathrm{MSB}\right\rangle \), respectively.

  3. 3.

    Let us calculate the number of \(|1\rangle \) inside the selection mask \(\left| W \right\rangle \) for each pair (r,c), i.e.,

    $$\begin{aligned} \left| n \right\rangle =\sum _{rw=1}^w {\sum _{cw=1}^w {\left| {W\left( {rw,cw} \right) } \right\rangle }}. \end{aligned}$$
  4. 4.

    Let us compare \(|n\rangle \) and \(|t\rangle \). If \(|n\rangle > |t\rangle \), then \(\left| {\hbox {I}_\mathrm{MSB} \left( {\hbox {r,c}} \right) } \right\rangle =| 1 \rangle \), else \(\left| {\hbox {I}_\mathrm{MSB} \left( {\hbox {r,c}} \right) } \right\rangle =| 0 \rangle \).

Then, we present the complete quantum algorithm.

figure b

Figure 7 shows us a numerical example (top-right) of \(3\times 3\) filter window for selection mask, where in that portion of the noisy \(\left| \hbox {I}_\mathrm{MSB} \right\rangle \), the number of \(|1\rangle \) is greater than the number of \(|0\rangle \), and then, the denoised \(\left| \hbox {I}_\mathrm{MSB} \right\rangle \) will be \(|1\rangle \).

The computational complexity of this quantum algorithm is \(O( ROW\times COL\times \) \(w\times w )\); however, although it is not a two-dimensional convolution, they have the same computational cost [14–17]. Quantum Boolean mean filter and Boolean mean filter have the same filtering performance, and both have a better performance than original and traditional mean filter (discrete and classical), see Sect. 3.2.

Working with CBS frees us from the influence that superposition and entanglement have normally when we work with generic cubits. That is, we are in a very special borderline case, i.e., it is similar to classical Boolean [28]. In fact, there is no difference between quantum Boolean and pure Boolean (classical) regarding their results in a filtering context. The quantum Boolean version has the same computational cost of classical Boolean version. Besides, for this algorithm, we will seek that \(|\psi \rangle \) be CBS (all the time), because it is easier its state treatment in the presence of quantum decoherence. On the other hand, the quantum decoherence time depends on the implementation technology of the quantum computer and not the quantum algorithm itself [1]. However, it is easier a collapse of the wave function with generic qubits that with CBS, the state is more stable in a quantum Boolean context than in a generic quantum context, in special after measurement of the state.

Finally, we present the classical Boolean version of mean filter, e.g., in MATLAB\(^{\circledR }\) [27] code outside quantum computer.

figure c

2.4 Quantum-to-classical interface (Q2CI)

Here, we recover each denoised \(|\psi \rangle \) from quantum algorithm, and we introduce it to the Q2CI. The output of such interface will be the \(\hbox {I}_\mathrm{MSB}\) of each color, which will be used alongside the other bitplanes to reconstruct each color component of the denoised image, and then, we turn to reconstruct the entire final denoised image. See Fig. 8.

Fig. 8
figure 8

Quantum-to-classical interface

Full size image

As we can see in previous sections, there is a direct and automatic correspondence between [0, 1] and [\(| 0 \rangle , | 1 \rangle \)]. Such correspondence (and in that order) will be the classical-to-quantum interface. In the same way, but in reverse order, there is a direct and automatic correspondence between [\(|0\rangle , |1\rangle \)] and [0, 1]. In this correspondence, but in that order, we know it as a quantum-to-classical interface. Unlike [34], the measurement is not a problem, since it does not alter the outcome measure. Therefore, it is not necessary and estimator after measurement as in [34].

In Table 1, we can see these statements, where left column represents the state before measurement, while right column represents the state after that, for CBS and generic state (see Sect. 2), where \(\hat{{M}}_m\) means measurement operator, and \(|\psi \rangle _{pm}\) is the post-measurement quantum state in its generic form [1–22].

Table 1 Measurement outcome with CBS and generic state
Full size table

In Fig. 8, we can see first the quantum algorithm, whose output is directed to the interface, which begins with the measurement operator, which measures the projection on the \(z\) axis (for this reason, it is called \(\hbox {Measurement}_\mathrm{z}\)), i.e., \(\alpha \). That is to say, it is only necessary to measure the \(z\) axis as in the case of the previous interface.

The Q2CI continues with a classical inverter, i.e., \(\hbox {I}_\mathrm{MSB}=1-\alpha \). This latter task is performed by a classical invertor, see Fig. 8.

As we can see in Figs. 3 and 4, \(\alpha \) is inverted with respect to \(\hbox {I}_\mathrm{MSB}\), i.e., if \(\hbox {I}_\mathrm{MSB} = 0\), then \(\alpha = 1\), when \(| \psi \rangle =| 0 \rangle \); however, if \(\hbox {I}_\mathrm{MSB} =1\), then \(\alpha = 0\), when \(|\psi \rangle =| 1 \rangle \). That is to say, here too, it is only necessary to consider the \(z\) axis of Bloch’s sphere when we work with CBS (see Figs. 3, 4), i.e., when we work with one qubit only, which is all that is used in this technology.

Table 1 is the cornerstone of this methodology called quantum Boolean image processing in general, and quantum Boolean image denoising in particular. It will allow us (among others):

  1. (a)

    to build more robust interfaces with respect to measurement noise (decoherence [35–42]),

  2. (b)

    to ignore the problem of quantum measurement [1, 22, 43], which was above mentioned,

  3. (c)

    a lower computational and memory cost [28], working only with MSB, and

  4. (d)

    to export this criterion beyond the quantum image processing [29, 30].

2.5 Bit reassembling and color recomposition

We take each denoised \(\hbox {I}_\mathrm{MSB}\) and its corresponding remaining untouched bitplanes, and we reassemble each color component with them, thus, and with the latter, we recompose the image. This latter task is performed by a own MATLAB\(^{\circledR }\) function [27] called reassembler(), see the following code:

figure d

3 Metrics and simulations

In this section, we present a set of metrics for these experiments which are well knowledge in digital image processing [14–17], and which consists in the comparison between: original versus classical mean filtered, and original versus quantum Boolean mean filtering algorithms (outside and inside quantum computer) respectively.

3.1 Metrics

Below, we present the most conspicuous metrics used in digital image processing [14–17].

3.1.1 Mean absolute error (MAE)

This is a conspicuous metric for these cases, which is a quantity used to measure how close forecasts or predictions are to eventual outcomes. The mean absolute error (MAE) for gray scale images is given by

$$\begin{aligned} \hbox {MAE}=\frac{\sum \limits _{r,c} {\left| {I_\mathrm{original} (r,c)-I_\mathrm{denoised} (r,c)} \right| } }{R\times C} \end{aligned}$$
(3)

which for two \(R \times C\) (rows-by-columns) images \(I_\mathrm{original}\) and \(I_\mathrm{denoised,}\) where \(I_\mathrm{denoised}\) means classical processed image, or quantum processed image, interchangeably.

3.1.2 Mean square error (MSE)

MSE indicates average square error of the pixels throughout the image between the original image \(I_\mathrm{original}\) and the classical or quantum processed image \(I_\mathrm{denoised}\), see Figs. 9 and 10. A lower MSE indicates a smaller difference between both images. This means that there is a significant filter concordance. Nevertheless, it is necessary to be very careful with the edges. The formula for the MSE calculation for grayscale images is

$$\begin{aligned} \hbox {MSE}=\frac{\sum \limits _{r,c} {\left( {I_\mathrm{original} (r,c)-I_\mathrm{denoised} (r,c)} \right) ^{2}} }{R\times C} \end{aligned}$$
(4)

Here, \(R\times C\) pixels is the size of the images too, including original image \(I\).

Fig. 9
figure 9

Complete classical image denoising, where MF means mean filtering

Full size image
Fig. 10
figure 10

\(3\times 3\) averaging kernel often used in mean filtering

Full size image

3.1.3 Peak signal-to-noise ratio (PSNR)

PSNR is a term for the ratio between the maximum possible power of an \(I_\mathrm{original}\) and the power of corrupting difference that affects the fidelity of the classical or quantum processed image representation regarding original representation. Because many \(I_\mathrm{original}\) have a very wide dynamic range, PSNR will be expressed in terms of the logarithmic decibel scale.

We will use it as a measure of quality of coincidence between original and classical or quantum denoised versions. It is most easily defined via the mean squared error (MSE) which for two \(R\times C\) (rows-by-columns) gray scale images \(I_\mathrm{original}\) and \(I_\mathrm{denoised}\), that is to say:

$$\begin{aligned} \hbox {PSNR}=10\log _{10} \left( {\frac{\max \left( {I_\mathrm{original} } \right) ^{2}}{\hbox {MSE}}} \right) =20\log _{10} \left( {\frac{\max \left( {I_\mathrm{original} } \right) }{\sqrt{\hbox {MSE}}}} \right) \end{aligned}$$
(5)

Here, \(\max \left( {I_\mathrm{original} } \right) \) is the maximum pixel value of the image. When the pixels are represented using 8 bits per sample, this is 255. More generally, when samples are represented using linear pulse code modulation (PCM) with \(B\) bits per sample, maximum possible value of \(\max \left( {I_\mathrm{original} } \right) \) is \(2^{B}-1\). For color images with three red–green–blue (RGB) values per pixel, the definition of PSNR is the same except the MSE is the sum over all squared value differences divided by image size and by three.

Typical values for the PSNR are between 30 and 50 dB, where higher is better.

3.2 Simulations

In Fig. 9, we can see the complete classical image denoising procedure, which will serve to any type of convolution mask filter.

However, in this case, we use the classical mean filter. The idea of mean filtering is simply to replace each pixel value in an image with the mean (“average”) value of its neighbors, including itself. This has the effect of eliminating pixel values which are unrepresentative of their surroundings. Mean filtering is usually thought of as a convolution filter. Like other convolutions, it is based around a kernel, which represents the shape and size of the neighborhood to be sampled when calculating the mean. Often, a \(3\times 3\) square kernel is used, as shown in Fig. 10, although larger kernels (e.g., \(5\times 5\) squares) can be used for more severe smoothing. (Note that a small kernel can be applied more than once in order to produce a similar but not identical effect as a single pass with a large kernel.)

For these experiments, all images are subjected to MATLAB\(^{\circledR }\) functions explained before, plus others built-in functions which (among other) separate the original image into its color components [27], e.g., the noise was generated using a MATLAB\(^{\circledR }\) R2014a (Mathworks, Natick, MA) [27] built-in function called imnoise. The noise type was salt & pepper, with a noise density of 0.05.

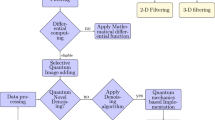
In Fig. 11, we can see the complete quantum Boolean image denoising (for color images). Besides, we can appreciate the seven-level decomposition, processing and recomposition of the noisy image. In detail, we can observe level of color decomposition, bit slicing, classical-to-quantum interface, quantum Boolean mean filtering, quantum-to-classical interface, bit reassembling and, finally, color recomposition.

Fig. 11
figure 11

Complete quantum Boolean image denoising (for color images), where, QuBo, QuBoMF, cl2qu and qu2cl means quantum Boolean, quantum Boolean mean filtering, classical to quantum and quantum to classical, respectively. We must note that: (1) we work with bitplane 7 (MSB) only, while the remaining 7 directly passed to the reconstruction process, i.e., not even they are affected by interfaces, and (2) converters have built-in interfaces; however, we do not show them to avoid complicating the figure

Full size image

On the other hand, first image is Agus in Miami (Fig. 12), which is a color bitmap file format (lossless) [44] of 1,326-by-1,326 pixels with 24 bits per pixel (bpp).

Fig. 12
figure 12

Denoising for Agus in Miami

Full size image

Figure 12 (top-left) shows us the original image used in this experiment; noisy image (top-right); the filtered images, processed by using classical mean filter (middle-left), and quantum Boolean mean filter techniques (middle-right), respectively. Besides, Fig. 12 (down-center) shows the difference pixel-to-pixel between classical denoised versus original (noiseless) and quantum Boolean denoised versus original (noiseless), too. As we can see, there are values of pixels where the difference between two versions is remarkably sensitive.

Figure 13 (top-left) shows us the original noiseless \(\hbox {I}_\mathrm{MSB}\) (from red color component) used in this experiment; noisy \(\hbox {I}_\mathrm{MSB}\) (top-right); the denoised \(\upalpha \), processed by using QBMF (down-left), and the denoised \(\hbox {I}_\mathrm{MSB}\) (down-right), respectively.

Fig. 13
figure 13

Bitplane 7 (MSB) of the red component for Agus in Miami (Color figure online)

Full size image

In Table 2, we can see MAE, MSE and PSNR results for classical and quantum Boolean among original and denoised images. The results are slightly better quantum version than the classical version.

Table 2 Metric of denoising for Agus in Miami: classical versus quantum Boolean
Full size table

This difference in favor of the quantum version is telling us a mismatch between the classical representation of the mean filtering and its quantum Boolean counterpart. This can only be because the noise is concentrated almost exclusively (but fully) in the MSB which is where operates the quantum Boolean version.

Second image is Angelina (Fig. 14), which is a color bitmap file format (lossless) of 1,348-by-1,078 pixels with 24 bits per pixel (bpp).

Fig. 14
figure 14

Denoising for Angelina

Full size image

We have the same noise as in the previous case.

Figure 14 (top-left) shows us the original image used in this experiment; noisy image (top-right); the filtered images, processed by using classical mean filter (middle-left), and quantum Boolean mean filter techniques (middle-right), respectively. Besides, Fig. 14 (down-center) shows the difference pixel-to-pixel between classical denoised versus original (noiseless) and quantum Boolean denoised versus original (noiseless), too. As we can see, there are values of pixels where the difference between two versions is remarkably sensitive here too. However, such is less than in the previous case. It has to do with a lower edges richness and texture level of Angelina versus Agus in Miami. Others important responsible factors for this difference are constituted by: (a) Agus in Miami has higher values in its LUMA [14–17]; (b) Agus in Miami has more brightness and contrast; and (c) Agus in Miami is larger than Angelina.

This later attribute seems irrelevant to naked eye; however, it is not, since, to process more qubits, it automatically increases the detrimental intervention of bad (or poorly) modeled noise. Besides, a larger image means more openness in the time window of the process which may be more exposed to quantum decoherence [22, 35–42]. This is a topic that should be further investigated if we want to process images of very high resolution in a quantum computer.

Figure 15 (top-left) shows us the original noiseless \(\hbox {I}_\mathrm{MSB}\) (from red color component) used in this experiment; noisy \(\hbox {I}_\mathrm{MSB}\) (top-right); the denoised \(\alpha \), processed by using QBMF (down-left), and the denoised \(\hbox {I}_\mathrm{MSB}\) (down-right), respectively.

Fig. 15
figure 15

Bitplane 7 (MSB) of the red component for Angelina (Color figure online)

Full size image

In Table 3, we can see MAE, MSE and PSNR results for classical and quantum Boolean among original and denoised images. Here too, the results are slightly better quantum version than the classical version.

Table 3 Metric of denoising for Angelina: classical versus quantum Boolean
Full size table

Finally, last image is Lena (Fig. 16), which is a color bitmap file format (lossless) of 512-by-512 pixels with 24 bits per pixel (bpp).

In this case, identical considerations to previous cases are used regarding present noise in the image. Tests with other types of noise gave identical comparative results

Fig. 16
figure 16

Denoising for Lena

Full size image

Figure 16 (top-left) shows us the original image used in this experiment; noisy image (top-right); the filtered images, processed by using classical mean filter (middle-left), and quantum Boolean mean filter techniques (middle-right), respectively. Besides, Fig. 16 (down-center) shows the difference pixel-to-pixel between classical denoised versus original (noiseless) and quantum Boolean denoised versus original (noiseless), too.

Figure 17 (top-left) shows us the original noiseless \(\hbox {I}_\mathrm{MSB}\) (from red color component) used in this experiment; noisy \(\hbox {I}_\mathrm{MSB}\) (top-right); the denoised \(\upalpha \), processed by using QBMF (down-left), and the denoised \(\hbox {I}_\mathrm{MSB}\) (down-right), respectively.

Fig. 17
figure 17

Bitplane 7 (MSB) of the red component for Lena (Color figure online)

Full size image

In Table 4, we can see MAE, MSE and PSNR results for classical and quantum Boolean among original and denoised images. Here too, the results are slightly better quantum version than the classical version.

Table 4 Metric of denoising for Lena: classical versus quantum Boolean
Full size table

Based on the analysis of the comparison between Agus, Angelina and Lena, we can understand why Lena is showing the best fit between classical and quantum Boolean version of filters. This can be seen clearly in the metrics of Tables 2, 3 and 4, where we obtain the lower difference between MAE and MSE among noiseless original and the respective denoised versions from three images so far treated. In return, this image has the highest difference value of PSNR among noiseless original and the respective denoised versions from three images so far treated. The reasons are clear: (a) Lena has lower values in its LUMA [14–17]; (b) Lena has less brightness and contrast; and (c) Lena is the smallest.

4 Conclusions and future works

A quantum Boolean image denoising methodology was presented in this work. A classical Boolean version of such methodology was presented too. As we have seen, the quantum Boolean version of the filter works with CBS, exclusively. To achieve this, we first decompose the image into its three color components, i.e., red, green and blue. Then, we get the bitplanes for each color, e.g., 8 bits per pixel, i.e., 8 bitplanes per color. From then on, we work with the bitplane corresponding to the MSB of each color, exclusive manner. After a classical-to-quantum interface (which includes a classical inverter), we have a quantum Boolean version of the image within the quantum machine. This methodology (which works with CBS, no other) allowed us to avoid the problem of quantum measurement, which alters the results of the measured except in the case of CBS. Summing up, this methodology will enable: (1) a simpler development of logic quantum operations, where they will closer to those used in the classical logic operations, and (2) building simple and robust classical-to-quantum and quantum-to-classical interfaces. Said so far is extended to quantum algorithms outside image processing too. After filtering of the inverted version of MSB (inside quantum machine), the result passes through a quantum-classical interface (which involves another classical inverter) and then proceeds to reassemble each color component and finally the ending filtered image. Finally, this methodology minimizes the impact of decoherence [45–50], not only for quantum image denoising but also for quantum image segmentation [51].

In a special section on metrics and simulations, we use MAE, MSE, and peak signal-to-noise ratio (PSNR) as metrics to compare the original noiseless image versus its denoised versions, i.e., classical and quantum Boolean. The chosen denoising methods for simulations were the classic mean filter and its quantum Boolean version. The results of both simulations (outside and inside of quantum computer, respectively) show the existence of notable differences between them, which are obvious considering that each version of the algorithm is implemented in completely different spaces. However, although they were different, the quantum Boolean results were superior to those obtained by the classical technique, that is to say, all images gave more appropriate metric values. The latter is clearly seen in the computer simulations.

Clearly, the next step is the application of this technique to signal and video processing on a quantum computer [29, 30], and thus, we may exploit all its computational power and huge storage capacity. It is right to think that quantum computers will have more and more ability to absorb the computational cost of an almost unlimited number of operations in unit time in the near future. This way, quantum technology will become the main platform for multimedia real-time implementations (such as processing, storage and transmission of music and video) which combined with quantum cryptography will allow it to become the epitome of multimedia on mobile. Thus, the new quantum technology will get move completely to the current digital technology in every today imaginable and unimaginable application.

Finally, the classical technique (i.e., mean filtering) was implemented in MATLAB\(^{\circledR }\) R2014a (Mathworks, Natick, MA) [27] on a notebook with Intel\(^{\circledR }\) Core\(^\mathrm{TM}\) i5 CPU M 430 @ 2.27 GHz and 6 GB RAM on Microsoft\(^{\circledR }\) Windows 7\({\copyright }\) Home Premium 32 bits. Besides, a simulated version of quantum implementations was done on a GPU cluster, NVIDIA\(^{\circledR }\) Tesla\({\copyright }\) 2050 GPU [52] with a peak performance of approximately 500 GFLOPS, with an achieved performance of approximately 250 GFLOPS in OpenCL. The GPU needed approximately 2.5 GB of bandwidth with InfiniBand connectivity at quad data rate (QDR) QLogic\(^{\circledR }\) [53] or 40 GB speeds.