Development of a Finite Element Program for Determining Mat Pressure in the Canning Process of a Catalytic Converter

Abstract

A catalytic converter in the automotive exhaust system, consists of a substrate in the center, a mat outside the substrate and a can outside the mat. Since the substrate is brittle, it is wrapped in mats and press-fitted into a can. If the mat pressure developed during the canning process is excessive, it might cause the fracture of the substrate. A finite element program for finding mat pressures on the substrate in the canning process was developed in Microsoft EXCEL. It is a user-friendly program with easy input and graphical output. By modeling the substrate, the mat and the can as simply as possible, fixing the number of elements and iterations and taking into account only a small part of the output radial distance changes in the current step to calculate the input pressure in the next step, the material nonlinear problem was solved successfully in Microsoft EXCEL. The solutions were compared to ABAQUS solutions and found to be accurate.

1 Introduction

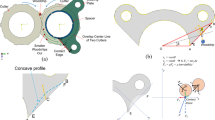
A catalytic converter is a vehicle emissions control device that converts toxic pollutants in exhaust gases to less toxic pollutants [1]. It consists of a substrate in the center, a mat outside the substrate and a can outside the mat as shown in Fig. 1. A substrate is a ceramic body with a number of small axial openings through which the exhaust gas passes. To increase the surface area exposed to the exhaust gas, the wall thickness of the openings were reduced. Then it is more likely that the substrate will be subjected to brittle fracture. Since the substrate is brittle, it is wrapped in a soft mat and inserted into a steel can. It is called canning.

Fig. 1

Substrate, mat and can in a catalytic converter

The contact pressure on the substrate depends mainly on how much the mat is compressed between the substrate and the can. If the contact pressure is too low, the substrate would slide, hit the can and be damaged when the car is in severe acceleration or deceleration. On the contrary, if the contact pressure is too high, the substrate would be damaged due to the contact pressure itself.

It is important to know the contact pressure on the substrate in the canning process. Kyoung [2] predicted the mat pressure distribution either in the canning process or under operation conditions using commercial software. He assumed that the mat material follows the hyperfoam model.

Instead of using commercial software, a small finite element analysis can be carried out in Microsoft EXCEL. Its matrix manipulation capability enables it to carry out the analysis. Several authors [3–7] used EXCEL to solve finite element problems. Using EXCEL to solve such problems is shown to be common when teaching the FEM to students. Because the finite element program in EXCEL cannot be fully-flexible, only very small number of elements was used in their applications. The first author of this paper was interested in the finite element analysis using EXCEL and published a book on it [8]. In this paper, a finite element program was developed in EXCEL and the mat pressure distribution in the canning process was predicted. It was a rather large-size problem for the program and furthermore the iteration process to get a converged solution was required.

2 Finite Element Analysis

A finite element program for finding the contact pressure on the substrate in canning of a catalytic converter was developed in EXCEL. It is a user-friendly program with easy input and graphical output. To check the accuracy of our solution, it was compared with the solution computed in ABAQUS.

2.1 Geometry of the Substrate Outer Surface

The substrate is of circular or oval section. The profile of an oval section is constructed from two circular arcs shown in Fig. 2. The first arc with its center at $\left( {{\text{x}}_{1} ,0} \right)$ and radius ${\text{r}}_{1}$ subtends an angle $\uptheta_{1}$. The second arc with center at $\left( {0,{\text{y}}_{2} } \right)$ and radius ${\text{r}}_{2}$ subtends an angle $\uptheta_{2}$.

Fig. 2

Creation of an oval section by combining two arcs

The semi-major and minor axes of an oval section are

$$a = {\text{x}}_{1} + {\text{r}}_{1}$$

(1)

$$b = y_{2} + {\text{r}}_{2}$$

(2)

Note that $y_{2}$ is negative.

The sum of the subtended angles is

$$\theta_{1} + \theta_{2} = 90^\circ$$

(3)

The horizontal and vertical distances from the origin to the point P where the two arcs are connected are

$$x_{1} + r_{1} \,{ \cos }\uptheta_{1} = r_{2} \,{ \sin }\uptheta_{2}$$

(4)

$$r_{1} \,{ \sin }\uptheta_{1} = r_{2} \,{ \cos }\uptheta_{2} + y_{2}$$

(5)

We have five Eqs. (1)–(5) with eight unknowns. Three of eight unknowns should be given to determine all unknowns.

2.2 Finite Element Modeling of the Substrate, Mat and Can

A finite element program was developed in EXCEL. Using matrix multiplication, matrix transverse and matrix inverse functions in EXCEL, we can construct a finite element equation and solve it. Due to difficulties in creating fully-automatic program in EXCEL, however, it is difficult to develop a program for a large-sized problem and even more difficult to develop a non-linear program.

The problem should be idealized as far as possible to be solved in EXCEL. Noting that the material of a substrate is softer than the steel but sufficiently hard compared to the material of a mat, the substrate can be idealized as being rigid. Then it is not necessary to model the substrate itself. Only the profile of a substrate is needed to calculate the gap between the substrate outer surface and the can inner surface.

The material of a mat shows a material nonlinearity as shown in Fig. 3. We found that it was not needed to model the mat. Only the mat pressure was calculated from the gap between the substrate and can and applied on the can inner surface.

Fig. 3

Nonlinear compression behavior of a mat

The can was assumed to be 2-dimensional and can resist both bending and membrane stresses. It was modeled as a beam.

It is not easy to develop a flexible, i.e. being able to adapting itself to different number of elements or different number of iterations, program in EXCEL. Therefore we conveniently fixed the number of elements and the number of iterations. In this way, a dedicated special finite element program using 35 elements and 20 iterations was developed.

2.3 Finite Element Procedures

• (a) Input a, b and $x_{1}$. Calculate $y_{2} , r_{1}$, $r_{2}$, $\theta_{1}$ and $\theta_{2}$ sequentially.

  $$y_{2} = b - r_{2}$$

  (6)
  $$r_{1} = a - x_{1}$$

  (7)
  $$r_{2} = \frac{{\left( {a^{2} + b^{2} - 2ar_{1} } \right)}}{{2(b - r_{1} )}}$$

  (8)
  $$\theta_{1} = \cos^{ - 1} \frac{{x_{1} }}{{r_{2} - r_{1} }}$$

  (9)
  $$\theta_{2} = \frac{\pi }{2} - \theta_{1}$$

  (10)

• (b) Input $t_{m}$ and $g_{t}$. Calculate $\epsilon$.

  $$\epsilon = \frac{{g_{t} }}{{t_{m} }} - 1$$

  (11)

• (c) Input $\mu_{i}$ and $\alpha_{i}$, i.e. coefficients and exponents in Ogden hyperfoam model. The values are listed in Table 1. Calculate $p_{m}$.

  Table 1 Input mechanical properties and dimensions

  $$p_{m} = \frac{2}{1 + \epsilon}\sum\limits_{i = 1}^{N} {\frac{{\mu_{i} }}{{\alpha_{i} }}\left[ {(1 + \epsilon )^{{\alpha_{i} }} - 1} \right]}$$

  (12)

• (d) Determine the number of elements in each arc so that the element size in each arc similar to each other. In this way, the first arc is equally divided into 19 elements and the second arc into 16 elements. Nodes #17–#35 are on the first arc and node #1–#17 are on the second arc.

  $$\frac{{N_{2} }}{{N_{1} }} \approx \frac{{r_{2} \theta_{2} }}{{r_{1} \theta_{1} }}$$

  (13)

• (e) Model the can as a 2-dimensional beam. Construct element stiffness matrices and assemble them.

The beam is of rectangular cross section with a unit width and thickness t. The sectional area and second moment of inertia are

$$A = t$$

(14)

$$I_{z} = t^{3} /12$$

(15)

The beam in Fig. 4 can resist uniform tension and compression as well as bending. The element stiffness matrix in local coordinate system is

$$\frac{{EI_{z} }}{{L^{3} }}\left[ {\begin{array}{*{20}l} \alpha \hfill & 0 \hfill & 0 \hfill & { - \alpha } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {12} \hfill & {6L} \hfill & 0 \hfill & { - 12} \hfill & {6L} \hfill \\ 0 \hfill & {6L} \hfill & {4L^{2} } \hfill & 0 \hfill & { - 6L} \hfill & {4L^{2} } \hfill \\ { - \alpha } \hfill & 0 \hfill & 0 \hfill & \alpha \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - 12} \hfill & { - 6L} \hfill & 0 \hfill & {12} \hfill & { - 6L} \hfill \\ 0 \hfill & {6L} \hfill & {4L^{2} } \hfill & 0 \hfill & { - 6L} \hfill & {4L^{2} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {u_{1}^{{\prime }} } \hfill \\ {v_{1}^{{\prime }} } \hfill \\ {\theta_{z1} } \hfill \\ {u_{2}^{{\prime }} } \hfill \\ {v_{2}^{{\prime }} } \hfill \\ {\theta_{z2} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {F_{{x{\prime }1}} } \\ {F_{{y{\prime }1}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {M_{z1} } \\ {F_{{x{\prime }2}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {F_{{y{\prime }2}} } \\ {M_{z2} } \\ \end{array} } \\ \end{array} } \right\}$$

(16)

where $\upalpha = AL^{2} /I_{z}$. Note that the nodes are on the mid-surface of the can.

Fig. 4

Forces and moment on a beam element

Converting it into global coordinate system in Fig. 5

Fig. 5

Global and local coordinate system

$$\frac{{EI_{z} }}{{L^{3} }}\left[ {\begin{array}{*{20}l} c \hfill & { - s} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ s \hfill & c \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & c \hfill & { - s} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & s \hfill & c \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \alpha & 0 & 0 & { - \alpha } & 0 & 0 \\ 0 & {12} & {6L} & 0 & { - 12} & {6L} \\ 0 & {6L} & {4L^{2} } & 0 & { - 6L} & {4L^{2} } \\ { - \alpha } & 0 & 0 & \alpha & 0 & 0 \\ 0 & { - 12} & { - 6L} & 0 & {12} & { - 6L} \\ 0 & {6L} & {4L^{2} } & 0 & { - 6L} & {4L^{2} } \\ \end{array} } \right]$$

(17)

$$\left[ {\begin{array}{*{20}c} c & s & 0 & 0 & 0 & 0 \\ { - s} & c & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & c & s & 0 \\ 0 & 0 & 0 & { - s} & c & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{1} } \\ {v_{1} } \\ {\theta_{z1} } \\ {u_{2} } \\ {v_{2} } \\ {\theta_{z2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {F_{x1} } \\ {F_{y1} } \\ {M_{z1} } \\ {F_{x2} } \\ {F_{y2} } \\ {M_{z2} } \\ \end{array} } \right\}$$

where ${\text{c}} = \cos \theta$, ${\text{s}} = \sin \theta$.

The force vector is

$$\left\{ {\begin{array}{*{20}c} {F_{x1} } \\ {F_{y1} } \\ {M_{z1} } \\ {F_{x2} } \\ {F_{y2} } \\ {M_{z2} } \\ \end{array} } \right\} = p_{m} \frac{L}{2}\left\{ {\begin{array}{*{20}c} { - \sin \theta } \\ {\cos \theta } \\ 0 \\ { - \sin \theta } \\ {\cos \theta } \\ 0 \\ \end{array} } \right\}$$

(18)

The global finite element equations are constructed by assembling them.

$$[K]\{ u\} = \{ f\}$$

(19)

The equations can be solved by multiplying the inverse matrix $[K]^{ - 1}$ on both sides.

$$\{ {\text{u}}\} = [K]^{ - 1} \{ f\}$$

(20)

• (f) The gap between the substrate and the can changed due to the deformation of the can.

The radial distance to the mat—can interface in the radial direction toward node i is

$$R_{i}^{*} = \sqrt {\left[ {\left( {r_{1} + g_{t} } \right){ \cos }\frac{{(36 - i)\theta_{1} }}{{N_{1} }} + u_{i} } \right]^{2} + \left[ {\left( {r_{1} + g_{t} } \right){ \sin }\frac{{(36 - i)\theta_{1} }}{{N_{1} }} + v_{i} } \right]^{2} } \quad ({\text{i}} = 17 - 36)$$

(20a)

$$R_{i}^{*} = \sqrt {\left[ {\left( {r_{2} + g_{t} } \right){ \sin }\frac{{(i - 1)\theta_{2} }}{{N_{2} }} + u_{i} } \right]^{2} + \left[ {\left( {r_{2} + g_{t} } \right){ \cos }\frac{{(i - 1)\theta_{2} }}{{N_{2} }} + v_{i} } \right]^{2} } \quad ({\text{i}} = 1 - 17)$$

(20b)

If we took the whole change into account in calculating new mat pressures, the iteration might not converge. Only a small part $\upeta$ of the radial distance change should be taken into account to avoid diverging. In the first iteration, a very small $\upeta$ was used and after that increased gradually to accelerate the convergence. For example, $\upeta = 0.0 6- 0. 4 8$ was used in the iteration shown in Fig. 6. The deformed shape from the converged displacements was plotted in Fig. 7.

Fig. 6

Converged horizontal and vertical displacements at nodes on y = 0 and x = 0

Fig. 7

Deformed shape of a can (deformation amplification factor 5)

$$R_{i} = (1 -\upeta)R_{i - 1} +\upeta\,R_{i}^{*}$$

(21)

• (g) Determine new $\epsilon$.

$$\epsilon = \frac{{R_{i} - r_{i} }}{{t_{m} }} - 1$$

(22)

Repeat step (c)–(g) until the iteration number 20 is reached.

The deformed can surface was drawn together with the undeformed can surface and the substrate outer surface in Fig. 7. The can deformation is amplified by a factor of 5.

2.4 Comparison with ABAQUS Solution

Using ABAQUS, the substrate and mat as well as the can were modeled with plane strain elements as shown in Fig. 8a. Note that nearly half the undeformed mat is outside the can at the beginning. Contact at the substrate—mat interface and at the mat—can interface were activated. Furthermore, at the mat—can interface shrink fit was activated [9, 10]. The shrink-fitted mat inside the can is shown in Fig. 8b.

Fig. 8

Coarse mesh created in ABAQUS

To check the effect of mesh refinement, both a coarse mesh and a fine mesh were created. In the coarse mesh shown in Fig. 8, the can was divided into 72 * 4 elements while in the fine mesh it was divided into 144 * 8 elements.

The displacements at the selected five points (a)–(e) on the can mid-surface were compared to the solution given by our program. The displacements fell in the region ${\text{u}} \le 0$ and ${\text{v}} \ge 0$ as shown in Fig. 9. See the deformed shape in Fig. 7. The can tends to become more circular due to the mat pressure. It is interesting to note that the displacements became closer to the solution given by our program as the mesh was refined. Note that the more efficient beam elements were used in our program while the plane strain elements were used in ABAQUS.

Fig. 9

Comparison of displacement components at five selected nodes

To see the pressure distribution, the minimum principal stress was plotted in Fig. 10. Along the mat—can interface, the mat pressure had its minimum at x = 0 and the maximum at y = 0. In the radial direction, the mat pressure decreased as the radial distance increased. It is interesting to note that the pressure became closer to the solution given by our program as the mesh was refined. The mat pressures by our program in Fig. 11 were on the mat—can interface.

Fig. 10

Contour plot of the minimum principal stress in ABAQUS

Fig. 11

Comparison of mat pressure versus radial distance along x = 0 and y = 0

Let’s consider the equilibrium of radial forces on the mat element neglecting the tangential forces in Fig. 12. It is found that the mat pressure is inversely proportional to the radial distance. Since the mat pressure on the substrate is the most important pressure, the pressures in the mat were converted to the pressure on the substrate.

Fig. 12

Equilibrium of radial forces on the mat element

Along the first and second arc, respectively

$$p_{e} = pr/r_{1} \quad {\text{and}}\quad p_{e} = pr/r_{2}$$

(23)

As shown in Fig. 13, the equivalent pressure, i.e. the converted pressures on the substrate were nearly constant. It tells us that the inverse proportionality holds between the mat pressure and the radial distance. It is interesting to note that the equivalent pressures became also closer to the solution given by our program as the mesh was refined.

Fig. 13

Comparison of equivalent pressure, i.e. converted mat pressure on the substrate

3 Conclusions

A finite element program for finding mat pressures on the substrate in canning of a catalytic converter was developed on Microsoft EXCEL. It is a user-friendly program with easy input and graphical output. By modeling the substrate, mat and can as simply as possible, fixing the number of elements and iterations and taking only a small part of the output radial distance change in the current step into account to calculate the input pressure in the next step, the material nonlinear problem was solved successfully.

To check the accuracy of our program’s solution, the same problem was modeled more realistically and solved using ABAQUS. To check the effect of mesh refinement in the ABAQUS mode, both a coarse mesh and a fine mesh were used. Both the can displacements and the mat pressures were in good agreement with our program solution. Furthermore, as the mesh was refined, the ABAQUS solution approached our program’s solution. Hence the accuracy of our program solution was confirmed.

It was determined that the mat pressure is inversely proportional to the radial distance from each arc center. The pressure on the substrate outer surface can be determined from the pressure on the can inner surface by the inverse proportionality.