A Cartesian Grid Method for Solving Stokes Equations with Discontinuous Viscosity and Singular Sources

Abstract

In this paper, we present a new finite difference scheme for solving incompressible, steady stokes equations in discontinuous domains. While solving two phase Stokes equations, across some interfaces, there are discontinuities in the pressure, viscosity and velocity. Since, these jump conditions are coupled together, it is difficult to discretise and solve the system of equations accurately. We apply the augmented approach introduced by Li et al. (Int J Numer Meth. Fluids 44:33–53, 2004) to decouple these jump conditions. A new finite difference method is then developed and presented to solve the resulting augmented system of Stokes equations. Points of intersection of grid lines and the interface are used as a node in the finite difference stencil and jump conditions are then used to determine the values at these intersection points. Numerical solutions are compared with the corresponding analytical solutions and those of the augmented immersed interface method. The method is found to be second order accurate for almost all the variables in the infinity norm.

1 Introduction

The incompressible, two phase Stokes equations with discontinuities in the viscosity and with singular source terms are often encountered in many practical applications in CFD. Over the last few decades, there has been an ongoing quest for new numerical methods to solve fluid problems with interfaces. Most of the numerical works on such problems involved mainly the use of immersed boundary (IBM) [1] or immersed interface (IIM) methods [2] on Cartesian grids. In the present work, a new immersed interface finite difference scheme, based on Cartesian coordinates, is presented for solving Stokes equations with arbitrary immersed interfaces in two dimensions. The originality of the scheme lies in the use of additional values at interfacial points (points at which grid lines intersect the interface) as nodes in finite difference stencil, which allows straightforward use of the standard finite difference approximations. Jump conditions of the variable and flux are then used to determine these interfacial values.

The paper is arranged as follows. Section 2 deals with mathematical formulation which covers governing equations, jump conditions and their discretisation procedure. Section 3 deals with the numerical results and Sect. 4 with the conclusion.

2 Mathematical Formulation

2.1 Governing Equations and the Jump Conditions

Assume that Ω is a domain in R² and Γ is an arbitrary piecewise smooth curve in Ω as shown in Fig. 1a. Level set formulation introduced by Osher and Sethian [3] is used to represent the interface Γ. Square domain consists of the union of two sub-domains Ω⁺ and Ω⁻ separated by a closed interface Γ. Two dimensional steady Stokes equations can be represented as

Fig. 1

a Uniform cartesian grid in two-dimensions with interface Γ separating the whole domain into two separate sub domains Ω ⁻ and Ω ⁺. b Geometry at an irregular point (x _i ,y _j ) and its normal projection (x _α , y _α ) on Γ; (ξ,η) is the local coordinate system aligned with Γ at (x _α , y _α )

$$\nabla p = \mu \Delta {\text{u}} + G + \int\limits_{\varGamma } {F(s)\delta (x - X(s))ds} ,\,\,\,\,\,\,\,\,x \in \varOmega ,$$

(1)

$$\nabla {\text{u}} = 0,\,\,\,x \in \varOmega ,\,$$

(2)

where u = (u, v) denotes the velocity vector, p denotes the pressure, F(s) is the singular source term, G(x) denotes the bounded force which may be discontinuous across Γ as well when Γ is parameterized by s. The viscosity μ is supposed as a piecewise constant

$$\mu = \left\{ {\begin{array}{*{20}c} {\mu^{ + } ,} \hfill & {\varGamma > 0} \hfill \\ {\mu^{ - } ,} \hfill & {\varGamma < 0} \hfill \\ \end{array} } \right.$$

Assume Γ ∈ C², $\hat{F}_{1}$(s) ∈ C¹, and $\hat{F}_{2}$(s) ∈ C¹ where $\hat{F}_{1}$(s) = F(s) · n and $\hat{F}_{2}$(s) = F(s); n is the normal and τ is tangential to the interface, respectively. Jump conditions across Γ can be written as.

$$[p] = 2\left[ {\mu \frac{{\partial \varvec{u}}}{\partial \xi } \cdot \varvec{n}} \right] + \hat{F}_{1} ,$$

(3)

$$\left[ {\frac{\partial p}{\partial \xi }} \right] = \left[ {\varvec{G} \cdot \varvec{n}} \right] + \frac{{\partial \hat{F}_{2} }}{\partial n} + 2\left[ {\mu \frac{{\partial^{2} }}{{\partial \eta^{2} }}(\varvec{u} \cdot \varvec{n})} \right],$$

(4)

$$\left[ {\mu \frac{{\partial \varvec{u}}}{\partial \xi } \cdot\varvec{\tau}} \right] + \left[ {\mu \frac{{\partial \varvec{u}}}{\partial \eta } \cdot \varvec{n}} \right] + \hat{F}_{2} = 0,$$

(5)

$$\left[ {\mu \Delta \cdot \varvec{u}} \right] = 0.\,$$

(6)

Balancing force along the n-axis at Γ gives us the jump condition (3) while the balancing forces along the τ-axis at Γ gives the jump condition (5). Applying the divergence operator to Eq. (1) gives jump condition (4) while the last jump condition (6) is derived from incompressibility condition ∇ · u = 0.

Since, these jump conditions are coupled together, it is difficult to discretise and solve the system of equations accurately. We therefore apply the augmented approach introduced by Li et al. in 2007 [4] to decouple these jump conditions. Jumps ([μu](s), [μv](s)) = ([μu](s), [μv](s)) are introduced as two augmented variables so that these jump conditions can be decoupled. Denote

$$\varvec{q} = (q_{1} ,q_{2} )^{T} = \left( {[\tilde{u}],[\tilde{v}]} \right)^{T}$$

Let p, u and v denote the solutions of the system of Eqs. (1)–(2). Then, the variables $\tilde{u}$,$\tilde{v}$, p and q satisfy the following set of equations:

$$\left\{ \begin{aligned} & \Delta p = \nabla \cdot \varvec{G} \\ & [p] = \hat{F}_{1} - 2\frac{{\partial \varvec{q}}}{\partial \tau } \cdot\varvec{\tau}\\ & \left[ {\frac{\partial p}{\partial n}} \right] = \frac{{\partial \hat{F}_{2} }}{\partial \tau } + 2\frac{{\partial^{2} }}{{\partial \eta^{2} }}(\varvec{q} \cdot \varvec{n}) + \left[ {\varvec{G} \cdot \varvec{n}} \right] \\ \end{aligned} \right.$$

(7)

$$\left\{ \begin{aligned} & \Delta \tilde{u} = p_{x} \, - \, \varvec{ G}_{1} , \\ & [\tilde{u}] = q_{1} ,\,\,\left[ {\frac{{\partial \tilde{u}}}{\partial n}} \right] = \,\left( {\hat{F}_{2} + \frac{{\partial \varvec{q}}}{\partial \tau } \cdot \varvec{n}} \right)\sin \theta - \left( {\frac{{\partial \varvec{q}}}{\partial \tau } \cdot\varvec{\tau}} \right)\cos \theta , \\ \end{aligned} \right.$$

(8)

$$\left( \begin{aligned} & \Delta \tilde{v} = p_{y} - \varvec{G}_{2} , \\ & [\tilde{v}] = q_{2} ,\, \, \left[ {\frac{{\partial \tilde{v}}}{\partial n}} \right] = - \left( {\hat{F}_{2} + \frac{{\partial \varvec{q}}}{\partial \tau } \cdot \varvec{n}} \right)\cos \theta - \left( {\frac{{\partial \varvec{q}}}{\partial \tau } \cdot\varvec{\tau}} \right)\sin \theta , \\ & \left[ {\frac{{\tilde{u}}}{\mu }} \right] = 0,\,\,\,\,\,\,\,\,\left[ {\frac{{\tilde{v}}}{\mu }} \right] = 0 \\ \end{aligned} \right.$$

(9)

Here, θ denotes the angle between x-axis and n-axis. These jump conditions are derived and explained in detail in [4]. It is worth mentioning that this system of partial differential equations is an elliptic system in which we have to solve all the equations simultaneously. If q is known to us, pressure jump conditions can be calculated. Hence pressure Eq. (7) can be solved independently. After solving for the pressure, u and v can be solved from the Eqs. (8) and (9) respectively.

2.2 Discretisation Procedure

Consider a uniform cartesian grid [a, b] × [c, d] in the whole domain as shown in Fig. 1a. The grid points are denoted by (x_i, y_j) for 0 ≤ i ≤ m, 0 ≤ j ≤ n. These grid points are categorised into two classes: regular and irregular grid points. A grid point is classified as irregular if the finite difference stencil resulting from the corresponding derivatives intersects Γ. Otherwise; it is termed as a regular grid point.

For regular grid points, finite difference approximations of arbitrary order, derived from a Taylor series expansion can be directly used. We use a Higher Order Compact (HOC) finite difference scheme proposed by kalita et al. [5] for discretisation. The idea is to use the original partial differential equation to substitute the leading truncation error terms in the finite difference equation. We begin by considering a general poisson equation ∇²u = f in variable u and forcing function f defined on the whole domain. For example, HOC finite difference formulation at a regular point (x_i, y_j) for $\frac{{\partial^{2} u}}{{\partial x^{2} }}$ can be written as

$$\frac{{\partial^{2} u}}{{\partial x^{2} }} = \delta x^{2} u_{i,j} - \frac{{dx^{2} }}{12}\left( {\frac{{\partial^{2} f}}{{\partial x^{2} }} - \delta x^{2} \delta y^{2} u_{i,j} } \right)$$

(10)

Here, δx² and δy² denote the standard central difference approximations respectively. The jump conditions across the interface can be written as

$$[u] = u^{ + } - u^{ - } = \hat{C}$$

(11)

$$[u_{\xi } ] = u_{\xi }^{ + } - u_{\xi }^{ - } = \sigma ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,[u_{\eta } ] = u_{\eta }^{ + } - u_{\eta }^{ - } = \lambda .$$

(12)

with [.] denoting the jump, the superscripts “+” and “−” represent the variables in the Ω⁺ and Ω⁻ regions respectively. Since the jump conditions are usually defined in normal (ξ-axis) or tangential (η-axis) direction of the interface, we introduce local coordinates (ξ, η) aligned with the interface at (X, Y) (see Fig. 1b), as

$$\begin{aligned} & \xi = (x - x_{\alpha } )\cos \theta + (y - y_{\alpha } )\sin \theta , \\ & \eta = - (x - x_{\alpha } )\sin \theta + (y - y_{\alpha } )\cos \theta , \\ \end{aligned}$$

where θ is the angle between +ve x-axis and the normal direction. Transforming the jump condition on u through local coordinate system and then differentiating it with respect to x and y yields

$$[u_{x} ] = [u_{\xi } ]\cos \theta - [u_{\eta } ]\sin \theta$$

(13)

$$[u_{y} ] = [u_{\xi } ]\sin \theta + [u_{\eta } ]\cos \theta$$

(14)

Since, Taylor series expansion, which provides the platform for finite difference approximations, is not valid for non-smooth functions, standard approximations fail to yield correct numerical solutions near the interface. Hence, a new modified finite difference is developed to discretise the governing equation at irregular points. We use standard central difference formulas including interfacial points (points at which grid lines intersect the interface) nodes in the stencil. The two jump conditions are then used to determine the values at these interfacial points at a desired order of accuracy. We consider a dimension by dimension splitting approach for discretization. We will only derive the one dimensional formula on the segment [x_i−1, x_i+2] × {y_j}. Other cases are duplication. For example, consider the situation shown in Fig. 2.

Fig. 2

Schematic diagram of general uniform grid stencil on the segment [x _i−1, x _i+2 ] × {y _j } with an interface Γ located at point x _α between irregular nodes x _i and x _i+1

For the irregular grid point “x_i” depicted in Fig. 2, we discretise the derivative using the nodes x_i−1, x_i and the interfacial point x as

$$\frac{{\partial^{2} u}}{{\partial x^{2} }} = \frac{{\frac{{u^{ - } - u_{i} }}{{x_{\alpha } - x_{i} }} - \frac{{u_{i} - u_{i - 1} }}{dx}}}{{\frac{{x_{\alpha } - x_{i} }}{2} + \frac{dx}{2}}}$$

(15)

Second order accurate one sided finite difference formula for $u_{x}^{ - }$ using three points on the left side of Γ can be written as

$$u_{x}^{ - } = \frac{{dx\left( {dx + 2dx_{\alpha }^{ - } } \right)u^{ - } - \left( {dx + dx_{\alpha }^{ - } } \right)^{2} u_{i} + \left( {dx_{\alpha }^{ - } } \right)^{2} u_{i - 1} }}{{dx\,dx_{\alpha }^{ - } \left( {dx + dx_{\alpha }^{ - } } \right)}}$$

(16)

Similarly expression for $u_{x}^{ + }$ can be written as

$$u_{x}^{ + } = \frac{{ - dx\left( {dx + 2dx_{\alpha }^{ + } } \right)u^{ + } + \left( {dx + dx_{\alpha }^{ + } } \right)^{2} u_{i + 1} - \left( {dx_{\alpha }^{ + } } \right)^{2} u_{i + 2} }}{{dx\,dx_{\alpha }^{ + } \left( {dx + dx_{\alpha }^{ + } } \right)}}$$

(17)

Substituting the values of $u_{x}^{ - }$ and $u_{x}^{ + }$ into Eq. (13), we get an equation in two unknowns u⁺ and u⁻. The first jump condition Eq. (11) is the second equation in variables u⁺ and u⁻. This system of two equations in two unknown variables can be easily solved analytically to find initial values of u⁺ and u⁻. These values can be substituted in the approximation given in Eq. (16). It is worth mentioning that we have considered the quantities u_i−1, u_i, u_i+1 and u_i+2 as constants in our system of equations. The reason is that, the initial guess is normally set equal to zero at all grid nodes. These values are updated at every iteration and the numerical solution is iterated till it converges towards the correct solution.

Special cases might arise when there is a scarcity of irregular points or when the grid point coincides with the interfacial point. In the former case, one can use a first order accurate formula for $u_{x}^{ - }$ or $u_{x}^{ + }$ that will only involve u_i and u_i+1 as nodes in the stencil. In the latter case, the grid point may be considered lying in either Ω⁺-region or Ω⁻-region and the modified difference scheme can be employed.

3 Results and Discussion

Two numerical examples are presented to check the efficiency of our methodology. Level set function ϕ is given as ϕ = x² + y² − 1 and the analytical solution is known under different situations. Denote by $L_{p}^{\infty }$ and $L_{u}^{\infty }$, infinity norm of error at all the grid nodes for pressure and velocity, respectively and $L_{u}^{\infty } = \left( {\frac{{L_{u}^{\infty } + L_{v}^{\infty } }}{2}} \right)$.

Example 1

We start with an example where the velocity is smooth and pressure, viscosity are discontinuous at the interface. The exact solution of pressure and velocity is given by

$$\begin{aligned} & p = \left\{ {\begin{array}{*{20}c} {0,\,\,\,\,\varGamma \le 0} \\ {1,\,\,\,\varGamma > 0} \\ \end{array} } \right. \\ & u = y(x^{2} + y^{2} - 1),\,\,\,\,(x,y) \in \varOmega ,\,\,\,\,\,\,\,\,\,\,v = - x(x^{2} + y^{2} - 1),\,\,\,\,\,(x,y) \in \varOmega . \\ \end{aligned}$$

and the viscosity μ is

$$\mu = \left\{ {\begin{array}{*{20}c} {0.5,\,\,\,\,\varGamma \le 0} \\ {1,\,\,\,\varGamma > 0} \\ \end{array} } \right.$$

The normal and tangential force density components can be calculated from the jump conditions as $\hat{F}_{1}$  = −1 and $\hat{F}_{2}$  = −1. The external forcing term G is given by G = (−4y, 4x) outside and G = (−8y, 8x) inside Γ.

Table 1 shows the grid refinement analysis of the error infinity norm of our computed results and compares the respective orders of accuracies with the results of Li et al. [4]. Second order accuracy is reported by our numerical simulations for both pressure and velocities, which are comparable to those reported by Ref. [4].

Table 1 Grid refinement analysis and comparison of infinity error norms of the computed results of the present scheme with those of Li et al. [4]

Example 2

In the second example, the quantities u, v and p are kept unchanged inside the interface but they are all set equal to zero outside. The velocity is now discontinuous and force density components are $\hat{F}_{1}$ = −1 and $\hat{F}_{2}$ = −2. The external forcing term G is given value zero outside Γ.

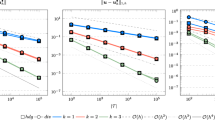
We compare our computed results for both pressure and velocity with Le et al. [4] in Table 2. One can see from the table that our computed error infinity norm, for both pressure and velocity, is better than those of Le et al. [4]. Least square fit line of the absolute errors in log-log plots in Fig. 3 shows second order accuracy of our scheme, for both pressure and velocity.

Table 2 Grid refinement analysis and comparison of infinity error norms of the computed results of the present scheme with those of Li et al. [4]

Fig. 3

Linear regression analysis using log-log scale for both pressure and velocity. Negative of slopes of these regression lines show order of accuracy

4 Conclusion

In this paper, we present a new finite difference scheme for Stokes flows in domains with discontinuities due to the presence of immersed circular interfaces. Augmented approach developed by Li et al. [4] is employed to decouple the jump conditions of pressure and velocity. Recently developed HOC scheme is then used for discretisation at the points away from the interface which produces least third order accuracy on a compact stencil. A new modified finite difference scheme is developed and implemented at irregular points. Interfacial points (points where interface intersects the grid lines) are used as nodes in the finite difference stencil and jump conditions across the interface are used to determine the values at these interfacial points. Studies confirm that our scheme has overall second order of accuracy and it produces better results than the augmented immersed interface method. However, order of accuracy can be increased further by involving more number of grid nodes in the finite difference stencil used at irregular points. As stokes flow represents a two-phase flow, through the two numerical experiments presented in the current study, our scheme can be easily extended to solve multiphase flows with both fixed and moving boundaries.