Development of Pressure-Robust Discontinuous Galerkin Finite Element Methods for the Stokes Problem

Abstract

Pressure-robustness is an essential demand for the incompressible fluid simulation. In this paper, we develop the enhanced discontinuous Galerkin (DG) finite element methods for solving Stokes equations in the primary velocity-pressure formulation to achieve pressure-robustness. The velocity reconstruction operator has been designed for discontinuous functions and utilized to modify the external source assembling. The new schemes stay almost the same as that in the existing DG schemes but only differ for the source terms. The conforming discontinuous Galerkin and symmetric interior penalty DG have been employed to demonstrate the enhancement. Optimal-order error estimates are established for the corresponding numerical approximation in various norms. Several numerical experiments are performed to validate our theoretical conclusions.

1 Introduction

In this paper, we consider the Stokes problem: find the velocity $\mathbf{u}$ and the pressure p such that

$$\begin{aligned} -\nu \varDelta \mathbf{u}+\nabla p= & {} \mathbf{f}\quad \text{ in }\;\Omega , \end{aligned}$$

(1)

$$\begin{aligned} \nabla \cdot \mathbf{u}= & {} 0\quad \text{ in }\;\Omega , \end{aligned}$$

(2)

$$\begin{aligned} \mathbf{u}= & {} 0\quad \text{ on }\; \partial \Omega , \end{aligned}$$

(3)

where $\Omega$ is a polygonal or polyhedral domain in $\mathbb {R}^d\; (d=2,3)$. Here $\nu$ is the kinematic viscosity and $\mathbf{f}$ is the external body force. The Stokes equation has been widely used in realistic applications. In order to derive a stable finite element numerical scheme, the finite element pairs for velocity and pressure need to satisfy the inf-sup condition. However the classical stable finite element methods for incompressible Stokes problem are usually not pressure-robust, i.e., their velocity error is pressure dependent, for example [8, 11, 15, 24], shown as follows,

$$\begin{aligned} \Vert \nabla (\mathbf{u}-\mathbf{u}_h)\Vert \le C\inf _{\mathbf{w}\in \mathbf{V}_h}\Vert \nabla (\mathbf{u}-\mathbf{w})\Vert +\frac{1}{\nu }\inf _{q\in W_h}\Vert p-q\Vert . \end{aligned}$$

Here $\mathbf{V}_h$ and $W_h$ are the stable finite element spaces to approximate velocity and the pressure. We observe that a pressure dependent term that can be relatively large in the case of small viscosity $\nu$. This may cause the bad simulations in many cases: as $\nu \ll 1$, one may observe large errors in velocity; bad approximation or singularity in pressure may affect the velocity simulation due to the coupling of velocity and pressure. To reduce these coupling effects, one would have to assume that the pressure is smooth enough and also employ higher scheme order, which may introduce extra difficulties in the simulations.

The concept of pressure-robustness has been proposed to remove the pressure dependency in velocity simulation. In this category, nowadays, many divergence-free elements have been developed for two dimensional problems [9, 29] and three dimensional problems [35]. The enrichment of the H(div; $\Omega$)-conforming elements with divergence-free rational shape-functions has been proposed in [12, 13]. Cockburn [7] and Wang [30] proposed divergence free schemes, which introduced tangential penalty to modify the variational formulation. Chen proposed to introduce a discrete dual curl operator [5] to implement divergence free MAC scheme on triangular grids. There are other approaches such as adding grad-div stabilization [16, 26, 27] and etc. An alternative method to get pressure independent approximation is introduced recently by Linke [20, 21] as employing a divergence preserving velocity reconstruction operator. a velocity reconstruction is presented in [20] to map discrete divergence free test functions onto exactly divergence free test functions which is applied only on the right hand side for the Stokes equations. A sequence of papers are investigating approaches for discontinuous pressure elements [2, 17, 20,21,22] and continuous pressure elements [18, 19]. With the help of velocity reconstruction, the pressure-robust schemes leading to a pressure independent velocity error estimate [20, 21, 23,24,25]

$$\begin{aligned} \Vert \nabla (\mathbf{u}-\mathbf{u}_h)\Vert \le C\inf _{\mathbf{w}\in V_h}\Vert \nabla (\mathbf{u}-\mathbf{w})\Vert . \end{aligned}$$

Such schemes can be directly used in the existing inf-sup stable schemes [4, 8] to achieve the robustness without compromising the computational accuracy.

In this paper, we focus on developing new pressure-robust numerical discretizations by modifying the existing discontinuous Galerkin scheme for viscosity dependent Stokes equations with the velocity reconstruction technique. The conforming discontinuous Galerkin [32] (CDG) and symmetric interior penalty discontinuous Galerkin (IPDG) finite element methods will be employed to demonstrate the enhancement. Comparing to the existing CDG and IPDG schemes for Stokes equation, our scheme only modifies the body force assembling but remains the same stiffness matrix. The rigorous error analysis is shown for the desired pressure-robustness and convergence results. Several numerical experiments are carried out for demonstrating the advantages of the new schemes.

This paper is organized as follows. Brief review regarding basis functions and velocity reconstruction operator will be presented in Sect. 2. The discretization is developed in Sect. 3 and the well-posedness is discussed in the same section. Then the error equations are given in Sect. 4. Our main results regarding error estimates are stated in Sect. 5. Section 6 presents several numerical examples for Stokes equations. Finally, this paper is summarized with concluding remarks in Sect. 7.

2 Preliminary

We use standard definitions for the Sobolev spaces $H^s(D)$ and their associated inner products $(\cdot , \cdot )_{s,D}$, norms $\Vert \cdot \Vert _{s,D}$, and seminorms $|\cdot |_{s,D}$ for $s\ge 0$. When $D = \Omega$, we drop the subscript D in the norm and inner product notation. We shall also assume the source term $\mathbf{f}\in \mathbf{L}^2(\Omega )$. In the following, we shall assume C is a generic constant which may take different values in different locations.

2.1 Finite Element Spaces

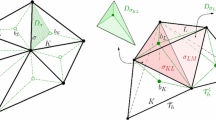
Let ${{\mathcal {T}}}_h$ be a partition of the domain $\Omega$ consisting of shape-regular triangles in two dimensional space or tetrahedrons in three dimensional space. Denote by ${{\mathcal {E}}}_h$ the set of all flat faces in ${{\mathcal {T}}}_h$, and let $\mathcal{E}_h^0={{\mathcal {E}}}_h\backslash \partial \Omega$ be the set of all interior faces. For $k\ge 1$ and given ${{\mathcal {T}}}_h$, define two finite element spaces, for approximating velocity

$$\begin{aligned} {\mathbf{V}_{h}} = \left\{ \mathbf{v}\in {{\varvec{{L}}}}{^{2}}(\Omega ): \mathbf{v}{|_{T}}\in [{P_{k}}(T)]^{d}, \;\;\forall T\in {{{\mathcal {T}}}_{h}} \right\} \end{aligned}$$

(4)

and for approximating pressure

$$\begin{aligned} W_h =\left\{ q\in L_0^2(\Omega ): \ q|_T\in P_{k-1}(T),\;\;\forall T\in {{\mathcal {T}}}_h\right\} . \end{aligned}$$

(5)

Let $T_1$ and $T_2$ be two elements in ${{\mathcal {T}}}_h$ sharing $e\in {{\mathcal {E}}}_h$. For $e\in {{\mathcal {E}}}_h$ and $\mathbf{v}\in {\mathbf{V}_{h}}+{{{\varvec{{H}}}}_{0}}^{1}(\Omega )$, the jump ${[\![}\mathbf{v}{]\!]}$ is defined as

$$\begin{aligned} {[\![}\mathbf{v}{]\!]}=\mathbf{v}\quad \mathrm{if} \;e\subset \partial \Omega ,\quad {[\![}\mathbf{v}{]\!]}=\mathbf{v}|_{T_1}-\mathbf{v}|_{T_2}\;\; \mathrm{if} \;e\in {{\mathcal {E}}}_h^0. \end{aligned}$$

(6)

The order of $T_1$ and $T_2$ is not essential. For $e\in {{\mathcal {E}}}_h$ and $\mathbf{v}\in {\mathbf{V}_{h}}+{{{\varvec{{H}}}}_{0}^{1}}(\Omega )$, the average ${\{\{}\mathbf{v}{\}\}}$ is defined as

$$\begin{aligned} {\{\{}\mathbf{v}{\}\}}=0\quad \mathrm{if} \;e\subset \partial \Omega ,\quad {\{\{}\mathbf{v}{\}\}}=\frac{1}{2}(\mathbf{v}|_{T_1}+\mathbf{v}|_{T_2})\;\; \mathrm{if} \;e\in {{\mathcal {E}}}_h^0, \end{aligned}$$

(7)

For a function $\mathbf{v}\in \mathbf{V}_h+{{{\varvec{{H}}}}_{0}}^{1}(\Omega )$, its weak gradient $\nabla _w\mathbf{v}|_T\in [\mathbf{RT} _{k}(T)]^{d}$ is a piecewise polynomial tensor satisfies the following equation for each $T\in {{\mathcal {T}}}_h$,

$$\begin{aligned} (\nabla _w\mathbf{v},\ \tau )_T = -(\mathbf{v},\ \nabla \cdot \tau )_T+ {\langle }{\{\{}\mathbf{v}{\}\}}, \ \tau \cdot \mathbf{n}{\rangle }_{\partial T}\quad \forall \tau \in [\mathbf{RT} _{k}(T)]^{d}, \end{aligned}$$

(8)

and its weak divergence $\nabla _w\cdot \mathbf{v}|_T\in P_{k-1}(T)$ is a piecewise polynomial satisfies the following equation for each $T\in {{\mathcal {T}}}_h$,

$$\begin{aligned} ( \nabla _{w}\cdot \mathbf{v},\ q)_T = -(\mathbf{v},\ \nabla q)_T+{\langle }{\{\{}\mathbf{v}{\}\}}\cdot \mathbf{n},\ q{\rangle }_{\partial T}\quad \forall q\in P_{k-1}(T). \end{aligned}$$

(9)

First we introduce two semi-norms ${|\!|\!|}\mathbf{v}{|\!|\!|}$ and $\Vert \mathbf{v}\Vert _{1,h}$ for any $\mathbf{v}\in \mathbf{V}_h+{{{\varvec{{H}}}}_{0}}^{1}(\Omega )$ as follows:

$$\begin{aligned} {|\!|\!|}\mathbf{v}{|\!|\!|}^2= & {} \sum _{T\in {{\mathcal {T}}}_h}(\nabla _w\mathbf{v},\nabla _w\mathbf{v})_T, \end{aligned}$$

(10)

$$\begin{aligned} \Vert \mathbf{v}\Vert _{1,h}^2= & {} \sum _{T\in {{\mathcal {T}}}_h}\Vert \nabla \mathbf{v}\Vert _T^2+\sum _{e\in {{\mathcal {E}}}_h}h_e^{-1}\Vert {[\![}\mathbf{v}{]\!]}\Vert _{e}^2. \end{aligned}$$

(11)

The following lemma has been established in [1, 33].

Lemma 1

Both $\Vert \mathbf{v}\Vert _{1,h}$ and ${|\!|\!|}\mathbf{v}{|\!|\!|}$ define a norm for $\mathbf{v}\in \mathbf{V}_h$ and the following norm equivalence holds true

$$\begin{aligned} C_1\Vert \mathbf{v}\Vert _{1,h}\le {|\!|\!|}\mathbf{v}{|\!|\!|}\le C_2 \Vert \mathbf{v}\Vert _{1,h} \quad \forall \mathbf{v}\in \mathbf{V}_h. \end{aligned}$$

(12)

2.2 Velocity Reconstruction Operators and Their Properties

Let ${{\mathbb {Q}}}_h$, $\mathbf{Q}_h$ and $Q_h$ be the element-wise defined $L^2$ projections onto the local spaces $[\mathbf{RT} _{k}(T)]^{d}$, $[P_{k}(T)]^{d}$ and $P_{k-1}(T)$ for $T\in {{\mathcal {T}}}_h$, respectively. Below, we shall introduce another projection operator $\varPi _h$.

Definition 1

For $\mathbf{v}\in \mathbf{V}_h$, we define the projection $\varPi _h \mathbf{v}\in \mathbf{RT} _{k-1}(T)$ such that $\varPi _h\mathbf{v}\in H(\text {div},\Omega )$ and $\varPi _h\mathbf{v}\cdot \mathbf{n}= 0$, $\nabla \cdot \varPi _h\mathbf{v}\in P_{k-1}(T)$ on each $T\in {{\mathcal {T}}}_h$ and satisfies:

$$\begin{aligned} (\varPi _h\mathbf{v},\;\mathbf{w})_T= & {} (\mathbf{v},\;\mathbf{w})_T \quad \forall \mathbf{w}\in [P_{k-2}(T)]^d,\quad k\ge 2 \end{aligned}$$

(13)

$$\begin{aligned} {\langle }\varPi _h\mathbf{v}\cdot \mathbf{n},\; q{\rangle }_{\partial T}= & {} {\langle }{\{\{}\mathbf{v}{\}\}}\cdot \mathbf{n},\; q{\rangle }_{\partial T}\quad \forall q\in P_{k-1}(e), e\subset {\partial T}. \end{aligned}$$

(14)

Remark 1

The similar velocity reconstruction can also be employed for $\mathbf{v}\in {H_{0}^{1}}(\Omega )$ and such reconstruction just follows the definition of Raviart–Thomas interpolation operator [3].

Lemma 2

For $\mathbf{v}\in \mathbf{V}_h+{{{\varvec{{H}}}}_{0}^{1}}(\Omega )$, there exists a projection $\varPi _h \mathbf{v}\in \mathbf{RT} _{k-1}(T)$ such that $\varPi _h\mathbf{v}\in H_0(\text {div},\Omega ):=\{\mathbf{v}\in H(\text {div},\Omega ),\mathbf{v}\cdot \mathbf{n}|_{\partial \Omega } = 0\}$, $\nabla \cdot \varPi _h\mathbf{v}\in P_{k-1}(T)$ on each $T\in {{\mathcal {T}}}_h$ and satisfies:

$$\begin{aligned} \Vert \varPi _h\mathbf{v}-\mathbf{v}\Vert\le & {} Ch\Vert \mathbf{v}\Vert _{1,h}, \end{aligned}$$

(15)

Lemma 3

Let $\varvec{\phi }\in {{{\varvec{{H}}}}_{0}^{1}}(\Omega )$, then the following equations hold true on $T\in {{\mathcal {T}}}_h$

$$\begin{aligned} \nabla _w \phi= & {} {{\mathbb {Q}}}_h\nabla \varvec{\phi }, \end{aligned}$$

(16)

$$\begin{aligned} \nabla _w\cdot \phi= & {} Q_h\nabla \cdot \varvec{\phi }, \end{aligned}$$

(17)

$$\begin{aligned} \nabla \cdot \varPi _h\phi= & {} \nabla _w\cdot \varvec{\phi }, \end{aligned}$$

(18)

$$\begin{aligned} \nabla _w\cdot \varPi _h\phi= & {} \nabla _w\cdot \varvec{\phi }. \end{aligned}$$

(19)

Proof

Using (8) and integration by parts, we have that for any $\tau \in [\mathbf{RT}_{k}(T)]^{d}$

$$\begin{aligned} (\nabla _w \varvec{\phi },\tau )_T= & {} -(\varvec{\phi },\nabla \cdot \tau )_T +\langle {\{\{}\varvec{\phi }{\}\}},\tau \cdot \mathbf{n}\rangle _{{\partial T}}\\= & {} -(\varvec{\phi },\nabla \cdot \tau )_T +\langle \varvec{\phi },\tau \cdot \mathbf{n}\rangle _{{\partial T}}\\= & {} ({{\mathbb {Q}}}_h\nabla \phi ,\tau )_T, \end{aligned}$$

which implies the desired identity (16). Similarly, we can prove (17). It follows from (13) and (14) that for any $q\in P_{k-1}(T)$,

$$\begin{aligned} (\nabla \cdot \varPi _h\varvec{\phi }, q)_T= & {} -(\varPi _h\varvec{\phi }, \nabla q)_T+{\langle }\varPi _h\varvec{\phi }\cdot \mathbf{n},q{\rangle }_{\partial T}\\= & {} -(\varvec{\phi }, \nabla q)_T+{\langle }{\{\{}\varvec{\phi }{\}\}}\cdot \mathbf{n},q{\rangle }_{\partial T}\\= & {} (\nabla _w\cdot \varvec{\phi },q)_T, \end{aligned}$$

which proves (18). Similarly, for any $q\in P_{k-1}(T)$

$$\begin{aligned} (\nabla _w\cdot \varPi _h\varvec{\phi }, q)_T= & {} -(\varPi _h\varvec{\phi }, \nabla q)_T+{\langle }{\{\{}\varPi _h\varvec{\phi }{\}\}}\cdot \mathbf{n},q{\rangle }_{\partial T}\\= & {} -(\varvec{\phi }, \nabla q)_T+{\langle }\varPi _h\varvec{\phi }\cdot \mathbf{n},q{\rangle }_{\partial T}\\= & {} -(\varvec{\phi }, \nabla q)_T+{\langle }{\{\{}\varvec{\phi }{\}\}}\cdot \mathbf{n},q{\rangle }_{\partial T}\\= & {} (\nabla _w\cdot \varvec{\phi },q)_T. \end{aligned}$$

We have proved the lemma. $\square$

For any function $\varphi \in H^1(T)$, the following trace inequality holds true (see [31] for details):

$$\begin{aligned} \Vert \varphi \Vert _{e}^2 \le C \left( h_T^{-1} \Vert \varphi \Vert _T^2 + h_T \Vert \nabla \varphi \Vert _{T}^2\right) . \end{aligned}$$

(20)

3 Numerical Schemes

For the sake of notation simplification, the following notations will also be employed,

$$\begin{aligned} (u,v)_{\mathcal {T}_h}:=\sum _{T\in \mathcal {T}_h}(u,v)_T,\ \langle u,v\rangle _{\partial \mathcal {T}_h}:=\sum _{T\in \mathcal {T}_h}\langle u,v\rangle _{\partial T},\; \langle u,v\rangle _{\mathcal {E}_h}:=\sum _{e\in \mathcal {E}_h}\langle u,v\rangle _e. \end{aligned}$$

For functions $\mathbf{w},\mathbf{v}\in \mathbf{V}_h$ and $q\in W_h$, define

$$\begin{aligned} A_h(\mathbf{w},\mathbf{v}):=(\nabla _w\mathbf{w},\nabla _w\mathbf{v})_{\mathcal {T}_h},\; B_h(\mathbf{v},q) = -(\nabla _w\cdot \mathbf{v},q). \end{aligned}$$

Besides, we shall also employ the notations in the interior penalty discontinuous Galerkin finite element methods. With each edge/face $e\in \mathcal {E}_h^0$, we associate a unit normal vector $\mathbf{n}_e$. If e is on the boundary $\partial \Omega$, then $\mathbf{n}_e$ is taken to be the unit ourward vector normal to $\partial \Omega$. Define the following bilinear terms for $\mathbf{w},\mathbf{v}\in \mathbf{V}_h$ and $q\in W_h$,

$$\begin{aligned} \mathcal {A}_h(\mathbf{w},\mathbf{v})= & {} (\nabla \mathbf{w},\nabla \mathbf{v})_{\mathcal {T}_h} - \langle {\{\{}\nabla \mathbf{w}{\}\}}\mathbf{n}_e,{[\![}\mathbf{v}{]\!]}\rangle _{\mathcal {E}_h} \\&- \langle {\{\{}\nabla \mathbf{v}{\}\}}\mathbf{n}_e,{[\![}\mathbf{w}{]\!]}\rangle _{\mathcal {E}_h} +\frac{\eta }{h_e}\langle {[\![}\mathbf{w}{]\!]},{[\![}\mathbf{v}{]\!]}\rangle _{\mathcal {E}_h}, \end{aligned}$$

where $\eta$ is a penalty parameter which is strictly positive and big enough to guarantee stability. Also define

$$\begin{aligned} \mathcal {B}_h(\mathbf{v},q) = -(\nabla \cdot \mathbf{v}, q)_{\mathcal {T}_h}+\langle {\{\{}q{\}\}},{[\![}\mathbf{v}\cdot \mathbf{n}_e{]\!]}\rangle _{\mathcal {E}_h}. \end{aligned}$$

In the following, we shall first cite the classical discontinuous Galerkin schemes as Algorithms 1 and 3, and then propose the enhanced pressure robust discontinuous Galerkin schemes in Algorithms 2 and 4.

Algorithm 1

(Conforming Discontinuous Galerkin (CDG) Scheme [34])

A finite element method for (1)–(3) is seeking $\mathbf{u}_h\in \mathbf{V}_h$ and $p_h\in W_h$ such that for all $\mathbf{v}\in \mathbf{V}_h$ and $q\in W_h$,

$$\begin{aligned} \nu A_h(\mathbf{u}_h,\mathbf{v})+B_h(\mathbf{v},p_h)= & {} (\mathbf{f},\mathbf{v}), \\ {B_h}(\mathbf{u}_h,q)= & {} 0. \end{aligned}$$

Algorithm 2

(Enhanced CDG Scheme)

A new finite element method for (1)–(3) is seeking $\mathbf{u}_h\in \mathbf{V}_h$ and $p_h\in W_h$ such that for all $\mathbf{v}\in \mathbf{V}_h$ and $q\in W_h$,

$$\begin{aligned} \nu A_h(\mathbf{u}_h,\mathbf{v})+B_h(\mathbf{v},p_h)= & {} (\mathbf{f},\varPi _h\mathbf{v}) \end{aligned}$$

(21)

$$\begin{aligned} {B_h}(\mathbf{u}_h,q)= & {} 0. \end{aligned}$$

(22)

Algorithm 3

(Interior Penalty Discontinuous Galerkin (IPDG) Scheme [28]) A finite element method for (1)–(3) is seeking $\mathbf{u}_h\in \mathbf{V}_h$ and $p_h\in W_h$ such that for all $\mathbf{v}\in \mathbf{V}_h$ and $q\in W_h$

$$\begin{aligned} \nu \mathcal {A}_h(\mathbf{u}_h,\mathbf{v})+\mathcal {B}_h(\mathbf{v},p_h)= & {} (\mathbf{f},\mathbf{v}),\\ \mathcal {B}_h(\mathbf{u}_h,q)= & {} 0. \end{aligned}$$

Algorithm 4

(Enhanced IPDG Scheme) A new finite element method for (1)–(3) is seeking $\mathbf{u}_h\in \mathbf{V}_h$ and $p_h\in W_h$ such that for all $\mathbf{v}\in \mathbf{V}_h$ and $q\in W_h$

$$\begin{aligned} \nu \mathcal {A}_h(\mathbf{u}_h,\mathbf{v})+\mathcal {B}_h(\mathbf{v},p_h)= & {} (\mathbf{f},\varPi _h\mathbf{v}), \end{aligned}$$

(23)

$$\begin{aligned} \mathcal {B}_h(\mathbf{u}_h,q)= & {} 0. \end{aligned}$$

(24)

Here, one can prove the equivalence of $B_h(\mathbf{v},q)$ and $\mathcal {B}_h(\mathbf{v},q)$ for $\mathbf{v}\in \mathbf{V}_h$ and $q\in W_h$ as follows,

$$\begin{aligned} B_h(\mathbf{v},q)= & {} -\sum _{T\in \mathcal {T}_h}\int _T\nabla _w\cdot \mathbf{v}q dT = \sum _{T\in \mathcal {T}_h}\left( - \int _{\partial T}{\{\{}\mathbf{v}{\}\}}\cdot \mathbf{n}q ds+\int _T\mathbf{v}\cdot \nabla q dT\right) \nonumber \\= & {} \sum _{T\in \mathcal {T}_h}\left( \int _{\partial T}(\mathbf{v}-{\{\{}\mathbf{v}{\}\}})\cdot \mathbf{n}q ds -\int _T\nabla \cdot \mathbf{v}q dT\right) \nonumber \\= & {} \mathcal {B}_h(\mathbf{v},q). \end{aligned}$$

(25)

Then together with the modifications in the source terms, we have the following remarks.

Remark 2

Algorithm 1 only differs Algorithm 3 in the terms $A_h(\mathbf{w},\mathbf{v})$ and $\mathcal {A}_h(\mathbf{w},\mathbf{v})$. However, Algorithms 1 is parameter/stabilizer free but Algorithm 3 requires the penalty parameter $\eta$ to be large enough for the sake of stability.

Remark 3

The stiffness matrix produced by Algorithm 2 is the same as that in Algorithm 1; the stiffness matrix of Algorithm 4 is the same as that in Algorithm 3. The only modification in Algorithm 2/Algorithm 4 is the external source assembling. Through such minor modification, we can enhance the classical schemes with the desire pressure-robustness.

Lemma 4

There exists a positive constant $\beta$ independent of h such that for all $\rho \in W_h$

$$\begin{aligned} \sup _{\mathbf{v}\in \mathbf{V}_h}\frac{B_h(\mathbf{v},\rho )}{{|\!|\!|}\mathbf{v}{|\!|\!|}}\ge \beta \Vert \rho \Vert . \end{aligned}$$

(26)

Proof

For any given $\rho \in W_h\subset L_0^2(\Omega )$, it is known [10] that there exists a function $\tilde{\mathbf{v}}\in {{{\varvec{{H}}}}_{0}^{1}}(\Omega )$ such that

$$\begin{aligned} \frac{(\nabla \cdot \tilde{\mathbf{v}},\rho )}{\Vert \tilde{\mathbf{v}}\Vert _1}\ge C\Vert \rho \Vert , \end{aligned}$$

(27)

where $C>0$ is a constant independent of h. Let $\mathbf{v}=\varPi _h{\tilde{\mathbf{v}}}\in \mathbf{V}_h$. Here $\varPi _h$ is the Raviart Thomas (RT) interpolation operator to the space $\mathbf{RT} _{k-1}(T)$, which belongs to the finite element space $\mathbf{V}_h$. It follows from the equivalence of norms (12), trace inequality (20) and ${\tilde{\mathbf{v}}}\in {{{\varvec{{H}}}}_{0}^{1}}(\Omega )$,

$$\begin{aligned} {|\!|\!|}\mathbf{v}{|\!|\!|}^2\le & {} C\Vert \mathbf{v}\Vert _{1,h}^2=C(\sum _{T\in {{\mathcal {T}}}_h}\Vert \nabla \mathbf{v}\Vert _T^2+\sum _{e\in {{\mathcal {E}}}_h^0}h_e^{-1}\Vert {[\![}\mathbf{v}{]\!]}\Vert _{e}^2)\nonumber \\\le & {} C \sum _{T\in {{\mathcal {T}}}_h}\Vert \nabla \varPi _h{\tilde{\mathbf{v}}}\Vert _T^2+\sum _{e\in {{\mathcal {E}}}_h^0}h_e^{-1}\Vert {[\![}\varPi _h{\tilde{\mathbf{v}}}-{\tilde{\mathbf{v}}}{]\!]}\Vert _{e}^2\nonumber \\\le & {} C\sum _{T\in \mathcal {T}_h}\Vert \nabla \varPi _h{\tilde{\mathbf{v}}}\Vert _T^2 + h^{-2}\Vert \varPi _h{\tilde{\mathbf{v}}}-{\tilde{\mathbf{v}}}\Vert _T^2 + \Vert \nabla \varPi _h{\tilde{\mathbf{v}}}-\nabla {\tilde{\mathbf{v}}}\Vert _T^2 \nonumber \\\le & {} C\Vert {\tilde{\mathbf{v}}}\Vert _1^2. \end{aligned}$$

(28)

The last step used (15) and the property of RT interpolation. It follows from (18) and (19) that

$$\begin{aligned} (\nabla _w\cdot \mathbf{v},\;\rho )= & {} (\nabla _w\cdot \varPi _h\tilde{\mathbf{v}},\;\rho )=(\nabla \cdot \tilde{\mathbf{v}},\;\rho ). \end{aligned}$$

Using the above Eqs. (28) and (27), we have

$$\begin{aligned} \frac{|B_h(\mathbf{v},\rho )|}{{|\!|\!|}\mathbf{v}{|\!|\!|}} = \frac{|(\nabla _w\cdot \mathbf{v},\rho )|}{{|\!|\!|}\mathbf{v}{|\!|\!|}}\ge & {} \frac{|(\nabla \cdot \tilde{\mathbf{v}},\rho )|}{C\Vert \tilde{\mathbf{v}}\Vert _1}\ge \beta \Vert \rho \Vert , \end{aligned}$$

for a positive constant $\beta$. This completes the proof. $\square$

Remark 4

The similar proof of inf-sup condition for IPDG can be found in Proposition 10 in [14] and Proposition 4.4 in [6].

Remark 5

The well-posedness of the scheme can be found in [34] for Algorithm 1. The proof of existence, uniqueness, and stability of Algorithm 3 can be found in [28]. Since Algorithms 2 and 4 share the same stiffness matrices as Algorithms 1 and 3, the new proposed Algorithms 2 and 4 directly inherit the well-posedness results. Here, we shall cite the following inequalities needed by later sections,

$$\begin{aligned}&\forall \mathbf{v},\mathbf{w}\in \mathbf{V}_h+{{{\varvec{{H}}}}_{0}^{1}},\; \mathcal {A}_h(\mathbf{w},\mathbf{v})\le C_1\Vert \mathbf{w}\Vert _{1,h}\Vert \mathbf{v}\Vert _{1,h}, \end{aligned}$$

(29)

$$\begin{aligned}&\forall \mathbf{v}\in \mathbf{V}_h, \mathcal {A}_h(\mathbf{v},\mathbf{v})\ge C_2\Vert \mathbf{v}\Vert _{1,h}^2 \end{aligned}$$

(30)

$$\begin{aligned}&\forall \rho \in W_h,\; \sup _{\mathbf{v}\in \mathbf{V}_h}\frac{\mathcal {B}_h(\mathbf{v},\rho )}{\Vert \mathbf{v}\Vert _{1,h}}\ge \beta \Vert \rho \Vert , \end{aligned}$$

(31)

where $\beta$, $C_1$, and $C_2$ are a positive constants independent of h.

4 Error Equations

In this section, we will derive the equations that the errors satisfy for the enhanced CDG scheme (Algorithm 2) and enhanced IPDG scheme (Algorithm 4). Let $\mathbf{e}_h=\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h$, ${\varvec{\epsilon }}_h=\mathbf{u}-\mathbf{u}_h$ and $\varepsilon _h=Q_hp-p_h$.

4.1 Error Equations for CDG Scheme in Algorithm 2

Lemma 5

The following error equations hold true for any $(\mathbf{v},q)\in \mathbf{V}_h\times W_h$,

$$\begin{aligned} \nu A_h(\mathbf{e}_h,\mathbf{v})+B_h(\mathbf{v},\varepsilon _h)= & {} \nu \ell _1(\mathbf{u},\mathbf{v})-\nu \ell _2(\mathbf{u},\mathbf{v})+\nu \ell _3(\mathbf{u},\mathbf{v}), \end{aligned}$$

(32)

$$\begin{aligned} B_h(\mathbf{e}_h,\ q)= & {} \ell _4(\mathbf{u},q), \end{aligned}$$

(33)

where

$$\begin{aligned} \ell _1(\mathbf{u},\ \mathbf{v})= & {} {\langle }(\nabla \mathbf{u}-{{\mathbb {Q}}}_h(\nabla \mathbf{u}))\cdot \mathbf{n},\;\mathbf{v}-{\{\{}\mathbf{v}{\}\}}{\rangle }_{\partial {{\mathcal {T}}}_h}, \end{aligned}$$

(34)

$$\begin{aligned} \ell _2(\mathbf{u},\mathbf{v})= & {} (\nabla _w (\mathbf{u}-\mathbf{Q}_h\mathbf{u}),\nabla _w\mathbf{v})_{{{\mathcal {T}}}_h}, \end{aligned}$$

(35)

$$\begin{aligned} \ell _3(\mathbf{u},\mathbf{v})= & {} (\varDelta \mathbf{u}, \varPi _h\mathbf{v}-\mathbf{v})_{{{\mathcal {T}}}_h}, \end{aligned}$$

(36)

$$\begin{aligned} \ell _4(\mathbf{u},q)= & {} {\langle }{\{\{}\mathbf{u}-\mathbf{Q}_h\mathbf{u}{\}\}}\cdot \mathbf{n},q{\rangle }_{\partial {{\mathcal {T}}}_h}. \end{aligned}$$

(37)

Proof

For a $\mathbf{v}\in \mathbf{V}_h$, we test (1) by $\varPi _h\mathbf{v}$ to obtain

$$\begin{aligned} -\nu (\varDelta \mathbf{u},\;\varPi _h\mathbf{v})+(\nabla p,\ \varPi _h\mathbf{v})=(\mathbf{f},\; \varPi _h\mathbf{v}), \end{aligned}$$

(38)

which implies

$$\begin{aligned} -\nu (\varDelta \mathbf{u},\;\mathbf{v})+(\nabla p,\ \varPi _h\mathbf{v})=(\mathbf{f},\; \varPi _h\mathbf{v})+\nu \ell _3(\mathbf{u},\mathbf{v}), \end{aligned}$$

(39)

Integration by parts and the fact $\langle \nabla \mathbf{u}\cdot \mathbf{n},\;{\{\{}\mathbf{v}{\}\}}\rangle _{\partial {{\mathcal {T}}}_h}=0$ give

$$\begin{aligned} -(\varDelta \mathbf{u},\;\mathbf{v})=(\nabla \mathbf{u},\nabla \mathbf{v})_{{{\mathcal {T}}}_h}- \langle \nabla \mathbf{u}\cdot \mathbf{n},\mathbf{v}-{\{\{}\mathbf{v}{\}\}}\rangle _{\partial {{\mathcal {T}}}_h}. \end{aligned}$$

(40)

It follows from integration by parts, (8) and (16),

$$\begin{aligned} (\nabla \mathbf{u},\nabla \mathbf{v})_{{{\mathcal {T}}}_h}= & {} ({{\mathbb {Q}}}_h\nabla \mathbf{u},\nabla \mathbf{v})_{{{\mathcal {T}}}_h}\nonumber \\= & {} -(\mathbf{v},\nabla \cdot ({{\mathbb {Q}}}_h\nabla \mathbf{u}))_{{{\mathcal {T}}}_h}+\langle \mathbf{v}, {{\mathbb {Q}}}_h\nabla \mathbf{u}\cdot \mathbf{n}\rangle _{\partial {{\mathcal {T}}}_h}\nonumber \\= & {} ({{\mathbb {Q}}}_h\nabla \mathbf{u}, \nabla _w \mathbf{v})_{{{\mathcal {T}}}_h}+\langle \mathbf{v}-{\{\{}\mathbf{v}{\}\}},{{\mathbb {Q}}}_h\nabla \mathbf{u}\cdot \mathbf{n}\rangle _{\partial {{\mathcal {T}}}_h}\nonumber \\= & {} ( \nabla _w \mathbf{u}, \nabla _w \mathbf{v})_{{{\mathcal {T}}}_h}+\langle \mathbf{v}-{\{\{}\mathbf{v}{\}\}},{{\mathbb {Q}}}_h\nabla \mathbf{u}\cdot \mathbf{n}\rangle _{\partial {{\mathcal {T}}}_h}. \end{aligned}$$

(41)

Combining (40) and (41) gives

$$\begin{aligned} -(\varDelta \mathbf{u},\;\mathbf{v})= & {} (\nabla _w \mathbf{u},\nabla _w\mathbf{v})_{{{\mathcal {T}}}_h}-\ell _1(\mathbf{u},\mathbf{v}). \end{aligned}$$

(42)

Using integration by parts, $\varPi _h\mathbf{v}\in H_0(\text {div},\Omega )$ and (18), we have

$$\begin{aligned} (\nabla p,\ \varPi _h\mathbf{v})= & {} -(p,\nabla \cdot \varPi _h\mathbf{v})_{{{\mathcal {T}}}_h}+{\langle }p, \varPi _h\mathbf{v}\cdot \mathbf{n}{\rangle }_{\partial {{\mathcal {T}}}_h}\nonumber \\= & {} -(Q_hp,\nabla \cdot \varPi _h\mathbf{v})_{{{\mathcal {T}}}_h}\nonumber \\= & {} -(Q_hp,\nabla _w\cdot \mathbf{v})_{{{\mathcal {T}}}_h}. \end{aligned}$$

(43)

Substituting (42) and (43) into (39) gives

$$\begin{aligned} \nu (\nabla _w\mathbf{u},\nabla _w\mathbf{v})_{{{\mathcal {T}}}_h}-(Q_hp,\nabla _w\cdot \mathbf{v})_{{{\mathcal {T}}}_h}=(\mathbf{f},\varPi _h\mathbf{v})+\nu \ell _1(\mathbf{u},\mathbf{v})+\nu \ell _3(\mathbf{u},\mathbf{v}). \end{aligned}$$

(44)

The difference of (44) and (21) implies

$$\begin{aligned} \nu (\nabla _w{\varvec{\epsilon }}_h,\nabla _w\mathbf{v})_{{{\mathcal {T}}}_h}-(\varepsilon _h,\nabla _w\cdot \mathbf{v})_{{{\mathcal {T}}}_h}=\nu \ell _1(\mathbf{u},\mathbf{v})+\nu \ell _3(\mathbf{u},\mathbf{v})\quad \forall \mathbf{v}\in \mathbf{V}_h. \end{aligned}$$

(45)

Adding and subtracting $(\nabla _w\mathbf{Q}_h\mathbf{u}-\nabla _w\mathbf{u},\nabla _w\mathbf{v})_{{{\mathcal {T}}}_h}$ in (45), we have

$$\begin{aligned} \nu (\nabla _w\mathbf{e}_h,\nabla _w\mathbf{v})_{{{\mathcal {T}}}_h}-(\varepsilon _h,\nabla _w\cdot \mathbf{v})_{{{\mathcal {T}}}_h}=\nu \ell _1(\mathbf{u},\mathbf{v})-\nu \ell _2(\mathbf{u},\mathbf{v})-\nu \ell _3(p,\mathbf{v}), \end{aligned}$$

(46)

which implies (32).

Testing Eq. (2) by $q\in W_h$ and using (9) give

$$\begin{aligned} (\nabla \cdot \mathbf{u},\;q)= & {} -(\mathbf{u},\;\nabla q)_{{{\mathcal {T}}}_h}+{\langle }\mathbf{u}\cdot \mathbf{n},q{\rangle }_{\partial {{\mathcal {T}}}_h}\\= & {} -(\mathbf{Q}_h\mathbf{u},\;\nabla q)_{{{\mathcal {T}}}_h}+{\langle }\mathbf{u}\cdot \mathbf{n},q{\rangle }_{\partial {{\mathcal {T}}}_h}\\= & {} (\nabla _w\cdot \mathbf{Q}_h\mathbf{u},\;q)_{{{\mathcal {T}}}_h}+{\langle }{\{\{}\mathbf{u}-\mathbf{Q}_h\mathbf{u}{\}\}}\cdot \mathbf{n},\;q{\rangle }_{\partial {{\mathcal {T}}}_h}\\= & {} (\nabla _w\cdot \mathbf{Q}_h\mathbf{u},\;q)_{{{\mathcal {T}}}_h}+\ell _4(\mathbf{u},q). \end{aligned}$$

which implies

$$\begin{aligned} (\nabla _w\cdot \mathbf{Q}_h\mathbf{u},\;q)_{{{\mathcal {T}}}_h}=-\ell _4(\mathbf{u},q). \end{aligned}$$

(47)

The difference of (47) and (22) implies (33). We have proved the lemma. $\square$

The following lemma will be used in the $L^2$ error estimate.

Lemma 6

For any $(\mathbf{v},q)\in \mathbf{V}_h\times W_h$, then we have,

$$\begin{aligned} \nu A_h({\varvec{\epsilon }}_h,\varPi _h\mathbf{v})+B_h(\mathbf{v},\varepsilon _h)=\nu \ell _1(\mathbf{u},\varPi _h\mathbf{v})\quad \forall \mathbf{v}\in V_h. \end{aligned}$$

(48)

Proof

Letting $\mathbf{v}=\varPi _h\mathbf{v}$ in (42), we have

$$\begin{aligned} -(\varDelta \mathbf{u},\;\varPi _h\mathbf{v})= & {} (\nabla _w \mathbf{u},\nabla _w\varPi _h\mathbf{v})_{{{\mathcal {T}}}_h}-\ell _1(\mathbf{u},\varPi _h\mathbf{v}). \end{aligned}$$

(49)

Combining (49) and (43) with (38) gives

$$\begin{aligned} \nu (\nabla _w\mathbf{u},\nabla _w\varPi _h\mathbf{v})_{{{\mathcal {T}}}_h}-(Q_hp,\nabla _w\cdot \mathbf{v})_{{{\mathcal {T}}}_h}=(\mathbf{f},\varPi _h\mathbf{v})+\nu \ell _1(\mathbf{u},\varPi _h\mathbf{v}). \end{aligned}$$

(50)

Letting $\mathbf{v}=\varPi _h\mathbf{v}$ in (21) gives

$$\begin{aligned} \nu (\nabla _w\mathbf{u}_h,\ \nabla _w\varPi _h\mathbf{v})-(\nabla _w\cdot \varPi _h\mathbf{v},\;p_h)= & {} (f,\;\varPi _h\mathbf{v}). \end{aligned}$$

(51)

Using (19), the Eq. (51) becomes

$$\begin{aligned} \nu (\nabla _w\mathbf{u}_h,\ \nabla _w\varPi _h\mathbf{v})-(\nabla _w\cdot \mathbf{v},\;p_h)= & {} (f,\;\varPi _h\mathbf{v}), \end{aligned}$$

(52)

The difference of (50) and (52) implies

$$\begin{aligned} \nu (\nabla _w{\varvec{\epsilon }}_h,\nabla _w\varPi _h\mathbf{v})_{{{\mathcal {T}}}_h}-(\varepsilon _h,\nabla _w\cdot \mathbf{v})_{{{\mathcal {T}}}_h}=\nu \ell _1(\mathbf{u},\varPi _h\mathbf{v})\quad \forall \mathbf{v}\in \mathbf{V}_h. \end{aligned}$$

(53)

By the definitions of ${A}_h,B_h$, we have proved the lemma. $\square$

4.2 Error Equations for IPDG Scheme in Algorithm 4

Lemma 7

The following error equations hold true for IPDG scheme: any $(\mathbf{v},q)\in \mathbf{V}_h\times W_h$,

$$\begin{aligned} \nu \mathcal {A}_h({\varvec{\epsilon }}_h,\mathbf{v})+\mathcal {B}_h(\mathbf{v},\varepsilon _h)= & {} \nu \ell _3(\mathbf{u},\mathbf{v}), \end{aligned}$$

(54)

$$\begin{aligned} \mathcal {B}_h(\mathbf{e}_h,\ q)= & {} \ell _4(\mathbf{u},q). \end{aligned}$$

(55)

Proof

Since the equivalence of $B_h(\mathbf{v},q)$ and $\mathcal {B}_h(\mathbf{v},q)$ as (25) for $\mathbf{v}\in \mathbf{V}_h,q\in W_h$, (55) follows from (33). For a $\mathbf{v}\in \mathbf{V}_h$, we test (1) by $\varPi _h\mathbf{v}$ to obtain (39). The definition of $\mathcal {A}_h(\cdot ,\cdot )$ gives

$$\begin{aligned} -(\varDelta \mathbf{u},\mathbf{v})= & {} \mathcal {A}_h(\mathbf{u},\mathbf{v}) = \mathcal {A}_h(\mathbf{u},\mathbf{v}), \end{aligned}$$

(56)

Substituting the above to (39), (43), and using the equivalence of $B_h(\cdot ,\cdot )$ and $\mathcal {B}_h(\cdot ,\cdot )$ as (25), we have

$$\begin{aligned} \nu \mathcal {A}_h(\mathbf{u},\mathbf{v})+\mathcal {B}_h(\mathbf{v},Q_hp)=(\mathbf{f},\; \varPi _h\mathbf{v})+\nu \ell _3(\mathbf{u},\mathbf{v}). \end{aligned}$$

The difference of the above equation and (23) gives (54). $\square$

Lemma 8

For any $(\mathbf{v},q)\in \mathbf{V}_h\times W_h$, then we have,

$$\begin{aligned} \nu \mathcal {A}_h({\varvec{\epsilon }}_h,\varPi _h\mathbf{v})_{{{\mathcal {T}}}_h}+\mathcal {B}_h(\mathbf{v},\varepsilon _h)_{{{\mathcal {T}}}_h}=0 \quad \forall \mathbf{v}\in V_h. \end{aligned}$$

(57)

Proof

Letting $\mathbf{v}= \varPi _h\mathbf{v}$ in (56), we have

$$\begin{aligned} -(\varDelta \mathbf{u},\varPi _h \mathbf{v})= & {} \mathcal {A}_h(\mathbf{u},\varPi _h\mathbf{v}). \end{aligned}$$

Combining $(\nabla p,\varPi _h\mathbf{v}) = \mathcal {B}_h(\mathbf{v},Q_hp)$ with (38), we obtain

$$\begin{aligned} \nu \mathcal {A}_h(\mathbf{u},\varPi _h\mathbf{v})+\mathcal {B}_h(\mathbf{v},Q_hp)=(\mathbf{f},\; \varPi _h\mathbf{v}), \end{aligned}$$

and thus the conclusion follows by taking the difference of the above equations and (23). $\square$

5 Main Results

5.1 Error Estimates in Energy Norm

Optimal order error estimates will be derived in this section for the velocity $\mathbf{u}_h$ and pressure $p_h$ in ${|\!|\!|}\cdot {|\!|\!|}$ norm and in the $L^2$ norm, respectively. The following equations hold true for ${\{\{}\mathbf{v}{\}\}}$ defined in (7),

$$\begin{aligned} \Vert \mathbf{v}-{\{\{}\mathbf{v}{\}\}}\Vert _e=\Vert {[\![}\mathbf{v}{]\!]}\Vert _e\quad \mathrm{if} \;e\subset \partial \Omega ,\quad \Vert \mathbf{v}-{\{\{}\mathbf{v}{\}\}}\Vert _e=\frac{1}{2}\Vert {[\![}\mathbf{v}{]\!]}\Vert _e\;\; \mathrm{if} \;e\in {{\mathcal {E}}}_h^0. \end{aligned}$$

(58)

Lemma 9

Let $(\mathbf{w},\rho )\in {{\varvec{{H}}}}^{k+1}(\Omega )\times H^k(\Omega )$ and $(\mathbf{v},q)\in \mathbf{V}_h\times W_h$. Then, the following estimates hold true

$$\begin{aligned} |\ell _1(\mathbf{w},\ \mathbf{v})|\le & {} Ch^{k}|\mathbf{w}|_{k+1}{|\!|\!|}\mathbf{v}{|\!|\!|}, \end{aligned}$$

(59)

$$\begin{aligned} |\ell _2(\mathbf{w},\ \mathbf{v})|\le & {} Ch^{k}|\mathbf{w}|_{k+1}{|\!|\!|}\mathbf{v}{|\!|\!|}, \end{aligned}$$

(60)

$$\begin{aligned} |\ell _3(\mathbf{w},\ \mathbf{v})|\le & {} Ch^{k}|\mathbf{w}|_{k+1}{|\!|\!|}\mathbf{v}{|\!|\!|}. \end{aligned}$$

(61)

$$\begin{aligned} |\ell _4(\mathbf{w},q)\le & {} Ch^{k}|\mathbf{w}|_{k+1}\Vert q\Vert . \end{aligned}$$

(62)

Proof

Using the Cauchy–Schwarz inequality, the trace inequality (20), (58) and (12), we have

$$\begin{aligned} |\ell _1(\mathbf{w},\ \mathbf{v})|= & {} |\sum _{T\in {{\mathcal {T}}}_h}{\langle }\mathbf{v}-{\{\{}\mathbf{v}{\}\}},\ \nabla \mathbf{w}\cdot \mathbf{n}-{{\mathbb {Q}}}_h(\nabla \mathbf{w})\cdot \mathbf{n}{\rangle }_{\partial T}| \\\le & {} C \sum _{T\in {{\mathcal {T}}}_h}\Vert \nabla \mathbf{w}-{{\mathbb {Q}}}_h\nabla \mathbf{w}\Vert _{{\partial T}} \Vert \mathbf{v}-{\{\{}\mathbf{v}{\}\}}\Vert _{\partial T}\\\le & {} C \left( \sum _{T\in {{\mathcal {T}}}_h}h_T\Vert (\nabla \mathbf{w}-{{\mathbb {Q}}}_h\nabla \mathbf{w})\Vert _{{\partial T}}^2\right) ^{\frac{1}{2}} \left( \sum _{e\in {{\mathcal {E}}}_h}h_e^{-1}\Vert {[\![}\mathbf{v}{]\!]}\Vert _e^2\right) ^{\frac{1}{2}} \\\le & {} Ch^{k}|\mathbf{w}|_{k+1}{|\!|\!|}\mathbf{v}{|\!|\!|}. \end{aligned}$$

It follows from (8), integration by parts, (20) and (58) that for any $\mathbf{q}\in [\mathbf{RT} _{k-1}(T)]^{d}$,

$$\begin{aligned} |(\nabla _w(\mathbf{w}-\mathbf{Q}_h\mathbf{w}), \mathbf{q})_{T}|= & {} |-(\mathbf{w}-\mathbf{Q}_h\mathbf{w}, \nabla \cdot \mathbf{q})_{T}+{\langle }\mathbf{w}-{\{\{}\mathbf{Q}_h\mathbf{w}{\}\}}, \mathbf{q}\cdot \mathbf{n}{\rangle }_{{\partial T}}|\nonumber \\= & {} |(\nabla (\mathbf{w}-\mathbf{Q}_h\mathbf{w}), \mathbf{q})_{T}+{\langle }\mathbf{Q}_h\mathbf{w}-{\{\{}\mathbf{Q}_h\mathbf{w}{\}\}}, \mathbf{q}\cdot \mathbf{n}{\rangle }_{{\partial T}}|\nonumber \\\le & {} \Vert \nabla (\mathbf{w}-\mathbf{Q}_h\mathbf{w})\Vert _T\Vert \mathbf{q}\Vert _T+Ch^{-1/2}\Vert {[\![}\mathbf{Q}_h\mathbf{w}{]\!]}\Vert _{\partial T}\Vert \mathbf{q}\Vert _T\nonumber \\\le & {} \Vert \nabla (\mathbf{w}-\mathbf{Q}_h\mathbf{w})\Vert _T\Vert \mathbf{q}\Vert _T+Ch^{-1/2}\Vert {[\![}\mathbf{w}-\mathbf{Q}_h\mathbf{w}{]\!]}\Vert _{\partial T}\Vert \mathbf{q}\Vert _T\nonumber \\\le & {} Ch^k|\mathbf{w}|_{k+1, T}\Vert \mathbf{q}\Vert _T. \end{aligned}$$

(63)

Letting $\mathbf{q}=\nabla _w\mathbf{v}$ in (63) and taking summation over T, we have

$$\begin{aligned} |\ell _2(\mathbf{w},\ \mathbf{v})|= & {} |(\nabla _w (\mathbf{w}-\mathbf{Q}_h\mathbf{w}),\nabla _w\mathbf{v})_{{{\mathcal {T}}}_h}|\\\le & {} Ch^{k}|\mathbf{w}|_{k+1}{|\!|\!|}\mathbf{v}{|\!|\!|}. \end{aligned}$$

If $k = 1$, it follows from Cauchy–Schwarz inequality and (15) that

$$\begin{aligned} |\ell _3(\mathbf{w},\ \mathbf{v})|= & {} |\sum _{T\in {{\mathcal {T}}}_h}(\varDelta \mathbf{w}, \varPi _h\mathbf{v}-\mathbf{v})_{T}| \le \sum _{T\in {{\mathcal {T}}}_h}\Vert \varDelta \mathbf{w}\Vert _T\Vert \varPi _h\mathbf{v}-\mathbf{v}\Vert _T\nonumber \\\le & {} Ch|\mathbf{w}|_{2} \Vert \mathbf{v}\Vert _{1,h}. \end{aligned}$$

If $k\ge 2$, denote by $Q_{k-2,T}$ the $L^2$ projection onto $P_{k-2}(T)$. It follows from the definition of $Q_{k-2,T}$, (13) and (15) that

$$\begin{aligned} |\ell _3(\mathbf{w},\ \mathbf{v})|= & {} |\sum _{T\in {{\mathcal {T}}}_h}(\varDelta \mathbf{w}, \varPi _h\mathbf{v}-\mathbf{v})_{T}|\\= & {} |\sum _{T\in {{\mathcal {T}}}_h}(\varDelta \mathbf{w}-Q_{k-2,T}(\varDelta \mathbf{w}), \varPi _h\mathbf{v}-\mathbf{v})_{T}|\\\le & {} Ch^{k}|\mathbf{w}|_{k+1} \Vert \mathbf{v}\Vert _{1,h}. \end{aligned}$$

Similarly we have

$$\begin{aligned} |\ell _4(\mathbf{w},q)|= & {} |\sum _{T\in {{\mathcal {T}}}_h}{\langle }{\{\{}\mathbf{w}-\mathbf{Q}_h\mathbf{w}{\}\}}\cdot \mathbf{n},q{\rangle }_{\partial T}|\\\le & {} C \sum _{T\in {{\mathcal {T}}}_h}\Vert \mathbf{w}-\mathbf{Q}_h\mathbf{w}\Vert _{{\partial T}} \Vert q\Vert _{\partial T}\\\le & {} C \left( \sum _{T\in {{\mathcal {T}}}_h}h_T^{-1}\Vert \mathbf{w}-\mathbf{Q}_h\mathbf{w}\Vert _{{\partial T}}^2\right) ^{\frac{1}{2}} \left( \sum _{T\in {{\mathcal {T}}}_h}h_T\Vert q\Vert _e^2\right) ^{\frac{1}{2}}\\\le & {} Ch^{k}|\mathbf{w}|_{k+1}\Vert q\Vert . \end{aligned}$$

We have proved the lemma. $\square$

Theorem 1

Let $(\mathbf{u}_h,p_h)\in \mathbf{V}_h\times W_h$ be the solutions from Algorithms 2 or 4. Assume $\eta$ is chosen big enough when Algorithm 4 is employed. Then, the following error estimates hold true

$$\begin{aligned} \Vert \mathbf{u}-\mathbf{u}_h\Vert _{1,h}\le & {} Ch^{k}|\mathbf{u}|_{k+1}, \end{aligned}$$

(64)

$$\begin{aligned} \Vert Q_hp-p_h\Vert\le & {} C\nu h^{k}|\mathbf{u}|_{k+1}. \end{aligned}$$

(65)

Proof

• 1). We first prove the results for Algorithm 2. It follows from (32) that for any $\mathbf{v}\in \mathbf{V}_h$

  $$\begin{aligned} |(\varepsilon _h,\;\nabla _w\cdot \mathbf{v})_{{{\mathcal {T}}}_h}|= & {} |\nu (\nabla _w\mathbf{e}_h,\; \nabla _w\mathbf{v})_{{{\mathcal {T}}}_h}-\ell _1(\mathbf{u},\mathbf{v})+\nu \ell _2(\mathbf{u},\mathbf{v})-\nu \ell _3(\mathbf{u},\mathbf{v})|\nonumber \\\le & {} C\nu ({|\!|\!|}\mathbf{e}_h{|\!|\!|}+h^k|\mathbf{u}|_{k+1}){|\!|\!|}\mathbf{v}{|\!|\!|}. \end{aligned}$$

  (66)

  Then the estimate (66) and the inf-sup condition (26) yield

  $$\begin{aligned} \Vert \varepsilon _h\Vert\le & {} C\nu ({|\!|\!|}\mathbf{e}_h{|\!|\!|}+h^k|\mathbf{u}|_{k+1}). \end{aligned}$$

  (67)

  By letting $\mathbf{v}=\mathbf{e}_h$ in (32) and $q=\varepsilon _h$ in (33) and subtracting the two resulting equations, we have

  $$\begin{aligned} \nu {|\!|\!|}\mathbf{e}_h{|\!|\!|}^2= & {} |\nu \ell _1(\mathbf{u},\mathbf{e}_h)-\nu \ell _2(\mathbf{u},\mathbf{e}_h)+\nu {\ell _3(\mathbf{u},\mathbf{e}_h)}-\ell _4(\mathbf{u},\varepsilon _h)|. \end{aligned}$$

  (68)

  It then follows from (59)–(62) and (67) that

  $$\begin{aligned} \nu {|\!|\!|}\mathbf{e}_h{|\!|\!|}^2\le & {} C\nu h^{k}|\mathbf{u}|_{k+1}{|\!|\!|}\mathbf{e}_h{|\!|\!|}+Ch^k|\mathbf{u}|_{k+1}\Vert \varepsilon _h\Vert \nonumber \\\le & {} C\nu h^{k}|\mathbf{u}|_{k+1}{|\!|\!|}\mathbf{e}_h{|\!|\!|}+C\nu h^k|\mathbf{u}|_{k+1}({|\!|\!|}\mathbf{e}_h{|\!|\!|}+h^k|\mathbf{u}|_{k+1})\nonumber \\\le & {} C\nu h^{2k}|\mathbf{u}|^2_{k+1}+\frac{\nu }{2}{|\!|\!|}\mathbf{e}_h{|\!|\!|}^2 \end{aligned}$$

  (69)

  which implies

  $$\begin{aligned} {|\!|\!|}\mathbf{e}_h{|\!|\!|}\le & {} Ch^{k}|\mathbf{u}|_{k+1}. \end{aligned}$$

  (70)

  It follows from (12)

  $$\begin{aligned} \Vert \mathbf{e}_h\Vert _{1,h}\le C{|\!|\!|}\mathbf{e}_h{|\!|\!|}\le & {} Ch^{k}|\mathbf{u}|_{k+1}. \end{aligned}$$

  (71)

  The estimate (71) and the triangle inequality imply (64). The pressure error estimate (65) follows immediately from (67) and (70).

• 2). Next, we prove the convergence results for Algorithm 4. By (54) and the continuity of $\mathcal {A}_h(\cdot ,\cdot )$ in (29), we have

  $$\begin{aligned} |{\mathcal {B}_h(\mathbf{v},\varepsilon _h)}|\le & {} |{\nu \ell _3(\mathbf{u},\mathbf{v})| + |\nu \mathcal {A}_h({\varvec{\epsilon }}_h,\mathbf{v})}|\\\le & {} C\nu \left( h^k|\mathbf{u}|_{k+1}+\Vert {\varvec{\epsilon }}_h\Vert _{1,h}\right) \Vert \mathbf{v}\Vert _{1,h}, \end{aligned}$$

  and thus by the inf-sup condition (31), it gives

  $$\begin{aligned} \Vert \varepsilon _h\Vert \le C\nu \left( h^k|\mathbf{u}|_{k+1}+\Vert {\varvec{\epsilon }}_h\Vert _{1,h}\right) . \end{aligned}$$

  (72)

  By (12), coercivity of bilinear form $\mathcal {A}_h(\cdot ,\cdot )$, (54), (55), (61), and (62), we have

  $$\begin{aligned} \nu {|\!|\!|}\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h{|\!|\!|}\le & {} C \nu \Vert \mathbf{Q}_h\mathbf{u}-\mathbf{u}_h\Vert _{1,h}^2 \le C \nu \mathcal {A}_h(\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h,\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h)\\= & {} \nu \mathcal {A}_h(\mathbf{Q}_h\mathbf{u}-\mathbf{u}+\mathbf{u}-\mathbf{u}_h,\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h)\\= & {} \nu \mathcal {A}_h(\mathbf{Q}_h\mathbf{u}-\mathbf{u},\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h)+\nu \ell _3(\mathbf{u},\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h)-\ell _4(\mathbf{u},\varepsilon _h)\\\le & {} C\nu h^{k}|\mathbf{u}|_{k+1}{|\!|\!|}\mathbf{e}_h{|\!|\!|}+Ch^k|\mathbf{u}|_{k+1}\Vert \varepsilon _h\Vert \\\le & {} C\nu h^{k}|\mathbf{u}|_{k+1}{|\!|\!|}\mathbf{e}_h{|\!|\!|}+C\nu h^k|\mathbf{u}|_{k+1}({|\!|\!|}\mathbf{e}_h{|\!|\!|}+h^k|\mathbf{u}|_{k+1})\\\le & {} C\nu h^{2k}|\mathbf{u}|^2_{k+1}+\frac{\nu }{2}{|\!|\!|}\mathbf{e}_h{|\!|\!|}^2 \end{aligned}$$

  and thus

  $$\begin{aligned} {|\!|\!|}\mathbf{e}_h{|\!|\!|}\le C\nu h^k|\mathbf{u}|_{k+1}. \end{aligned}$$

  Then the above estimate combines with (72) completes the proof of this lemma.

$\square$

Remark 6

In comparison, we also cite the following convergence results for energy error estimate of Algorithms 1 and 3, which can be found in [28, 34]. Let $(\mathbf{u}_h,p_h)\in \mathbf{V}_h\times W_h$ be the solutions from Algorithms 1 or 3. Assume $\eta$ is chosen big enough when Algorithm 3 is employed. We have

$$\begin{aligned} \Vert \mathbf{u}-\mathbf{u}_h\Vert _{1,h}\le & {} Ch^{k}\left( |\mathbf{u}|_{k+1}+\frac{1}{\nu }\Vert p\Vert _k\right) , \end{aligned}$$

(73)

$$\begin{aligned} \Vert Q_hp-p_h\Vert\le & {} C h^{k}\left( \nu |\mathbf{u}|_{k+1}+\Vert p\Vert _k\right) . \end{aligned}$$

(74)

It is noted that the pressure dependency has been removed in Theorem 1.

5.2 Error Estimates in $L^2$-Norm

In this section, the $L^2$-error estimate for the velocity approximation is investigated. Recall that $\mathbf{e}_h=\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h$, ${\varvec{\epsilon }}_h=\mathbf{u}-\mathbf{u}_h$ and $\varepsilon _h=Q_hp-p_h$. Consider the dual problem of seeking $({\varvec{\psi }},\xi )$ such that

$$\begin{aligned} -\nu \varDelta {\varvec{\psi }}+\nabla \xi&=\varPi _h{\varvec{\epsilon }}_h&\quad \text{ in }\;\Omega , \end{aligned}$$

(75)

$$\begin{aligned} \nabla \cdot {\varvec{\psi }}&=0&\quad \text{ in }\;\Omega , \end{aligned}$$

(76)

$$\begin{aligned} {\varvec{\psi }}&= 0&\quad \text{ on }\;\partial \Omega . \end{aligned}$$

(77)

Assume that the dual problem has the ${{\varvec{{H}}}}^{2}(\Omega )\times H^1(\Omega )$-regularity in the sense that the solution $({\varvec{\psi }},\xi )\in {{\varvec{{H}}}}^{2}(\Omega )\times H^1(\Omega )$ satisfies

$$\begin{aligned} \nu \Vert {\varvec{\psi }}\Vert _{2}+\Vert \xi \Vert _1\le C\Vert \varPi _h{\varvec{\epsilon }}_h\Vert . \end{aligned}$$

(78)

Theorem 2

Let $(\mathbf{u}_h,p_h)\in \mathbf{V}_h\times W_h$ be the solutions of Algorithms 2 or 4. Assume that (78) holds true and $\eta$ is chosen big enough if Algorithm 4 is employed. Then we have

$$\begin{aligned} \Vert \mathbf{u}-\mathbf{u}_h\Vert \le Ch^{k+1}|\mathbf{u}|_{k+1}. \end{aligned}$$

(79)

Proof

• 1). First we shall prove the $L^2$-error estimate for CDG scheme in Algorithm 2. Testing (75) by $\varPi _h{\varvec{\epsilon }}_h$ gives

  $$\begin{aligned} (\varPi _h{\varvec{\epsilon }}_h, \varPi _h{\varvec{\epsilon }}_h)= & {} -\nu (\varDelta {\varvec{\psi }},\;\varPi _h{\varvec{\epsilon }}_h)+(\nabla \xi ,\ \varPi _h{\varvec{\epsilon }}_h). \end{aligned}$$

  (80)

  It is obvious

  $$\begin{aligned} -(\varDelta {\varvec{\psi }},\varPi _h{\varvec{\epsilon }}_h)= & {} -(\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h)+(\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h). \end{aligned}$$

  (81)

  To estimate the first term on the right hand side of (81), we use integration by parts and the fact ${\langle }\nabla {\varvec{\psi }}\cdot \mathbf{n},{\{\{}{\varvec{\epsilon }}_h{\}\}}{\rangle }_{\partial {{\mathcal {T}}}_h}=0$ to obtain

  $$\begin{aligned} -(\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h)= & {} (\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}-{\langle }\nabla {\varvec{\psi }}\cdot \mathbf{n},\ {\varvec{\epsilon }}_h- {\{\{}{\varvec{\epsilon }}_h{\}\}}{\rangle }_{\partial {{\mathcal {T}}}_h}\\= & {} ({{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}+(\nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\\&-{\langle }\nabla {\varvec{\psi }}\cdot \mathbf{n},\ {\varvec{\epsilon }}_h- {\{\{}{\varvec{\epsilon }}_h{\}\}}{\rangle }_{\partial {{\mathcal {T}}}_h}\\= & {} -(\nabla \cdot {{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}+{\langle }{{\mathbb {Q}}}_h\nabla {\varvec{\psi }}\cdot \mathbf{n},\ {\varvec{\epsilon }}_h{\rangle }_{\partial {{\mathcal {T}}}_h}\\&+(\nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}-{\langle }\nabla {\varvec{\psi }}\cdot \mathbf{n},\ {\varvec{\epsilon }}_h- {\{\{}{\varvec{\epsilon }}_h{\}\}}{\rangle }_{\partial {{\mathcal {T}}}_h}\\= & {} ({{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}+{\langle }{{\mathbb {Q}}}_h\nabla {\varvec{\psi }}\cdot \mathbf{n},\ {\varvec{\epsilon }}_h-{\{\{}{\varvec{\epsilon }}_h{\}\}}{\rangle }_{\partial {{\mathcal {T}}}_h}\\&+(\nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}-{\langle }\nabla {\varvec{\psi }}\cdot \mathbf{n},\ {\varvec{\epsilon }}_h- {\{\{}{\varvec{\epsilon }}_h{\}\}}{\rangle }_{\partial {{\mathcal {T}}}_h}\\= & {} ({{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}+(\nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}-\ell _1({\varvec{\psi }},{\varvec{\epsilon }}_h), \end{aligned}$$

  which implies

  $$\begin{aligned} -(\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h)= & {} ({{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\nonumber \\+ & {} (\nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}-\ell _1({\varvec{\psi }},{\varvec{\epsilon }}_h). \end{aligned}$$

  (82)

  It follows from (16) that

  $$\begin{aligned} ({{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}= & {} (\nabla _w {\varvec{\psi }},\;\nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\nonumber \\= & {} (\nabla _w \varPi _h(\mathbf{Q}_h{\varvec{\psi }}),\;\nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\nonumber \\+ & {} (\nabla _w ({\varvec{\psi }}-\varPi _h(\mathbf{Q}_h{\varvec{\psi }})),\;\nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}. \end{aligned}$$

  (83)

  The Eq. (47) implies

  $$\begin{aligned} (\varepsilon _h,\nabla _w\cdot \mathbf{Q}_h{\varvec{\psi }})_{{{\mathcal {T}}}_h}=-\ell _4({\varvec{\psi }},\varepsilon _h). \end{aligned}$$

  (84)

  Using the Eqs. (48) and (84), we have

  $$\begin{aligned} \nu (\nabla _w \varPi _h(\mathbf{Q}_h{\varvec{\psi }}),\;\nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}=\nu \ell _1(\mathbf{u},\varPi _h(\mathbf{Q}_h{\varvec{\psi }}))-\ell _4({\varvec{\psi }},\varepsilon _h). \end{aligned}$$

  (85)

  It follows from (83) and (85)

  $$\begin{aligned} \nu ({{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}= & {} \nu \ell _1(\mathbf{u},\varPi _h(\mathbf{Q}_h{\varvec{\psi }}))-\ell _4({\varvec{\psi }},\varepsilon _h)\nonumber \\+ & {} \nu (\nabla _w ({\varvec{\psi }}-\varPi _h(\mathbf{Q}_h{\varvec{\psi }})),\;\nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}. \end{aligned}$$

  (86)

  Using (82) and (86), we have

  $$\begin{aligned} -\nu (\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h)= & {} \nu \ell _1(\mathbf{u},\varPi _h(\mathbf{Q}_h{\varvec{\psi }}))-\ell _4({\varvec{\psi }},\varepsilon _h)+\nu (\nabla _w ({\varvec{\psi }}-\varPi _h(\mathbf{Q}_h{\varvec{\psi }})),\;\nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\nonumber \\+ & {} \nu (\nabla {\varvec{\psi }}-\mathbf{Q}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}-\nu \ell _1({\varvec{\psi }},{\varvec{\epsilon }}_h). \end{aligned}$$

  (87)

  Using (87), (81) becomes

  $$\begin{aligned} -\nu (\varDelta {\varvec{\psi }},\varPi _h{\varvec{\epsilon }}_h)&=\nu \ell _1(\mathbf{u},\varPi _h(\mathbf{Q}_h{\varvec{\psi }}))-\ell _4({\varvec{\psi }},\varepsilon _h)+\nu (\nabla _w ({\varvec{\psi }}-\varPi _h(\mathbf{Q}_h{\varvec{\psi }})),\;\nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\nonumber \\&\quad +\nu (\nabla {\varvec{\psi }}-\mathbf{Q}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}-\nu \ell _1({\varvec{\psi }},{\varvec{\epsilon }}_h) +\nu (\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h). \end{aligned}$$

  (88)

  It follows from integration by parts and (2), (17) and (22) that

  $$\begin{aligned} (\nabla \xi ,\ \varPi _h{\varvec{\epsilon }}_h)= & {} -(\xi ,\ \nabla \cdot \varPi _h{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}+{\langle }\xi ,\; \varPi _h{\varvec{\epsilon }}_h\cdot \mathbf{n}{\rangle }_{\partial {{\mathcal {T}}}_h}\nonumber \\= & {} -(\xi ,\ \nabla \cdot \varPi _h{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\nonumber \\= & {} -(Q_h\xi ,\ \nabla \cdot \varPi _h{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\nonumber \\= & {} -(Q_h\xi ,\ \nabla _w\cdot {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}\nonumber \\= & {} -(Q_h\xi ,\ \nabla _w\cdot \mathbf{u})_{{{\mathcal {T}}}_h}+(Q_h\xi ,\ \nabla _w\cdot \mathbf{u}_h)_{{{\mathcal {T}}}_h}\nonumber \\= & {} 0. \end{aligned}$$

  (89)

  Combining (89) and (88) with(80), we have

  $$\begin{aligned} \nu \Vert \varPi _h{\varvec{\epsilon }}_h\Vert ^2\le & {} |\nu \ell _1(\mathbf{u},\varPi _h(\mathbf{Q}_h{\varvec{\psi }}))|+|\ell _4({\varvec{\psi }},\varepsilon _h)|+|\nu (\nabla _w ({\varvec{\psi }}-\varPi _h(\mathbf{Q}_h{\varvec{\psi }})),\;\nabla _w{\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}|\nonumber \\+ & {} |\nu (\nabla {\varvec{\psi }}-\mathbf{Q}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}|+|\nu \ell _1({\varvec{\psi }},{\varvec{\epsilon }}_h)| +|\nu (\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h)|\nonumber \\= & {} \nu T_1+T_2+\nu T_3+\nu T_4+\nu T_5+\nu T_6. \end{aligned}$$

  (90)

  Next we estimate all the terms on the right hand side of (90). Using the Cauchy–Schwarz inequality, (20), adding and subtracting $\mathbf{Q}_h{\varvec{\psi }}$, (15) and the definitions of $\mathbf{Q}_h$ and ${{\mathbb {Q}}}_h$ we obtain

  $$\begin{aligned} T_1= & {} |\ell _1(\mathbf{u},\varPi _h(\mathbf{Q}_h{\varvec{\psi }}))|\le \left| \langle (\nabla \mathbf{u}-{{\mathbb {Q}}}_h\nabla \mathbf{u})\cdot \mathbf{n},\; \varPi _h(\mathbf{Q}_h{\varvec{\psi }})-{\{\{}\varPi _h(\mathbf{Q}_h{\varvec{\psi }}){\}\}}\rangle _{\partial {{\mathcal {T}}}_h} \right| \\\le & {} C\left( \sum _{T\in {{\mathcal {T}}}_h}h_T\Vert (\nabla \mathbf{u}-{{\mathbb {Q}}}_h\nabla \mathbf{u})\Vert ^2_{\partial T}\right) ^{1/2} \left( \sum _{T\in {{\mathcal {T}}}_h}h_T^{-1}\Vert {[\![}\varPi _h(\mathbf{Q}_h{\varvec{\psi }})-{\varvec{\psi }}{]\!]}\Vert ^2_{\partial T}\right) ^{1/2} \\\le & {} C\left( \sum _{T\in {{\mathcal {T}}}_h}\Vert \nabla \mathbf{u}-{{\mathbb {Q}}}_h\nabla \mathbf{u}\Vert ^2_T+h_T^2\Vert \nabla \mathbf{u}-{{\mathbb {Q}}}_h\nabla \mathbf{u}\Vert _{1,T}^2\right) ^{1/2}\\&\quad \left( \sum _{T\in {{\mathcal {T}}}_h}h_T^{-2}\Vert \varPi _h(\mathbf{Q}_h{\varvec{\psi }})-{\varvec{\psi }}\Vert ^2_T+\Vert \varPi _h(\mathbf{Q}_h{\varvec{\psi }})-{\varvec{\psi }}\Vert _{1,T}^2 \right) ^{1/2} \\\le & {} Ch^{k+1}|\mathbf{u}|_{k+1}\Vert {\varvec{\psi }}\Vert _2. \end{aligned}$$

  It follows from (62) and (65) that

  $$\begin{aligned} T_2= & {} |\ell _4({\varvec{\psi }},\varepsilon _h)|\le Ch\Vert {\varvec{\psi }}\Vert _2\Vert \varepsilon _h\Vert \le C\nu h^{k+1}|\mathbf{u}|_{k+1}|{\varvec{\psi }}|_2. \end{aligned}$$

  It follows from (63) and (64) that

  $$\begin{aligned} T_3= & {} |(\nabla _w({\varvec{\psi }}-\varPi _h(\mathbf{Q}_h{\varvec{\psi }})),\;\nabla _w {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}|\\ {}\le & {} C{|\!|\!|}{\varvec{\epsilon }}_h{|\!|\!|}{|\!|\!|}{\varvec{\psi }}-\varPi _h(\mathbf{Q}_h{\varvec{\psi }}){|\!|\!|}\\\le & {} Ch^{k+1}|\mathbf{u}|_{k+1}|{\varvec{\psi }}|_2. \end{aligned}$$

  The estimates (12) and (64) imply

  $$\begin{aligned} T_4= & {} |(\nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }},\ \nabla {\varvec{\epsilon }}_h)_{{{\mathcal {T}}}_h}|\\\le & {} C\left( \sum _{T\in {{\mathcal {T}}}_h}\Vert \nabla {\varvec{\epsilon }}_h\Vert _T^2\right) ^{1/2} \left( \sum _{T\in {{\mathcal {T}}}_h}\Vert \nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }}\Vert _T^2\right) ^{1/2}\\\le & {} C\left( \sum _{T\in {{\mathcal {T}}}_h}(\Vert \nabla (\mathbf{u}-\mathbf{Q}_h\mathbf{u})\Vert _T^2+\Vert \nabla (\mathbf{Q}_h\mathbf{u}-\mathbf{u}_h)\Vert _T^2)\right) ^{1/2}\\&\quad \,\times&\left( \sum _{T\in {{\mathcal {T}}}_h}\Vert \nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }}\Vert _T^2\right) ^{1/2}\\\le & {} Ch|{\varvec{\psi }}|_2(h^k|\mathbf{u}|_{k+1}+{|\!|\!|}\mathbf{e}_h{|\!|\!|})\\\le & {} Ch^{k+1}|\mathbf{u}|_{k+1}|{\varvec{\psi }}|_2. \end{aligned}$$

  Using (12) and (64), we obtain

  $$\begin{aligned} T_5= & {} |\ell _1({\varvec{\psi }},{\varvec{\epsilon }}_h)|=\left| {\langle }(\nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }})\cdot \mathbf{n},\ {\varvec{\epsilon }}_h-{\{\{}{\varvec{\epsilon }}_h{\}\}}{\rangle }_{\partial {{\mathcal {T}}}_h}\right| \\\le & {} \sum _{T\in {{\mathcal {T}}}_h} h_T^{1/2}\Vert \nabla {\varvec{\psi }}-{{\mathbb {Q}}}_h\nabla {\varvec{\psi }}\Vert _{\partial T}h_T^{-1/2}\Vert {[\![}{\varvec{\epsilon }}_h{]\!]}\Vert _{\partial T}\\\le & {} Ch\Vert {\varvec{\psi }}\Vert _2(\sum _{T\in {{\mathcal {T}}}_h}h_T^{-1}(\Vert {[\![}\mathbf{e}_h{]\!]}\Vert ^2_{\partial T}+\Vert {[\![}\mathbf{u}-\mathbf{Q}_h\mathbf{u}{]\!]}\Vert ^2_{\partial T}))^{1/2}\\\le & {} Ch\Vert {\varvec{\psi }}\Vert _2({|\!|\!|}\mathbf{e}_h{|\!|\!|}+(\sum _{T\in {{\mathcal {T}}}_h}h_T^{-1}\Vert {[\![}\mathbf{u}-\mathbf{Q}_h\mathbf{u}{]\!]}\Vert ^2_{\partial T})^{1/2}\\\le & {} Ch^{k+1}|\mathbf{u}|_{k+1}|{\varvec{\psi }}|_2. \end{aligned}$$

  Using (15), (64) and (78), we have

  $$\begin{aligned} T_6= & {} |(\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h)| \le Ch\Vert {\varvec{\psi }}\Vert _2\Vert {\varvec{\epsilon }}_h\Vert _{1,h}\\\le & {} Ch^{k+1}\Vert \mathbf{u}\Vert _{k+1}\Vert {\varvec{\psi }}\Vert _2. \end{aligned}$$

  Combining all the estimates above with (90) yields

  $$\begin{aligned} \nu \Vert \varPi _h{\varvec{\epsilon }}_h\Vert ^2\le C\nu h^{k+1}|\mathbf{u}|_{k+1}\Vert {\varvec{\psi }}\Vert _2. \end{aligned}$$

  Using (78), we have

  $$\begin{aligned} \Vert \varPi _h{\varvec{\epsilon }}_h\Vert \le C h^{k+1}|\mathbf{u}|_{k+1}. \end{aligned}$$

  It follows from the triangle inequality, the above estimate and (64)

  $$\begin{aligned} \Vert {\varvec{\epsilon }}_h\Vert\le & {} \Vert {\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h\Vert +\Vert \varPi _h{\varvec{\epsilon }}_h\Vert \nonumber \\\le & {} Ch \Vert {\varvec{\epsilon }}_h\Vert _{1,h}+ C h^{k+1}|\mathbf{u}|_{k+1}\nonumber \\\le & {} C h^{k+1}|\mathbf{u}|_{k+1}. \end{aligned}$$

  (91)

  We have completed the proof for Algorithm 2.

• 2). Next we shall prove the results for Algorithm 4. Testing (75) by $\varPi _h{\varvec{\epsilon }}_h$ gives

  $$\begin{aligned} \nu (\varPi _h{\varvec{\epsilon }}_h, \varPi _h{\varvec{\epsilon }}_h)= & {} -\nu (\varDelta {\varvec{\psi }},\varPi _h{\varvec{\epsilon }}_h)+(\nabla \xi ,\varPi _h{\varvec{\epsilon }}_h). \end{aligned}$$

  (92)

  Similarly as (89), by using the equivalence property in (25), we have

  $$\begin{aligned} (\nabla \xi ,\ \varPi _h{\varvec{\epsilon }}_h) = 0. \end{aligned}$$

  (93)

  By subtracting and adding $\nu (\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h)$ to (92) and using (93), we obtain

  $$\begin{aligned} \nu (\varPi _h{\varvec{\epsilon }}_h,\varPi _h{\varvec{\epsilon }}_h)= & {} -\nu (\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h)+\nu (\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h)\nonumber \\= & {} \nu \mathcal {A}_h({\varvec{\psi }},{\varvec{\epsilon }}_h)+\nu (\varDelta {\varvec{\psi }},{\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h) . \end{aligned}$$

  (94)

  Here we have used the definition of bilinear form $\mathcal {A}_h(\cdot ,\cdot ).$ Next by subtracting and adding $\varPi _h\mathbf{Q}_h{\varvec{\psi }}$, using (57), (25) and (47), it implies

  $$\begin{aligned} \nu \mathcal {A}_h({\varvec{\psi }},{\varvec{\epsilon }}_h)= & {} \nu \mathcal {A}_h({\varvec{\psi }}- \varPi _h\mathbf{Q}_h{\varvec{\psi }},{\varvec{\epsilon }}_h) + \nu \mathcal {A}_h(\varPi _h\mathbf{Q}_h{\varvec{\psi }},{\varvec{\epsilon }}_h)\\= & {} \nu \mathcal {A}_h({\varvec{\psi }}- \varPi _h\mathbf{Q}_h{\varvec{\psi }},{\varvec{\epsilon }}_h) -\mathcal {B}_h(\mathbf{Q}_h{\varvec{\psi }},\varepsilon _h)\\= & {} \nu \mathcal {A}_h({\varvec{\psi }}- \varPi _h{\varvec{\psi }},{\varvec{\epsilon }}_h) -\ell _4({\varvec{\psi }},\varepsilon _h). \end{aligned}$$

  Combining (94) and above equation gives

  $$\begin{aligned} \nu \Vert \varPi _h{\varvec{\epsilon }}_h\Vert ^2\le & {} \nu \Vert {\varvec{\psi }}-\varPi _h{\varvec{\psi }}\Vert _{1,h}\Vert {\varvec{\epsilon }}_h\Vert _{1,h} + \nu \Vert {\varvec{\psi }}\Vert _2\Vert {\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h\Vert + |\ell _4({\varvec{\psi }},\varepsilon _h)|\\\le & {} C\left( \nu h \Vert {\varvec{\psi }}\Vert _2\Vert {\varvec{\epsilon }}_h\Vert _{1,h}+h|{\varvec{\psi }}|_2\Vert \varepsilon _h\Vert \right) \\\le & {} C\nu h^{k+1}\Vert \varPi _h{\varvec{\epsilon }}_h\Vert \; |\mathbf{u}|_{k+1}. \end{aligned}$$

  Canceling the common factors in the above estimate and combining (15) (64), we finally prove estimate

  $$\begin{aligned} \Vert {\varvec{\epsilon }}_h\Vert\le & {} \Vert {\varvec{\epsilon }}_h-\varPi _h{\varvec{\epsilon }}_h\Vert + \Vert \varPi _h{\varvec{\epsilon }}_h\Vert \\\le & {} Ch\Vert {\varvec{\epsilon }}_h\Vert _{1,h}+h^{k+1}|\mathbf{u}|_{k+1}\\\le & {} Ch^{k+1}|\mathbf{u}|_{k+1}. \end{aligned}$$

$\square$

Remark 7

We also cite the $L^2$ error estimate for Algorithms 1 and 3 for comparison. Let $(\mathbf{u}_h,p_h)\in \mathbf{V}_h\times W_h$ be the solutions from Algorithms 1 or 3. Assume $\eta$ is chosen big enough when Algorithm 3 is employed. We have

$$\begin{aligned} \Vert \mathbf{u}-\mathbf{u}_h\Vert \le Ch^{k+1}\left( \Vert \mathbf{u}\Vert _{k+2}+\frac{1}{\nu }\Vert p\Vert _{k+1}\right) . \end{aligned}$$

The pressure dependent term $\frac{1}{\nu }\Vert p\Vert _{k+1}$ has been eliminated in Theorem 2. Thus, we claim that Algorithms 2 and 4 are pressure-robust schemes.

6 Numerical Experiments

In this section, several numerical experiments will be carried out to validate our theoretical conclusions in Theorems 1 and 2 and compare the results for the non-pressure-robust schemes. By using discontinuous elements with degree $k\ge 1$, we are expecting the optimal rate in convergence as follows,

$$\begin{aligned} H^1 \text {-seminorm for velocity:}&\Vert \nabla {\varvec{\epsilon }}_h\Vert :=\Vert \nabla (\mathbf{u}-\mathbf{u}_h)\Vert \approx \mathcal {O}(h^{k}),\\ L^2 \text {-norm for velocity:}&\Vert {\varvec{\epsilon }}_h\Vert := \Vert \mathbf{u}-\mathbf{u}_h\Vert \approx \mathcal {O}(h^{k+1})\\ L^2 \text {-norm for pressure:}&\Vert \varepsilon _h\Vert :=\Vert p-Q_hp\Vert \approx \mathcal {O}(h^k). \end{aligned}$$

We shall test the following two-dimensional problem on the uniform triangular grid with mesh size h. Let $\Omega = (0,1)\times (0,1)$, and the exact solutions with homogeneous Dirichlet boundary condition for velocity, are chosen as follows for testing:

$$\begin{aligned} \mathbf{u}=\begin{pmatrix} \; 10x^2(x-1)^2y(y-1)(2y-1)\\ -10x(x-1)(2x-1)y^2(y-1)^2 \end{pmatrix},\ p = 10(2x-1)(2y-1). \end{aligned}$$

Table 1 Example 6.1. Error profiles and convergence results for CDG schemes with $k = 1$

Table 2 Example 6.1. Error profiles and convergence results for CDG schemes with $k = 2$

Table 3 Example 6.1. Error profiles and convergence results for CDG schemes with $k = 3$

6.1 Test 1—Convergence Tests for CDG Schemes

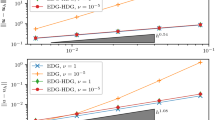
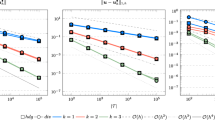
The first test has been carried out for testing the convergence results for the proposed enhanced Algorithm 2 and non-pressure-robust Algorithm 1. The error profiles and convergence results are reported in Table 1, 2 and 3. We observe:

• The convergence orders for varying polynomial degrees are all optimal as expected.

• In the case of $k = 1,2$, as we reduce the values in $\nu$, the velocity errors produced by Algorithm 2 will be increased by a factor of $\frac{1}{\nu }$, though optimal rates in convergence can still be achieved. Such increasing errors are due to the non-pressure-robustness in the scheme. In contrast to the velocity error, the pressure error will remain the same as we decrease the values in $\nu$. This confirms the results in Remarks 6 and 7.

• In the case of $k = 1,2$, all the errors are smaller than the non-pressure-robust scheme Algorithm 1 and thus Algorithm 2 outperforms Algorithm 1. Furthermore, the velocity errors remain the same for varying values in $\nu$; the pressure errors are reduced by a factor of $\nu$. This validates the robustness in our proposed schemes.

• When the simulation approximates velocity by $[P_3(T)]^2$ element and approximates pressure by $P_2(T)$ element, the pressure has been fully resolved. In this case, one can observe that the velocity errors produced by Algorithms 1 and 2 are comparable. However, due to the introduced inconsistency errors, the pressure error from Algorithm 2 is slightly larger than that from Algorithm 1, though both two types errors are at the same magnitude.

• All the above observations agree with our theoretical conclusions.

6.2 Test 2—Convergence Test for IPDG Schemes

In this section, we shall compare the numerical performance for our proposed enhance scheme with classical IPDG finite element methods. In all the computation, we take $\eta = 4k^2$. The numerical results and error profiles are reported in Table 4, 5 and 6. The similar numerical conclusions as 6.1 can be obtained. Again, we validate the theoretical conclusions.

Table 4 Example 6.2. Error profiles and convergence results for IPDG schemes with $k = 1$

Table 5 Example 6.2. Error profiles and convergence results for IPDG schemes with $k = 2$

Table 6 Example 6.2. Error profiles and convergence results for IPDG schemes with $k = 3$

7 Conclusion

In this paper, we investigate the velocity reconstruction techniques for enhancing the pressure-robustness in the existing DG scheme. Both theoretical analysis and numerical experiments have been provided to show the optimal rate in convergence and pressure-robustness. By only modifying the source term, our new schemes can achieve the desired pressure-robust features with minimal efforts. Both theoretical analysis and numerical experiments are provided to demonstrate the advantages in the new schemes. In the future, we shall investigate more applications in the incompressible fluid simulation and time dependent problems.