Keywords

1 Introduction

The mechanical impedance of the human ankle plays a major role in lower-extremity functions which involve mechanical interaction of the foot with a contacting surface, including shock-absorption during foot-strike or maintenance of upright posture. Precise quantitative measurement of ankle mechanical impedance may support deeper understanding of how the ankle supports these functions and other aspects of locomotion and its neural control, and may provide essential data for the design of improved therapeutic procedures to address deficiencies of balance and/or locomotion.

Recently, there have been a few lower extremity power prostheses that control the mechanical impedance at their joints. Notable examples are a transfemoral powered prosthesis by Sup et al. [1–4] and a transtibial powered prosthesis by Au et al. [5–7]. The former includes a controller that adjusts the impedance of the ankle and knee joints at different phases of gait. The latter, which later transitioned into the commercially available ankle-foot prosthesis BiOM, has an active ankle joint with a finite-state machine to generate appropriate ankle impedance and torque at each phase of gait [8, 9]. While both prostheses have advanced the state-of-the-art, their designs are confined to the sagittal plane. Even level walking in a straight line requires the ankle to function in both the sagittal and frontal planes. Additionally, normal daily activity includes more gait scenarios such as turning, traversing slopes, steering, and adapting to uneven terrain profiles. This suggests that the next advance in lower extremity assistive devices is to extend their design and control to the frontal plane. To do that, we need a better understanding of the multi-variable mechanical impedance of the human ankle, and that is the subject of this study.

Several prior studies have addressed ankle mechanical impedance. Lamontagne et al. [10] reported the viscoelastic behavior of relaxed ankle plantarflexors. Other researchers compared dorsi-flexion/plantar-flexion (DP) ankle stiffness of unimpaired and neurologically-impaired subjects [11–15]. Dynamic compliance of the human ankle using band-limited Gaussian torque perturbations was estimated by Mirbagheri et al. [16]. Kearney and Hunter [17, 18] and Weis et al. [19, 20] used a similar system identification approach to estimate the passive and active dynamic stiffness of the ankle joint in DP. Also, Mirbagheri et al. [21] and Kearney et al. [22] used a similar method to estimate the intrinsic and reflexive components of ankle dynamic stiffness. Intrinsic and reflex contributions to ankle stiffness in dorsiflexion at different levels of voluntary muscle co-contraction were measured by Sinkjaer et al. [23]. Kirsch and Kearney [24] estimated ankle mechanical impedance in DP by superimposing small stochastic motion perturbations during a large stretch imposed upon active triceps surae muscles. Winter et al. [25], Morasso and Sanguineti [26], and Loram and Lakie [27, 28] measured the ankle stiffness during quiet standing. Davis and Deluca [29], Palmer [30], and Hansen et al. [31] measured ankle stiffness during locomotion.

All of these studies were confined to the sagittal plane. In the frontal plane, Saripalli and Wilson [32] studied the variation of ankle stiffness under different weight-bearing conditions. Zinder et al. [33] studied dynamic stabilization and ankle stiffness in the inversion/eversion direction (IE) by applying a sudden perturbation in the frontal plane at a time of upright posture during bipedal weight-bearing stance. Roy et al. estimated the ankle stiffness in both DP and IE for unimpaired subjects [34] and subjects with chronic hemiparesis [35] but coupling between these degrees of freedom was not assessed.

All of this prior work characterized ankle mechanical impedance in single degrees of freedom (DOF) and did not address the multi-variable character of the ankle. Yet the ankle is a biomechanically complex joint with multiple DOFs. Its major anatomical axes do not intersect and they are far from orthogonal, which could introduce a biomechanical coupling between DP and IE. Furthermore, single DOF ankle movements are rare in normal lower-extremity actions and the control of multiple ankle DOFs may present unique challenges [36]. In previous work by some of the authors [37–40], the multi-variable ankle mechanical impedance of young unimpaired subjects with maximally relaxed muscles was measured in static condition. In the study reported here, we extend the estimation to the dynamic condition. Preliminary reports of part of this work were presented in [41–43].

We chose to use stochastic frequency-domain methods to estimate ankle dynamic mechanical impedance. A singular advantage of this approach is that, although it requires an assumption of linear dynamics (which may be justified by assuming smoothness and using small perturbations) it requires no a-priori assumption about the order or dynamic structure of the system under investigation. In particular, it does not require the common assumption in previous work that ankle mechanical impedance is composed of inertia, damping, and stiffness, but is applicable to more complex, higher-order dynamics.

Stochastic excitation using hydraulic actuators has been used in prior research [18, 17, 22, 19–21, 23, 44]. Hydraulic actuators have intrinsically high output mechanical impedance, which cannot substantially be reduced by force feedback control, especially at higher frequencies, and that means they essentially impose motion perturbations [45, 46]. However, imposing motion perturbations requires care to avoid applying excessive force to subjects’ joints.

Previously, we presented a multi-variable stochastic method to estimate upper extremity mechanical impedance by applying pseudo-random torque perturbations [47]. In the work reported here, we adapted that method to estimate human ankle mechanical impedance using Anklebot, a wearable robot designed for the study and treatment of the ankle [34]. The principal adaptation was to obviate direct force measurement by using an accurate characterization of the robot’s dynamic behavior.

Remarkably, we found that, despite the non-orthogonality of the ankle joint’s anatomical axes and the geometric complexity of its musculo-skeletal kinematics, the relaxed ankle’s multivariable mechanical impedance is predominantly orthogonal and aligned with its principal axes in the sagittal and frontal planes.

2 Methods

2.1 Subject

This study reports the results on one young male subject with no reported biomechanical or neuromuscular disorder. This participant gave written informed consent to participate as approved by the Michigan Technological University institutional review board.

2.2 Experimental Setup

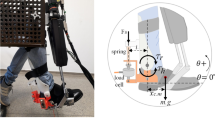
In general, we define ankle mechanical impedance as a dynamic operator that maps a time-history of angular displacement onto a corresponding time-history of torque. This dynamic operator was measured for DP and IE simultaneously using a wearable robot, Anklebot (Interactive Motion Technologies, Inc.), the device used in previous work [37–39, 41, 43, 42]. Described in detail in [34], it is backdrivable with low friction and allows human subjects to move the foot freely in three DOF relative to the shank. Of those, two DOF are actuated by two nearly-parallel linear actuators attached to the leg (through a shoe and knee-brace) and aligned approximately between the knee and the ball of the foot. The sum of the actuator forces generates a dorsi-flexion/plantar-flexion torque; their difference generates an inversion/eversion torque. Anklebot is able to apply actively controllable torques up to 23 N-m (DP) and 15 N-m (IE) simultaneously. Position information is provided by two linear incremental encoders (Renishaw) with a resolution of 5 × 10−6 m mounted on the traction drives. Torque is measured by current sensors (Burr-Brown 1NA117P), which provide a measure of motor torque with a nominal resolution of 2.59 × 10−6 N-m.

2.3 Experimental Protocol

Estimation of ankle mechanical impedance consisted of two steps. First, the subject was seated wearing a knee brace and the Anklebot (Fig. 6.1a). A proportional position controller prevented the ankle joint from drifting and guaranteed safe and stable data capture. Gains of 5, 10 or 15 N-m/rad were used in separate tests. With the subject’s foot clear of the ground and his ankle gently held in a neutral position with the sole at a right angle to the tibia, subject was instructed to relax fully and allow the machine to move the foot. Two uncorrelated pseudo-random command voltage sequences with 100 Hz bandwidth and 60 s long, were applied simultaneously to the actuators to produce torque perturbations that rotated the subject’s foot in all directions in the frontal and sagittal planes while remaining within the natural limits of the joint. Actuator displacements and command voltages were recorded. The second step repeated this procedure while the human subject was wearing the knee brace with the mounted Anklebot, except that the shoe was connected to the Anklebot actuators but was not worn by the human subject (Fig. 6.1b). This approach provided characterization of the apparatus dynamics including possible dynamic effects from the combined structure of the seat and human body.

Fig. 6.1
figure 1

Test setup. (a) Anklebot fully attached to a human subject while suspended using a compliant strap. (b) Anklebot partially attached to a human subject while suspended using a compliant strap. (c) Anklebot attached to ankle mockup

Full size image

To validate this procedure it was also applied to a physical “mockup” of the ankle, consisting of two wooden blocks, one corresponding to the shank, the other to the foot (Fig. 6.1c) and connected at right angles by a stainless steel plate weakened by slots. By design, the rotational stiffness of this plate was highly anisotropic to allow assessment of our method’s ability to detect the directional structure of ankle impedance. The shank block was secured to a horizontal table. A connector similar to that used in the Anklebot shoes was secured to the foot block. To avoid plastic deformation of the steel plates, the magnitude of the random signals used with this mockup was 60 % of the magnitude used with human subjects. For comparison, the inertia of the foot block and the stiffness of the steel plate were estimated from their geometric and material properties.

2.4 Analysis Methods

The measured variables were the displacements X L and X R and commanded forces F L and F R in the left and right actuators, respectively. The ankle torques and angles were estimated from a kinematic model of the relation between actuator displacement and joint angular displacement depicted in Fig. 6.2:

Fig. 6.2
figure 2

Schematic of Anklebot and its geometrical parameters

Full size image
$$ {\tau}_{dp}=\left({F}_R+{F}_L\right){x}_{{\mathit{tr}}, {\mathit{len}}} $$
(6.1)
$$ {\theta}_{{\mathit{dp}}}={\theta}_{{\mathit{dp}}, {\mathit{offset}}}+ \arctan \left(\frac{X_R+{X}_L}{2{x}_{{\mathit{tr}}, {\mathit{len}}}}\right) $$
(6.2)
$$ {\tau}_{ie}=\frac{1}{2}\left({F}_R-{F}_L\right){x}_{{\mathit{tr}}, {\mathit{width}}} $$
(6.3)
$$ {\theta}_{ie}={\theta}_{{\mathit{ie}}, {\mathit{offset}}}+ \arctan \left(\frac{X_R-{X}_L}{x_{{\mathit{tr}}, {\mathit{width}}}}\right) $$
(6.4)

where τ dp and τ ie are joint torques and θ dp and θ ie are angles in DP and IE directions, respectively. θ dp,offset and θ ie,offset are the angles at which the ankle will be centered with respect to the coronal and sagittal planes, respectively. In the experiments in this study, their values were zero. The other parameters in Eqs. 6.1, 6.2, 6.3, and 6.4 are described in Fig. 6.2.

Voltage inputs to the actuators generated forces that resulted in ankle motion. A “natural” or strictly proper description of this system is as a mechanical admittance (force input, motion output). Assuming linear dynamics, admittance Y(f) in DP-IE space is a 2 × 2 matrix of transfer functions.

$$ \left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\}=\mathbf{Y}(f)\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}=\left[\begin{array}{ll}\hfill {Y}_{11}(f)\hfill & \hfill {Y}_{12}(f)\hfill \\ {Y}_{21}(f)\hfill & \hfill {Y}_{22}(f)\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\} $$
(6.5)

If this matrix is non-singular, its inverse is mechanical impedance, Z(f) = Y − 1(f), a matrix of transfer functions relating input angles to output torques.

$$ \left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}=\mathbf{Z}(f)\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\}=\left[\begin{array}{ll}\hfill {Z}_{11}(f)\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\} $$
(6.6)

A proportional controller with a diagonal gain matrix with identical elements prevented the ankle from drifting from its neutral position.

$$ \boldsymbol{\uptau} =\mathbf{K}\left({\boldsymbol{\uptheta}}_o-\boldsymbol{\uptheta} \right)+{\boldsymbol{\uptau}}_p $$
(6.7)

where \( \boldsymbol{\uptau} ={\left\{\begin{array}{ll}\hfill {\tau}_{dp}\hfill & \hfill {\tau}_{ie}\hfill \end{array}\right\}}^T \) is a vector of applied ankle torques, \( \boldsymbol{\uptheta} ={\left\{\begin{array}{ll}\hfill {\theta}_{dp}\hfill & \hfill {\theta}_{ie}\hfill \end{array}\right\}}^T \) is a vector of ankle angles, K is a diagonal gain matrix that determines Anklebot stiffness that prevents the foot from drifting, subscript o denotes the neutral ankle angle, and subscript p denotes perturbation torques. The ankle and Anklebot form a multivariable closed-loop system.

$$ \boldsymbol{\uptheta} ={\left(\mathbf{1}+\mathbf{YK}\right)}^{-1}\mathbf{Y}\left(\mathbf{K}{\boldsymbol{\uptheta}}_o+{\boldsymbol{\uptau}}_p\right) $$
(6.8)

The closed-loop admittance matrix is θ = (1 + YK)− 1 Yτ p . The closed-loop impedance matrix is its inverse, τ p  = Y − 1(1 + YK)θ = (Z + K)θ, i.e.

$$ {\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}}_p=\left[\begin{array}{ll}\hfill {Z}_{11}(f)+ K\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)+ K\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\} $$
(6.9)

The mechanical impedance of the system under test is

$$ \mathbf{Z}(f)=\left[\begin{array}{ll}\hfill {Z}_{11}(f)\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)\hfill \end{array}\right]=\left[\begin{array}{ll}\hfill \frac{\tau_{dp}(f)}{\theta_{dp}(f)}- K\hfill & \hfill \frac{\tau_{dp}(f)}{\theta_{ie}(f)}\hfill \\ \frac{\tau_{ie}(f)}{\theta_{dp}(f)}\hfill & \hfill \frac{\tau_{ie}(f)}{\theta_{ie}(f)}- K\hfill \end{array}\right] $$
(6.10)

where the impedance functions τ x (f)/θ y (f) x, y = dp, ie are determined from experimental measurements.

Although the system naturally behaves as a mechanical admittance, expressing it as a mechanical impedance simplifies separating the robot dynamics from the human ankle dynamics. The foot and shoe share the same motion, consequently the torque exerted by the actuator is the sum of the torques required to move the foot and shoe; the output mechanical impedance of the robot adds to the human ankle mechanical impedance. The human ankle mechanical impedance is obtained by subtracting the estimate for robot and shoe alone from the estimate for robot, shoe, and ankle as follows.

$$ \mathbf{Z}\left|{}_{ankle}=\mathbf{Z}\right|{}_{ankle+ Anklebot\kern0.5em and\kern0.5em shoe}-\mathbf{Z}\Big|{}_{Anklebot\kern0.5em and\kern0.5em shoe} $$
(6.11)

Frequency-domain stochastic methods were used to estimate the mechanical impedance matrices. Sixty seconds of data were sampled at 200 Hz yielding 12,000 samples. Welch’s averaged, modified periodogram method of spectral estimation, as implemented in MATLAB was used to estimate one-sided auto- and cross-power spectral densities of the torque and angle sequences in the DP and IE directions. A periodic Hamming window with a length of 512 samples was used with an FFT length of 1,024 samples, yielding a spectral resolution of 0.195 Hz. Power spectral density functions were estimated by averaging their values calculated from 45 data windows with 50 % overlap (256 samples). The standard error of the impedance plots was determined by dividing the standard deviation of impedances at each frequency by \( \sqrt{45} \). Elements of the mechanical impedance matrix are presented in Appendix as described in [48]. Moreover, partial coherence functions were estimated to measure the linear dependency between each input and output after removing the effects of the other inputs in the multivariable case (see Appendix).

3 Results

3.1 Validation Using the Ankle Mockup

Because of the modest torques applied to the physical mockup, its displacements were small (root-mean square actuator displacement was 2.5, 2.4 and 2.3 mm when proportional gains were 5, 10 and 15 Nm/rad, respectively) supporting a linear description of its dynamics. Figure 6.3a shows the partial coherences obtained when the stochastic estimation procedure was applied to the mockup in actuator coordinates (the forces and displacements of the actuators) with proportional gain 10 N-m/rad. The diagonal elements exhibited partial coherences greater than 0.8 at most frequencies from 0 to 50 Hz, averaging 0.86 in the DP and 0.89 in the IE directions over this range. The off-diagonal elements exhibited partial coherences typically greater than 0.8 from 0 to 20 Hz, decreasing to 0.6 at about 30 or 40 Hz and averaging 0.68 from X R to F L and 0.75 from X L to F R from 0 to 50 Hz. These results demonstrated that, despite the known nonlinearities of the Anklebot actuators (including static friction, primarily due to the traction drives, and “cogging” due to the permanent magnet motors [34]), the linear methods we used gave satisfactory results.

Fig. 6.3
figure 3

Partial coherences of the mockup impedance matrix, (a) in actuator coordinates; (b) in joint coordinates

Full size image

Figure 6.3b shows the partial coherences obtained when the recorded data were first transformed to DP-IE joint coordinates (as detailed in Eqs. 6.1, 6.2, 6.3 and 6.4) before applying the stochastic estimation procedure. Results obtained with four values of the proportional gain (K = 0, 5, 10 and 15 N-m/rad) are superimposed, showing that all yielded essentially identical results, along with the results obtained when the actuators were disconnected from the foot block (with K = 5 N-m/rad). In this case, the partial coherences of the off-diagonal elements declined to extremely low values, less than 0.2 at most frequencies, averaging less than 0.05 from θ ie to τ dp and from θ dp to τ ie from 0 to 50 Hz for all values of proportional gain. As shown by the partial coherences in Fig. 6.3a, this cannot be attributed to nonlinear dynamics but is due to low signal strength. By design, there is essentially no coupling between the DP and IE degrees of freedom of the mockup; its impedance matrix is essentially diagonal with zero entries in the off-diagonal positions. Confirming this account, the partial coherences of the diagonal elements increased, becoming greater than 0.8 and close to 0.9 at almost all frequencies between 0 and 50 Hz, averaging more than 0.9 from θ dp to τ dp and from θ ie to τ ie , respectively, over this range for all value of proportional gain, indicating that the diagonal elements of a linear model accounted for more of the data variance in joint coordinates.

Figure 6.4 shows Bode plots of the magnitude and phase of the actuator and mockup diagonal mechanical impedances. The impedance of the actuator alone was as expected. A permanent-magnet motor driven by a current-controlled amplifier is competently modeled as a force-controlled actuator retarded by an output impedance dominated by a combination of inertia and damping, and that is consistent with these observations. The estimated mechanical impedance of the mockup was obtained by subtraction as described above. Results obtained with four values of the proportional gain, K, are superimposed, and demonstrate that the method was extremely insensitive to this parameter.

Fig. 6.4
figure 4

Diagonal elements of the mockup impedance matrix in joint coordinates

Full size image

A linear second-order model, based on the mockup physical parameters, is also superimposed. In DP the parameter values are inertia: 0.017 kg-m2; damping: 0.4 N-m-s/rad; stiffness: 40.2 N-m/rad. Parameter values in IE are inertia: 0.004 kg-m2; damping: 0.5 N-m-s/rad; stiffness: 191 N-m/rad. The model exhibited an undamped natural frequency at 7.7 Hz in DP.

In IE the undamped natural frequency appears to be at 34.8 Hz. However, in both DP and IE, the phase plots showed evidence of returning towards zero degrees, suggesting the presence of a dynamic zero, which may be due to un-modeled resonance, e.g., due to the metal bracket that was mounted on the foot block. As a result, the data at frequencies greater than 30 Hz should be interpreted with caution. Theoretical calculation of the foot block moment of inertia in the DP direction yielded 0.0176 kg-m2, which differed from the DP model parameter by 3.4 %. Theoretical calculation of the steel plate stiffness in bending yielded 40.0 N-m/rad, which differed from the DP model parameter by 0.5 %.

3.2 Human Ankle Mechanical Impedance

3.2.1 Coherences

The torques applied to the ankle evoked small angular displacements (root-mean square displacement was 2.48° in DP and 2.70° in IE) consistent with linear analysis. Figure 6.5a shows a representative example of the partial coherences obtained when the stochastic estimation procedure was applied in joint coordinates. Over a frequency range from 0 to 50 Hz, both of the diagonal elements of the impedance matrix exhibited a partial coherence averaging 0.93, with a minimum of 0.84 at 0.78 Hz for Z 11 and 0.87 at 3.12 Hz for Z 21. A proportional gain of K = 10 N-m/rad was used to prevent the ankle from drifting from its neural position. Almost identical results were obtained with proportional gains of K = 5 and 15 N-m/rad. In contrast, over the same frequency range the off-diagonal elements of the impedance matrix exhibited low coherence averaging 0.06. Below 10 Hz the off-diagonal partial coherence improved slightly, peaking at 0.41 at 2.15 Hz for Z 12 and 0.37 at 5.6 Hz for Z 21 but yielding averages over 0 to 10 Hz of 0.19 for Z12 and 0.20 for Z21. As indicated from the validation tests, this indicates weak coupling between DP and IE throughout most of the frequency range.

Fig. 6.5
figure 5

Partial coherence plots of the diagonal elements of the impedance matrix for Anklebot attached to a human ankle with proportional gain K = 10 N-m/rad, (a) in joint coordinates; (b) in actuator coordinates

Full size image

Applying the stochastic estimation procedure in actuator coordinates improved the off-diagonal partial coherences (Fig. 6.5b), which averaged 0.18 from 30 to 50 Hz; 0.15 from 0 to 50 Hz; 0.15 from 0 to 30 Hz; and 0.22 from 0 to 10 Hz. However, the diagonal partial coherences remained high, averaging 0.93 from 0 to 50 Hz, indicating that a linear description with principal axes in the sagittal and frontal planes accounted for almost all of the data variance under these conditions.

3.2.2 Mechanical Impedance About Principal Axes

Figure 6.6 shows Bode plots of the diagonal impedance magnitude and phase in the DP and IE directions with their associated standard errors for this subject. Included in the plot are data obtained during both steps of the procedure, with and without the human subject. The estimated mechanical impedance of the ankle was obtained by subtraction of these complex vectors as described above.

Fig. 6.6
figure 6

Diagonal elements of the mechanical impedance matrix for Anklebot attached to a human ankle, Anklebot alone, and a human ankle with proportional gain K = 10 N-m/rad. (a) DP direction; (b) IE direction

Full size image

At all frequencies, the mechanical impedance in DP was greater than in IE. For example, at low frequencies the impedance magnitude approached an asymptote from which the static impedance (i.e., stiffness) could be estimated. The stiffness in DP was 23.0 dB (14.1 N-m/rad), whereas the stiffness in IE was 17.1 dB (7.1 N-m/rad), 2.0 times smaller. This is consistent with results reported elsewhere [19, 20, 34, 37–39, 17, 18].

Figure 6.7 shows the directional variation of ankle impedance magnitude in DP-IE coordinates. The plots were generated by rotational transformation of the time-history of the torque and angle data from 0° to 90° in 5° increments before performing stochastic identification to find the ankle impedance in two orthogonal directions. To display the directional variation, the impedance magnitude was averaged over two frequency ranges: 0–3 Hz and 3–5 Hz, where the inertia makes minimal contribution to impedance. In the lowest frequency range (0–3 Hz) the average impedance magnitude was greater in DP than IE, resulting in a characteristic “peanut” shape. In the 3–5 Hz range the average impedance in the DP direction increased more than in the IE direction, accentuating this “peanut” shape. Interestingly, the peanut shape was not precisely aligned with the anatomical axes but tilted approximately 20° counter clockwise.

Fig. 6.7
figure 7

Spatial variation of ankle impedance magnitude over different frequency ranges. The radius represents impedance magnitude (Nm/rad). Angles 0°, 90°, 180°, and 270° correspond to eversion, dorsiflexion, inversion, and plantarflexion, respectively

Full size image

3.2.3 Low-Frequency Impedance

At lower frequencies, the mechanical impedance of the ankle passive tissues and lower extremity muscles was evident. To estimate a “break frequency” dividing these two regions, the intersection between a horizontal line through the mean low-frequency magnitude and a straight line least-squares best fit to the magnitude plot at higher frequencies was computed. In DP the mean magnitude between 0.7 and 5 Hz averaged 27.9 dB and the estimated break frequency averaged 5.8 Hz. In IE, the mean magnitude between 0.7 and 8 Hz averaged 22.0 dB and the estimated break frequency averaged 8.8 Hz.

Below this break frequency neither the magnitude nor phase plots were consistent with a simple damped spring, but indicated more complex dynamics. In DP there was a substantial increase of impedance magnitude in the vicinity of 3 Hz, with a corresponding increase of phase below this frequency and decline above it. In IE a similar phenomenon was observed, also in the vicinity of 3 Hz. The mean impedance magnitude in IE between 3 and 8 Hz was 23.1 dB. This exceeded the mean magnitude between 0.7 and 3 Hz, 19.7 dB. On average, the “mid-frequency” impedance magnitude exceeded the static impedance by a factor of 1.9.

Similar results were obtained in DP. The mean impedance magnitude in DP between 3 and 8 Hz was 29.6 dB. This exceeded the mean magnitude between 0.7 and 3 Hz, 26.6 dB. This “mid-frequency” impedance magnitude exceeded the static impedance by a factor of 2.0. Furthermore, the “mid-frequency” impedance magnitude in DP exceeded that in IE by a factor of 2.1.

3.2.4 High-Frequency Impedance

In both DOF there was clear evidence that, above the break frequencies, the magnitude plot increased with frequency, consistent with the expected predominance of inertial behavior. Purely inertial behavior corresponds to a slope of 40 dB/decade. In DP, a straight line least-squares best fit to the magnitude plot above 10 Hz yielded an average slope of 37.0 dB/decade. In IE, a straight line least-squares best fit to the magnitude plot above 10 Hz showed an average slope of 49.6 dB/decade.

Predominantly inertial behavior should also be accompanied by monotonic convergence of phase towards 180° with increasing frequency. However, though phase initially increased around the break frequencies, at still greater frequencies (in the vicinity of 20 Hz) it declined, indicating the presence of higher modes of vibration.

4 Discussion

This study presented a method for estimating the multi-variable mechanical impedance of the human ankle. The method was applied to one young male subject with no biomechanical or neurological disorders to identify his relaxed ankle mechanical impedance in DP and IE simultaneously.

Spatial variation of ankle impedance magnitude in the low frequency range was not precisely aligned with the anatomical axes but tilted approximately 20° counter clockwise. The maximum magnitude of the impedance in the DP direction can be achieved by projecting the maximum ankle impedance magnitude onto the DP axis. It implies multiplying the maximum magnitude by cosine (20°) that is 0.94. This led to one unanticipated result of this study, that multivariable ankle mechanical impedance was predominantly oriented along axes in the sagittal plane (DP) and frontal plane (IE) with little coupling between these DOF. Using DP-IE joint coordinates, the diagonal elements of the mechanical impedance matrix exhibited partial coherences close to unity over a frequency range from 0 to as high as 60 Hz, indicating that a linear model of DP and IE impedance with zero cross-coupling would account for almost all of the variance in the data.

However, the musculo-skeletal anatomy of the human ankle is not simply organized along axes in the sagittal and frontal planes. Although the tibiotalar articulation (primarily responsible for dorsi-plantar flexion) may be approximated as a revolute joint with axis perpendicular to the sagittal plane (but see Ref. [49] for the single axis representation of the overall rotation of the ankle), the axis of the subtalar articulation (primarily responsible for inversion-eversion) is perpendicular to neither the sagittal nor frontal planes [36]. Furthermore, the lines of action of several musculo-tendon actuators (e.g., tibialis anterior, peroneus longus) lie neither in the sagittal nor frontal planes [50]. As a result, their tensions contribute both DP and IE torques simultaneously.

Given this biomechanical complexity, the lack of coupling we observed is remarkable. Ankle mechanical impedance arises from an interplay of skeletal, muscular and possibly neural factors, and contributes to several aspects of lower-limb function, including shock-absorption at foot-strike. The momentum absorbed by the leading leg at foot-strike is directed primarily in the plane of progression, the sagittal plane. Any coupling in the multivariable ankle mechanical impedance would re-direct this momentum to evoke displacement in the frontal plane, about the axis of lowest ankle impedance, eversion/inversion. It may, therefore, be advantageous to minimize the coupling between degrees of freedom. Hence the lack of coupling we observed may represent a functional adaptation of the ankle as a whole.

4.1 Dynamic Complexity of Ankle Mechanical Impedance

Although the Anklebot and its actuators include known nonlinearities, the linear methods used yielded a satisfactory and physically meaningful characterization of the mockup. In joint angle coordinates, the partial coherences for the off-diagonal elements of the impedance matrix were essentially zero—as they should have been, given the physical lack of coupling in the device.

Conversely, the partial coherences for the diagonal elements of the impedance matrix were close to unity at frequencies up to 40 Hz (Fig. 6.3b). Thus, despite the limitations of our apparatus, our methods were accurate over the frequency range of interest for studies of the biomechanics and neural control of the ankle.

The stochastic identification procedure we used exerted a random vibratory torque on the ankle. That vibratory input might have evoked abnormal neural activity which, in turn, may have affected the apparent mechanical impedance of the ankle. However, because we imposed a random vibratory torque, rather than motion, the “natural” low-pass character of the limb admittance resulted in a relative attenuation of ankle motion at higher frequencies and that may have mitigated this possible source of artifact. As matters turned out, the estimates of static mechanical impedance derived from the stochastic identification procedure used here corresponded well with independent measurements made using very slow ramp perturbations designed to minimize spurious activation of muscle spindles [37–39].

A pronounced deviation from second-order mass, spring and damper dynamics was observed at lower frequencies where inertial forces become insignificant and visco-elastic behavior predominates. We estimated a break frequency between “higher” and “lower” regions by intersecting a horizontal line through the low-frequency region (0.7–5 Hz in DP; 0.7 and 8 Hz in IE) with a straight line that best described the rate of magnitude increase at higher frequencies (10–30 Hz); the result was 5.8 Hz in DP and 8.8 Hz in IE. Substantially below these break frequencies, around 2–4 Hz, we observed a non-monotonic change of phase with frequency and a corresponding increase of impedance magnitude. The mean impedance magnitude in a “mid-frequency” region (3–5 Hz in DP and 3–8 Hz in IE) was substantially greater than the static stiffness of the joint: 1.9 times in IE and 2.0 times in DP.

We considered whether this phenomenon might be an artifact of our experimental apparatus and took steps to eliminate it. The lower limb and Anklebot were suspended from a highly compliant elastic support (the blue straps in Fig. 6.1a and b). As a result, resonant modes of vibration due to interaction between the lower limb and the frame supporting the subject were around 0.3 Hz, substantially lower than the frequency range we measured . In a further attempt to eliminate this possible artifact, the behavior of the Anklebot and shoe was measured without the human limb present (Fig. 6.1b) and the result subtracted from measurements with the limb present. Even though the Anklebot was arguably the dominant mass contributing to this resonance (it weighs ∼3.5 Kg) its frequency was lower with the limb present (around 0.15 Hz) that eliminated it as a possible artifact. On the other hand, the impedance magnitude plots from the experiment on the mockup did not show this “mid-frequency” phenomenon that led us to investigate the possible contribution of the shoe. An experiment similar to that depicted in Fig. 6.1a, b but using a foot block that could be fit tightly into the shoe did not show this phenomenon, indicating that our apparatus is unlikely to be a source of artifact. Nevertheless, whether the phenomenon we observed is an artifact of our methods or a property of human biomechanics remains to be resolved definitively in future work.

4.2 Ankle Mechanical Impedance in the Sagittal and Frontal Planes

The importance of minimizing coupling between sagittal and frontal plane motions was reinforced by our observation that ankle mechanical impedance in IE was substantially smaller than in DP. This is unsurprising at higher frequencies where inertia dominates, as the foot’s moment of inertia about the DP axis is clearly greater than about the IE axis. However, IE mechanical impedance was also smaller at lower frequencies, resulting in similar break frequencies. This remarkable observation suggests that neuro-muscular mechanical impedance may have co-evolved with skeletal inertia to produce a dynamically uniform response to perturbations. Static impedance (stiffness) was smaller in IE than DP by more than a factor of two. Mid-frequency impedance was smaller in IE than DP by more than a factor of 3. Because the foot obviously has smaller inertia in IE than DP, this may simply reflect a functional preference to maintain a uniform dynamic response to perturbations in any direction—comparable transient perturbations would be resisted by comparable neuro-muscular responses. Of course, the validity of these speculations remains to be tested by further experimentation.

Although the data reported here were obtained with muscles relaxed, preliminary results with active muscles indicate a similar trend [51]. This is a clinically important finding and indicates the direction of rotation in which the ankle is most vulnerable. Lower frontal-plane mechanical impedance indicates a greater tendency for the foot to roll. Perturbations, e.g., from uneven ground, may evoke excessive displacement and possibly injury of the ankle. That is consistent with the observation that most ankle-related injuries occur in the frontal plane rather than in the sagittal plane [52].

In this chapter, we presented a method for estimating the multivariable mechanical impedance of the human ankle in non-load bearing conditions. This approach may provide information necessary for the design and development of the next generation of lower extremity assistive robots with more anthropomorphic ankle joint dynamics.

Modulation of ankle impedance is a significant characteristic of the human ankle during gait. However, considering the bandwidth limitations of actuators in the current state of technology, modulation of the impedance of an artificial ankle may be facilitated if the ankle joint is primarily designed with an intrinsic passive mechanical impedance similar to that of the human ankle. For example, a multi-axis ankle-foot prosthesis may have a passive mechanical impedance in both sagittal and frontal planes similar to human ankle impedance. Similarly, orthotic or exoskeletal assistive robots may be tailored for each individual user, such that the hybrid system of injured human ankle and assistive device possesses a passive mechanical impedance similar to the average unimpaired human ankle.

Incorporating design features that allow these devices to mimic the mechanical impedance of the human ankle in both sagittal and frontal planes may increase their weight and complexity; but this may be offset by their advantages. A more anthropomorphic ankle joint may improve gait dynamics and, as a result, lower the overall metabolic cost of gait, as well as reduce the occurrence of secondary injuries. Multi-axial orthotic and prosthetic ankle joints promise to allow better accommodation to terrains with different profiles of elevation and inclination. They also may offer better maneuverability that may, in turn, lead to increased mobility and hence improve general health and well-being.