The Residual Stress Decomposition Method (RSDM): A Novel Direct Method to Predict Cyclic Elastoplastic States

Abstract

Instead of approaching the steady state behavior of an elastic–perfectly plastic structure, under cyclic loading, through time consuming incremental time-stepping calculations, one may alternatively use direct methods. A common feature of these methods is to estimate directly these cyclic states, profiting, thus, big savings in computer time. The elastic shakedown is the most important, in terms of structural safety, cyclic state. Most of the existing methods address this state through the solution of an optimization problem. In this work, a novel direct method that has a more physical understanding and may predict any cyclic steady stress state is exposed. The method is based on the expected cyclic nature of the residual stress distribution at the steady cycle. Having evaluated the elastic stress part of the total stress to equilibrate the external load, the unknown residual stress part is decomposed into Fourier series, whose coefficients are evaluated iteratively by satisfying compatibility and equilibrium with zero loads at time points inside the cycle. A computationally simple way to account for plasticity is considered. The procedure converges uniformly to a residual stress field which is either constant, marking the loading to be below the elastic shakedown limit, or to a cyclic residual stress field, from which possible alternating plasticity or ratcheting conditions may be realized. The procedure is formulated within the finite element method. A von Mises yield surface is typically used. Examples of application to a truss and a two dimensional plate under plane stress or strain are discussed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Nowadays structures are continuously designed to withstand repeated thermo-mechanical loading that forces them to enter the plastic regime. Such loading conditions are encountered either in civil or mechanical engineering. Typical examples of such structures are buildings and bridges under seismic loading on the one hand and nuclear reactors and aircraft gas propulsion engines on the other.

The life cycle assessment of such a structure constitutes an important task for a structural engineer. However, the long term response of a structure, subjected to a given thermo-mechanical loading which exhibits inelastic time independent plastic strains, is quite complex, because of the need to perform lengthy and expensive incremental calculations, especially for structures with a high degree of redundancy. In the case that the long term response turns out to be a stabilized state there are procedures called direct methods, which may lead directly to these states. Scleronomic or rheonomic stable materials guarantee the existence of such states [1]. Thus direct methods search for this asymptotic state right from the start of the calculations.

The most well known cyclic state is the elastic shakedown. The search for this state is based on the lower [2] and upper bound [3] shakedown theorems of plasticity. The formulation of these problems is normally done using mathematical programming (MP). One may refer to various such procedures like a nonlinear Newton-type algorithm [4] or the interior point methods (e.g. [5, 6]).

There are also very few approaches that are not based on MP. Internal parameters are introduced in [7] which characterize local inelastic mechanisms. Another procedure is the Linear Matching Method (LMM) [8] which is a generalization of the elastic compensation method [9] and is based on matching a linear problem to a plasticity problem. A sequence of linear solutions, with spatially varying moduli, is generated that provide upper bounds that monotonically converge to the least upper bound.

The method was further extended beyond shakedown, for loadings that can be decomposed into constant and time varying components, so as to provide an upper bound estimation of the ratchet boundary [10].

Besides the knowledge of safety margins, it is important to be able to determine the long-term effects on a structure for a given cyclic loading. For this purpose, an alternative to the cumbersome incremental procedure is a method called Direct Cycle Analysis (DCA) originally suggested in [11] and implemented in the commercial program Abaqus [12]. The main assumption of the method is that the displacements at the steady cycle will become cyclic. The method is quite involved and appears to be a mixture of an incremental and an iterative procedure. The displacements are decomposed into Fourier series whose coefficients are evaluated in an iterative way by linking them with the coefficients of the Fourier series of the out-of-balance load vector. This vector is evaluated as in an incremental procedure, and static admissibility is enforced by leading it to zero. The procedure seems to be suited for the cases of alternating plasticity but fails to converge for loadings that are close to ratcheting as also mentioned in [12] since, because of its main assumption, it can’t predict such a case.

A new direct method to predict any long-term cyclic state of an elastic-perfectly structure under a given cyclic loading was quite recently suggested [13]. The method focuses on the cyclic nature of the residual stresses at the steady state. The method has been called Residual Stress Decomposition Method (RSDM) and is based on decomposing the residual stresses in Fourier series inside a cycle of loading. The decomposition of the residual stresses, so as to find a simplified way to predict creep cyclic steady stress states, was originally proposed in [14].

In the RSDM the coefficients of the Fourier series are evaluated in an iterative way by integrating the residual stress rates over the cycle. By satisfying equilibrium and compatibility at time points inside the cycle one may evaluate these rates. Plastic effects are accounted for by adding the elastic and the residual stress at the cycle points. If the sum exceeds the yield surface, the plastic strain rate may be represented by the stress in excess of the yield surface. This excess stress provides then input for iteration. If the plastic strain rates stabilize, in the form of a converged residual stress vector, the procedure stops. One can easily distinguish any of the three different cases, shakedown, alternating plasticity or ratcheting. A one-dimensional truss and a two-dimensional plate with a hole under plane stress have demonstrated in [13] the application of the procedure. For the plate, results are, in the present work, extended to include plane strain conditions. The whole approach is shown to be stable and computationally efficient, with uniform convergence.

2 Cyclic Steady-States

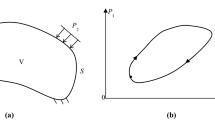
Let us consider a body of volume V and surface S. On one part of S we have zero displacement conditions and on the other part of the surface a cyclic loading of the form (1) is applied.

$$ \mathbf{P}(t) = \mathbf{P}(t + nT) $$

(1)

where P(t) is the set of loads that act on S; t is the time point inside the cycle, T is the period of the cycle, n=1,2,… , denotes the number of full cycles. Bold letters are used, herein, to denote vectors and matrices.

Let us suppose that our structure is made of an elastic-perfectly plastic material. At any time point τ=t/T inside the cycle the structure will develop a stress field σ(τ) which may be decomposed into an elastic part σ ^el(τ), that equilibrates the external loading P(τ) assuming a completely elastic behavior, and a self-equilibrating residual stress part ρ(τ) that is due to inelasticity. Therefore:

$$ \boldsymbol{\sigma} (\tau) = \boldsymbol{\sigma} ^{\mathrm{el}}( \tau) + \boldsymbol{\rho} (\tau). $$

(2)

An analogous decomposition holds for the strain rates:

$$ \dot{\boldsymbol{\varepsilon}} = \dot{\mathbf{e}}^{\mathrm {el}}(\tau ) + \dot{ \boldsymbol{\varepsilon}} _{r}(\tau). $$

(3)

The residual strain rate itself may be decomposed into an elastic and a plastic part [15]. Thus the final compatibility equation is expressed as:

$$ \dot{\boldsymbol{\varepsilon}} = \dot{\mathbf{e}}^{\mathrm {el}}(\tau ) + \dot{ \boldsymbol{\varepsilon}} _{r}^{\mathrm{el}}(\tau) + \dot{ \boldsymbol{ \varepsilon}} ^{\mathrm{pl}}(\tau). $$

(4)

The elastic strain rates are related to the stress rates through the elasticity matrix D, whereas the plastic strain rate vector through the gradient of the flow rule:

$$ \begin{aligned} & \dot{\boldsymbol{\sigma}} ^{\mathrm{el}}(\tau) = \mathbf{D} \cdot\dot{\mathbf{e}}, \\ & \dot{\boldsymbol{\rho}} (\tau) = \mathbf{D} \cdot\dot{\boldsymbol{ \varepsilon}} _{r}^{\mathrm{el}}, \\ & \dot{\boldsymbol{\varepsilon}} ^{\mathrm{pl}} = \lambda\cdot \frac{\partial f}{\partial\boldsymbol{\sigma}} \end{aligned} $$

(5)

where f is the yield surface.

Based on the Drucker’s stability postulate for rheonomic or scleronomic materials it may be proved [16] that there always exists an asymptotic cyclic state that the stresses and strain rates stabilize and become periodic with the same period of the cyclic loading.

Depending on the amplitude of the load three different asymptotic states may be realized, based on the existence or not of the plastic strain rates:

• (a) Elastic shakedown, meaning $\dot{\boldsymbol{\varepsilon}} ^{\mathrm{pl}} \to \mathbf{0}$.

• (b) Plastic shakedown, meaning $\dot{\boldsymbol{\varepsilon}} ^{\mathrm{pl}} \ne\mathbf{0},\ \mathrm{but} \int_{0}^{T} \dot{\boldsymbol{\varepsilon}} ^{\mathrm {pl}}dt = \mathbf{0}$.

• (c) Ratcheting, meaning $\dot{\boldsymbol{\varepsilon}} ^{\mathrm {pl}} \ne\mathbf{0},\ \mbox{and } \int_{0}^{T} \dot{\boldsymbol{\varepsilon}} ^{\mathrm{pl}}dt \ne \mathbf{0}$.

3 The Residual Stress Decomposition Method (RSDM)

Since the elastic stress under a cyclic load is cyclic, a cyclic steady stress state renders the residual stress distribution to be also cyclic. One may thus exploit this cyclic nature, decompose the residual stresses into Fourier series, and try to find the unknown Fourier coefficients. In this way we may write:

$$ \boldsymbol{\rho} (\tau) = \frac{1}{2}\mathbf{a}_{0} + \sum_{k = 1}^{\infty} \bigl\{ \cos(2k\pi\tau) \cdot\mathbf{a}_{k} + \sin(2k\pi\tau) \cdot\mathbf{b}_{k} \bigr\}. $$

(6)

Differentiating the above with respect to τ one may write the following expression for the derivative:

$$ \dot{\boldsymbol{\rho}} (\tau) = 2\pi\sum _{k = 1}^{\infty} \bigl\{ - k\sin(2k\pi\tau) \cdot \mathbf{a}_{k} + k\cos(2k\pi\tau) \cdot\mathbf{b}_{k} \bigr\}. $$

(7)

Making use of (7) and the orthogonality properties of the trigonometric functions one may get expressions for the Fourier coefficients of the cosine and sine series in terms of the residual stress derivatives:

$$ \begin{aligned} & \mathbf{a}_{k} = - \frac{1}{k\pi} \int_{0}^{1} \sin(2k\pi\tau) \cdot\dot{ \boldsymbol{\rho}} (\tau) d\tau, \\ & \mathbf{b}_{k} = \frac{1}{k\pi} \int_{0}^{1} \cos(2k\pi\tau) \cdot\dot{\boldsymbol{\rho}} (\tau) d\tau. \end{aligned} $$

(8)

A more involved formula proves to be needed for the constant term, which uses the information at the beginning and at the end of the cycle [13]:

$$ \frac{1}{2}\mathbf{a}_{0,e} = \Biggl( \frac{1}{2} \mathbf{a}_{0,b} + \sum_{k = 1}^{\infty} \mathbf{a}_{k,b} \Biggr) - \sum_{k = 1}^{\infty} \mathbf{a}_{k,e} + \int_{0}^{1} \dot{ \boldsymbol{\rho}} (\tau) d\tau $$

(9)

where the subscripts b and e denote the beginning and the end of the cycle respectively. As seen from Eqs. (8) and (9), because of (7), there is an implicit dependence of the Fourier coefficients and thus an iterative scheme may be used to estimate them, once the residual stress derivatives are calculated.

To find these derivatives one seeks to satisfy compatibility and equilibrium at some predefined time points inside the cycle. To this end we assume that our structure is discretized with finite elements (FEs). Using the rates of displacements of the nodes of the FE mesh one may write:

$$ \dot{\boldsymbol{\varepsilon}} = \mathbf{B} \cdot\dot {\mathbf{r}}. $$

(10)

From Eqs. (4) and (5) we may write:

$$ \dot{\boldsymbol{\rho}} = \mathbf{D} \cdot\bigl( \dot {\boldsymbol{ \varepsilon}} - \dot{\mathbf{e}}^{\mathrm{el}} - \dot{\boldsymbol {\varepsilon}} ^{\mathrm{pl}} \bigr). $$

(11)

Since the strain rates are kinematically admissible, the residual stress rates are self-equilibrated, and fixed supports have been assumed, one may write, for a virtual strain field $\delta\dot{\boldsymbol{\varepsilon}}$, using the Principle of Virtual Work (PVW):

$$ \int_{V} \delta\dot{\boldsymbol{\varepsilon}} ^{T} \cdot\dot{\boldsymbol{\rho}} dV = 0. $$

(12)

Combining (10), (11) and (12), we end up with:

$$ \biggl(\int_{V} \mathbf{B}^{T} \cdot \mathbf{D} \cdot\mathbf{B} dV \biggr) \cdot\dot{\mathbf{r}} = \int _{V} \mathbf{B}^{T} \cdot\dot{\boldsymbol{\sigma}} ^{\mathrm{el}}dV + \int_{V} \mathbf{B}^{T} \cdot \mathbf{D} \cdot\dot{ \boldsymbol{\varepsilon}} ^{\mathrm{pl}} dV $$

(13)

or equivalently:

$$ \mathbf{K} \cdot\dot{\mathbf{r}} = \dot{\mathbf{R}} + \int _{V} \mathbf{B}^{T} \cdot\mathbf{D} \cdot\dot{ \boldsymbol{\varepsilon}} ^{\mathrm{pl}}dV $$

(14)

where K is the stiffness matrix, $\dot{\mathbf{R}}$ is the rate vector of the external forces acting on the structure at the cycle time τ.

Plastic straining will occur whenever the total stress (Eq. (2)) exceeds the yield surface (Fig. 1). In such a case, the returning back on the yield surface will be, according to the closest point projection [17], along the vector $\overrightarrow{\mathrm{CB}}$, with the plastic strain rate $\dot{\boldsymbol{\varepsilon}} ^{\mathrm{pl}}$ directed along $\overrightarrow{\mathrm{BC}}$. We use, instead, the vector $\overrightarrow{\mathrm{CA}}$ which is −σ _p. This vector is a ‘radial return’ type of mapping along the known $\overrightarrow{\mathrm{OC}}$. It may be easily determined, especially for a von Mises yield surface. It is an equivalent measure for the plastic straining in the sense that they either both exist or not.

Fig. 1

Estimation of plastic straining (von Mises yield surface)

3.1 Numerical Procedure

An iterative procedure has been written that updates the Fourier coefficients inside an iteration [13].

Firstly we solve for the external loading and its cycle rate assuming elastic behavior, and obtain, for each cycle point τ, the elastic stress σ ^el(τ) and the elastic stress rate $\dot{\boldsymbol{\sigma}} ^{\mathrm{el}}(\tau)$ at each Gauss point (GP) of a continuum finite element.

Let us suppose that after the completion of the iteration (μ) an estimate of the distribution of the Fourier coefficients $\mathbf{a}_{0}^{(\mu)},\mathbf{a}_{k}^{(\mu )},\mathbf{b}_{k}^{(\mu)}$ has been made. The following steps are now followed:

• 1. For a specific cycle point τ we compute ρ ^(μ)(τ), at each GP, using (6):

  $$ \boldsymbol{\rho} ^{(\mu)}(\tau) = \frac{1}{2}\mathbf{a}_{0}^{(\mu)} + \sum_{k = 1}^{\infty} \bigl\{ \cos(2k\pi\tau) \cdot\mathbf{a}_{k}^{(\mu)} + \sin(2k\pi\tau) \cdot \mathbf{b}_{k}^{(\mu)} \bigr\}. $$

  (15)

• 2. Evaluate at each GP the total stress σ ^(μ)(τ), using (2):

  $$ \boldsymbol{\sigma} ^{ ( \mu )}(\tau) = \boldsymbol{\sigma} ^{\mathrm{el}}(\tau) + \boldsymbol{\rho} ^{ ( \mu )}(\tau). $$

  (16)

• 3. Calculate whether, at each GP, $\bar{\sigma} ^{(\mu)}(\tau) > \sigma_{Y}$. In such a case compute $\boldsymbol{\sigma} _{p}^{(\mu)}(\tau)$:

  $$ \xi= \frac{\bar{\sigma} ^{ ( \mu )}(\tau) - \sigma_{Y}}{\bar{\sigma } ^{ ( \mu )}(\tau)} \Rightarrow\boldsymbol{\sigma} _{p}^{(\mu)} ( \tau) = \xi\cdot\boldsymbol{\sigma} ^{ ( \mu )} ( \tau). $$

  (17)

• 4. Assemble for the whole structure the rate vector of the nodal forces $\dot{\mathbf{R}}\boldsymbol{'}(\tau)$, which is the r.h.s. of Eqs. (13)–(14):

  $$ \dot{\mathbf{R}\boldsymbol{'}}(\tau) = \dot{\mathbf{R}}(\tau) + \int_{V} \mathbf{B}^{T} \cdot\boldsymbol{\sigma} _{p}^{ ( \mu )}(\tau)dV. $$

  (18)

• 5. Solve the following iterative form of Eq. (14) and obtain $\dot{\mathbf{r}}^{(\mu )}(\tau)$:

  $$ \mathbf{K}\dot{\mathbf{r}}^{ ( \mu )}(\tau) = \dot{\mathbf{R} \boldsymbol{'}}(\tau). $$

  (19)

• 6. Evaluate at each GP the residual stress derivative rates, using (11):

  $$ \dot{\boldsymbol{\rho}} ^{ ( \mu )}(\tau) = \mathbf{DB}\dot{ \mathbf{r}}^{ ( \mu )}(\tau) - \dot{\boldsymbol{\sigma}} ^{\mathrm{el}}(\tau) - \boldsymbol{\sigma} _{p}^{ ( \mu )}(\tau). $$

  (20)

• 7. Repeat the steps 1–6 for all the assumed cycle points.

• 8. Perform a numerical integration over the cycle points and update the Fourier coefficients, making use of Eqs. (8) and (9):

  $$ \begin{aligned} \mathbf{a}_{k}^{ ( \mu+ 1 )} &= - \frac{1}{k\pi} \int_{0}^{1} \bigl\{ \bigl[ \dot{ \boldsymbol{\rho}} ^{ ( \mu )} ( \tau ) \bigr] ( \sin2k\pi \tau ) \bigr\}d\tau, \\ \mathbf{b}_{k}^{ ( \mu+ 1 )} & = \quad\frac{1}{k\pi} \int _{0}^{1} \bigl\{ \bigl[ \dot{\boldsymbol{\rho}} ^{ ( \mu )} ( \tau ) \bigr] ( \cos2k\pi\tau ) \bigr\}d\tau, \\ \frac{\mathbf{a}_{0}^{ ( \mu+ 1 )}}{2} &= - \sum_{k = 1}^{\infty} \mathbf{a}_{k}^{ ( \mu+ 1 )} + \frac{\mathbf{a}_{0}^{ ( \mu )}}{2} + \sum _{k = 1}^{\infty} \mathbf {a}_{k}^{ ( \mu )} + \int_{0}^{1} \bigl[ \dot{\boldsymbol{\rho}} ^{(\mu)} ( \tau ) \bigr]d\tau. \end{aligned} $$

  (21)

• 9. From the updated Fourier coefficients evaluate the updated distribution of the residual stresses, at all the Gauss points, using (15), and check the convergence through their norms at the end of the cycle:

  $$ \frac{\Vert \boldsymbol{\rho} ^{ ( \mu+ 1 )}(1) \Vert _{2} - \Vert \boldsymbol{\rho} ^{ ( \mu )}(1) \Vert _{2}}{\Vert \boldsymbol {\rho} ^{ ( \mu+ 1 )}(1) \Vert _{2}} \le \mathit{tol} $$

  (22)

  where tol is a specified tolerance.

If (22) holds, the procedure stops as we have reached a cyclic stress state (cs), and ρ ^(μ)=ρ ^(μ+1)=ρ ^cs; otherwise we go back to step 1 and repeat the process.

Once a cyclic stress state has been attained, we look at $\boldsymbol {\sigma} _{p}^{\mathrm{cs}} = \boldsymbol{\sigma} _{p}^{(\mu)} = \boldsymbol{\sigma} _{p}^{(\mu+ 1)}$, which was evaluated during the last iteration. We may determine the nature of the obtained solution, for each GP, by evaluating the following integral over the cycle:

$$ \alpha_{i} = \int_{0}^{1} \sigma _{p,i}^{\mathrm{cs}}(\tau)d\tau $$

(23)

with i spanning all the components of $\boldsymbol{\sigma} _{p}^{\mathrm{cs}}(\tau)$.

Depending on the values of α _i we may have:

• (a) If α _i ≠0, a state of ratcheting exists at this GP. If α _i =0, we check the value of $\sigma_{p,i}^{\mathrm {cs}}(\tau)$ for every cycle point τ.

• (b) If $\sigma_{p,i}^{\mathrm{cs}}(\tau) \ne0$, the Gauss point is in a state of reverse plasticity, since this must hold for pairs of cycle points of equal value but of alternating sign.

• (c) If $\sigma_{p,i}^{\mathrm{cs}}(\tau) = 0$, the point has remained either elastic or has developed an elastic shakedown state.

For the case of all the Gauss points being either elastic or in a state of elastic shakedown, our structure, under the given external loading, will also shake down. On the other hand, if sufficient GPs are in a state of ratcheting, at the steady state, our structure will undergo incremental collapse. This, numerically, may be easily proved here, through the singularity of the stiffness matrix, which can be evaluated just at the end of the converged steady cycle, by zeroing the elasticity matrix D at the ratcheting GPs.

4 Application Examples

The method is applied to two structures one being a one dimensional and the other a two dimensional plate element with a hole under plane stress or plane strain conditions. A value of 10⁻⁴ for the tolerance proved quite accurate to stop the iterations.

4.1 Pin Jointed Framework

The truss structure (Fig. 2) that consists of five members, whose properties are listed in Table 1, was chosen as a first example of application of the proposed method. Material data was assumed as E=0.21×10⁵ kN/cm², σ _y =36 kN/cm², whereas L=200 cm.

Fig. 2

Five bar truss example

Table 1 Properties of the truss elements

A simple two node plane truss element was used to analyze the structure. The only change that needs to be applied in the numerical procedure, presented for the continuum, is to use the axial stress in each bar, for this one-dimensional problem, instead of the effective stress used for the continuum.

The truss was subjected to concentrated cyclic loads F ₀ and F _c which are applied at nodes 3 and 4 respectively. Two cases of loading have been considered which lead to different cyclic steady states.

• (a) The first cyclic loading case has the following variation with time:

  $$F_{c} ( t ) = 100\sin ( 2\pi t/T ), \qquad F_{0} = 400~\mathrm{kN}. $$

The procedure predicts that the structure will shakedown. The constant in time steady state residual stress may be seen in Fig. 3(a). In Fig. 3(b) one may also see the distribution of the total stress, for bar 1, inside the cycle, where nowhere the yield stress is exceeded. Analogous behavior is observed, of course, for all the other bars.

• (b) The second cyclic loading case has the following variation with time:

  $$F_{c} ( t ) = 200\sin( 2\pi t/T ), \qquad F_{0} = 200~\mathrm{kN}. $$

Fig. 3

Steady state stress distributions inside a cycle for element 1 (load case a—shakedown): (a) residual stress, (b) total stress

For this loading case the RSDM predicts that the structure is going to suffer from alternating plasticity. In Fig. 4 one may see the uniform convergence of the procedure towards the final steady state.

Fig. 4

Convergence of the iterative procedure—truss example (load case b)

The distribution of the cyclic residual stress predicted for the middle bar 1 inside the steady cycle may be seen in Fig. 5. The procedure shows that in the steady state the middle bar suffers plastic strain rates, of alternating nature. These strains spread within the time intervals [0.169, 0.362] and [0.638, 0.851], inside the cycle, rendering the total plastic strain over the cycle (parameter α ₁—expression (23), also equal to the total area under the curve, Fig. 6) equal to zero.

Fig. 5

Predicted steady state residual stress distribution for element 1 inside a cycle (load case b—alternating plasticity)

Fig. 6

Predicted $\sigma _{p}^{\mathrm{cs}}(t)$ distribution at steady state inside a cycle for element 1 (load case b—alternating plasticity)

The results for both the two loading cases agree well with those in [18].

4.2 Plate with a Central Hole

The second example of application is the classical problem of a square plate having a circular hole in its center. The plate is subjected to two biaxial uniform loads applied at the edges of the plate. Due to the symmetry of the structure and the loading, only one quarter of the plate is considered.

The boundary conditions as well as its finite element mesh discretization are shown in Fig. 7. The ratio between the diameter d of the hole and the length L of the plate is equal to 0.2. Also the ratio of the depth of the plate and its length is equal to 0.05. Ninety-eight, eight-noded, isoparametric elements with 3×3 Gauss integration points were used.

Fig. 7

The geometry, loading, and the finite element mesh of a quarter of a plate

The material data used was: Young’s modulus E=0.21×10⁵ kN/cm², Poisson’s ratio ν=0.3 and yield stress σ _y =36 kN/cm².

Both plane stress and plain strain conditions have been examined as the procedure 3.1 may be applied to both of them.

The same vectors $\boldsymbol{\sigma} = \{ \begin{array}{cccc} \sigma_{xx} & \sigma _{yy} & \sigma_{xy} & \sigma_{zz} \end{array} \}^{T}$ and $\boldsymbol{\rho} = \{ \begin{array}{cccc} \rho_{xx} & \rho_{yy} & \rho_{xy} & \rho_{zz} \end{array} \}^{T}$ may be utilized at a GP for both cases. For each of the two cases the corresponding 3×3 elasticity matrix D should be used. As far as the fourth element of the stress vector is concerned, for the plane stress problem $\sigma_{zz}^{\mathrm{el}},\rho_{zz} = 0$. The same holds for their derivatives.

For a plane strain problem, on the other hand, we should have $\sigma _{zz}^{\mathrm{el}} = \nu ( \sigma_{xx}^{\mathrm{el}} + \sigma_{yy}^{\mathrm{el}} )$, ρ _zz =ν(ρ _xx +ρ _yy ). The same, of course, holds for their derivatives. The non existence of the corresponding out of plane plastic strain is assured by setting σ _p,zz =0.

Three different loading cases were taken into account, which lead the structure to either shakedown, reverse plasticity or ratcheting. Results are plotted for the generally most highly stressed points of the plate GP 1 or GP 2, depending on the loading case.

• (a) The first cyclic loading case has the following variation with time:

  $$P_{y} ( t ) = 0.65\sigma_{y}\sin^{2} ( \pi t/T ),\qquad P_{x} ( t ) = 0. $$

The predicted by the procedure behavior for the structure is a shakedown state and this complies with the fact that this loading is below the shakedown boundary estimated in [19]. In Fig. 8 the computed by the RSDM steady-state residual stress distribution is plotted for the GP 2, for both plane stress and plane strain conditions. This residual stress distribution is unique and will be the same with the one that would be predicted from an incremental step-by-step analysis, e.g. [12] (see also examples in [13]). The total stress distribution for this point is plotted in Fig. 9. In Fig. 10 one may also see the convergence towards the final steady states.

• (b) The second cyclic loading case has the following variation with time:

  $$P_{y} ( t ) = 0.7223\sigma_{y}\sin^{2} ( \pi t/T ),\qquad P_{x} ( t ) = 0. $$

Fig. 8

Residual stress distribution at GP 2 inside a cycle at steady state under plane stress and plane strain conditions (load case a—shakedown)

Fig. 9

Effective total stress distribution at GP 2 inside a cycle at steady-state (load case a—shakedown), plane stress and plane strain condition

Fig. 10

Convergence of the iterative procedure (load case a—shakedown)

The value of this load, at many cycle points, is in excess of the shakedown limit computed by using a plane stress modeling, and below the shakedown limit assuming a plane strain condition [19]. The present numerical procedure (RSDM) also shows that this loading will lead the plate to shakedown for plane strain, but assuming plane stress conditions the loading leads some GPs to reverse plasticity. So, for the plane strain case, in Figs. 11, 12 one may see the computed by the RSDM steady-state residual stress distribution for the GP 2 and its effective total stress distribution, respectively.

Fig. 11

Residual stress distribution at GP 2 inside a cycle at steady-state (load case b—shakedown), plane strain case

Fig. 12

Effective total stress distribution at GP 2 inside a cycle at steady-state (load case b—shakedown), plane strain case

On the other hand, for plane stress modelling, we plot, for the most strained point GP 2, the variation of the yy component of the excess stress vector $\boldsymbol {\sigma} _{p}^{\mathrm{cs}}$, which has the biggest values from the three components (Fig. 13). We may see that plastic straining occurs, alternately, inside the time intervals [0, 0.04], [0.45, 0.55] and [0.96, 1] at the steady cycle.

• (c) The third cyclic loading case involves two loads, one constant in time and one varying with time:

  $$P_{y} ( t ) = 0.5\sigma_{y}\sin^{2} ( \pi t/T ),\qquad P_{x} ( t ) = 0.93\sigma_{y}. $$

Fig. 13

Predicted cyclic steady-state distribution of the yy component of the stress vector at GP 2 (load case b—alternating plasticity), plane stress case

This loading, at many cycle points, is above the ratcheting boundary. The results for GP 1, assuming plane strain conditions, may be seen in Fig. 14, where plastic straining of the same positive sign inside the cycle intervals [0, 0.11] and [0.89, 1] at the steady cycle is observed. On the other hand, with a plane stress modeling, one may observe that plastic strains of the same positive sign appear during the whole cycle (Fig. 15). For both cases the xx direction of the component of the excess stress vector $\boldsymbol{\sigma} _{p}^{\mathrm{cs}}$, which has the biggest values from the three components, is plotted. This ratcheting behavior is observed also for quite a few GPs around the structure, which definitely constitutes incremental collapse mechanisms for both plane strain and plane stress conditions that may be seen in Figs. 16, 17 respectively. We may observe that we have a much more spreading of ratcheting for the case of plane stress than for the case of plane strain.

Fig. 14

Predicted cyclic steady-state distribution of the xx component of the stress vector at GP 1 (load case c—ratcheting), plane strain condition

Fig. 15

Predicted cyclic steady-state distribution of the xx component of the stress vector at GP 1 (load case c—ratcheting), plane stress condition

Fig. 16

Ratcheting mechanism—RSDM (plane strain condition)

Fig. 17

Ratcheting mechanism—RSDM (plane stress condition)

In Fig. 18 one may see the convergence of the RSDM for this loading case, for both plane stress and plain strain conditions.

Fig. 18

Convergence of the iterative procedure (load case c)

Reviewing the examples considered herein, we note that, within the adopted tolerance, the number of iterations ranged from a minimum of 80 for the case of reverse plasticity of the truss example, to a maximum number of 740 for the case of ratcheting of the plate example, under plane strain. The total CPU-time required to solve this last example was just 260 s, using an Intel Core i7 at 2.93 GHz with 4096 MB RAM.

The number of time points inside the cycle should be enough so that it may adequately represent the applied loading. Fifty time points inside the cycle were used for all the examples considered herein. Three terms of the Fourier series were found enough to represent the residual stress decomposition. The RSDM procedure proved to be quite stable, no matter which asymptotic behavior was reached. Another important fact of the computational efficiency of the approach is that the stiffness matrix needs to be decomposed once and for all at the start of the calculations.

5 Concluding Remarks

The Residual Stress Decomposition Method (RSDM) is a direct method that proves to be a simple and efficient procedure to estimate the long-term effects of the cyclic loading on a structure. For a given time history of this loading it may equally predict any possible steady state either it is elastic shakedown or alternating plasticity or ratcheting.

The method, although currently developed for elastic-perfectly plastic material and the von Mises yield surface, has the potential of extension to other types of behavior and yield surfaces.

It also appears to have the potential to provide safety margins for a cyclic loading the exact history of which is not known, but only its variation ranges, and work is being done towards this direction.