Advances of the RSDM-S: Robustness and Fast Convergence Issues

Abstract

The Residual Stress Decomposition Method (RSDM) is an iterative numerical procedure which has been developed to estimate, in a direct way, the kind of asymptotic stress states under cyclic loading of inelastic structures. The method was the basis to formulate another numerical procedure, which was named RSDM-S, to establish safety margins for elastic shakedown under mechanical and/or thermal loads. The method exploits the expected cyclic nature of the residual stresses of the asymptotic cycle state. Starting from a load factor high above shakedown an iterative procedure shrinks the loading domain until the conditions of the limit cycle, which marks the shakedown state, are met. The procedure consists of two loops an external incremental that reduces the load factor and an internal iterative loop that establishes a cyclic state for the current load factor. The current work refers to advancements of the method in terms of robustness and fast convergence. It discusses the efficiency of the numerical scheme used which is proved to have a continuous descent towards the shakedown factor with superlinear convergence. Examples of application of structures undergoing various kinds of cyclic actions like, mechanical or thermomechanical loads or cyclic imposed displacements are presented, and shakedown domains are constructed.

1 Introduction

The last decades, structures and structural components are designed to operate beyond the elastic limit in favor of material savings. Especially in case of cyclic thermomechanical loadings the allowable stresses may be greater than the yield limit. The amplitude of the cyclic load will determine the magnitude of the inelastic strains, which will be responsible either for the failure due to alternating plastic straining (low cycle fatigue) and/or incremental plastic straining (ratcheting), or for safety, through elastic shakedown. Thus, the post-elastic response of structures due to cyclic thermal and mechanical loads is always a major concern for the designer engineer.

Apart from the thermomechanical loads, support excitations due to repeated accidental loads, such as the earthquakes, may establish a pattern of cyclic imposed displacements to the structures.

The induced stresses, due to seismic actions, undergo many complete reversals in a small period like the duration of an earthquake. Designing such structures to behave elastically during earthquakes, without damage, may render the project economically unviable. Consequently, it may be necessary for the structure to suffer some damage and therefore dissipate energy input, during the earthquake. Thus, the same question arises whether after a sequence of imposed cyclic displacements, the post-elastic response will lead to a long-term stabilization of the damage, with an effect to extend the life cycle of a structure.

Previous years, in order to study the post-elastic response of a structure, one should perform step-by-step inelastic analysis based on a specific time-history. In this way one could be sure that, the structure would end up to a safe or unsafe asymptotic state. Besides the fact that this approach is time consuming and may have convergence problems, no general answer of safety will be given except for the specific load history. However, a class of numerical methods, called Direct Methods exists, (a most recent compilation of these methods may be found in [13], which may provide safety margins for any load combinations. These methods have a much lower computational cost as they bypass the transient deformation stages and search the asymptotic states, in a direct way, right from the start of the calculations.

Most direct methods deal with the shakedown problem as being a constrained optimization problem, described by the theorems of [11] and [6]. The structure is discretized with many finite elements (FE) and large-scale nonlinear mathematical programming (MP) problems must be solved. Towards this direction, general-purpose efficient optimization algorithms, like the interior point method (IPM) or conic programming, are often employed, as part of the method. These may be combined with other algorithms to assess the behavior of materials that require a high degree of intensive computational burden (e.g. [3]).

A strain driven algorithm that converts the MP problem of the lower bound shakedown theorem to an equivalent incremental-iterative problem of fictitious elastoplastic steps has been proposed and recently applied to the analysis of fiber-based 3D framed structures [10]

The linear matching method (LMM) is an iterative method that produces a sequence of linear elastic solutions by modifying the elastic moduli of the various parts of the structure so that the stress equals the yield stress. Thus, in this respect each time it matches a linear problem to a plasticity problem. The method was developed in the context of shakedown [14]. The method was expanded and employed, since then, to many applications in problems of structural mechanics, e.g. to find ratcheting limits [2, 8], and more recently in shakedown with hardening and thermal effects [9]

A simplified Direct Method originally conceived for creep problems [15, 16] was further developed and applied to account for plastic behavior [18]. The metod was called Residual Stress Decomposition method (RSDM) [19]. It is an iterative stress driven direct method which can predict the final asymptotic state of a cyclically loaded structure (either shakedown, or alternating plasticity or incremental collapse). In this asymptotic stress state, the residual stresses have cyclic behavior, thus they can be decomposed in Fourier series whose coefficients may be calculated in an iterative manner by satisfying compatibility and equilibrium at time points inside the cycle. The method was formulated to calculate the shakedown limit (RSDM-S) of structures subjected to cyclic thermomechanical loads and multidimensional loading domains [20,21,22].

An upgrade of the RSDM-S appeared quite recently [17]. The upgrade was both in the robustness and the numerical efficiency. The robustness is guaranteed as the sequence of the iterative steps is theoretically proved to be monotonically decreasing towards the final solution. A numerical scheme that possesses a superlinear convergence makes it a very fast procedure. The method was also formulated to cater for cyclic imposed displacements.

In the present work, these issues of robustness and convergence are further discussed and analyzed. The efficiency of the approach is further demonstrated through new applications to structures under mechanical, thermomechanical, or imposed displacements, simulating earthquake loading.

2 Theoretical Background

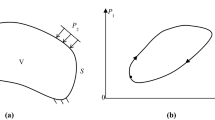
Let a body of volume V with surface S be subjected to mechanical load P, applied on a part of the surface S_f, prescribed displacements $\overline{{\varvec{u}} }$, applied on another part S_pr and fixed displacements on another part S_u (Fig. 1).

Fig. 1

Reproduced from [17]. Copyright © Elsevier Masson SAS. All rights reserved

Body subjected to forces and imposed displacements.

The mechanical load and prescribed displacements are applied periodically with period T. One may assume that the minimum values of the cyclic load or prescribed displacements are zero and the starred quantities represent the maximum values (Fig. 2). It has been proved [7] that if a structure shakes down under a cyclic loading program containing the vertices of the loading domain, then it will shake down for any loading path contained in this domain. Such a cyclic program may be seen in Fig. 2, in either the time domain (a), or the loading domain (b).

Fig. 2

Reproduced from [17]. Copyright © Elsevier Masson SAS. All rights reserved

Independent cyclic loading (mechanical (and/or) imposed displacement) variation over one time period a in time domain, b in loading domain.

This domain may be isotropically varied if multiplied with a load factor γ. Thus, the idea behind RSDM-S is to find the largest loading domain for which shakedown occurs, by moving from a large value of γ to smaller ones.

In response to the cyclic loading program, the stresses in the structure at a cycle point τ = t/T (where this point is either a point in the time domain or a vertex in the loading domain) are decomposed into an elastic part ${{\varvec{\upsigma}}}_{{}}^{el}$, in response to the applied external cyclic actions, and a residual stress part ${{\varvec{\uprho}}}$. In the search for the shakedown factor γ, the elastic stresses are themselves multiplied by this factor. Thus, the total stress vector can now be written:

$${{\varvec{\upsigma}}}(\tau ) = \gamma {{\varvec{\upsigma}}}_{{}}^{el} (\tau ) + {{\varvec{\uprho}}}(\tau )$$

(1)

The elastic response of the loads and the prescribed displacements may be obtained by separating the two actions and superposing their effects [17]. Two different finite element (FE) problems are solved which provide the corresponding to the two actions elastic strain rates ${\dot{\mathbf{\varepsilon }}}_{L}^{el}$, ${\dot{\mathbf{\varepsilon }}}_{pr}^{el}$; on the other hand, plasticity introduces residual strains. Thus, one may write for the total strain rate ${\dot{\mathbf{\varepsilon }}}$:

$${\dot{\mathbf{\varepsilon }}} = {\dot{\mathbf{\varepsilon }}}_{L}^{el} + {\dot{\mathbf{\varepsilon }}}_{pr}^{el} + {\dot{\mathbf{\varepsilon }}}_{r}^{el} + {\dot{\mathbf{\varepsilon }}}^{pl}$$

(2)

Where ${\dot{\mathbf{\varepsilon }}}^{pl}$ are the plastic strains and ${\dot{\mathbf{\varepsilon }}}_{r}^{el}$ is the residual elastic straining. Since both terms ${\dot{\mathbf{\varepsilon }}}$ and ${\dot{\mathbf{\varepsilon }}}_{L}^{el} + {\dot{\mathbf{\varepsilon }}}_{pr}^{el}$ in (2) are kinematically admissible, the sum:

$${\dot{\mathbf{\varepsilon }}}_{r} = {\dot{\mathbf{\varepsilon }}}_{r}^{el} + {\dot{\mathbf{\varepsilon }}}^{pl}$$

(3)

is also kinematically admissible. In a FE environment this may be expressed as ${\dot{\mathbf{\varepsilon }}}_{r} = {\mathbf{B}}{\kern 1pt} {\dot{\mathbf{r}}}_{r}$, where B is the well-known FE compatibility matrix between strains and FE nodal displacements.

The elastic term ${\dot{\mathbf{\varepsilon }}}_{r}^{el}$ is related to the residual stress via the elastic material matrix D. Thus, one may write:

$${\dot{\mathbf{\varepsilon }}}_{r} = {\mathbf{D}}^{ - 1} {{\dot{\varvec{\rho}} + \dot{\mathbf\varepsilon}}}^{pl} \to {\dot{\varvec\rho}} = {\mathbf{D}\dot{\mathbf{\varepsilon}}}_{r} - {\mathbf{D}\dot{\mathbf{\varepsilon}}}^{pl}$$

(4)

Expressing residual strain compatibility and equilibrium of residual stresses with zero loads, one may write, from the principle of virtual work (PVW):

$$\int\limits_{V} {{\mathbf{B}}^{\rm T} \cdot {\dot{\varvec{\rho }}}dV} = 0$$

$$\to \int\limits_{V} {({\mathbf{B}}^{{\mathbf{T}}} {\mathbf{DB}})} dV{\dot{\mathbf{r}}}_{r} = \int\limits_{V} {{{\mathbf{B}}^{T} {\mathbf{D}\dot{\mathbf{\varepsilon}}}}^{pl} dV} \to {\mathbf{K\dot{r}}}_{r} = \int\limits_{V} {{\mathbf{B}}^{T} {{\mathbf{D}\dot{\mathbf{\varepsilon}}}}^{pl} dV}$$

(5)

with K being the standard stiffness matrix.

The cyclic nature of the residual stresses at the asymptotic cycle (e.g., [4]) allows their decomposition in Fourier series.

$${{\varvec{\uprho}}}(\tau ) = \frac{1}{2}{\mathbf{a}}_{0}^{{}} + \sum\limits_{k = 1}^{n} {\left\{ {\cos (2k\pi \tau ) \cdot {\mathbf{a}}_{k}^{{}} + \sin (2k\pi \tau ) \cdot {\mathbf{b}}_{k}^{{}} } \right\}}$$

(6)

with the values of the Fourier coefficients being given, [18,19,20].

$${\mathbf{a}}_{k}^{{}} = - \frac{1}{k\pi }\int\limits_{0}^{1} {\left\{ {\left[ {{\dot{\varvec{\rho }}}\left( \tau \right)} \right]\left( {\sin 2k\pi \tau } \right)} \right\}d\tau }$$

(7)

$${\mathbf{b}}_{k}^{{}} = \quad \frac{1}{k\pi }\int\limits_{0}^{1} {\left\{ {\left[ {{\dot{\varvec{\rho }}}\left( \tau \right)} \right]\left( {\cos 2k\pi \tau } \right)} \right\}d\tau }$$

(8)

The basis of the RSDM-S are the Eqs. (6)–(8). Very good accuracy was attained by keeping just three terms of the series, i.e. n = 3.

An upgraded numerical scheme of the RSDM-S has been very recently presented [17]. It consists of an inner and an outer loop. The outer incremental type loop updates the shakedown factor, which is then used in the inner loop to iteratively update the Fourier coefficients found by performing time integration over the values of ${\dot{\varvec{\rho}}}$ evaluated (Eqs. (4) and (5)) at the vertices of the loading domain. The iterations of the internal loop stop when a cyclic solution has been established. This is manifested when two successive values of φ, defined by (9), coincide within a certain accuracy:

$$\varphi = \sum\limits_{k = 1}^{n} {\left\| {{\mathbf{a}}_{k}^{{}} } \right\|} + \sum\limits_{k = 1}^{n} {\left\| {{\mathbf{b}}_{k}^{{}} } \right\|}$$

(9)

If we denote by $\gamma^{(\mu )}$, the value of the current shakedown factor inside an outer iteration μ, the following formula is used to update it for the first two iterations:

$$\gamma^{(\mu + 1)} = \gamma^{(\mu )} - \varphi (\gamma^{(\mu )} )$$

(10)

whereas for the next outer iterations the following formula is used:

$$\gamma_{{}}^{{\left( {\mu + 1} \right)}} = \gamma_{{}}^{\left( \mu \right)} - \frac{{\gamma_{{}}^{\left( \mu \right)} - \gamma_{{}}^{{\left( {\mu - 1} \right)}} }}{{\varphi \left( {\gamma_{{}}^{\left( \mu \right)} } \right) - \varphi \left( {\gamma_{{}}^{{\left( {\mu - 1} \right)}} } \right)}} \cdot \varphi \left( {\gamma_{{}}^{\left( \mu \right)} } \right)$$

(11)

The proposed relationship is a regular falsi procedure for finding the zero of the function $\varphi (\gamma )$, defined at the points of the convergence of the inner loops. Thus, the convergence of the outer loops is superlinear (e.g., [5]).

Given that $\gamma^{(\mu )} > \gamma^{(\mu + 1)}$, for the corresponding values of $\varphi$, it will hold that $\varphi (\gamma^{(\mu )} ) > \varphi (\gamma^{(\mu + 1)} )$. This is an important assumption to prove that $\varphi$ is a monotonously descending function, as assumed in Fig. 3.

Fig. 3

Reproduced from [17]. Copyright © Elsevier Masson SAS. All rights reserved

Convergent sequence of solutions.

The proof of the monotonicity may be found in [17] and is illustrated in the present work (Fig. 4). It is related to the fact that because of (7) and (8) the norms of the vectors of the coefficients of the Fourier series are directly related to the norms of the residual stress rate vectors which in turn are directly related to the plastic strain vector (Eq. (4)). The value of φ, on the other hand is proportional to the length of this vector (Eq. 9), which, since it is measured through the radial return rule, is the distance from the yield surface when the total stress exceeds it. Thus, the proof is obvious, from Fig. 4, where one may see the total stress vectors OA and OB at the end of iteration μ and at the start of iteration μ + 1, respectively, with both points A and B located on the elastic stress vector ${{\varvec{\upsigma}}}^{el}$.

Fig. 4

Proof of the descending sequence of $\varphi (\gamma )$

Initial starting point of the descending algorithm may be considered as three or four times the maximum elastic limit which is located at one of the vertices of the loading domain.

3 Examples of Application

In the present work, the updated RSDM-S is used to evaluate load and displacement shakedown limits in new examples. The results are validated either by performing step-by-step analyses or by comparing with the corresponding results of the bibliography. All examples highlight the speed and the accuracy of the RSDM-S.

3.1 The Simple Frame

The first example is the simple sway frame of Fig. 5a, as introduced in [12].

Fig. 5

a Geometry and loads, b Loading cycle

Two distributed loads (P₁ and P₂) act independently, varying from the value “0” to the maximum values $P_{1}^{*}$ and $P_{2}^{*}$, as shown in Fig. 5b. The mechanical properties were E = 20,000 kN/cm², $\nu$ =0.3, σ_y = 10 kN/cm². The RSDM-S was run considering five time points of the loading cycle (the vertices of the loading domain). 350 brick elements were used for the discretization (Fig. 6).

Fig. 6.

Reproduced from [17]. Copyright © Elsevier Masson SAS. All rights reserved

2D view and 3D view of the frame using 350 brick elements.

Different shakedown limits were calculated, considering different ratios of P₁/P₂. The shakedown domain is presented in Fig. 7.

Fig. 7

Shakedown domain

In all the cases the convergence appeared quite smooth. In Fig. 8 one may see such a convergence at point A, which was accomplished in twelve iterations.

Fig. 8

Convergence diagram for point A

It is pointed out that, the results are in good agreement with those presented [12].

3.2 The Slab with the Hole

The numerical efficiency of the upgraded RSDM-S is further demonstrated also in the case of thermomechanical loading. The benchmark problem of the square plate with a circular hole in its center is selected. The structure is subjected to both thermal and distributed mechanical loads (Fig. 9a). The mechanical load is applied at the edge of the slab and is uniformly distributed. The temperature ranges from the inner to the outer edge according to the formulae:

$$\theta (r,t) = \theta_{0} + \frac{{\Delta \theta * \ln \left( {\frac{2.5D}{r}} \right)}}{\ln (5)}$$

(12)

Fig. 9

a Geometry, b loading Discretization of the slab

Due to the symmetry of the geometry and the loading, only one quarter of the plate is discretized (Fig. 9b). Let D be the diameter of the circle, L the length of the slab and d the thickness, then $D/L = 0.2$,$d/L = 0.05$. In the present work, L is equal to 20 cm. The boundary conditions along the X-axis and the Y-axis are considered rolled. Results for the cyclic thermal load θ and the cyclic load P varying proportionally from 0 to $\theta_{{}}^{*}$ and $P_{{}}^{*}$ will be investigated. The material properties are E = 180 GPa, v = 0.3 and σ_y = 200 MPa. The model consists of 220 brick elements.

The RSDM-S converged in 15 external iterations. The corresponding shakedown domain for different ratios of ${\uptheta }^{*}/{P}^{*}$ is presented in Fig. 10.

Fig. 10

Shakedown domain for the holed slab. The value σ_t corresponds to the maximum thermal stress developed in the structure

3.3 90 ^ο Pipe Elbow

Pipe elbows are met in almost all types of piping systems. Being parts of machinery configurations, pipelines, and industrial facilities, they are often subjected to earthquake loads. Thus, these components usually undergo cyclic loads and/or imposed cyclic displacements.

In the present example, the shakedown domain for a typical 90^ο steel pipe bend subjected to cyclic out of plane-imposed displacement is investigated. The steel elbow, of a yield stress of 360 MPa, consists of two straight pipes with an 8-inch outer diameter, 8.18 mm depth and of an equal length of 1.10 m. The left end of the pipe is considered fixed and the imposed displacement is applied at the right support with direction along the horizontal axis Z, as shown in Fig. 11.

Fig. 11

The configuration of the pipe elbow

The cross section was divided into three layers along the thickness with the structure being discretized with 10,528 hexagonal brick elements. The elbow is subjected to horizontal cyclic imposed displacement varying from 0 to u*. The yield displacement turned out to be u_y = 18 mm.

According to the RSDM-S the shakedown displacement is equal to u_sh = 32 mm. The convergence is quite good and the procedure is completed in 11 iterations, as shown in Fig. 12.

Fig. 12

Convergence diagram of the RSDM-S in the case of imposed displacement

The shakedown limit produced by the RSDM-S was validated with results obtained by step-by-step analyses using the Abaqus software [1]. Two analyses were run, considering the amplitude of the imposed displacement higher and lower than the shakedown limit.

In the first case, the imposed displacement was equal to 60 mm and the plastic strain was found to be always increasing (ratcheting). The most stressed point was point A located near the fixed support. For this point, the accumulated plastic strain at the end of the 16th cycle of loading is shown in Fig. 13.

Fig. 13

Contour of equivalent plastic strain at the last loading cycle

The evolution of the equivalent plastic strain from cycle to cycle for the point A may be seen in Fig. 14.

Fig. 14

Plastic strain diagram in case of 60 mm

In the case where the imposed displacement was set equal to 20 mm, the plastic deformation appeared and locked around 1%. 50 cycles were used and the shakedown condition met right from the first cycle as presented in Fig. 15.

Fig. 15

Plastic strain diagram in the case of 20 mm

4 Convergence Issues

To underline the numerical efficiency of the method, the following remarks can be made concerning its convergence characteristics:

Both the internal and the external loops are controlled through the iterative values of $\varphi$ (Eq. (9)) [17]. Internal loop iterations stop when the relative difference between two successive values of $\varphi$ is of a tolerance of 10^–3, whereas the external loop iterations stop when the value of $\varphi$ reaches the tolerance of 10^–4.

Convergence evolution towards the shakedown factor is plotted against the external loop iterations, where the load factor changes value. There is no standard number of internal loop iterations (internal loops have linear convergence), but due to the external superlinear convergence, the number of external incremental-like loops limits the total number of iterations. For all the different loading cases of the examples considered herein, to reach the final shakedown factor, this total number never exceeded 120 iterations (for example, for the elbow problem with the larger number of finite elements, it was 87). In each iteration, the number of elastic solutions (Eq. 5) equals the number of vertices of the loading domain; the stiffness matrix used to find these solutions is formed and decomposed only once (at the very beginning of the procedure). Additionally, it should be noted that even with n = 1, as the number of terms of the Fourier series, the results are almost identical.

5 Concluding Remarks

The RSDM-S is a direct method that is used to establish shakedown domains. In the present work a recent update of the approach that appeared in the literature is elaborated further. Closely linked to the robustness of the procedure, the proof of the method’s continuous descent towards the shakedown load factor is demonstrated graphically. At the same time, the superlinear convergence of the external incremental-like outer loop which guarantees fast convergence is underlined. Further structural examples to the already published ones, undergoing diverse cyclic loading actions from thermomechanical loading to imposed displacements are discussed and construction of corresponding shakedown domains are presented.