Abstract
The simulation of systems with dynamics on strongly varying time scales is quite challenging and demanding with regard to possible numerical methods. A rather naive approach is to use the smallest necessary time step to guarantee a stable integration of the fast frequencies. However, this typically leads to unacceptable computational loads. Alternatively, multirate methods integrate the slow part of the system with a relatively large step size while the fast part is integrated with a small time step. In this work, a multirate integrator for constrained dynamical systems is derived in closed form via a discrete variational principle on a time grid consisting of macro and micro time nodes. Being based on a discrete version of Hamilton’s principle, the resulting variational multirate integrator is a symplectic and momentum preserving integration scheme and also exhibits good energy behaviour. Depending on the discrete approximations for the Lagrangian function, one obtains different integrators, e.g. purely implicit or purely explicit schemes, or methods that treat the fast and slow parts in different ways. The performance of the multirate integrator is demonstrated by means of several examples.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Mechanical systems with dynamics on varying time scales, in particular those including highly oscillatory motion, impose challenging questions for numerical integration schemes. Tiny step sizes are required to guarantee a stable integration of the fast frequencies. However, for the simulation of the slow dynamics, integration with a larger time step is accurate enough. Here, small time steps increase integration times unnecessarily, especially for costly function evaluations. Typical examples of systems exhibiting dynamics on different time scales can be found in astrophysics, where depending on the distances between planets, the resulting gravitational forces can be extremely strong or weak leading to different time scales for a flight trajectory through space, or in molecular dynamics, where locally extremely high frequencies superpose global folding processes. In multibody dynamics, such systems occur e.g. in combustion engines with chain drives or in vehicle dynamics, or generally in systems being composed of rigid and elastic parts with varying and in particular with high stiffness. In this chapter, variational integrators are constructed for the efficient and structure preserving simulation of such systems.
1.1 Variational Integrators
The key feature of variational integrators is that they are based on a discrete variational formulation of the underlying system, e.g. a discrete version of Hamilton’s principle for conservative mechanical systems. More concretely, the time stepping schemes are derived from a discrete variational principle based on a discrete action function that approximates the continuous one. This is opposed to the standard derivation of integration methods that start with a continuous equation of motion and replace the continuous quantities, in particular the derivatives with respect to time, by discrete approximations. The variational theory of discrete mechanics provides a theoretical framework that parallels continuous variational dynamics. Discrete analogues to the Euler-Lagrange equations, Noether’s theorem, and the Legendre transform are derived from a discrete Lagrangian by performing similar steps as in the continuous theory. The resulting time stepping schemes are structure preserving, i.e. they are symplectic-momentum conserving and exhibit good energy behaviour, meaning that no artificial dissipation is present and the energy error stays bounded over longterm simulations. There exist many works on symplectic integrators like [12, 13, 15, 16, 18, 25, 27] to mention just a few. A detailed introduction and a survey on the history and literature on the variational view of discrete mechanics is given in [24]. Choosing different variational formulations (e.g. Hamilton, Lagrange-d’Alembert, Hamilton-Pontryagin, etc.), variational integrators have been developed for classical conservative mechanical systems (for an overview see [19, 20]), forced [13] and controlled [26] systems, constrained systems (holonomic [21, 22] and nonholonomic systems [14]), nonsmooth systems [7], stochastic systems [5], and multiscale systems [30]. In this chapter, we focus on holonomically constrained systems in the framework of discrete variational mechanics for which the constraints are enforced using Lagrange multipliers. Thus, a discrete version of the index 3 DAEs is solved.
1.2 Integration Methods for Multirate Systems
For systems comprising fast and slow dynamics, different integration methods have been developed to save computational work while preserving the accuracy of the simulation. Here, the methods distinguish with respect to the simulation goals and the structure of the underlying system (for an overview of numerical methods for oscillatory, multiscale Hamiltonian systems see e.g. [6]).
Considering systems with a slow potential that is expensive to evaluate while the fast potential is cheap to evaluate, splitting methods have been developed to accurately capture the slow dynamics without resolving the fast one. One possibility to achieve this is via implicit-explicit methods that treat the fast potential implicitly and the slow one explicitly as e.g. the so called impulse method (see e.g. [12, 17]). This method can also be interpreted as a particular variational splitting method found in the literature under the name IMEX [28]. To refine the resolution for the fast dynamics associated with the fast potential, smaller time steps can be used to perform its implicit time integration. If a structure preserving integrator is used, the composition ensures that its properties are inherited. The explicit treatment of the expensive potential certainly decreases computational costs, however, here, the fast integration is performed for all variables, also the slow degrees of freedom.
Another alternative for the efficient simulation of multirate systems is averaging. Here one is not interested in resolving the fast dynamics, but considers it to be sufficient to feed an average of the fast dynamics into the slow equations of motion. HMM (heterogeneous multiscale methods [32]) aim to link models at different scales and provides a general framework for designing and analysing very heterogeneous, multiscale or even multiphysics problems. Relying on a top-down strategy, the missing information is filled in an incomplete model on the macro scale by estimating what happens on the micro scale through averaging. Thereby, one avoids the isolated pointwise evaluation of oscillatory functions, instead relies on averaged quantities. FLAVORS (flow averaging integrators [30]) are another example of averaging methods. These integrators are formulated using variational methods and the average of the flow is performed via a splitting and resynchronisation technique.
The separation of the unknowns into fast and slow degrees of freedom enables to resolve the fast dynamics in an efficient way if different time grids are used for different parts of the system. These multirate integration methods (for an overview see e.g. [10–12] and references therein) integrate the slow part of the system with a relatively large step size while the fast part is integrated with a small time step. Thereby, main challenges are the identification of fast and slow parts (e.g. either by separating the system’s energy or by defining disjunct sets of degrees of freedom), the synchronisation of their different dynamics and in particular the treatment of mixed parts as they often appear when fast and slow dynamics are coupled either via potentials or by constraints. Furthermore, resonance phenomena impose restrictions on the combination of large and small time steps. Hence, another challenge is the stability analysis of multirate stepping schemes as done for linear problems e.g. in [3, 8]. Similar to our approach, the latter work is based on a variational derivation, however the resulting multirate schemes are different from those presented here. There are many examples in the literature where multirate schemes based on backward differentiation formulas (BDF) or Runge-Kutta methods are applied e.g. to electric circuit systems [11, 29, 31], but also to mechanical problems [2]. However, most of them do not focus on the preservation of the underlying system’s structure. The aim of this chapter is to develop a structure preserving multirate integrator based on variational mechanics.
1.3 Contribution and Outline
Sections 2 and 3 give an overview of Lagrangian dynamics. Basic definitions and properties such as energy conservation, symplecticity and Noether’s theorem are revisited in the continuous and the discrete setting, respectively. In particular, the variational formulation for constrained variational mechanics including the Lagrange multiplier theorem is presented. The variational framework provides the basis for the derivation of the variational multirate integrator described in Sect. 4. The multirate integrator is derived in closed form via a discrete variational principle on a time grid consisting of macro and micro time nodes and thus falls into the class of structure preserving integrators which generally exhibit very good longterm stability. The use of different quadrature rules in the approximation of the appearing integrals and its influence on the degree of coupling in the resulting system of discrete equations of motion, the number of necessary function evaluations and the possibility to treat fast and slow parts in an implicit or an explicit way, respectively, is discussed. The performance of the variational multirate integrator is demonstrated by means of a standard benchmark problem for multirate integration, the Fermi-Pasta-Ulam problem, and for an example from constrained multibody dynamics in Sect. 5.
2 Lagrangian Dynamics
Basic definitions and properties of Lagrangian dynamics like the conservation of energy, symplecticity and Noether’s theorem are recalled in Sect. 2.1, before Lagrangian dynamics subject to scleronomic, holonomic constraints is considered in Sect. 2.2. All notation has been introduced in [23, 24], where a large part of the theory presented here can be found.
2.1 Lagrangian Dynamics—Definitions and Properties
Consider an n-dimensional mechanical system in a configuration manifold Q⊆ℝn with configuration vector q(t)∈Q and velocity vector \(\dot{q}(t) \in T_{q(t)}Q\) in the tangent space, where t denotes the time variable in the bounded interval [t
0,t
N
]⊂ℝ. Let, the Lagrangian L:TQ→ℝ of the mechanical system consists of the difference of the kinetic energy \(T(\dot{q})\) and a potential U(q). Let  denote the space of smooth curves q:[t
0,t
N
]→Q satisfying q(t
0)=q
0 and q(t
N
)=q
N
, where q
0,q
N
∈Q are fixed endpoints. For
denote the space of smooth curves q:[t
0,t
N
]→Q satisfying q(t
0)=q
0 and q(t
N
)=q
N
, where q
0,q
N
∈Q are fixed endpoints. For  , the action integral is defined as
, the action integral is defined as
Requiring that the first variation of this action vanishes, i.e. \(\delta\mathfrak{S}=0\), Hamilton’s principle of stationary action yields the Euler-Lagrange equations of motion of a conservative mechanical system
2.1.1 Energy Conservation
The total energy E:TQ→ℝ of a Lagrangian L is given by
It is conserved along a solution of the Euler-Lagrange equations (1). More generally, solutions of (1) can be identified with the Lagrangian flow F L :[t 0,t N ]×TQ→TQ that takes a given initial state \((q(t_{0}), \dot{q}(t_{0}))\in TQ\) forward in time to the actual state at t∈[t 0,t N ] via \(F^{t}_{L}:TQ \rightarrow TQ\) with \(F^{t}_{L}: (q(t_{0}), \dot{q}(t_{0})) \mapsto(q(t), \dot{q}(t))\). In other words, \(E \circ F^{t}_{L}=E\) for all t∈[t 0,t N ], i.e. the total energy is conserved along the Lagrangian flow.
2.1.2 Symplecticity
For hyperregular Lagrangians, the Lagrangian two form Ω L :T(TQ)×T(TQ)→ℝ (being a two form means that Ω L is a skew symmetric bilinear form on TQ) is symplectic, i.e. it is a closed, weakly nondegenerate two form. A coordinate expression of the Lagrangian symplectic form is given by
where Einstein’s summation convention is used. An important property of the Lagrangian flow is that it is symplectic in the sense that it preserves the Lagrangian symplectic form, i.e.
where \(( F^{t}_{L} )^{*}(\varOmega_{L})\) denotes the pull back of Ω L . As a consequence of symplecticity, the volume in state space is conserved.
2.1.3 Noether’s Theorem
Another key property of the Lagrangian flow is its behaviour with respect to the action of a Lie group G (with Lie algebra \(\mathfrak {g}\)). The Lagrangian is said to be G-invariant, if the Lie group acts on the configuration via ϕ:G×Q→Q and on the velocity via the tangent lift ϕ TQ:G×TQ→TQ and \(L \circ\phi_{g}^{TQ}=L\) holds for all g∈G with \(\phi^{TQ}_{g}(q,\dot{q})=\phi^{TQ}(g,(q,\dot{q}))\). In this case, the group is said to be a symmetry of the Lagrangian, leading to a momentum map \(J_{L}:TQ \rightarrow\mathfrak{g}^{*}\) that is preserved along the Lagrangian flow, so that \(J_{L} \circ F^{t}_{L}=J_{L}\) for all times t∈[t 0,t N ].
Example 1
Some classical examples of symmetries are the invariance of the Lagrangian with respect to translation and rotation, leading to the conservation of total linear momentum and total angular momentum, respectively.
2.2 Constrained Lagrangian Dynamics
Now, let the motion be constrained by the vector valued function of holonomic, scleronomic constraints requiring g(q)=0∈ℝm. It is assumed that 0∈ℝm is a regular value of the constraints, such that
is an (n−m)-dimensional submanifold, called constraint manifold. Just as C can be embedded in Q via i:C→Q, its 2(n−m)-dimensional tangent bundle
can be embedded in TQ in a natural way by tangent lift Ti:TC→TQ. Here and in the sequel G(q)=Dg(q) denotes the m×n Jacobian of the constraints. Note that according to (2), admissible velocities are constrained to the null space of the constraint Jacobian.
A Lagrangian L:TQ→ℝ can be restricted to L
C=L
|TC
:TC→ℝ. To investigate the relation of the dynamics of L
C on TC and the dynamics of L on TQ, the following notation is used. Let q
0,q
N
∈C be fixed endpoints and consider  and the corresponding space of curves in C denoted by
and the corresponding space of curves in C denoted by  . Furthermore, set
. Furthermore, set  to be the space of curves λ:[t
0,t
N
]→ℝm with no boundary conditions.
to be the space of curves λ:[t
0,t
N
]→ℝm with no boundary conditions.
Theorem 1
Suppose that 0 is a regular value of the scleronomic holonomic constraints g:Q→ℝm and set C=g −1(0)⊂Q. Let L:TQ→ℝ be a Lagrangian and L C=L |TC its restriction to TC. Then the following statements are equivalent:
-
(i)
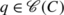 extremises the action integral
\(\mathfrak{S}^{C}(q)= \int_{t_{0}}^{t_{N}} L^{C}(q, \dot{q}) \, dt\)
and hence solves the Euler-Lagrange equations for
L
C.
extremises the action integral
\(\mathfrak{S}^{C}(q)= \int_{t_{0}}^{t_{N}} L^{C}(q, \dot{q}) \, dt\)
and hence solves the Euler-Lagrange equations for
L
C. -
(ii)
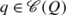 and
and
 satisfy the constrained Euler-Lagrange equations
$$ \begin{aligned}[c] \frac{\partial L(q,\dot{q})}{\partial{q}} - \frac{d}{dt} \biggl(\frac {\partial L(q,\dot{q})}{\partial\dot{q}} \biggr) - G^T(q) \cdot{\lambda} & = {0} \\ {g}({q}) & = {0} \end{aligned} $$(3)
satisfy the constrained Euler-Lagrange equations
$$ \begin{aligned}[c] \frac{\partial L(q,\dot{q})}{\partial{q}} - \frac{d}{dt} \biggl(\frac {\partial L(q,\dot{q})}{\partial\dot{q}} \biggr) - G^T(q) \cdot{\lambda} & = {0} \\ {g}({q}) & = {0} \end{aligned} $$(3) -
(iii)
 extremise
$$ \bar{\mathfrak{S}}(q, { \lambda})= \int_{t_0}^{t_N} L(q, \dot{q}) - g^T(q)\cdot{\lambda} \, dt $$(4)
extremise
$$ \bar{\mathfrak{S}}(q, { \lambda})= \int_{t_0}^{t_N} L(q, \dot{q}) - g^T(q)\cdot{\lambda} \, dt $$(4)and hence, solve the Euler-Lagrange equations for the augmented Lagrangian \(\bar{L}:T(Q \times\mathbb {R}^{m}) \rightarrow\mathbb{R}\) defined by \(\bar{L}({q}, {\lambda}, \dot{q}, \dot{{\lambda}}) = L(q, \dot{q}) - g^{T}(q)\cdot{\lambda}\).
The proof given in [24] makes use of the Lagrange multiplier theorem (see e.g. [1]). The term −G T(q)⋅λ∈(TC)⊥ in (3)1 represents the constraint forces that prevent the system from deviation of the constraint manifold. As can be seen, the constrained system on TC is a standard Lagrangian systems and so it has the usual conservation properties. In particular, the constrained Lagrangian system L C:TC→ℝ has a flow map that preserves the symplectic two form \(\varOmega_{L^{C}} = (Ti)^{*}\varOmega_{L}\). Furthermore, Noether’s theorem holds for both, the unconstrained as well as the constrained case. Thus, if the lifted group action leaves L C on TC invariant, the same momentum map is preserved.
3 Discrete Variational Dynamics
The variational theory of discrete mechanics provides a theoretical framework that parallels continuous variational dynamics. Discrete analogues to the Euler-Lagrange equations, the symplectic structure and Noether’s theorem are derived from a discrete Lagrangian by performing similar steps as in the continuous theory.
3.1 Discrete Variational Dynamics—Definitions and Properties
Corresponding to TQ, the discrete state space is defined by Q×Q which is locally isomorphic to TQ. For a discrete time grid {t
0,t
0+Δt,…,t
0+NΔt=t
N
} with N∈ℕ and constant step size Δt∈ℝ, let  denote the space of discrete trajectories q
d
:{t
0,t
0+Δt,…,t
0+NΔt=t
N
}→Q satisfying q
d
(t
0)=q
0 and q
d
(t
N
)=q
N
for given q
0,q
N
∈Q. A continuous trajectory q:[t
0,t
N
]→Q is replaced by a discrete trajectory \({q}_{d}=\{q_{k}\}_{k=0}^{N}\). Here, q
k
=q
d
(t
0+kΔt) is viewed as an approximation to q(t
0+kΔt).
denote the space of discrete trajectories q
d
:{t
0,t
0+Δt,…,t
0+NΔt=t
N
}→Q satisfying q
d
(t
0)=q
0 and q
d
(t
N
)=q
N
for given q
0,q
N
∈Q. A continuous trajectory q:[t
0,t
N
]→Q is replaced by a discrete trajectory \({q}_{d}=\{q_{k}\}_{k=0}^{N}\). Here, q
k
=q
d
(t
0+kΔt) is viewed as an approximation to q(t
0+kΔt).
According to the key idea of variational integrators, the variational principle is discretised rather than the resulting equations of motion. The action integral is approximated in a time interval [t k ,t k+1] using the discrete Lagrangian L d :Q×Q→ℝ via
The quadrature used to approximate the integral in (5) determines the actual time stepping scheme (6) and in particular its order of accuracy. For  , variation of the discrete action sum
, variation of the discrete action sum
reads

Requiring its stationarity for all \(\{ \delta{q}_{k}\}_{k=1}^{N-1}\) and δq 0=δq N =0 yields the discrete (unconstrained) Euler-Lagrange equations
For a given initial configuration q 0=q(t 0)∈Q and initial velocity \(\dot{q}(t_{0})\in T_{q_{0}}Q\) with corresponding initial conjugate momentum
the first discrete configuration can be computed by solving
Then for two given subsequent configurations, (6) can be used to integrate forward in time. See [23, 24] for the theory on (discrete) Legendre transforms.
3.1.1 Symplecticity
The discrete object corresponding to the Lagrangian flow is the discrete Lagrangian map \(F_{L_{d}}: Q \times Q \rightarrow Q \times Q\) with \(F_{L_{d}}: (q_{k-1},q_{k})\mapsto(q_{k}, q_{k+1})\) according to (6). One can show that the discrete Lagrangian map inherits the properties we summarised for the continuous Lagrangian flow. That means the discrete Lagrangian symplectic form with coordinate expression
is preserved under the discrete Lagrangian map, i.e.
and we say that \(F_{L_{d}}\) is symplectic.
3.1.2 Energy Behaviour
Due to the symplecticity of the discrete Lagrangian map, backward error analysis can be used to prove that no energy is dissipated numerically, see [12]. As a consequence, the total energy oscillates (with a small amplitude) close to the real value and no energy is gained or lost artificially along the discrete trajectory q d . Thus, the integration runs very stable, even when relatively large time steps are used. We speak about good longterm energy behaviour.
On the other hand, for exactly energy conserving time stepping schemes, the energy is conserved up to numerical accuracy, see e.g. [4] and many references therein. It is well known [9] that numerical integrators based on constant time steps cannot be symplectic and exactly energy conserving at the same time.
3.1.3 Discrete Noether’s Theorem
Consider a given discrete Lagrangian system L d :Q×Q→ℝ which is invariant under the lift ϕ Q×Q:G×(Q×Q)→Q×Q of the action ϕ:G×Q→Q, i.e. \(L_{d} \circ\nobreak\phi_{g}^{Q \times Q} = L_{d}\) for all g∈G. Then the corresponding discrete Lagrangian momentum map \(J_{L_{d}}: Q \times Q \rightarrow\mathfrak{g}^{*}\) is a conserved quantity of the discrete Lagrangian map, such that \(J_{L_{d}} \circ F_{L_{d}} =J_{L_{d}}\). Note that discrete momentum maps are conserved exactly, i.e. up to the numerical accuracy to which the (often nonlinear) discrete equations of motion are solved.
Example 2
As in the continuous case, most common classical examples are the conservation of total linear momentum and total angular momentum, when the discrete Lagrangian is invariant with respect to translation and rotation, respectively. In general, a value of the momentum map can be computed from the initial data, and this value is exactly preserved along the discrete trajectory.
3.2 Constrained Discrete Variational Dynamics
Let q
0,q
N
∈C be fixed end points. Consider  and let
and let  denote the corresponding set of discrete trajectories in C. Furthermore, let
denote the corresponding set of discrete trajectories in C. Furthermore, let  be the set of maps λ
d
:{t
0,t
0+Δt,…,t
0+NΔt=t
N
}→ℝm with no boundary conditions. Then, \(\lambda_{d}=\{\lambda_{k}\}_{k=0}^{N-1}\) with λ
k
=λ
d
(t
k
) approximates the Lagrange multiplier λ(t
k
) at t
k
=t
0+kΔt.
be the set of maps λ
d
:{t
0,t
0+Δt,…,t
0+NΔt=t
N
}→ℝm with no boundary conditions. Then, \(\lambda_{d}=\{\lambda_{k}\}_{k=0}^{N-1}\) with λ
k
=λ
d
(t
k
) approximates the Lagrange multiplier λ(t
k
) at t
k
=t
0+kΔt.
To include scleronomic holonomic constraints in the discrete variational principle, the integral over [t k ,t k+1] of the scalar product of the constraints and the corresponding Lagrange multiplier in (4) is approximated by the trapezoidal rule
whereby \({g}_{d}^{T}({q}_{k})=\Delta t{g}^{T}({q}_{k})\) is used and let \({G}^{T}_{d}({q}_{k})= D{g}_{d}^{T}({q}_{k})\).
Analogue to Theorem 1, the relation between the constrained discrete Lagrangian system on Q×Q and that corresponding to a discrete Lagrangian restricted to C×C is stated in the following theorem which has again been taken from [24].
Theorem 2
Suppose that 0 is a regular value of the scleronomic holonomic constraints g:Q→ℝm and set C=g −1(0)⊂Q. Let L d :Q×Q→ℝ be a discrete Lagrangian and \(L^{C}_{d}=L_{d _{| C \times C}}\) its restriction to C×C. Then the following statements are equivalent:
-
(i)
 extremises the discrete action
\(\mathfrak{S}^{C}_{d}=\mathfrak{S}_{d _{| C \times C}}\)
and hence solves the discrete Euler-Lagrange equations for
\(L^{C}_{d}\).
extremises the discrete action
\(\mathfrak{S}^{C}_{d}=\mathfrak{S}_{d _{| C \times C}}\)
and hence solves the discrete Euler-Lagrange equations for
\(L^{C}_{d}\). -
(ii)
 and
and
 satisfy the constrained discrete Euler-Lagrange equations
satisfy the constrained discrete Euler-Lagrange equations

-
(iii)
 extremise
\(\bar{\mathfrak{S}}_{d}({q}_{d}, {\lambda}_{d})= \mathfrak{S}_{d}({q}_{d}) - \langle{\lambda}_{d}, {g}_{d}({q}_{d}) \rangle\)
and hence, solve the Euler-Lagrange equations for the augmented Lagrangian
\(\bar{L}_{d}:(Q \times\mathbb {R}^{m}) \times(Q \times\mathbb{R}^{m}) \rightarrow\mathbb{R}\)
defined by
$$\bar{L}_d({q}_k, {\lambda}_k, {{q}_{k+1}},{{\lambda}_{k+1}}) = L_d({q}_k, {{q}_{k+1}}) - \frac{1}{2} g^T_d({q}_{k}) \cdot{\lambda}_{k}- \frac{1}{2} g^T_d({q}_{k+1}) \cdot{\lambda}_{k+1} $$
extremise
\(\bar{\mathfrak{S}}_{d}({q}_{d}, {\lambda}_{d})= \mathfrak{S}_{d}({q}_{d}) - \langle{\lambda}_{d}, {g}_{d}({q}_{d}) \rangle\)
and hence, solve the Euler-Lagrange equations for the augmented Lagrangian
\(\bar{L}_{d}:(Q \times\mathbb {R}^{m}) \times(Q \times\mathbb{R}^{m}) \rightarrow\mathbb{R}\)
defined by
$$\bar{L}_d({q}_k, {\lambda}_k, {{q}_{k+1}},{{\lambda}_{k+1}}) = L_d({q}_k, {{q}_{k+1}}) - \frac{1}{2} g^T_d({q}_{k}) \cdot{\lambda}_{k}- \frac{1}{2} g^T_d({q}_{k+1}) \cdot{\lambda}_{k+1} $$
As in the continuous case, the structure preservation properties remain untouched by the presence of constraints, the constrained discrete Lagrangian map preserves the standard discrete symplectic form on C×C and the same discrete momentum maps that are preserved in the discrete unconstrained case (again, the preserved value can be computed as the continuous momentum maps at the initial condition).
4 Variational Multirate Integrator
Having reviewed Lagrangian dynamics for constrained systems in the time continuous case in Sect. 2 and in the discrete setting in Sect. 3, we now focus on constrained systems with dynamics on different time scales.
4.1 Slow and Fast Potential and Constraints
Let the fact that the Lagrangian contains slow and fast dynamics be characterised by the possibility to additively split the potential energy U(q)=V(q)+W(q) into a slow potential V and a fast potential W. Then, the constrained Euler-Lagrange equations of motion on a time interval [t 0,t N ]⊂ℝ
can be derived via Hamilton’s principle requiring stationarity of the action. See Sect. 5 for examples of such additively split potentials.
4.2 Slow and Fast Variables
We further assume that the n-dimensional configuration variable q can be divided into n s slow variables q s∈Q s and n f fast variables q f∈Q f such that Q s×Q f=Q and q=(q s,q f) with n s+n f=n. Let the fast potential depend of the fast degrees of freedom only, i.e. W=W(q f) while the slow potential V=V(q) depends on the complete configuration variable as does the constraint function g=g(q). With these assumptions, the Euler-Lagrange equations (7) take the form
Remark 1
If in addition, the slow potential depends on the slow variables only and on top of that the kinetic energy does not contain any entries coupling \(\dot{q}^{s}\) and \(\dot{q}^{f}\), then the system is completely decoupled and simulation can be performed independently in parallel, without any exchange of information. This case is trivial and we focus on the scenario described above. Note that the inclusion of additional potentials or constraint functions depending on the fast or the slow variable only is straightforward.
4.3 Discrete Variational Principle on Macro and Micro Grid
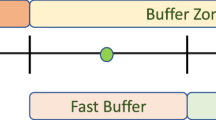
Rather than choosing one time grid for the approximation as for standard variational integrators, for the multirate integrator, two different time grids are introduced, see Fig. 1. With the time steps ΔT and Δt (where ΔT≥Δt), a macro time grid {t k =kΔT∣k=0,…,N} and a micro time grid \(\{t^{m}_{k}=k\Delta T + m \Delta t \mid k=0,\ldots ,N-1, m=0,\ldots,p\}\) are defined. Note that except for the boundary nodes t 0,t N , two micro time nodes coincide with a macro time node, i.e. \(t_{k-1}^{p}=t_{k}^{0}=t_{k}\) for k=1,…,N−1, and ΔT=pΔt, see Fig. 1. The macro time grid provides the domain for the discrete macro trajectory of the slow variables
and the discrete micro trajectory of the fast variables lives on the micro grid
Since the constraints depend on the complete configuration variables, the Lagrange multipliers cannot be separated in a fast and a slow part and must be computed on the fine time grid. Thus, the discrete trajectory of Lagrange multipliers takes the form
Note that \(t_{k-1}^{p}=t_{k}^{0}\) and therefore also \(q_{k-1}^{f,p}=q_{k}^{f,0}\) and \(\lambda_{k-1}^{p}=\lambda_{k}^{0}\) hold.
As an approximation to \(\bar{\mathfrak{S}}\) in (4), the augmented discrete action is defined as
The discrete Lagrangian L d =T d −V d −W d approximates \(\int_{t_{k}}^{t_{k+1}}L(q, \dot{q}) \, dt\) and reads
while h d is approximating \(\int_{t_{k}}^{t_{k+1}}g(q)^{T}\cdot\lambda \, dt\). Omitting the arguments of L d and h d , stationarity of the discrete action

with independent variations \(\delta q_{k}^{s}\) for k=0,…,N and \(\delta q_{k}^{f,m}, \delta\lambda_{k}^{m}\) for k=0,…,N−1 and m=0,…,p yields the discrete Euler-Lagrange equations. Let k=0 and assume that an initial configuration \((q_{0}^{s},q_{0}^{f,0})\) being consistent with the constraints, i.e. \(g((q_{0}^{s},q_{0}^{f,0}))=0\), and an initial conjugate momentum \((p_{0}^{s},p_{0}^{f,0})\) is given. Then for k=0, the unknowns \({q_{1}^{s}, q_{0}^{f,1},\ldots,q_{0}^{f,p}}\) and \(\lambda_{0}^{0},\ldots,\lambda_{0}^{p-1}\) are determined by solving the following set of equations for m=1,…,p−1.
These equations can be considered as initial conditions, since they determine the unknowns in the first macro time interval from given initial data. Note that variation with respect to \(\lambda_{0}^{0}\) is unnecessary, since the initial configuration does fulfil the constraints a priori. Analog to the variational integrators for constrained systems on a single time grid as described in Sect. 3.2 (see also e.g. [21, 24]), here variation with respect to \(\lambda_{0}^{m}\) yields the condition \(g((q_{0}^{s},q_{0}^{f,m}))=0\). Therefore, the last condition \(g((q_{1}^{s},q_{0}^{f,p}))=0\) is composed by contributions from variation with respect to the multipliers \(\lambda_{0}^{p}\) and \(\lambda_{1}^{0}\) (which are equal) which is ensured using the Dirac delta in the last equation. To proceed further in time for k=1,…,N−1 (assuming that \(q_{k-1}^{s},q_{k}^{s},q_{k-1}^{f,0},\ldots,q_{k-1}^{f,p}\) are given), solving the following discrete Euler-Lagrange equations for m=1,…,p−1 determines \({q_{k+1}^{s}, q_{k}^{f,1},\ldots,q_{k}^{f,p}}\) and \(\lambda_{k}^{0},\ldots,\lambda_{k}^{p-1}\).
Again, at the macro nodes the constraint equations include an additional term which is added using the Dirac delta. Note however, that this term does not exist at the very end node t N .
Remark 2
Due to the variational derivation of the multirate integrator, we can state that a discrete symplectic form is preserved along the discrete solution trajectory. Furthermore, if the discrete Lagrangian is invariant under a group action on the macro grid, then the corresponding momentum map is preserved at the macro time nodes \(\{t_{k}\}_{k=0}^{N}\).
4.4 Discrete Action—Influence of Quadrature
The quadrature rules in use for the discrete Lagrangian (9) and the discrete constraint term in (8) determine the degree of coupling between the discrete equations (10) and (11), respectively. This can range from a fully implicit scheme over variants being explicit in the macro and implicit in the micro quantities to fully explicit schemes. We consider Lagrangians of the form \(L(q,\dot{q}) = T(\dot{q}) - V(q)-W(q^{f})\).
4.4.1 Kinetic Energy
Assume that the kinetic energy can be decomposed in a contribution from the fast and the slow variables, i.e.
where M s and M f are the mass matrices for the slow and fast variables, respectively, yielding the total mass matrix as M=diag(M s,M f). In the sequel the velocities \(\dot{q}^{s}\) and \(\dot{q}^{f}\) are approximated using backward difference operators on the macro and micro grid. Then the discrete kinetic energy is defined on the time interval [t k ,t k+1] as

4.4.2 Constraints
The discrete function h d approximates the integral \(\int_{t_{k}}^{t_{k+1}}g(q)^{T}\cdot\lambda\, dt\). Similar to the approximation on a standard time grid as described in Sect. 3.2 (see also [21]), a trapezoidal rule is used here.

For the discrete constraint function g d , an intuitive example is the following.
Example 3
The slow variables q s can be linearly interpolated between \(q_{k}^{s}\) and \(q_{k+1}^{s}\) on the micro time grid as
Then, the discrete constraint function reads
4.4.3 Potential Energy
When standard variational integrators are used for problems with very stiff potentials, their discrete counterparts are often based on midpoint evaluations of the continuous potentials such that the corresponding integration scheme is implicit. On the other hand, softer potentials can be approximated by evaluations of the continuous potential on the left or right node yielding explicit schemes (at least as long as there are no constraints present), which are of course much cheaper regarding the computational costs. For the multirate integrator, a large variety of combinations is possible.
Example 4
(Implicit fast and explicit slow forces)
Let’s first consider a special case where the dynamics is not subject to any constraints. Then, choosing an affine combination as approximation in the slow potential that involves only macro nodes
with 0≤α≤1 and a micro node based midpoint rule in the fast potential
leads to discrete conservative forces in the discrete Euler-Lagrange equations which are explicit for the slow potential and implicit for the fast one. Thus, only few evaluations of the gradient of V are necessary which is advantageous when the slow potential’s evaluation is very costly compared to the fast one. The resulting scheme can be interpreted as a variational splitting method which is symmetric and symplectic, since it is a symmetric composition of symmetric and symplectic methods. When this method is formulated with \(\alpha=\frac {1}{2}\) on only one time grid with a constant time step (i.e. Δt=ΔT and p=1) and without splitting the configuration variable into fast and slow variables, one obtains the IMEX method in [28] which is an example of an impulse method, see [12] and references therein.
Example 5
(Fully implicit scheme)
In this example, the slow variables are interpolated according to (12) and then midpoints are inserted into the slow potential
and into the fast potential as in (14). As a result, the discrete Euler-Lagrange equations are fully coupled and have to be solved simultaneously using an iteration method. Another quadrature yielding a fully implicit scheme for 0≤α≤1 is given by
Example 6
(Fully explicit scheme)
In the absence of constraints, using the affine combination of the slow potential evaluated at the macro nodes in (13) and the affine combination of micro node evaluations of the fast potential
with 0≤α≤1 leads to discrete Euler-Lagrange equations (11) that can subsequently be solved without iteration, i.e. first \(q_{k}^{f,1}\) is obtained from \((\mathrm{DEL})_{k}^{f,0}\), then \((\mathrm{DEL})_{k}^{f,m}\) yields \(q_{k}^{f,m+1}\) for m=1,…,p−1. At any time, \(q_{k+1}^{s}\) can be computed from \((\mathrm{DEL})_{k}^{s}\). For \(\alpha=\frac{1}{2}\), this choice of quadrature leads to the scheme in [8] for the special case that a synchronised time grid is used there.
More general multirate schemes are obtained for different choices and combinations of quadrature. Depending on the complexity of the evaluation of the potential functions and their gradients, the computational costs of the overall simulation is heavily influenced by the choice of quadrature.
5 Numerical Examples
5.1 Fermi-Pasta-Ulam Problem
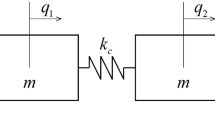
The performance of the presented multirate approach is first demonstrated by means of the Fermi-Pasta-Ulam (FPU) problem (see e.g. [12]). Consider 2l unit point masses that are chained together by soft and stiff springs as shown in Fig. 2. With an appropriate choice of the coordinates it is possible to separate the slow and the fast variables of the multirate system. The slow variables \(q^{s}_{i},\,i=1,\ldots,l\), correspond to the location of i-th stiff spring’s centre, while the length of i-th stiff spring is a fast variable \(q^{f}_{i},\,i=1,\ldots,l\). The Lagrangian is composed by the kinetic energy of slow and fast variables and the spring potentials

where the second term is the soft spring potential V((q s,q f)) depending on the complete configuration variable, while the third term is the stiff potential W(q f) that depends on the spring lengths only and includes the stiffness ω∈ℝ which is supposed to be large. For this system, no constraints are present. The Fermi-Pasta-Ulam problem is a multirate system, i.e. it shows different behaviour on different time scales (confirm [12]). The vibration of the stiff linear springs takes place on the time scale ω −1, while ω 0 is the time scale of the soft nonlinear springs’ motion. Furthermore, on the time scale ω, energy exchanges among the stiff springs. For the simulations, we consider 6 point masses (i.e. l=3) with mass m=1 and the stiffness of the stiff springs is ω=50. The system has an initial displacement \(q^{s}_{1}(0) =1\) and an initial extension \(q^{f}_{1}(0)=\omega^{-1}\), initial velocities are \(\dot{q}^{s}_{1}(0) =1\) and \(\dot{q}^{f}_{1}(0)=1\). All remaining initial values are zero.
In this simulation, the quadrature (16) with α=1 is used for the slow potential and the midpoint rule (14) for the fast one. As a reference solution, a standard variational integrator (p=1) with the time step ΔT=0.01 is used. This time step is small enough to resolve the fast oscillations of the stiff springs’ extensions. In the left hand side plot in Fig. 3, the configuration and momentum of the first slow and the first fast variable (i.e. the first stiff spring’s centre and the length of the first stiff spring) are shown. Using a bigger time step ΔT=0.3, the fast motion cannot be captured anymore as can be seen on the right hand side of Fig. 3.
Keeping a macro time step of ΔT=0.3, the multirate variational integrator is used for a different number of intermediate micro steps. In Fig. 4, micro (red solid) and macro (blue dashed) solutions for configuration and momentum of the first slow and the first fast variable are shown for p=10 micro steps on the left and for p=30 micro steps on the right. For an increasing number of micro steps, the approximation of the fast variables becomes better. For p=30, the micro step size Δt=0.01 is equal to the step size of the standard variational integrator in the reference solution. As a result, the discrete solution of the fast variable nicely coincides with the reference solution although the macro solution alone (red solid) does not resolve the fast dynamics.
In Fig. 5, the exchange of energy between the stiff springs (blue dashed, black dash-dotted, cyan dashed) is shown. The total oscillatory energy, i.e. the sum of the stiff springs’ energy (red solid) remains close to a constant value (this is called an adiabatic invariant of the Hamiltonian system, see [12]) which is nicely visible in Fig. 5(a) for the reference solution. Using the macro time step T=0.3 and p=1 (Fig. 5(b)), the total energy oscillates much more and cannot be considered a constant value anymore. However, for p=10 (Fig. 5(c)) and p=30 (Fig. 5(d)) micro steps the oscillations become smaller, and for p=30 the same qualitative long term energy behaviour as for the reference solution is obtained.
Computational costs for different examples of quadrature rules are depicted in Fig. 6. Computation times for the simulation of t N =30 seconds are shown in the left hand side plot for the fully implicit scheme (Example 5: (14) and (15)) and on the right hand side for a quadrature leading to an explicit treatment of the fast potential and an implicit treatment of the slow potential (Example 4: (14) and (13)). All simulations are based on a constant micro time step of Δt=0.01. For an increasing number p of micro steps per macro time step (thus for an increasing macro step ΔT=pΔt), the computational costs decrease as expected. Thus, the resolution for the fast dynamics stays constant and fine enough, while the overall computational costs get lower since the number of slow potential evaluations decreases.
5.2 Triple Spherical Pendulum
For the triple spherical pendulum in Fig. 7, the slow variable q s=q 1∈ℝ3 is the placement of the large mass (\(m_{1}^{\mathrm{slow}}=100\)), while q f=(q 2,q 3)∈ℝ6 contains the placements of the two smaller masses (\(m_{2}^{\mathrm {fast}}=m_{3}^{\mathrm{fast}}=2\)). The slow potential energy reads \(V(q)=q^{T}\cdot M\cdot\bar{g}\) with the constant mass matrix M∈ℝ9×9 and the gravity vector \(\bar{g} \in\mathbb {R}^{9}\) acting in the negative e 3-direction with acceleration 9.81. Massless rigid links of lengths l 1=20 and l 2=3 connect the large mass to the origin and the first small mass to the large one, respectively. They give rise to a purely slow constraint \(g^{s}(q^{s})=\frac {1}{2}(q_{1}^{2}-l^{2}_{1})\) and a constraint \(g^{sf}(q)=\frac {1}{2}((q_{2}-q_{1})^{2}-l^{2}_{2})\) coupling the slow and the first fast mass. Both constraints are combined into the vector valued constraint function g=(g s,g sf). The second small mass is connected to the first one by a linear spring with the stiffness ω=5000, thus the fast potential takes the form \(W(q^{f})=\frac{1}{2}\omega ((q_{3}-q_{2})^{2}-l_{3}^{2})\) where l 3=3 is the length of the unstretched spring. Initially, the triple pendulum is aligned with the e 1-axis and the spring is prestretched by 2. The slow mass has an initial velocity of \(\dot{q}^{s}(0)=(0,2,-3)\) and the fast masses’ initial velocity is \(\dot{q}^{f}(0)=(0,3l_{2},-l_{2},l_{2}+l_{3},5(l_{2}+l_{3}),-(l_{2}+l_{3}))\).
In the simulation of the triple pendulum’s dynamics, the midpoint evaluation (14) is used in the fast potential. Since the gravity potential is a linear function, it yields a constant force vector, which is independent of the choice of quadrature. The two left hand side plots in Fig. 8 show the evolution of the configuration and conjugate momentum of the second fast mass, being computed via a standard variational integrator (p=1) with ΔT=0.001 as a reference solution. The right hand side plots show the results from the variational multirate scheme with ΔT=0.08 and p=5, while the corresponding results for p=10 and p=20 are depicted in Fig. 9. The lines connect the values at the macro nodes and the intermediate micro node values are indicated by little crosses. One can see clearly, that the macro grid with ΔT=0.08 is too coarse to resolve the fast motion. For an increasing number of micro nodes, the fast oscillations of the second small mass become more and more visible. Finally, a numerical indicator for the variational character of the proposed method is given in Fig. 10. The triple pendulum’s Lagrangian is invariant with respect to rotation about the gravitational axis, thus the corresponding angular momentum component L 3 is conserved exactly along the trajectory. The algorithm does conserve L 3 to numerical accuracy, independent of the macro or micro time step size.
6 Conclusion
A unified framework for the derivation of different multirate integrators for constrained dynamical systems is presented. All schemes are derived in closed form via a discrete variational principle on a time grid consisting of macro and micro time nodes. Being based on a discrete version of Hamilton’s principle, the resulting variational multirate integrators are symplectic and momentum preserving integration schemes and also exhibit good energy behaviour. The choice of quadrature in the slow and fast potentials of the system can be adapted to the simulation goal like e.g. a low number of function evaluations of a costly potential or obtaining a partly of fully explicit scheme. In particular, if the number of micro nodes is large enough, fast oscillations can be resolved without solving for the slow variables on the micro grid. This leads to savings in the computational costs. This unified variational framework allows the analysis of a large class of multirate schemes, which has to be done in future work with particular focus on stability problems caused by resonance phenomena.
References
Abraham, R., Marsden, J.E., Ratiu, T.: Manifolds, Tensor Analysis, and Applications. Springer, New York (1988)
Arnold, M.: Multi-rate time integration for large scale multibody system models. In: Proceedings of the IUTAM Symposium on Multiscale Problems in Multibody System Contacts, Stuttgart, Germany (2006)
Barth, E., Schlick, T.: Extrapolation versus impulse in multiple-timestepping schemes. II. Linear analysis and applications to Newtonian and Langevin dynamics. J. Chem. Phys. 109, 1633–1642 (1998)
Betsch, P., Leyendecker, S.: The discrete null space method for the energy consistent integration of constrained mechanical systems. Part II: Multibody dynamics. Int. J. Numer. Methods Eng. 67(4), 499–552 (2006)
Bou-Rabee, N., Owhadi, H.: Stochastic variational integrators. IMA J. Numer. Anal. 29, 421–443 (2008)
Cohen, D., Jahnke, T., Lorenz, K., Lubich, C.: Numerical integrators for highly oscillatory Hamiltonian systems: a review. In: Analysis, Modeling and Simulation of Multiscale Problems, pp. 553–576 (2006)
Fetecau, R.C., Marsden, J.E., Ortiz, M., West, M.: Nonsmooth Lagrangian mechanics and variational collision integrators. SIAM J. Appl. Dyn. Syst. 2(3), 381–416 (2003)
Fong, W., Darve, E., Lew, A.: Stability of asynchronous variational integrators. J. Comput. Phys. 227, 8367–8394 (2008)
Ge, Z., Marsden, J.E.: Lie-Poisson Hamilton-Jacobi theory and Lie-Poisson integrators. Phys. Lett. A 133(3), 134–139 (1988)
Gear, C.W., Wells, R.R.: Multirate linear multistep methods. BIT 24, 484–502 (1984)
Günther, M., Kærnø, A., Rentrop, P.: Multirate partitioned Runge-Kutta methods. BIT Numer. Math. 41(3), 504–514 (2001)
Hairer, E., Wanner, G., Lubich, C.: Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations. Springer, New York (2004)
Kane, C., Marsden, J.E., Ortiz, M., West, M.: Variational integrators and the Newmark algorithm for conservative and dissipative mechanical systems. Int. J. Numer. Methods Eng. 49(10), 1295–1325 (2000)
Kobilarov, M., Marsden, J.E., Sukhatme, G.S.: Geometric discretization of nonholonomic systems with symmetries. Discrete Contin. Dyn. Syst., Ser. S 1(1), 61–84 (2010)
Leimkuhler, B., Patrick, G.: A sympletic integrator for Riemannian manifolds. J. Nonlinear Sci. 6, 367–384 (1996)
Leimkuhler, B., Reich, S.: Symplectic integration of constrained Hamiltonian systems. Math. Comput. 63, 589–605 (1994)
Leimkuhler, B., Reich, S.: Simulating Hamiltonian Dynamics. Cambridge University Press, Cambridge (2004)
Lew, A., Marsden, J.E., Ortiz, M., West, M.: An overview of variational integrators. In: Finite Element Methods: 1970’s and Beyond, pp. 85–146. CIMNE, Barcelona (2003)
Lew, A., Marsden, J.E., Ortiz, M., West, M.: An overview of variational integrators. In: Franca, L.P., Tezduyar, T.E., Masud, A. (eds.) Finite Element Methods: 1970’s and Beyond, pp. 98–115. CIMNE, Barcelona (2004)
Lew, A., Marsden, J.E., Ortiz, M., West, M.: Variational time integrators. Int. J. Numer. Methods Eng. 60(1), 153–212 (2004)
Leyendecker, S., Marsden, J.E., Ortiz, M.: Variational integrators for constrained dynamical systems. Z. Angew. Math. Mech. 88, 677–708 (2008)
Leyendecker, S., Ober-Blöbaum, S., Marsden, J.E., Ortiz, M.: Discrete mechanics and optimal control for constrained systems. Optim. Control Appl. Methods 31(6), 505–528 (2010)
Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry. Springer, New York (1994)
Marsden, J.E., West, M.: Discrete mechanics and variational integrators. Acta Numer. 10, 357–514 (2001)
McLachlan, R., Quispel, G.: Geometric integrators for ODEs. J. Phys. A 39(19), 5251–5286 (2006)
Ober-Blöbaum, S., Junge, O., Marsden, J.E.: Discrete mechanics and optimal control: an analysis. ESAIM Control Optim. Calc. Var. 17(2), 322–352 (2010)
Reich, S.: Momentum conserving symplectic integrations. Physica D 76(4), 375–383 (1994)
Stern, A., Grinspun, E.: Implicit-explicit integration of highly oscillatory problems. Multiscale Model. Simul. 7, 1779–1794 (2009)
Striebel, M., Bartel, A., Günther, M.: A multirate ROW-scheme for index-1 network equations. Appl. Numer. Math. 59, 800–814 (2009)
Tao, M., Owhadi, H., Marsden, J.E.: Nonintrusive and structure preserving multiscale integration of stiff ODEs, SDEs, and Hamiltonian systems with hidden slow dynamics via flow averaging. Multiscale Model. Simul. 8(4), 1269–1324 (2010)
Verhoeven, A., Tasić, B., Beelen, T.G.J., ter Maten, E.J.W, Mattheij, R.M.M.: BDF compound-fast multirate transient analysis with adaptive stepsize control. J. Numer. Anal. Ind. Appl. Math. 3(3–4), 275–297 (2008)
Weinan, E., Engquist, B., Li, X., Ren, W., Vanden-Eijnden, E.: Heterogeneous multiscale methods: a review. Commun. Comput. Phys. 2(3), 367–450 (2007)
Acknowledgements
This chapter was partly developed and published in the course of the Collaborative Research Centre 614 “Self-Optimizing Concepts and Structures in Mechanical Engineering” funded by the German Research Foundation (DFG) under grant number SFB 614.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Leyendecker, S., Ober-Blöbaum, S. (2013). A Variational Approach to Multirate Integration for Constrained Systems. In: Samin, JC., Fisette, P. (eds) Multibody Dynamics. Computational Methods in Applied Sciences, vol 28. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-5404-1_5
Download citation
DOI: https://doi.org/10.1007/978-94-007-5404-1_5
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-5403-4
Online ISBN: 978-94-007-5404-1
eBook Packages: EngineeringEngineering (R0)



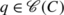 extremises the action integral
extremises the action integral
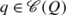 and
and
 satisfy the constrained Euler-Lagrange equations
satisfy the constrained Euler-Lagrange equations
 extremise
extremise
 extremises the discrete action
extremises the discrete action
 and
and
 satisfy the constrained discrete Euler-Lagrange equations
satisfy the constrained discrete Euler-Lagrange equations

 extremise
extremise









