Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Good runnability (performance) of webs and other axially moving bands and belts depends on the realized velocity and in-plane tension. Web breaks and instability are the most serious threats to good runnability. Arisen fracture and instability modes cause problems, e.g., for paper machines and printing presses. In practice, web instability in the form of buckling occurs when tension applied to the webs is less than some critical value, and extension of a safe stability range is realized by increasing the tension. However, a web break occurs when tension exceeds some critical value. Thus, the increase of the in-plane tension has opposite influences on the web stability and fracture. Both criteria are significant from the viewpoint of increased productivity demands, which mean faster production speeds and a longer safe production time interval (longevity).

Several studies related to the stable web movement exist in the literature. Vibrations of travelling membranes and thin plates were first studied by Archibald and Emslie [1], Miranker [11], Swope and Ames [18], Mote [12], Simpson [16], Chonan [4], and Wickert and Mote [22], concentrating on various aspects of free and forced vibrations. Stability of travelling rectangular membranes and plates was first studied by Ulsoy and Mote [19], Lin and Mote [9, 10], and Lin [8]. Recently, the behaviour of axially moving materials has been studied by, e.g., Shin et al. [15], Wang et al. [20], and Banichuk et al. [2].

In [2], buckling of an axially moving elastic plate was studied. The critical velocity and the corresponding buckling shapes were studied analytically as functions of problem parameters.

The field of fracture mechanics was developed by Irwin [7], based on the early papers of Inglis [6], Griffith [5], and Westergard [21]. Linear elastic fracture mechanics (LEFM), assuming a small plastic zone ahead of the crack tip, was first applied to paper material by Seth and Page [14], who measured fracture toughness of different paper materials. Swinehart and Broek [17] determined fracture toughness of paper using both the stress intensity factor and the strain energy release rate. They found that the measured crack length and fracture toughness were in a good agreement with the LEFM theory.

In this study, the product of critical buckling velocity and a safe time (longevity) will be taken as a maximized productivity function. We will evaluate analytically the performance criterion as a function of the applied tension and other problem parameters, and will study the problem of finding the optimal tension that maximizes the considered criterion.

2 Basic Relations and Formulation of the Optimization Problem

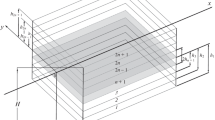
Consider an elastic web travelling at a constant velocity V 0 in the x direction and being simply supported by a system of rollers located at x=0,ℓ,2ℓ,3ℓ,… (Fig. 21.1). A rectangular element Ω i , i=1,2,3,…, of the web

$$ \varOmega_{i}=\bigl\{(x,y): i\ell\leq x\leq(i+1)\ell,\ -b \leq y \leq b\bigr\} $$
(21.1)

is considered in a Cartesian coordinate system, where ℓ and b are prescribed geometric parameters. Additionally, assume that the considered web is represented as an elastic plate having constant thickness h, the Poisson ratio ν, the Young modulus E, and bending rigidity D. The plate elements in (21.1) have small initial surface cracks (Fig. 21.1) of the length a with a given upper bound a 0, i.e.,

$$ 0<a\leq a_{0}, $$

and are subjected to homogeneous tension T, acting in the x direction.

Fig. 21.1
figure 1

Top: A travelling web having an initial crack, and being supported by a system of rollers. Bottom: A travelling web under cyclic tension, which is produced by the Earth’s gravity

Full size image

The sides of the plate element (i=1,2,3,…)

$$\varGamma_{\ell}= \{ x=0,\ -b\leq y\leq b \} \quad\text{and} \quad \varGamma_{r}= \{ x=\ell,\ -b\leq y\leq b \} $$

are simply supported, and the sides

$$\varGamma_{-}= \{ y=-b,\ 0\leq x\leq\ell\} \quad\text{and} \quad \varGamma_{+}= \{ y=b,\ 0\leq x\leq\ell\} $$

are free of traction.

Consider the following scenario where the web is moving under cyclic in-plane tension and fatigue crack growth is realized. Suppose that the web is subjected to a cyclic tension T that varies in the given limits

$$T_{\min}\leq T\leq T_{\max}, $$

where

$$T_{\min}=T_{0}-\Delta T, \qquad T_{\max}=T_{0}+ \Delta T. $$

Above ΔT>0 is a given parameter such that

$$ T_{0}-\Delta T>0 \quad\text{and} \quad\frac{\Delta T}{T_{0}} \ll1. $$
(21.2)

For one cycle, the tension increases from T=T min up to T=T max (the loading process) and then decreases from T=T max to T=T min (the unloading process). The loading and unloading processes are supposed to be quasistatic: the dynamical effects are excluded.

The cyclic tension T may be produced by different imperfections. One cause of cyclic tension could be elastic vibrations of the rollers resulting in small changes in the distance between the rollers. In this case, the number of tension cycles may be very large. Another cause of cyclic tension could be the Earth’s gravity [3] (see Fig. 21.1).

The product of the moving web velocity V 0 and the process time t f can be considered a productivity criterion (performance function), i.e.,

$$ J=m_0V_{0}t_{\mathrm{f}}, \quad m_0=2bm. $$
(21.3)

Here, m is the mass per unit area of the middle surface of the band. In (21.3), the velocity V 0 is taken from the safe interval

$$0<V_{0}<V_{0}^{\mathrm{cr}}, $$

where \(V_{0}^{\mathrm{cr}}\) is the critical buckling speed.

A safe interval for the safe functioning time (the number of cycles) is written as

$$0<t_{\mathrm{f}}<t_{\mathrm{f}}^{\mathrm{cr}} \quad\text{or} \quad 0<n<n^{\mathrm{cr}}, $$

where \(t_{\mathrm{f}}^{\mathrm{cr}}\) and n cr are, respectively, the time interval and the total number of cycles before fatigue fracture. For a small cycle time period τ and a big number of cycles n, we assume that t f=nτ (approximately). Note that the critical buckling velocity \(V_{0}^{\mathrm{cr}}\) and the critical functioning time \(t_{\mathrm{f}}^{\mathrm{cr}}\) (the critical number of cycles n cr) depend on the parameters of the average in-plane tension T 0, and the admissible variance ΔT, i.e.

$$V_{0}^{\mathrm{cr}}=V_{0}^{\mathrm{cr}}(T_{0}, \Delta T), \qquad t_{\mathrm{f}}^{\mathrm{cr}}=t_{\mathrm{f}}^{\mathrm {cr}}(T_{0}, \Delta T), \qquad n^{\mathrm{cr}}=n^{\mathrm{cr}}(T_{0},\Delta T). $$

Consequently, the maximum value of the productivity criterion for the given values T 0 and ΔT is evaluated as

$$J(T_{0},\Delta T) = m_0 V_{0}^{\mathrm{cr}}(T_{0}, \Delta T)t_{\mathrm{f}}^{\mathrm{cr}}(T_{0},\Delta T) =m_0 \tau V_{0}^{\mathrm{cr}}(T_{0},\Delta T)n^{\mathrm{cr}}(T_{0},\Delta T). $$

The optimal average (mean) in-plane tension T 0 is found from a solution of the following optimization problem:

$$ J^{*}=\max_{T_{0}} J(T_{0},\Delta T). $$
(21.4)

To solve the formulated optimization problem (21.4), we will use the explicit analytical expressions for the values \(V_{0}^{\mathrm{cr}}\) and n cr. The value of T 0, giving the maximal production J ∗, is denoted by \(T_{0}^{*}\).

3 Evaluation of the Web Longevity and the Critical Buckling Velocity

To evaluate n cr, let us apply the fatigue crack growth theory. Suppose that the web contains one initial crack of length a 0. The process of fatigue crack growth under cyclic tension (loading) can be described by the following equation [13] and the initial condition:

$$ \frac{\mathrm{d}a}{\mathrm{d}n}=C(\Delta K)^{k}, \quad(a)_{n=0} = a_{0}. $$
(21.5)

Here the variance ΔK of the stress intensity factor K is determined with the help of formulae

$$ \begin{gathered} \Delta K=K_{\max}-K_{\min}, \quad K_{\max}=\beta\sigma_{\max }\sqrt{\pi a}, \\ K_{\min} = \beta\sigma_{\min}\sqrt{\pi a}, \quad \sigma_{\max}=\frac{T_{\max}}{h}, \quad\sigma_{\min} = \frac{T_{\min}}{h}. \end{gathered} $$
(21.6)

In (21.5), C and k are material constants. In (21.6), h is the thickness of the web, n is the number of cycles, and σ max, K max, σ min and K min are, respectively, the maximum and minimum values of the stress σ and the stress intensity factor K in any given loading cycle. For the considered case, the surface crack geometric factor is β=1.12.

Using (21.5) and (21.6), we write the crack growth equation in the following form:

$$ \frac{\mathrm{d}a}{\mathrm{d} n}=C\kappa_{0}^{k}a^{k/2},\quad \kappa_{0}=\frac{2\beta\sqrt{\pi }}{h}\Delta T. $$
(21.7)

It follows from (21.7) and the initial condition in (21.5) that for considered values of the parameter k≠2, we will have

$$ n=A \biggl[\frac{1}{a_{0}^{(k-2)/2}}-\frac{1}{a^{(k-2)/2}} \biggr], \quad A= \frac{2}{(k-2)C\kappa_{0}^{k}}. $$
(21.8)

Take into account that the unstable crack growth is obtained after n=n cr cycles when the critical crack length a cr satisfies the limiting relation

$$(K_{\max})_{a=a_{\mathrm{cr}}}=K_{\mathrm{C}}, $$

or, in another form, we have

$$ \beta\frac{T_{\max}}{h}\sqrt{\pi a_{\mathrm{cr}}}=K_{\mathrm{C}}. $$
(21.9)

Note that σ max and T max (σ min and T min) are the maximum (minimum) stresses and tensions in the uncracked web, where the crack is located. Using (21.9) and the inequality ΔT/T 0≪1 in (21.2), we obtain

$$a_{\mathrm{cr}}=\frac{1}{\pi} \biggl(\frac{K_{\mathrm{C}}h}{\beta T_{\max}} \biggr)^{2}\approx\frac{1}{\pi} \biggl(\frac{K_{\mathrm{C}}h}{\beta T_{0}} \biggr)^{2} $$

and, by (21.8), we will have the following expression for the critical number of cycles:

$$ n^{\mathrm{cr}} = (n)_{a=a_{\mathrm{cr}}} = A \biggl[\frac {1}{a_{0}^{(k-2)/2}}- \biggl( \frac{\sqrt{\pi}\beta T_{0}}{K_{\mathrm{C}}h} \biggr)^{k-2} \biggr]. $$
(21.10)

From the condition of positiveness of the expression in (21.10), we find the maximum value of admissible tensions:

$$ T_{0}\leq\frac{1}{\sqrt{\pi a_{0}}}\frac{K_{\mathrm{C}}h}{\beta}\equiv T_{0}^{\mathrm{M}}. $$
(21.11)

In the special case k=2, we can find the critical number of cycles to be

$$ n^{\mathrm{cr}}=B \ln\biggl[\frac{1}{\pi a_{0}} \biggl(\frac{K_{\mathrm{C}}h}{\beta T_{0}} \biggr)^{2} \biggr], \quad B=\frac{1}{C\kappa_{0}^{2}}, $$
(21.12)

and the tension limit \(T_{0}^{\mathrm{M}}\) is expressed by (21.11).

The dependence of the critical number of cycles n cr on the average tension T 0 and the problem parameter k is shown in Fig. 21.2 using dimensionless quantities (defined below in (21.18) and (21.21)).

Fig. 21.2
figure 2

Dependence of the (dimensionless) critical number of cycles \(\tilde{n}^{\mathrm{cr}}\) on the (dimensionless) average tension \(\tilde{T}_{0}\) for different values of the Paris constant k

Full size image

Stationary equations describing the behaviour of the web with the applied boundary conditions form the following eigenvalue problem (a buckling problem):

$$ \everymath{\displaystyle} \begin{array}{rl@{\quad}l} \bigl(mV_{0}^{2}-T_{0} \bigr) \frac{\partial^{2}w}{\partial x^{2}} +D \biggl(\frac {\partial^{4}w}{\partial x^{4}} +2\frac{\partial^{4}w}{\partial x^{2}\partial y^{2}} + \frac{\partial^{4}w}{\partial y^{4}} \biggr) & =0, & \text{in } \varOmega, \\[12pt] w=0, \qquad\frac{\partial^{2}w}{\partial x^{2}} & =0, & \text{on } \varGamma_{\ell} \text{ and } \varGamma_{r}, \\[12pt] \frac{\partial^{2}w}{\partial y^{2}} +\nu\frac{\partial ^{2}w}{\partial x^{2}} & =0, & \text{on } \varGamma_{-} \text{ and } \varGamma_{+}, \\[12pt] \frac{\partial^{3}w}{\partial y^{3}}+(2-\nu)\frac{\partial^{3}w}{\partial x^{2}\partial y} & = 0, & \text{on } \varGamma_{-} \text{ and } \varGamma_{+}. \end{array} $$
(21.13)

Here D=Eh 3/(12(1−ν 2)), and m is the mass per unit area of the middle surface of the plate, and we denote the eigenvalue

$$\lambda=\gamma^{2}=\frac{\ell^{2}}{\pi^{2}D}\bigl(mV_{0}^{2}-T_{0} \bigr). $$

The critical instability (buckling mode) velocity of the travelling plate, as was shown by [2], is given by

$$ \bigl(V_{0}^{\mathrm{cr}}\bigr)^{2} = \frac{T_{0}}{m} + \frac{\gamma_{*}^{2}}{m}\frac{\pi^{2}D}{\ell^{2}}, $$
(21.14)

where \(\gamma_{*}^{2}=\lambda_{*}\) is the minimal eigenvalue of the problem (21.13). The parameter γ=γ ∗ is found as the root of the equation (see Fig. 21.3)

$$ \varPhi(\gamma,\mu)-\varPsi(\gamma,\nu)=0, $$
(21.15)

where

$$ \begin{gathered} \varPhi(\gamma,\mu)=\tanh\biggl(\frac{\sqrt {1-\gamma}}{\mu } \biggr)\coth\biggl(\frac{\sqrt{1+\gamma}}{\mu} \biggr), \\ \varPsi(\gamma,\nu)=\frac{\sqrt{1+\gamma}}{\sqrt{1-\gamma }}\frac{(\gamma+\nu-1)^{2}}{(\gamma-\nu+1)^{2}}, \quad\mu= \frac{\ell}{\pi b}. \end{gathered} $$
(21.16)
Fig. 21.3
figure 3

Behaviour of Φ and Ψ as functions of γ

Full size image

As it is seen from (21.15) and (21.16), the root γ=γ ∗ depends on ν and μ and does not depend on the other problem parameters, including the value of tension T 0. Consequently, the critical instability velocity, defined in (21.14), is increased with the increasing of tension T 0. However, the increasing of T 0 is limited due to initial damages and other imperfections.

4 Optimization and Performance Function

The most important factor for runnability and stability of moving bands, containing initial imperfections, is the applied tension. To find a safe and optimal T 0 maximizing the performance function is our considered problem. To perform this task, let us represent the optimized functional (21.3) as a function of the average tension T 0. If we take into account explicit expressions for n cr, in (21.10), and for \(V_{0}^{\mathrm{cr}}\), in (21.14), use (21.3), and perform necessary algebraic transformations, assuming that k≠2, we will have

$$J(T_{0}) = m_0\tau V_{0}^{\mathrm{cr}}(T_{0})n^{\mathrm{cr}}(T_{0}) = J_{0} \biggl[1+\frac{1}{D} \biggl(\frac{\ell}{\gamma_{*}\pi} \biggr)^{2}T_{0} \biggr]^{1/2} \biggl[1- \biggl( \frac{\beta\sqrt{\pi a_{0}}}{hK_{\mathrm{C}}}T_{0} \biggr)^{k-2} \biggr], $$

where

$$ J_{0}=\frac{4b\tau\pi a_0\gamma_{*}\sqrt{D m}}{(k-2)C\ell} \biggl(\frac{h}{2\beta\Delta T\sqrt{\pi a_0}} \biggr)^{k}. $$
(21.17)

The performance function J is proportional to the multiplier J 0 and, consequently, the optimized tension T 0 does not depend on this parameter.

For convenience of the following estimations and reduction of characteristic parameters, we introduce the dimensionless values

$$ \tilde{J} = \frac{J}{J_{0}}, \qquad\tilde{T}_{0} = \frac{T_{0}}{T_{0}^{\mathrm{M}}} = \frac{\beta\sqrt{\pi a_{0}}}{K_{\mathrm{C}}h}T_{0}, \qquad g= \frac{K_{\mathrm{C}}h}{\beta D\sqrt{\pi a_{0}}} \biggl(\frac{\ell}{\gamma_{*}\pi} \biggr)^{2}, $$
(21.18)

and represent the optimized functional and the interval of optimization as

$$ \tilde{J}(\tilde{T}_{0}) = (1+g\tilde{T}_{0} )^{1/2} \bigl(1-\tilde{T}_{0}^{k-2} \bigr), \quad k>2 $$
(21.19)

with

$$ 0<\tilde{T}_{0}<1. $$
(21.20)

In other words,

$$\tilde{J}(\tilde{T}_{0}) = \tilde{V}_{0}^{\mathrm{cr}}( \tilde{T}_{0})\,\tilde{n}^{\mathrm{cr}}(\tilde{T}_{0}) $$

with

$$ \tilde{V}_{0}^{\mathrm{cr}}(\tilde{T}_{0}) = (1+g \tilde{T}_{0} )^{1/2} \quad\text{and} \quad \tilde{n}^{\mathrm{cr}}(\tilde{T}_{0}) = 1-\tilde{T}_{0}^{k-2}. $$
(21.21)

In the special case k=2, we will use the expressions (21.3), (21.12) and (21.14) and perform algebraic transformations. We will have

$$J(T_{0}) = m_0\tau V_{0}^{\mathrm{cr}}(T_{0})n^{\mathrm{cr}}(T_{0}) = J_{1} \biggl[1 +\frac{1}{D} \biggl(\frac{\ell}{\gamma_{*}\pi} \biggr)^{2}T_{0} \biggr]^{1/2} \ln\biggl( \frac{hK_{\mathrm{C}}}{\beta\sqrt{\pi a_{0}}}\frac{1}{T_{0}} \biggr) $$

with

$$J_{1}=\frac{4b\tau\pi\gamma_{*}\sqrt{D m}}{C\ell} \biggl(\frac{h}{2\beta\Delta T\sqrt{\pi}} \biggr)^{2}. $$

Using the dimensionless values \(\tilde{J}=J/J_{1}\) and \(\tilde{T}_{0}\), g from (21.18), we find

$$ \tilde{J}(\tilde{T}_{0}) = \ln\biggl(\frac{1}{\tilde{T}_{0}} \biggr) (1 +g\tilde{T}_{0} )^{1/2}, \quad0<\tilde{T}_{0}<1. $$
(21.22)

It is seen from (21.22) that

$$ 0=(\tilde{J})_{\tilde{T}_{0}=1}\leq\tilde{J}(\tilde{T}_{0})\leq( \tilde{J})_{\tilde{T}_{0}=0} = \infty, \quad0<\tilde{T}_{0}<1. $$
(21.23)

Note that (21.23) also holds in the case k<2, when

$$\tilde{J}(\tilde{T}_{0})={-}(1+g\tilde{T}_{0} )^{1/2} \bigl(1-\tilde{T}_{0}^{k-2} \bigr) $$

and

$$J_{0}=\frac{4b\tau\pi a_{0}\gamma_{*}\sqrt{D m}}{(2-k)C\ell} \biggl(\frac{h}{2\beta\Delta T\sqrt{\pi a_{0}}} \biggr)^{k}. $$

Thus, in the case k≤2, the optimum is \(\tilde{T}_{0}=0\), meaning that the model omits the effect of the critical speed. However, for most materials k≈3 or bigger.

5 Results and Discussion

The optimization problem (21.19)–(21.20) was solved numerically for different values of k: for k=2.5, k=3, and k=3.5. The material parameters were chosen to describe a paper material. Young’s modulus was E=109 Pa, the Poisson ratio was ν=0.3, the mass per unit area was m=0.08 kg/m2, and the strain energy rate over density was G C/ρ=10 J m/kg. The size of the rectangular element (Ω i ) was ℓ×2b=0.1 m×10 m, and the surface crack geometric factor was β=1.12. The material constants in (21.5) were k=2.5, 3, 3.5, and C=10−14. Paper fracture toughness K C was calculated from the relation \(G_{\mathrm{C}}=K_{\mathrm{C}}^{2}/E\) [7]. The variance in tension was chosen to be small, ΔT=0.1 N/m. The investigated values of initial crack lengths were a 0=0.005 m, 0.01 m,0.05 m, 0.1 m. As illustrated in Fig. 21.1, the length of one cycle was assumed to be 2ℓ. This value was used to approximate the cycle time period τ by \(\tau=2\ell/V_{0}^{\mathrm{cr}}\) after the value of \(V_{0}^{\mathrm{cr}}\) was evaluated by the optimization.

In Fig. 21.4, the dimensionless performance function (21.19) is plotted for k=2.5, 3, 3.5. It is seen that the value of optimal tension \(\tilde{T}_{0}^{*}\) is increased with increasing the value of k.

Fig. 21.4
figure 4

Performance (\(\tilde{J}\)) dependence on tension (\(\tilde {T}_{0}\)) (dimensionless quantities)

Full size image

In Tables 21.1 and 21.2, the results of the non-dimensional optimization problem (21.19)–(21.20) are shown for the considered values of the parameters k and a 0. In Table 21.1, the values of the productivity function \(\tilde{J}\) at the optimum are shown. It can be noted that an increase in the length of the initial crack a 0 decreases productivity. The values of productivity seem to increase when k is increased. However, one must take into account that also J 0, in (21.17), depends on k, which affects the actual productivity \(J=J_{0}\tilde{J}\). In Table 21.2, the optimal values of the dimensionless tension \(\tilde{T}_{0}^{*}\) are shown. It is seen that the dimensionless tension values slightly decrease when the crack size is increased.

Table 21.1 Dependence of the optimum of \(\tilde{J}\) (performance) on the parameters k (Paris constant) and a 0 (m, initial crack length)
Full size table
Table 21.2 Dependence of the optimal tension \(\tilde{T}_{0}^{*}\) on the parameters k (Paris constant) and a 0 (m, initial crack length)
Full size table

Since the actual optimal productivity, the actual tension, and the related critical speed and the critical number of cycles are of interest, these values were found at the optimum and are shown in Tables 21.3 and 21.4. Note that several assumptions have been made. Firstly, the Paris constant C=10−14 is assumed to be independent of k, and both of the values are not measured for paper but were chosen to be close to the typical values of some known materials. Secondly, the cycle time period τ is approximated assuming that one cycle length is 2ℓ, and using the relation, \(\tau=2\ell/V_{0}^{\mathrm{cr}}\).

Table 21.3 Left: Dependence of the optimal tension \(T_{0}^{*}\) (N/m) on the parameters k (Paris constant) and a 0 (m, initial crack length). Right: Critical velocity \(V_{0}^{\mathrm{cr}}\) (m/s) at the optimum, depending on the parameters k and a 0
Full size table
Table 21.4 Left: Dependence of the optimum of J (kg, performance) on the parameters k (Paris constant) and a 0 (m, initial crack length). Right: The number of cycles n cr at the optimum, depending on the parameters k and a 0
Full size table

The actual optimal tension \(T_{0}^{*}\) is calculated from (21.18), that is \(T_{0}^{*}=T_{0}^{\mathrm{M}}\tilde{T}_{0}^{*}\). Since \(T_{0}^{\mathrm{M}}\) only depends on fixed values, and the material parameters in \(T_{0}^{\mathrm{M}}\) are measured and known for paper material, the results for the actual optimal tension, shown in Table 21.3 (left), are comparable and quite reliable. The results for the optimal tension \(T_{0}^{*}\) are also illustrated as a colorsheet in Fig. 21.5.

Fig. 21.5
figure 5

A colorsheet showing the dependence of the optimal tension \(T_{0}^{*}\) (N/m) on the parameters k (Paris constant) and a 0 (m, initial crack length). Note the logarithmic scale of a 0

Full size image

In Table 21.3 (right), the critical velocities corresponding to the optimal values of tension \(V_{0}^{\mathrm{cr}}(T_{0}^{*})\) are shown. The values of velocities can be calculated directly from (21.14) using the values in Table 21.3 (left). As expected, the velocities decrease as a 0 is increased.

The actual optimal number of cycles \(n^{\mathrm{cr}}(T_{0}^{*})\) and the actual optimal productivity J ∗ are more difficult to predict, since they depend on the Paris constant C, which is not known for paper materials. As mentioned above, the same value of C, C=10−14, is used for all investigated values of k, which may not be reasonable. Since the value of κ 0 defined in (21.7) is big (in this case ΔT>h), then \(\kappa_{0}^{k}\) increases with the increase in k. Keeping C constant, we see from (21.7) that the crack growth rate may be bigger with a bigger value of k depending on the value of a k/2, which is small. This means that the number of cycles may be the smaller the greater the value of k is, which can also be seen from (21.8): the greater the value of k, the smaller the value of A. In the results in Table 21.4 (right), it can be seen that the effect of κ 0 is big, and the number of cycles at the optimum decreases remarkably when k is increased. This also results in a decrease in the optimal productivity J ∗, which is shown in Table 21.4 (left).

Comparing the results in Tables 21.1 and 21.4 (left), we therefore make no conclusion about the effect of k on the actual performance J ∗. The qualitative result of the decrease in the performance J ∗ when a 0 is increased is, however, reported.

6 Conclusion

In this study, the problems of safety analysis and optimization of a moving elastic web travelling between two rollers at a constant axial velocity were investigated. Instability of the web (transverse buckling) and its fatigue crack growth under a cyclic in-plane tension were included in the study. The expressions for the critical buckling velocity and the number of cycles before the fracture (longevity of the web) as a function of in-plane tension and other problem parameters were used to formulate analytically an optimization problem, in which the productivity was maximized. The optimal tension maximizing the productivity function was found.

The optimal values of tension seemed to be very sensitive to the length of the initial crack. It was found that the greater the initial crack, the smaller the optimal tension and, consequently, the smaller the maximal productivity.

It should be noted that the critical velocity of the (paper) web was considered in vacuum, and the effects of the surrounding fluid were excluded in this study, and remain as topics for future research. Thus, the results are to be interpreted as approximate.