Optimization of Axially Moving Layered Web

Abstract

The stability analysis and optimization of elastic web travelling between two rollers with a constant velocity are presented. The mathematical model for a layered travelling web (continuous isotropic composite plate) is developed restricting the consideration to one open draw. The layered plate with various mechanical properties of layers is considered and analytical expressions for the effective characteristics are derived. As a result the composed structure can be considered as an isotropic homogeneous plate and the obtained formulas for computation of critical velocity can be applied. Then the isoperimetric optimization problem is formulated and studied. The total mass of the layered plate is considered as an isoperimetric condition. The critical divergence velocity is taken as an optimized quality criterion. To this end consisted in maximization of the web stability and for maximization of the divergence velocity with respect to material distribution, the evolutionary optimization method (genetic algorithm) is applied. The number of materials is supposed to be given. Applying the genetic algorithm these materials are distributed on the plate thickness (provide the optimal plate consisted of some layers of different thickness) and the critical velocity is maximized under the constraint on the total mass of the structure. Numerical results are presented for different sets of problem parameters.

1 Introduction

Travelling flexible strings, membranes, beams and plates are the most common models of axially moving continua [1]. Previous studies of these models described by the second and fourth order differential equations focus on aspects of free vibration including the nature of wave propagation in moving media and the effects of axial motion on the frequency spectrum and eigenfunctions. It has been shown that the natural frequency of each mode decreases when transport speed increases and that the travelling string, beam, panel and plate will experience divergence instability at a sufficiently high speed (see, for example, [1, 2]).

This work concentrates on stability analysis and optimization of elastic web travelling between two rollers with a constant velocity. We present a model for a layered travelling web (continuous isotropic composite plate) restricting the consideration to one open draw. The web is mechanically simply supported at the inflow and outflow ends of the span, with the rest boundaries of the span unsupported. The considered part of the layered web is effectively isotropic, homogeneous and occupies the domain having a rectangular shape in plan. The web is symmetrically composed with respect to a middle plane and is consisted of elastic layers characterized by some important parameters (mass per unit area, Young modular, Poisson ratio and distances from the middle plane).

In this study we consider the layered plate with various mechanical properties of layers and derive analytical expressions for the effective characteristics. As a result we can consider the composed structure as an isotropic homogeneous plate and apply the obtained formulas for computation of critical velocity. Then the isoperimetric optimization problem is formulated and studied. As an isoperimetric condition it is considered the total mass of the layered plate. The critical divergence velocity is taken as an optimized quality criterion.

To this end consisted in maximization of the web stability and for maximization of the divergence velocity with respect to material distribution, we apply the evolutionary optimization method (genetic algorithm) [3, 4]. This algorithm was developed in [4] and effectively applied with some modifications in [5, 6] for layered structures. The number of materials is supposed to be given. Applying the genetic algorithm we distribute these materials on the plate thickness (provide the optimal plate consisted of some layers of different thickness) and maximize the critical velocity under the constraint on the total mass of the structure. Numerical results are presented for different sets of problem parameters. It is noted that the considered problem and applied approach can be generalized and also used for the cases with incomplete data concerning the properties of materials [7].

2 Problem Formulation

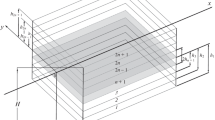
In this paper we present a model for a layered travelling web (continuous isotropic composite plate), restricting the consideration to one open draw. The web is mechanically simply supported at the inflow ($x = 0$) and outflow ($x = l$) ends of the span, with the rest of boundaries of the span unsupported ($y = b$ and $y = - b$). The considered part of the layered web is effectively isotropic and occupies the region $\varOmega = \{ (x,y,z):$ $0 < x < l, - b < y < b, - H/2 < z < H/2\}$ in the rectangular global coordinate system x, y, z. The web is travelling at a constant velocity $V_{0}$ in the x-direction. The length l, the width 2b, the total thickness H, and the velocity $V_{0}$ of the web are the given positive numbers. The web is symmetrically composed with respect to a middle plane and consisted of $2n + 1$ odd number elastic layers characterized by mass per unit area $m_{i}$, Young’s modulus $E_{i}$, Poisson’s ratio $\nu_{i}$ and distances $h_{i}$ from the middle plane. Extreme layers have number of 1 and $2n + 1$ (see Fig. 1).

Fig. 1.

Layers.

Taking into account the stacking symmetry with respect to middle plane ($z = 0$) and that the layers are pasting together we obtain the plate with the following effective bending rigidity $D^{ef}$, Poisson’s ratio $\nu^{ef}$, and mass per unit area $m^{ef}$

$$ D^{ef} = \frac{2}{3}\left[ {\frac{{E_{n + 1} h_{n + 1}^{3} }}{{1 - \nu_{n + 1}^{2} }} + \sum\limits_{i = 1}^{n} {\frac{{E_{i} }}{{1 - \nu_{i}^{2} }}\left( {h_{i}^{3} - h_{i + 1}^{3} } \right)} } \right] $$

(1)

$$ \nu^{ef} = \frac{2}{{3D^{ef} }}\left[ {\frac{{E_{n + 1} \nu_{n + 1} h_{n + 1}^{3} }}{{1 - \nu_{n + 1}^{2} }} + \sum\limits_{i = 1}^{n} {\frac{{E_{i} \nu_{i} }}{{1 - \nu_{i}^{2} }}\left( {h_{i}^{3} - h_{i + 1}^{3} } \right)} } \right] $$

(2)

$$ m^{ef} = m_{n + 1} + 2\sum\limits_{i = 1}^{n} {m_{i} } $$

(3)

The dynamical out-of-plane mechanical behavior of the moving homogeneous isotropic web is described by the following differential equations and boundary conditions ($\Delta^{2}$ is a biharmonic operator)

$$ m\left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2V_{0} \frac{{\partial^{2} w}}{\partial x\partial t} + V_{0}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) - T_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }} + D\Delta^{2} w = 0 $$

(4)

$$ \left( w \right)_{x = 0,l} \, = \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)_{x = 0,l} \, = 0, - b \le y \le b $$

(5)

$$ \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)_{y = \pm b} = \left( {\frac{{\partial^{3} w}}{{\partial y^{3} }} + \left( {2 - \nu } \right)\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}} \right)_{y = \pm b} = 0,0 \le x \le l $$

(6)

Here the transverse (out-of-plane) displacement of the web is denoted by the function $w = w\left( {x,y,t} \right)$ and the mechanical constant tension, applied at the web ends $(x = 0,l)$ is denoted by $T_{0}$.

In the case of homogeneous isotropic moving web with parameters m, D, $\nu$ the explicit expression has been found for the critical divergence (instability) velocity $V_{0}^{div}$ [1]. This expression can be also used for the considered effective layered homogeneous and isotropic web movement described by the presented boundary value problem. Assuming $m = m^{ef}$, $D = D^{ef}$, $\nu = \nu^{ef}$ we will have

$$ \left( {V_{0}^{div} } \right)^{2} = \frac{{T_{0} }}{{m^{ef} }} + \frac{{\gamma_{ * }^{2} \pi^{2} D^{ef} }}{{m^{ef} l^{2} }} $$

(7)

where constant $\gamma_{ * }$ is a root of the following transcendental equation

$$ \begin{aligned}\Phi \left( {\gamma ,\mu } \right) -\Psi \left( {\gamma ,\nu^{ef} } \right) = 0 \\\Phi \equiv \tanh \left( {\frac{{\sqrt {1 - \gamma } }}{\mu }} \right)\coth \left( {\frac{{\sqrt {1 + \gamma } }}{\mu }} \right) \\\Psi \equiv \frac{{\sqrt {1 +\upgamma} \left( {\upgamma +\upnu^{ef} - 1} \right)^{2} }}{{\sqrt {1 -\upgamma} \left( {\upgamma -\upnu^{ef} + 1} \right)^{2} }},\upmu = \frac{l}{\pi b} \\ \end{aligned} $$

(8)

Thus, for each layered web with symmetrical internal structure and given parameters $m_{i}$, $E_{i}$, $\upnu_{i}$ ($i = 1,2, \ldots ,n + 1$) we can obtain the values $m^{ef}$, $D^{ef}$, $\upnu^{ef}$ and consequently to determine the critical divergence velocity $V_{0}^{div}$ using to this end the presented expression. Using the expression for $V_{0}^{div}$ we will consider the following optimization problem consisted in maximization of the web stability, i.e. maximization of $V_{0}^{div}$ by means of the layers variation. To this end it is convenient to use natural parametrization.

Taking into account that each of the given materials can be enumerated with one parameter, we apply natural parametrization using the scalar variable t that takes given values $t_{1}$, $t_{2}$, …, $t_{s}$,…, $t_{r}$, i.e.

$$ t \in \left\{ {t_{1} ,t_{2} , \ldots ,t_{s} , \ldots ,t_{r} } \right\} $$

If the layers are characterized by Young’s modulus E, Poissons’s ratio $\nu$, mass per unit area m then

$$ E_{s} = E\left( {t_{s} } \right),\nu_{s} = \nu \left( {t_{s} } \right),m_{s} = m\left( {t_{s} } \right) $$

Thus the layered optimized plate consists of discrete set of layers (materials), distributed along the z-axis and characterized by the set of parameters $\left\{ {E_{s} ,\nu_{s} ,m_{s} } \right\}$, $s = 1,2, \ldots ,r$. Distribution of the parameters ($E(z)$, $\nu (z)$, $m(z)$) along the web depth are given by piece-wise constant functions defined of the segment $0 \le z \le H/2$. For each point $z \in \left[ {0,H/2} \right]$ these functions take some values from given finite set, i.e. $E\left( z \right) \in \left\{ {E_{s} } \right\}$, $\nu \left( z \right) \in \left\{ {\nu_{s} } \right\}$, $m\left( z \right) \in \left\{ {m_{s} } \right\}$, $s = 1,2, \ldots ,r$.

In what follows, we apply discussed parametrization (Fig. 2) of the essential parameters using the piece-wise constant function $t = t(z)$ ($z \in \left[ {0,H/2} \right]$) taking the value $t = t_{s} = s$ from the given set, i.e. $t \in \left\{ {t_{s} = s} \right\}$ and such as the following equalities are satisfied:

Fig. 2.

Piece-wise constant distribution of material properties.

$$ E_{s} = E\left( {t\left( z \right)} \right)_{{t = t_{s} = s}} ,\upnu_{s} =\upnu\left( {t\left( z \right)} \right)_{{t = t_{s} = s}} ,m_{s} = m\left( {t\left( z \right)} \right)_{{t = t_{s} = s}} $$

(9)

3 Problem of Optimization

Using this representation we consider the problem of maximization of critical divergence function $V_{0}^{div}$ (or $\left( {V_{0}^{div} } \right)^{2}$) with a mass constraint

$$ \left( {V_{0}^{div} } \right)_{ * } = \mathop {\hbox{max} }\limits_{t} V_{0}^{div} \left( {t\left( z \right)} \right) $$

(10)

$$ m^{ef} = m^{ef} \left( {t\left( z \right)} \right) \le M_{0} $$

(11)

$$ t\left( z \right) \in \left\{ {t_{s} } \right\}:z_{i - 1} < z < z_{i} ,\quad i = 1,2, \ldots ,n + 1,s = 1,2, \ldots ,r,z_{1} = H/2,z_{n + 1} = 0 $$

(12)

where $M_{0} > 0$ is a given constant.

To solve the optimization problem (10)–(12) in general case, i.e. taking into account the isoperimetric inequality (11), let us apply the approach (method of penalty function), based on maximization of the augmented functional $J^{a}$ defined by the formulae

$$ J^{a} = V_{0}^{div} - \lambda \left( {m^{ef} - M_{0} } \right) $$

(13)

$$ \begin{aligned} \lambda = 0,{\text{if }}\left( {m^{ef} - M_{0} } \right) \le 0 \hfill \\ \lambda = \lambda_{0} > 0,{\text{ otherwise}} \hfill \\ \end{aligned} $$

(14)

where $\lambda_{0}$ is a positive penalty multiplier.

4 Genetic Algorithm

Solution of the problem of the functional $J^{a}$ (13) maximization for the various values of the problem parameters $M_{0}$, H, $T_{0}$ and material characteristics presented in Table 1 is performed with the help of a genetic algorithm [3, 4].

Table 1. Characteristics of materials.

We apply this algorithm of global optimization to overcome the complexity caused by local extremums arising in the considered problem. It is supposed that the interval $\left[ {0,H/2} \right]$ of the variable z is divided by the points $z_{i} ,i = 0,2, \ldots ,n + 1$ into $n + 1$ subintervals. For each i-subinterval ($i = 1, \ldots ,n + 1$) the values E, $\nu$, m can take the constant values corresponding to the chosen materials.

The index of the material can take the values form 1 to 3. Population under consideration consists of N individuals represented admissible piece-wise homogeneous webs. The number N is supposed to be even and kept constant in the population renewal process. Each j-individual of the population is described by the set of values $t\left( {j,i} \right)$ representing the design variables at a node. The “best” individual, i.e. the set $t_{ * } \left( {j,i} \right)$ maximizing the augmented functional, is sought by using the genetic algorithm.

The first step of algorithm consist in initialization of the population, that is assigning random values taken from $\left[ {1,2,3} \right]$ to all elements $t\left( {j,i} \right),i = 1, \ldots ,n + 1$. For all created individuals ($j = 1,2, \ldots ,N$) of the initial population we compute the augmented functional $J^{a} \left( j \right)$ and find the individuals having the maximal value of the functional. Using the initial data and the next step of the algorithm, it is possible to determine a new population consisting of N individuals, and so to successively maximize the functional $J^{a}$.

At the second step of the algorithm we select N/2 individual pairs, “parents”, to obtain N/2 pairs of individuals, “children”, which constitute new population. Selection of the first parent (“a”) is performed by a following manner. Some natural number N^T is chosen and then N^T individuals are selected randomly. From this set of individuals we preserve and use only one individual having the maximal value of augmented functional $J^{a}$. Similarly we find the second parent (“b”) and put together the first pair of individuals. All together we choose N/2 such pairs.

The third step of algorithm consists in obtaining of two children from each pair of parents. For this purpose we generate some random value $p_{r}$ from interval $[0,1]$ and a random natural number $n_{r}$ from $\left[ {1,2, \ldots ,n + 1} \right]$. If $p_{r} \le p_{co}$ ($p_{co}$ is the crossover probability, given constant value) then the values of design variables of children at the nodes $\left[ {1,2, \ldots ,n_{r} } \right]$ are copied from their parents “a” and “b”, but the meaning of these values at the nodes $\left[ {n_{r} + 1, \ldots ,n + 1} \right]$ are obtained with the help of crossover. The latter means that for child “a” we copy the values in the corresponding nodes of the parent “b” and vice versa.

Successive sorting of all parent pairs and performing of described operations lead to N individuals (children), that compose the new population.

The fourth step of the algorithm consists in mutation of the new population. This step is necessary to avoid staying at the local maximum of the functional. To realize the mutation procedure we take some small (~0.005) parameter $p_{m}$ (probability of mutation). Then for all nodes of each individual of the population we generate a random number $p_{r}$ from interval $\left[ {0,1} \right]$. If $p_{r} \le p_{m}$ then the value of design variable at this node is replaced by the arbitrary value satisfying given constraint. For the next population, we compute the functionals $J^{a} \left( j \right)$ and select the best individual. Then we go to the second step of applied algorithm. Note that if the best child from the new population is worse than the best parent from the previous population then we replace it by this parent. This makes the process of finding of global maximum a monotonic one.

The optimal distribution of material $t\left( z \right)$ was determined with the help of the genetic algorithm. Here the parameters of computational process were taken as $n = 10$, $N = 10$, $N^{T} = 4$, $p_{co} = 0.5$, $p_{m} = 0.05$. Calculations were completed after 500 generations. Characteristics of materials considered as admissible for optimal design of the non-homogeneous isotropic layered web are presented in Table 1.

The results of numerical solution for the case of $\lambda = 0$ (no constraint on $m^{ef}$) and for the cases when $M_{0} = 430;420;410$ (g/m²) are presented in Fig. 3 (variants a–d) for the following problem parameters: $l = 1.2$ m, $b = 0.47$ m, $T_{0} = 16$ N/m, $H = 10^{ - 3}$ m. Material 1 is shown by white color, material 2 and material 3 are shown by red and blue colors respectively.

Fig. 3.

Material distributions.

The dependence of the constant $\gamma_{ * }$ on the Poisson’s ratio $\nu^{ef}$ for considered problem parameters is presented in Fig. 4.

Fig. 4.

The dependence of the constant $\gamma_{ * }$ on the Poisson’s ratio $\upnu^{ef}$.

5 Appendix

The calculus of effective moduli $D^{ef}$, $\nu^{ef}$, and $m^{ef}$ has been performed in the paper with the help of the formulas (1)–(3). The formula (3) for effective mass $m^{ef}$ per unit area of the layered web is obtained by direct summation of the corresponding masses (the summation is taken over $2n + 1$ layers).

Let us derive more complicated formulas (1) and (2) for effective bending rigidity $D^{ef}$ and effective Poissons’s ratio $\nu^{ef}$ of the considered non-homogeneous layered web. To this end we apply the formulas for stresses and strains and will use the expression for bending moment

$$ \int\limits_{ - H/2}^{H/2} {\sigma_{x} zdz = \left( {\int\limits_{ - H/2}^{H/2} {\frac{{z^{2} E\left( z \right)dz}}{{1 - \left( {\nu \left( z \right)} \right)^{2} }}} } \right)} \frac{{\partial^{2} w}}{{\partial x^{2} }} = D^{ef} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) $$

(15)

Taking into account the symmetry of internal web structure, i.e.

$$ E\left( z \right) = E\left( { - z} \right),\nu \left( z \right) = \nu \left( { - z} \right) $$

(16)

we find the expression for effective bending rigidity in the form

$$ D^{ef} = 2\int\limits_{0}^{H/2} {\frac{{z^{2} E\left( z \right)}}{{1 - \left( {\nu \left( z \right)} \right)^{2} }}dz} $$

(17)

Using mechanical and geometric characteristics of the web layers $E_{i}$, $\nu_{i}$, $h_{i}$ we evaluate the integral in (17). We will have the following formula

$$ D^{ef} = \frac{2}{3}\frac{{E_{n + 1} }}{{1 - \nu_{n + 1}^{2} }}h_{n + 1}^{3} + \frac{2}{3}\sum\limits_{i = 1}^{n} {\frac{{E_{i} }}{{1 - \nu_{i}^{2} }}\left( {h_{i}^{3} - h_{i + 1}^{3} } \right)} $$

(18)

that coincides with (1).

In analogous manner we derive the formula for effective Poisson’s ratio of non-homogeneous isotropic layered web. Thus, we obtain

$$ \upnu^{ef} = \frac{2}{{D^{ef} }}\int\limits_{0}^{H/2} {\frac{{z^{2}\upnu\left( z \right)E\left( z \right)}}{{1 - \left( {\upnu\left( z \right)} \right)^{2} }}dz} = \frac{2}{{D^{ef} }}\left[ {\frac{{\upnu_{n + 1} E_{n + 1} h_{n + 1}^{3} }}{{1 -\upnu_{n + 1}^{2} }} + \sum\limits_{i = 1}^{n} {\frac{{E_{i}\upnu_{i} }}{{1 -\upnu_{i}^{2} }}\left( {h_{i}^{3} - h_{i + 1}^{3} } \right)} } \right] $$

(19)

that coincides with (2).