Keywords

1 Introduction

We construct and investigate iteration methods for the finite dimensional constrained saddle point problem

(2.1)

where \(f\in\mathbb{R}^{N_{x}}\) and \(g\in\mathbb{R}^{N_{\lambda}}\) are given vectors, and the following assumptions hold:

  1. (A1)

    Operator \(A:\mathbb {R}^{N_{x}}\rightarrow \mathbb {R}^{N_{x}}\) is continuous, strictly monotone and coercive;

  2. (A2)

    \(C\in \mathbb {R}^{N_{\lambda}\times N_{x}}\), N λ ≤N x , is a full rank matrix: \(\operatorname {rank}C = N_{\lambda}\);

  3. (A3)

    P=∂Φ, Q=∂Ψ, where \(\varPhi: \mathbb {R}^{N_{x}} \rightarrow\bar{\mathbb {R}}\) and \(\varPsi: \mathbb {R}^{N_{\lambda}} \rightarrow \bar{\mathbb {R}}\) are proper, convex and lower semi-continuous functions.

Different particular cases of the problem (2.1) arise if grid approximations (finite difference, finite element, etc.) are used to approximate variational inequalities or optimal control problems. Specifically, introducing the dual variables to the grid approximations of the variational inequalities with constraints for the gradient of a solution leads to (2.1) with Q=0. Approximations of the control problems with control function in the right-hand side of a linear differential equation or in the boundary conditions give rise to the saddle point problem (2.1) with Q=0 and linear A. Finally, we note that mixed and hybrid finite element schemes for the 2-nd order variational inequalities with pointwise constraints to the solution imply (2.1) with P=0.

The solution methods for large-scale unconstrained saddle point problems are thoroughly investigated. The state-of-the-art for this problem can be found in the survey paper [1] and in the book [6]. Constrained saddle point problems arising from the Lagrangian approach for solving variational inequalities in mechanics and physics are considered in [8–10] (see also the bibliography therein). Namely, the convergence of Uzawa-type, Arrow-Hurwitz-type, and operator-splitting iterative methods are investigated in these books.

The development of the efficient numerical methods designed to solve state-constrained optimal control problems represents severe numerical challenges. The construction of the effective iterative solution methods for them is an actual problem. The achievements in this field during the past two decades are reported in the book [5] and the articles [2–4, 11–15, 21]. The augmented Lagrangian method as well as regularization and penalty methods have been investigated for particular classes of the state-constrained optimal control problems. Adjustment schemes for the regularization parameter of a Moreau–Yosida-based regularization and for the relaxation parameter of interior point approaches to the numerical solution of pointwise state constrained elliptic optimal control problems have been constructed. Lavrentiev regularization has been applied to transform the state constraints to the mixed control-state constraints in the linear-quadratic elliptic control problem with pointwise constraints on the state. The interior point methods and the primal-dual active set strategy have been applied to the transformed problem.

In this article, we prove convergence of the iterative solution methods for the saddle point problem (2.1). The sufficient conditions of convergence for the iterative methods are presented in the form of matrix inequalities and give rise to constructing appropriate preconditioners and allow choosing the iterative parameter. Applications of the general convergence results to sample examples of the variational inequalities and optimal control problems, as well as several numerical results, are included. The results of this article are founded in the previous papers [16–19] by the authors.

2 Iterative Methods for the Saddle-Point Problem

2.1 Existence of the Solutions

Consider the problem (2.1) and suppose that it has a nonempty set of solutions X={(x,λ)}. Below we present the existence results for the cases P=0 or Q=0, which are mostly interesting for the applications included in the article. Note that the assumptions (A1)–(A3) ensure the uniqueness of the component x.

Lemma 2.1

Let the assumptions (A1)–(A3) be fulfilled and P=0. Let also the operator A be uniformly monotone, i.e.,

$$ (Ax-Ay,x-y)\ge \alpha\|x-y \|_{A_0}^2\quad\alpha>0, \\ $$
(2.2)

and Lipshitz-continuous

$$ \|Ax-Ay\|_{A_0^{-1}}\le \beta\|x-y\|_{A_0} $$
(2.3)

with a symmetric and positive definite matrix \(A_{0}\in\mathbb{R}^{N_{x}\times N_{x}}\). Then, the problem (2.1) has a unique solution (x,λ).

Lemma 2.2

([17])

Let the assumptions (A1)–(A3) be fulfilled, Q=0, and

$$\operatorname {int}\operatorname {dom}\varPhi\cap\bigl\{x\in\mathbb{R}^{N_x}:\, Cx=g\bigr\}\neq \emptyset. $$

Then, the problem (2.1) has a nonempty set of solutions X={(x,λ)} with a uniquely defined component x.

2.2 Iteration Methods

We consider two iteration methods for solving (2.1): a preconditioned Uzawa-type method

$$ \begin{aligned} Ax^{k+1}+P \bigl(x^{k+1}\bigr)-C^T \lambda^k & \ni f, \\ \frac{1}{\tau}B_{\lambda}\bigl(\lambda^{k+1} - \lambda^k \bigr) +Q\bigl(\lambda^{k+1}\bigr)+Cx^{k+1} & \ni g \end{aligned} $$
(2.4)

and a preconditioned Arrow-Hurwitz-type method

$$ \begin{aligned} \frac{1}{\tau}B_{x} \bigl(x^{k+1} - x^k\bigr)+Ax^{k}+P \bigl(x^{k+1}\bigr)-C^T \lambda^k & \ni f, \\ \frac{1}{\tau}B_{\lambda}\bigl(\lambda^{k+1} - \lambda^k \bigr) +Q\bigl(\lambda^{k+1}\bigr)+Cx^{k+1} & \ni g. \end{aligned} $$
(2.5)

Preconditioners B x and B λ are supposed to be symmetric and positive definite matrices, τ>0 is an iteration parameter.

In the forthcoming theorem, we give sufficient conditions of the convergence for the iterative method (2.4).

Theorem 2.1

([17])

Let the operator A be uniformly monotone (2.2). If

$$ B_{\lambda}>\frac{\tau}{2\alpha} CA_0^{-1}C^T, $$
(2.6)

then the iterations of the method (2.4) converge to a solution of (2.1) starting from any initial guess λ 0.

Note 1

Since the component x of the exact solution (x,λ), as well as the components x k of the iterations belong to \(D(P)\subset \operatorname {dom}\varPhi\), it is sufficient for A to be a uniform monotone operator only on \(\operatorname {dom}\varPhi\).

Note 2

  1. (a)

    In [6], it is proved that the positive eigenvalues μ of two generalized eigenvalue problems

    $$CA_0^{-1}C^T=\mu B_{\lambda} \quad \mbox{and} \quad C^T B_{\lambda}^{-1} C=\mu A_0 $$

    with symmetric and positive definite matrices A 0 and B λ coincide. Owing to this inequality, (2.6) is equivalent to the inequality

    $$ A_0>\frac{\tau}{2\alpha} C^T B_{\lambda}^{-1} C. $$
    (2.7)
  2. (b)

    The inequality

    $$(Ax-Ay, x-y)>\frac{\tau}{2} \bigl(C^TB_{\lambda}^{-1}C(x-y), x-y\bigr) \quad \forall x\neq y $$

    replaces both (2.2) and (2.6).

  3. (c)

    If A is linear then we can take A 0=0/5(A+A T) and the inequalities (2.6) and (2.7) become, respectively (cf. [18]):

    $$B_{\lambda}>\frac{\tau}{2} CA_0^{-1}C^T \quad\mbox{and} \quad A_0>\frac{\tau}{2} C^T B_{\lambda}^{-1} C. $$
  4. (d)

    In the case of a potential operator A:A=∇Ξ, where Ξ is a differentiable convex function, the method (2.4) is just the preconditioned Uzawa method applied to finding a saddle point of the Lagrangian

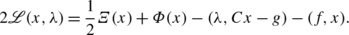
The sufficient conditions for the choice of the preconditioning matrices B x and B λ and iterative parameter τ>0 required to ensure the convergence of the Arrow–Hurwitz-type method (2.5) are given by

Theorem 2.2

([17])

Let the operator A be uniformly monotone (2.2) and Lipshitz-continuous (2.3). If

$$ \bigl(2\alpha- \tau\mu_{\max} \beta^2\bigr) A_0>\tau\,C^TB_{\lambda}^{-1}C, $$
(2.8)

where \(\mu_{\max}=\lambda_{\max}(B_{x}^{-1/2}A_{0}B_{x}^{-1/2})\) is the maximal eigenvalue of the matrix \(B_{x}^{-1/2}A_{0}B_{x}^{-1/2}\), then iterations of the method (2.5) converge to a solution of (2.1) starting from any initial guess (x 0,λ 0).

Note 3

It is sufficient for A to be a uniform monotone and Lipshitz-continuous operator only on \(\operatorname {dom}\varPhi\) (cf. Note 1).

Note 4

  1. (a)

    The choice B x =A 0 gives the best limit for the iterative parameter τ ensuring the convergence of the method. In this case, the inequality (2.8) reads

    $$A_0>\frac{\tau}{2\alpha- \tau\beta^2} \,C^TB_{\lambda}^{-1}C, $$

    and further choice of a preconditioner B λ is similar to the case of the method (2.4).

  2. (b)

    If A is linear then the sufficient convergence condition (2.8) can be replaced by the following sharper condition:

    $$A>\frac{\tau}{2} \bigl(AB_x^{-1}A^T+C^TB_{\lambda}^{-1}C \bigr). $$

2.3 Stopping Criterion

One possible stopping criterium for an iterative process is based on the evaluation of residual norms. Namely, when solving the problem (2.1) by an iterative method we find not only the pair (x k,λ k)—approximations of the exact solution (x,λ), but also uniquely defined selections γ k∈P(x k), δ k∈Q(λ k). Let us define the residual vectors

$$r_x^k=f-Ax^k-\gamma^k+C^T \lambda^k, \qquad r_{\lambda}^k=g- \delta^k-Cx^k. $$

Lemma 2.3

Let the operator A be uniformly monotone (2.2). Then the error estimate

$$ \bigl\|x-x^k\bigr\|_{A_0}\le c_1 \bigl\|r_x^k\bigr\|_{A_0^{-1}}+c_2 \bigl\|\lambda- \lambda^k\bigr\|^{1/2}\bigl\|r_{\lambda}^k \bigr\|^{1/2} \quad\forall k $$
(2.9)

is valid for the methods (2.4) and (2.5). Constants c 1 and c 2 depend only on the constant α of uniform monotonicity of operator A.

Since ∥λ−λ k∥→0 for k→∞, then the inequality (2.9) gives an estimate for the error \(\|x-x^{k}\|_{A_{0}}\) throughout the norms \(\|r_{x}^{k}\|_{A_{0}^{-1}}\) and \(\|r^{k}_{\lambda}\|\).

Note 5

In the Uzawa-type method for the saddle point problem, the inclusion Ax−B T λ+∂φ(x)∋f is solved exactly on each iteration. Due to this fact, \(r^{k}_{x}=0\) and the estimate (2.9) reads

$$ \bigl\|x-x^k\bigr\|_{A_0}\le c_2 \bigl\| \lambda-\lambda^k\bigr\|^{1/2}\bigl\|r_{\lambda}^k \bigr\|^{1/2} \quad\forall k, $$
(2.10)

whence

$$\bigl\|x-x^k\bigr\|=o\bigl(\bigl\|r_{\lambda}^k\bigr\|^{1/2} \bigr) \quad\mbox{for } k \rightarrow\infty. $$

3 Application to Variational Inequalities

Now we consider the application of the previous results to a sample example of the variational inequality: find u∈V such that ∀v∈V

$$ \int_{\varOmega} a(x)\, k(\nabla u) \cdot \nabla(v-u)\, \mathrm{d} x +\int_{\varOmega} |\nabla v|\, \mathrm{d}x-\int _{\varOmega} |\nabla u|\, \mathrm{d}x\ge \int_{\varOmega} f (v-u)\, \mathrm{d} x. $$
(2.11)

Here \(H_{0}^{1}(\varOmega)\subset V\subset H^{1}(\varOmega)\), a(x)>0, and \(k(\bar{t}): \mathbb{R}^{2} \rightarrow\mathbb{R}^{2}\) is a continuous and uniformly monotone vector-function:

$$ \bigl(k(\bar{t}_1) - k(\bar{t}_2) \bigr)\cdot(\bar{t}_1-\bar{t}_2) \ge \sigma_0 |\bar{t}_1- \bar{t}_2|^2 \quad\forall\bar{t}_i,\ \sigma_0>0. $$
(2.12)

We construct a simple finite element approximation of (2.11) in the case of polygonal domain Ω. Let \(\overline{\varOmega}= \bigcup_{e\in T_{h}} e\) be a conforming triangulation of \(\overline{\varOmega}\) [7], where T h is a family of N e non-overlapping closed triangles e (finite elements) and h is the maximal diameter of all e∈T h . Further \(V_{h}\subset H_{0}^{1}(\varOmega)\) is the space of the continuous and piecewise linear functions (linear on each e∈T h ), while U h ∈L 2(Ω) is the space of the piecewise constant functions. Define f h ∈U h and a h ∈U h by the equalities

$$f_h(x)=|e|^{-1}\int_{t\in e} f(t)\, \mathrm{d} t,\qquad a_h(x)=|e|^{-1}\int_{t\in e} a(t)\, \mathrm{d} t,\quad\forall x\in e,\ |e|=\operatorname {meas}e. $$

The finite element approximation of the problem (2.11) satisfies the relation

(2.13)

In order to formulate (2.13) in a vector-matrix form, we first define the vectors \(u\in\mathbb{R}^{N_{u}}\) and \(w\in\mathbb{R}^{N_{e}}\) of the nodal values of functions u h ∈V h and w h ∈U h , respectively. We correspond a vector valued function \(\bar{q}_{h}=(q_{1h}, q_{2h})\in U_{h}\times U_{h}\) to the vector \(q=(q_{11}, q_{21},\ldots, q_{1i}, q_{2i},\ldots,q_{1N_{e}},q_{2N_{e}}) \in \mathbb {R}^{2 N_{y}}\), where q 1i =q 1h (x), q 2i =q 2h (x) for x∈e i . Further, we define the matrix \(L\in\mathbb{R}^{N_{u}\times N_{y}}\) and the operator \(k: \mathbb{R}^{N_{y}}\rightarrow\mathbb{R}^{N_{y}}\) by the equalities

$$(Lu, q)=\int_{\varOmega} \nabla u_h(x)\cdot\bar{q}_h(x) \,\mathrm{d}x, \qquad \bigl(k(p),q\bigr)=\int_{\varOmega} a_h(x) k\bigl(\bar{p}_h(x)\bigr) \cdot\bar{q}_h(x) \,\mathrm{d}x, $$

diagonal matrix \(D=\operatorname {diag}(a_{1}, a_{1},\ldots, a_{i}, a_{i},\ldots,a_{N_{e}},a_{N_{e}})\in \mathbb {R}^{N_{y}\times N_{y}}\) with the entries a i =a h (x) for x∈e i , and vector \(f\in\mathbb{R}^{N_{u}}\), (f,u)=∫ Ω f h (x)u h (x) dx. Finally, let the convex function be defined by the relation

$$\theta(p)=\sum_{j=1}^{N_e} |e_j|\,\bigl(p_{2j}^2+p_{2j-1}^2 \bigr)^{1/2}. $$

Now, the discrete variational inequality (2.13) can be written in the form

$$u\in\mathbb{R}^{N_u}:\bigl(D\,k(Lu), L(v-u)\bigr)+\theta(Lv)- \theta(Lu) \ge (f,v-u) \quad\forall v\in\mathbb{R}^{N_u} $$

or, equivalently, as the inclusion

$$ L^T D k(Lu)+L^T \partial\theta(Lu) \ni f. $$
(2.14)

We will construct different saddle point problems using the inclusion (2.14).

3.1 Variational Inequality with the Linear Main Operator

First, let us consider the discrete problem approximating variational inequality with the linear differential operator: k(∇u)=∇u. The corresponding discrete inclusion is

$$L^T\, D\, Lu+L^T \partial\theta(Lu)\ni f. $$

Denoting p=Lu, we transform it to one of the following three systems:

(2.15)
(2.16)
(2.17)

The matrix of the first two equations in the system (2.15) is positive definite and block diagonal. Thus, the Uzawa-type method (2.4), being applied to this system, can be effectively implemented. On the other side, the saddle point problems (2.16) and (2.17) contain degenerate matrices and , respectively, so, the iterative method (2.4) cannot be applied for their solution. We realize different equivalent transformations of (2.16) and (2.17) by using the equation Lu=p, to obtain the systems with positive definite matrices A i . In particular, we can get the system corresponding to the augmented Lagrangian method

(2.18)

The matrix in (2.18) is symmetric and positive definite for any r>0. However, it is not block diagonal or block triangle. In view of this, the method (2.4) cannot be effectively implemented (while it converges for this problem). The most well-known methods for solving (2.18) are the so-called Algorithms 2–6 (see [8, 9]), based on the block relaxation technique to inverse A r and updating of the Lagrange multipliers λ. Instead of (2.18) we construct the systems with positive definite and block triangle 2×2 left upper blocks:

(2.19)
(2.20)

Lemma 2.4

Let 0<r<4. Then the matrices

(2.21)

in the systems (2.19) and (2.20) are energy equivalent to the block diagonal and positive definite matrix

with the constants depending only on r:

$$\alpha_i(r) ( A_0x,x)\le \bigl(A_i[r]x,x \bigr)\le \beta_i(r) (A_0x,x) \quad\forall x,\ i=2,3. $$

As the matrices A 2[r] and A 3[r] defined in (2.21) are block triangle, the Uzawa-type iterative method (2.4) can be easily implemented for the solution of the systems (2.19) and (2.20). Owing to Theorem 2.1, the most reasonable preconditioner is B λ =D −1. The convergence result in the particular case r=1 reads as follows:

Theorem 2.3

([18])

Let r=1. Then the method (2.4) with B λ =D −1 applied to the systems (2.19) and (2.20) converges provided that \(0<\tau<\frac{1}{2}\).

Implementation of the method (2.4) for (2.19) and (2.20) includes solving a system of linear equations with the matrix L T DL and solving an inclusion of the form cDp+∂θ(p)∋F, c=const with a known vector F. In the example under consideration, the matrix D is diagonal and the multivalued operator ∂θ is block-diagonal with 2×2 blocks. Because of this, the inclusion cDp+∂θ(p)∋F can be easily solved by the direct methods.

3.2 Variational Inequality with Non-linear Main Operator

To construct saddle point problems for the inclusion (2.14) with the non-linear main operator, we proceed similarly to the linear case. Namely, by using Lagrange multipliers λ and the equation Lu=p, we construct saddle point problems with uniformly monotone operators in the space of the vectors x=(u,p)T. Consider two of them:

(2.22)
(2.23)

The systems (2.22) and (2.23) contain block-triangle operators

Lemma 2.5

Let the uniform monotonicity property (2.12) with the constant σ 0 hold and 0<r<4σ 0. Then the operators A 1 and A 2 are uniformly monotone:

$$ (A_ix_1-A_ix_2, x_1-x_2)\ge \alpha_i \|x_1-x_2\|^2_{A_0}, \quad \alpha_i =\alpha_i(r,\sigma_0)>0,\ i=1,2, $$
(2.24)

where is the positive definite matrix.

Lemma 2.6

Let the function k be Lipschitz-continuous:

$$ \bigl(k(\bar{t}_1) - k(\bar{t}_2)\bigr) \cdot(\bar{s}) \le \sigma_1 |\bar{t}_1- \bar{t}_2| |\bar{s}|\quad\forall\bar{t}_i, \bar{s}. $$
(2.25)

Then the operators A 1 and A 2 are Lipschitz-continuous:

$$ \|A_ix_1-A_ix_2 \|_{A_0^{-1}}\le \beta_i \|x_1-x_2 \|_{A_0}, \quad\beta_i =\beta_i(r, \sigma_1),\ i=1,2. $$
(2.26)

Application of Lemmas 2.5 and 2.6 and Theorem 2.1 gives the following result:

Theorem 2.4

Let 0<r<4σ 0. Then the Uzawa-type iterative method (2.4) with the preconditioner B λ =D −1 applied for solving (2.22) and (2.23) converges if

$$0<\tau<\frac{2\alpha_2 r}{1+r}. $$

Implementation of the method (2.4) for (2.23) includes solving a system of linear equations with the matrix L T DL and solving the inclusion Dk(p)+∂θ(p)∋F with a known vector F. This inclusion can be effectively solved because the operator k is diagonal and ∂θ is a 2×2 block diagonal operator.

Implementation of (2.4) for the problem (2.22) requires solving the system of nonlinear equations L T k(Lu)+L T λ=0 by an inner iterative method. Thus, the effectiveness of the algorithm depends also on the effectiveness of an inner iterative method. Instead of the Uzawa-type method we can apply the Arrow–Hurwitz-type iterative method (2.5) for the problem (2.22) with B λ =D −1 and . The results of Lemmas 2.5 and 2.6 and Theorem 2.2 yield

Theorem 2.5

Let 0<r<4σ 0. Then the iterative method (2.5) for the problem (2.22)

$$ \begin{aligned} \frac{r}{\tau}L^TDL \bigl(u^{k+1}-u^k\bigr)+ L^Tk \bigl(Lu^k\bigr)+L^T\lambda^k & = 0, \\ \frac{1}{\tau}D\bigl(p^{k+1}-p^k\bigr)-rDLu^k+rDp^k+ \partial\theta\bigl(p^{k+1}\bigr) -\lambda^k & \ni0, \\ \frac{1}{\tau}\bigl(\lambda^{k+1} - \lambda^k\bigr)+ D\bigl(L u^{k+1}-p^{k+1}\bigr) & = 0 \end{aligned} $$
(2.27)

converges if

$$\tau<\frac{2\alpha_1}{\beta_1+(1+r)/r}. $$

It is easy to see that the implementation of (2.27) includes the same steps as the implementation of the method (2.4) for (2.23).

3.3 Variational Inequality with Pointwise Constraints both for the Solution and Its Gradient

Consider the variational inequality: find \(u\in U_{ad}=\{u\in H^{1}_{0}(\varOmega): u(x)\ge 0 \mbox{ in } \varOmega\}\), such that for all v∈U ad

$$\int_{\varOmega} a(x) k\bigl(|\nabla u|\bigr) \nabla u\cdot\nabla(v-u)\, \mathrm{d} x+\int_{\varOmega} \bigl(|\nabla v|-|\nabla u|\bigr)\, \mathrm{d} x\ge \int_{\varOmega} f (v-u)\, \mathrm{d} x, $$

where a(x)>0 and the vector-function \(k(|\bar{t}|) \bar{t}\) satisfies (2.12). After approximation of this variational inequality, we obtain the discrete variational inequality

$$\bigl(D\,k(Lu), L(v-u)\bigr)+\theta(Lv)-\theta(Lu) +\varphi(v)-\varphi(u) \ge (f,v-u) \quad\forall v\in \mathbb {R}^{N_u}, $$

where φ is the indicator function of the constraint set \(\{u\in \mathbb {R}^{N_{u}}: u_{i}\ge 0\ \forall i\}\), while all other notations are the same as above. We write this variational inequality in the form of inclusion

$$L^T\, D\, k(Lu)+L^T \partial\theta(Lu)+\partial \varphi(u)\ni f. $$

We proceed as before and construct the saddle point problems

(2.28)
(2.29)

Both iterative methods, (2.4) and (2.5), can be applied for solving these saddle point problems because the results of Theorems 2.1 and 2.2 are valid with the operator P defined by P(x)=(∂φ(u),∂θ(p))T. But now, the implementation of the Uzawa-type iterative method (2.4) for (2.29) includes the solution of the finite dimensional obstacle problem—the inclusion

$$rL^TDLu+\partial\varphi(u)\ni rL^TDp-L^T \lambda $$

with the symmetric and positive definite matrix rL T DL, and the implementation of this method for (2.28) includes the solution of the problem with the non-linear operator

$$L^T k(Lu)+\partial\varphi(u)\ni-L^T \lambda. $$

The Arrow–Hurwitz-type method (2.5) with preconditioners and B λ =D −1 being applied to (2.28) or (2.29) converges and it can be easily implemented. On the other hand, in this case the maximal eigenvalue μ max of the matrix \(B_{x}^{-1/2}A_{0}B_{x}^{-1/2}\) depends on condition numbers of the matrices D and L T L, thus, on the mesh step h. Convergence of the corresponding iterative methods is guaranteed for the very small iterative parameter τ, and numerical experiments demonstrate slow convergence of the Arrow–Hurwitz-type method (2.5).

3.4 Results of Numerical Experiments

We have solved a number of 1D and 2D linear and non-linear variational inequalities using the simplest finite element and finite difference approximations and applying the Uzawa-type method. The main purpose of the numerical experiments was to observe the dependence of the number of iterations upon the mesh step h and iterative parameter τ. We also compared proposed iterative algorithms with well-known algorithms for saddle point problems constructed via an augmented Lagrangian technique. Several numerical results are reported below.

Consider the following one-dimensional variational inequality

$$u\in K: \int_0^1 u^{\prime} \bigl(v^{\prime}-v^{\prime}\bigr)\,\mathrm{d} x\ge \int _0^1 f (v-u)\, \mathrm{d}x \quad\forall v\in K $$

with the set of constraints \(K=\{u\in H^{1}_{0}(0,1): |u^{\prime}(x)|\le 1 \mbox{ for } x\in(0,1)\}\). Finite element approximation with piecewise linear elements on the uniform grid leads to the inclusion L T Lu+L T ∂θ(Lu)∋f, where the matrix L corresponds to the approximation of the first order derivative. We solve the corresponding saddle point problems:

Problem 2.1

The saddle point problem with (which corresponds to (2.19)).

Problem 2.2

The saddle point problem with (which corresponds to (2.15)).

We use the stopping criterion

$$\bigl\|u-u^*\bigr\|_{L_2}= \Biggl( h \sum_{i=1}^n \bigl(u_i-u^*_i\bigr)^2 \Biggr)^{1/2}<10^{-4}, $$

where h=n −1 is the mesh step and u ∗ is the known exact solution, and the initial guess λ=0. Table 2.1 demonstrates the dependence of the number of iterations n it upon the iterative parameter and the number of the grid nodes for Problem 2.1.

Table 2.1 Dependence of n it on τ and n for Problem 2.1
Full size table

For Problem 2.2 the optimal iterative parameter was found τ=0.4 and the number of iterations to achieve the accuracy \(\|u-u^{*}\|_{L_{2}}<10^{-4}\) for the grids with the number of nodes from n=50 to n=500 000 was equal to 12.

Now we consider two-dimensional variational inequalities with linear differential operators

(2.30)
(2.31)

We set Ω=(0,1)×(0,1) and construct finite difference approximations on uniform grids. These finite difference schemes can be written in the form of the inclusion L T Lu+L T ∂θ(Lu)∋f, where the rectangular matrix L corresponds to the approximation of the gradient operator. We have studied the following two saddle point problems:

Problem 2.3

2D saddle point problem with the matrix .

Problem 2.4

2D saddle point problem with the matrix (which corresponds to the augmented Lagrangian method with r=1).

We use the stopping criterion

$$\bigl\|u-u^*\bigr\|_{L_2}= \Biggl(h^{2} \sum _{i,j=1}^n \bigl(u_{ij}-u^*_{ij} \bigr)^2 \Biggr)^{1/2}<10^{-3}, $$

where n=h −1 is the number of nodes in one direction and u ∗ is the known exact solution. Table 2.2 contains results for the variational inequality (2.30).

Table 2.2 Left: The Uzawa method with the preconditioner B λ equals to the unit matrix for Problem 2.3, the initial guess λ=0. Right: Algorithm 2 for Problem 2.4, corresponding to the augmented Lagrangian method, the initial guess λ=0, p=0
Full size table

For the discrete saddle point problems corresponding to (2.31) the results were similar. Namely, for both aforementioned methods and grids with the number of nodes n=100,200,400 the accuracy \(\|u-u^{*}\|_{L_{2}}<10^{-3}\) was achieved within 19 iterations for τ=1.2, which was found as numerically optimal.

Finally, we consider a two-dimensional variational inequality associated with the non-linear differential operator

$$ \int_{\varOmega} k\bigl(| \nabla u |\bigr)\nabla u\cdot \nabla(v-u) \,\mathrm{d}x \ge C \int_{\varOmega} (v-u) \,\mathrm{d}x, \quad\forall v \in K, $$
(2.32)

where Ω=(0,1)×(0,1), \(k(t) t=\sqrt{t}\) and \(K=\{u\in H^{1}_{0}(\varOmega):|\nabla u(x)|\le 1 \mbox{ in } \varOmega\}\). We constructed a finite difference approximation of (2.32) on the uniform grid. According to the theory the iterative parameter was taken τ=1/2. Since the exact solution was not known we estimated the norms of the residuals \(\|r_{\lambda}\||_{L_{2}}\) (see the estimate (2.10)). Calculations were made for different amount of nodes in one direction. For all grids, we observed typical dependence of norms of the residuals upon the iteration number: very fast decreasing during the first iterations with further deceleration. After 20–25 iterations the norm \(\|u^{k}-u^{k-1}\|_{L_{2}}\) became very close to zero and the vector u k could be taken as the exact solution. The calculation results for the case n=500 are given in Table 2.3, where \(\delta u=\|u^{k}-u^{100}\|_{L_{2}}\) is the norm of the difference between the current iteration and the 100th iteration which was taken as the exact solution.

Table 2.3 2D non-linear saddle point problem; C=10, τ=1/2, n=500
Full size table

In the computations performed for 1D and 2D variational inequalities, the following features were observed:

  • The dependence of the rate of convergence for the method (2.4) on the parameters r and τ=τ(r) was quite low;

  • The number of iterations did not depend on the mesh size h=1/n;

  • In all cases the Uzawa-type method (2.4) applied to transformed saddle point problems with the block triangle A was similar by a rate of convergence to Algorithm 2 applied to the saddle point problem constructed via the augmented Lagrangian technique.

4 Application to Optimal Control Problems

Consider the following elliptic boundary value problem:

$$ \int_{\varOmega}\sum _{i,j=1}^{2} \biggl(a_{ij} \frac{\partial y}{\partial x_j} \frac{\partial z}{\partial x_i}+a_0 y z \biggr) \,\mathrm{d}x=\int_{\varOmega}(f+ \chi_0 u) z \,\mathrm{d}x \quad\forall z\in H^1_0( \varOmega). $$
(2.33)

Here Ω 0⊆Ω, \(\chi_{0}\equiv\chi_{\varOmega_{0}}\) is the characteristic function of the domain Ω 0, the function f∈L 2(Ω) is fixed, while u∈L 2(Ω 0) is a variable control function. Coefficients a ij (x) and a 0(x) are continuous in \(\overline{\varOmega}\) and satisfy the following ellipticity assumptions:

$$\sum_{i, j=1}^{2}a_{ij}(x) \xi_j \xi_i\ge c_0 \sum _{i=1}^{2}\xi_i^2, \qquad a_0(x)\ge 0 \quad\forall x\in \overline{\varOmega},\ c_0=\mathrm{const}>0. $$

Define the goal functional

$$J(y,f)=\frac{1}{2}\int_{\varOmega_1}(y-y_d)^2 \,\mathrm{d}x+\frac {1}{2}\int_{\varOmega_0} u^2 \,\mathrm{d}x $$

with a given function y d (x)∈L 2(Ω 1), Ω 1⊆Ω, and the sets of the constraints

$$Y_{ad}=\bigl\{y\,{\in}\, V: y(x)\ge 0 \ \forall x\,{\in}\,\varOmega\bigr\},\qquad U_{ad}=\bigl\{u\,{\in}\, L_2(\varOmega_0): \bigl|u(x)\bigr| \le u_d \ \forall x\,{\in}\, \varOmega_0\bigr\}. $$

The optimal control problem reads as follows:

$$ \min_{(y,u)\in Z} J(y,u),\qquad Z=\bigl\{(y,u):y\in Y_{ad},\ u\in U_{ad}, \mbox{ Eq.~(2.33) holds} \bigr\}. $$
(2.34)

We suppose that the set Z is non-empty. Then, the problem (2.34) has a unique solution (cf., e.g., [20]).

Construct a finite element approximation of the problem (2.34) in the case of polygonal domains Ω, Ω 0 and Ω 1. Let a triangulation of Ω be consistent with Ω 0 and Ω 1. Define the spaces of the continuous and piecewise linear functions (linear on each triangle of the triangulation) on the domain Ω (\(V_{h}\subset H^{1}_{0}(\varOmega)\)) and on the subdomains Ω 0 and Ω 1. Let functions f, u and y d be continuous and f h , u h and y d h be their piecewise linear interpolations. We use the quadrature formulas

where x α are the vertices of e, and \(|e|=\operatorname {meas}e\). Finite element approximations of the state equation, the goal function, and the constraints are as follows:

(2.35)

The state equation (2.35) has a unique solution y h and the following stability inequality holds:

$$ S^{1/2}_{\varOmega}\bigl(|y_h|^2 \bigr)\le k_a \bigl(S^{1/2}_{\varOmega} \bigl(f_h^2\bigr)+S^{1/2}_{\varOmega_0} \bigl(u_h^2\bigr) \bigr) $$
(2.36)

with a constant k a independent on h. The finite element approximation of the optimal control problem (2.34) is

$$ \begin{cases} \displaystyle\min_{(y_h,u_h)\in Z_{h}} J_{h}(y_h,u_h),\\ Z_{h}=\{(y_h,u_h):\,y_h\in Y^h_{ad}, u_h\in U^h_{ad}, \mbox{ Eq. (2.35) holds}\}. \end{cases} $$
(2.37)

To obtain the matrix-vector form of (2.37), we define the vectors of nodal values \(y\in \mathbb {R}^{N_{y}}\), \(u\in \mathbb {R}^{N_{u}}\) and the matrices

Then, the discrete optimal control problem can be written in the form

$$\min_{Ly=Mf+Su} \biggl\{\frac{1}{2} (K y,y)-(K y_d,y)+\theta(y)+ \frac{1}{2} (M_0u,u)+\varphi(u) \biggr\}, $$

where \(\theta(y)=I_{Y_{ad}}(y)\) and \(\varphi(u)=I_{U_{ad}}(u)\) are the indicator functions of the sets \(Y_{ad}=\{y\in \mathbb {R}^{N_{y}}: y_{i}\ge 0 \ \forall i\}\) and \(U_{ad}=\{u \in \mathbb {R}^{N_{u}}: |u_{i}|\le u_{d}\ \forall i\}\), respectively. The corresponding saddle point problem reads as follows:

(2.38)

In the problem (2.38), the stiffness matrix L is positive definite, and M>0, M 0>0, K≥0 are diagonal matrices. The main feature of (2.38) is that K is a degenerate matrix. We transform the system (2.38) to obtain a positive definite and block triangle left upper 2×2 block. To this end we add to the first inclusion in (2.38) the last equation multiplying by −rML −1, r>0, and obtain the saddle point problem

(2.39)

with

and \(\tilde{g}= (\tilde{f}, 0)^{T}\), \(\tilde{f}=K y_{d}+rML^{-1}Mf\).

Lemma 2.7

Let \(0<r<\frac{4}{k_{a}^{2}}\), where the constant k a is defined in (2.36). Then, the matrix A[r] is an energy equivalent to with constants depending only on r. In particular,

$$\bigl(A[r]x,x\bigr)\ge \alpha\bigl(A^0x,x\bigr),\quad\alpha= \alpha(r,k_a)>0. $$

We solve (2.39) by using the iterative Uzawa-type method (2.4) with the preconditioner B λ =L M −1 L T:

$$ \begin{aligned} (K+rM)y^{k+1} +\partial\theta \bigl(y^{k+1}\bigr) -rML^{-1}S u^{k+1} & \ni L^T \lambda^{k} +\tilde{f}, \\ M_0 u^{k+1}+ \partial\varphi\bigl(u^{k+1}\bigr) & \ni-S^T \lambda^{k}, \\ \frac{1}{\tau}L M^{-1} L^T\bigl(\lambda^{k+1} - \lambda^k\bigr) +Ly^{k+1}-Su^{k+1} & \ni M f. \end{aligned} $$
(2.40)

Theorem 2.6

([18])

The iterative method (2.40) converges if

$$0<\tau< \frac{2 \alpha}{k_a^2 +1}. $$

Along with the iterative method (2.40) we can use the gradient method for the regularized problem. Namely, let us change the indicator function \(\theta(y)=I_{Y_{ad}}(y)\) of the constraint set \(Y_{ad}=\{y\in\mathbb{R}^{N_{y}}:\, y_{i}\ge 0 \; \forall i\}\) by the differentiable function

$$\displaystyle\theta_{\varepsilon}(y)=\frac{1}{\varepsilon} \bigl(M y^-, y^- \bigr). $$

For the corresponding regularized saddle point problem we can apply the “traditional” gradient method

$$ \begin{gathered} Ly^{k+1}=Su^{k}+M f, \\ L^T \lambda^{k+1}= (K+rM)y^{k+1} +\nabla \theta_{\varepsilon}\bigl(y^{k+1}\bigr) -rML^{-1}S u^{k}-\tilde{f}, \\ M_0\frac{u^{k+1}-u^{k}}{\tau}+M_0 u^{k+1}+ \partial \varphi\bigl(u^{k+1}\bigr)+S^T \lambda^{k+1}\ni0. \end{gathered} $$
(2.41)

Theorem 2.7

([19])

The iterative method (2.41) converges if

$$0< \tau< \frac{2 \varepsilon}{k_a^2(1+\varepsilon) +r\varepsilon}. $$

When implementing any of the iterative methods (2.40) or (2.41) we have to solve the systems of linear equations with matrices L and L T, and to solve two inclusions with diagonal operators M 0+∂φ and K+rM+∂θ.

4.1 Numerical Experiments

Problem 2.5

A control- and state-constrained optimal control problem with observation in the whole domain Ω=(0,1)×(0,1): minimize the goal functional

$$\frac{1}{2}\int_{\varOmega} {y^{2}(x)\,\mathrm{d}x}+\frac{1}{2}\int_{\varOmega}{u^{2}(x)\,\mathrm{d}x} $$

under the constraints

$$ \begin{array}{rl@{\quad }l@{\qquad }rl@{\quad }l} -\Delta y & =f+u, & x \in\varOmega, & y(x) &=0, & x \in\partial\varOmega, \\[6pt] y(x) & \ge 0, & x \in\varOmega, & \bigl|u(x)\bigr| &\le 1, & x \in \varOmega. \end{array} $$
(2.42)

We constructed a finite difference approximation of this problem on the uniform grid. The corresponding saddle point problem has the form (2.38) with unit matrices K, M 0 and S. Therefore, we can use the preconditioned Uzawa-type method (2.40) for solving this saddle point problem without its transformation. The results of the calculations are reported in Table 2.4, where F ∗=J(y,u) is the value of the discrete goal function on the known exact solution (y,u) (y=3(sin(6πx 1 x 2))+ for the corresponding grid), while F=J(y k,v k) is its value on the current iteration; \(\mathit{Err}=(\|y^{k}-y\|_{L_{2}}^{2}+\|u^{k}-u\|^{2}_{L_{2}})^{\frac{1}{2}}\).

Table 2.4 The Uzawa-type method for Problem 2.5, y=3(sin(6πx 1 x 2))+
Full size table

Problem 2.6

A control- and state-constrained optimal control problem with observation in the part Ω 1=(0,0.7)×(0,1) of the domain Ω=(0,1)×(0,1): minimize the goal functional

$$\frac{1}{2}\int_{\varOmega_{1}} y^{2}(x)\,\mathrm{d}x +\frac{1}{2} \int _{\varOmega} u^{2}(x)\,\mathrm{d}x $$

under the constraints (2.42). We constructed a finite difference approximation of this problem on the uniform grid. The corresponding saddle point problem has the form (2.38) with the degenerate matrix K. We transformed it to the problem of the form (2.39) with r=1 and applied the Uzawa-type method (2.40) for its solution. The corresponding calculation results are included in Table 2.5.

Table 2.5 The Uzawa-type method for Problem 2.6
Full size table

Problem 2.7

A state-constrained optimal control problem with observation in the whole domain: minimize the goal functional

$$J(y,u)=\frac{1}{2} \int_{\varOmega} (y-y_{d})^{2} \,\mathrm{d}x + \frac{1}{2} \int_{\varOmega} u^{2} \,\mathrm{d}x $$

under the constraints

$$\begin{gathered} -\Delta y=f+u,\quad x\in\varOmega, \qquad y(x)=0,\quad x\in \partial\varOmega, \\ y(x)\le 0.5,\quad x\in\varOmega. \end{gathered} $$

We constructed a finite difference approximation on the uniform grid and applied the Uzawa-type method (2.40) and the gradient method (2.41) for solving the corresponding discrete saddle point problems. We compared the calculated iterations with the exact solution y, calculated by using a great deal of convergent iterations. Table 2.6 contains the results for the case f=20, h=10−2, F ∗=44.1789. The notations are Err y =∥y−y k∥, δy k=∥y k−1−y k∥.

Table 2.6 Uzawa-type and gradient methods for Problem 2.7
Full size table

Along with the Uzawa-type and regularization methods, we have also applied the Douglas-Rachford splitting method for solving state-constrained optimal control problems. We have found that none of the methods could be defined as the efficient one in all situations. More numerical experiments should be made to define the classes of the optimal control problems and the corresponding iterative methods which are the most efficient for their solving.