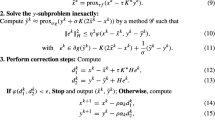A primal–dual prediction–correction algorithm for saddle point optimization

Abstract

In this paper, we introduce a new primal–dual prediction–correction algorithm for solving a saddle point optimization problem, which serves as a bridge between the algorithms proposed in Cai et al. (J Glob Optim 57:1419–1428, 2013) and He and Yuan (SIAM J Imaging Sci 5:119–149, 2012). An interesting byproduct of the proposed method is that we obtain an easily implementable projection-based primal–dual algorithm, when the primal and dual variables belong to simple convex sets. Moreover, we establish the worst-case ${\mathcal {O}}(1/t)$ convergence rate result in an ergodic sense, where t represents the number of iterations.

1 Introduction

Consider the following saddle-point optimization problem:

$$\begin{aligned} \min _{y\in \mathcal{{Y}}}\;\max _{x\in \mathcal{{X}}}\;\varPhi (x,y):=\langle y, Ax\rangle +\frac{\nu }{2}\Vert By-b\Vert ^2, \end{aligned}$$

(1.1)

where $\mathcal{{X}}$ and $\mathcal{{Y}}$ are two nonempty, closed and convex subsets of ${\mathbb R}^m$ and ${\mathbb R}^n$, respectively; $A\in {\mathbb R}^{n\times m}$ and $B\in {\mathbb R}^{n\times n}$ are two given matrices; $b\in {\mathbb R}^n$ is a given (observation) vector; $\nu >0$ serves as a tuning parameter; $\langle \cdot , \cdot \rangle$ denotes the standard inner product of vectors; and $\Vert \cdot \Vert$ is the Euclidean norm. It is well documented in the literature that the saddle point problem (1.1) has many applications in diverse areas such as constrained optimization duality, zero-sum games, and image processing (see [4–6, 8–10, 13]), amongst others.

To solve the saddle point problem (1.1), Chambolle and Pock [4] introduced the so-called first-order primal–dual algorithm (FOPDA), which has been successfully applied to solve many image restoration problems. In recent years, primal–dual methods have been extensively studied for solving convex optimization and saddle point problems arising in signal/image processing, computer vision, and machine learning (see [12] for a recent overview on such primal–dual algorithmic advancements). As pointed out in [4], the primal–dual hybrid gradient (PDHG) method [11, 15] as well as the Arrow–Hurwicz–Uzawa method [1] are special cases of the FOPDA method. Although the conditions for global convergence of FOPDA are weaker than those in [1, 15], the numerical results reported in [2, 10] show that FOPDA [4] performs better in practice when its parameters are set beyond their theoretically guaranteed limits. Motivated by these results, He and Yuan [10] introduced a new class of primal–dual based prediction–correction algorithms where the range of the involved parameters in [4] was extended to further augment the performance of FOPDA. Subsequently, Cai et al. [2] presented an improved version of He and Yuan’s algorithm with a new correction step, which further weakens the conditions assumed in [10] and also improves its computational efficiency.

In this paper, we propose another primal–dual algorithm, which aims to bridge the gap between the algorithms in [2, 10]. As a byproduct, we also obtain a partially linearized primal–dual algorithm, which only requires two projections during the prediction stage. This resulting linearized version of our algorithm is relatively easier to implement as compared to the algorithms in [2, 4, 10] as long as the projections of $\mathcal{{X}}$ and $\mathcal{{Y}}$ are readily available as closed-form solutions or are simple enough to compute numerically. Recently, Chambolle and Pock [3] established the ${\mathcal {O}}(1/t)$ convergence rate of the FOPDA method in an ergodic sense. In a similar fashion, in the third contribution of this work, we also establish the ${\mathcal {O}}(1/t)$ convergence rate for the proposed algorithm, which further serves to provide an interesting complement to the methods introduced in [2, 10].

The remainder of this paper is organized as follows. In Sect. 2, we begin by summarizing some basic notations and definitions, and follow this up by deriving an equivalent variational characterization of the saddle point problem (1.1). In Sect. 3, we propose the algorithmic framework of the primal–dual based prediction–correction method and briefly address its connections to existing primal–dual algorithms. More importantly, we describe a simplified projection-based primal–dual method obtained by virtue of appropriately chosen parameters. In Sect. 4, we establish the ${\mathcal {O}}(1/t)$ convergence rate of the proposed method in an ergodic sense, and finally, Sect. 5 summarizes the contributions of this paper and presents extensions for future research.

2 Preliminaries

In this section, we begin by summarizing some notations and definitions, and moreover, we reformulate the saddle point problem (1.1) as a variational inequality, which serves to facilitate the subsequent convergence analysis.

Let ${\mathbb R}^n$ be an n-dimensional Euclidean space. The symbol $^\top$ represents the transpose. For a given symmetric and positive definite matrix H, we let $\Vert x\Vert _H=\sqrt{\langle x, Hx\rangle }$ be the H-norm of x. Furthermore, we denote $\Vert N\Vert$ to be the matrix 2-norm of an arbitrary matrix N.

Let $\varOmega$ be a convex subset of ${\mathbb R}^n$. We denote $P_{\varOmega }(\cdot )$ to be the projection of $(\cdot )$ onto $\varOmega$ under the Euclidean norm, that is,

$$\begin{aligned} P_{\varOmega }(v):=\arg \min \left\{ \Vert u-v\Vert \;|\; u\in \varOmega \right\} , \quad \forall v\in {\mathbb R}^n. \end{aligned}$$

Now, let $(x^*,y^*)$ be a solution of the saddle point problem (1.1). Then, from saddle point optimality conditions, we get,

$$\begin{aligned} \max _{x\in \mathcal{{X}}}\left\{ \langle x, A^{\top }y^*\rangle +\frac{\nu }{2}\Vert By^*-b\Vert ^2\right\}&\le \langle x^*, A^{\top }y^*\rangle +\frac{\nu }{2}\Vert By^*-b\Vert ^2 \\&\le \min _{y\in \mathcal{{Y}}}\left\{ \langle x^*, A^{\top }y\rangle +\frac{\nu }{2}\Vert By-b\Vert ^2\right\} , \end{aligned}$$

which reduces to the following pair of variational inequalities:

$$\begin{aligned} \left\{ \begin{array}{ll} \langle x-x^*, -A^\top y^*\rangle \ge 0, &{} \;\;\forall x\in \mathcal{{X}},\\ \langle y-y^*, Ax^*+\nu B^\top (By^*-b)\rangle \ge 0, &{} \;\;\forall y\in \mathcal{{Y}}.\end{array}\right. \end{aligned}$$

The above variational characterization can be compactly rewritten as a problem of finding ${\varvec{u}}^*\in \varOmega$, such that

$$\begin{aligned} \langle {\varvec{u}}-{\varvec{u}}^*,F({\varvec{u}}^*)\rangle \ge 0,\;\quad \forall {\varvec{u}}\in \varOmega , \end{aligned}$$

(2.1a)

where

$$\begin{aligned} {\varvec{u}}:=\left( \begin{array}{l} x\\ y\end{array}\right) , \; F({\varvec{u}}):=\left( \begin{array}{l} -A^\top y\\ Ax+\nu B^\top (By-b)\end{array}\right) , \;\;\;\hbox {and}\;\; \varOmega :=\mathcal{{X}}\times \mathcal{{Y}}. \end{aligned}$$

(2.1b)

It is easy to verify that the underlying mapping F defined in (2.1b) is monotone, i.e.,

$$\begin{aligned} \langle {\varvec{u}}_1-{\varvec{u}}_2,~F({\varvec{u}}_1)-F({\varvec{u}}_2)\rangle \ge 0,\;\;\quad \forall {\varvec{u}}_1,\; {\varvec{u}}_2\in \varOmega . \end{aligned}$$

Throughout this paper, our convergence analysis is based on the variational characterization (2.1) and the associated theory of variational inequalities.

3 Algorithm

To begin with, define:

$$\begin{aligned} M: =\left( \begin{array}{ccc}\frac{1}{\tau }I&{} &{} A^\top \\ \theta A &{} &{}\frac{1}{\sigma }I+2\rho B^\top B\end{array}\right) \quad \text {and}\quad H: =\left( \begin{array}{ccc}\frac{1}{\tau }I&{}&{} 0 \\ 0 &{}&{} \frac{1}{\sigma }I+2\rho B^\top B\end{array}\right) , \end{aligned}$$

(3.1)

where $\tau$, $\theta$, $\sigma$, $\rho$ are given constants such that both M and H are positive definite, denoted using standard notation as $M\succ 0$ and $H\succ 0$.

We are now ready to formally present the algorithmic framework of the primal–dual prediction–correction algorithm where, for the sake of notational convenience, we have represented ${\varvec{u}}:=(x,y)$ and $\lambda _{\max }(B^\top B)$ denotes the maximum eigenvalue of $B^\top B$.

Remark 3.1

When we set $\rho :=0$ in (3.2c), Algorithm 1 reduces to the first algorithm proposed in [10]. Besides, if we set $\rho :=\nu$, while taking H as the identity matrix and

$$\begin{aligned} \alpha _k^*:=\frac{\langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k, {\widetilde{M}}({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle }{\Vert M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\Vert ^2},\quad \mathrm{where}\quad \widetilde{M}: =\left( \begin{array}{ccc}\frac{1}{\tau }I&{} &{} A^\top \\ \theta A &{}&{} \frac{1}{\sigma }I+\nu B^\top B\end{array}\right) , \end{aligned}$$

(3.5)

as the step size [instead of $\alpha _k$ in (3.3)], the iterative scheme then coincides with the algorithm introduced in [2]. Clearly, Algorithm 1 can be regarded as an extension of the respective methods proposed in [2, 10].

Note that the y-related subproblem (3.2c) is essentially a constrained minimization problem if $\mathcal{{Y}}$ is a proper subset of ${\mathbb R}^n$. In this situation, Algorithm 1 fails to be easily implemented when $\rho :=0$ (as is the case in [2, 4, 10]). Indeed, observe that, when taking $\rho :=-\nu /2$, the iterative schemes (3.2a) and (3.2c) amount to two projection steps, given by,

Clearly, the projection steps (3.6a) and (3.6b) are computationally easier to implement than the original projection operators introduced in [2, 4, 10], as long as the sets $\mathcal{{X}}$ and $\mathcal{{Y}}$ are relatively simple. It is worthwhile to note that such a linearization strategy has appeared in a recent work [14], where the authors only considered the case of a fixed $\theta =1$ in (3.2b), and showed that this variant yields significant computational benefits.

4 Convergence results

In this section, we first prove that Algorithm 1 is globally convergent to a solution of (1.1). Our secondary goal is to establish the worst-case ${\mathcal {O}}(1/t)$ convergence rate result in an ergodic sense, which is not estimated in [2, 10]. In our analysis, we impose the same assumptions on the parameters $\tau$, $\sigma$, and $\delta$, as stated in [10].

Lemma 4.1

Let $\{{\varvec{u}}^{k}:=(x^{k}, y^{k})\}$ be generated by Algorithm 1. Then, we have

$$\begin{aligned} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^{k}, F({{\widetilde{{\varvec{u}}}}}^{k}) +M({{\widetilde{{\varvec{u}}}}}^{k}-{\varvec{u}}^k)\rangle \ge 0, \;\;\forall {\varvec{u}}\in \varOmega , \end{aligned}$$

(4.1)

where M is as given in (3.1).

Proof

By invoking the first-order optimality conditions of (3.2a) and (3.2c), we have

$$\begin{aligned} \left\{ \begin{array}{l} \langle x-{\widetilde{x}}^{k}, -A^\top y^{k}+\frac{1}{\tau }({\widetilde{x}}^{k}-x^k)\rangle \ge 0,\;\; \forall x\in \mathcal{{X}},\\ \langle y-{\widetilde{y}}^{k}, A\bar{x}^{k}+\nu B^\top (B{\widetilde{y}}^{k}-b)+ \left( \frac{1}{\sigma }I+2\rho B^\top B\right) ({\widetilde{y}}^k-y^k)\rangle \ge 0,\; \forall y\in \mathcal{{Y}}. \end{array}\right. \end{aligned}$$

Using the notation in (2.1), together with (3.2b), yields the desired inequality (4.1). $\square$

Lemma 4.2

Let ${\varvec{u}}^*:=(x^*,y^*)$ be an arbitrary solution of (1.1). Then, the sequences $\{{\varvec{u}}^k\}$ and $\{{{\widetilde{{\varvec{u}}}}}^k\}$ generated by Algorithm 1 satisfy the following property:

$$\begin{aligned} \langle {\varvec{u}}^k-{\varvec{u}}^*, M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle \ge \langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k, M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle . \end{aligned}$$

(4.3)

Proof

Note that the inequality (4.1) holds for any ${\varvec{u}}\in \varOmega$. As a consequence, we have

$$\begin{aligned} \langle {\varvec{u}}^*-{{\widetilde{{\varvec{u}}}}}^{k}, F({{\widetilde{{\varvec{u}}}}}^{k}) +M({{\widetilde{{\varvec{u}}}}}^{k}-{\varvec{u}}^k)\rangle \ge 0, \;\;\forall {\varvec{u}}^*\in \varOmega . \end{aligned}$$

(4.4)

On the other hand, it follows from (2.1) that

$$\begin{aligned} \langle {{\widetilde{{\varvec{u}}}}}^k- {\varvec{u}}^*, F({\varvec{u}}^*)\rangle \ge 0. \end{aligned}$$

(4.5)

Adding (4.4) and (4.5) yields

$$\begin{aligned} \langle {{\widetilde{{\varvec{u}}}}}^k-{\varvec{u}}^*, F({\varvec{u}}^*)- F({{\widetilde{{\varvec{u}}}}}^k)\rangle \ge \langle {\varvec{u}}^*-{{\widetilde{{\varvec{u}}}}}^k,M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle , \end{aligned}$$

which together with the monotonicity of F implies that

$$\begin{aligned} \langle {{\widetilde{{\varvec{u}}}}}^k-{\varvec{u}}^*,M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle \ge 0. \end{aligned}$$

Thus, we conclude that

$$\begin{aligned} \langle {\varvec{u}}^k-{\varvec{u}}^*, M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle \ge \langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k, M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle , \end{aligned}$$

and the assertion of this lemma is obtained. $\square$

Remark 4.1

When $\rho =\nu$, note that the matrix M can be expressed as the sum of two parts

$$\begin{aligned} M={\widetilde{M}} + N,\quad \mathrm{where}\quad N:=\left( \begin{array}{ccc} 0 &{}&{} 0 \\ 0 &{}&{} \rho B^\top B\end{array}\right) , \end{aligned}$$

and ${\widetilde{M}}$ is as previously defined in (3.5). Consequently, the term on the right hand side of (4.3) satisfies

$$\begin{aligned} \langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k, M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle&= \langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k, {\widetilde{M}}({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle + \rho \Vert B(y^k-{\widetilde{y}}^k)\Vert ^2 \\&\ge \langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k, {\widetilde{M}}({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle , \end{aligned}$$

and this validates the reasonableness of the choice of step size used in [2].

It is easy to verify that the matrix H, defined in (3.1), is always positive definite under the condition that $\rho >-1/(2\sigma \lambda _{\max }(B^\top B))$. Therefore, it follows that

$$\begin{aligned} \langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k , M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle \ge \frac{\delta }{1+\delta }\Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2>0, \quad \forall {\varvec{u}}^k\ne {{\widetilde{{\varvec{u}}}}}^k. \end{aligned}$$

(4.6)

A formal proof of this result is presented below, following a similar line of reasoning as used in [10, 11].

Lemma 4.3

Let H and M be defined as (3.1). If the parameters $\tau$ and $\sigma$ satisfy

$$\begin{aligned} \tau \sigma \frac{(1+\theta )^2}{4}< \frac{1}{\Vert A^\top A\Vert }, \end{aligned}$$

we have

$$\begin{aligned} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}, M({\varvec{u}}-{{\widetilde{{\varvec{u}}}}})\rangle \ge \frac{\delta }{1+\delta }\Vert {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}\Vert _H^2>0,\quad \forall {\varvec{u}}\ne {{\widetilde{{\varvec{u}}}}}, \end{aligned}$$

where

$$\begin{aligned} \delta := \frac{2}{1+\theta } \sqrt{\frac{1}{\tau \sigma \Vert A^\top A\Vert }}-1 >0. \end{aligned}$$

Proof

Under the assumed condition that $\delta >0$, it holds that

$$\begin{aligned} \tau (1+\delta )\Vert A^\top A\Vert \frac{(1+\theta )^2}{4}=\frac{1}{\sigma (1+\delta )}. \end{aligned}$$

Using the Cauchy–Schwarz inequality yields

$$\begin{aligned}&(1+\theta )\langle y-{\widetilde{y}}, A(x-{\widetilde{x}})\rangle \\&\quad \ge -(\tau (1+\delta )\Vert A^\top A\Vert )\frac{(1+\theta )^2}{4}\Vert y-{\widetilde{y}}\Vert ^2-\frac{1}{\tau (1+\delta )\Vert A^\top A\Vert }\Vert A(x-{\widetilde{x}})\Vert ^2 \\&\quad =-\frac{1}{\sigma (1+\delta )}\Vert y-{\widetilde{y}}\Vert ^2-\frac{1}{\tau (1+\delta )\Vert A^\top A\Vert }\Vert A(x-{\widetilde{x}})\Vert ^2 \\&\quad \ge -\frac{1}{1+\delta }\left( \frac{1}{\tau }\Vert x-{\widetilde{x}}\Vert ^2+\frac{1}{\sigma }\Vert y-{\widetilde{y}}\Vert ^2 \right) . \end{aligned}$$

On the other hand,

$$\begin{aligned} \Vert {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}\Vert _{H}^2&=\frac{1}{\tau }\Vert x-{\widetilde{x}}\Vert ^2+\frac{1}{\sigma }\Vert y-{\widetilde{y}}\Vert ^2+2\rho \Vert y-{\widetilde{y}}\Vert _{B^\top B}^2 \\&\ge \frac{1}{\tau }\Vert x-{\widetilde{x}}\Vert ^2+\frac{1}{\sigma }\Vert y-{\widetilde{y}}\Vert ^2. \end{aligned}$$

Combining the above inequalities leads to

$$\begin{aligned} \frac{1}{1+\delta }\Vert {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}\Vert _{H}^2 +(1+\theta )\langle y-{\widetilde{y}}, A(x-{\widetilde{x}})\rangle \ge 0. \end{aligned}$$

For any ${\varvec{u}}\ne {{\widetilde{{\varvec{u}}}}}$, we get

$$\begin{aligned}&\langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}, M({\varvec{u}}-{{\widetilde{{\varvec{u}}}}})\rangle \\&\quad =\Vert {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}\Vert _{H}^2+(1+\theta ) \langle y-{\widetilde{y}}, A(x-{\widetilde{x}})\rangle \\&\quad =\frac{\delta }{1+\delta }\Vert {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}\Vert _H^2+\frac{1}{1+\delta }\Vert {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}\Vert _{H}^2+(1+\theta ) \langle y-{\widetilde{y}}, A(x-{\widetilde{x}})\rangle \\&\quad \ge \frac{\delta }{1+\delta }\Vert {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}\Vert _H^2>0. \end{aligned}$$

Hence, the assertion of this lemma is proved. $\square$

Therefore, it follows from Lemma 4.3 that the inequality (4.6) holds. Then, an immediate consequence to (4.3) and (4.6) is that,

$$\begin{aligned} \langle H({\varvec{u}}^k-{\varvec{u}}^*),H^{-1}M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle \ge \frac{\delta }{1+\delta }\Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2>0,\quad \forall {\varvec{u}}^k\ne {{\widetilde{{\varvec{u}}}}}^k. \end{aligned}$$

Obviously, the above inequality indicates that, at any iteration k of the algorithm, $-H^{-1}M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)$ is a descent direction of the distance function $\frac{1}{2}\Vert {\varvec{u}}-{\varvec{u}}^*\Vert _H^2$, which also ensures that the correction step (3.3) is well defined.

Theorem 4.1

Let ${\varvec{u}}^*$ be an arbitrary solution of (1.1). Then, there exists a constant $c>0$ such that the sequence $\{{\varvec{u}}^k\}$ generated by Algorithm 1 satisfies

$$\begin{aligned} \Vert {\varvec{u}}^{k+1}-{\varvec{u}}^*\Vert _H^2 \le \Vert {\varvec{u}}^k-{\varvec{u}}^*\Vert _H^2 - c\Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2. \end{aligned}$$

(4.7)

Proof

Recalling the iterative scheme (3.3), we have

$$\begin{aligned}&\Vert {\varvec{u}}^{k+1}-{\varvec{u}}^*\Vert _H^2 \nonumber \\&\quad = \Vert {\varvec{u}}^k-\gamma \alpha _k H^{-1}M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)-{\varvec{u}}^*\Vert _H^2 \nonumber \\&\quad =\Vert {\varvec{u}}^k-{\varvec{u}}^*\Vert _H^2 - 2\gamma \alpha _k\langle {\varvec{u}}^k-{\varvec{u}}^*,M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle + \gamma ^2\alpha _k^2\Vert H^{-1}M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\Vert _H^2 \nonumber \\&\quad \le \Vert {\varvec{u}}^k-{\varvec{u}}^*\Vert _H^2 - 2\gamma \alpha _k\langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k,M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle + \gamma ^2\alpha _k^2\Vert H^{-1}M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\Vert _H^2 \nonumber \\&\quad =\Vert {\varvec{u}}^k-{\varvec{u}}^*\Vert _H^2 - \gamma (2-\gamma )\alpha _k\langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k,M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle \nonumber \\&\quad \le \Vert {\varvec{u}}^k-{\varvec{u}}^*\Vert _H^2 - \gamma (2-\gamma )\alpha _k \frac{\delta }{1+\delta } \Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2. \end{aligned}$$

(4.8)

It follows from the definition of $\alpha _k$, defined by (3.4), that

$$\begin{aligned} \alpha _k&:=\frac{({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)^\top M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)}{\Vert H^{-1}M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\Vert _H^2} \\&\ge \frac{\delta \Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2}{(1+\delta )\Vert M^\top H^{-1}M\Vert \Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert ^2} \\&\ge \frac{\delta \lambda _{\min }(H)}{(1+\delta )\Vert M^\top H^{-1}M\Vert } \\&=\frac{\delta \cdot \min \left\{ \frac{1}{\tau },\frac{1}{\sigma }+2\rho \lambda _{\min }(B^\top B)\right\} }{(1+\delta )\Vert M^\top H^{-1}M\Vert } \\&:=\alpha _{\min } >0, \end{aligned}$$

where $\lambda _{\min }(\bullet )$ denotes the minimum eigenvalue of a matrix $(\bullet )$.

Therefore, we conclude from (4.8) that

$$\begin{aligned} \Vert {\varvec{u}}^{k+1}-{\varvec{u}}^*\Vert _H^2\le \Vert {\varvec{u}}^k-{\varvec{u}}^*\Vert _H^2 -\left( \frac{\gamma (2-\gamma )\delta \alpha _{\min }}{1+\delta }\right) \Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2. \end{aligned}$$

Setting $c:=\left( \gamma (2-\gamma ){\delta }\alpha _{\min }\right) /({1+\delta })$ completes the proof. $\square$

The above theorem proves that the sequence $\{{\varvec{u}}^k\}$ generated by Algorithm 1 is Fejér monotone with respect to the solution set of (2.1). Following the line of reasoning presented in [10, Theorem 3.7] (see also [2, 4]), we can also prove that Algorithm 1 enjoys global convergence. Therefore, we only state the following theorem and refer the reader to the aforementioned references for a detailed proof of this result.

Theorem 4.2

The sequence $\{{\varvec{u}}^k\}$ generated by Algorithm 1 is globally convergent to a solution point of (1.1).

Next, we prove that Algorithm 1 has a worst-case ${\mathcal {O}}(1/t)$ convergence rate in an ergodic sense. We begin this analysis with a fundamental inequality proved in the following lemma.

Lemma 4.4

Let the sequences $\{{\varvec{u}}^k\}$ and $\{{{\widetilde{{\varvec{u}}}}}^k\}$ be generated by Algorithm 1. Then, the following inequality

$$\begin{aligned} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,F({\varvec{u}})\rangle +\frac{1}{2\gamma \alpha _k}\left( \Vert {\varvec{u}}-{\varvec{u}}^k\Vert _H^2 - \Vert {\varvec{u}}-{\varvec{u}}^{k+1}\Vert _H^2\right) \ge \frac{(2-\gamma )\delta }{2(1+\delta )}\Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2,\nonumber \\ \end{aligned}$$

(4.9)

holds for all ${\varvec{u}}\in \varOmega$, where H is as defined in (3.1).

Proof

Rearranging the terms in (4.1), we get

$$\begin{aligned} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,F({{\widetilde{{\varvec{u}}}}}^k)\rangle \ge \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle . \end{aligned}$$

(4.10)

It follows from the monotonicity of F that

$$\begin{aligned} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,F({\varvec{u}})\rangle \ge \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,F({{\widetilde{{\varvec{u}}}}}^k)\rangle ,\quad \forall {\varvec{u}}\in \varOmega . \end{aligned}$$

Clearly, from (4.10), we have

$$\begin{aligned} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,F({\varvec{u}})\rangle \ge \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle ,\quad \forall {\varvec{u}}\in \varOmega . \end{aligned}$$

(4.11)

Note that the correction step (3.3) can be rewritten as

$$\begin{aligned} {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k = \frac{1}{\gamma \alpha _k}M^{-1}H({\varvec{u}}^k-{\varvec{u}}^{k+1}), \end{aligned}$$

and consequently, we have

$$\begin{aligned} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k, M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle = \frac{1}{\gamma \alpha _k} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k, H({\varvec{u}}^k-{\varvec{u}}^{k+1})\rangle . \end{aligned}$$

(4.12)

An application, on the right hand side of (4.12), of the following equality

$$\begin{aligned} \langle {\varvec{a}}-{\varvec{b}},H({\varvec{c}}-{\varvec{d}})\rangle = \frac{1}{2}\left( \Vert {\varvec{a}}-{\varvec{d}}\Vert _H^2-\Vert {\varvec{a}}-{\varvec{c}}\Vert _H^2\right) +\frac{1}{2}\left( \Vert {\varvec{c}}-{\varvec{b}}\Vert _H^2-\Vert {\varvec{d}}-{\varvec{b}}\Vert _H^2\right) \end{aligned}$$

with settings ${\varvec{a}}:={\varvec{u}}$, ${\varvec{b}}:={{\widetilde{{\varvec{u}}}}}^k$, ${\varvec{c}}:={\varvec{u}}^k$, and ${\varvec{d}}:={\varvec{u}}^{k+1}$, yields

$$\begin{aligned}&\langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,H({\varvec{u}}^k-{\varvec{u}}^{k+1})\rangle \nonumber \\&\quad =\frac{1}{2}\left( \Vert {\varvec{u}}-{\varvec{u}}^{k+1}\Vert _H^2-\Vert {\varvec{u}}-{\varvec{u}}^k\Vert _H^2\right) +\frac{1}{2}\left( \Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2-\Vert {\varvec{u}}^{k+1}-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2\right) . \end{aligned}$$

(4.13)

The last term of (4.13) satisfies

$$\begin{aligned}&\frac{1}{2}\left( \Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2-\Vert {\varvec{u}}^{k+1}-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2\right) \nonumber \\&\quad =\frac{1}{2}\left( \Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2 - \Vert {\varvec{u}}^k-\gamma \alpha _k H^{-1}M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2\right) \nonumber \\&\quad =\frac{1}{2}\gamma (2-\gamma )\alpha _k\langle {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k,M({\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k)\rangle \nonumber \\&\quad \ge \frac{\delta \gamma (2-\gamma )\alpha _k}{2(1+\delta )}\Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2 , \end{aligned}$$

(4.14)

where the first equality comes from (3.3) and the second inequality follows from (4.6). Combining (4.11), (4.12), (4.13), and (4.14) leads to

$$\begin{aligned} \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,F({\varvec{u}})\rangle \ge \frac{1}{2\gamma \alpha _k}\left( \Vert {\varvec{u}}-{\varvec{u}}^{k+1}\Vert _H^2-\Vert {\varvec{u}}-{\varvec{u}}^k\Vert _H^2\right) +\frac{(2-\gamma )\delta }{2(1+\delta )}\Vert {\varvec{u}}^k-{{\widetilde{{\varvec{u}}}}}^k\Vert _H^2, \end{aligned}$$

and the desired result is obtained by rearranging the terms in the above inequality. $\square$

Theorem 4.3

For any integer $t>0$, we denote

$$\begin{aligned} {\bar{\varvec{u}}_t}=\frac{1}{\varUpsilon _t}\sum _{k=0}^t \alpha _k{{\widetilde{{\varvec{u}}}}}^k,\quad \text {with} \quad \varUpsilon _t= \sum _{k=0}^t \alpha _k , \end{aligned}$$

(4.15)

where ${{\widetilde{{\varvec{u}}}}}^k$ ($k=0,1,\cdots ,t$) are generated by Algorithm 1 and $\alpha _k$ is given by (3.4). Then, we have ${\bar{\varvec{u}}_t}\in \varOmega$ and

$$\begin{aligned} \langle {\bar{\varvec{u}}_t}-{\varvec{u}}, F({\varvec{u}})\rangle \le \frac{1}{2\gamma \alpha _{\min }(t+1)}\Vert {\varvec{u}}-{\varvec{u}}^0\Vert _H^2. \end{aligned}$$

Proof

First, as a direct consequence of (4.9), we have

$$\begin{aligned} \alpha _k \langle {\varvec{u}}-{{\widetilde{{\varvec{u}}}}}^k,F({\varvec{u}})\rangle +\frac{1}{2\gamma }\Vert {\varvec{u}}-{\varvec{u}}^k\Vert _H^2\ge \frac{1}{2\gamma }\Vert {\varvec{u}}-{\varvec{u}}^{k+1}\Vert _H^2,\quad \forall {\varvec{u}}\in \varOmega . \end{aligned}$$

Summing the above inequality over $k=0,1,\cdots ,t$ results in

$$\begin{aligned} \left\langle \varUpsilon _t {\varvec{u}}-\sum _{k=0}^t\alpha _k {{\widetilde{{\varvec{u}}}}}^k,F({\varvec{u}})\right\rangle + \frac{1}{2\gamma }\Vert {\varvec{u}}-{\varvec{u}}^0\Vert _H^2\ge 0,\quad \forall {\varvec{u}}\in \varOmega . \end{aligned}$$

As $\alpha _k\ge \alpha _{\min }$, we have $\varUpsilon _t\ge (t+1)\alpha _{\min }$ and

$$\begin{aligned} \frac{1}{\varUpsilon _t} \le \frac{1}{(t+1)\alpha _{\min }}. \end{aligned}$$

Therefore,

$$\begin{aligned} \left\langle \frac{1}{\varUpsilon _t}\sum _{k=0}^t \alpha _k{{\widetilde{{\varvec{u}}}}}^k-{\varvec{u}},F({\varvec{u}})\right\rangle \le \frac{1}{2\gamma \varUpsilon _t}\Vert {\varvec{u}}-{\varvec{u}}^0\Vert _H^2\le \frac{1}{2\gamma \alpha _{\min }(t+1)}\Vert {\varvec{u}}-{\varvec{u}}^0\Vert _H^2, \end{aligned}$$

and the assertion of this theorem is obtained. $\square$

The foregoing theorem shows that for a given arbitrary compact set ${\mathcal D}\subset \varOmega$, after t iterations of Algorithm 1, we obtain an approximate solution ${\bar{\varvec{u}}_t}$, given by (4.15), for the variational inequality (2.1) [and equivalently for the saddle point problem (1.1)] such that

$$\begin{aligned} \sup \left\{ \langle {\bar{\varvec{u}}_t} - {\varvec{u}}, F({\varvec{u}})\rangle \right\} \le \epsilon , \end{aligned}$$

where $\epsilon :=\frac{d^2}{2\gamma \alpha _{\min }(t+1)}$, with $d:=\sup \{\Vert {\varvec{u}}-{\varvec{u}}^0\Vert _H\;|\;{\varvec{u}}\in \varOmega \}$. Hence, the ${\mathcal {O}}(1/t)$ convergence rate of Algorithm 1 is established in an ergodic sense.

5 Conclusion

In this paper, we introduced a primal–dual prediction–correction algorithm for solving a saddle point optimization problem. The proposed algorithm enjoys an algorithmic framework that bridges the gap between the approaches described in [2] and [10]. As a byproduct, we also obtain a projection-based primal–dual algorithm by choosing an appropriate proximal parameter, which is comparatively easier to implement than the methods described in [2, 4, 10], as long as the projections of both $\mathcal{{X}}$ and $\mathcal{{Y}}$ are simple enough to be computed. Furthermore, we also established that our proposed algorithm is globally convergent with a worst-case ${\mathcal {O}}(1/t)$ convergence rate in an ergodic sense, which supports the numerical performance reported in [2, 10] from a theoretical perspective.

In conclusion, note that the computational experience reported in several previous works in the literature has indicated that the speed of convergence of the PDHG method is highly sensitive with respect to the choice of the values of $\tau$ and $\sigma$. Most recently, the authors [7] proposed an adaptive version of PDHG to accelerate its numerical performance. Taking a cue from this approach, we can also gainfully employ an adaptive strategy for the acceleration of our method, and the results of this research are forthcoming.