Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

Much work on mathematics teacher knowledge has drawn on the earlier conceptualisations of Shulman (1986). In brief, his model of teacher knowledge, prompted more by concerns about inadequate teacher education programmes rather than individual teacher competence, comprised three components: subject matter content knowledge, pedagogical content knowledge and curricular knowledge. More recently, a number of researchers have developed frameworks that essentially present mathematics teacher knowledge in generalised forms that acknowledge not only the role of subject matter knowledge in successful teaching – an understanding of the substantive and syntactic properties of mathematics – but also transformative pedagogic knowledge, whereby subject matter knowledge is made amenable to multiple presentations. Such models include, for example, Sherin’s (2002) discussion of content knowledge complexes, reflecting the automated and simultaneous application of both content and pedagogic content knowledge, Rowland, Huckstep, and Thwaites’ (2005) four-dimensional model of primary preservice teacher knowledge, and the University of Michigan team’s model incorporating common content knowledge, specialized content knowledge, horizon knowledge, knowledge of content and students and knowledge of content and teaching (Ball, Thames, & Phelps, 2008). All such models can be construed as representations or developments of Shulman’s (1986) content and pedagogical content knowledge. However, such categorisations, in their presentations of essentially personal attributes, seem to locate teacher knowledge within the individual. While this is not of itself problematic, it is difficult to understand, particularly in the light of the arguments below, how such frameworks are not consequences of particular cultural contexts drawing on both systemic imperatives and didactic folklore.

As can be seen from the above, with few exceptions, most mathematics teacher knowledge research has been undertaken by US-based researchers, many of whom seem to have overlooked the possibility that teachers’ mathematical knowledge, as manifested in their observable behaviour, is a cultural construction, as evidenced by other US-based researchers (Hiebert et al., 2003; Schmidt et al., 1996; Stigler, Gallimore, & Hiebert, 2000). In this paper, a framework for analysing teachers’ mathematical knowledge that explicitly acknowledges the cultural discourse in which mathematics teaching and learning occur is proposed. It does not seek to replace existing models, but to complement them. Admittedly, some teacher knowledge researchers have acknowledged the limitations of work undertaken in single cultural contexts (Ball et al., 2008), but few have considered whether frameworks developed in one cultural context are applicable in another (although the studies of An, Kulm, and Wu (2004) and Delaney, Ball, Hill, Schilling, and Zopf (2008) are exceptions). This is an issue of some salience. For example, discussing Spanish teachers’ subject knowledge, Escudero and Sánchez (2007, p. 314) examine several textbook representations of Thales’ theorem, one of which reads “if several parallel straight lines (AA´, BB´, CC´) are cut by two transversal lines (AC, A´C´), the ratio of any two segments of one of these transversals is equal to the ratio of the corresponding segments of the other transversal”. Such presentations, largely unknown in current English texts, not only highlight differences in curricular expectations, but also provoke the reaction that whether they are categorised as common or specialised content knowledge is probably of less importance than whether they should be required knowledge of teachers working within curriculum frameworks that do not privilege them. Thus, in an attempt to shift teacher knowledge from the personal construct embedded in much recent research, this paper considers teacher knowledge as a social construction located within particular cultural contexts.

Mathematical Knowledge in Teaching: A Culturally-Located Model

It is probably not an unreasonable conjecture that not only are teachers’ actions reflections of their goals, but also that their goals reflect an idealised view of what it is they want to achieve for their students. In this respect, Reeve and Jang (2006) describe two forms of long term goals focused respectively on learner autonomy and learner conformity, while others, in accordance with psychological research, have discussed goals as focused on learner mastery or learner performance (Wolters & Daugherty, 2007). In respect of this study, the professional goals and ambitions teachers have for their students are construed as idealised learning outcomes relating to knowledge, skills and dispositions that are addressed by an equally idealised set of didactics that may or may not be linked with learner autonomy or conformity, mastery or performance orientation. In this manner, teachers’ long term goals reflect an idealised curriculum. For example, an idealised curriculum may relate to learner acquisition of adaptive expertise, or the flexible application of an integrated and connected set of concepts and procedures (Baroody, 2003; Kilpatrick, Swafford, & Findell, 2001). Another may reflect Dutch expectations in which learner experiences and teachers’ structuring of mathematics are located in problems that are imaginably real to the learner (Van den Heuvel-Panhuizen, 2003). Importantly, Andrews’ (2007a) investigation of English and Hungarian mathematics teachers’ professional goals found most English teachers articulating goals concerning mathematics as applicable number and the means by which learners are prepared for a world beyond school, while their Hungarian colleagues privileged mathematics as problem-solving and logical thinking. Such differences highlight two characteristics of the idealised curriculum: it is located in individual experience and it is articulable.

According to Hufton and Elliott (2000, p. 117) teachers’ practices are so “deep in the background of the schooling process … so taken-for-granted … as to be beneath mention”. In this regard, a number of researchers have attempted to “reveal taken-for-granted and hidden aspects of teaching” (Hiebert et al., 2003, p. 3) and have unveiled unnoticed but culturally-located practices characteristic of the systems under scrutiny (Schmidt et al., 1996; Stigler et al., 2000). The consensus seems to be that teachers employ pedagogical strategies which, through repeated enactment, are not only typical of a country’s lessons, but also beneath their consciousness (Cogan & Schmidt, 1999). This sense of typicality has found confirmation in Andrews’ research in which mathematics teachers from four European countries have been observed to behave, at least as far as seven generic learning outcomes and ten generic didactic strategies are concerned, in ways that align them closely with their national colleagues and distinguish them from their overseas colleagues (Andrews, 2007b, 2009a, 2009b). Explanations suggest that cultures “shape the classroom processes and teaching practices within countries, as well as how students, parents and teachers perceive them” (Knipping, 2003, p. 282). Thus, it seems that teachers’ actions, in addition to being informed by individuals’ idealised curricula, are informed by culturally-located and beneath articulation received curricula. The received curriculum, characterised by its hidden, inarticulable, properties is amenable only to inference and can be construed as a set of collective practices and goals.

Of course, irrespective of the idealised and received curricular determinants of their actions, most teachers work within systemically defined curricular frameworks, which the second international mathematics study described as intended curricula – systemically located expectations of learner outcomes which frequently reflect historical values and imperatives. An assumption too frequently made in mathematics education circles is that mathematics curricula, particularly in culturally similar countries, share many similarities and few substantial differences. In this regard, a brief analysis of the mathematics curricula of Flanders and Hungary and their expectations with regard to linear equations, the countries and topic represented in this chapter, is salient.

The Flemish curriculum for mathematicsFootnote 1 in the first grade of secondary education is located in three domains: number theory, algebra and geometry. Within each strand are three core objectives concerning (1) concept formation and knowledge of facts; (2) procedures; and (3) cohesion between concepts. The particular expectations for simple linear equations are:

  • First grade of secondary education: Use letters to represent generalisations and unknowns, solve equations of the first degree with one unknown and simple problems, which can be converted to such an equations.

  • Second grade of secondary education: Solve equations of the first and second degree in one unknown, and problems which can be converted into such equations.

The generic expectations focus on issues concerning language, problem solving as both a mathematical activity and as a means modelling the real world, ‘the importance and the need for providing proof, which is inherent in mathematics’, and a need for students to ‘develop self-regulation by focusing on the problem, planning, executing and monitoring the solution process; develop self-confidence as a result of successfully solving mathematical problems; develop a sense of independence and determination in tackling problems’.

The Hungarian curriculumFootnote 2 for grades 5–8 (upper primary) includes an introduction locating the learning of mathematics within a developmental framework, acknowledging explicitly the transition from concrete and inductive to abstract and deductive. It addresses the affective domain while making no concession to ensure that children are presented with intellectually challenging mathematics. These aims are supported by five broad themes concerning the application of acquired mathematical concepts: the development of a mathematical approach; problem-solving skills and logical thinking; the application of acquired learning methods and thinking; and developing the right attitude towards learning. Curriculum content is also characterised according to five broad themes, namely: methods of thinking, algebra and arithmetic, mathematical relations, functions and sequences, geometry, and probability and statistics. First degree equations with a single unknown are covered in each of the 4 years. Students should

  • Year 5: Solve simple equations of the first degree by deduction, breaking down, checking by substitution along with simple problems expressed verbally.

  • Year 6: Solve simple equations of the first degree and one variable with freely selected method.

  • Year 7: Solve simple equations of the first degree by deduction and the balance principle. Interpret texts and solve verbally expressed problems. Solve equations of the first degree and one variable by the graphical method.

  • Year 8: Solve deductively equations of the first degree in relation to the base set and solution set. Analyse texts and translate them into the language of mathematics. Solve verbally expressed mathematical problems.

Such details highlight differences in the underlying systemic conceptions of mathematics and its teaching and, it is argued, confirm that teachers’ expected subject knowledge is clearly a function of the system in which they work. For example, the Hungarian curriculum’s developmental framework, reflected in the annual visitation and incremental conceptual growth of linear equations, differs markedly from the espoused expectations of the Flemish.

In sum, teachers’ mathematical knowledge in teaching is a social construction drawing, inter alia, on the culturally-located idealised, received and intended curricula. It is conjectured that the closer the three are aligned, the more coherent both subject knowledge and its didactic manifestation are likely to be; although if systemic expectations are limited, then even closely aligned curricula may result in limited opportunities for learning. Also, of course, if the three curricula are unaligned, then the result may be didactic anarchy, as in the case of Mrs. Oublier whereby reform-oriented practices were incorporated alongside unconsciously held traditional beliefs about mathematics teaching and normative classroom behaviours (Cohen, 1990). In this chapter, the tripartite framework of idealised, received and intended curricula is examined from the perspective of its explaining variation in the ways in which teachers present mathematics to their students. To achieve this objective, two sequences of lessons taught on linear equations to students in grade 8 in Flanders and Hungary are examined. Each sequence was taught by a teacher defined locally as effective in the manner of the learner’s perspective study (Clarke, 2006).

The Project

Funded by the European Union, the Mathematics Education Traditions of Europe (METE) project examined aspects of mathematics teaching in Belgium (Flanders), England, Finland, Hungary and Spain. The main dataset comprised video recordings of four sequences of lessons taught in each country on agreed topics by teachers defined locally, in the manner of the learner’s perspective study (Clarke, 2006) as effective. After recording, videotapes were downloaded and compressed for ease of sharing and coded against a generic schedule developed in a bottom-up and iterative manner during the first year of the project. Full details of this process can be seen in Andrews (2007c), although it is probably sufficient to say that the final coding schedule comprised seven generic learning outcomes and ten generic didactic strategies which project colleagues thought, on the basis of a year’s live observations, reflected well their perceptions of the mathematics teaching of the five countries.Footnote 3 Codes were applied to the episodes of a lesson, where an episode was defined “as that part of a lesson in which the teacher’s observable didactic intention remained constant” (Andrews, 2007c, p. 499), with no limit to the number of codes that could be applied. The only criterion was the presence of a learning outcome or didactic strategy at some point during the episode. Several quantitative analyses have been undertaken and these have proved effective in highlighting similarities and differences in the emphases found in the respective countries’ episodes (Andrews, 2007b, 2009a, 2009b). However, much work has still to be done in respect of qualitative analyses, and this chapter represents a first pass at that process.

Two sequences of four lessons on the topic of linear equations, taught to grade 8 students in Flanders and Hungary, are reported below. The topic was chosen because it reflects an important transition as mathematics passes from concrete and inductive to abstract and deductive. Particularly pertinent to the analysis presented in this chapter is research highlighting a distinction between arithmetical and algebraic equations. On one hand, arithmetic equations, with the unknown on one side only, are generally assumed to be susceptible to undoing (Filloy & Rojano, 1989). On the other hand, algebraic (non-arithmetic) equations, with unknowns on both sides, cannot be solved by arithmetic-based approaches and require not only that the learner “understand that the expressions on both sides of the equals sign are of the same nature (or structure)” (Filloy & Rojano, 1989, p. 19), but also that they are able to operate on the unknown as an entity and not a number. Thus, arithmetic equations are procedural, while algebraic or non-arithmetic equations are structural (Kieran, 1992). The choice of these two sequences was based on the availability of English language mathematics curricula, and because they provided interesting similarities and differences in the ways the two teachers concerned – Pauline in Flanders and Eva in Hungary – conceptualised and presented this iconic topic to their students. These similarities and differences, drawing on the generic learning outcomes and didactic strategies exploited in the METE project, can be seen in Table 7.1. In respect of similarities of learning outcomes, for example, both teachers emphasised student acquisition of conceptual knowledge and procedural knowledge, while neither attended to derived knowledge. However, there were substantial differences in the emphases placed on structural knowledge, mathematical efficiency and problem solving. Thus, the two teachers offer interesting and culturally different contexts for discussing the proposed framework.

Table 7.1 Percentage of all Flemish and Hungarian episodes coded for each of the generic learning outcomes and didactic strategies alongside the same for Pauline and Eva
Full size table

Both teachers were in their late twenties with between 6 and 7 years’ experience. The Flemish lessons were drawn from a middle track class in an unremarkable comprehensive in a provincial university city while the Hungarian derived from a Budapest gimnazium. Each sequence is reported as accurately as data permit. Videographers were instructed to focus on the teachers whenever they were speaking. Teachers wore radio-microphones while a static microphone was placed strategically to capture as much student talk as possible. Lessons were transcribed and subtitles constructed so that colleagues from each country could watch any lesson from another. Thus, any description of a lesson will be informed by several layers of interpretation and choice – videographer, transcriber, interpreter and writer. The descriptions below are also informed by a decision to focus attention on the activities and tasks teachers present and the manner in which they implemented them. As Thompson, Carlson, and Silverman (2007, p. 416) observe, “… tasks do not have agency. Tasks do not elicit behavior any more than a hammer elicits hammering”. Thus, the manner in which the two teachers presented their tasks and the means by which this presentation facilitated student agency informed the interpretation and reporting of the two sequences. The order of the two sequences is determined by nothing other than alphabetical order.

Pauline

Pauline’s class comprised 25 grade 8 students of average attainment. It was clear from conversations between teacher and students that simple linear equations had been covered earlier in the students’ learning of mathematics; an experience, drawing on a vocabulary of task and outcome, where the unknown was always located on the right hand side of an equation and solved by a process of intuitive undoing.

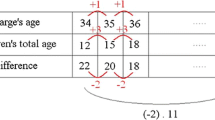
The first lesson began with Pauline posing a problem involving characters from the cartoon series The Simpsons: if Bart, Lisa and Maggie, are 7, 5 and 0 years old respectively and their mother, Marge, is 34 years old, in how many years would the sum of the children’s ages equal their mother’s? Pauline drew a table of values before completing, collaboratively, the first three columns.

Marge’s age

34

35

36

…

Children’s total age

12

15

18

…

Individual completion of the remaining columns was followed by a discussion during which the solution of 11 years and the fact that with every year’s increase in Marge’s age the sum of the children’s increased by three were agreed. Pauline then introduced an unknown, x, to represent the number of years to pass before the two sums would be equal. This led, after several closed questions, to her writing that Marge would acquire 34 + x years, while the children would reach 7 + x, 5 + x and 0 + x respectively. Lastly, she wrote 34 + x = 7 + x + 5 + x + 0 + x, which she simplified to 34 + x = 12 + 3x.

After this Pauline demonstrated how each of the two rows of the table of values could be represented graphically to show an intersection after 11 years. This brief exposure to an alternative approach was followed by her modelling, by means of questions and the introduction of the balance, the solution to x + 7 = 9. She sketched the left-hand image of the two below and asked how the unknown, x, could be found. A student suggested that removing seven from both sides would not only maintain the balance but also provide a unique value for x, as reflected in the second image. The process was then summarised symbolically as shown. This was followed by Pauline modelling, by means of the bracketed process, solutions to x – 2 = 10, 3x = 8 and \(\frac{x}{3}=7\).

figure 7_a_186043_1_En

Full size image

Finally, in this particular episode, Pauline drew the table below on an OHT and explained, with no reference to the balance or any questions posed to her class, the relationship between each of her four exemplars to their respective formalisations. During this time, she included aspects of the history of equations on the same slide and their significance in the work of, for example, Descartes.

a = b

⇒

a + c = b + c

  

a – c = b – c

  

a. c = b. c

  

a: c = b: c

The lesson ended with an exercise involving problems of the form, x – 3 = 10, 200 – x = 20 and so on. The solutions to these were to be placed in a crossword-like grid.

The second lesson began with students continuing the exercise started the previous lesson. After several minutes Pauline initiated a class discussion focused on particular difficulties. For example, she spent some time discussing the solution to \(\frac{2x}{3}\,=\,30\) and how division by \(3/2\) was equivalent to multiplying by its inverse. The class then returned to the exercise before answers were presented on the overhead projector and students corrected their own work. During both periods of seatwork Pauline circulated the room helping individuals. In this early part of the lesson, a student asked whether they should continue to use the balance method and was told that, for the time being, she should continue to use it.

In the next phase of the lesson, Pauline wrote 6(x – 5) – 8 = x – 3 on the board and indicated to her students that this was a substantially more difficult equation than those previously experienced but that, if they concentrated on what she was about to show them, they would soon be able to solve it confidently. When asked about the differences between this new equation and those solved earlier, one student commented that there was an x in both the task and the outcome. Pauline commented that they were no longer to think about equations as task and outcome but to talk about left terms and right terms. Following this, Pauline began a formal treatment in which the algebra, including actions, was written on the left side of the board and justificatory annotations on the right. Throughout the process Pauline questioned continuously. The following is what she wrote.

$$\qquad\qquad\qquad\qquad\qquad\qquad 6(x - 5) - 8 = x - 3 \qquad\qquad(1)\ \textrm{Eliminate brackets}$$

A discussion followed in which Pauline drew from her students notions of associativity and commutativity before settling on distributivity as the warrant for what she was about to do. This included an aside, written on a different board, during which she discussed which rule would be applied to 6.(5x). A student initially proposed the brackets rule (de haakjes regel) before Pauline steered them to associativity.

$$6x - 30 - 8 = x - 3 (2)\ \textrm{Calculate if possible}$$
$$\begin{array}{rl}\,\,6x - 38 &\,\,{=}\, x - 3 \\ - x({\textrm{ }}) - x \\ 6x - 38 - x &\,\,{=}\, - 3 \\ \end{array}$$

Although this was not annotated, Pauline asserted the need to collect like terms and, in particular, get the unknowns to one side and the numbers to the other.

$$\qquad\qquad\qquad 5x - 38 = - 3\quad \qquad(3)\ \textrm{Get x in one term and the rest in the other}$$

+ 38() + 38

$$ 5x = - 3 + 38\quad \quad\qquad\qquad\qquad\qquad(4)\ \textrm{Calculate if possible}$$
$$5x = 35$$

:5( ):5 (5) Divide both terms by the coefficient of x (Pauline encouraged her students to use the expression factor of x)

$$x = \frac{{35}}{5}$$
$$x = 7$$

Having obtained a solution and discussed the uniqueness of the value obtained, Pauline undertook a check. This took the following form.

$$\begin{array}{rl} 6 \cdot (7 - 5) - 8 &\,{=}\,\, 7 - 3 \\ 6 \cdot 2 - 8 &\,{=}\,\, 4 \\ 12 - 8 &\,{=}\,\, 4 \\ 4 &\,{=}\,\, 4 \\ \end{array}$$

The third and fourth lessons followed similar forms. They began with Pauline revisiting the equations posed at the end of the previous lesson by means of closed questions supplemented by overhead transparencies on which she had prepared solutions. Subsequently, students were invited to work on selected problems from their text while she circulated the room helping individuals before further discussion of solutions. One point of interest arose during the public solution to an equation in which all coefficients were fractions; Pauline explained to her students that by rewriting all fractions over a common denominator and then multiplying the whole equation by the common denominator reduced the equation to one with integer coefficients that could be solved as all those that had gone before.

Eva

This sequence of lessons was taught to a class of 20 grade 7 students in a Budapest gimnazium. The first lesson began with Eva presenting several open sentences, some of which were mathematical, to revisit notions of truth and the role of the basic set in determining the validity of a statement. This was followed by a brief discussion in which she defined an equation as comprising two expressions connected by an equals sign and that such expressions may or may not contain variables or unknowns depending on circumstances. Throughout, Eva wrote much on the board, although it is not clear whether or not students were expected to make notes. Next, Eva posed an exercise in which three open sentences were to be solved in relation to a basic set defined as integers in the range –3≤ □ ≤ 3. The open sentences were 5 – □ = 8, 5 – □ > 6 and □.2 = 7.

Once solutions or ideas had been shared, Eva posed several oral problems like, “Kala is twice as old as her sister. The sum of their ages is 24, how old are they?” Each was solved individually before students shared their solution strategies. At the close of this episode, Eva commented that such problems could be solved mentally with the application of logic.

Eva now split the class into four groups. Each was given a different word problem for translating into an equation. Eva made it clear that she did not expect the equation to be solved, just constructed. The first group’s problem was:

Some friends went on a trip. The first day they covered just 2 km. The second day they covered 2/10 of the remaining journey. If they covered 6 km on the second day, how long was their journey?

Each group worked for several minutes before a representative demonstrated how its equation had been derived from the text. Eventually, all four stories had been heard and four identical equations, 0,2.(x – 2) = 6, had been written on the board. This process lasted many minutes with Eva offering many prompts before all the equations had emerged correctly. She then recounted the story for each equation before inviting approaches to their solution. A volunteer proposed a thinking backwards strategy and, showing no anxiety concerning division by 0,2, obtained a value of x = 32. Eva then checked this solution against the text of each problem.

This was followed by a new word problem:

On two consecutive days, the same weight of potatoes was delivered to the school’s kitchen. On the first day, 3 large bags and 2 bags of 10 kg were delivered. On the second day, 2 large bags and 7 bags of 10 kg were delivered. If the weight of each large bag was the same, what weight of potatoes was in the large bag?

As before, Eva asked her students to construct an equation and soon, despite some hesitation concerning units, a girl wrote on the board 3x + 20 = 2x + 70. Eva asked whether their intuitive strategies would be sufficient and suggested that the balance principle would be able to help them. The class was questioned as to what this meant and several contributed suggestions indicating their understanding of its function in relation to equations. With help from her students, Eva wrote

$$\begin{array}{rl} 3x + 20 &\,{=}\,\, 2x + 70| - 20 \\ 3x &\,{=}\,\, 2x + 50| - 2x \\ x &\,{=}\,\, 50{\textrm{ kg}} \\ \end{array}$$

She reminded the class of the need to check and did so, substituting 50 back into each expression separately before comparing for equality. Lastly, she posed some algebraic equations for homework.

The second lesson began with Eva, by means of much questioning, revisiting the previous lesson. When her students reached the potato problem, she reminded them of the scale principle and, having reminded them of the importance of specifying the meaning of x, drew the following.

Drawing on what her students suggested, Eva then rubbed out two small bags on each side, leaving.

Finally, she erased two large bags from each side to show that one large bag balanced 5 bags of 10 kg.

On completion of the drawings, Eva asked students how the diagrams could be represented symbolically. The students offered sufficient for her to repeat what she had written on the board the previous lesson. At this point, she reminded her class of the importance of checking and did so.

Eva then set about checking the previous lesson’s homework. With contributions from various students, some oral and others written on the board, the class worked publicly through solutions to several equations with the unknown on both sides. Throughout, Eva focused her students on the balance principle and, in relation to one particular problem, highlighted the difficulty of expressing negative terms on the scales. On several occasions, more than one solution was reported for an equation with all being compared and points concerning elegance and efficiency made. In every case, Eva insisted that solutions were checked.

After this, an exercise was set. The first, 10a – 4 + 3a –11a = 2 + 4a + 4 – 7a, was solved collectively with Eva orchestrating the process. Then students worked quietly on their own before Eva paused to consider the solution to an apparently problematic equation; 7.(2 – c) + 5 – 4.(c – 8) = –4 – 3.(c + 3). A student went to the board and, after prompting, eliminated the brackets before completing the rest unproblematically. Finally, two similar equations were set for homework.

The third and fourth lessons, following the sharing of homework solutions, comprised sequentially posed and publicly solved equations. Some were located entirely within a world of mathematics while others were first derived from word problems. One word problem, by way of example, was “A stake is driven through a pond into the ground. If 1/4 of the stake’s length is in the ground, 3/5 in water and 2.8 m above the water, how long is the stake?” Thus, in this and other equations, coefficients were frequently fractions.

Discussion

In the following, the two sequences of lessons are examined for their similarities and key differences. This provides a basis for evaluating the effectiveness of the tripartite curriculum as a complementary framework to the Shulman-related model discussed above. To facilitate this process, the percentages, drawn from Andrews (2009a, 2009b), of all Flemish and Hungarian episodes coded for each of the generic learning outcomes and didactic strategies are presented in Table 7.1, alongside the same summary statistics for the episodes of each of the two teachers. Details of the codes are beyond this chapter, although working definitions can be seen in Table 7.2. Each teacher is discussed separately with the intended curriculum being considered before the received and idealised, due to the former being a systemic bench mark. As above, Pauline is considered first.

Table 7.2 Working definitions of the codes used in Andrews (2009a, 2009b)Footnote

In the table, the abbreviation K refers to ‘knowledge’.

Full size table

Pauline

Firstly, in respect of the intended curriculum and the particular expectations relating to equations, Pauline unambiguously and consistently addressed letters as unknowns and solutions to first degree equations. There were occasional episodes in which concept formation was addressed, as in her use of the Simpsons’ problem and the invocation of the balance when solving x + 7 = 9. She placed considerable emphasis on the development of students’ procedural knowledge. Indeed, it could be argued that the key objective of all four lessons was the development of procedural fluency. Also, despite her use of terminology relating to arithmetical structures as well as the extended and formalised discussion of the use of the denominator during the fourth lesson, there were few attempts to address cohesion between topics. In respect of generic expectations, problem solving was limited to challenging context-independent equations with no attempt to derive equations and then solve them. In a similar vein, Pauline made no attempt to engage her students in real world modelling. Lastly, there were several occasions when Pauline seemed to have been caught off-guard by her students’ suggestions. In each case, she promised to address students’ concerns or suggestions once she had completed her planned activity but never did, indicating rare opportunities for students to acquire self-regulatory competence. Overall, the resonance between the systemic expectations and Pauline’s observed behaviour is strong in some areas and weak in others. Her competence with the substantive and syntactic knowledge pertaining to equations seemed secure, although her application of that knowledge to contexts other than those of mathematics itself seemed limited. In short, her mathematical knowledge in teaching appeared less resonant with the intended curriculum than Flemish authorities might have wished.

Secondly, there are aspects of Pauline’s practice that resonate with what the literature indicates is a Flemish mathematics education tradition, although, as will be discussed below, there is also variation from it. For example, Pauline’s failure to address in any significant manner mathematical problem solving and unambiguous emphasis on procedural knowledge accords with earlier findings that Flemish mathematics teaching is largely transmissive (Waeytens, Lens, & Vandenberghe, 1997) and privileges declarative knowledge and lower-order procedural skills (Janssen, De Corte, Verschaffel, Knoors, & Colemont, 2002) above those of problem solving and adaptive expertise (Verschaffel, De Corte, & Borghart, 1997). When the quantitative data derived from Pauline’s lessons are considered, it would seem that she placed greater emphasis on procedural knowledge and lower emphases on conceptual knowledge, structural knowledge and reasoning than her Flemish colleagues (Andrews, 2009a). Moreover, in respect of her didactic emphases, she questioned and shared more rarely than her colleagues and this, coupled with a tendency to coach and assess more frequently (Andrews, 2009b), could be construed not only as distinguishing her practice from the Flemish collective, but further evidence of a teacher who, through frequent checks that students were succeeding with the work set, places great value in procedural competence. In summary, the evidence highlights elements of Pauline’s received curriculum that identify her with her colleagues and elements that suggest divergence from it.

Thirdly, in respect of the idealised curriculum, some conjectures are possible. Pauline attempted neither to engage her students in translating word problems into manipulable symbolic forms nor to offer them opportunities to model real world situations. Moreover, on the single occasion she derived an equation from a word problem – in this case an algebraic equation – she abandoned it and introduced the balance as a strategy for solving arithmetic equations. However, introducing analytical approaches to solve equations amenable to a process of reversal is didactically unproductive (Pirie & Martin, 1997; Nogueira de Lima & Tall, 2008). Additionally, when she derived the equation, little input was sought from her students, reflecting a practice whereby the problems posed, despite being mathematically challenging, were never resolved in a genuinely collaborative manner, with collectively undertaken activity always leading to a predetermined outcome. These latter observations, further supported by her frequent use of pre-prepared OHTs comprising model solutions, allude to a conception of teaching in which the role of the teacher is to structure learners’ opportunities so tightly that not only is her students’ learning trajectory entirely predetermined but also any potential deviations are thwarted. Thus, in sum, Pauline’s idealised curriculum, despite the complexity of the problems posed, seemed to reflect a teacher-centred and procedurally-focused perspective on mathematics teaching and learning. The totality of the above suggests that her idealised curriculum was at odds with elements of the intended curriculum and, in the characteristics of her observed practice, that her received curriculum also diverged from that of the Flemish collective.

Eva

In terms of the intended curriculum, Eva’s lessons show adherence to systemic developmental expectations, with the explicit curriculum content of the 4 years of equations being observed at various times in the first two lessons. For example, the year 5 and year 6 objectives were observed subsequent to the activity in which each of four groups translated a word problem into the same equation. The emphasis on the balance was not only introduced at the end of the first lesson, but also repeated systematically at the start of the second, where clear links were made between the concrete and abstract. The early emphasis on the translation of word problems, an objective of the year 7 curriculum, was observed in all four lessons, while relating the solving of equations to the base and solution sets was explicitly addressed at the start of the first lesson in a manner that indicated that this was not an unfamiliar aspect of their work. Problem solving skills were regularly addressed in both the translation of complex word problems into equations and the expectation that the students would solve non-routine equations involving unknowns on both sides along with negative numbers, fractions and brackets in various manifestations. Also, the constant sharing of solutions provided ample opportunity for students to engage with and explain their mathematical reasoning. In sum, the evidence suggests that Eva adhered closely to systemic expectations in respect of her presentation of both linear equations and generic learning outcomes.

In respect of the received curriculum, some interesting insights emerged. Firstly, Eva’s use of the balance in solving the potato problem reflected very closely a lesson observed by Andrews (2003) in which the teacher, László, not only presented pictures of the balance alongside a symbolic representation but also located his entire exposition around a physical balance and small bags containing an unknown number of glass marbles. Thus, it is not inconceivable that such presentations form part of a received didactic culture. Eva’s lessons not only adhered closely to a previously observed cycle of problem posing, solving and sharing (Andrews, 2003; Szendrei & Torok, 2007) but also reflected a tradition in which concrete materials and drawings are used to scaffold students’ learning of mathematics (Depaepe, De Corte, Op’t Eynde, & Verschaffel, 2005). The problems posed were frequently difficult. For example, the translation from text to symbols of some of the word problems leading to the shared equations of lesson one, and the pole driven through water into the ground of lesson four were challenging, and presented not inconsiderable difficulty for some students. Additionally, Eva’s constant invocation of brackets, negatives and fractions imparted a different sense of difficulty in accordance with earlier findings that Hungarian teachers operate with the general rather than the particular (Andrews, 2003), while her consistently high expectations in respect of procedural competence resonated closely with earlier observations (Andrews, 2003, 2007b, 2009a; Depaepe et al., 2005). Thus, there is considerable evidence that Eva’s classroom behaviours, as manifestations of her received curriculum, resonate closely with what the literature says of Hungarian teachers generally. However, when compared with her colleagues, the data presented in Table 7.1 show, as with Pauline above, lower emphases on conceptual knowledge, structural knowledge and reasoning and a substantially increased emphasis on procedural knowledge. In respect of her didactic practices, the same table shows little substantial variation between Eva’s practice and that of her colleagues other than a lower emphasis on explicit motivational strategies.

In relation to her idealised curriculum, several inferences can be made. The ways in which Eva facilitated the collective construction of both procedural and conceptual knowledge through the use of non-routine problems reflects, it is argued, social constructivist principles. Moreover, her frequent use of realistic word problems, as construed by the Dutch realistic mathematics education tradition as imaginably real (Van den Heuvel-Panhuizen, 2003), presents an atypical perspective from the Hungarian norm in which teachers rarely pose problems related to any context other than mathematics itself (Andrews, 2003). Also, the manner in which Eva constructed her students’ engagement with both conceptual and procedural elements indicates an implicit emphasis on their acquisition of adaptive expertise. Thus, it seems that Eva’s idealised curriculum is located in beliefs about collectively constructed knowledge, which, supported by the systematic use of realistic problems, facilitate her ambitions concerning learner acquisition of adaptive expertise.

In sum, despite some apparent discrepancies, the evidence indicates a close resonance between the three curricula: the intended is reflected closely in Eva’s observed practice. Eva’s received curriculum resonates well with both the intended and the collective Hungarian, which seems equally resonant with her idealised. There are differences, but it could be argued that Eva’s use of realistic problems allows her to not only address the intended curriculum with authority but also raise her practice above that of the collective received.

Conclusion

Quantitative analyses indicated that Pauline’s and Eva’s observable learning objectives differed from the collectives of their respective countries. For example, both were observed to privilege procedural knowledge while simultaneously placing lower emphases on conceptual knowledge, structural knowledge and reasoning. This highlights, I propose, the significance not only of acknowledging the cultural context in which teaching and learning occur, but also the topic under scrutiny. The lessons above were both on linear equations, a topic with limited opportunities for teachers to focus on, say, conceptual and structural knowledge, particularly when compared with many topics in, say, geometry. In similar vein, linear equations present fewer opportunities for high-level reasoning but many more opportunities for procedural work than would the angle properties of polygons; both Pauline and Eva offered considerable variation in respect of the exercises they posed, drawing on a various forms of coefficients, exploiting brackets in different ways and so on. This would be in contrast to the limited procedural opportunities embedded in, say, the angle sum of a triangle. Thus, their observable behaviours may not have deviated quite as far from the collective received curriculum as initially suggested. Other deviations from the received curricula, as in Pauline’s lower emphasis on questioning and sharing, are conjectured to reflect individual idealised curricula and are not necessarily topic related.

Of course, it would have been possible to analyse the subject knowledge manifestations of both Pauline and Eva against existing frameworks. For example, Pauline’s apparent reluctance to deviate from her planned sequences of activity could be construed as low-level contingency (Rowland et al., 2005). However, whether or not this reluctance is a reflection of, essentially, a deficit in her pedagogic repertoire or a desire not to deviate from a well-defined and articulated procedure is difficult to determine. What is clear, although possible explanations can be found in her idealised curriculum, is that her observed behaviours set her apart from both the intended expectations of her educational system and the received practices of her colleagues. In similar vein, would the content knowledge observed in Eva’s lessons be manifestations of Ball et al.’s (2008) common or specialised content knowledge? The answer to this, I propose, requires acknowledgement of both intended and received curricula. For example, the expectations of mathematics for all learners in Hungary, at least as far as the intended and received curricula indicate, are high. Consequently, common content knowledge in that country would be qualitatively different from countries where systemic expectations are low. In summary, the above shows that mathematical knowledge in teaching is a relative and not an absolute construct and confirms that the proposed tripartite curriculum model provides a worthwhile, but complementary, alternative to existing frameworks.