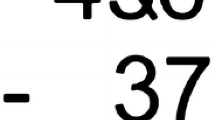“Mathematical knowledge for teaching”: adapting U.S. measures for use in Ireland

Abstract

This article describes a study in which measures of mathematical knowledge for teaching developed in the United States were adapted to measure mathematical knowledge for teaching in Ireland. When adapting the measures it was not assumed that the mathematical knowledge used by Irish and U.S. teachers is the same. Instead psychometric and interview-based methods were used to determine a correspondence between the constructs being measured, and ensure the integrity of item performance in the Irish context. The study found overlap between the knowledge that is used to teach in both Ireland and the United States, and that the items tapped into this knowledge. However, specific findings confirm the usefulness of conducting extensive checks on the validity of items used in cross-national contexts. The process of adaptation is described to provide guidance for others interested in using the items to measure mathematical knowledge for teaching outside the United States. The process also enabled the authors to raise questions about the assumptions that lie behind the practice-based construct of mathematical knowledge for teaching.

Introduction

The last two decades have seen growing interest in cross-national studies of teaching and learning. The Trends in International Mathematics and Science Study (TIMSS) and the Program for International Student Assessment (PISA) have demonstrated strengths and weaknesses in student achievement across developing and industrialized countries. As these results have been disseminated, there has been a lively effort by scholars interested in determining which aspects of high-achieving countries’ mathematics instruction matter (Stigler and Hiebert 1999). The quantity and quality of teachers’ mathematical knowledge has been one leading area of interest (An et al. 2004; Ma 1999). However, while student-level measures such as those included in TIMSS and PISA are carefully investigated for neutrality with regard to language and culture, measures of teacher knowledge are not.

This article argues for and provides an initial example of the cross-cultural adaptation of a set of measures of teacher knowledge. It argues that beyond the literal translation needed to convert items from one language to another, test developers need to carefully account for differences in the culture of teaching mathematics itself. Several studies suggest that the work of teaching in the United States differs from the work of teaching elsewhere (e.g., Cogan and Schmidt 1999; Santagata 2004; Schmidt et al. 1996; Stigler and Hiebert 1999). Stigler and Hiebert (1999), for instance, claim that different beliefs about the nature of mathematics, the nature of learning, the role of the teacher, the structure of a lesson, and how to respond to individual differences among students lead to different teaching practices in the United States and Japan. Others claim that the spread of global models of schooling influence national education systems (Meyer et al. 1992). Even if this is true the global models interact with national laws, customs and expectations, and local influences could still affect how lessons are planned, for example valuing mathematical reasoning over memorization (LeTendre et al. 2001). If the work of teaching differs from one country to another, an instrument to measure knowledge for teaching needs to be sensitive to such differences.

This is especially true for the measures we describe here, which were intended to capture “mathematical knowledge for teaching” (MKT), or the mathematics teachers use in classrooms, a construct that are explained in more detail below. In addition to the differences in mathematics teaching identified in the above literature, there may be less visible—but critically important, from a measurement perspective—differences in key tasks of teaching mathematics. For instance, the use of mathematical terms and conventions might differ; the presence and prevalence of particular content strands at particular grades might differ; the typical responses of students might vary. Given that the MKT items were intended to measure teachers’ use of classroom mathematics in the United States, cross-national variability in classroom mathematics would threaten the interpretation of results from studies in other countries.

This article emerged from an attempt by the lead author¹ to use the U.S. items to measure the mathematical knowledge held by primary teachers in Ireland. Before using the U.S. items to investigate Irish teachers mathematical knowledge, a pilot study was deemed necessary to investigate how multiple choice items would be selected and adapted. Therefore the pilot study centers on the selection, adaptation, and evaluation of items, some of which would be used in a subsequent study of Irish teachers’ mathematical knowledge for teaching. This article is based on the pilot study and represents an attempt to identify and respond to issues that arise in adapting MKT items for use in another country. Ireland was particularly appealing because the language of instruction (English) was largely held constant; this allowed for greater attention to the other issues of adaptation that might arise. It was also anticipated that the multiple-choice items could subsequently be used in Ireland, in pre-tests and post-tests, to measure how mathematical knowledge grows during pre-service teacher education, during professional development interventions, or with teaching experience (Hill and Ball 2004). Eventually, following extensive cross-national validation, it is possible that the items could be used to compare teachers’ mathematical knowledge for teaching across countries.

As the literature on test adaptation recommends, we did not assume the items could be used in Ireland without modification. Because these items were based on a construct that emerged from studying the practice of mathematics teaching in the United States, we made item adaptation a study in itself prior to using the items as a measuring instrument. We asked: what methodological challenges were encountered when attempting to use the items outside the United States? What choices did we make when adapting the items and why did we make them? How did we evaluate the success of the adaptations? What did these initial explorations suggest about the suitability of the U.S. measures for studying mathematical knowledge of teachers in Ireland? Answering these questions would help us solve the immediate problem of adapting the measures for Ireland. Moreover, it would be of help to other researchers who wished to adapt the measures for use in their countries, and would lead to greater understanding of the construct of mathematical knowledge for teaching.

In answering the questions, we begin with an overview of research on teachers’ knowledge of mathematics and on other instances of translating tests from one country to another. We then describe the methods used in the current study. The methods included a moderate-scale pilot of an untimed written test administered to teachers (n = 100) and follow-up interviews with five teachers after administering the pilot. In the results section, we outline how psychometric analyses allowed us to fine-tune our understanding of how the translated² items performed in Ireland. Note our interest in this article is not about how teachers perform on the items but in how the adapted items perform in a new setting. A well-performing item is one that generally high-scoring teachers answer correctly and one that low-scoring teachers get wrong. We conclude by discussing the findings and recommending steps that researchers might take when adapting measures of teacher knowledge from one country to another.

Background

Several studies over the past two decades have investigated how teachers acquire mathematical knowledge and how they apply it when teaching mathematics (e.g., Ball 1990; Borko et al. 1992; Eisenhart et al. 1993; Stein et al. 1990). Building on this work and on Shulman’s (1986) hypothesis about a professionally useful form of subject matter knowledge called “pedagogical content knowledge,” scholars at the University of Michigan have been developing a theory about the mathematics that primary school teachers need to know. This knowledge, called mathematical knowledge for teaching (MKT), not only includes aspects of pedagogical content knowledge, but also incorporates subject matter knowledge, both common and specialized. The relationship between pedagogical content knowledge and subject matter knowledge in the construct of mathematical knowledge for teaching can be seen in Fig. 1 (from Hill et al. 2007). The figure illustrates that MKT consists of disciplinary knowledge, including both mathematical knowledge that is held by well-educated adults and mathematical knowledge that is specialized to the work of teaching. In addition to disciplinary knowledge, MKT includes pedagogical content knowledge, that is knowledge of how to make mathematical ideas understandable to students and knowledge of what students find difficult in mathematics and students’ typical perceptions and misconceptions (Shulman 1986).

Fig. 1

Mathematical knowledge for teaching (Hill et al. 2007)

The concept of mathematical knowledge for teaching emerged from studying records of practice of mathematics teaching, and identifying the recurrent tasks teachers do that require mathematical knowledge, reasoning, and insight (Ball and Bass 2003a; Ball et al. 2005). For example, teachers analyze the mathematical steps that produce students’ errors. They also design explanations, assess students, pose and respond to mathematical questions, evaluate the quality of teaching materials, deploy representations, explain concepts, and show why procedures work. Such tasks demand mathematical knowledge (Ball and Bass 2000, 2003b).

In order to learn more about the mathematical knowledge that is needed for teaching, the researchers developed assessment items that could measure the MKT held by large numbers of teachers. These items, developed by the Learning Mathematics for Teaching (LMT) project, require teachers to identify the most appropriate answer for multiple-choice questions that are based on school- and classroom-related scenarios.

Preliminary psychometric analyses, including factor analyses of U.S. teachers’ responses to the items, support the existence of the mathematical knowledge for teaching construct and suggest that this construct has specific dimensions or domains (Hill et al. 2004). Four domains of mathematical knowledge for teaching have been hypothesized and analyses support the existence of the first three. The four dimensions are common content knowledge (CCK), specialized content knowledge (SCK), knowledge of content and students (KCS) and knowledge of content and teaching (KCT) (Ball et al. 2005). CCK and SCK are subject matter knowledge and KCS and KCT, along with knowledge of curriculum, are a form of pedagogical content knowledge (Ball et al. 2006). Common content knowledge refers to the mathematical knowledge and skill possessed by any well-educated adult, e.g., correctly subtracting 75−18. Specialized content knowledge is mathematical knowledge and skill used by teachers in their work but not generally held by well-educated adults, e.g., knowing alternative algorithms for calculating 75−18. Knowledge of content and students includes knowing about both mathematics and students, e.g., recognizing why a student might give the answer 63 to 75−18. Knowledge of content and teaching involves knowing about both mathematics and teaching, e.g., knowing instructional advantages of different representations of 75−18. Although these domains have been identified in the U.S., the domains of knowledge may differ in other settings.

Nevertheless, mathematics educators in other countries have expressed interest in using these measures. Some further believe that the items could be used to compare knowledge of teachers in different countries. The comparative interest may have been prompted by the use of high-profile tests such as the Trends in International Mathematics and Science Study (TIMSS), which measured students’ mathematical achievement across countries. Indeed some studies have already compared U.S. and Chinese teachers’ knowledge of mathematics (e.g., An et al. 2004; Ma 1999) and these studies concluded that the Chinese teachers’ knowledge of mathematics for teaching was generally superior to that of U.S. teachers.

Unfortunately, these studies typically provide little information as to how the measurement instruments were adapted for use outside the United States. For example, An et al. (2004) state that “questionnaires were prepared first in English and then translated into Chinese” (p. 151), but little information is given about translation issues that arose in the research. This is critical, because misunderstandings of terms can alter whether and how instruments discern teacher knowledge. These problems even occur without translating items into a different language; Borko and her colleagues described how multiple possible interpretations of what is meant by “to provide an explanation for” (1992, p. 212) caused problems for one student teacher. If the meaning of a mathematical practice can be misunderstood in one language, there is room for even more misunderstanding when terms are translated into a second language.

Ma does not explicitly describe how the mathematical teaching tasks she uses, which were developed in the United States (Ball 1988), were adapted for use with Chinese teachers. In several places throughout her book she places in context, explains or refers to the Chinese words for particular expressions, mathematical conventions, units of measurement, mathematics teaching practices and mathematical terms. In many cases these notes are placed in footnotes, giving the impression that they are supplementary, even though they may be central to the main data. Further, the teaching tasks themselves may or may not have been appropriate as contexts for evaluating Chinese teachers’ use of mathematical knowledge. Indeed, Ma (1999) changed the context of a “subtraction with regrouping” scenario from one that assessed U.S. teachers’ ability to evaluate textbook selections to one that assessed how Chinese teachers would approach teaching the problem and what prior knowledge students needed. Changing the context of an item may alter how teachers respond to it, but Ma did not discuss how this change might have affected her comparison of U.S. and Chinese teachers’ mathematical knowledge.

International comparative studies in other fields over the last 20 years have led to the development of guidelines for translating or adapting tests from one country to another (Grisay 2002; Hambleton et al. 2005; Maxwell 1996). This literature provides extensive descriptions of how items were adapted and tested for equivalence in different countries, including those where the same language is spoken but where other differences exist. Many of the recommended procedures can be applied to translating mathematical knowledge for teaching items, such as using translators who are native speakers of the target language, who know the target culture and who have expertise in both subject matter and test development methods. Furthermore, these studies discuss how psychometric data can be used to evaluate the success of adapting the measures. Yet the process of translating mathematical knowledge for teaching items is also different from other kinds of item translation.

One difference is that the mathematical knowledge for teaching items were not initially designed to be used in other settings. In fact, they were deliberately designed to reflect the work of teaching in one country, the United States. In contrast, when developing items for TIMSS in 2003, National Research Coordinators from each participating country contributed to the design and preparation of the test instrument (Chrostowski and Malak 2004). This lack of input from potential international users of the items makes translation more difficult because there is a greater risk that items may be biased in favor of U.S. teachers and unlike the PISA studies only one source language for items exists (e.g., Grisay 2002).

A second way in which translating MKT items is different from translating TIMSS or PISA items is that they are grounded not in the discipline of mathematics, but in the practice of teaching mathematics. This makes adapting the items more costly in terms of time and expertise. Like in TIMSS and PISA, one needs to recruit professional translators and apply procedures such as double translation and reconciliation. In addition, however, one needs to recruit and train multi-disciplinary teams expert in mathematics, in measures development, and in the practice of teaching in the country for which items are being adapted. Such teams can advise on how well the items relate to mathematics teaching in particular countries and can identify areas of MKT not measured by the items.

A third difference also relates to the content being measured. Tests such as TIMSS and PISA measure mathematical knowledge, which is commonly assumed to be universal.³ Notwithstanding this common belief, comparative studies of mathematics achievement generally have been criticized for their assumption of an “idealized international curriculum, defined by a common set of performance tasks” (Keitel and Kilpatrick 1999). Keitel and Kilpatrick further say that “no allowance is made for different aims, issues, history and context across the mathematics curricula of the systems being studied” (p. 243). We argue that these and many more potential differences exist in the mathematical knowledge used for teaching in different countries. Actual and potential areas of difference in mathematical knowledge for teaching across countries relate to teachers, students, mathematics and teaching materials and include:

• what teachers do during mathematics lessons. For example, the amount of time teachers devote to whole class instruction compared to working with groups or individuals varies across countries (Stigler et al. 1987);

• teachers’ conceptions about mathematics and about mathematics teaching. For example one study of teachers from England and Hungary linked different conceptions about mathematics and mathematics teaching to the presence of mathematics wall displays in English classrooms, a feature absent in Hungarian classrooms (Andrews and Hatch 2000);

• the classroom contexts in which the knowledge is used. Some teachers, for example, work in linguistically homogenous classrooms whereas others work in multilingual classrooms. In multilingual situations teachers must use their mathematical knowledge to explain concepts and to understand students’ thinking processes without always understanding students’ language (Gorgorió and Planas 2001);

• differences in the types and sophistication of the explanations students make (Silver et al. 1995). Teachers may need different levels of knowledge to respond appropriately to typical explanations in their country;

• responding to student errors. In some countries teachers might decide to mitigate a student’s error whereas teachers elsewhere have been found to express disappointment at errors through the use of harsh or ironic comments (Santagata 2004);

• the presence and prevalence of specific mathematical topics. For example, the grade level at which topics appear have been found to differ among countries (e.g., Fuson et al. 1988);

• the mathematical language used in the school. Spellings, units of measurement and punctuation have been found to vary among English speaking countries (Chrostowski and Malak 2004);

• the content of the textbooks. This can vary from country to country making different demands on, and providing different supports to, teachers (e.g., Mayer et al. 1995).

All of these potential differences in the practice of teaching mathematics render guidelines available from previous studies only partially helpful in this translation endeavor. Translation guidelines from TIMSS and PISA offer an informative starting point, but additional challenges can be expected if MKT items are translated for use outside the United States.

Nevertheless, despite the many potential differences, it seems probable that some degree of overlap exists between mathematical knowledge for teaching in different countries. For example, one common content item asks respondents whether the statement, “0 is an even number,” is true. The answer depends on the definition of even numbers and it cannot vary among countries unless a fundamental mathematical assumption is changed. Moreover, it is likely that this is something that should be known by all teachers, (for example when teaching students to classify numbers as odd or even in early grades or when deciding whether the sum or product of two numbers is odd or even in higher grades). If agreement among countries is likely on the importance of such common content knowledge, other items, especially those that relate to knowledge of students and to specialized content knowledge, may reflect knowledge that varies from country to country.

In order to help specify how differences might occur, we describe mathematics teaching in the two countries central to our analysis. The measures originate in the United States where there is no centralized mathematics curriculum and at a policy level, mathematics teaching is influenced by the work of the National Council of Teachers of Mathematics (NCTM) and particularly the Council’s Curriculum and Evaluation Standards for School Mathematics (1989) and its Principles and Standards for School Mathematics (2000).⁴ Mathematics education in the Republic of Ireland has been less well documented and a brief overview is presented here to describe the context for which the measures were translated from the U.S. version.

In Ireland disagreements about the teaching of mathematics have never caught the imagination of media or the public in the way that characterized the “Math Wars” in the United States (Wilson 2003). Nevertheless a study by Walsh (2006) of inspectors’ reports, curriculum documents, test results, notes for teachers, and small scale studies between 1922 and 1990 reveals a persistent, silent war being waged between the aspirations of policy makers and curriculum designers on one hand and the practice of teachers in teaching mathematics on the other. Teachers were continuously encouraged to emphasize applications of mathematics, the use of concrete materials and problems based on students’ experiences and interests, the promotion of thinking and the centrality of language and oral discussion. Although some of these were observed in practice, the predominant picture in schools for most of the 70 years was one of over-reliance on textbooks, emphasis on mechanical and routine aspects of mathematics and difficult vocabulary in textbooks. In general, students were considered to perform well in arithmetic but less well in algebra, geometry and problem solving (Walsh 2006).

A revised curriculum was introduced in 1999 which was structured around interconnected strands (number, algebra, shape and space, measures, and data) spanned by mathematical skills. The curriculum advocated principles such as building on previous knowledge, teaching informed by assessment, teaching using constructivist and guided discovery methods, using language effectively and accurately, manipulating materials to support concept acquisition, calculating mentally and estimating, using technology to support mathematical processes, and problem solving (Government of Ireland 1999). Although the date scheduled for full implementation, 2002, was relatively recent, the initial signs are that in many classrooms little has changed (Government of Ireland 2005; Murphy 2004; National Council for Curriculum and Assessment 2005).

In summary, the United States has been working at reforming mathematics instruction longer than Ireland, with more resources, and with arguably more success. This may change the nature of MKT. However, at policy level at least, the content standards of the National Council of Teachers of Mathematics are similar to the strands of the Irish primary mathematics curriculum and the NCTM process standards (National Council of Teachers of Mathematics 2000) are similar to the Irish curriculum skills (Government of Ireland 1999).

Method

Ireland is a good first testing-ground for efforts to translate the U.S. items. Ireland differs from the United States in many features such as size, history, diversity and cultural activities, such as sports. The countries also share similarities. Speaking in 2000, the Deputy Prime Minister of Ireland, Mary Harney, claimed that “spiritually” the Irish are “a lot closer to Boston than Berlin”.⁵ Formal collaboration between the two countries occurs on many issues, including education.⁶ These differences and similarities make Ireland a suitable location to begin investigating how to adapt the measures of mathematical knowledge for teaching for use outside the United States; we might expect to find some, but not radical, differences between the two countries. For example, similar algorithms are found in both countries but minor differences in layout may be noticed. Furthermore, because English is the principal language of public schooling in both countries, we could study the effect of using the measures of mathematical knowledge in a different country without the added complication of translating from one language to another.

Both qualitative and quantitative methods were used to describe, and analyze the success of, the adaptations to items. Qualitatively, we documented the process of selecting items, and then carefully recorded the adaptations made for Ireland. When making the adaptations, we conducted a focus-group interview with four practicing Irish teachers and with one mathematician. In addition we conducted follow-up interviews with five (different) teachers after they had completed the test, to learn about their responses to the items. Quantitatively, we studied how the measures performed psychometrically in a pilot study.

Approximately 110 item stems⁷ developed by the LMT project were available for selection. These items had previously been piloted on various survey forms in the United States on samples of teachers ranging in number from 104 to 659.⁸ The items were mainly piloted in California’s Mathematics Professional Development Institutes between 2001 and 2003 (Hill 2004a–d).

The items were administered to a convenience sample of 100 Irish primary teachers⁹ in summer 2004. The teachers were attending summer institutes in a range of curriculum areas including visual arts, language, social, environmental and scientific education, and mathematics. These courses last for twenty hours over five days and teachers who attend them during their holidays may take three days of extra personal vacation during the following school year. The lead author approached teachers doing these courses in six centers and invited them to participate in the study. Teachers were told that it would take about 90 minutes to complete the test, and participants were offered a token of appreciation. Teachers were required to complete the survey in the presence of the researcher and no time limit was imposed.

After completing the questionnaire, follow-up interviews were conducted with five teachers. A convenience sample of teachers who were willing to spend one extra hour answering questions about the test was selected. Teachers who completed the questionnaire towards the end of the testing period were more likely to be invited to do the interview than those who did the test earlier and only teachers who completed the questionnaire in Dublin were asked to participate in the interviews. The interviews were intended to yield data about how well teachers believed the items reflected the work of teaching mathematics in primary schools in Ireland. About seven general questions were asked to elicit teachers’ general opinion on the items, the extent to which they related to the work of primary teaching, the authenticity of the characters in the questions, the clarity of the language, and the questions that respondents are likely to find difficult. The teachers were also asked if they could think of teaching situations, not reflected in the chosen items, where they draw on their mathematical knowledge. In addition, 16 questions from the test were selected and interviewees were asked to state what answer they gave and why they chose that answer and not another answer. These interviews were recorded and transcribed.

Teachers’ responses to the multiple-choice items were compiled and analyzed quantitatively using psychometric methods. Previously, item difficulties and slopes (how well items discriminate among teachers with similar levels of knowledge) were calculated in the U.S. context but it was important to independently calculate item difficulties based on Irish teachers’ responses. Specifically, we wanted to know how the U.S. items performed in Ireland, because this would shed light on whether they were measuring similar constructs in the two countries. We entered the responses of the Irish teachers into BILOG-MG (Zimowski et al. 1996) and conducted three psychometric analyses: we inspected the point biserial correlation estimates from Ireland and compared them to the U.S. point biserial estimates; we calculated Cronbach’s alpha for each domain of the test; and we compared the relative item difficulties from a one-parameter Item Response Theory (IRT) model in each setting. We chose a one-parameter (Rasch) model because the sample size was too small to use a two-parameter model. The point biserial correlation indicates how an item correlates with all other items. The higher an item’s point biserial correlation, the stronger the relationship between the item and the construct being measured. Another way of thinking about this is that the higher the point biserial correlation, the better the item can discriminate between individuals who are closer together on the underlying construct. An item which has a low point biserial correlation discriminates poorly, in that it is mostly measuring noise. Difficulty refers to the difficulty of items vis-à-vis one another. Bilog-MG (Zimowski et al. 1996) reports item difficulties in standard deviations, on a scale where 0 represents the average teacher ability. Difficulties lower than 0 describe easier items and higher difficulties reflect more difficult items. Scale reliability measures the consistency of test-takers’ scores achieved over multiple items or over multiple testing occasions. A widely used measure of reliability from classical test theory is Cronbach’s alpha and it is reported on a 0–1 scale. Higher figures indicate that the item responses are highly correlated and that they are consistently measuring the same thing. Another way of thinking about this is that it measures the amount of “observed individual differences ... that is attributable to true variance” (Cronbach and Shavelson 2004, p. 401) in teachers’ mathematical knowledge for teaching. If the point biserial correlations, the difficulty levels and the overall reliabilities differed among countries, this would suggest that the items were performing differently across cultures.

Results

This article is primarily about how the items performed in a setting outside the United States rather than how teachers performed on the items. Therefore the results begin with a description of how items were selected for inclusion in the test. Changes to the items are then carefully documented because these changes might affect how teachers respond to the items. Next we present the results of interviews with five teachers after they had completed the test. Finally, we present the findings from psychometric analyses of item performance in Ireland and the United States.

Item selection

The lead author selected items for use in Ireland based on his knowledge of the work of teaching mathematics in Irish primary schools and on results from psychometric analyses of item pilots in the U.S. From the bank of approved items, 39 item stems were selected for use. Nine of the 110 U.S. item stems available at the time were excluded from consideration because they related to topics that are not generally taught at primary school level in Ireland, but instead appear mainly in the secondary school curriculum. The topics included division of fractions by fractions, abundant numbers, division of a whole number by a non-unit fraction, rotational symmetry, coordinate geometry, equations with two variables, linear functions, and exponential growth.

The final set of items selected for the Irish study contained items from each of four scales that had been identified in the U.S. studies: content knowledge (including CCK and SCK) of number and operations, content knowledge of patterns, functions and algebra, content knowledge of geometry, and a further set of number and operations items which required knowledge of content and students (KCS). Ten additional item stems were used: three “items-in-progress” belonging to the LMT Project and seven written specifically for use in Ireland. These ten item stems do not form part of the analysis in this article because they have not been subjected to the rigorous item vetting process (Bass and Lewis 2005). The total number of items selected in each mathematical strand and in each domain of the construct is summarized in Table 1.

Table 1 Number of items in each category chosen for pilot test of items in Ireland

The most important criterion for selecting items was alignment with the knowledge of primary mathematics teaching and its mathematical demands in Ireland. As in any situation where items developed exclusively in a country are selected for use in the second, we could not choose items to reflect MKT used in the second country (Ireland in this case) that does not arise in the first.

Item adaptation

After item selection and initial adaptations by the lead author, items were reviewed in advance of test administration by a focus group of four experienced, practicing Irish teachers who helped determine whether the items reflected situations that would arise in Irish classrooms. Further modifications of items followed, based on the focus group discussion. Finally, one Irish mathematician critiqued the changes to determine if they were mathematically sound. The instructions to the focus group teachers and to the mathematician, none of whom had prior knowledge of the construct of mathematical knowledge for teaching, were to accept items without change, or to propose adaptations to items so that they sounded realistic to Irish teachers and so that they preserved mathematical integrity.

We compiled a table listing all the changes that were made to the items in adapting them for use in Ireland. Of the 42 item stems that were originally written in the United States only 7 were unchanged. Having considered different ways of categorizing the changes that were made to the items, we decided that the following four categories best summarize the changes:

• 1. Changes related to the general cultural context;

• 2. Changes related to the school cultural context;

• 3. Changes related to mathematical substance;

• 4. Other changes.

Translations that related to the general cultural context included: changing people’s names to make them sound more familiar to Irish teachers; altering spellings to reflect differences between U.S. and British English; adapting non-mathematical language and culturally specific activities to give the items a local flavor. This category of changes is summarized in Table 2. These changes are important in making the items appear authentic to Irish teachers and similar changes were made to TIMSS items (Maxwell 1996).

Table 2 Exemplars of general contextual changes made to items and frequency of changes

The second category of changes related to the cultural context of the school or of the education system in general. This included language used in school and structural features of the wider education system. Examples are given in Table 3. Adapting language related to the general context or to the school context of the items is important so that teachers in a second location are not distracted by unfamiliar terms or contexts. Knowledge of the education system in the “target” country is required to make such changes. These changes do not affect the mathematical substance of the items and therefore are unlikely to compromise the items’ ability to measure mathematical knowledge for teaching.

Table 3 Exemplars of school contextual changes made to items and frequency of changes

In contrast to the previous two categories, the third category related to the mathematical substance of the items. Units of measurement were changed; such changes were similar to ones made for TIMSS and PISA, although fewer were necessary in those assessments because most participating countries used a common system of measurement (metric) (Maxwell 1996; Wilson and Xie 2004). Of the 98 items that originated in the LMT database, 12 items (12%) required adaptation of the measurement units. In some cases, these translations were straightforward and the sense of the item was preserved. For example, $20 might become €20 or 10 yards might become 10 metres. In most cases such adaptations are similar to context changes such as changes of names and spellings.

Not all changes of measurement units, however, were so straightforward. In four items, the numerical quantity also had to be changed in order to preserve the sense of the item. For example, sweets are often sold by the ounce in the United States, but sweets are rarely sold by the analogous unit in Ireland, the gram. This prompted further changes in the item: instead of a graph in intervals of single ounces, the item now required a graph in intervals of ten grams. This type of change was more problematic than the general cultural changes mentioned earlier because it risks making the mathematics more difficult for one population taking the test.

Other mathematical changes referred more specifically to teachers’ mathematical knowledge and are less likely than the one just described to have occurred in TIMSS or PISA (see Table 4). They included changes to the mathematical language that is used in schools, changes to representations that are commonly used in schools and changes to anticipated student responses. The mathematical language used in Irish schools differs in some ways from language that is used in the U.S., resulting in changes to 17% of the items. In most cases, precise translations for the terms were possible. When teaching place value, for instance, in Ireland the term unit is used in the national curriculum whereas one is typically used in the United States. A right-angled triangle in Ireland is more commonly called a right triangle in the United States. Students in the United States encounter input-output machines and Irish students use function machines. In the United States a flat shape is called a plane figure or a 2-D figure whereas in Ireland it is called a 2-D shape. In each of these cases an exact translation from the U.S. to the Irish term is possible. The term “polygon,” however, is frequently used in school texts in the United States and rarely in Irish texts, where the term 2-D shape is preferred. The problem is that polygon and 2-D shape are not synonyms because the set of 2-D shapes includes circles, semicircles and ovals and the set of polygons does not. Therefore, qualifying statements (e.g., a 2-D shape with straight sides) may need to accompany the terms in a particular country.

Table 4 Exemplars of mathematical changes to items and frequency of changes

Representations of mathematical ideas can also vary from country to country. Take, for example, an item that included a representation of a factor tree. Although the changes (see Table 4) may seem superficial to a mathematician, all four Irish teachers who saw the U.S. representation prior to the pilot test agreed that it needed to be modified in order to appear familiar to Irish teachers. With the item changed as recommended by the teachers, 74% of the 100 Irish teachers responded correctly to this item. In the subsequent large scale study, where the U.S. diagram was included unchanged, only 58% of a different sample of 503 Irish teachers responded correctly. It is possible that the unfamiliar diagram distracted Irish teachers in the second study, negatively impacting their scores.

The four Irish focus-group teachers also believed that the method used by a student to multiply two single-digit numbers, a × b, (multiplying a by b − 3 and then skip counting three multiples of a; e.g., 6 × 9 solved by calculating 6 × 6 = 36, 42, 48, 54), in a U.S. item would be unusual in Ireland and they agreed that multiplying two numbers and counting on in ones would be more likely. However counting in ones for 3 × a would also be unrealistic so the context was changed to have the student in the Irish item count on a ones. As a result the mathematical demand of the item was slightly changed from calculating a × b to calculating a × (b − 2) (see Table 4). This change again highlights a challenge faced in adaptation. Is the mathematical knowledge in this item about knowing how students are likely to respond to a computational task? If so, the adaptation seems to be appropriate. If, however, the mathematical knowledge being measured is a teacher’s ability to apply the distributive property, (8 × 7) = (5 × 7) + (3 × 7), then the change is not appropriate because it simply makes the same task easier, (6 × 7) = (5 × 7) + (1 × 7). In order to assist the accuracy of translation in the 2000 PISA study, test developers provided a “short description of the Question Intent” (Grisay 2002, p. 60) for each item; this feature could be developed for the mathematical knowledge for teaching items in the future.

The final category refers to changes not necessitated by cultural requirements. These included deletion of an answer choice, alterations to visual appearance (e.g., font size or typeface), further clarification of an item or alteration to the meaning of a distractor. Because these changes were not made in response to possible differences in mathematical knowledge, and the items had previously been through a rigorous development process in the US (see Bass and Lewis 2005), the changes were unnecessary. It is conceivable, however, that in some cultures (e.g., where multiple-choice formats are unfamiliar to potential respondents) such changes may be necessary. Such changes may be problematic because they could make an item easier or more difficult; they may make it more or less discriminating; and they may also change how effectively the items measure the underlying construct. In this instance, however, they do not shed light on the cross-cultural nature of the construct of mathematical knowledge for teaching and therefore they will not be discussed further here.

Figures 2 and 3 provide an example of how some of the principles, identified above, were applied and they illustrate how an item was adapted. This specific item was not used in the Irish test but a similar one was included.¹⁰

• There are no people’s names in the item, no change needed there.

• The $ sign would have been changed to a € (Euro) but the values still make sense.

• No change needed because of different school mathematical language.

• No change needed because of differences in the education system.

• “Taffy” could be changed to toffee, but making toffee is not an activity that is familiar to most Irish children so that part would be changed to a scenario involving making Rice Krispie™ buns.

• A final type of change adjusted the item to account for a difference in the Irish primary curriculum which requires students to divide whole numbers by unit fractions (and not to divide fractions by fractions) so 1¼ was changed to 3.¹¹

The original item is reproduced in Fig. 2 and the changes that were made are reflected in the rewritten item in Fig. 3.

Fig. 2

How an item looked before adaptation

Fig. 3

How an item looked after adaptation (changes underlined)

Follow-up interviews

After the items were adapted and administered, we interviewed five of the Irish teacher–respondents about the items in the test. We wanted to investigate how successful the translation of the items from the U.S. context had been by asking if the items sounded authentic to Irish teachers and whether the items related to the work of teaching mathematics in Ireland.

Four of the five teachers interviewed believed that the teachers and the students described in the items seemed authentic and the fifth teacher remarked only that several of the characters had Irish names. Most of the teachers also commented that the language in the items was clear, although two commented that some of the mathematical terms were unfamiliar. One teacher was unsure of the meanings of congruent and tessellate and another teacher also included congruent, tetrahedron, and polygon among the terms that were difficult. These unfamiliar terms, which were both specific and exceptional in the test as a whole, point to terms that might need to be translated or explained in a future administration of the questionnaire.¹² One of the teachers suggested that “if you’re doing shapes with a class, you’re going to look at [the relevant vocabulary] beforehand and you’re going to kind of study it and know exactly what [the students] ask you” (Pilot transcript 2358). This does not, however, prepare a teacher for responding to a question or a statement from a student that occurs out of context.

Interview participants also identified as difficult, items featuring materials not commonly available in Irish schools. One such item referred to tetrominoes and another to algebra tiles. Two of the teachers said they did not understand the item that used the algebra tiles: “I never saw that sort of illustration. I didn’t understand that at all. I couldn’t work that out” (Pilot transcript 1291). A third respondent found it “a bit taxing” because “you’re transferring algebraic thinking into graphics” (Pilot transcript 2346).

When the Irish teachers were asked if they thought that the mathematics in the items was the kind that teachers encounter in Irish classrooms, they all agreed that, in general, it was. Three teachers qualified their answers to this question. One believed that most Irish students would not produce the type of mathematics produced by the hypothetical students in some of the U.S. questions. Another teacher speculated as to why this might be. He commented that some of the mathematics included in the items would not be observed in an Irish classroom. He noted that a relatively high proportion—25 out of 108—of the items in the Irish test related to patterns, functions and algebra and Irish students do not currently spend much time on the algebra strand of the curriculum. Consequently, if the algebra items, for example, included in the Irish questionnaire are based around mathematical conjectures, questions or other utterances that Irish students are unlikely to produce in class, it is possible that these items do not reflect mathematical knowledge that Irish teachers use when teaching mathematics. Since 1999, however, algebra has been a specific strand of the Irish primary mathematics curriculum.

Notwithstanding these comments from the interviewees, all the Irish teachers commented that the items seemed authentic based on their teaching experience. Items relating to content or contexts that were unclear, difficult or unlikely to occur in Irish classrooms were exceptional.

Overall the follow-up interviews we conducted demonstrated their potential to yield important data in relation to translating items. We collected data that helped us to explain unexpected responses and reasons for errors that may be country-specific and that suggested alternative, credible response options that are not currently included in the items. The interview data also helped us to check if the characters in the questions seemed authentic to teachers and if the situations arose when teaching mathematics in the new setting. In addition, we used the interviews to identify language that caused difficulty for respondents in the new setting. We found the interview data to be less effective for identifying content that arises in the work of teaching, but that is not covered by the items and which might form the basis of future items.

Because we interviewed only five teachers, we do not claim to have definitively resolved all the issues raised in the previous paragraph. We have, however, identified areas that are worthy of further investigation and gathered evidence to support the potential of more systematic use of follow-up interviews in future translation of MKT items.

Psychometric analyses

Data from the sample of 100 Irish teachers were analyzed and compared to data obtained from teachers in the United States. Although neither group of teachers constituted a random sample, IRT models are considered to be robust to this difficulty, because IRT is focused on comparing items, rather than individuals. We began by inspecting point biserial correlations for number and operations content knowledge (CCK and SCK) items. The point biserial correlations of content knowledge items in both settings were not on an interval scale so we first performed a Fisher Z transformation on them. Figure 4 correlates the U.S. and Irish Fisher Z transformed biserial correlations of content knowledge items. In general there is a moderate correlation between the point biserials (r = 0.43) but item 1d, which is more than two standard errors from a best-fit line between the two sets of estimates, is a clear outlier.

Fig. 4

A regression line fitted to a scatter plot of the U.S. and Irish Fisher Z transformed biserial correlations

Item 1d required the respondent to consider whether a representation was an accurate representation of one-fourth (see Fig. 5a). Like items 1a, 1b and 1c, the only adaptations were a change of name and a change in school language in the item stem. Although many respondents in both countries believed that the representation reproduced in Fig. 5(a) represented one-fourth, the follow-up interviews indicate that some Irish teachers believed that it represented one-eighth. Three of the five teachers interviewed expressed uncertainty about whether the dark line was deliberately or unintentionally only on the upper part of the horizontal line. One teacher commented: “That struck me, ‘that’s one-eighth’ the minute I saw it. It didn’t strike me as a quarter” (Pilot transcript 2346). The combination of evidence from the interviews and the point biserial correlations suggest that this item surfaces a difference between how U.S. and Irish teachers interpret linear representations of fractions. Several Irish teachers appeared to consider it as an area, rather than a linear representation, with just 62% of them identifying it as one fourth. In the United States, 95% of respondents correctly identified the diagram as representing one-fourth. This conjecture is supported by the finding of the subsequent study of Irish teachers where the representation was changed so that the number line was shaded above and below the line (see Fig. 5b). Selection and adaptation of items for the subsequent national study of Irish teachers’ mathematical knowledge for teaching was informed by findings from the pilot study. Of 503 sampled teachers in the second study, the percentage that correctly identified the fraction as one-fourth in the revised diagram rose to 92%, much closer to the U.S. finding. It is possible, however, that the Irish teachers continued to use an area conception of fractions rather than a linear one when answering this question so an alternative representation may be needed if the goal were to elicit Irish teachers’ understanding of linear representations of fractions. This result shows that teachers’ performance on items across countries can be sensitive to what may appear to be minor differences in representation.

Fig. 5

(a) Linear representation of a fraction from a content knowledge item in the actual study (b) Revised linear representation of a fraction from a content knowledge item in the follow-up study

In the number concepts and operations knowledge of content and students (KCS) domain, one item had a negative point-biserial correlation score of −0.051, indicating that respondents who scored well on other items in this subtest were slightly more likely to get this wrong than right. The item asked teachers to identify similar errors that students made when adding three two-digit numbers, such as failing to heed place value, and failing to note a carry of 2 tens rather than 1 ten. Our initial hypothesis for this difference centered on the fact that the algorithm is typically recorded differently in Ireland. In the second study, where the algorithm was recorded as it usually is in Ireland, the point biserial correlation rose to 0.306. Again what appeared to be a minor variation in the layout of an algorithm may have affected teacher performance on the item (Table 5).

Table 5 Point biserial correlation estimates for number and operations content knowledge items ordered by estimates on Irish test form

After examining point biserial correlations, we inspected relative item difficulties to determine whether the same items, in general, were easy and difficult in both countries. Overall, Fig. 6 and Table 6 show quite a strong correlation (0.74) between the items that Irish and U.S. teachers found difficult. We did, however, identify three outliers. Item 1d, which featured the linear fraction representation, was relatively more difficult for Irish teachers and two other items (1a and 1c) relating to the same stem on the topic of representations of ¼ were relatively more difficult for U.S. than Irish teachers. Items 1a and 1c require respondents to state whether or not different representations—one area model and one discrete model—show ¼. Without further investigation no obvious reason emerges to explain the why these items were relatively more difficult for the U.S. teachers.

Fig. 6

A regression line fitted to a scatter plot of the relative difficulties of items in the Irish and U.S. versions of the number concepts and operations section of the test

Table 6 Difficulty estimates for number and operations content knowledge items with equated Irish difficulty estimates

We also calculated Cronbach’s alpha for each domain of the test (Table 7). We cannot specifically compare these estimates to those obtained in the United States because the items on the forms were different. However, the estimates are broadly similar to some of the early results obtained in the United States (see Hill et al. 2004). The greatest difference can be seen in the domain of knowledge of students and content (numbers and operations). The knowledge of students and content reliabilities are noticeably lower than those found in the other three domains in both settings, but in Ireland, the measure is lower than any of the U.S. measures. This may indicate that students have different misconceptions or difficulties or that they approach problems differently in the two countries, but further study would be needed to establish why.

Table 7 Coefficient alpha results for each domain of the test piloted in Ireland

Discussion

Adapting items developed in one country to measure teachers’ mathematical knowledge in another enables researchers to build on expertise that has been developed by international research groups. We have shown, however, that translating such measures from one setting to another fairly similar setting is a non-trivial process. Despite the relative similarities between the United States and Ireland, we found differences in mathematical language, in measurement units, in representations of mathematical concepts, and in knowledge of students and content. Although such differences may be dismissed as mathematically trivial, some evidence pointed to teachers’ performances on items being sensitive to apparently minor variations in items. With non-English speaking countries, or in countries with markedly different ways of teaching mathematics, many more changes may be required. Therefore, explicit guidelines for adapting teaching knowledge items need to be developed. Based on the follow-up interviews and on the psychometric analyses we believe that our adaptations were generally appropriate and that the results section of this article provides working guidelines on which those adapting items in future can build. If future translations based on these guidelines are documented, researchers will be better placed to interpret test results because the changes made, or the absence of changes, may help to explain differences in teachers’ scores which are not attributable to differences in their knowledge. Further, apparent differences in knowledge may be accounted for by differences in the mathematical knowledge used by the teachers in the respective countries.

Those who wish to adapt measures of teachers’ mathematical knowledge will also have to grapple with other issues as we did in the United States–Ireland project. A key question is: what constitutes the mathematical knowledge for teaching in a particular country and who has the expertise to decide this? Much can be agreed with little argument. Teachers in a country need to have deep understanding of algorithms used for arithmetic operations, to be able to manipulate commonly used materials and to know terms that appear in the curriculum. Although the school curriculum is an important factor in determining mathematical knowledge, other factors also influence the mathematical knowledge that a teacher needs: typical forms of classroom interaction, materials available and assessment procedures used, for example. All of these factors need to be considered when determining the mathematical knowledge used in teaching in a particular country.

One particular issue is that some mathematics topics appear in different grade levels in each country, leading, in the current study, to exclusion of U.S. items based on topics that do not appear in the Irish curriculum. The decision to remove items because they are based on topics that do not appear in the Irish primary curriculum illustrates one challenge faced in using the test outside the United States. Knowing curriculum content is one component of teachers’ mathematical knowledge, but few would argue that teachers need to know only the mathematics of the curriculum. Should teachers be able to divide fractions by fractions, for example, and be able to respond to students’ questions about division of fractions by fractions even if such content is not included in the primary school curriculum? Discussion among teachers, teacher educators and mathematicians with expertise in the theory of mathematical knowledge for teaching and/or in local knowledge of teaching offers one way to resolve this issue.

Another issue centers on the lexicon for mathematics teaching. Many item adaptations required paying close attention to mathematical language and considering how terms might be more or less familiar to teachers from each country. Referring to an earlier example, it could be argued that because the terms polygon and 2-D shape describe particular mathematical concepts, the term polygon (or equivalent) should be included in the mathematical discourse of Irish teachers and 2-D shape (or equivalent) should be part of the mathematical discourse of U.S. teachers, even if curricula in each setting do not use such terminology. A question therefore is what should be included in the lexicon and how should it change among elementary, middle and high school teachers in the United States and between primary and secondary teachers in Ireland? The question can be addressed by studying the language teachers use and encounter when working at particular grade levels, in particular countries and examining the mathematical accuracy and adequacy of the terminology used.

This study identified knowledge that Irish teachers currently hold, but we do not claim that this is all the mathematics that Irish teachers need to know. Teachers may know what they know for historical, social or cultural reasons and this knowledge may influence how teachers teach. Teaching methods change. Teacher preparation evolves. Curricula are reformed. Teachers may need to acquire new knowledge and a measure of mathematical knowledge must be able to accommodate such knowledge. Think about Gulliver among the Lilliputians, for example. If the Lilliputians had limited their measurement of height to themselves they would have had no way to measure the height of Gulliver when he arrived in their land. Similarly, if their measurement scale was built with only people the size of Gulliver in mind, it is possible that the intervals would not measure the locals precisely because the intervals would be too far apart. When we pilot our measures we are both measuring current knowledge and developing measures that can be used to measure knowledge that we believe is useful in teaching mathematics, even if that knowledge is not currently widely held among teachers. This causes a tension when adapting measures because if, for example, Irish teachers score poorly on a particular item compared to U.S. teachers, this may be because the item is tapping into knowledge that Irish teachers do not use in teaching. Whether it is knowledge that Irish teachers should use in their teaching or whether that knowledge is peripheral to the work of teaching in Ireland, requires a judgment call on the part of the test translator.

The writers of teacher assessments can support the adaptation process in at least two ways. If test authors define the “Question Intent” for each item, adapters could try to maintain the integrity of the intent in their translation. Test developers could also investigate the possibility of training multi-disciplinary, multilingual teams to vet items prior to their being used in new countries. When items have been selected and adapted based on decisions and criteria outlined above, changes to items might be submitted for approval to a team of educators and mathematicians with expert knowledge of the mathematical knowledge for teaching construct, prior to administering the survey. This would help ensure that the adaptations did not compromise the ability of the items to measure MKT.

When comparing teachers’ knowledge across countries, it is possible that adaptation of items from one country alone may not be sufficient. One needs to be cognizant of identifying potential new material for items that reflect distinctive aspects of mathematical knowledge for teaching as observed in the new setting; aspects that are not currently reflected in the item bank developed based on studying the practice of mathematics teaching in the United States. For example in Ireland a national mathematics curriculum exists for mathematics teaching and a third grade teacher can be expected to know the mathematics that a pupil entering the class from second grade can be expected to have encountered previously. This knowledge will not be tapped in the existing U.S. items. Another specific example is that the Irish curriculum requires students to draw, construct and deconstruct nets of 3-D shapes (Government of Ireland 1999) but no U.S. items featuring nets have been developed to date.

This research has benefits for practicing elementary school teachers, particularly for teachers in the country for which the items are adapted. Pre-service and in-service mathematics education can be improved because the measures would allow professional developers to measure teacher learning rather than just teachers’ level of satisfaction with professional workshops (Wilson and Berne 1999). The process of adapting the measures also has the potential to inform teachers about differences in MKT from country to country. Such awareness could help teachers to prepare for teaching in new settings and could enable teacher mobility across countries.

As with any study, the current study has some limitations. First, the sample size of 100 Irish teachers was small, restricting the analyses we could conduct. Of these teachers, only five were interviewed about their responses to items. Further, the timing of these interviews, prior to analyzing data, meant that the items discussed in detail were not necessarily the items that performed differently than in the U.S. Third, the forms that were used in the Irish test consisted of different items than on any single U.S. form and this made psychometric comparisons problematic. Fourth, we did not have analogous interview data with U.S. teachers to compare their views of the items. Finally, although we speak of the United States as an entity, the data were drawn from a handful of states and it is possible that the construct may differ among other U.S. states to a similar or greater extent than it differs between Ireland and the states where U.S. data were collected. Despite these limitations, novel and multiple sources of data were used to explore how mathematical knowledge for teaching may differ across two countries.

We now return to summarize our answers to the four research questions. First, we encountered four methodological challenges when using U.S. items to measure MKT in Ireland. One significant challenge is deciding what MKT is core for primary school teaching across countries and what is specific to a country, determined by factors such as its curriculum, pupil interaction patterns, assessment procedures, mathematical language and the teaching materials available. In other words, if MKT in the United States and in Ireland were represented on a Venn Diagram, what would be in each of the sections A, B, C? (See Fig. 7). A second challenge arose because the items originated exclusively in the U.S. Therefore, familiarity with education and culture in both settings was needed to translate the items for Ireland. A third challenge arose from the fact that we found teachers’ performances on some items to be sensitive to what might appear to be minor variations in representations. Fourth, in one item deciding on an appropriate translation was hampered by not having a “question intent” to accompany the question.

Fig. 7

Mathematical knowledge for teaching in the United States and Ireland

With regard to our second research question, when adapting the items most changes were made so that the U.S. originating items would appear realistic to teachers in Ireland. For this reason names, spellings, cultural activities, features of schools, measurement units, representations of concepts, mental arithmetic approaches used by students and school mathematical language were changed. We envisaged that other changes to the format of questions may be needed in a setting where multiple-choice questions may not be familiar to potential respondents. We evaluated the success of the adaptations by using follow-up interviews in which we asked the Irish teachers if the items appeared authentic to them and if the mathematics was of the kind that Irish teachers encounter. We also evaluated the item adaptations by looking at how the point biserial correlation estimates correlated between Ireland and the United States. Finally, the initial explorations suggest that with the translations described above the vast majority of elementary school items developed in the United States were suitable for use with primary teachers in Ireland. The process also revealed instances where translating items, from one primarily English-speaking setting to another, was problematic and it raised questions about adapting MKT items that need further investigation. These questions include: to which adaptations were teachers’ performances on items more sensitive? Why are some items more difficult for teachers in one setting than another? and why do KCS items have lower reliability measures than other items in both settings?

This article has described methodological challenges that arise when using U.S. measures of mathematical knowledge for teaching to measure such knowledge in other countries. It suggests that international comparisons of teachers’ mathematical knowledge need to be considered in the light of differences that may exist in the knowledge that teachers use in each country. Much work remains to be done to reach a greater understanding of the relationship and interaction between mathematics teaching and mathematical knowledge for teaching in the United States and elsewhere.