Keywords

2010 Mathematics Subject Classification

1 Introduction

The prey predator dynamics has been extensively discussed by several investigators [4, 15, 16]. Leslie and Gower proposed a prey-predator model under the assumption that there is a correlation between reduction in population of predator and its preferred food [10]. Even, another prey-predator model has been introduced by Leslie in which carrying capacity of predator population depends commensurately upon prey population [10, 11]. Later, May incorporated Holling type functional response in this model [15]. On account of the functional responses of types I, II and III, the model produced a wide range of dynamics and investigators explored global stability of equilibrium point, occurrence of chaos and periodicity in the system [2, 5, 7, 9]. Sokol and Howell [19] introduced a Holling type IV functional response in the model which fitted their experimental data significantly better. The functional response IV is characterized by inflation in predation rate with prey population to utmost at a threshold prey density beyond which predation rate drops [6]. Whereas, in case of other functional responses the predation rate inflates with prey density. In another study [3], a model with functional response IV numerically demonstrated different dynamics at significant levels of prey interference in comparison to the other functional responses. Li and Xiao investigated Leslie–Gower model with functional response IV which manifested limit cycles and bifurcation [12]. Models incorporating time delays with Holling type IV functional response are extensively studied by Jiang and Lian [8, 13]. They explored complex dynamics in the system and demonstrated stability, periodic orbits and direction of bifurcating periodic orbits.

The employment of feedback control in complex systems generated significant interest after influential work by Ott [17]. The method is so simple and convenient that it appears to be remarkable for biological problem. Not much of research has been done in this area pertaining to ecological systems [14, 18].

By studying a Leslie–Gower prey-predator model with Holling’s functional response of type IV, it is shown in this paper that an appropriately chosen control approach can render an unstable system into one that is globally stable.

2 The Mathematical Model

Let the density of prey and predator population be X(t) and Y(t) respectively. It is assumed that prey population is growing logistically with Holling’s functional response of type IV

$$\begin{aligned} \nonumber \frac{dX}{dT}= & {} rX\left( 1-\frac{X}{K}\right) -\frac{mXY}{X^2+a}\\ \frac{dY}{dT}= & {} s\left( 1-\frac{Y}{n X}\right) Y. \end{aligned}$$
(1)

where r is the intrinsic growth of prey species with carrying capacity K. m denotes per capita consumption rate of the predator and the constant a denotes the number of prey required to make maximum rate just half. s is the growth rate of the logistically growing population Y and n is magnitude of food quality of prey for reproduction in predator population. All the parameters are assumed to be taken positive. The following set of non-dimensional variables and parameters helps reduce the number of parameters from 6 to 3:

$$t=rT,~ x=X/K, ~y=mY/rK^2 \quad \mathrm {and}$$
$$\alpha =a/K^2, ~\beta =mn/Kr,~ \gamma =s/r$$

This leads to non-dimensional form of the system

$$\begin{aligned} \nonumber \frac{dx}{dt}= & {} x\left( 1-x\right) -\frac{xy}{x^2+\alpha }\\ \frac{dy}{dt}= & {} \gamma \left( 1-\frac{ y}{\beta x}\right) y. \end{aligned}$$
(2)

The initial conditions for the system (2) are:

$$\begin{aligned} x\ge 0, y\ge 0. \end{aligned}$$
(3)

From the biological point of view, the equilibrium point lying in the positive quadrant \(R^2\) is of interest for the dynamics of the system. The interior equilibrium point \(E^*=(x^{*}, y^*)\) can be obtained from the equations:

$$1-x=\frac{y}{x^2+\alpha }, \quad y=\beta x.$$

It is seen that the system (2) exhibits Hopf bifurcation and admits a limit cycle under certain conditions (refer [12]).

The main objective of this paper is to show that a dynamic balance can be reached and the system (2) can be stabilized both locally and globally by suitably chosen feedback linearization design.

3 Feedback Linearization

Feedback linearization fully or partly transforms the primary nonlinear system into an equivalent linear system. This approach is entirely different from the traditional Jacobian approach.

3.1 Approximate Linearization

In the present section, an effort is made to stabilize the system (2) by employing approximate linearization.

Theorem 1

The feedback control law u stabilizes the closed-loop system (2), where u is

$$u=k_{1}(x-x^{*})+k_{2}(y-y^{*})$$
$$\begin{aligned} k_{1}> & {} \frac{(k_{2}-\gamma )\left( 1-2x^{*}-\frac{(\alpha -{x^{*}}^2)\beta x^{*}}{({x^{*}}^2+\alpha )^2}\right) }{\frac{x^{*}}{{x^{*}}^2+\alpha }}-\beta \gamma \\ k_{2}< & {} \gamma +2x^{*}+\frac{(\alpha -{x^{*}}^2)\beta x^{*}}{({x^{*}}^2+\alpha )^2}-1. \end{aligned}$$

Proof

A linear control u is exerted on the system (2) as

$$\begin{aligned} \nonumber \frac{dx}{dt}= & {} x\left( 1-x\right) -\frac{xy}{x^2+\alpha }\\ \frac{dy}{dt}= & {} \gamma \left( 1-\frac{ y}{\beta x}\right) y+u. \end{aligned}$$
(4)

Transformations \(v=x-x^{*}\) and \(w=y-y^{*}\) reduce the system (4) to

$$\begin{aligned} \nonumber \dot{v}= & {} (v+x^{*})\left( 1-(v+x^{*})\right) -\frac{(v+x^{*})(w+y^{*})}{(v+x^{*})^2+\alpha } \\ \dot{w}= & {} (w+y^{*})\left( \gamma -\frac{\gamma (w+y^{*})}{\beta (v+x^{*})}\right) +u. \end{aligned}$$
(5)

where \(x^{*}\) and \(y^{*}\) are equilibrium values. The linearized form of (5) can be written as

$$\begin{aligned} \dot{\mathbf{U }}=A\mathbf U +Bu \end{aligned}$$
(6)

where

$$\mathbf U =\left( \begin{array}{c} v \\ w \\ \end{array} \right) , ~ A=\left( \begin{array}{cc} 1-2x^{*}-\frac{(\alpha -{x^{*}}^2)\beta x^{*}}{({x^{*}}^2+\alpha )^2} &{} -\frac{x^{*}}{{x^{*}}^2+\alpha } \\ \beta \gamma &{} -\gamma \\ \end{array} \right) , ~ B=\left( \begin{array}{c} 0 \\ 1\\ \end{array} \right) . $$

In linear feedback, each control variable takes as a linear combination of state variables. In our case

$$\begin{aligned} u=K\mathbf U . \end{aligned}$$
(7)

where row vector \( K=\left( \begin{array}{cc} k_{1} &{} k_{2} \\ \end{array} \right) \) represents a constant feedback. Using (7), (6) can be written as

$$\begin{aligned} \dot{\mathbf{U }}=(A+BK)\mathbf U =C\mathbf U \end{aligned}$$
(8)

and

$$C=A+BK=\left( \begin{array}{cc} 1-2x^{*}-\frac{(\alpha -{x^{*}}^2)\beta x^{*}}{({x^{*}}^2+\alpha )^2} &{} -\frac{x^{*}}{{x^{*}}^2+\alpha } \\ \beta \gamma +k_{1} &{} -\gamma +k_{2} \\ \end{array} \right) .$$

The trace and determinant of matrix C are

$$\begin{aligned} Trace ~C= & {} 1-2x^{*}-\frac{(\alpha -{x^{*}}^2)\beta x^{*}}{({x^{*}}^2+\alpha )^2}-\gamma +k_{2}\\ det~ C= & {} \left( 1-2x^{*}-\frac{(\alpha -{x^{*}}^2)\beta x^{*}}{({x^{*}}^2+\alpha )^2}\right) (-\gamma +k_{2})+\left( \beta \gamma +k_{1}\right) \left( \frac{x^{*}}{{x^{*}}^2+\alpha }\right) . \end{aligned}$$

It follows from the Routh–Hurwitz criterion that the controlled system (8) is stable iff

$$Trace~ C<0,~ det ~C>0.$$

Thus suitably chosen \(k_{1}\) and \(k_{2}\) such that

$$\begin{aligned} k_{2}<\gamma +2x^{*}+\frac{(\alpha -{x^{*}}^2)\beta x^{*}}{({x^{*}}^2+\alpha )^2}-1< 0 \end{aligned}$$
(9)

and

$$\begin{aligned} k_{1}>\frac{(k_{2}-\gamma )\left( 1-2x^{*}-\frac{(\alpha -{x^{*}}^2)\beta x^{*}}{({x^{*}}^2+\alpha )^2}\right) }{\frac{x^{*}}{{x^{*}}^2+\alpha }}-\beta \gamma . \end{aligned}$$
(10)

would make the system (8) stable.

3.2 Exact Linearization

In the previous section, a control law was obtained, using approximate linearization approach, locally. In this section, another approach known as exact linearization, is employed which makes the system locally as well as globally stable.

The nonlinear system is assumed to be of the form

$$\begin{aligned} \nonumber \dot{\mathbf{X }}= & {} f(\mathbf X )+g(X)u^{'},\quad \mathbf X (0)=\mathbf X _{0} \\ \tilde{X}= & {} h(\mathbf X ) \end{aligned}$$
(11)

where \(\mathbf X \in {R}^{n}\) and \(u^{'}\in {R}^{m}\) are state vector and input vector respectively. \(\tilde{X}\in {R}^{m}\)is output vector having continuous derivatives where f, g are continuous vector on \({R}^{n}\) with \(f(0)=0\).

The feedback control is employed as

$$\begin{aligned} u^{'}=\alpha (\mathbf X )+\beta (\mathbf X )v \end{aligned}$$
(12)

where v is an external reference input. Further, a change of variable \(z=\varPhi (\mathbf X )\) is introduced that transforms the nonlinear system into a linear controllable system.

The original system (2) with control term can be written as

$$\begin{aligned} \dot{\mathbf{X }}=\left( \begin{array}{c} x\left( 1-x\right) -\frac{xy}{x^2+\alpha }\\ y\left( \gamma -\frac{\gamma y}{\beta x}\right) \\ \end{array} \right) +\left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right) u^{'} \end{aligned}$$
(13)

Here \(u^{'}\) is an exerted control introducing an output \(\tilde{X}=x-x^{*}\) stands for chasing of prey population. Theorem 2 is the main result of this section.

Theorem 2

The closed loop system (13) is globally asymptotically stable provided the feedback control law is

$$\begin{aligned} u^{'}=-x(x^2+\alpha )-y+\frac{x^2+\alpha }{x}-\frac{(\alpha -x^2)\beta }{(x^2+\alpha )}. \end{aligned}$$
(14)

Proof

Using the transformations be \(\bar{x}=x-x^{*}, \bar{y}=y-y^{*}\), the system (13) can be rewritten as

$$\begin{aligned} \nonumber \dot{\bar{\mathbf{X }}}= & {} f(\bar{\mathbf{X }})+g(\bar{\mathbf{X }})u^{'} \\ \tilde{X}= & {} h(\bar{\mathbf{X }})=\bar{x} \end{aligned}$$
(15)

where

$$ f(\bar{\mathbf{X }})=\left( \begin{array}{c} (\bar{x}+x^{*})\left( 1-(\bar{x}+x^{*})\right) -\frac{(\bar{x}+x^{*})(\bar{y}+y^{*})}{(\bar{x}+x^{*})^2+\ alpha}\\ (\bar{y}+y^{*})\left( \gamma -\frac{\gamma (\bar{y}+y^{*})}{\beta (\bar{x}+x^{*})}\right) \\ \end{array} \right) ,\quad g(\bar{\mathbf{X }})=\left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right) $$
$$ \text {and} \quad \bar{\mathbf{X }}=\left( \begin{array}{c} \bar{x} \\ \bar{y} \\ \end{array} \right) . $$

As \(h(\bar{\mathbf{X }})=\bar{x}\), then

$$\begin{aligned} L_{f}h(\bar{\mathbf{X }})=\dot{\bar{x}}=x\left( 1-x\right) -\frac{xy}{x^2+\alpha }, \end{aligned}$$
(16)

obviously,

$$\begin{aligned} {L_{g}L_{f}^{r-1}h(\bar{\mathbf{X }})}={L_{g}L_{f}^{2-1}h(\bar{\mathbf{X }})}=-\frac{x}{x^2+\alpha }\ne 0. \end{aligned}$$
(17)

Here r is relative degree. For the particular system \(r=2\).

Letting

$$\begin{aligned} z=\varPhi (\bar{\mathbf{X }}) =\left( \begin{array}{c} h(\bar{\mathbf{X }}) \\ L_{f}h(\bar{\mathbf{X }}) \\ \end{array} \right) =\left( \begin{array}{c} \bar{x} \\ \dot{\bar{x}} \\ \end{array} \right) \end{aligned}$$
(18)

which denotes change of variables and \(h(\bar{\mathbf{X }})\) and \(L_{f}h(\bar{\mathbf{X }})\) being linearly independent, it is global diffeomorphism. Describing

$$\begin{aligned} \nonumber \dot{z}_{1}= & {} z_{2} \\ \dot{z}_{2}= & {} v \end{aligned}$$
(19)

in the new z-coordinate system, where v is a input relating to actual input \(u^{'}\) by

$$v=L^2_{f}h(\bar{\mathbf{X }})+L_{g}L_{f}h(\bar{\mathbf{X }})u^{'},~~ {L_{g}L_{f}h(\bar{\mathbf{X }})}\ne 0$$

The Brunovsky canonical form is written as (see [1])

$$\begin{aligned} u^{'}=\frac{1}{L_{g}L_{f}h(\bar{\mathbf{X }})}(-z_{1}-z_{2}-L_{f}^{2}h(\bar{\mathbf{X }})). \end{aligned}$$
(20)

Accordingly, the system (2) converts into the linear system and the Brunovsky linear system is absolutely controllable [1]. Hence the system (13) is globally stable (ref. [18]).

From (20), the control law \(u^{'}\) can be written as

$$\begin{aligned} u^{'}=-x(x^2+\alpha )-y+\frac{x^2+\alpha }{x}-\frac{(\alpha -x^2)\beta }{(x^2+\alpha )}. \end{aligned}$$
(21)

Hence the proof.

4 Numerical Simulation

In the current section, numerical simulations are given to validate the analytic results for the stabilization of the system (2). Let us consider the following set of parameters [8]:

$$\begin{aligned} \alpha =0.2, \beta =1.2, \gamma =0.02. \end{aligned}$$
(22)

For this choice of parameters, system (2) shows limit cycle and corresponding oscillating time series, respectively for initial values (0.1578, 0.18935). Analysis suggests that system (2) exhibits periodic orbits and thrashing time series (see Figs. 1 and 2).

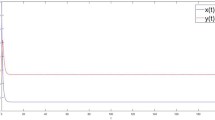
By employing feedback control with approximate linearization (see Sect. 3.1), a control law \(u=K\mathbf U \) is achieved with \(K=\left( \begin{array}{cc} 1 &{} ~~0.27\\ \end{array} \right) \) through which system attains asymptotic stability. In Fig. 3, the time series converges to equilibrium point of the system (2).

In exact linearization (see Sect. 3.2), the control law (14) as given in Theorem 2, i.e.

$$\begin{aligned} \nonumber u^{'}= & {} -x(x^2+0.2)-y+\frac{(x^2+0.2)}{x}+\frac{(0.2-x^2)1.2}{(x^2+0.2)} \end{aligned}$$

makes system (2) globally stable. Time series plotted in Fig. 4 shows that solution trajectory approaches to equilibrium point \(E^{*}(0.0025, 0.2005)\).

Fig. 1
figure 1

Closed loop of original system (2)

Full size image
Fig. 2
figure 2

Oscillating time series of original system (2)

Full size image
Fig. 3
figure 3

Approximate linearization

Full size image
Fig. 4
figure 4

Exact linearization

Full size image

5 Conclusions

The Leslie–Gower prey-predator model with Holling type IV functional response shows periodic solutions and bifurcations [8, 12]. In this paper, it is shown that desired control laws can be determined using feedback (approximate and exact) linearizations that can bring the system into order such that its positive equilibrium solution becomes locally and globally stable.

Feedback linearization approaches are important methods to deal with nonlinear dynamical systems. Results of this study further show that control theory has a vital role to play even in biological sciences.