Design Optimization of Shell and Tube Heat Exchanger Using Differential Evolution Algorithm

Abstract

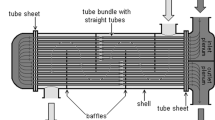
Shell and tube heat exchangers (STHE) are the most common type of heat exchangers widely used in various kinds of industrial applications. Cost minimization of these heat exchangers is of prime concern for designers as well as for users. Heat exchanger design involves processes such as selection of geometric and operating parameters. Generally, different exchangers geometries are rated to identify those that satisfy a given heat duty and a set of geometric and operational constraints. In the present study we have considered minimization of total annual cost as an objective function. The different variables used include shell internal diameter, outer tube diameter and baffle spacing for which two tube layout viz. triangle and square are considered. The optimization tool used is differential evolution (DE) algorithm, a nontraditional stochastic optimization technique. Numerical results indicate that, DE can be used effectively for dealing with such types of problems.

1 Introduction

Heat exchangers are devices that facilitate heat transfer between two fluids at different temperatures. They are used in industrial process to recover heat between two process fluids. The shell-and-tube heat exchangers (STHE) are probably the most common type of heat exchangers applicable for a wide range of operating temperatures and pressures.

The design of STHEs, including thermodynamic and fluid dynamic design, cost estimation and optimization, represents a complex process containing an integrated whole of design rules and empirical knowledge of various fields. There are many previous studies on the optimization of heat exchanger. Investigators have used different optimization techniques considering different objective functions like minimum entropy generation and minimum cost of STHEs to optimize heat exchanger design.

Some studies have focused on a single geometric parameter like optimal baffle spacing while some have considered optimizing a variety of geometrical and operational parameter of STHEs.

Strategies applied for solving such problems vary from traditional mathematical methods to sophisticated non-traditional optimization methods such as genetic algorithms (GA), differential evolution (DE), particle swarm optimization (PSO) etc. Relevant literature can be found in [1–7].

In the present study we have considered the cost optimization of STHE and have employed DE for solving the optimization model.

The remaining of the paper is divided into three sections. In Sect. 2, we discuss the DE optimization technique, in Sect. 3, mathematical model considered is discussed in brief. In Sect. 4, we give numerical results and finally in Sect. 5, the conclusions based on the present study are given.

2 Differential Evolution (DE)

DE, an evolutionary algorithm, was proposed by Storn and Price [8, 9]. The main operators of DE are mutation, crossover and selection to guide the search process. The algorithm uses mutation operation as a search mechanism; crossover operation is applied to induce diversity and selection operation is to direct the search toward the potential regions in the search space.

DE starts with a set of solutions, which is randomly generated when no preliminary knowledge about the solution space is available. This set of solution is called population.

Let $P^{G} = \{ X_{i}^{G} , \, i = 1,2, \ldots NP\}$ be the population at any generation G which contain NP individuals where an individual can be defined as a D dimensional vector such as $X_{i}^{G} = \left( {x_{1,i}^{G} ,x_{2,i}^{G} \ldots , \, x_{D,i}^{G} } \right).$

For basic DE (DE/rand/1/bin) mutation, crossover and selection operations are defined as below:

• i. Mutation: For each target vector $X_{i}^{G}$, mutant vector $V_{i}^{G + 1}$ is defined by:

$$ V_{i}^{G} = X_{r1}^{G} + F(X_{r2}^{G} - X_{r3}^{G} ) $$

(1)

Where $r_{1} ,r_{2} ,r_{3} ,r_{4} ,r_{5} \in 1,2, \ldots NP$ are randomly chosen integers, distinct from each other and also different from the running index i. F is a real and constant factor having value between [0, 2] and controls the amplification of differential variation $\left( {X_{r2}^{G} -X_{r3}^{G} } \right)$.

• ii. Crossover: Crossover is introduced to increase the diversity of perturbed parameter vectors $V_{i}^{G} = \left( {v_{1,i}^{G} ,v_{2,i}^{G} \ldots v_{D,i}^{G} } \right)$.

Let $U_{i}^{G} = \left( {u_{1,i}^{G} ,u_{2,i}^{G} \ldots, u_{D,i}^{G} } \right)$ as the trial vector then $U_{i}^{G}$ is defined as:

$$ u_{{j,i}}^{G} = \left\{ {\begin{array}{*{20}l} {v_{{j,i}}^{G} ,} & {if\,Cr < rand(0\,1)\forall j = jrand} \\ {x_{{j,i}}^{G} } & {otherwise} \\ \end{array} } \right. $$

(2)

rand(0, 1) is uniform random number between 0 and 1; Cr is the crossover constant takes values in the range [0, 1] and jrand ∈ 1, 2,…, D; is the randomly chosen index.

• iii. Selection: It decides which vector $\left( {X_{i}^{G}\,{\text{or}}\,U_{i}^{G} } \right)$ should be a member of next generation G + 1. During the selection operation we generate a new population $P^{G + 1} = \left\{ {X_{i}^{G + 1} ,\quad i = 1,{ 2}, \ldots ,NP} \right\}$ for next generation G + 1 by choosing the best vector between trial vector and target vector.

$$ X_{i}^{{G + 1}} = \left\{ {\begin{array}{*{20}l} {U_{i}^{G} ,} & {if\,f(U_{i}^{G} ) < f(X_{i}^{G} )} \\ {X_{i}^{G} } & {otherwise} \\ \end{array} } \right. $$

(3)

Thus the points obtained after selection are either better or at par with the points of the previous generation.

3 Mathematical Model

• A. Objective Function

• Total cost C_t is taken as the objective function, which includes capital investment (C_i), energy cost (C_e), annual operating cost (C_o) and total discounted operating cost (C_tod) [10]. This optimization function is subjected to design variables d₀, D_s and B.

  $$ {\text{Minimize}}\;{\text{C}}_{\text{t}} = {\text{C}}_{\text{i}} + {\text{C}}_{\text{tod}} $$

  • (a) Capital investment includes cost of purchase, instalment and piping for heat exchanger and shell side and tube side pumps multiplied by annualization factor.

$$ {\text{C}}_{\text{i}} = A_{f} \left( {{\text{C}}_{\text{ps}} + {\text{ C}}_{\text{pt}} + {\text{ C}}_{\text{he}} } \right) $$

Capital cost is calculated by using halls correlation and it depends on exchanger surface area (A).

$$ {\text{C}}_{\text{i}} = a_{1} + \, a_{2} \;A^{{a_{3} }} $$

Where a ₁ = 8000, a ₂ = 259.2 and a ₃ = 0.93 for stainless steel is used as material of construction for both shell and tubes.

• (b) Total operating cost is cost of energy required to operate pumps. This is given by

$$ {\text{C}}_{\text{o}} = {\text{PC}}_{\text{e}} {\text{H}} $$

And total discounted total cost is given by

$$ {\text{C}}_{\text{od}} = \mathop \sum \limits_{x = 1}^{ny} \frac{\text{Co}}{{(1 + i)^{x} }} $$

• B. Heat Transfer equations

• Heat transfer between fluids in shell and tube is due to convection currents in liquids and conduction in wall of tube. But as steal is highly conducting material and thickness of tube walls is assumed to be very small, resistance offered to conduction heat transfer in tube walls is ignored. Depending on flow pattern, tube side heat transfer coefficient is calculated by following correlation.

  $$ h_{t} = \frac{{k_{t} }}{{d_{i} }}\left[ {3.657 + \frac{{0.0677(Re_{t} Pr_{t} \left( {\frac{{d_{i} }}{L}} \right))^{{1.33^{1/3} }} }}{{1 + 0.1Pr_{t} (Re_{t} \left( {\frac{{d_{i} }}{L}} \right))^{0.3} }}} \right] $$

  (if Re_t < 2,300 [10])

  $$ h_{t} = \frac{{k_{t} }}{{d_{i} }}\left[ {\frac{{(\frac{{f_{t} }}{8})(Re_{t} - 1000)Pr_{t} }}{{1 + 12.7\left( {\frac{{f_{t} }}{8}} \right)^{\frac{1}{2}} (Pr_{t}^{\frac{2}{3}} - 1)}}\left( {1 + \frac{{d_{i} }}{L}} \right)^{0.67} } \right] $$

  (if 2300 < Re_t < 10,000 [10])

  $$ h_{t} = 0.027\frac{{k_{t} }}{{d_{0} }}Re_{t}^{0.8} Pr_{t}^{1/3} \left( {\frac{{\mu_{t} }}{{\mu_{wt} }}} \right)^{0.14} $$

  (If Re_t > 10,000 [10])

Where f_t is Darcy friction factor given by

$$ f_{t} = \left( {1.82\log 10^{{Re_{t} }} - 1.64} \right)^{ - 2} $$

Re_t is Reynolds number which is given by

$$ Re_{t} = \frac{{\rho_{t} v_{t} d_{i} }}{{\mu_{t} }} $$

Flow velocity at tube side is given by

$$ v_{t} = \frac{{m_{t} }}{{\left( {\pi /4} \right)d_{t}^{2} \rho_{t} }}\left( {\frac{n}{{N_{t} }}} \right) $$

• N_t is the number of tubes and n is the number of tube passes. Total number of tubes (N_t) is depended on shell diameter and tube diameter. These can be approximated by the equation

  $$ N_{t} = C\left( {\frac{{D_{s} }}{{d_{0} }}} \right)^{{n_{1} }} $$

• C and n₁ are coefficients that take values according to flow arrangement and number of passes. These coefficients are given Table 1 for different flow arrangements.

  Table 1 Value of C and n₁ coefficients

Tube side prandtl number (Pr_t) is given by

$$ Pr_{t} = \frac{{\mu_{t} C_{pt} }}{{k_{t} }} $$

Also d_i = 0.8 d_o

Kerns formulation [11] is used to find shell side heat transfer coefficient of segmental baffle shell and tube heat exchanger

$$ h_{s} = 0.36\frac{{k_{t} }}{{d_{e} }}Re_{s}^{0.55} Pr_{s}^{1/3} \left( {\frac{{\mu_{s} }}{{\mu_{wts} }}} \right)^{0.14} $$

Where d_e is shell hydraulic diameter and computed as

$$ d_{e} = \frac{{4\left( {S_{t}^{2} - \left( {\pi d_{0}^{2} /4} \right)} \right)}}{{\pi d_{0} }} $$

(for square pitch)

$$ d_{e} = \frac{{4\left( {0.43S_{t}^{2} - \left( {0.5\pi d_{0}^{2} /4} \right)} \right)}}{{0.5\pi d_{0} }} $$

(for triangular pitch)

Cross sectional area normal to flow direction is determined by

$$ \begin{aligned} A_{s} & = D_{s} B\left( {1 - \frac{{d_{0} }}{{S_{t} }}} \right) \\ v_{s} & = \frac{{m_{s} }}{{\rho_{s} A_{s} }} \\ \end{aligned} $$

Reynolds number for shell side follows,

$$ Re_{s} = \frac{{m_{s} d_{e} }}{{A_{s} \mu_{s} }} $$

Prandtl number for shell side follows,

$$ Pr_{s} = \frac{{\mu_{s} C_{ps} }}{{k_{s} }} $$

The overall heat transfer coefficient (U) depends on both the tube side and shell side heat transfer coefficients and fouling resistances are given by

$$ U = \frac{1}{{\left( {1/h_{s} } \right) + R_{fs} + \left( {d_{0} /d_{i} } \right)\left( {R_{ft} + \left( {1/h_{t} } \right)} \right)}} $$

Considering the cross flow between adjacent baffle, the logarithmic mean temperature difference (LMTD) is determined by,

$$ LMTD = \frac{{\left( {T_{hi} - T_{co} } \right) - \left( {T_{ho} - T_{ci} } \right)}}{{\log \left( {\left( {T_{hi} - T_{co} } \right)/\left( {T_{ho} - T_{ci} } \right)} \right)}} $$

The correction factor F for the flow configuration involved is found as a function of dimensionless temperature ratio for mostflow configuration of interest, [12, 13]

$$ \begin{aligned} F & = \frac{{\sqrt {R^{2} + 1} }}{R - 1} \\ & *\frac{{\ln \left( {\left( {1 - P} \right)/\left( {1 - PR} \right)} \right)}}{{\ln \left( {\left( {2 - PR - P + P\sqrt {R^{2} + 1} } \right)/\left( {2 - PR - P - P\sqrt {R^{2} + 1} } \right)} \right)}} \\ \end{aligned} $$

Where R is a coefficient given by,

$$ R = \frac{{\left( {T_{hi} - T_{ho} } \right)}}{{\left( {T_{co} - T_{ci} } \right)}} $$

And P is the efficiency given by,

$$ P = \frac{{\left( {T_{co} - T_{ci} } \right)}}{{\left( {T_{hi} - T_{ci} } \right)}} $$

Considering overall heat transfer coefficient, the heat exchanger surface area (A) is computed by,

$$ A = \frac{Q}{U*F*LMTD} $$

For sensible heat transfer

$$ Q = m_{h} C_{ph} \left( {T_{hi} - T_{ho} } \right) = m_{c} C_{pc} \left( {T_{co} - T_{ci} } \right) $$

Based on total heat exchanger surface area (A) the necessary tube length (L) is,

$$ L = \frac{A}{{\pi d_{0} t}} $$

• C. Pumping Power

• The power required to pump the fluid into the shell and tube heat exchanger is a function of the pressure drop allowance which is actually the static fluid pressure which may be expended to drive the fluid through the exchanger. There is a very close physical and economic affinity between pressure drop and heat transfer for every type of heat exchanger. Increasing the flow velocity will result in rise of heat transfer coefficient (for a constant heat capacity in a heat exchanger). This results in a compact exchanger design and reduced investment cost. But we cannot neglect the fact that increase in flow velocity will cause more pressure drop which will result in additional running cost. For this reason pressure drop is considered with heat transfer in order to find best solution for the system.

Tube side pressure drop includes distributed pressure drop along the tube length and concentrated pressure losses in elbows and in the inlet and outlet nozzle [11]

$$ \begin{aligned} \varDelta P_{t} & = \varDelta P_{tubelength} + \varDelta P_{tubeelbow} \\ \varDelta P_{t} & = \frac{{\rho_{t} v_{t}^{2} }}{2}\left( {\frac{L}{{d_{i} }}f_{t} + p} \right)n \\ \end{aligned} $$

Different values of constant p are considered by different authors. Kern [13] assumed p = 4, while Sinnot et al. [14] assume dp = 2.5.

The shell side pressure drop is,

$$ \varDelta P_{s} = f_{s} \left( {\frac{{\rho_{s} v_{s}^{2} }}{2}} \right)\left( \frac{L}{B} \right)\left( {\frac{{D_{s} }}{{D_{e} }}} \right), $$

Where,

$$ f_{s} = 2b_{0} Re_{s}^{ - 0.15} $$

And b₀ = 0.72 [15] valid for Re_s < 40,000

Considering pumping efficiency $(\eta )$, pumping power computed by,

$$ P = \frac{1}{\eta }\left( {\frac{{m_{t} }}{{\sigma_{t} }}\varDelta P_{t} - \frac{{m_{s} }}{{\sigma_{s} }}\varDelta P_{s} } \right) $$

• D. Design constraints for feasible design

• Design of heat exchanger is constrained by various factors. Those can be classified into geometric and operating constraints.

• Operating constraints

• Maximum allowed pressure drop on both shell and tube side of heat exchanger. These pressure drops are directly proportional to maximum pump capacity available. Upper bounds of pressure drops are given by

  $$ \begin{aligned} \varDelta {\text{P}}_{\text{t}} \le & \, \, \varDelta {\text{P}}_{\text{tmax}} \\ \varDelta {\text{P}}_{\text{s}} \le &\, \, \varDelta {\text{P}}_{\text{smax}} \\ \end{aligned} $$

Velocity range allowed for both shell and tube sides. Velocity of fluid above certain value can cause erosion or flow induced tube vibrations and lower velocities can cause fowling. These bounds are given by

$$ \begin{aligned} {\text{V}}_{\text{tmin}} \le &\, {\text{V}}_{\text{t}} \le {\text{V}}_{\text{tmax}} \\ {\text{V}}_{\text{smin}} \le &\, {\text{V}}_{\text{s}} \le {\text{V}}_{\text{smax}} \\ \end{aligned} $$

Recommended velocity by Sinnot on tube side are 1–2.5 m/s and 0.3–1 m/s on shell side.

• Geometric constraints

• Length and diameter of shell and tube heat exchanger can be restricted due to space constraints.

  $$ \begin{aligned} {\text{D}}_{\text{s}} &\, \le {\text{D}}_{\text{smax}} \\ {\text{L}}_{\text{t}} &\, \le {\text{L}}_{\text{tmax}} \\ \end{aligned} $$

In case of baffle spacing, higher spacing can cause bypassing, reduced cross flow along with low heat transfer coefficient and lower spacing can lead to higher heat transfer coefficient in expense of higher pressure drops in shell side fluid

$$ {\text{B}}_{ \hbox{min} } \le {\text{B}} \le {\text{B}}_{ \hbox{max} } $$

4 Numerical Results and Discussions

• A. Parameter settings of DE

• DE has certain control parameters which are to be set by the user. In the present study the following parameter setting is considered:

  • Population size—50

  • Scale factor F—0.5, 0.8

  • crossover rate Cr—0.5, 0.9

  • maximum number of iterations—100

  • B. Experimental settings

• We executed the algorithm 50 times and recorded the mean value.

• Programming language used is DEVC++.

• Random numbers are generated using rand() the inbuilt function of DEVC++.

• The effectiveness of the present approach using DE is assessed by analyzing the following case study:1.44 (MW) duty, kerosene crude oil exchanger [16].

• C. Results and comparison

• In this section, numerical results are given in Tables 1 and 2. In Table 1 results are given on the basis of different parameter settings (denoted as 1,2,3 in Table 2) of DE. The values given by setting 2 (Cr = 0.9, F = 0.5) are optimum. Hence, we can see that parameter setting 2 (Cr = 0.9, F = 0.5) perform better in the comparison of other settings.

  Table 2 Results by DE with different parameter settings

We observed that the numerical results obtained using DE are either better or at par with the results available in literature. It was observed that DE was able to achieve the optimal design variables successfully (Table 3).

Table 3 Comparison of results with GA and PSO

5 Conclusion

Heat exchangers are an integral component of all thermal systems. Their designs should be adapted well to the applications in which they are used; otherwise their performances will be deceiving and their costs excessive. Heat exchanger design can be a complex task, which requires a suitable optimization technique for a proper solution. The present work shows the effectiveness of differential evolution optimization algorithm. This technique can be easily modified to suit optimization of various thermal systems.