Keywords

1 Introduction

Uncertainty quantification is important in the assessing and predicting performance of complex engineering systems, especially given limited experimental or real-world data. Simulation of complex physical systems involves multiple levels of modeling, ranging from the material to component to subsystem to system. Interacting models and simulation codes from multiple disciplines (multiple physics) may be required, with iterative analyses between some of the codes. As the models are integrated across multiple disciplines and levels, the problem becomes more complex, and assessing the predictive capability of the overall system model becomes more difficult. Many factors contribute to the uncertainty in the prediction of the system model including inherent variability in model input parameters, sparse data, measurement error, modeling errors, assumptions, and approximations.

The various sources of uncertainty in performance prediction can be grouped into three categories:

  • Physical variability

  • Data uncertainty

  • Model error

1.1 Physical Variability

This type of uncertainty also referred to as aleatory or irreducible uncertainty arises from natural or inherent random variability of physical processes and variables, due to many factors such as environmental and operational variations, construction processes, and quality control. This type of uncertainty is present both in system properties (e.g., material strength, porosity, diffusivity, geometry variations, chemical reaction rates) and external influences and demands on the system (e.g., concentration of chemicals, temperature, humidity, mechanical loads). As a result, in model-based prediction of system behavior, there is uncertainty regarding the precise values for model parameters and model inputs, leading to uncertainty about the precise values of the model output. Such quantities are represented in engineering analysis as random variables, with statistical parameters, such as mean values, standard deviations, and distribution types, estimated from observed data or in some cases assumed. Variations over space or time are modeled as random processes.

1.2 Data Uncertainty

This type of uncertainty falls under the category of epistemic uncertainty (i.e., knowledge or information uncertainty) or reducible uncertainty (i.e., the uncertainty is reduced as more information is obtained). Data uncertainty occurs in different forms. In the case of a quantity treated as a random variable, the accuracy of the statistical distribution parameters depends on the amount of data available. If the data is sparse, the distribution parameters themselves are uncertain and may need to be treated as random variables. Alternatively, information may be imprecise or qualitative, or as a range of values, based on expert opinion. Both probabilistic and non-probabilistic methods have been explored to represent epistemic uncertainty. Measurement error (either in the laboratory or in the field) is another important source of data uncertainty.

1.3 Model Error

This results from approximate mathematical models of the system behavior and from numerical approximations during the computational process, resulting in two types of error in general – solution approximation error and model form error. The performance assessment of a complex system involves the use of several analysis models, each with its own assumptions and approximations. The errors from the various analysis components combine in a complicated manner to produce the overall model error (described by both bias and uncertainty).

The roles of several types of uncertainty in the use of model-based simulation for performance assessment can be easily seen in the case of reliability analysis. Consider the probability of an undesirable event denoted by g(X) < k, which can be computed from Eq. (1):

$$ P\left( {g({\mathbf{X}}) < k} \right) = \int\limits_{{g({\mathbf{X}}) < k}} {{{f}_{{\mathbf{X}}}}({\mathbf{x}}){\text{d}}{\mathbf{x}}} $$
(1)

where X is the vector of input random variables, f X (x) is the joint probability density function of X, g(X) is the model output, and k is the regulatory requirement in performance assessment. Every term on the right-hand side of Eq. (1) has uncertainty. There is inherent variability represented by the vector of random variables X, data uncertainty (due to inadequate data) regarding the distribution type and distribution parameters of f X (x), and model errors in the computation of g(X). Thus, it is necessary to systematically identify the various sources of uncertainty and develop the framework for including them in the overall uncertainty quantification in the performance assessment of engineering systems.

The uncertainty analysis methods covered in this chapter are grouped by sections along the four major groups of analysis activities that are needed for performance assessment under uncertainty:

  1. 1.

    Input uncertainty quantification

  2. 2.

    Uncertainty propagation analysis (includes model error quantification)

  3. 3.

    Model calibration, verification, validation, and extrapolation

  4. 4.

    Probabilistic performance assessment

A brief summary of the analysis methods covered in the four groups is as follows:

  • Input uncertainty quantification: Physical variability of parameters can be quantified through random variables by statistical analysis. Parameters that vary in time or space are modeled as random processes or random fields with appropriate correlation structure. Data uncertainty that leads to uncertainty in the distribution parameters and distribution types can be addressed using confidence intervals and Bayesian statistics. Recent methods to include several sources of data uncertainty, namely, sparse data, interval data, and measurement error, are discussed in this chapter.

  • Uncertainty propagation analysis: Both classical and Bayesian probabilistic approaches can be investigated to propagate inherent variability and data uncertainty through individual sub-models and the overall system model. To reduce the computational expense, surrogate models can be constructed using several different techniques. Methods for sensitivity analyses in the presence of uncertainty are discussed. The uncertainty in the overall model output also includes model errors and approximations in each step of the analysis; therefore, approaches to quantify model error are included in the discussion.

  • Model calibration, verification, validation, and extrapolation: Model calibration is the process of adjusting model parameters to obtain good agreement between model predictions and experimental observations. Both classical and Bayesian statistical methods are discussed for model calibration with available data. One particular concern is how to properly integrate different types of data, available at different levels of the model hierarchy. Assessment of the “correct” implementation of the model is called verification, and assessment of the degree of agreement of the model response with the available physical observation is called validation. Model verification and validation activities help to quantify model error (both model form error and solution approximation error). A Bayesian network framework is discussed for quantifying the confidence in model prediction based on data, models, and activities at various levels of the system hierarchy. Such information is available in heterogeneous formats from multiple sources, and a consistent framework to integrate such disparate information is important.

  • Performance assessment: Limit state-based reliability analysis methods are available to help quantify the assessment results in a probabilistic manner. Monte Carlo simulation with high-fidelity analyses modules is computationally expensive; hence, surrogate (or abstracted) models are frequently used with Monte Carlo simulation. In that case, the uncertainty or error introduced by the surrogate model also needs to be quantified.

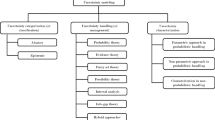
Figure 1 shows the four groups of activities within a conceptual framework for systematic quantification, propagation, and management of various types of uncertainty. The methods discussed in this chapter address all the four steps shown in Fig. 1. The different steps of analysis in Fig. 1 are not strictly sequential. While uncertainty has been dealt with using probabilistic as well as non-probabilistic (e.g., fuzzy sets, possibility theory, evidence theory) formats in the literature, this chapter will only focus on probabilistic analysis.

Fig. 1
figure 1

Uncertainty quantification, propagation, and management

Full size image

In Fig. 1, the box “Data” in the input uncertainty quantification step includes laboratory data, historical field data, literature sources, and expert opinion. The box “Design changes” may refer to conceptual, preliminary, or detailed design, depending on the development stage. The boxes “Design changes” and “Risk management” are outside the scope of this chapter, although they are part of the overall uncertainty management framework.

2 Input Uncertainty Quantification

2.1 Physical Variability

Examples of model input variables with physical variability (i.e., inherent, natural variability) include:

  1. (a)

    Material properties (e.g., mechanical and thermal properties, soil properties, chemical properties)

  2. (b)

    Geometrical properties (e.g., Structural dimensions, concrete cover depth)

  3. (c)

    External conditions (e.g., mechanical loading, boundary conditions, physical processes such as freeze-thaw, chemical processes such as carbonation, chloride, or sulfate attack)

Many uncertainty quantification studies have only focused on quantifying and propagating the inherent variability in the input parameters. Well-established statistical (both classical and Bayesian) methods are available for this purpose.

In probabilistic analysis, the sample to sample variations (random variables) in the parameters are addressed by defining them as random variables with probability density functions (PDFs). Some parameters may vary not only from sample to sample (as is the case for random variables) but also in spatial or time domain. Parameter variation over time and space can be modeled as random processes or random fields.

Some well-known methods for simulating random processes are spectral representation (SR) [13], Karhunen-Loeve expansion (KLE) ([10, 18, 30]), and polynomial chaos expansion (PCE) ([18, 30, 37]). The PCE method has been used to represent the stochastic model output as a function of stochastic inputs.

Consider an example of representing a random process using KLE, expressed as

$$ \pi (x,\chi ) = \pi (x) + \sum\limits_{{i = 1}}^{\infty } \sqrt {{{{\lambda }_i}}} {{\xi }_i}(\chi ){{f}_i}(x) $$
(2)

where \( \pi (x) \) is the mean of the random process \( \pi (x,\chi ) \), \( {{\lambda }_i} \) and \( {{f}_i}(x) \) are eigenvalues and eigenfunctions of \( C({{x}_1},{{x}_2}) \), and \( {{\xi }_i}(\chi ) \) is a set of uncorrelated standard normal random variables (x is a space or time coordinate, and χ is an index representing different realizations of the random process). Using Eq. (2), realizations of the random process \( \pi (x,\chi ) \) can be easily simulated by generating samples of the random variables \( {{\xi }_i}(\chi ) \), and these realizations of \( \pi (x,\chi ) \) can be used in the reliability analysis.

Some boundary conditions (e.g., temperature and moisture content) might exhibit a recurring pattern over shorter periods and also a trend over longer periods. Both can be numerically represented by a seasonal model using an autoregressive integrated moving average (ARIMA) method generally used for linearFootnote 1 nonstationaryFootnote 2 processes [5]. This method can be used to predict the temperature or the rainfall magnitudes in the future so that it can be used in the durability analysis of the structures under future environmental conditions.

It may also be important to quantify the statistical correlations between some of the input random variables. Many previous studies on uncertainty quantification simply assume either zero or full correlation, in the absence of adequate data. A Bayesian approach may be pursued for this purpose, as described in Sect. 2.2.

2.2 Data Uncertainty

This section discusses methods to quantify uncertainty due to limited statistical data and measurement errors (ε exp). Data may also be available in interval format (e.g., expert opinion). A Bayesian approach, consistent with the framework proposed in Fig. 1, can be used in the presence of data uncertainty. The prior distributions of different physical variables and their distribution parameters can be based on available data and expert judgment, and these are updated as more data becomes available through experiments, analysis, or real-world experience.

Data qualification is an important step in the consideration of data uncertainty. All data points may not have equal weight; a careful investigation of data quality will help to assign appropriate weights to different data sets.

2.2.1 Sparse Statistical Data

For any random variable that is quantitatively described by a probability density function, there is always uncertainty in the corresponding distribution parameters due to small sample size. As testing and data collection activities are performed, the state of knowledge regarding the uncertainty changes and a Bayesian updating approach can be implemented. The Bayesian approach also applies to joint distributions of multiple random variables, which also helps to include the uncertainty in correlations between the variables. A prior joint distribution is assumed (or individual distributions and correlations are assumed) and then updated as data becomes available.

Instead of assuming a well-known prior distribution form (e.g., uniform, normal) for sparse data sets, either empirical distribution functions or flexible families of distributions based on the data can be constructed. A bootstrappingFootnote 3 technique can then be used to quantify the uncertainty in the distribution parameters. The empirical distribution function is constructed by ranking the observations from lowest to highest value and assigning a probability value to each observation. Examples of flexible distribution families include the Johnson family, Pearson family, gamma distribution, and stretched exponential distribution (e.g., [48]). Recently, Sankararaman and Mahadevan [43] developed a likelihood-based approach to construct nonparametric probability distributions in the presence of both sparse and interval data.

Transformations have been proposed from a non-probabilistic to probabilistic format, through the maximum likelihood approach [25, 40]. Such transformations have attracted the criticism that information is either added or lost in the process. Two ways to address the criticism are to (1) construct empirical distribution functions based on interval data collected from multiple experts or experiments [9] and (2) construct flexible families of distributions with bounds on distribution parameters based on the interval data, without forcing a distribution assumption (McDonald et al. 2008). These can then be treated as random variables with probability distribution functions and combined with other random variables in a Bayesian framework to quantify the overall system model uncertainty. The use of families of distributions will result in multiple probability distributions for the output, representing the contributions of both physical variability and data uncertainty. The nonparametric approach of Sankararaman and Mahadevan [43] also has the ability to quantify the contributions of aleatory and epistemic uncertainty to the probabilistic representation of an uncertain variable.

2.2.2 Measurement Error

The measurement error in each input variable in many studies (e.g., [1]) is assumed to be independent and identically distributed (IID) normal with zero mean and an assumed variance, i.e., \( {{\varepsilon }_{{\exp }}}\sim N\left( {0,\sigma_{{\exp }}^2} \right) \). Due to the measurement uncertainty, the distribution parameter σ exp cannot be obtained as a deterministic value. Instead, it is a random variable with a prior density τ(σ exp). Thus, when new data is available after testing, the distribution of σ exp can be easily updated using the Bayesian theorem. Another way to represent measurement error \( {{\varepsilon }_{{\exp }}} \) is through an interval only, and not as a random variable.

3 Uncertainty Propagation Analysis

In this section, methods to quantify the contributions of different sources of uncertainty and error as they propagate through the system analysis model, including the contribution of model error, are discussed, in order to quantify the overall uncertainty in the system model output.

This section covers two issues: (1) quantification of model output uncertainty, given input uncertainty (both physical variability and data uncertainty), and (2) quantification of model error (due to both model form selection and solution approximations).

Several uncertainty analysis studies, including a study with respect to the proposed Yucca Mountain high-level waste repository, have recognized the distinction between physical variability and data uncertainty [16, 17]. As a result, these methods evaluate the variability in an inner loop calculation and data uncertainty in an outer loop calculation.

3.1 Propagation of Physical Variability

Various probabilistic methods (e.g., Monte Carlo simulation and first-order or second-order analytical approximations) have been studied for the propagation of physical variability in model inputs and model parameters [14] expressed through random variables and random process or fields. Stochastic finite element methods (e.g., [10, 15]) have been developed for single discipline problems, in structural, thermal, and fluid mechanics. An example of such propagation is shown in Fig. 2. Several types of combinations of system analysis model and statistical analysis techniques are available:

  • Monte Carlo simulation with the deterministic system analysis as a black-box (e.g., [39]) to estimate model output statistics or probability of regulatory compliance

  • Monte Carlo simulation with a surrogate model to replace the deterministic system analysis model (e.g., [10, 18, 19, 47]), to estimate model output statistics or probability of regulatory compliance

  • Local sensitivity analysis using finite difference, perturbation, or adjoint analyses, leading to estimates of the first-order or second-order moments of the output (e.g., [3])

  • Global sensitivity and effects analysis and analysis of variance in the output (e.g., [4])

Fig. 2
figure 2

Example of physical variability propagation

Full size image

These techniques are generic and can be applied to engineering systems with multiple component modules and multiple physics. However, most applications of these techniques have only considered physical variability. The techniques need to include the contribution of data uncertainty and model error to the overall model prediction uncertainty. Computational effort is a significant issue in practical applications, since these techniques involve a number of repeated runs of the system analysis model. The system analysis may be replaced with an inexpensive surrogate model in order to achieve computational efficiency; this is discussed in Sect. 3.3 of this report. Efficient Monte Carlo techniques have also been pursued to reduce the number of system model runs, including Latin hypercube sampling (LHS) [8, 32] and importance sampling [28, 50].

When multiple requirements are defined, computation of the overall probability of satisfying multiple performance criteria requires integration over a multidimensional space defined by unions and intersections of individual events (of satisfaction or violation of individual criteria).

3.2 Propagation of Data Uncertainty

Three types of data uncertainty were discussed in Sect. 2. Sparse point data results in uncertainty about the parameters of the probability distributions describing quantities with physical variability. In that case, uncertainty propagation analysis takes a nested implementation. In the outer loop, samples of the distribution parameters are randomly generated, and for each set of sampled distribution parameter values, probabilistic propagation analysis is carried out as in Sect. 3.1. This results in the computation of multiple probability distributions of the output or confidence intervals for the estimates of probability of failure.

In the case of measurement error, choice of the uncertainty propagation technique depends on how the measurement error is represented. If the measurement error is represented as a random variable, it is simply added to the measured quantity, which is also a random variable due to physical variability. Thus, a sum of two random variables may be used to include both physical variability and measurement error in a quantity of interest. If the measurement error is represented as an interval, one way to implement probabilistic analysis is to represent the interval through families of distributions or upper and lower bounds on probability distributions, as discussed in Sect. 2.2.1. In that case, multiple probabilistic analyses, using the same nested approach as in the case of sparse data, can be employed to generate multiple output distributions or confidence intervals for the model output. The same approach is possible for interval variables that are only available as a range of values, as in the case of expert opinion.

Propagation of uncertainty is conceptually very simple but computationally quite expensive to implement, especially when both physical variability and data uncertainty are to be considered. The presence of both types of uncertainty requires a nested implementation of uncertainty propagation analysis (simulation of data uncertainty in the outer loop and simulation of physical variability in the inner loop). If the system model runs are time-consuming, then uncertainty propagation analysis could be prohibitively expensive. One way to overcome the computational hurdle is to use an inexpensive surrogate model to replace the detailed system model, as discussed next.

3.3 Surrogate Models

Surrogate models (also known as response surface models) are frequently used to replace the expensive system model and used for multiple simulations to quantify the uncertainty in the output. Many types of surrogate modeling methods are available, such as linear and nonlinear regression, polynomial chaos expansion, Gaussian process modeling (e.g., Kriging model), splines, moving least squares, support vector regression, relevance vector regression, neural nets, or even simple lookup tables. For example, Goktepe et al. [12] used neural network and polynomial regression models to simulate expansion of concrete specimens under sulfate attack. All surrogate models require training or fitting data, collected by running the full-scale system model repeatedly for different sets of input variable values. Selecting the sets of input values is referred to as statistical design of experiments, and there is extensive literature on this subject. Two types of surrogate modeling methods are discussed below that might achieve computational efficiency while maintaining high accuracy in output uncertainty quantification. The first method expresses the model output in terms of a series expansion of special polynomials such as Hermite polynomials and is referred to as a stochastic response surface method (SRSM). The second method expresses the model output through a Gaussian process and is referred to as Gaussian process modeling.

3.3.1 Stochastic Response Surface Method (SRSM)

The common approach for building a surrogate or response surface model is to use least squares fitting based on polynomials or other mathematical forms based on physical considerations. In SRSM, the response surface is constructed by approximating both the input and output random variables and fields through series expansions of standard random variables (e.g., [18, 19, 47]). This approach has been shown to be efficient, stable, and convergent in several structural, thermal, and fluid flow problems. A general procedure for SRSM is as follows:

  1. (a)

    Representation of random inputs (either random variables or random processes) in terms of Standard Random Variables (SRVs) by K-L expansion, as in Eq. (2).

  2. (b)

    Expression of model outputs in chaos series expansion. Once the inputs are expressed as functions of the selected SRVs, the output quantities can also be represented as functions of the same set of SRVs. If the SRVs are Gaussian, the output can be expressed a Hermite polynomial chaos series expansion in terms of Gaussian variables. If the SRVs are non-Gaussian, the output can be expressed by a general Askey chaos expansion in terms of non-Gaussian variables [10].

  3. (c)

    Estimation of the unknown coefficients in the series expansion. The improved probabilistic collocation method [19] is used to minimize the residual in the random dimension by requiring the residual at the collocation points equal to zero. The model outputs are computed at a set of collocation points and used to estimate the coefficients. These collocation points are the roots of the Hermite polynomial of a higher order. This way of selecting collocation points would capture points from regions of high probability [45].

  4. (d)

    Calculation of the statistics of the output that has been cast as a response surface in terms of a chaos expansion. The statistics of the response can be estimated with the response surface using either Monte Carlo simulation or analytical approximation.

3.3.2 Kriging or Gaussian Process Models

Gaussian process (GP) models have several features that make them attractive for use as surrogate models. The primary feature of interest is the ability of the model to “account for its own uncertainty.” That is, each prediction obtained from a Gaussian process model also has an associated variance or uncertainty. This prediction variance primarily depends on the closeness of the prediction location to the training data, but it is also related to the functional form of the response. For example, see Fig. 3, which depicts a one-dimensional Gaussian process model. Note how the uncertainty bounds are related to both the closeness to the training points, as well as the shape of the curve.

Fig. 3
figure 3

Gaussian process model with uncertainty bounds

Full size image

The basic idea of the GP model is that the output quantities are modeled as a group of multivariate normal random variables. A parametric covariance function is then constructed as a function of the inputs. The covariance function is based on the idea that when the inputs are close together, the correlation between the outputs will be high. As a result, the uncertainty associated with the model prediction is small for input values that are close to the training points and large for input values that are not close to the training points. In addition, the GP model may incorporate a systematic trend function, such as a linear or quadratic regression of the inputs (in the notation of Gaussian process models, this is called the mean function, while in Kriging, it is often called a trend function). The effect of the mean function on predictions which interpolate the training data is small, but when the model is used for extrapolation, the predictions will follow the mean function very closely.

Within the GP modeling technique, it is also possible to adaptively select the design of experiments to achieve very high accuracy. The method begins with an initial GP model built from a very small number of samples, and then one intelligently chooses where to generate subsequent samples to ensure the model is accurate in the vicinity of the region of interest. Since the GP model provides the expected value and variance of the output quantity, the next sample may be chosen in the region of highest variance, if the objective is to minimize the prediction variance. The method has been shown to be both accurate and computationally efficient for arbitrarily shaped functions [2].

3.4 Sensitivity Analysis

Sensitivity analysis serves several important functions: (1) identification of dominant variables or sub-models, thus helping to focus data collection resources efficiently; (2) identification of insignificant variables or sub-models of limited significance, helping to reduce the size of the problem and computational effort; and (3) quantification of the contribution of solution approximation error. Both local and global sensitivity analysis techniques are available to investigate the quantitative effect of different sources of variation (physical parameters, models, and measured data) on the variation of the model output. The primary benefit of sensitivity analysis to uncertainty analysis is to enable the identification of which physical parameters have the greatest influence on the output [6, 42]).

Sensitivity analysis can be local or global. Local sensitivity analysis utilizes first-order derivatives of system output quantities with respect to the parameters. It is usually performed for a nominal set of parameter values. Global sensitivity analysis typically uses statistical sampling methods, such as Latin Hypercube Sampling, to determine the total uncertainty in the system output over the entire range of the input uncertainty and to apportion that uncertainty among the various parameters.

3.5 Model Error Quantification

Model errors may relate to governing equations, boundary and initial condition assumptions, loading description, and approximations or errors in solution algorithms (e.g., truncation of higher order terms, finite element discretization, curve-fitting models for material damage such as S-N curve). Overall model error may be quantified by comparing model prediction and experimental observation, properly accounting for uncertainties in both. This overall error measure combines both model form and solution approximation errors, so it needs to be considered in two parts. Numerical errors in the model prediction can be quantified first, using sensitivity analysis, uncertainty propagation analysis, discretization error quantification, and truncation (residual) error quantification. The measurement error in the input variables can be propagated to the prediction of the output. The error in the prediction of the output due to the measurement error in the input variables is approximated by using a first-order sensitivity analysis [36]. Then the model form error can be quantified based on all the above errors, following the approach illustrated for a heat transfer problem by Rebba et al. [36].

3.5.1 Solution Approximation Error

Several components of prediction error, such as discretization error (denoted by ε d) and uncertainty propagation analysis error (ε s) can be considered. Several methods to quantify the discretization error in finite element analysis are available in the literature. However, most of these methods do not quantify the actual error; instead, they only quantify some indicator measures to facilitate adaptive mesh refinement. The Richardson extrapolation (RE) method comes closest to quantifying the actual discretization error [38]. (In some applications, the model is run with different levels of resolution, until an acceptable level of accuracy is achieved; formal error quantification may not be required).

Errors in uncertainty propagation analysis (ε s) are method-dependent, i.e., sampling error occurs in Monte Carlo methods and truncation error occurs in response surface methods (either conventional or polynomial chaos-based). For example, sampling error could be assumed to be a Gaussian random variable with zero mean and variance given by σ 2/N where N is the number of Monte Carlo runs and σ 2 is the original variance of the model output [41]. The truncation error is simply the residual error in the response surface.

Rebba et al. [36] and Liang and Mahadevan [26] used the above concept to construct a surrogate model for finite element discretization error in structural analysis, using the stochastic response surface method (SRSM). Gaussian process models may also be employed for this purpose. Both options are helpful in quantifying the solution approximation error.

3.5.2 Model form Error

The overall prediction error is a combination of errors resulting from numerical solution approximations and model form selection. A simple way is to express the total observed error (difference between prediction and observation) as the sum of the following error sources:

$$ {{\varepsilon }_{\rm{obs}}} = {{\varepsilon }_{\rm{num}}} + {{\varepsilon }_{\rm{model}}} - {{\varepsilon }_{{{ \exp }}}} $$
(3)

where ε num, ε model, and ε exp represent numerical solution error, model form error, and output measurement error, respectively. However, solution approximation error results from multiple sources and is probably a nonlinear combination of various errors such as discretization error, round-off and truncation errors, and stochastic analysis errors. One option is to construct a regression model consisting of the individual error components [36]. The residual of such a regression analysis will include the model form error (after subtracting the experimental error effects). By denoting ε obs as the difference between the data and prediction, i.e., ε obs = y exp − y pred, we can construct the following relation by considering a few sources of numerical solution error [36]:

$$ {{\varepsilon }_{\rm{obs}}} = f({{\varepsilon }_{\rm{h}}},{{\varepsilon }_{\rm{d}}},{{\varepsilon }_{\rm{s}}}) + {{\varepsilon }_{\rm{model}}} - {{\varepsilon }_{{{ \exp }}}} $$
(4)

where ε h, ε d, and ε s represent output error due to input parameter measurement error, finite element discretization error, and uncertainty propagation analysis error, respectively, all of which contribute to numerical solution error. Rebba et al. [36] illustrated the estimation of model form error using the above concept for a one-dimensional heat conduction problem, using a polynomial chaos expansion for the input-output model as well as numerical solution error. Kennedy and O’Hagan [24] calibrated Gaussian process surrogate models for both the input-output model and the model form error (which is also referred to as model discrepancy or model inadequacy term). Both approaches incorporate the dependence of model error on input values.

4 Model Calibration, Validation and Extrapolation

After quantifying and propagating the physical variability, data uncertainty, and model error for individual components of the overall system model, the probability of meeting performance requirements (and our confidence in the model prediction) needs to be assessed based on extrapolating the model to field conditions (which are uncertain as well), where sometimes very limited or no experimental data is available. Rigorous verification, validation, and calibration methods are needed to establish credibility in the modeling and simulation. Both classical and Bayesian statistical methodologies have been investigated during recent years. The methods have the capability to consider multiple output quantities or a single model output at different spatial and temporal points.

This section discusses methods for (1) calibration of model parameters, based on observation data; (2) validation assessment of the model, based on observation data; and (3) estimation of confidence in the extrapolation of model prediction from laboratory conditions to field conditions.

4.1 Model Calibration

Two types of statistical techniques may be pursued for model calibration uncertainty, the least squares approach and the Bayesian approach. The least squares approach estimates the values of the calibration parameters that minimize the discrepancy between model prediction and experimental observation. This approach can also be used to calibrate surrogate models or low-fidelity models, based on high-fidelity runs, by treating the high-fidelity results similar to experimental data.

The second approach is Bayesian calibration [24] using Gaussian process surrogate models. This approach is flexible and allows different forms for including the model errors during calibration of model parameters [31]. Recently, Sankararaman and Mahadevan [43] extended least squares, likelihood and Bayesian calibration approaches to include imprecise and unpaired input-output data sets, a commonly occurring situation when using historical data or data from the literature, where all the inputs to the model may not be reported.

Markov Chain Monte Carlo (MCMC) simulation is used for numerical implementation of the Bayesian updating analysis. Several efficient sampling techniques are available for MCMC, such as Gibbs sampling, the Metropolis algorithm, and the Metropolis-Hastings algorithm [11].

4.2 Model Validation

Model validation involves comparing prediction with observation data (either historical or experimental) when both have uncertainty. Since there is uncertainty in both model prediction and experimental observation, it is necessary to pursue rigorous statistical techniques to perform model validation assessment rather than simple graphical comparisons, provided data is even available for such comparisons. Statistical hypothesis testing is one approach to quantitative model validation under uncertainty, and both classic and Bayesian statistics have been explored. Classical hypothesis testing is a well-developed statistical method for accepting or rejecting a model based on an error statistic (see e.g., [46]). Validation metrics have been investigated in recent years based on Bayesian hypothesis testing [29, 33, 34, 49], reliability-based methods [35], and risk-based decision analysis [22, 23]. Ling and Mahadevan [27] provide detailed discussion of the interpretations of various metrics, their mathematical relationships, and implementation issues, with the example of a MEMS device reliability prediction problem and validation data.

In Bayesian hypothesis testing, we assign prior probabilities for the null and alternative hypotheses; let these be denoted as P(H 0) and P(H a) such that P(H 0) + P(H a) = 1. Here, H 0 : model error < allowable limit, and H a: model error > allowable limit. When data D is obtained, the probabilities are updated as P(H 0 | D) and P(H a | D) using the Bayesian theorem. Then, a Bayesian factor [20] B is defined as the ratio of likelihoods of observing D under H 0 and H a; i.e., the first term in the square brackets on the right-hand side of Eq. (5):

$$ \frac{{P\left( {{{H}_0}|D} \right)}}{{P\left( {{{H}_{\rm{a}}}|D} \right)}} = \left[ {\frac{{P\left( {D|{{H}_0}} \right)}}{{P\left( {D|{{H}_{\rm{a}}}} \right)}}} \right]\frac{{P\left( {{{H}_0}} \right)}}{{P\left( {{{H}_{\rm{a}}}} \right)}} $$
(5)

If B > 1, the data gives more support to H 0 than H a. Also, the confidence in H 0, based on the data, comes from the posterior null probability P(H 0 | D), which can be rearranged from the above equation as \( \frac{{P\left( {{{H}_0}} \right)B}}{{P\left( {{{H}_0}} \right)B + 1 - P\left( {{{H}_0}} \right)}} \). Typically, in the absence of prior knowledge, we may assign equal probabilities to each hypothesis, and thus, P(H 0) = P(H a) = 0.5. In that case, the posterior null probability can be further simplified to B/(B + 1). Thus, a B value of 1.0 represents 50 % confidence in the null hypothesis being true.

The Bayesian hypothesis testing is also able to account for uncertainty in the distribution parameters (mentioned in Sect. 2). For such problems, the validation metric (Bayesian factor) itself becomes a random variable. In that case, the probability of the Bayesian factor exceeding a specified value can be used as the decision criterion for model acceptance/rejection.

Notice that model validation only refers to the situation when controlled, target experiments are performed to evaluate model prediction, and both the model runs and experiments are done under the same set of input and boundary conditions. The validation is done only by comparing the outputs of the model and the experiment. Once the model is calibrated, verified, and validated, it may be investigated for confidence in extrapolating to field conditions different from laboratory conditions. This is discussed in the next section.

4.3 Overall Uncertainty Quantification

While individual methods for calibration, verification, and validation have been developed as mentioned above, it is necessary to integrate the results from these activities for the purpose of overall uncertainty quantification in the model prediction. This is not trivial because of several reasons. First, the solution approximation errors calculated as a result of the verification process need to be accounted for during calibration, validation, and prediction. Second, the result of validation may lead to a binary result, i.e., the model is accepted or rejected; however, even when the model is accepted, it is not completely correct. Hence, it is necessary to account for the degree of correctness of the model in the prediction. Third, calibration and validation are performed using independent data sets, and it is not straightforward to compute their combined effect on the overall uncertainty in the response.

The issue gets further complicated when system-level behavior is predicted based on a hierarchy of models. As the complexity of the system under study increases, there may be several components and subsystems at multiple levels of hierarchy, which integrate to form the overall multilevel system. Each of these components and subsystems is represented using component-level and subsystem-level models which are mathematically connected to represent the overall system model which is used to study the underlying system. In each level, there is a computational model with inputs, parameters, outputs, experimental data (hopefully available for calibration and validation separately), and several sources of uncertainty – physical variability, data uncertainty (sparse or imprecise data, measurement errors, expert opinion), and model uncertainty (parameter uncertainty, solution approximation errors, and model form error).

Recent studies by the author and coworkers have demonstrated that the Bayesian network methodology provides an efficient and powerful tool to integrate multiple levels of models, associated sources of uncertainty and error, and available data at multiple levels and in multiple formats. While the Bayesian approach can be used to perform calibration and validation individually for each model in the multilevel system, it is not straightforward to integrate the information from these activities in order to compute the overall uncertainty in the system-level prediction. Sankararaman and Mahadevan [44] extend the Bayesian approach to integrate and propagate information from verification, calibration, and validation activities in order to quantify the margins and uncertainties in the overall system-level prediction.

Bayesian networks [21] are directed acyclic graphical representations with nodes to represent the random variables and arcs to show the conditional dependencies among the nodes. Data in any one node can be used to update the statistics of all other nodes. This property makes the Bayesian network a powerful tool to integrate information generated from multiple activities and to quantify the uncertainty in prediction under actual usage conditions [29].

Figure 4 shows an illustrative Bayesian network for confidence extrapolation. An ellipse represents a random variable, and a rectangle represents observed data. A solid line arrow represents a conditional probability link, and a dashed line arrow represents the link of a variable to its observed data if available. The probability densities of the variables Ω, z, and y are updated using the validated data Y. The updated statistics of Ω, z, and y are then used to estimate the updated statistics of the decision variable d (i.e., assessment metric). In addition, both model prediction and predictive experiments are related to input variables X via physical parameters Φ. Note that there is no observed data available for d; yet we are able to calculate the confidence in the prediction of d, by making use of observed data in several other nodes and propagation of posterior statistics through the Bayesian network.

Fig. 4
figure 4

Bayes network

Full size image

The Bayesian network thus links the various simulation codes and corresponding experimental observations to facilitate two objectives: (1) uncertainty quantification and propagation and (2) confidence assessment in system behavior prediction in the application domain, based on data from the laboratory domain, expert opinion, and various computational models at different levels of the system hierarchy.

5 Conclusion

Uncertainty quantification in performance assessment involves consideration of three sources of uncertainty – inherent variability, information uncertainty, and model errors. This chapter surveyed probabilistic methods to quantify the uncertainty in model-based prediction due to each of these sources and addressed them in four stages – input characterization based on data; propagation of uncertainties and errors through the system model; model calibration, validation, and extrapolation; and performance assessment. Flexible distribution families as well as a nonparametric Bayesian approach were discussed to handle sparse data and interval data. Methods to quantify model errors resulting from both model form selection and solution approximation were discussed. Bayesian methods were discussed for model calibration, validation, and extrapolation. An important issue is computational expense, when iterative analysis between multiple codes is necessary. Uncertainty quantification multiplies the computational effort of deterministic analysis by an order of magnitude. Therefore, the use of surrogate models, sensitivity and screening analyses, and first-order approximations of overall output uncertainty are available to reduce the computational expense.

Many of the methods described in the chapter have been applied to mechanical systems that are small in size or time-independent, and the uncertainties considered were not very large. None of these simplifications are available in the case of long-term performance assessment of civil infrastructure systems, and real-world data to validate long-term model predictions are not available. Thus, the extrapolations are based on laboratory data or limited term observations and come with large uncertainty. The application of the methods described in this chapter to such complex systems needs to be investigated. However, it should be recognized that the benefit of uncertainty quantification is not so much in predicting the actual failure probability or similar measures but in facilitating engineering decision-making, such as comparing different design and analysis options, performing sensitivity analyses, and allocating resources for uncertainty reduction through further data collection and/or model refinement.