Failure Probability Bounds Using Multicut-High-Dimensional Model Representation

Abstract

The structural reliability analysis in presence of mixed uncertain variables demands more computation as the entire configuration of fuzzy variables needs to be explored. Moreover, the existence of multiple design points plays an important role in the accuracy of results as the optimization algorithms may converge to a local design point by neglecting the main contribution from the global design point. Therefore, in this chapter, a novel uncertain analysis method for estimating the failure probability bounds of structural systems involving multiple design points in presence of mixed uncertain variables is presented. The proposed method involves weight function to identify multiple design points, multicut-high dimensional model representation technique for the limit state function approximation, transformation technique to obtain the contribution of the fuzzy variables to the convolution integral, and fast Fourier transform for solving the convolution integral. The proposed technique estimates the failure probability accurately with significantly less computational effort compared to the direct Monte Carlo simulation. The methodology developed is applicable for structural reliability analysis involving any number of fuzzy and random variables with any kind of distribution. The numerical examples presented demonstrate the accuracy and efficiency of the proposed method.

1 Introduction

Reliability analysis taking into account the uncertainties involved in a structural system plays an important role in the analysis and design of structures. Due to the complexity of structural systems, the information about the functioning of various structural components has different sources, and the failure of systems is usually governed by various uncertainties, all of which are to be taken into consideration for reliability estimation. Uncertainties present in a structural system can be classified as aleatory uncertainty and epistemic uncertainty. Aleatory uncertainty information can be obtained as a result of statistical experiments and has a probabilistic or random character. Epistemic uncertainty information can be obtained by the estimation of the experts and in most cases has an interval or fuzzy character. When aleatory uncertainty is only present in a structural system, then the reliability estimation involves determination of the probability that a structural response exceeds a threshold limit, defined by a limit state function influenced by several random parameters. Structural reliability can be computed by adopting probabilistic method involving the evaluation of multidimensional integral [1, 2].

In first- or second-order reliability method (FORM/SORM), the limit state functions need to be specified explicitly. Alternatively, the simulation-based methods such as Monte Carlo techniques require more computational effort for simulating the actual limit state function repeated times. The response surface concept was adopted to get separable and closed form expression of the implicit limit state function in order to use fast Fourier transform (FFT) to estimate the failure probability [3]. The high-dimensional model representation (HDMR) concepts were applied for the approximation of limit state function at the MPP and FFT techniques to evaluate the convolution integral for estimation of failure probability [4]. In this method, efforts are required in evaluating conditional responses at a selected input determined by sample points, as compared to full-scale simulation methods.

Further, the main contribution to the reliability integral comes from the neighborhood of design points. When multiple design points exist, available optimization algorithms may converge to a local design point and thus erroneously neglect the main contribution to the value of the reliability integral from the global design point(s). Moreover, even if a global design point is obtained, there are cases for which the contribution from other local or global design points may be significant [5]. In that case, multipoint FORM/SORM is required for improving the reliability analysis [6]. In the presence of only epistemic uncertainty in a structural system, possibilistic approaches to evaluate the minimum and maximum values of the response are available [7, 8].

All the reliability models discussed above are based on only one kind of uncertain information, either random variables or fuzzy input, but do not accommodate a combination of both types of variables. However, in some engineering problems with mixed uncertain parameters, using one kind of reliability model cannot obtain the best results. To determine the failure probability bounds of a structural system involving both random and fuzzy variables, the entire configuration of the fuzzy variables needs to be explored. Hence, the computational effort involved in estimating the bounds of the failure probability increases tremendously in the presence of multiple design points and mixed uncertain variables.

This chapter explores the potential of coupled multicut-HDMR (MHDMR)-FFT technique in evaluating the reliability of a structural system with multiple design points, for which some uncertainties can be quantified using fuzzy membership functions while some are random in nature. Comparisons of numerical results have been made with direct MCS method to evaluate the accuracy and computational efficiency of the present method.

2 High Dimensional Model Representation

High dimensional model representation (HDMR) is a general set of quantitative model assessment and analysis tools for capturing the high dimensional relationships between sets of input and output model variables [4, 9]. Let the N-dimensional vector $\user2{x} = \{ {{x}_1},{{x}_2}, \ldots, {{x}_N}\}$ represent the input variables of the model under consideration and the response function as $g(\user2{x})$. Since the influence of the input variables on the response function can be independent and/or cooperative, HDMR expresses the response $g(\user2{x})$ as a hierarchical correlated function expansion in terms of the input variables as

$$ \begin{array}{lll} g\left( {x} \right) = & {{g}_0} +\sum\limits_{{i = 1}}^N {{{g}_i}\left( {{{x}_i}} \right)} +\sum\limits_{{1 \le {{i}_1} < {{i}_2} \le N}}{{{g}_{{{{i}_1}{{i}_2}}}}\left( {{{x}_{{{{i}_1}}}},{{x}_{{{{i}_2}}}}} \right)} + \ldots \cr&+\sum\limits_{{1 \le {{i}_1} < \ldots < {{i}_l} \le N}}{{{g}_{{{{i}_1}{{i}_2} \ldots {{i}_l}}}}\left({{{x}_{{{{i}_1}}}},{{x}_{{{{i}_2}}}}, \ldots, {{x}_{{{{i}_l}}}}}\right)} + \cdots + {{g}_{{12...N}}}\left( {{{x}_1},{{x}_2}, \ldots, {{x}_N}} \right),\end{array} $$

(1)

where ${{g}_0}$ is a constant term representing the zeroth-order component function or the mean response of $g(\user2{x})$. The function ${{g}_i}\left( {{{x}_i}} \right)$ is a first-order term expressing the effect of variable ${{x}_i}$ acting alone, although generally nonlinearly, upon the output $g(\user2{x})$. The function ${{g}_{{{{i}_1}{{i}_2}}}}\left( {{{x}_{{{{i}_1}}}},{{x}_{{{{i}_2}}}}} \right)$ is a second-order term which describes the cooperative effects of the variables ${{x}_{{{{i}_1}}}}$ and ${{x}_{{{{i}_2}}}}$ upon the output $g(\user2{x})$. The higher order terms give the cooperative effects of increasing numbers of input variables acting together to influence the output $g(\user2{x})$. The last term ${{g}_{{12, \cdots, N}}}\left( {{{x}_1},{{x}_2}, \ldots, {{x}_N}} \right)$ contains any residual dependence of all the input variables locked together in a cooperative way to influence the output $g(\user2{x})$. The expansion functions are determined by evaluating the input–output responses of the system relative to the defined reference point c along associated lines, surfaces, subvolumes, etc., in the input variable space. This process reduces to the following relationship for the component functions in Eq. (1):

$$ {{g}_0} = g\left( \user2{c} \right), $$

(2)

$$ {{g}_i}\left( {{{x}_i}} \right) = g\left( {{{x}_i},{{\user2{c}}^i}} \right) - {{g}_0}, $$

(3)

$$ {{g}_{{{{i}_1}{{i}_2}}}}\left( {{{x}_{{{{i}_1}}}},{{x}_{{{{i}_2}}}}} \right) = g\left( {{{x}_{{{{i}_1}}}},{{x}_{{{{i}_2}}}},{{\user2{c}}^{{{{i}_1}{{i}_2}}}}} \right) - {{g}_{{{{i}_1}}}}\left( {{{x}_{{{{i}_1}}}}} \right) - {{g}_{{{{i}_2}}}}\left( {{{x}_{{{{i}_2}}}}} \right) - {{g}_0}, $$

(4)

where the notation $g\left( {{{x}_i},{{\user2{c}}^i}} \right) = g\left( {{{c}_1},{{c}_2}, \ldots, {{c}_{{i - 1}}},{{x}_i},{{c}_{{i + 1}}}, \ldots, {{c}_N}} \right)$ denotes that all the input variables are at their reference point values except ${{x}_i}$. The ${{g}_0}$ term is the output response of the system evaluated at the reference point c. The higher order terms are evaluated as cuts in the input variable space through the reference point. Therefore, each first-order term ${{g}_i}\left( {{{x}_i}} \right)$ is evaluated along its variable axis through the reference point. Each second-order term ${{g}_{{{{i}_1}{{i}_2}}}}\left( {{{x}_{{{{i}_1}}}},{{x}_{{{{i}_2}}}}} \right)$ is evaluated in a plane defined by the binary set of input variables ${{x}_{{{{i}_1}}}}$ and ${{x}_{{{{i}_2}}}}$ through the reference point, etc. The first-order approximation of $g(\user2{x})$ is as follows:

$$ \tilde{g}\left( \user2{x} \right) \equiv g\left( {{{x}_1},{{x}_2}, \ldots, {{x}_N}} \right) = \sum\limits_{{i = 1}}^N {g\left( {{{c}_1}, \ldots, {{c}_{{i - 1}}},{{x}_i},{{c}_{{i + 1}}}, \ldots, {{c}_N}} \right)} - \left( {N - 1} \right)g\left( \user2{c} \right). $$

(5)

The notion of 0th, 1st, etc., in HDMR expansion should not be confused with the terminology used either in the Taylor series or in the conventional least-squares-based regression model. It can be shown that the first-order component function ${{g}_i}\left( {{{x}_i}} \right)$ is the sum of all the Taylor series terms which contain and only contain variable ${{x}_i}$. Hence, first-order HDMR approximations should not be viewed as first-order Taylor series expansions nor do they limit the nonlinearity of $g(\user2{x})$.

3 Multicut-HDMR

The main limitation of truncated cut-HDMR expansion is that depending on the order chosen sometimes it is unable to accurately approximate $g(\user2{x})$, when multiple design points exist on the limit state function or when the problem domain is large. In this section, a new technique based on MHDMR is presented for approximation of the original implicit limit state function, when multiple design points exist. The basic principles of cut-HDMR may be extended to more general cases. MHDMR is one extension where several cut-HDMR expansions at different reference points are constructed, and the original implicit limit state function $g(\user2{x})$ is approximately represented not by one but by all cut-HDMR expansions. In the present work, weight function is adopted for identification of multiple reference points closer to the limit surface.

Let ${{\user2{d}}^1},{{\user2{d}}^2}, \ldots, {{\user2{d}}^{{{{m}_d}}}}$ be the ${{m}_d}$ identified reference points closer to the limit state function based on the weight function. MHDMR approximation of the original implicit limit state function is based on the principles of cut-HDMR expansion, where individual cut-HDMR expansions are constructed at different reference points ${{\user2{d}}^1},{{\user2{d}}^2}, \ldots, {{\user2{d}}^{{{{m}_d}}}}$ by taking one at a time as follows:

$$ \begin{array}{lll}{ {{g}^k}\left( {x} \right) = g_{{_0}}^k + \sum\limits_{{i = 1}}^N {g_{{_i}}^k\left( {{{x}_i}} \right)} + \sum\limits_{{1 \le {{i}_1} < {{i}_2} \le N}} {g_{{_{{{{i}_1}{{i}_2}}}}}^k\left( {{{x}_{{{{i}_1}}}},{{x}_{{{{i}_2}}}}} \right)} + \ldots} \hfill \\{+ \sum\limits_{{1 \le {{i}_1} < ... < {{i}_l} \le N}} {g_{{_{{{{i}_1}{{i}_2}...{{i}_l}}}}}^k\left( {{{x}_{{{{i}_1}}}},{{x}_{{{{i}_2}}}}, \ldots, {{x}_{{{{i}_l}}}}} \right)} + \ldots + g_{{_{{12...N}}}}^k\left( {{{x}_1},{{x}_2}, \ldots, {{x}_N}} \right); \hfill } & {k = 1,2, \ldots, {{m}_d}} \\\end{array} . $$

(6)

The original implicit limit state function $g(\user2{x})$ is approximately represented by blending all locally constructed ${{m}_d}$ individual cut-HDMR expansions as follows:

$$ g\left( \user2{x} \right) \cong \sum\limits_{{k = 1}}^{{{{m}_d}}} {{{\lambda }_k}\left( \user2{x} \right)} \left[ {g_{{_0}}^k + \sum\limits_{{i = 1}}^N {g_{{_i}}^k({{x}_i})} + \ldots + g_{{_{{12 \cdots N}}}}^k({{x}_1},{{x}_2}, \ldots, {{x}_N})} \right]. $$

(7)

The coefficients ${{\lambda }_k}\left( \user2{x} \right)$ possess the properties

$$ {{\lambda }_k}\left( {x} \right) =\left\{\begin{array}{llll}\\1 \quad {{\text{if}}\;{ }{x}\;{\text{is}}\;{\text{in}}\;{\text{any}}\;{\text{cut}}\;{\text{subvolume}}\;{\text{of}}\;{\text{the}}\;k{\text{-th}}\;{\text{reference}}\;{\text{point}}\;{\text{expansions}}} \\0 \quad{{\text{if}}\;{x}\;{\text{is}}\;{\text{in}}\;{\text{any}}\;{\text{cut}}\;{\text{subvolume}}\;{\text{of}}\;{\text{other}}\;{\text{reference}}\;{\text{point}}\;{\text{expansions}}} \\\end{array} \right. $$

(8)

and

$$ \sum\limits_{{k = 1}}^{{{{m}_d}}} {{{\lambda }_k}\left( \user2{x} \right)} = 1. $$

(9)

There are a variety of choices to define ${{\lambda }_k}\left( \user2{x} \right)$. In the present study, the metric distance ${{\alpha }_k}\left( \user2{x} \right)$ from any sample point to the reference point ${{\user2{d}}^k};\quad k = 1,2, \ldots, {{m}_d}$

$$ {{\alpha }_k}\left( \user2{x} \right) = {{\left[ {\sum\limits_{{i = 1}}^N {{{{\left( {{{x}_i} - d_i^k} \right)}}^2}} } \right]}^{{\frac{1}{2}}}};\quad d_i^k \equiv k{\text{-th}}{\text{reference}}{\text{point}} $$

(10)

is used to define

$$ {{\lambda }_k}\left( \user2{x} \right) = \frac{{{{{\bar{\lambda }}}_k}(\user2{x})}}{{\sum\limits_{{s = 1}}^{{{{m}_d}}} {{{{\bar{\lambda }}}_s}(\user2{x})} }}, $$

(11)

where

$$ {{\bar{\lambda }}_k}(\user2{x}) = \prod\limits_{{s = 1;{ }s \ne k}}^{{{{m}_d}}} {{{\alpha }_s}\left( \user2{x} \right)} . $$

(12)

The coefficients ${{\lambda }_k}\left( \user2{x} \right)$ determine the contribution of each locally approximated function to the global function. The properties of the coefficients ${{\lambda }_k}\left( \user2{x} \right)$ imply that the contribution of all other cut-HDMR expansions vanishes except one when x is located on any cut line, plane, or higher dimensional (≤ l) subvolumes through that reference point, and then the MHDMR expansion reduces to single point cut-HDMR expansion. As mentioned above, the l-th-order cut-HDMR approximation does not have error when x is located on these subvolumes. When ${{m}_d}$ cut-HDMR expansions are used to construct an MHDMR expansion, the error-free region in input x space is ${{m}_d}$ times that for a single reference point cut-HDMR expansion; hence, the accuracy will be improved. Therefore, first-order MHDMR approximations of the original implicit limit state function with ${{m}_d}$ reference points can be expressed as

$$ \tilde{g}\left( \user2{x} \right) \cong \sum\limits_{{k = 1}}^{{{{m}_d}}} {{{\lambda }_k}\left( \user2{x} \right)\left[ {\sum\limits_{{i = 1}}^N {{{g}^k}\left( {d_1^k, \ldots, d_{{i - 1}}^k,{{x}_i},d_{{i + 1}}^k, \ldots, d_N^k} \right)} - \left( {N - 1} \right){{g}^k}\left( {{{\user2{d}}^k}} \right)} \right]} . $$

(13)

4 Weight Function

The most important part of MHDMR approximation of the original implicit limit state function is identification of multiple reference points closer to the limit state function. The proposed weight function is similar to that used by Kaymaz and McMahon [10] for weighted regression analysis. Among the limit state function responses at all sample points, the most likelihood point is selected based on closeness to zero value, which indicates that particular sample point is close to the limit state function.

In this study, two types of procedures are adopted for identification of reference points closer to the limit state function, namely, (1) first-order method and (2) second-order method. The procedure for identification of reference points closer to the limit state function using first-order method proceeds as follows: (a) $n{ }\left( { = 3,5,7\;{\text{or}}\;9} \right)$ equally spaced sample points ${{\mu }_i} - {{{\left( {n - 1} \right){{\sigma }_i}}} \left/ {2} \right.}$, ${{\mu }_i} - {{{\left( {n - 3} \right){{\sigma }_i}}} \left/ {2} \right.}$, …, ${{\mu }_i}$, …, ${{\mu }_i} + {{{\left( {n - 3} \right){{\sigma }_i}}} \left/ {2} \right.}$, ${{\mu }_i} + {{{\left( {n - 1} \right){{\sigma }_i}}} \left/ {2} \right.}$ are deployed along each of the random variable axis ${{x}_i}$ with mean ${{\mu }_i}$ and standard deviation ${{\sigma }_i}$, through an initial reference point. Initial reference point is taken as mean value of the random variables. (b) The limit state function is evaluated at each sample point. (c) Using the limit state function responses at all sample points, the weight corresponding to each sample point is evaluated using the following weight function:

$$ {{w}^I} = { \exp }\left( { - \frac{{g\left( {{{c}_1}, \ldots, {{c}_{{i - 1}}},{{x}_i},{{c}_{{i + 1}}}, \ldots, {{c}_N}} \right) - {{{\left. {g\left( \user2{x} \right)} \right|}}_{{{ \min }}}}}}{{\left| {{{{\left. {g\left( \user2{x} \right)} \right|}}_{{{ \min }}}}} \right|}}} \right). $$

(14)

Second-order method of identification of reference points closer to the limit state function proceeds as follows: (a) A regular grid is formed by taking $n{ }\left( { = 3,5,7{\text{ or }}9} \right)$ equally spaced sample points ${{\mu }_{{{{i}_1}}}} - {{{\left( {n - 1} \right){{\sigma }_{{{{i}_1}}}}}} \left/ {2} \right.}$, ${{\mu }_{{{{i}_1}}}} - {{{\left( {n - 3} \right){{\sigma }_{{{{i}_1}}}}}} \left/ {2} \right.}$, …, ${{\mu }_{{{{i}_1}}}}$, …, ${{\mu }_{{{{i}_1}}}} + {{{\left( {n - 3} \right){{\sigma }_{{{{i}_1}}}}}} \left/ {2} \right.}$, ${{\mu }_{{{{i}_1}}}} + {{{\left( {n - 1} \right){{\sigma }_{{{{i}_1}}}}}} \left/ {2} \right.}$ along the random variable ${{x}_{{{{i}_1}}}}$ axis with mean ${{\mu }_{{{{i}_1}}}}$ and standard deviation ${{\sigma }_{{{{i}_1}}}}$ and $n{ }\left( { = 3,5,7{\text{ or }}9} \right)$ equally spaced sample points ${{\mu }_{{{{i}_2}}}} - {{{\left( {n - 1} \right){{\sigma }_{{{{i}_2}}}}}} \left/ {2} \right.}$, ${{\mu }_{{{{i}_2}}}} - {{{\left( {n - 3} \right){{\sigma }_{{{{i}_2}}}}}} \left/ {2} \right.}$, …, ${{\mu }_{{{{i}_2}}}}$, …, ${{\mu }_{{{{i}_2}}}} + {{{\left( {n - 3} \right){{\sigma }_{{{{i}_2}}}}}} \left/ {2} \right.}$, ${{\mu }_{{{{i}_2}}}} + {{{\left( {n - 1} \right){{\sigma }_{{{{i}_2}}}}}} \left/ {2} \right.}$ along the random variable ${{x}_{{{{i}_2}}}}$ axis with mean ${{\mu }_{{{{i}_2}}}}$ and standard deviation ${{\sigma }_{{{{i}_2}}}}$, through an initial reference point. Initial reference point is taken as mean value of the random variables. (b) The limit state function is evaluated at each sample point. (c) Using the limit state function responses at all sample points, the weight corresponding to each sample point is evaluated using the following weight function:

$$ {{w}^{{II}}} = { \exp }\left( { - \frac{{g\left( {{{c}_1}, \ldots, {{c}_{{{{i}_1} - 1}}},{{x}_{{{{i}_1}}}},{{c}_{{{{i}_1} + 1}}}, \ldots, {{c}_{{{{i}_2} - 1}}},{{x}_{{{{i}_1}}}},{{c}_{{{{i}_2} + 1}}}, \ldots, {{c}_N}} \right) - {{{\left. {g\left( \user2{x} \right)} \right|}}_{{{ \min }}}}}}{{\left| {{{{\left. {g\left( \user2{x} \right)} \right|}}_{{{ \min }}}}} \right|}}} \right). $$

(15)

Sample points ${{\user2{d}}^1},{{\user2{d}}^2}, \ldots, {{\user2{d}}^{{{{m}_d}}}}$ with maximum weight are selected as reference points closer to the limit state function for construction of ${{m}_d}$ individual cut-HDMR approximations of the original implicit limit state function locally. In this study, two types of sampling schemes, namely, FF and SF, are adopted. Figure 1a shows FF sampling scheme involving first-order method of identification of reference points and blending of locally constructed individual first-order HDMR approximations at different identified reference points using the coefficients ${{\lambda }_k}\left( \user2{x} \right)$ to form MHDMR approximation $\tilde{g}\left( \user2{x} \right)$. Figure 1b shows SF sampling scheme involving second-order method of identification of reference points and blending of locally constructed individual first-order HDMR approximations to form MHDMR approximation.

Fig. 1

MHDMR approximation of original limit state function, with (a) FF sampling scheme and (b) SF sampling scheme

5 Failure Probability Bounds

Let the N-dimensional input variables vector $\user2{x} = \{ {{x}_1},{{x}_2}, \ldots, {{x}_N}\}$, which comprises of r number of random variables and f number of fuzzy variables, be divided as $\user2{x} = \{ {{x}_1},{{x}_2}, \ldots, {{x}_r},{{x}_{{r + 1}}},{{x}_{{r + 2}}}, \ldots, {{x}_{{r + f}}}\}$ where the subvectors $\{ {{x}_1},{{x}_2}, \ldots, {{x}_r}\}$ and $\{ {{x}_{{r + 1}}},{{x}_{{r + 2}}}, \ldots, {{x}_{{r + f}}}\}$, respectively, group the random variables and the fuzzy variables, with $N = r + f$. Then, the first-order approximation of $\tilde{g}(\user2{x})$ can be divided into three parts: the first part with only the random variables, the second part with only the fuzzy variables, and the third part is a constant which is the output response of the system evaluated at the reference point c as follows:

$$ \tilde{g}\left( \user2{x} \right) = \sum\limits_{{i = 1}}^r {g\left( {{{x}_i},{{\user2{c}}^i}} \right)} + \sum\limits_{{i = r + 1}}^N {g\left( {{{x}_i},{{\user2{c}}^i}} \right)} - \left( {N - 1} \right)g\left( \user2{c} \right). $$

(16)

The joint membership function of the fuzzy variables part is obtained using suitable transformation of the variables $\{ {{x}_{{r + 1}}},{{x}_{{r + 2}}}, \ldots, {{x}_N}\}$ and interval arithmetic algorithm. Using this approach, the minimum and maximum values of the fuzzy variables part are obtained at each α-cut. Using the bounds of the fuzzy variables part at each α-cut along with the constant part and the random variables part in Eq. (16), the joint density functions are obtained by performing the convolution using FFT in the rotated Gaussian space at the MPP, which upon integration yields the bounds of the failure probability.

5.1 Transformation of Fuzzy Variables

Optimization techniques are required to obtain the minimum and maximum values of a nonlinear response within the bounds of the interval variables. This procedure is computationally expensive for problems with implicit limit state functions, as optimization requires the function value and gradient information at several points in the iterative process. But, if the function is expressed as a linear combination of interval variables, then the bounds of the response can be expressed as the summation of the bounds of the individual variables. Therefore, fuzzy variables part of the nonlinear limit state function in Eq. (16) is expressed as a linear combination of intervening variables by the use of first-order HDMR approximation in order to apply an interval arithmetic algorithm as follows:

$$ \sum\limits_{{i = r + 1}}^N {g\left( {{{x}_i},{{\user2{c}}^i}} \right)} = {{z}_1} + {{z}_2} + \ldots + {{z}_f}, $$

(17)

where ${{z}_i} = {{\left( {{{\beta }_i}{{x}_i} + {{\gamma }_i}} \right)}^{\kappa }}$ is the relation between the intervening and the original variables with $\kappa$ being order of approximation taking values $\kappa = 1$ for linear approximation, $\kappa = 2$ for quadratic approximation, $\kappa = 3$ for cubic approximation, and so on. The bounds of the intervening variables can be determined using transformations [11]. If the membership functions of the intervening variables are available, then at each α-cut, interval arithmetic techniques can be used to estimate the response bounds at that level.

5.2 Estimation of Failure Probability Using FFT

Concept of FFT can be applied to the problem if the limit state function is in the form of a linear combination of independent variables and when either the marginal density or the characteristic function of each basic random variable is known. In the present study, HDMR concepts are used to express the random variables part along with the values of the constant part and the fuzzy variables part at each α-cut as a linear combination of lower order component functions. The steps involved in the proposed method for failure probability estimation as follows:

• 1. If $\user2{u} = {{\left\{ {{{u}_1},{{u}_2}, \ldots, {{u}_r}} \right\}}^T} \in {{\Re }^r}$ is the standard Gaussian variable, let ${{\user2{u}}^{{k*}}} = {{\left\{ {u_1^{{k*}},u_2^{{k*}}, \ldots, u_r^{{k*}}} \right\}}^T}$ be the MPP or design point, determined by a standard nonlinear constrained optimization. The MPP has a distance ${{\beta }_{\rm{HL}}}$, which is commonly referred to as the Hasofer–Lind reliability index. Construct an orthogonal matrix $\user2{R} \in {{\Re }^{{r \times r}}}$ whose r-th column is ${{\user2{\alpha }}^{{k*}}} = {{{{{\user2{u}}^{{k*}}}}} \left/ {{{{\beta }_{\rm{HL}}}}} \right.}$, that is, $\user2{R} = \left[ {\left. {{{\user2{R}}_1}} \right|{{\user2{\alpha }}^{{k*}}}} \right]$, where ${{{\mathbf{R}}}_1} \in {{\Re }^{{r \times r - 1}}}$ satisfies ${{\user2{\alpha }}^{{k*T}}}{{\user2{R}}_1} = {0} \in {{\Re }^{{1 \times r - 1}}}$. The matrix R can be obtained, for example, by Gram–Schmidt orthogonalization. For an orthogonal transformation, $\user2{u}{\mathbf{= }}\user2{R}\user2{v}$.

• 2. Let $\user2{v} = {{\left\{ {{{v}_1},{{v}_2}, \ldots, {{v}_r}} \right\}}^T} \in {{\Re }^r}$ be the rotated Gaussian space with the associated MPP ${{\user2{v}}^{{k*}}} = {{\left\{ {v_1^{{k*}},v_2^{{k*}}, \ldots, v_r^{{k*}}} \right\}}^T}$. Note that in the rotated Gaussian space, the MPP is ${{\user2{v}}^{*}} = {{\left\{ {0,0, \ldots, {{\beta }_{\rm{HL}}}} \right\}}^T}$. The transformed limit state function $g(\user2{v})$ therefore maps the random variables along with the values of the constant part and the fuzzy variables part at each α-cut into rotated Gaussian space $\user2{v}$. First-order HDMR approximation of $g(\user2{v})$ in rotated Gaussian space $\user2{v}$ with ${{\user2{v}}^{{k*}}} = {{\left\{ {v_1^{{k*}},v_2^{{k*}}, \ldots, v_r^{{k*}}} \right\}}^T}$ as reference point can be represented as follows:

  $$ {{\tilde{g}}^k}\left( \user2{v} \right) \equiv {{g}^k}\left( {{{v}_1},{{v}_2}, \ldots, {{v}_r}} \right) = \sum\limits_{{i = 1}}^r {{{g}^k}\left( {v_1^{{k*}}, \ldots, v_{{i - 1}}^{{k*}},{{v}_i},v_{{i + 1}}^{{k*}}, \ldots, v_r^{{k*}}} \right)} - \left( {r - 1} \right)g\left( {{{\user2{v}}^{{k*}}}} \right). $$

  (18)

• 3. In addition to the MPP as the chosen reference point, the accuracy of first-order HDMR approximation in Eq. (18) may depend on the orientation of the first $r - 1$ axes. In the present work, the orientation is defined by the matrix R. In Eq. (18), the terms ${{g}^k}\left( {v_1^{{k*}}, \ldots, v_{{i - 1}}^{{k*}},{{v}_i},v_{{i + 1}}^{{k*}}, \ldots, v_r^{{k*}}} \right)$ are the individual component functions and are independent of each other. Equation (18) can be rewritten as

  $$ {{\tilde{g}}^k}\left( \user2{v} \right) = {{a}^k} + \sum\limits_{{i = 1}}^r {{{g}^k}\left( {{{v}_i},{{\user2{v}}^{{k{{*}^i}}}}} \right)}, $$

  (19)

  where ${{a}^k} = - \left( {r - 1} \right)g\left( {{{\user2{v}}^{{k*}}}} \right)$.

• 4. New intermediate variables are defined as

  $$ y_i^k = {{g}^k}\left( {{{v}_i},{{\user2{v}}^{{k{{*}^i}}}}} \right). $$

  (20)

  The purpose of these new variables is to transform the approximate function into the following form:

  $$ {{\tilde{g}}^k}\left( \user2{v} \right) = {{a}^k} + y_1^k + y_2^k + \cdots + y_r^k. $$

  (21)

• 5. Due to rotational transformation in v-space, component functions $y_i^k$ in Eq. (21) are expected to be linear or weakly nonlinear function of random variables ${{v}_i}$. In this work, both linear and quadratic approximations of $y_i^k$ are considered.

• 6. Let $y_i^k = {{b}_i} + {{c}_i}{{v}_i}$ and $y_i^k = {{b}_i} + {{c}_i}{{v}_i} + {{e}_i}v_i^2$ be the linear and quadratic approximations, where coefficients ${{b}_i} \in \Re$, ${{c}_i} \in \Re$, and ${{e}_i} \in \Re$ (nonzero) are obtained by least-squares approximation from exact or numerically simulated conditional responses ${{\left\{ {{{g}^k}\left( {v_i^1,{{\user2{v}}^{{k{{*}^i}}}}} \right),{{g}^k}\left( {v_i^2,{{\user2{v}}^{{k{{*}^i}}}}} \right), \cdots, {{g}^k}\left( {v_i^n,{{\user2{v}}^{{k{{*}^i}}}}} \right)} \right\}}^T}$at n sample points along the variable axis v _i . Then, Eq. (21) results in

  $$ {{\tilde{g}}^k}\left( \user2{v} \right) \equiv {{a}^k} + y_1^k + y_2^k + \cdots + y_r^k = {{a}^k} + \sum\limits_{{i = 1}}^r {\left( {{{b}_i} + {{c}_i}{{v}_i}} \right)} $$

  (22)

  and

  $$ {{\tilde{g}}^k}\left( \user2{v} \right) \equiv {{a}^k} + y_1^k + y_2^k + \cdots + y_r^k = {{a}^k} + \sum\limits_{{i = 1}}^r {\left( {{{b}_i} + {{c}_i}{{v}_i} + {{e}_i}v_i^2} \right)} . $$

  (23)

• 7. The global approximation is formed by blending of locally constructed individual first-order HDMR approximations in the rotated Gaussian space at different identified reference points using the coefficients ${{\lambda }_k}$:

  $$ \tilde{g}(\user2{v}) = \sum\limits_{{k = 1}}^{{{{m}_d}}} {{{\lambda }_k}} {{\tilde{g}}^k}(\user2{v}). $$

  (24)

• 8. Since ${{v}_i}$ follows standard Gaussian distribution, marginal density of the intermediate variables ${{y}_i}$ can be easily obtained by simple transformation (using chain rule):

  $$ {{p}_{{{{Y}_i}}}}\left( {{{y}_i}} \right) = {{p}_{{{{V}_i}}}}\left( {{{v}_i}} \right)\left| { \frac{{d{{v}_i}}}{{d{{y}_i}}} } \right|. $$

  (25)

• 9. Now, the approximation is a linear combination of the intermediate variables ${{y}_i}$. Therefore, the joint density of $\tilde{g}\left( \user2{v} \right)$, which is the convolution of the individual marginal density of the intervening variables ${{y}_i}$, can be expressed as follows:

  $$ {{p}_{{\tilde{G}}}}\left( {\tilde{g}} \right) = {{p}_{{{{Y}_1}}}}\left( {{{y}_1}} \right) * {{p}_{{{{Y}_2}}}}\left( {{{y}_2}} \right) * \ldots * {{p}_{{{{Y}_r}}}}\left( {{{y}_r}} \right), $$

  (26)

  where ${{p}_{{\tilde{G}}}}\left( {\tilde{g}} \right)$ represents joint density of the transformed limit state function $\tilde{g}\left( \user2{v} \right)$.

• 10. Applying FFT on both sides of Eq. (26) leads to

  $$ FFT\left[ {{{p}_{{\tilde{G}}}}\left( {\tilde{g}} \right)} \right] = FFT\left[ {{{p}_{{{{Y}_1}}}}\left( {{{y}_1}} \right)} \right]FFT\left[ {{{p}_{{{{Y}_2}}}}\left( {{{y}_2}} \right)} \right] \ldots FFT\left[ {{{p}_{{{{Y}_r}}}}\left( {{{y}_r}} \right)} \right]. $$

  (27)

• 11. By applying inverse FFT on both side of Eq. (27), joint density of $\tilde{g}(\user2{v})$ is obtained.

• 12. The probability of failure is given by the following equation:

  $$ {{P}_{\rm{F}}} = \int\limits_{{ - \infty }}^0 {{{p}_{{\tilde{G}}}}\left( {\tilde{g}} \right){\text{d}}\tilde{g}.} $$

  (28)

• 13. The membership function of failure probability can be obtained by repeating the above procedure at all confidence levels of the fuzzy variables part.

6 Numerical Examples

To evaluate the accuracy and the efficiency of the present method, comparisons of the estimated failure probability bounds, both by performing the convolution using FFT in conjunction with linear and quadratic approximations and MCS on the global approximation, have been made with that obtained using direct MCS. When comparing computational efforts by various methods in evaluating the failure probability, the number of original limit state function evaluations is chosen as the primary comparison tool in this chapter. This is because of the fact that number of function evaluations indirectly indicates the CPU time usage. For direct MCS, number of original function evaluations is same as the sampling size. While evaluating the failure probability through direct MCS, CPU time is more because it involves number of repeated actual finite-element analysis.

6.1 Parabolic Performance Function

The limit state function considered is a parabola of the form

$$ g\left( \user2{x} \right) = - x_1^2 - {{x}_2} + {{x}_3}, $$

(29)

where ${{x}_1}$ and ${{x}_2}$ are assumed to be independent standard normal variables. The variable ${{x}_3}$ is assumed to be fuzzy with triangular membership function having the triplet [5.0, 7.0, 9.0].

The initial reference point c is taken as, respectively, the mean values and nominal values of the random and fuzzy variables. The first-order HDMR approximation, which is constructed over the initial reference point, is divided into two parts: one with only the random variables and the other with the fuzzy variables. The joint membership function of the fuzzy part of limit state function is obtained using suitable transformation of the fuzzy variables. In this example, the joint membership function is same as the membership function of the fuzzy variable ${{x}_3}$. As shown in Fig. 2, the limit state function given by Eq. (28) is symmetric about ${{x}_2}$ for given value of ${{x}_3}$ (say the nominal value of ${{x}_3} = 7$ at $\alpha = 1$) and has two design points. The two actual design points of the limit state function shown in Fig. 2, obtained using recursive quadratic programming (RQP) algorithm, are (2.54, 0.49) and (−2.54, 0.49) with reliability indices ${{\beta }_1} = {{\beta }_2} = 2.588$.

Fig. 2

Limit state function

Table 1 illustrates computational details and identification of reference points ${{\user2{d}}^1},{{\user2{d}}^2}$ using FF sampling scheme with five equally spaced sample points ($n = 5$) along each of the variable axis. In Table 1, the values corresponding to $\alpha = {{0}^{{(L)}}}$ and $\alpha = {{0}^{{(R)}}}$, respectively, indicate the extreme left and right values of the limit state function $g(\user2{x})$ at zero confidence level (i.e., $\alpha = 0$). Table 1 shows two reference points ${{\user2{d}}^1} = \left( {2,0} \right)$ and ${{\user2{d}}^2} = \left( { - 2,0} \right)$ closer to the function. After identification of the two reference points (2, 0) and (−2, 0), local individual first-order HDMR approximations of the original limit state function are constructed at the two reference points by deploying $n = 5$ sample points along each of the variable axis. Local approximations of the original limit state function are blended together to form global approximation. The bounds of the failure probability are obtained both by performing the convolution using FFT in conjunction with linear and quadratic approximations and MCS on the global approximation.

Table 1 Identification of multiple design points with FF sampling

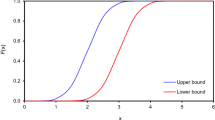
Figure 3 shows the membership function of the failure probability ${{P}_{\rm{F}}}$ estimated both by performing the convolution using FFT and MCS on the global approximation, as well as that obtained using direct MCS.

Fig. 3

Membership function of failure probability for parabolic performance function

In addition, effect of SF sampling scheme on the estimated membership function of the failure probability is studied. After identifying two reference points ${{\user2{d}}^1} = ( - 2,2)$ and ${{\user2{d}}^2} = (2,2)$ closer to the function producing maximum weight, the bounds of the failure probability are obtained. Figure 3 also shows the membership function of the failure probability obtained by the proposed method based on SF sampling scheme. The effect of number of sample points is studied by varying n from 3 to 9. It is observed that $n = 7$ provides the optimum number of function calls with acceptable accuracy in evaluating the failure probability with the present method.

6.2 Cantilever Steel Beam

A cantilever steel beam of 1.0 m with cross-sectional dimensions of (0.1 m × 0.01 m) is considered, as shown in Fig. 4, to examine the accuracy and efficiency of the proposed method for the membership function of failure probability estimation. The beam is subjected to an in-plane moment at the free end and a concentrated load at 0.4 m from the free end. The structure is assumed to have failed if the square of the von Mises stress at the support (at A in Fig. 4) exceeds specified threshold ${{V}_{{{ \max }}}}$. Therefore, the limit state function is defined as

$$ g(\user2{x}) = {{V}_{{{ \max }}}} - V(\user2{x}), $$

(30)

where $V(\user2{x})$ is the square of the von Mises stress, expressed as a quadratic operator on the stress vector.

Fig. 4

Cantilever steel beam

In this example, loads ${{x}_1}$ and ${{x}_2}$, modulus of elasticity of the beam E, and threshold quantity ${{V}_{{{ \max }}}}$ are taken as uncertain variables. The variations of E and ${{V}_{{{ \max }}}}$ are expressed as $E = {{E}_0}\left( {1 + \varepsilon {{x}_3}} \right)$ and ${{V}_{{{ \max }}}} = {{V}_{{{ \max }}}}_0\left( {1 + \varepsilon {{x}_4}} \right)$. Here, $\varepsilon$ is small deterministic quantity representing the coefficient of variation of the random variables and are taken to equal to 0.05, ${{E}_0} = 2 \times {{10}^5}{\text{ N/}}{{\text{m}}^{{2}}}$ denotes the deterministic component of modulus of elasticity, and ${{V}_{\rm{max0}}} = 6.15 \times {{10}^9}{\text{ N/}}{{\text{m}}^{{2}}}$ denotes the deterministic component of threshold quantity. All variables are assumed to be independent. The mean values of random variables ${{x}_1}$ and ${{x}_2}$ are 1 and 0, respectively, with the standard deviation of 1. The variables ${{x}_3}$ and ${{x}_4}$ are triangular fuzzy numbers with [0.0 2.0 4.0] and [0.0, 0.1, 0.2], respectively.

The limit state function given in Eq. (30) is approximated using first-order HDMR by deploying $n = 5$ sample points along each of the variable axis and taking, respectively, the mean values and nominal values of the random and fuzzy variables as initial reference point (1.0, 0.0, 2.0, 0.1). The approximated limit state function is divided into two parts, one with only the random variables along with the value of the constant part and the other with the fuzzy variables. The joint membership function of the fuzzy part of approximated limit state function is obtained using suitable transformation of the fuzzy variables. Using FF sampling scheme, the sample point $\user2{d} = \left( {1, - 2} \right)$ is identified as reference point closer to the limit state function producing maximum weight. In this case, since only one reference point is identified, local approximation is same as the global approximation. The bounds of the failure probability are obtained both by performing the convolution using FFT in conjunction with linear and quadratic approximations and MCS on the global approximation. Figure 5 shows the membership function of the failure probability estimated both by performing the convolution using FFT in conjunction with linear and quadratic approximations and MCS on the global approximation, as well as that obtained using direct MCS.

Fig. 5

Membership function of failure probability for cantilever steel beam

In addition, the membership function of the failure probability obtained by the proposed method based on SF sampling scheme is also shown in Fig. 5. The effect of number of sample points is studied by varying n from 3 to 9. It is observed that $n = 7$ provides the optimum number of function calls with acceptable accuracy in evaluating the failure probability with the present method.

6.3 80-Bar 3D Truss Structure

A 3D truss, shown in Fig. 6, is considered in this example to examine the accuracy and efficiency of the proposed method for the membership function of failure probability estimation. The loads at various levels are considered to be random, while the cross-sectional areas of the angle sections at various levels are assumed to be fuzzy as shown in Table 2.

Fig. 6

3D truss structure with 80 bars

Table 2 Properties of the uncertain variables

The maximum horizontal displacement at the top of the tower is considered to be the failure criterion, as given below:

$$ g\left( \user2{x} \right) = {{\Delta }_{{{ \lim }}}} - \Delta \left( \user2{x} \right). $$

(31)

The limiting deflection ${{\Delta }_{{{ \lim }}}}$ is assumed to be 0.15 m. The limit state function is approximated using first-order HDMR by deploying $n = 5$ sample points along each of the variable axis and taking, respectively, the mean values and nominal values of the random and fuzzy variables as initial reference point.

The approximated limit state function is divided into two parts, one with only the random variables along with the value of the constant part and the other with the fuzzy variables. The joint membership function of the fuzzy part of approximated limit state function is obtained using suitable transformation of the fuzzy variables. The two reference points closer to the function producing maximum weights, 1.0 and 0.977, are identified. After identification of two reference points, local first-order HDMR approximations are constructed at the reference points. The bounds of the failure probability are obtained both by performing the convolution using FFT in conjunction with linear and quadratic approximations and MCS on the global approximation. Figure 7 shows the membership function of the failure probability estimated both by performing the convolution using FFT and MCS on the global approximation, as well as that obtained using direct MCS.

Fig. 7

Membership function of failure probability for truss structure

In addition, effects of SF sampling scheme and the number of sample points on the estimated membership function of the failure probability are studied. Figure 7 also shows the membership function of the failure probability estimate obtained by the proposed method based on SF sampling scheme.

7 Summary and Conclusions

This chapter presented a novel uncertain analysis method for estimating the membership function of the reliability of structural systems involving multiple design points in the presence of mixed uncertain variables. The method involves MHDMR technique for the limit state function approximation, transformation technique to obtain the contribution of the fuzzy variables to the convolution integral and fast Fourier transform for solving the convolution integral at all confidence levels of the fuzzy variables. Weight function is adopted for identification of multiple reference points closer to the limit surface. Using the bounds of the fuzzy variables part at each confidence level along with the constant part and the random variables part, the joint density functions are obtained by (1) identifying the reference points closer to the limit state function and (2) blending of locally constructed individual first-order HDMR approximations in the rotated Gaussian space at different identified reference points to form global approximation and (3) performing the convolution using FFT, which upon integration yields the bounds of the failure probability. As an alternative, the bounds of the failure probability are estimated by performing MCS on the global approximation in the original space, obtained by blending of locally constructed individual first-order HDMR approximations of the original limit state function at different identified reference points.

The results of the numerical examples involving explicit hypothetical mathematical function and structural/solid-mechanics problems indicate that the proposed method provides accurate and computationally efficient estimates of the membership function of the failure probability. The results obtained from the proposed method are compared with those obtained by direct MCS. The numerical results show that the present method is efficient for structural reliability estimation involving any number of fuzzy and random variables with any kind of distribution. Two types of sampling schemes, namely, FF and SF, are adopted in this study for MHDMR approximation of the original limit state function construction. A parametric study is conducted with respect to the number of sample points n used in FF and SF sampling-based MHDMR approximation, and its effect on the estimated failure probability is investigated. An optimum number of sample points n must be chosen in approximation of the original limit state function.