Confidence Bounds on Failure Probability Using MHDMR

Abstract

The structural reliability analysis in presence of mixed uncertain variables demands more computation as the entire configuration of fuzzy variables needs to be explored. Moreover the existence of multiple design points plays an important role in the accuracy of results as the optimization algorithms may converge to a local design point by neglecting the main contribution from the global design point. Therefore, in this paper a novel uncertain analysis method for estimating the failure probability bounds of structural systems involving multiple design points in presence of mixed uncertain variables is presented. The proposed method involves weight function to identify multiple design points, multicut-high dimensional model representation technique for the limit state function approximation, transformation technique to obtain the contribution of the fuzzy variables to the convolution integral and fast Fourier transform for solving the convolution integral. In the proposed method, efforts are required in evaluating conditional responses at a selected input determined by sample points, as compared to full scale simulation methods. Therefore, the proposed technique estimates the failure probability accurately with significantly less computational effort compared to the direct Monte Carlo simulation. The methodology developed is applicable for structural reliability analysis involving any number of fuzzy and random variables with any kind of distribution. The accuracy and efficiency of the proposed method is demonstrated through two examples.

1 Introduction

Reliability analysis taking into account the uncertainties involved in a structural system plays an important role in the analysis and design of structures. Due to the complexity of structural systems the information about the functioning of various structural components has different sources and the failure of systems is usually governed by various uncertainties, all of which are to be taken into consideration for reliability estimation. Uncertainties present in a structural system can be classified as aleatory uncertainty and epistemic uncertainty. Aleatory uncertainty information can be obtained as a result of statistical experiments and has a probabilistic or random character. Epistemic uncertainty information can be obtained by the estimation of the experts and in most cases has an interval or fuzzy character. When aleatory uncertainty is only present in a structural system, then the reliability estimation involves determination of the probability that a structural response exceeds a threshold limit, defined by a limit state/performance function influenced by several random parameters. Structural reliability can be computed adopting probabilistic method involving the evaluation of multidimensional integral [1, 2]. In first- or second-order reliability method (FORM/SORM), the limit state functions need to be specified explicitly. Alternatively the simulation-based methods such as Monte Carlo techniques requires more computational effort for simulating the actual limit state function repeated times. The response surface concept was adopted to get separable and closed form expression of the implicit limit state function in order to use fast Fourier transform (FFT) to estimate the failure probability [3]. The High Dimensional Model Representation (HDMR) concepts were applied for the approximation of limit state function at the MPP and FFT technique to evaluate the convolution integral for estimation of failure probability [4]. In this method, efforts are required in evaluating conditional responses at a selected input determined by sample points, as compared to full scale simulation methods.

In addition, the main contribution to the reliability integral comes from the neighbourhood of design points. When multiple design points exist, available optimization algorithms may converge to a local design point and thus erroneously neglect the main contribution to the value of the reliability integral from the global design point(s). Moreover, even if a global design point is obtained, there are cases for which the contribution from other local or global design points may be significant [5]. In that case, multipoint FORM/SORM is required for improving the reliability analysis [6]. In the presence of only epistemic uncertainty in a structural system, possibilistic approaches to evaluate the minimum and maximum values of the response are available [7]. All the reliability models discussed above are based on only one kind of uncertain information; either random variables or fuzzy input, but do not accommodate a combination of both types of variables. However, in reality, for some engineering problems in which some uncertain parameters are random variables, others are interval or fuzzy variables, using one kind of reliability model cannot obtain the best results. To determine the bounds of reliability of a structural system involving both random and interval or fuzzy variables, every configuration of the interval variables needs to be explored. Hence, the computational effort involved in estimating the bounds of the failure probability increases tremendously in the presence of multiple design points and mixed uncertain variables. This paper explores the potential of coupled Multicut-HDMR (MHDMR)-FFT technique in evaluating the reliability of a structural system with multiple design points, for which some uncertainties can be quantified using fuzzy membership functions while some are random in nature. Comparisons of numerical results have been made with direct MCS method to evaluate the accuracy and computational efficiency of the present method.

2 Multi-cut High Dimensional Model Representation

High Dimensional Model Representation (HDMR) is a general set of quantitative model assessment and analysis tools for capturing the high-dimensional relationships between sets of input and output model [4, 8]. Let the N dimensional vector ${\mathbf{x}} = \{ x_{1} ,x_{2} , \ldots ,x_{N} \}$ represent the input variables of the model under consideration, and the response function as $g({\mathbf{x}}).$ Since the influence of the input variables on the response function can be independent and/or cooperative, HDMR expresses the response $g({\mathbf{x}})$ as a hierarchical correlated function expansion in terms of the input variables. The expansion functions are determined by evaluating the input-output responses of the system relative to the defined reference point c along associated lines, surfaces, subvolumes, etc. in the input variable space. The first-order approximation of $g({\mathbf{x}})$ is as follows:

$$ \tilde{g}({\mathbf{x}}) = \sum\limits_{i = 1}^{N} {g\left( {c_{1} , \ldots ,c_{i - 1} ,x_{i} ,c_{i + 1} , \ldots ,c_{N} } \right)} - \left( {N - 1} \right)g({\mathbf{c}}) $$

(1)

The notion of 0th, 1st, etc. in HDMR expansion should not be confused with the terminology used either in the Taylor series or in the conventional least-squares based regression model. It can be shown that, the first order component function $g_{i} (x_{i} )$ is the sum of all the Taylor series terms which contain and only contain variable $x_{i} .$ Hence first-order HDMR approximations should not be viewed as first-order Taylor series expansions nor do they limit the nonlinearity of $g({\mathbf{x}}) .$

The main limitation of truncated cut-HDMR expansion is that depending on the order chosen sometimes it is unable to accurately approximate $g({\mathbf{x}}) ,$ when multiple design points exist on the limit state function or when the problem domain is large. In this section, a new technique based on MHDMR is presented for approximation of the original implicit limit state function, when multiple design points exist. The basic principles of cut-HDMR may be extended to more general cases. MHDMR is one extension where several cut-HDMR expansions at different reference points are constructed, and the original implicit limit state function $g({\mathbf{x}})$ is approximately represented not by one, but by all cut-HDMR expansions. In the present work, weight function is adopted for identification of multiple reference points closer to the limit surface. Let ${\mathbf{d}}^{1} ,{\mathbf{d}}^{2} , \ldots ,{\mathbf{d}}^{{m_{d} }}$ be the ${{m_{d} }}$ identified reference points closer to the limit state function based on the weight function. The original implicit limit state function $g({\mathbf{x}})$ is approximately represented by blending all locally constructed ${{m_{d} }}$ individual cut-HDMR expansions as follows:

$$ g({\mathbf{x}}) \cong \sum\limits_{k = 1}^{{m_{d} }} {\uplambda_{k} \left( {\mathbf{x}} \right)} \left[ {g_{0}^{k} + \sum\limits_{i = 1}^{N} {g_{i}^{k} (x_{i} )} + \cdots + g_{12 \cdots N}^{k} \quad (x_{1} ,x_{2} , \ldots ,x_{N} )} \right] $$

(2)

The coefficients $\uplambda_{k} ({\mathbf{x}})$ determine the contribution of each locally approximated function to the global function. The properties of the coefficients $\uplambda_{k} ({\mathbf{x}})$ imply that the contribution of all other cut-HDMR expansions vanish except one when x is located on any cut line, plane, or higher dimensional (≤l) sub-volumes through that reference point, and then the MHDMR expansion reduces to single point cut-HDMR expansion. As mentioned above, the lth order cut-HDMR approximation does not have error when x is located on these sub-volumes. When m_d cut-HDMR expansions are used to construct a MHDMR expansion, the error free region in input x space is m_d times that for a single reference point cut-HDMR expansion, hence the accuracy will be improved. Therefore, first-order MHDMR approximations of the original implicit limit state function with m_d reference points can be expressed as

$$ \tilde{g}({\mathbf{x}}) \cong \sum\limits_{k = 1}^{{m_{d} }} {\uplambda_{k} ({\mathbf{x}})\left[ {\sum\limits_{i = 1}^{N} {g^{k} \left( {d_{1}^{k} , \ldots ,d_{i - 1}^{k} ,x_{i} ,d_{i + 1}^{k} , \ldots ,d_{N}^{k} } \right)} - \left( {N - 1} \right)g^{k} \left( {{\mathbf{d}}^{k} } \right)} \right]}. $$

(3)

3 Weight Function for Identification of Multiple Reference Points

The most important part of MHDMR approximation of the original implicit limit state function is identification of multiple reference points closer to the limit state function. The proposed weight function is similar to that used by Kaymaz and McMahon [9] for weighted regression analysis. Among the limit state function responses at all sample points, the most likelihood point is selected based on closeness to zero value, which indicates that particular sample point is close to the limit state function. In this study two types of procedures are adopted for identification of reference points closer to the limit state function, namely: (1) first-order method, and (2) second-order method. The procedure for identification of reference points closer to the limit state function using first-order method proceeds as follows: (a) $n( {=} 3,5,7\,{\text{or}}\,9)$ equally spaced sample points $\upmu_{i} - (n - 1)\upsigma_{i} /2,$ $\upmu_{i} - (n - 3)\upsigma_{i} /2,$ …, $\upmu_{i} ,$ …, $\upmu_{i} + (n - 3)\upsigma_{i} /2,$ $\upmu_{i} + (n - 1)\upsigma_{i} /2$ are deployed along each of the random variable axis $x_{i}$ with mean $\upmu_{i}$ and standard deviation $\upsigma_{i} ,$ through an initial reference point. Initial reference point is taken as mean value of the random variables ; (b) The limit state function is evaluated at each sample point; (c) Using the limit state function responses at all sample points, the weight corresponding to each sample point is evaluated using the following weight function,

$$ w^{\prime} = \exp \left( { - \frac{{g\left( {c_{1} , \ldots ,c_{i - 1} ,x_{i} ,c_{i + 1} , \ldots ,c_{N} } \right) - \left. {g({\mathbf{x}})} \right|_{\hbox{min} } }}{{\left| {\left. {g({\mathbf{x}})} \right|_{\hbox{min} } } \right|}}} \right). $$

(4)

Sample points ${\mathbf{d}}^{1} ,{\mathbf{d}}^{2} , \ldots ,{\mathbf{d}}^{{m_{d} }}$ with maximum weight are selected as reference points closer to the limit state function, for construction of $m_{d}$ individual cut-HDMR approximations of the original implicit limit state function locally. In this study, two types of sampling schemes, namely FF and SF are adopted.

4 Estimation of Failure Probability in Presence of Mixed Uncertain Variables

Let the N-dimensional input variables vector ${\mathbf{x}} = \{ x_{1} ,x_{2} , \ldots ,x_{N} \} ,$ which comprises of r number of random variables and f number of fuzzy variables be divided as, ${\mathbf{x}} = \{ x_{1} ,x_{2} , \ldots ,x_{r} ,x_{r + 1} ,x_{r + 2} , \ldots ,x_{r + f} \}$ where the subvectors $\{ x_{1} ,x_{2} , \ldots ,x_{r} \}$ and $\{ x_{r + 1} ,x_{r + 2} , \ldots ,x_{r + f} \}$ respectively group the random variables and the fuzzy variables, with $N = r + f .$ Then the first-order approximation of $\tilde{g}({\mathbf{x}})$ can be divided into three parts, the first part with only the random variables, the second part with only the fuzzy variables and the third part is a constant which is the output response of the system evaluated at the reference point c, as follows

$$ \tilde{g}({\mathbf{x}}) = \sum\limits_{i = 1}^{r} {g\left( {x_{i} ,{\mathbf{c}}^{i} } \right)} + \sum\limits_{i = r + 1}^{N} {g\left( {x_{i} ,{\mathbf{c}}^{i} } \right)} - (N - 1)g({\mathbf{c}}) $$

(5)

The joint membership function of the fuzzy variables part is obtained using suitable transformation of the variables $\{ x_{r + 1} ,x_{r + 2} , \ldots ,x_{N} \}$ and interval arithmetic algorithm. Using the bounds of the fuzzy variables part at each $\alpha$-cut along with the constant part and the random variables part, the joint density functions are obtained by performing the convolution using FFT in the rotated Gaussian space at the MPP, which upon integration yields the bounds of the failure probability . The steps involved in the proposed method for failure probability estimation as follows:

• (i) If ${\mathbf{u}} = \{ u_{1} ,u_{2} , \ldots ,u_{r} \}^{T} \in \Re^{r}$ is the standard Gaussian variable, let ${\mathbf{u}}^{k^{*}} = \left\{ {u_{1}^{k^{*}} ,u_{2}^{k^{*}} , \ldots ,u_{r}^{k^{*}} } \right\}^{T}$ be the MPP or design point, determined by a standard nonlinear constrained optimization. The MPP has a distance $\upbeta_{HL}$ which is commonly referred to as the Hasofer–Lind reliability index. Note that in the rotated Gaussian space the MPP is ${\mathbf{v}}^{*} = \{ 0,0, \ldots ,\upbeta_{HL} \}^{T} .$ The transformed limit state function $g({\mathbf{v}})$ therefore maps the random variables along with the values of the constant part and the fuzzy variables part at each $\upalpha$-cut, into rotated Gaussian space V. First-order HDMR approximation of $g({\mathbf{v}})$ in rotated Gaussian space V with ${\mathbf{v}}^{k^{*}} = \left\{ {v_{1}^{k^{*}} ,v_{2}^{k^{*}} , \ldots ,v_{r}^{k^{*}} } \right\}^{T}$ as reference point can be represented as follows:

  $$ \tilde{g}^{k} ({\mathbf{v}}) \equiv \sum\limits_{i = 1}^{r} {g^{k} \left( {v_{1}^{k^{*}} , \ldots ,v_{i - 1}^{k^{*}} ,v_{i} ,v_{i + 1}^{k^{*}} , \ldots ,v_{r}^{k^{*}} } \right)} - (r - 1)g({\mathbf{v}}^{k^{*}} ) $$

  (6)

• (ii) In addition to the MPP as the chosen reference point, the accuracy of first-order HDMR approximation may depend on the orientation of the first r − 1 axes. In the present work, the orientation is defined by the matrix. The terms $g^{k} \left( {v_{1}^{k^{*}} , \ldots ,v_{i - 1}^{k^{*}} ,v_{i} ,v_{i + 1}^{k^{*}} , \ldots ,v_{r}^{k^{*}} } \right)$ are the individual component functions and are independent of each other. Equation (6) can be rewritten as,

  $$ \tilde{g}^{k} ({\mathbf{v}}) = a^{k} + \sum\limits_{i = 1}^{r} {g^{k} \left( {v_{i} ,{\mathbf{v}}^{{k^{*i} }} } \right)} $$

  (7)

• (iii) New intermediate variables are defined as

  $$ y_{i}^{k} = g^{k} \left( {v_{i} ,{\mathbf{v}}^{{k^{*i} }} } \right) $$

  (8)

• (iv) The purpose of these new variables is to transform the approximate function into the following form

  $$ \tilde{g}^{k} \left( {\mathbf{v}} \right) = a^{k} + y_{1}^{k} + y_{2}^{k} + \cdots + y_{r}^{k} $$

  (9)

• (v) Due to rotational transformation in v-space, component functions $y_{i}^{k}$ are expected to be linear or weakly nonlinear function of random variables $v_{i} .$

• (vi) The global approximation is formed by blending of locally constructed individual first-order HDMR approximations in the rotated Gaussian space at different identified reference points using the coefficients $\uplambda_{k}$

  $$ \tilde{g}({\mathbf{v}}) = \sum\limits_{k = 1}^{{m_{d} }} {\uplambda_{k} } \tilde{g}^{k} ({\mathbf{v}}) $$

  (10)

• (vii) Since v_i follows standard Gaussian distribution, marginal density of the intermediate variables y_i can be easily obtained by transformation.

• (viii) Now the approximation is a linear combination of the intermediate variable. Therefore, the joint density of $\tilde{g}({\mathbf{v}}) ,$ which is the convolution of the marginal density of the intervening variables can be expressed as follows:

  $$ p_{{\tilde{G}}} \left( {\tilde{g}} \right) = p_{{Y_{1} }} \left( {y_{1} } \right) * p_{{Y_{2} }} \left( {y_{2} } \right) * \cdots * p_{{Y_{r} }} \left( {y_{r} } \right) $$

  (11)

• (ix) Applying FFT and inverse FFT on both side joint density of $\tilde{g}({\mathbf{v}})$ is obtained.

• (x) The probability of failure is given by the following equation

  $$ P_{F} = \int\limits_{ - \infty }^{0} {p_{{\tilde{G}}} \left( {\tilde{g}} \right)d\tilde{g}} . $$

  (12)

• (xi) The membership function of failure probability can be obtained by repeating the above procedure at all confidence levels of the fuzzy variables part.

5 Numerical Examples

5.1 Four Dimensional Quadratic Function

This example considers a hypothetical limit state function of the following form:

$$ \begin{aligned} g({\mathbf{x}}) & = \, {-} x_{1}^{2} - x_{2}^{2} - x_{3}^{2} - x_{4}^{2} + 9x_{1} + 11x_{2} + 11x_{3} + 11x_{4} \\ & \quad - x_{5}^{2} - 4.6x_{5} + x_{6}^{2} + 4.7x_{6} + 11 \\ \end{aligned} $$

(13)

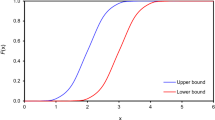
where $x_{1} ,x_{2} ,x_{3} ,x_{4}$ are assumed to be normal variables with mean value as 5.0 and standard deviation value as 0.4, and $x_{5} ,x_{6}$ are assumed to be fuzzy variables with triangular membership function having the triplet [4.96, 5.0, 5.04]. Figure 1 shows the estimated membership function of the failure probability P_F by the proposed methods, as well as by using direct MCS. The failure probability estimated by the proposed MHDMR approximation with FF sampling scheme requires significantly less computational effort than direct MCS for the same accuracy.

Fig. 1

Membership function of failure probability

5.2 80-Bar 3D-Truss Structure

A 3D-truss, shown in Fig. 2, is considered in this example to examine the accuracy and efficiency of the proposed method for the membership function of failure probability estimation. The loads at various levels are considered to be random while the cross-sectional areas of the angle sections at various levels are assumed to be fuzzy. The maximum horizontal displacement at the top of the tower is considered to be the failure criterion, as given below.

$$ g({\mathbf{x}}) =\Delta _{\lim } -\Delta ({\mathbf{x}}) $$

(14)

Fig. 2

80-bar 3D-truss structure

The limiting deflection $\Delta _{\lim }$ is assumed to be 0.15 m. The limit state function is approximated using first-order HDMR by deploying n = 5 sample points along each of the variable axis and taking respectively the mean values and nominal values of the random and fuzzy variables as initial reference point. The two reference points closer to the function producing maximum weights, 1.0 and 0.977 are identified. After identification of two reference points, local first-order HDMR approximations are constructed at the reference points. The bounds of the failure probability are obtained both by performing the convolution using FFT in conjunction with linear and quadratic approximations and MCS on the global approximation. Figure 3 shows the membership function of the failure probability P_F estimated both by performing the convolution using FFT, and MCS on the global approximation, as well as that obtained using direct MCS. In addition, effects of SF sampling scheme and the number of sample points on the estimated membership function of the failure probability P_F are studied.

Fig. 3

Membership function of failure probability

6 Summary and Conclusion

This paper presented a novel uncertain analysis method for estimating the membership function of the reliability of structural systems involving multiple design points in the presence of mixed uncertain variables. The method involves MHDMR technique for the limit state function approximation, transformation technique to obtain the contribution of the fuzzy variables to the convolution integral and fast Fourier transform for solving the convolution integral at all confidence levels of the fuzzy variables. Weight function is adopted for identification of multiple reference points closer to the limit surface. Using the bounds of the fuzzy variables part at each confidence level along with the constant part and the random variables part, the joint density functions are obtained by (i) identifying the reference points closer to the limit state function and (ii) blending of locally constructed individual first-order HDMR approximations in the rotated Gaussian space at different identified reference points to form global approximation, and (iii) performing the convolution using FFT, which upon integration yields the bounds of the failure probability . As an alternative the bounds of the failure probability are estimated by performing MCS on the global approximation in the original space, obtained by blending of locally constructed individual first-order HDMR approximations of the original limit state function at different identified reference points. The results of the numerical examples indicate that the proposed method provides accurate and computationally efficient estimates of the membership function of the failure probability. The results obtained from the proposed method are compared with those obtained by direct MCS. The numerical results show that the present method is efficient for structural reliability estimation involving any number of fuzzy and random variables with any kind of distribution.