Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The intent of the paper is to show that the governing equation for simple mechanical systems may contain fractional derivatives. We consider three types of oscillator to which a semi-infinite Bernoulli-Euler beam is attached. It is shown that if the consideration is limited only to the oscillator, then the environment (i.e. the semi-infinite Bernoulli-Euler beam) adds a fractional derivative into the oscillator equation. Another system governed by a differential equation with fractional derivative is the suspension of the fluid-conveying-pipe. The eigenvector expansion method based upon transformation of the equation into a set of four semi-differential equations is utilised for solving the obtained differential equation with fractional derivatives.

2 Three Mechanical Systems

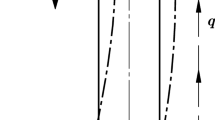
Consider a Single-Degree-Of-Freedom system and a semi-infinite Bernoulli-Euler beam x > 0, which is attached to mass m at x = 0, cf. Fig. 1.

Fig. 1
figure 1

Schematics of the first model

Full size image

The mass m is allowed to perform only vertical displacements and governed by the equation

$$\displaystyle{ m\dfrac{\mathrm{{d}}^{2}y} {\mathrm{d}{t}^{2}} = -\mathit{cy} + Q\bigg\vert _{x=0} + f(t)\;. }$$
(1)

where y is the absolute displacement of the mass m, f(t) is an external driving force, t is time and \(Q\big\vert _{x=0}\) is the shear force in the beam acting on the mass m.

The equation of the beam bending is as follows

$$\displaystyle{ \mathit{EI}\dfrac{{\partial }^{4}w} {\partial {x}^{4}} +\rho A\dfrac{{\partial }^{2}w} {\partial {t}^{2}} = 0\;,\quad 0 < x < \infty \;, }$$
(2)

where w(x, t) is the absolute displacement, EI is the bending stiffness of the beam, ρ is the mass density and A is the cross-sectional area. The condition of coupling of mass m and the beam is given by

$$\displaystyle{ y(t) = w(0,t)\;. }$$
(3)

The zero initial conditions are assumed, then the Laplace transformation gives

$$\displaystyle{{ \mathit{mp}}^{2}\bar{y}(p) + c\bar{y}(p) =\bar{ Q}(p)\bigg\vert _{ x=0} +\bar{ f}(p)\;, }$$
(4)
$$\displaystyle{ \mathit{EI}\dfrac{\mathrm{{d}}^{4}\bar{w}} {\mathrm{d}{x}^{4}} +\rho A{p}^{2}\bar{w} = 0\;,\quad 0 < x < \infty \;. }$$
(5)

The solution of Eq. (5) bounded at infinity is as follows

$$\displaystyle{ \bar{w}(x,p) = A_{2}\exp (\lambda _{2}x) + A_{4}\exp (\lambda _{4}x)\;. }$$
(6)

where the wave numbers are

$$\displaystyle{\lambda _{2} = -(1 + i)\beta \sqrt{p}\;,\quad \lambda _{4} = -(1 - i)\beta \sqrt{p}\;,\quad \beta = \root{4}\of{\rho A/4\mathit{EI}}}$$

for \(\sqrt{p} > 0\). The bending moment in the beam vanishes at x = 0

$$\displaystyle{\bar{M}\bigg\vert _{x=0} = -\mathit{EI}\dfrac{\mathrm{{d}}^{2}\bar{w}} {\mathrm{d}{x}^{2}} \bigg\vert _{x=0} = 2\mathit{EI}{i\beta }^{2}p(A_{ 2} - A_{4}) = 0\;.}$$

Hence, A 2 = A 4 and the shear force \(\bar{Q}\big\vert _{x=0}\) to be substituted into Eq. (4) is

$$\displaystyle{ \bar{Q}\bigg\vert _{x=0} = -\mathit{EI}\dfrac{\mathrm{{d}}^{3}\bar{w}} {\mathrm{d}{x}^{3}} \bigg\vert _{x=0} = -\mathit{EI}\left [\lambda _{2}^{3}A_{ 2} +\lambda _{ 4}^{3}A_{ 4}\right ] = -4{\mathit{EI}\beta }^{3}p\sqrt{p}\:A_{ 2}\;. }$$
(7)

As follows from Eq. (6) \(\bar{w}(0,p) =\bar{ y}(p) = 2A_{2}\), that allows one to establish the following relationship between the shear force \(\bar{Q}\big\vert _{x=0}\) and the beam displacement \(\bar{w}(0,p)\)

$$\displaystyle{ \bar{Q}\bigg\vert _{x=0} = -2{\mathit{EI}\beta }^{3}p\sqrt{p}\:\bar{y}(p)\;. }$$
(8)

Inserting the latter equation into Eq. (4) yields

$$\displaystyle{{ \mathit{mp}}^{2}\bar{y}(p) + 2{\mathit{EI}\beta }^{3}p\sqrt{p}\:\bar{y}(p) + c\bar{y}(p) =\bar{ f}(p)\;. }$$
(9)

Since the trivial initial conditions were assumed, Eq. (9) corresponds to the following ordinary differential equation for displacement y(t)

$$\displaystyle{ m\dfrac{\mathrm{{d}}^{2}y} {\mathrm{d}{t}^{2}} + 2{\mathit{EI}\beta }^{3}\dfrac{\mathrm{{d}}^{3/2}y} {\mathrm{d}{t}^{3/2}} + \mathit{cy} = f(t)\;. }$$
(10)

As seen from Eq. (10), the dynamics of mass m is governed by a single differential equation with a fractional derivative of the order \(3/2\).

Another mechanical system governed by the differential equation with a fractional derivative is obtained from the above system provided that the semi-infinite Bernoulli-Euler beam is clamped to a rigid mass m rather than it is simply supported. In this case the governing equation is as follows (the derivation is omitted as it is fully analogous to the previous one)

$$\displaystyle{ m\dfrac{\mathrm{{d}}^{2}y} {\mathrm{d}{t}^{2}} + 4{\mathit{EI}\beta }^{3}\dfrac{\mathrm{{d}}^{3/2}y} {\mathrm{d}{t}^{3/2}} + \mathit{cy} = f(t)\;. }$$
(11)

The third mechanical system consists of a disk attached to an angular spring and a semi-infinite Bernoulli-Euler beam, Fig. 2.

Fig. 2
figure 2

Schematics of the third model

Full size image

The beam is supposed to be clamped to the disc in such a way that the angle of rotation of the disk and that of the beam at x = 0 coincide. The differential equation of the disk is given as

$$\displaystyle{ J \dfrac{\mathrm{{d}}^{2}\varphi } {\mathrm{d}{t}^{2}} + 2\beta \mathit{EI} \dfrac{\mathrm{{d}}^{1/2}\varphi } {\mathrm{d}{t}^{1/2}} + k\varphi = m(t)\;. }$$
(12)

where J is the moment of the mass inertia, k is the angular stiffness of the spring and m(t) is the external driving moment. We omit the derivation however one can easily perform it by analogy with the above one. Again, a differential equation with a fractional derivative is obtained however, in contrast to Eqs. (10) and (11), the governing equation contains the fractional derivative of the order \(1/2\).

3 Mechanical System with a Pipeline Conveying Fluid

We consider now a pipeline conveying a heavy fluid. The pipe is assumed to perform bending vibration in the plane xz. The suspension of the pipe is assumed to be modeled by a spring of stiffness c and a dashpot b. The mass of the suspension is m and the velocity of the fluid is denoted by v, see Fig. 3.

Fig. 3
figure 3

Schematics of the suspended pipe conveying fluid

Full size image

The governing equation for the pipe bending vibration is as follows

$$\displaystyle{ \mathit{EI}\dfrac{{\partial }^{4}w} {\partial {x}^{4}} = -\big(\rho A\big)_{p}\dfrac{{\partial }^{2}w} {\partial {t}^{2}} -\big (\rho A\big)_{f}\:a_{z}\;. }$$
(13)

Here the subscripts p and f refer to the pipe and fluid respectively and a z denotes the fluid acceleration in direction z . Using the rule of determining the material derivative we obtain

$$\displaystyle{ a_{z} = \dfrac{{\partial }^{2}w} {\partial {t}^{2}} + 2v \dfrac{{\partial }^{2}w} {\partial {x}^{}\partial {t}^{}} + {v}^{2}\dfrac{{\partial }^{2}w} {\partial {x}^{2}} \;. }$$
(14)

Substituting Eq. (14) into Eq. (13) yields

$$\displaystyle{ \mathit{EI}\dfrac{{\partial }^{4}w} {\partial {x}^{4}} +\big (\rho A\big)_{f}\bigg(\dfrac{{\partial }^{2}w} {\partial {t}^{2}} + 2v \dfrac{{\partial }^{2}w} {\partial {x}^{}\partial {t}^{}} + {v}^{2}\dfrac{{\partial }^{2}w} {\partial {x}^{2}} \bigg) = 0\;, }$$
(15)

where the inertia term of the pipe is dropped under the assumption (ρ A) p  ≪ (ρ A) f which implies that the distributed mass of the pipe is much smaller than that of the conveyed fluid.

Assuming zero initial conditions for the beam and applying the Laplace transformation we obtain the following ordinary differential equation in the Laplace domain

$$\displaystyle{ \mathit{EI}\bar{{w}}^{\;IV } + (\rho A)_{ f}{v}^{2}\bar{{w}}^{\;II} + 2v(\rho A)_{ f}p\bar{{w}}^{\;I} + (\rho A)_{ f}{p}^{2}\bar{w} = 0\;. }$$
(16)

The eigenvalues λ n , n = 1, 2, 3, 4 are now the solutions of the equation

$$\displaystyle{{ \lambda }^{4} {+\beta }^{2}{\left (2\lambda \sqrt{\eta } +\beta p\right )}^{2} = 0\;,\quad \eta = \frac{{\beta }^{2}{v}^{2}} {4} \;,\quad \beta = \root{4}\of{\frac{(\rho A)_{f}} {\mathit{EI}} \:} > 0\;. }$$
(17)

Repeating the derivation of the second part of the paper we arrive at the following equation for the Laplace transform of the displacement y

$$\displaystyle{{ \mathit{mp}}^{2}\bar{y}(p) + 4{\mathit{EI}\beta }^{3}{p}^{3/2}\bar{w}(0,p) + p\left [b - (\rho A)_{ f}v\right ]\bar{w}(0,p) + c\bar{y}(p) = f(p) }$$
(18)

which corresponds to the following ordinary differential equation with a fractional derivative of order \(3/2\)

$$\displaystyle{ m\dfrac{\mathrm{{d}}^{2}y} {\mathrm{d}{t}^{2}} + 4{\mathit{EI}\beta }^{3}\dfrac{\mathrm{{d}}^{3/2}y} {\mathrm{d}{t}^{3/2}} + \left [b - (\rho A)_{f}v\right ]\dfrac{\mathrm{{d}}^{}y} {\mathrm{d}{t}^{}} + \mathit{cy} = f(t)\;. }$$
(19)

This equation governs the motion of the pipe suspension.

4 Eigenvector Expansion Method for Solving Differential Equation with Fractional Derivative

Equations (10)–(12), (19) are ordinary differential equations of second order with the derivatives of the order \(1/2\) or \(3/2\). We take Eq. (19) in the case f(t) = 0 and solve it by means of the eigenvector expansion method suggested in [1] for differential equations with fractional derivatives. To this end, we introduce a non-dimensional time τ = kt, \(k = \sqrt{c/m}\) and two non-dimensional system parameters

$$\displaystyle{ \delta = 2 \frac{{\mathit{EI}\beta }^{3}} {\:m\sqrt{k}\:}\;,\quad \epsilon = \frac{\:b - (\rho A)_{f}v\:} {mk} }$$
(20)

Then we can set Eq. (19) in the following form

$$\displaystyle{ {D}^{2}y + 4\delta {D}^{3/2}y +\varepsilon \mathit{Dy} + y = 0\;,\quad D = \dfrac{\mathrm{{d}}^{}} {\mathrm{d}{\tau }^{}} }$$
(21)

This equation can be represented in the normal form of four semi-differential equations by means of the substitution

$$\displaystyle{ z_{1} = {D}^{3/2}y(t)\;,\quad z_{ 2} = Dy(t)\;,\quad z_{3} = {D}^{1/2}y(t)\;,\quad z_{ 4} = y(t) }$$
(22)

which allow us to rewrite the latter equation in the matrix form

$$\displaystyle{\{\mathbf{A}\}{D}^{1/2}\{\mathbf{z}\} =\{ \mathbf{B}\}\{\mathbf{z}\}}$$

where {z} denotes the column composed of z n , n = 1, 2, 3, 4 in Eq. (22). Applying the standard methods of linear algebra yields the eigenvectors {Ψ} and eigenvalues λ j

$$\displaystyle{ \{\mathbf{A}\}\{\varPsi \}_{j} =\lambda _{j}\{\mathbf{B}\}\{\varPsi \}_{j} }$$
(23)

where the eigenvectors are orthonormalized, i.e.

$$\displaystyle{ \{\varPsi \}_{i}^{T}\{\mathbf{B}\}\{\varPsi \}_{ j} =\delta _{\mathit{ij}}\;,\quad \{\mathbf{A}\}\{\varPsi \}_{j} =\lambda _{j}\delta _{\mathit{ij}}\;. }$$
(24)

Let us notice at this place that the eigenvalues λ j of the matrix equation (23) have nothing in common with the eigenvalues of the differential equation (21). Namely the eigenvalues λ j are solutions of equation \({\lambda }^{4} + a\lambda + b = 0\) and are given by

$$\displaystyle{ \lambda _{1} =\bar{\lambda } _{2} = p + \mathit{iq}\;,\quad \lambda _{3,4} = -p \pm is }$$
(25)

where

$$\displaystyle\begin{array}{rcl} & & p = \sqrt{\:\kappa \:}\;,\quad q = \sqrt{\:\kappa + \frac{\delta } {2\sqrt{\kappa }}\:}\;,\quad s = \sqrt{\:\kappa - \frac{\delta } {2\sqrt{\kappa }}\:}\;, \\ & & \qquad \quad \kappa = \frac{{2}^{1/3}} {4} \left [{\left ({\delta }^{2} + \sqrt{{\delta }^{4 } - \frac{16} {27}}\:\right )}^{1/3} +{ \left ({\delta }^{2} -\sqrt{{\delta }^{4 } - \frac{16} {27}}\:\right )}^{1/3}\right ]\quad {}\end{array}$$
(26)

By means of the substitution {z} = {h}{Ψ} where matrix {Ψ} is built from the eigenvectors columns {Ψ} j we arrive at the system of four uncoupled semi-differential equations

$$\displaystyle{ {D}^{1/2}h_{ j} -\lambda _{j}h_{j}(t) = 0\;,\quad j = 1,2,3,4 }$$
(27)

Solving these equations with the help of Laplace transformation, applying the inverse Laplace transformation and satisfying the initial conditions, we obtain the sought-for result. We refer the reader to [1] for detail.

Obtaining a closed form solution assumes the well-known property of the Laplace transformation, namely the Laplace transform L[…] of a fractional derivative of order α of function \(\varphi (t)\) is as follows

$$\displaystyle{ L\big[{D}^{\alpha }\varphi (t)\big] = {p}^{\alpha }L\big[\varphi (t)\big] - C }$$
(28)

It follows from the formal definition of a fractional derivative of order α which is given by

$$\displaystyle{ {D}^{\alpha }\left \{\varphi (t)\right \} = \dfrac{\mathrm{{d}}^{}} {\mathrm{d}{t}^{}}\left \{ \frac{1} {\varGamma (1-\alpha )}\int \limits _{0}^{t}{(t-\tau )}^{-\alpha }\varphi (t)\:d\tau \right \} }$$
(29)

see [2]. Here C is the constant determined by the following condition

$$\displaystyle{ C = {D}^{\alpha -1}\varphi (t)\Bigr \rvert_{ t=0} }$$
(30)

It is worth mentioning that the value of C is not necessarily equal to zero even for the zero initial conditions for the system. There exists a seeming discrepancy between the number of initial conditions in the system (two initial conditions in the initial-value problem) and the number of the integration constants in the system (27) of four uncoupled semi-differential equations (four integration constants). This discrepancy is easily removed since the general expressions for the displacement and velocity contains some the functions which are unbounded at t → 0. The requirement that these functions must vanish provide us with two additional conditions, see [1] for detail.

5 Critical Velocity of the Fluid in the Pipe

We now proceed to analysis of stability of the suspension. Numerical analysis of free vibration of the pipe, i.e. under the assumption f(t) = 0, shows that the stability border is described by the condition \(\varepsilon =\delta\). Since parameter \(\varepsilon\) depends on the velocity of fluid from this condition one obtains the critical velocity of the flow

$$\displaystyle{ v_{\mathit{crit}} = \frac{b} {\rho A} + \root{4}\of{\;\frac{1} {8} \frac{\mathit{EI}} {\rho A} \frac{c} {m}\;} }$$
(31)

If this value is exceeded, i.e. v > v crit , then the suspension and hence the pipe are unstable.

6 Conclusion

It is shown that some mechanical systems are governed by differential equations with fractional derivatives. The eigenvector expansion method is used for solving the obtained equations with fractional derivatives and deriving closed-form solutions. For example, this closed form solution is appropriate for obtaining simple formula for the critical velocity for systems conveying fluids.