Primary and secondary resonances in pipes conveying fluid with the fractional viscoelastic model

Abstract

Nonlinear forced vibrations of a fractional viscoelastic pipe conveying fluid exposed to the time-dependent excitations is investigated in the present work. Attention is focused in particular on the primary and secondary resonances with the Kelvin–Voigt fractional order constitutive relationship model. The nonlinear geometric partial differential equations due to stretching effect have been expressed by assumptions with Von Karman’s strain-displacement relation and Euler–Bernoulli beam theory. Viscoelastic fractional model for damping and stiffness, and also plug flow model for fluid flow are considered to derive the equation of motion. Based on the Galerkin truncation, the coupled Fluid-Solid interaction nonlinear equation transferred to ordinary differential equations. The method of multiple scales is adopted to analyze steady-state solutions for the primary, superharmonic, and subharmonic resonances. Finally, the detailed parametric studies on the nonlinear dynamic behavior are discussed. Results delineate that the fractional derivative order and the retardation time have significant effects on the oscillation exhibited for different values of flow velocity.

1 Introduction

Pipes conveying fluid are one of the fundamental elements which are extensively encountered in many practical applications such as the oil extraction and transmission, hydraulic oil tubes, lubrication pipes, and military industries. There are numerous particular conditions which pipes conveying fluid will be excited by external excitations. In some cases, these external excitations may lead to dangerous effects and anomalous behaviors. The high amplitude excitations may result in nonlinear behaviors. Specifically, nonlinear resonances may be used in the field of damage detection. In the literature several techniques have been proposed to detect the damage and health monitoring, using nonlinear techniques [1,2,3,4,5,6]. More specifically, structural health monitoring based on the analyzing sub- and superharmonic responses describes and gives a physical interpretation to define parameters suitable for damage detection. There are excellent literature surveys that discuss comprehensively the problem of pipes conveying fluid. Païdoussis [7] thoroughly examined many problems that existed in the dynamics of pipes conveying fluid. The nonlinear dynamics of a pipe conveying fluids subjected to various supports have been studied completely in the past years due to its wide applications [8,9,10,11,12]. The forced vibration of an extensible curved pipe conveying fluid resting on a nonlinear elastic foundation subjected to external excitation was discussed by Ni et al. [13]. They found that the amplitude of the excitation can increase the amplitude of the response and jump frequency significantly, while the damping only has a significant effect on the peak value and the level of nonlinearity only have a significant effect on the jump frequency of steady-state responses, respectively. Steady-state response of a fluid conveying pipe with 3:1 internal resonance in the supercritical regime studied by Mao et al. [14]. They used an analytical method to solve the local responses around the nontrivial equilibrium configuration and investigated global bifurcations by the simulation method. They found the responses change bifurcations in the special region. Liu et al. [15] studied the forced oscillations of a cantilevered pipe conveying fluid under base excitations. They observed for low flow velocity, both the first and second modes primary resonances can be observed when the excitation frequency is either increased or decreased successively. Based on the absolute nodal coordinate formulation (ANC) and transfer matrix method (TMM), an efficient Riccati ANC–TMM was applied to nonlinear dynamics analysis of pipe conveying fluid with large deformations by Rong et al. [16]. Tang et al. [17] employed analytical methods to study the post-buckling behavior and nonlinear dynamics of a fluid conveying pipe made from a functionally graded material. They showed nonlinear frequency of the FGM pipe is increased with the increase of the initial amplitude but is decreased with the increase of the flow velocity and fluid density. Taylor et al. [18] used the methods of nonlinear dynamics including time histories, phase portraits, power spectra, and Poincaré sections to characterize the stability and bifurcation regions of a cantilevered pipe conveying fluid with symmetric constraints at the point of contact.

In recent years, various viscoelastic models have been taken into account to model the time-dependent behavior of materials such as synthetics, rubbers, and polymers. One of the models that perfectly describes the effect of time and loading history on material behavior, is fractional viscoelastic model [19,20,21,22,23]. Considering the accuracy of the viscoelastic fractional model, many researchers had been vastly used this model to describe the dynamic behavior of structures [24,25,26,27,28,29,30,31]. Agrawal [32] presented a general analytical technique for stochastic analysis of a continuous beam whose damping characteristic is described using a fractional derivative model. They emphasized this approach is very similar to the integral derivative model. A non-local two-dimensional foundation model with fractional calculus proposed by Failla et al. [33]. They found the volume forces are non-local and assumed to depend on the relative displacement between the interacting column elements through power-law distance-decaying attenuation functions. Therefore, they obtained the equilibrium equations in fractional differential equations. The stochastic response of fractionally damped beams studied by Di Lorenzo et al. [34]. They examined the influence of the fractional derivative order on the power spectral density response. They observed the damping effect in reducing the power spectral density amplitude for higher values of the fractional derivative order. They also found the fractional derivative term introduces in the system dynamics both effective damping and effective stiffness frequency-dependent terms. Spanos et al. [35] investigated nonlinear random vibrations of beams with fractional derivative elements which the nonlinear term arises from the assumption of moderately large beam displacements. They showed with this model, the beam response can be determined reliably via an optimal statistical linearization procedure. The non-local fractional Euler–Bernoulli beam theory formulated as a generalization of classical Euler–Bernoulli beams, utilizing fractional calculus presented by Sumelka et al. [36]. They showed this new model can give, qualitatively and quantitatively manner, a good approximation of the revealed experimental results. Di Paola et al. [37] proposed finite element method on fractional visco-elastic frames. Freundlich [38] studied the dynamic response of a simply supported viscoelastic beam of the fractional derivative Kelvin–Voigt model which subjected to a force traveling with a constant acceleration. They found in the case of a force moving at a constant velocity, the calculated maximum deflection of the beam decreases with the increasing order of fractional derivative. The dynamics of non-local fractional viscoelastic beams under stochastic agencies was investigated by Alotta et al. [39]. They emphasized due to the non-local terms in the involved coefficient matrices the set of coupled fractional differential equations can not be decoupled with the standard method of modal analysis. For this reason, the dynamic response of the beam studied using a fractional-order state-variable expansion and a complex modal transformation. Liaskos et al. [40] derived implicit analytic solutions for the linear stochastic partial differential beam equation with fractional derivative terms. Freundlich [41] studied transient vibrations of an Euler–Bernoulli cantilever beam with a rigid mass attached at the end and subjected to the base motion. The viscoelastic material properties described with the fractional derivative model of the Kelvin–Voigt type. He observed a decrease in the derivative order causes an increase in the vibration amplitudes of the beam. He also found the actual parameters of the fractional Kelvin–Voigt model should be determined by conducting appropriate experimental investigations. More recently, some scholars studied the dynamic stability of pipes conveying fluid with the fractional viscoelastic model. Sinir and Demir [42] modeled the pipe as an initially straight cable and examined the dynamic behavior of the pipe in the subcritical region. They observed the fractional viscosity, unlike classic viscosity, has even insignificantly changed the natural frequency of the system insignificantly. Tang et al. [43] studied the fractional dynamics of pipes excited by foundation vibration based on the fractional order differential theory. They found for the fractional models, as the foundation vibration amplitude increases, the response amplitude increases, but larger viscoelastic damping and the nonlinear coefficient can reduce the response amplitude. They also observed the ranges of the stable steady-state responses for the polymer-like material pipes, exhibit much larger than those of the previous pipe models. Nonlinear free vibration analysis of a fractional dynamic model for the viscoelastic pipe conveying fluid was examined by Tang et al. [44]. They showed that the amplitudes of the fluid conveying pipe constituted by the fractional viscoelastic material model display much higher than those predicted by the previous models. Javadi et al. [45] analyzed the stability of pipes conveying fluid with the fractional viscoelastic model. They found fractional order and the retardation time change the boundaries of divergence and flutter instabilities. They also showed for some fractional model parameters, increasing the damping may result in decreasing the system stability.

Due to the importance of the nonlinear resonance analysis for health monitoring and damage detection, this paper is devoted to examining nonlinear forced vibrations of a pipe conveying fluid exposed to the time-dependent excitations. Attention is focused on the primary, superharmonic and subharmonic responses with the Kelvin–Voigt fractional damping model. The nonlinear geometric partial differential equations due to stretching effect have been expressed by assumptions with Von Karman’s strain-displacement relation and Euler–Bernoulli beam theory. Viscoelastic fractional model for damping and stiffness, and also plug flow model for fluid flow are also considered to derive the equation of motion. Using the Galerkin method, the governing nonlinear partial differential equations are reduced to nonlinear ordinary differential equations. The perturbation technique is employed to analyze the steady-state solutions for primary and secondary responses. Finally, some numerical test cases have been examined to determine the influences of the fractional derivative order, the retardation time, the flow velocity, the harmonic concentrated force position and physical parameters on the nonlinear dynamic behavior.

2 Governing equation

Fig. 1

Schematic of a simply supported pipe conveying fluid

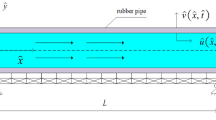
The schematic diagram of a simply supported pipe is shown in Fig. 1. The pipe has length of L, flexural rigidity EI, mass per unit length m and cross-sectional area A. The fluid is incompressible with the steady flow velocity U and mass per unit length M. The Cartesian coordinate system (x-z) is established where the components of u and w stand for the longitudinal and transverse displacements, respectively. As regards, the fractional viscoelastic model describes realistically dependence of response on deformation history and time-independent elastic response. The relationship between stress ($\hat{\sigma }$) and strain ($\hat{\varepsilon }$) of the fractional viscoelastic model can be expressed as:

$$\begin{aligned} \hat{\sigma } = C(\hat{\varepsilon } + \eta D_{}^\alpha \hat{\varepsilon } ) \end{aligned}$$

(1)

where $C$ , $\eta$ and $D_{}^\alpha$ are the elastic constitutive matrix, the retardation time and Caputo fractional operator respectively. The Caputo fractional operator is defined as follows:

$$\begin{aligned} D^{\alpha } f(t)= {\left\{ \begin{array}{ll} \frac{1}{\Gamma (1-\alpha )} \frac{\, \mathrm {d}}{\, \mathrm {d}t}\int _{0}^{t} \frac{1}{(t-\tau )^{\alpha }}f(\tau ) \, \mathrm {d}\tau &{} 0< \alpha <1, \\ \\ \tfrac{\, \mathrm {d}}{\, \mathrm {d}t}f(t) &{} \alpha = 1, \\ \end{array}\right. } \end{aligned}$$

(2)

which $\Gamma (\alpha )$ is the Gamma function and $\alpha$ is the order of the time fractional derivative. Newton’s second law can be used in the lateral direction for two elements of the pipe and the fluid. The wall normal reaction ($F_{z}$) force is imposed on the fluid element. The equation can be written as follows:

$$\begin{aligned} - {F_z} = M{a_{fz}} \end{aligned}$$

(3)

where $a_{fz}$ is the acceleration of the fluid element in the lateral direction. Assuming the plug flow model for the fluid flow, the acceleration of the fluid element can be written as:

$$\begin{aligned} {a_{fz}} = \frac{{{\partial ^2}w}}{{\partial {t^2}}} + 2U\frac{{{\partial ^2}w}}{{\partial x\partial t}} + {U^2}\frac{{{\partial ^2}w}}{{\partial {x^2}}} \end{aligned}$$

(4)

Similarly, for the pipe solid element the Newton’s second law can be expressed as:

$$\begin{aligned} \frac{{\partial {\tilde{Q}}}}{{\partial x}} + \frac{\partial }{{\partial x}}\left( T\frac{{\partial w}}{{\partial x}}\right) + {F_z} + F(x,t) = m{a_{pz}} \end{aligned}$$

(5)

where $F(x, t)$ and ${\tilde{Q}}(x,t)$ are the harmonic concentrated force and internal shear forces respectively. $T$ is the initial tension in the pipe which can be generated when the pipe is constrained in the axial direction. This is dependent on the difference between the pipe length and the distance between axial supports and in practical applications can be measured using strain gauges. Due to mid-plane stretching, using Von-Karman’s strain-displacement relation and assuming weak nonlinearities, ${\tilde{Q}}(x,t)$ for a simply supported Euler–Bernoulli beam is given by [46]:

$$\begin{aligned} \begin{aligned} {\tilde{Q}}(x,t)&= \frac{{\partial \tilde{\textit{M}}}}{{\partial x}} + N(x,t)\frac{{\partial w}}{{\partial x}}\\&= - \left( E + {E^*}\frac{\partial }{{\partial t}}\right) I\frac{{{\partial ^3}w}}{{\partial {x^3}}} + \frac{{EA}}{{2L}}\frac{{\partial w}}{{\partial x}}\int \limits _0^L {{{\left( {\frac{{\partial w}}{{\partial x}}} \right) }^2}dx} \end{aligned} \end{aligned}$$

(6)

which ${\tilde{M}}(x,t)$ and N(x, t) are stress resultants which can be obtained as

$$\begin{aligned} N(x,t)= & {} \int \limits _A^{} {{\widehat{\sigma }} \mathrm{{d}}A} = \frac{{EA}}{L}\int \limits _0^L {{{\left( {\frac{{\partial w}}{{\partial x}}} \right) }^2}} \mathrm{{d}}x \end{aligned}$$

(7)

$$\begin{aligned} M(x,t)= & {} \int \limits _A^{} {{\widehat{\sigma }} z\mathrm{{ d}}A = } \left( {E + {E^*}\frac{\partial }{{\partial t}}} \right) \int \limits _A^{} {z\mathrm{{ d}}A} - \left( {E + {E^*}\frac{\partial }{{\partial t}}} \right) \frac{{{\partial ^2}w}}{{\partial {x^2}}}\int \limits _A^{} {{z^2}\mathrm{{ d}}A} \nonumber \\= & {} - \left( {E + {E^*}\frac{\partial }{{\partial t}}} \right) I\frac{{{\partial ^2}w}}{{\partial {x^2}}} \end{aligned}$$

(8)

Because the x-axis crosses into the centroid of the cross-section of the pipe, $\int \limits _A^{} {\mathrm{{d}}A} = 0$ and $I = \int \limits _A^{} {{z^2}\mathrm{{ d}}A}$.

The pipe has internal dissipation that E* is the coefficient of Kelvin–Voigt damping model in material. Assuming T and U are constants in the pipe longitudinal direction and substituting Eq. (6) in Eq. (5), the nonlinearity equation of motion in the lateral direction can be derived as:

$$\begin{aligned}&\left( {E + {E^*}\frac{{{\partial ^\alpha }}}{{\partial t^\alpha }}} \right) I\frac{{{\partial ^4}w}}{{\partial {x^4}}} + M\left( {\frac{{{\partial ^2}w}}{{\partial {t^2}}} + 2U\frac{{{\partial ^2}w}}{{\partial x\partial t}} + {U^2}\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right) \nonumber \\&\quad + m\frac{{{\partial ^2}w}}{{\partial {t^2}}} - {T}\frac{{{\partial ^2}w}}{{\partial {x^2}}} - \frac{{EA}}{{2L}}\frac{{{\partial ^2}w}}{{\partial {x^2}}}\int \limits _0^L {{{\left( {\frac{{\partial w}}{{\partial x}}} \right) }^2}dx} = F(x,t) \end{aligned}$$

(9)

Furthermore, for simplicity of the parametric studies, the following dimensionless variables are defined:

$$\begin{aligned} \begin{aligned} \xi&=\frac{x}{L},\quad \lambda = \frac{w}{L},\quad \tau = \frac{t}{L}{\left( {\frac{{T}}{m}} \right) ^{1/2}},\quad u = U{\left( {\frac{M}{{{T}L}}} \right) ^{1/2}},\quad \varepsilon \chi = \frac{{EA}}{{T}},\quad \\ \beta&= \frac{M}{{M + m}},\quad \gamma = \frac{{EI}}{{{T}{L^2}}},\quad \eta = \frac{{{E^*}I}}{{{T}{L^2}}}{\left( {\frac{{T}}{{M{L^2}}}} \right) ^{\alpha /2}},\quad {{\tilde{F}} = F\left( {\frac{{mL}}{{M\beta {T}}}} \right) } \end{aligned} \end{aligned}$$

(10)

By substituting Eq. (10) into Eq. (9), the dimensionless form of equation can be obtained as:

$$\begin{aligned}&\frac{{{\partial ^2}\lambda }}{{\partial {\tau ^2}}} + \beta \left[ \gamma \frac{{{\partial ^4}\lambda }}{{\partial {\xi ^4}}} +\, \eta \frac{{{\partial ^\alpha }}}{{\partial {\tau ^\alpha }}}\left( \frac{{{\partial ^4}\lambda }}{{\partial {\xi ^4}}}\right) \right. \nonumber \\&\quad \left. +\,2u\frac{{{\partial ^2}\lambda }}{{\partial \tau \partial \xi }} + \frac{{{\partial ^2}\lambda }}{{\partial {\xi ^2}}}\left( {u^2} - 1 - \frac{1}{2}\varepsilon \chi \int \limits _0^1 {{{\left( \frac{{\partial \lambda }}{{\partial \xi }}\right) }^2}} d\xi \right) \right] = {\tilde{F}}(\xi ,\tau ) \end{aligned}$$

(11)

where associated boundary conditions are:

$$\begin{aligned} \lambda (0,\tau ) = \lambda (1,\tau ) = 0,\begin{array}{*{20}{c}} {}&{} \end{array}\frac{{{\partial ^2}\lambda (0,\tau )}}{{\partial {\xi ^2}}} = \frac{{{\partial ^2}\lambda (1,\tau )}}{{\partial {\xi ^2}}} = 0 \end{aligned}$$

(12)

The solutions of Eq. (11) can be written in the following modal expansion as:

$$\begin{aligned} \lambda (\tau ,\xi ) = \sum \limits _{n = 1}^\infty {{\psi _n}(\tau )} {\phi _n}(\xi ) \end{aligned}$$

(13)

which ${\psi _n}(\tau )$ and ${\phi _n}(\xi )$ are generalized coordinates and the mode shapes of the simply supported pipe, respectively. For the nonlinear forced vibrations, when the excitation frequency is equal to natural frequencies, primary resonance with limited amplitude is occurs. Whereas when the excitation frequency is a distinct multiplier of natural frequencies, subharmonic or superharmonic resonances may occur.

2.1 Primary resonance

To analyze the primary resonance, a concentrated excitation with small amplitude in position $\xi = {\xi _0}$ is applied. The external force subjected to the pipe conveying fluid is given by:

$$\begin{aligned} {\tilde{F}}(\xi ,\tau ) = \varepsilon {\bar{F}}\cos (\Omega \tau )\delta (\xi - {\xi _0}) \end{aligned}$$

(14)

which $\varepsilon$, $\Omega$, $\delta$ and ${\bar{F}}$ are the artificially introduced perturbation parameter, frequency of external, Dirac function and amplitude of force respectively. By considering the first two modes which lead to accurate and converged result [7] and substituting Eq. (14) into Eq. (11) and applying the Galerkin method, the following equations are obtained:

$$\begin{aligned}&{\ddot{\psi }_1}(\tau ) + {c_{11}}{\psi _1}(\tau ) + {c_{12}}\psi _1^3(\tau ) + {c_{13}}D_{}^\alpha {\psi _1}(\tau ) + {c_{14}}{\psi _1}(\tau )\psi _2^2(\tau ) + {c_{15}}{\dot{\psi } _2}(\tau ) = {f_1} \end{aligned}$$

(15)

$$\begin{aligned}&{\ddot{\psi } _2}(\tau ) + {c_{21}}{\psi _2}(\tau ) + {c_{22}}\psi _2^3(\tau ) + {c_{23}}D_{}^\alpha {\psi _2}(\tau ) + {c_{24}}\psi _1^2(\tau ){\psi _2}(\tau ) + {c_{25}}{\dot{\psi } _1}(\tau ) = {f_2} \end{aligned}$$

(16)

where the constant coefficients can be expressed as:

$${c_{j1}} = \beta \int\limits_0^1 {\left\{ {\sum\limits_{m = 1}^{mm} {[\gamma \phi _m^{(4)}(\xi )} + \left( {{u^2} - 1} \right){{\phi ''}_m}(\xi )]} \right\}{\phi _j}} (\xi ){\rm{d}}\xi {\rm{ }}$$

(17)

$${c_{j2}} = - \frac{1}{2}\varepsilon \chi \beta \int\limits_0^1 {\left\{ {\sum\limits_{m = 1}^{mm} {{{\phi ''}_m}(\xi )\int\limits_0^1 {{{\left( {{{\phi '}_m}(\xi )} \right)}^2}} {\rm{d}}\xi } } \right\}{\phi _j}} (\xi ){\rm{d}}\xi$$

(18)

$${c_{j3}} = \beta \eta \int\limits_0^1 {\left\{ {\sum\limits_{m = 1}^{mm} {\phi _m^{(4)}{\rm{(}}\xi {\rm{)}}} } \right\}{\phi _j}} {\rm{(}}\xi {\rm{)d}}\xi$$

(19)

$${c_{j4}} = - \frac{1}{2}\varepsilon \chi \beta \int\limits_0^1 {\sum\limits_{m = 1}^{mm} {\left\{ {{{\phi ''}_m}(\xi )\int\limits_0^1 {{{\left( {{{\phi '}_m}(\xi )} \right)}^2}} {\rm{d}}\xi } \right\}} {\phi _j}} {\rm{(}}\xi {\rm{)d}}\xi$$

(20)

$${c_{j5}} = 2\beta u\int\limits_0^1 {\left\{ {\sum\limits_{m = 1}^{mm} {{{\phi '}_m}{\rm{(}}\xi {\rm{) }}} } \right\}} {\phi _j}{\rm{(}}\xi {\rm{)d}}\xi$$

(21)

$${f_j} = \int\limits_0^1 {\varepsilon \bar F\cos (\Omega \tau ){\phi _j}(\xi )\delta (\xi - {\xi _0}){\rm{d}}\xi }$$

(22)

where j = 1…2 and mm = 2. In the case of primary resonance, the excitation frequency can be taken as:

$$\begin{aligned} \Omega \simeq \omega _n^{} + {\sigma _n}\varepsilon \end{aligned}$$

(23)

where ${\sigma _n}$ is the detuning parameter that quantifies the deviation of $\Omega$ from ${\omega _n}$. Assuming the weak nonlinearity, the method of multiple scales is applied directly to nonlinear ordinary differential equations to seek approximate solutions. By considering the first order expansion, solutions are assumed to be of the following form:

$$\begin{aligned} {\psi _1}(\tau ,\varepsilon )& = {} {\psi _{01}}({T_0},{T_1}) + \varepsilon {\psi _{11}}({T_0},{T_1}) \end{aligned}$$

(24)

$$\begin{aligned} {\psi _2}(\tau ,\varepsilon )& = {} {\psi _{02}}({T_0},{T_1}) + \varepsilon {\psi _{12}}({T_0},{T_1}) \end{aligned}$$

(25)

which ${T_0} = \tau$ and ${T_1} = \varepsilon \tau$ are fast and slow scale times respectively. The time derivatives are defined as fallow:

$$\begin{aligned} \frac{d}{{d\tau }}&= {} {D_0} + \varepsilon {D_1} \end{aligned}$$

(26)

$$\begin{aligned} \frac{{{d^2}}}{{d{\tau ^2}}}&= {} {\left( {{D_0} + \varepsilon {D_1}} \right) ^2} = {D_0}^2 + \varepsilon 2{D_0}{D_1} \end{aligned}$$

(27)

$$\begin{aligned} \frac{{{d^\alpha }}}{{d{\tau ^\alpha }}}&= {} {\left( {{D_0} + \varepsilon {D_1}} \right) ^\alpha } = {D_0}^\alpha + \varepsilon D_0^{\alpha - 1}{D_1} \end{aligned}$$

(28)

which ${D_n} = \frac{\partial }{{\partial {T_n}}}$ and the parameter $D_{}^\alpha ({e^{i{\omega _n}\tau }})$ is obtained by [46]

$$\begin{aligned} D_{}^\alpha ({e^{i{\omega _n}\tau }}) = {(i{\omega _n})^\alpha }{e^{i{\omega _n}\tau }} \end{aligned}$$

(29)

Substituting Eqs. (24) and (25) in Eqs. (15) and (16) and after the separation of zeroth- and first-order problems of the multiple-scales perturbation series yield: The order ${\varepsilon ^0}$ :

$$\begin{aligned}&{D_0}^2{\psi _{01}}({T_0},{T_1}) + {c_{11}}{\psi _{01}}({T_0},{T_1}) = 0 \end{aligned}$$

(30)

$$\begin{aligned}&{D_0}^2{\psi _{02}}({T_0},{T_1}) + {c_{21}}{\psi _{02}}({T_0},{T_1}) = 0 \end{aligned}$$

(31)

At order ${\varepsilon ^0}$, the general solution for Eqs. (30) and (31) can be expressed as:

$$\begin{aligned} {\psi _{01}}({T_0},{T_1}) = {A_1}({T_1}){e^{i{\omega _1}{T_0}}} + {{\bar{A}}_1}({T_1}){e^{ - i{\omega _1}{T_0}}} \end{aligned}$$

(32)

$$\begin{aligned} {\psi _{02}}({T_0},{T_1}) = {A_2}({T_1}){e^{i{\omega _2}{T_0}}} + {{\bar{A}}_2}({T_1}){e^{ - i{\omega _2}{T_0}}} \end{aligned}$$

(33)

For the ${\varepsilon ^1}$ order:

$$\begin{aligned}&{D_0}^2{\psi _{11}} + \omega _1^2{\psi _{11}}\nonumber \\&\quad = - 2[ {(i{\omega _1}){{A'}_1}({T_1}){e^{i{\omega _1}{T_0}}} + ( - i{\omega _1}){{{\bar{A}}'}_1}({T_1}){e^{ - i{\omega _1}{T_0}}}} ]\nonumber \\&\quad - {c_{12}}\left[ A_1^3({T_1}){e^{3i{\omega _1}{T_0}}} + {\bar{A}}_1^3({T_1}){e^{ - 3i{\omega _1}{T_0}}} + 3A_1^2({T_1}){{{\bar{A}}}_1}({T_1}){e^{i{\omega _1}{T_0}}} \right. \nonumber \\&\quad \left. + 3{A_1}({T_1}){{{\bar{A}}}_1}^2({T_1}){e^{ - i{\omega _1}{T_0}}} \right] \nonumber \\&\quad - {c_{13}}\left[ {{{(i{\omega _1})}^\alpha }A({T_1}){e^{i{\omega _1}{T_0}}} + {{(i{\omega _1})}^\alpha }{\bar{A}}({T_1}){e^{ - i{\omega _1}{T_0}}}} \right] \nonumber \\&\quad - {c_{14}}\left[ {{A_1}({T_1}){e^{i{\omega _1}{T_0}}} + {{{\bar{A}}}_1}({T_1}){e^{ - i{\omega _1}{T_0}}}} \right] \nonumber \\&\quad \left[ {A_2^2({T_1}){e^{2i{\omega _2}{T_0}}} + {\bar{A}}_2^2({T_1}){e^{ - 2i{\omega _2}{T_0}}} + 2{A_2}({T_1}){{{\bar{A}}}_2}({T_1})} \right] \nonumber \\&\quad - {c_{15}}\left[ {(i{\omega _2}){{A'}_2}({T_1}){e^{i{\omega _2}{T_0}}} + ( - i{\omega _2}){{{\bar{A}}'}_2}({T_1}){e^{ - i{\omega _2}{T_0}}}} \right] \nonumber \\&\quad + \frac{{{f_1}}}{2}({e^{i\Omega t}} + {e^{ - i\Omega t}}) \end{aligned}$$

(34)

$$\begin{aligned}&{D_0}^2{\psi _{21}} + \omega _2^2{\psi _{21}} \nonumber \\&\quad = - 2\left[ {(i{\omega _2}){{A'}_2}({T_1}){e^{i{\omega _2}{T_0}}} + ( - i{\omega _2}){{{\bar{A}}'}_2}({T_1}){e^{ - i{\omega _2}{T_0}}}} \right] \nonumber \\&\quad - {c_{22}}\left[ A_2^3({T_1}){e^{3i{\omega _2}{T_0}}} + {\bar{A}}_2^3({T_1}){e^{ - 3i{\omega _2}{T_0}}}\right. \nonumber \\&\quad \left. +\, 3A_2^2({T_1}){{{\bar{A}}}_2}({T_1}){e^{i{\omega _2}{T_0}}} +\,3{A_2}({T_1}){{{\bar{A}}}_2}^2({T_1}){e^{ - i{\omega _2}{T_0}}} \right] \nonumber \\&\quad - {c_{23}}\left[ {{{(i{\omega _2})}^\alpha }{A_2}({T_1}){e^{i{\omega _2}{T_0}}} + {{(i{\omega _2})}^\alpha }{{{\bar{A}}}_2}({T_1}){e^{ - i{\omega _2}{T_0}}}} \right] \nonumber \\&\quad - {c_{24}}\left[ {{A_2}({T_1}){e^{i{\omega _2}{T_0}}} + {{{\bar{A}}}_2}({T_1}){e^{ - i{\omega _2}{T_0}}}} \right] \left[ A_1^2({T_1}){e^{2i{\omega _1}{T_0}}}\right. \nonumber \\&\quad \left. + {\bar{A}}_1^2({T_1}){e^{ - 2i{\omega _1}{T_0}}} + 2{A_1}({T_1}){{{\bar{A}}}_1}({T_1}) \right] \nonumber \\&\quad - {c_{25}}\left[ {(i{\omega _1}){{A'}_1}({T_1}){e^{i{\omega _1}{T_0}}} + ( - i{\omega _1}){{{\bar{A}}'}_1}({T_1}){e^{ - i{\omega _1}{T_0}}}} \right] \nonumber \\&\quad + \frac{{{f_2}}}{2}({e^{i\Omega t}} + {e^{ - i\Omega t}}) \end{aligned}$$

(35)

Eliminating the secular and small-divisor terms yield the complex-valued modulation equation:

$$\begin{aligned}&\left[ {(2i{\omega _1}){{A'}_1}({T_1})} \right] + {c_{12}}\left[ {3A_1^2({T_1}){{{\bar{A}}}_1}({T_1})} \right] + {c_{13}}\left[ {{{(i{\omega _1})}^\alpha }A({T_1})} \right] \nonumber \\&\quad + \frac{{{f_1}}}{2}({e^{i{\sigma _1}{T_1}}}) + {c_{14}}\left[ {2{A_2}({T_1}){{{\bar{A}}}_2}({T_1}){A_1}({T_1})} \right] = 0 \end{aligned}$$

(36)

$$\begin{aligned}&\left[ {(2i{\omega _2}){{A'}_2}({T_1})} \right] + {c_{22}}\left[ {3A_2^2({T_1}){{{\bar{A}}}_2}({T_1})} \right] + {c_{23}}\left[ {{{(i{\omega _2})}^\alpha }{A_2}({T_1})} \right] \nonumber \\&\quad + \frac{{{f_2}}}{2}({e^{i{\sigma _1}{T_1}}}) + {c_{24}}\left[ {2{A_1}({T_1}){{{\bar{A}}}_1}({T_1}){A_2}({T_1})} \right] = 0 \end{aligned}$$

(37)

Assuming that the amplitude ${A_n}$ can be written as the polar form:

$$\begin{aligned} {A_n}({T_1}) = \frac{1}{2}{a_n}({T_1}){e^{i{Q_n}({T_1})}} \end{aligned}$$

(38)

Substituting ${A_1}({T_1})$ and ${A_2}({T_1})$ in Eqs. (36) and (37) results in:

$$\begin{aligned}&\left[ {(i{\omega _1})({{a'}_1}({T_1}) + i{a_1}{{Q'}_1}({T_1}))} \right] {e^{i{Q_1}({T_1})}} + {c_{12}}\frac{{3a_1^3({T_1})}}{8}{e^{i{Q_1}({T_1})}} + {c_{13}}{(i{\omega _1})^\alpha }\frac{1}{2}{a_1}({T_1}){e^{i{Q_1}({T_1})}}\nonumber \\&\quad + \frac{{{f_1}}}{2}{e^{i{\sigma _1}{T_1}}} + {c_{14}}\frac{1}{4}a_1^{}({T_1}){e^{i{Q_1}({T_1})}}a_2^2({T_1}) = 0\end{aligned}$$

(39)

$$\begin{aligned}&\left[ {(i{\omega _2})({{a'}_2}({T_1}) + i{a_2}{{Q'}_2}({T_1}))} \right] {e^{i{Q_2}({T_1})}} + {c_{22}}\frac{{3a_2^3({T_1})}}{8}{e^{i{Q_2}({T_1})}} + {c_{23}}{(i{\omega _2})^\alpha }\frac{1}{2}{a_2}({T_1}){e^{i{Q_2}({T_1})}}\nonumber \\&\quad + \frac{{{f_2}}}{2}{e^{i{\sigma _2}{T_1}}} + {c_{24}}\frac{1}{4}a_2^{}({T_1}){e^{i{Q_2}({T_1})}}a_1^2({T_1}) = 0 \end{aligned}$$

(40)

Equations (39) and (40) can be transferred to an autonomous system by eliminating term ${T_1}$

$$\begin{aligned} {\gamma _n}({T_1}) = {\sigma _n}{T_1} - {Q_n}({T_1}) \end{aligned}$$

(41)

Considering steady-state motion in this condition one can write:

$$\begin{aligned}&\frac{d}{{d{T_1}}}{a_n}({T_1}) = 0 \end{aligned}$$

(42)

$$\begin{aligned}&\frac{d}{{d{T_1}}}{\gamma _n}({T_1}) = 0 \end{aligned}$$

(43)

For steady-state motion of the first mode, when ${T_1} \rightarrow \infty$ the amplitude of ${a_2}({T_1}) = 0$ ,so Eq. (39) can be simplified as:

$$\begin{aligned} - {\omega _1}a_1^{}({T_1}){\sigma _1} + {c_{12}}\frac{{3a_1^3{{({T_1})}^{}}}}{8} + {c_{13}}{(i{\omega _1})^\alpha }\frac{1}{2}a_1^{}({T_1}) + \frac{1}{2}{f_1}{e^{i{\gamma _1}}} = 0 \end{aligned}$$

(44)

Similarly, steady-state motion of the second mode, when ${T_1} \rightarrow \infty$ the amplitude of ${a_1}({T_1}) = 0$, so Eq. (40) yields to:

$$\begin{aligned} - {\omega _2}a_2^{}({T_1}){\sigma _2} + {c_{22}}\frac{{3a_2^3{{({T_1})}^{}}}}{8} + {c_{23}}{(i{\omega _2})^\alpha }\frac{1}{2}a_2^{}({T_1}) + \frac{1}{2}{f_{2}}{e^{i{\gamma _2}}} = 0 \end{aligned}$$

(45)

By separating the real and imaginary parts, eliminating $\gamma$ and squaring, two equations can be obtained as follows:

$$\begin{aligned}&{\left( {{\sigma _1}{\omega _1}{a_1}({T_1}) - {c_{12}}\frac{{3a_1^3({T_1})}}{8} - \frac{{{c_{13}}{a_1}({T_1}){{({\omega _1})}^\alpha }}}{2}{{\mathrm{Re}}} {{(i)}^\alpha }} \right) ^2} + {\left( {\frac{{{c_{13}}{a_1}({T_1}){{({\omega _1})}^\alpha }}}{2}{\mathop {\mathrm{Im}}\nolimits } {{(i)}^\alpha }} \right) ^2} = f_1^2\end{aligned}$$

(46)

$$\begin{aligned}&{\left( {{\sigma _2}{\omega _2}{a_2}({T_1}) - \frac{{{c_{22}}3a_2^3({T_1})}}{8} - \frac{{{c_{23}}{a_2}({T_1}){{({\omega _2})}^\alpha }}}{2}{{\mathrm{Re}}} {{(i)}^\alpha }} \right) ^2} + {\left( {\frac{{{c_{23}}{a_2}({T_1}){{({\omega _2})}^\alpha }}}{2}{\mathop {\mathrm{Im}}\nolimits } {{(i)}^\alpha }} \right) ^2} = f_2^2 \end{aligned}$$

(47)

2.2 Superharmonic resonance

As already mentioned, in Eqs. (15) and (16) the nonlinear term ${x^3}$ due to stretching effect induce superharmonic (3:1) and subharmonic (1:3) resonances. In the following of examination of secondary resonance, an excitation with large amplitude is considered and also the excitation frequency is away from the natural frequency. For the superharmonic resonances the excitation frequency can be taken as:

$$\begin{aligned} 3\Omega \simeq \omega _n^{} + {\sigma _n}\varepsilon \end{aligned}$$

(48)

Again, the procedure of multiple scales method is applied and equating coefficients of ${\varepsilon ^0}$ and ${\varepsilon ^1}$ yields: The order ${\varepsilon ^0}$:

$$\begin{aligned} {D_0}^2{\psi _{01}}({T_0},{T_1}) + {c_{11}}{\psi _{01}}({T_0},{T_1})= & {} {f_1}\cos (\Omega t) \end{aligned}$$

(49)

$$\begin{aligned} {D_0}^2{\psi _{02}}({T_0},{T_1}) + {c_{21}}{\psi _{02}}({T_0},{T_1})= & {} {f_2}\cos (\Omega t) \end{aligned}$$

(50)

which the general solutions Eqs. (49) and (50) can be expressed as:

$$\begin{aligned} {\psi _{01}}({T_0},{T_1})\,= \,& {} {A_1}({T_1}){e^{i{\omega _1}{T_0}}} + {{\bar{A}}_1}({T_1}){e^{ - i{\omega _1}{T_0}}} + {\Lambda _1}({e^{i\Omega t}} + {e^{ - i\Omega t}}) \end{aligned}$$

(51)

$$\begin{aligned} {\psi _{02}}({T_0},{T_1})\,=\, & {} {A_2}({T_1}){e^{i{\omega _2}{T_0}}} + {{\bar{A}}_2}({T_1}){e^{ - i{\omega _2}{T_0}}} + {\Lambda _2}({e^{i\Omega t}} + {e^{ - i\Omega t}}) \end{aligned}$$

(52)

The terms of ${\Lambda _1}$ and ${\Lambda _2}$ can be obtained as:

$$\begin{aligned} {\Lambda _1}= & {} \frac{1}{2}\left( \frac{{{f_1}}}{{{\Omega ^2} - \omega _1^2}}\right) \end{aligned}$$

(53)

$$\begin{aligned} {\Lambda _2}= & {} \frac{1}{2}\left( \frac{{{f_2}}}{{{\Omega ^2} - \omega _2^2}}\right) \end{aligned}$$

(54)

Substituting the general solutions in terms of the order ${\varepsilon ^1}$ and eliminating secular term and small devisors yields:

$$\begin{aligned} (2i{\omega _1}){A'_1}({T_1}) + {c_{12}}\left[ {3A_1^2({T_1}){{{\bar{A}}}_1}({T_1}) + \Lambda _1^3 + 6{A_1}({T_1}){\Lambda ^2}} \right] + {c_{13}}{(i{\omega _1})^\alpha }{A_1}({T_1})= & {} 0 \end{aligned}$$

(55)

$$\begin{aligned} (2i{\omega _2}){A'_2}({T_1}) + {c_{22}}\left[ {3A_2^2({T_1}){{{\bar{A}}}_2}({T_1}) + \Lambda _2^3 + 6{A_2}({T_1})\Lambda _2^2} \right] + {c_{23}}{(i{\omega _2})^\alpha }{A_2}({T_1})= & {} 0 \end{aligned}$$

(56)

Substituting the polar form of ${A_n}({T_1})$, into Eqs. (55) and (56), and separating the real and imaginary, the modulation equations can be obtained as follows:

$$\begin{aligned}&{\left( {\left[ \frac{{3\Lambda _1^2{c_{12}}}}{{{\omega _1}}} - \sigma \right] {a_1}(T) + \frac{{3{c_{12}}a_1^3({T_1})}}{{8{\omega _1}}} + \frac{{{c_{13}}{a_1}({T_1}){{({\omega _1})}^{\alpha - 1}}}}{2}{\mathop {\mathrm{Re}}\nolimits } {{(i)}^\alpha }} \right) ^2}\nonumber \\&\quad + {\left( {\frac{{{c_{13}}{a_1}({T_1}){{({\omega _1})}^{\alpha - 1}}}}{2}{\mathop {\mathrm{Im}}\nolimits } {{(i)}^\alpha }} \right) ^2} = {\left( {\frac{{c_{12}^{}\Lambda _1^3}}{{\omega _1^{}}}} \right) ^2} \end{aligned}$$

(57)

$$\begin{aligned}&{\left( {\left[ \frac{{3\Lambda _2^2{c_{22}}}}{{{\omega _2}}} - {\sigma _2}\right] {a_2}(T) + \frac{{3{c_{22}}a_2^3({T_1})}}{{8{\omega _2}}} + \frac{{{c_{23}}{a_2}({T_1}){{({\omega _2})}^{\alpha - 1}}}}{2}{\mathop {\mathrm{Re}}\nolimits } {{(i)}^\alpha }} \right) ^2}\nonumber \\&\quad + {\left( {\frac{{{c_{23}}{a_2}({T_1}){{({\omega _2})}^{\alpha - 1}}}}{2}{\mathop {\mathrm{Im}}\nolimits } {{(i)}^\alpha }} \right) ^2} = {\left( {\frac{{c_{22}^{}\Lambda _2^3}}{{\omega _2^{}}}} \right) ^2} \end{aligned}$$

(58)

2.3 Subharmonic resonance

Within the range of subharmonic excitation, one will have:

$$\begin{aligned} \Omega \simeq 3\omega _n^{} + {\sigma _n}\varepsilon \end{aligned}$$

(59)

Setting the secular and small divisor terms equal to zero, yields:

$$\begin{aligned}&2i{\omega _1}{{A'}_1}({T_1}) + {c_{12}}\left( {3A_1^2({T_1}){{{\bar{A}}}_1}({T_1}) + 3{\bar{A}}_1^2({T_1}){\Lambda _1}{e^{i{\sigma _1}\varepsilon {T_0}}} + 6{A_1}({T_1})\Lambda _1^2} \right) \nonumber \\&\quad + {c_{13}}{(i{\omega _1})^\alpha }{A_1}({T_1}) = 0 \end{aligned}$$

(60)

$$\begin{aligned}&2i{\omega _2}{{A'}_2}({T_1}) + {c_{22}}\left( {3A_2^2({T_1}){{{\bar{A}}}_2}({T_1}) + 3A_2^2({T_1})\Lambda _2^{}{e^{i{\sigma _2}\varepsilon {T_0}}} + 6A_2^{}({T_1})\Lambda _2^2} \right) \nonumber \\&\quad + {c_{23}}{(i{\omega _2})^\alpha }{A_2}({T_1}) = 0 \end{aligned}$$

(61)

Separating Eqs. (60) and (61) into the real and imaginary parts and transferring to an autonomous system by eliminating term ${T_1}$ results in:

$$\begin{aligned}&{\left( {{\sigma _1} - \frac{{{c_{12}}9\Lambda _1^2}}{{\omega _1^{}}} - {c_{12}}\frac{{9a_1^2({T_1})}}{{8\omega _1^{}}} - \frac{{3{c_{13}}{{(\omega _1^{})}^{\alpha - 1}}}}{2}{\mathrm{Re}} {{\left( i \right) }^\alpha }} \right) ^2}\nonumber \\&\quad + {\left( {\frac{{3{c_{13}}{{(\omega _1^{})}^{\alpha - 1}}}}{2}{{\mathrm{Im}}} {{\left( i \right) }^\alpha }} \right) ^2} = {\left( {\frac{{9\Lambda _1^{}a_1^{}({T_1})}}{{4\omega _1^{}}}} \right) ^2} \end{aligned}$$

(62)

$$\begin{aligned}&{\left( {{\sigma _2} - \frac{{{c_{22}}9\Lambda _2^2}}{{{\omega _2}}} - {c_{22}}\frac{{9a_{^2}^2({T_1})}}{{8{\omega _2}}} - \frac{{3{c_{23}}{{({\omega _2})}^{\alpha - 1}}}}{2}{\mathrm{Re}} {{\left( i \right) }^\alpha }} \right) ^2}\nonumber \\&\quad + {\left( {\frac{{3{c_{23}}{{({\omega _2})}^{\alpha - 1}}}}{2}{{\mathrm{Im}}} {{\left( i \right) }^\alpha }} \right) ^2} = \frac{{81\Lambda _2^2a_2^2({T_1})}}{{16\omega _2^2}} \end{aligned}$$

(63)

3 Numerical results and discussion

In order to prove the validity of the numerical results, comparison study is done and after that, the effects of the fractional derivative order, the retardation time, harmonic concentrated force position and fluid velocity on the nonlinear dynamics are discussed.

3.1 Validation of the present study

To verify the proposed formulation and examine the accuracy of the numerical results, the validation process is performed with results available in the open literature. The comparison study is accomplished between the obtained results of this research and the results reported by Tang et al. [44] which studied the nonlinear free vibration of a fractional dynamic model for the viscoelastic pipe conveying fluid. They obtained the dynamic equation of motions for pipe by employing the Euler–Bernoulli beam theory and generalized Hamilton’s principle. In this reference, the multiple scale method is used to investigate the free vibration of the pipe. The response amplitude of the viscoelastic fractional pipe for the first mode has been depicted in Fig. 2. The characteristics of the system are: $\beta$ = 0.7, u = 1.6, $\varepsilon$ = 0.005 and ${\bar{\eta }}$ = $\gamma$ = $\chi$ = 1 which ${\bar{\eta }} = \eta /\varepsilon$ and initial condition is assumed as ${a_0}$ = 1. As can be seen, a good agreement for different values of $\alpha$ is obtained in this comparison.

Fig. 2

Comparison study of response amplitude versus the time for different values of the fractional order

3.2 Linear analysis

In order to find a better understanding of the physics of the considered problem, linear analysis has been done. In Fig. 3, the dimensionless dampings, and frequencies versus dimensionless flow velocity have been depicted for the viscoelastic model. As you can see, by increasing the dimensionless fluid velocity, divergence will occur for the first and second mode at ${u_{cr1}} \approx 3.3$ and ${u_{cr2}} \approx 6.4$ respectively. The flow velocity which the system experiences instability for the first time is defined as critical velocity. Thus, sub-critical flow velocity for this case is $u < 3.3$. Typically, the pipe at critical flow velocity undergoes a static pitchfork bifurcation and the amplitude of the buckled pipe. Therefore at the rest of the manuscript and in all of the numerical results and evaluations, flow velocity will be considered lower than critical flow velocity ($u < {u_{cr}}$).

Fig. 3

Dimensionless dampings and frequencies versus dimensionless flow velocity for $\alpha$ = $\chi$ = 1, $\beta$ = 0.2, $\varepsilon$ = $\eta$ = 0.005 and $F(x,t) = 0$

3.3 Primary resonance

The effects of the fractional derivative order, the retardation time, the location of the harmonic concentrated force and flow velocity on the primary responses of pipes conveying fluid will be discussed in this subsection. In order to investigate these effects, numerous test cases with assuming $\varepsilon = 0.005$ and $\gamma$ = $\chi$ = 1 are considered.

3.3.1 Effect of the fractional model

Fig. 4

Primary response amplitude for different values of $\alpha$ with ${\xi _0} = 0.5$, ${\bar{\eta }}$ = 1, u = 2, $\beta$ = 0.7, ${\bar{F}}$ = 10 and $\Omega = {\omega _1} + \varepsilon \sigma$

Fig. 5

Primary response amplitude for the first and second modes with ${\xi _0} = 0.25$, $\alpha$ = 0.5, ${\bar{\eta }}$ = 1, u =2, $\beta$ = 0.7 and ${\bar{F}}$ = 10

Figures 4 and 5 show the response amplitude for the condition ${\bar{\eta }}$ = 1, u = 2, ${\bar{F}}$ = 10 and $\beta$ = 0.7. In Fig. 4 the effect of fractional derivative order ($\alpha$) on the response amplitude have been analyzed. The harmonic concentrated force is also applied at ${\xi _0} = 0.5$ and $\Omega$ is close to the first natural frequency. It is found, by decreasing the value of $\alpha$, the peak amplitude increases. This result is expectable, because by decreasing $\alpha$, the fractional viscoelastic model will be close to elastic model without any damping. In Fig. 5 the response amplitude curve are indicated which the excitation frequency is close to the first and second natural frequency. In this case, investigation have been considered for $\alpha$ = 0.5 and ${\xi _0} = 0.25$. In Figs. 6 and 7 which correspond to the ${\bar{\eta }}$ = 1, u = 2, ${\bar{F}}$ = 10 and $\sigma$ = 0.1, the response amplitude versus $\beta$ are represented. In Fig. 6 the effects of $\alpha$ on the behavior of the response amplitude versus $\beta$ for ${\xi _0}$ = 0.5 are depicted. As you can see, by increasing $\beta$, the response amplitude decreases but the rate of decrease in the viscoelastic model is higher. This result can be justified by the fact that increasing $\beta$, the total mass of the system is also increasing which can be led to decreasing the response amplitude. The response amplitude versus $\beta$ when the excitation frequency is close to the first and second natural frequency for $\alpha$ = 0.3 and ${\xi _0} = 0.25$ is presented in Fig. 7. As you can see for both cases, by increasing $\beta$ the response amplitude decreases. Next, to assess the influence of the excitation amplitude on the response amplitude, other test cases have been considered. For these cases, properties are ${\bar{\eta }}$ = 1, u = 2, $\sigma$ = 0.1 and $\beta$ = 0.7. Effect of the excitation amplitude for different values of $\alpha$ has been depicted in Fig. 8 which correspond to ${\xi _0} = 0.5$. As is shown for small fractional derivative orders, the deviation of the system from linear behavior occurs in smaller values of the excitation amplitude. For $\alpha$=0.3 a nonlinear oscillation hysteresis is observed. When ${\bar{F}} < 48$ the system has a single small stable limit cycle oscillation (LCO). For $48< {\bar{F}} < 67$ two LCO can be found and for ${\bar{F}} > 67$ only a large stable LCO can be observed. To clarify the effects of $\eta$ on the response amplitude, another test case has been considered. As illustrated in Fig. 9, by decreasing ${\bar{\eta }}$ the peak response amplitude increases whereas the deviation of response frequency from excitation frequency decreases. It means, increasing damping results in more nonlinearity behavior.

Fig. 6

Primary response amplitude versus $\beta$ for different values of $\alpha$, with ${\xi _0}$ = 0.5, ${\bar{\eta }}$ = 1, u = 2, $\sigma$ = 0.1, ${\bar{F}}$ = 10 and $\Omega = {\omega _1} + \varepsilon \sigma$

Fig. 7

Primary response amplitude versus $\beta$ for the first and second modes with $\alpha$ = 0.3, ${\xi _0} = 0.25$, ${\bar{\eta }}$ = 1, u = 2, $\sigma$ = 0.1 and ${\bar{F}}$ = 10

Fig. 8

Primary response amplitude versus the excitation amplitude for different values of $\alpha$, with ${\xi _0} = 0.5$, ${\bar{\eta }}$ = 1, u = 2, $\sigma$ = 0.1, $\beta$ = 0.7 and $\Omega = {\omega _1} + \varepsilon \sigma$

Fig. 9

Primary response amplitude for different values of ${\bar{\eta }}$, with ${\xi _0}$ = $\alpha$ =0.5, u = 2, $\beta$ = 0.7, ${\bar{F}}$ =10 and $\Omega = {\omega _1} + \varepsilon \sigma$

3.3.2 Effects of flow velocity

Figure 10 represents the response amplitude curve for different values of u. As the flow velocity increases, the response amplitude increases too. As illustrated when the flow velocity reaches to near the critical velocity, the rate of increase is considerable. As stated earlier (see Fig. 3), by increasing the flow velocity, the structural stiffness is decreased which justify the system behavior shown in Fig. 10.

Fig. 10

Primary response amplitude for different values of u with ${\xi _0}$ = $\alpha$ = 0.5, ${\bar{\eta }}$ = 1, $\beta$ = 0.7, ${\bar{F}}$ = 10 and $\Omega = {\omega _1} + \varepsilon \sigma$

3.4 Superharmonic resonance

This subsection deals with the investigation on the effect of the fractional model, the location of the harmonic concentrated force and flow velocity on superharmonic responses.

3.4.1 Effect of the fractional model

Fig. 11

Superharmonic response amplitude for different values of $\alpha$ with ${\xi _0}$ = 0.5, ${\bar{\eta }}$ = 1, u = 3, $\beta$ = 0.7, ${\Lambda _{1}}$ = 1 and $3\Omega = {\omega _1} + \varepsilon \sigma$

Fig. 12

Superharmonic response amplitude for the first and second modes with ${\xi _0}$ = 0.25, $\alpha$ = 0.3, ${\bar{\eta }}$ = 1, u = 3, $\beta$ = 0.7, ${\Lambda _{2}}$ = 1 and ${\Lambda _{1}}$ = $\sqrt{2} /2.$

Fig. 13

Superharmonic response amplitude versus the excitation amplitude for different values of $\alpha$ with ${\xi _0}$ = 0.5, ${\bar{\eta }}$ = 2, $\sigma$ = 0.5, u = 3, $\beta$ = 0.7 and $3\Omega = {\omega _1} + \varepsilon \sigma$

Figures 11 and 12 depict superharmonic response amplitude with for ${\bar{\eta }}$ = 1, u = 3, $\beta$ = 0.7. The effect of $\alpha$ on the response amplitude is demonstrated in Fig. 11 which corresponds to ${\Lambda _1}$ = 1. As you can see, by decreasing the value of $\alpha$, the peak amplitude increases and shifts to the right. It is interesting that with the fractional model, superharmonic response amplitude is considerable in comparison with the conventional viscoelastic model. Figure 12 shows the comparisons between the response amplitude when the excitation is close to one-third of the first and second modes, respectively. In this case, parameters are assumed as: ${\Lambda _1}$ = $\sqrt{2} /2$ , ${\Lambda _2}$ = 1 = 1, $\alpha$ = 0.3 and ${\xi _0}$ = 0.25. It is observed when the excitation frequency is close to one-third of second mode natural frequency, the peak response amplitude and deviation of response frequency are bigger in comparison with the case that the excitation frequency is close to the one-third of the first mode natural frequency. Figure 13 discusses the variation of the response amplitude versus the excitation amplitude for different values of $\alpha$ for ${\xi _0}$ = 0.5, ${\bar{\eta }}$ = 2, u = 3, $\sigma$=0.5, $\beta$ = 0.7 and ${\Lambda _{1}}$ = 1. It is worth noting at the first, the rate of increase of the amplitude for smaller values of $\alpha$ is considerable. Figures 14 and 15 show the superharmonic response amplitude versus $\beta$ with ${\bar{\eta }}$ = 1, u = 2 and $\sigma$ = 0.3. The effects of $\alpha$ on the response amplitude versus $\beta$ has been presented in Fig. 14 which corresponded to ${\Lambda _{1}}$ = 1 and ${\xi _0}$ = 0.5. As illustrated in this graph, for larger values of $\beta$ the rate of increase for fractional model is higher than viscoelastic model. To analyze the effect of $\beta$ on the behavior of the system when the excitation frequency is close to the three times of the first and second natural frequency, another test case has been considered with $\alpha$ = 0.7, ${\Lambda _{2}}$ = 1 and ${\Lambda _{1}}$ = $\sqrt{2} /2$ . It is observed from Fig. 15 that with increasing $\beta$ the response amplitude which corresponded to $3\Omega = {\omega _1} + \varepsilon \sigma$ , is also increased whereas the response amplitude which corresponded to $3\Omega = {\omega _2} + \varepsilon \sigma$ , for $\beta > 0.15$ is decreased. Figure 16 is depicted to clarify the effects of ${\bar{\eta }}$ on the response amplitude. This figure shows like primary resonance, the peak amplitude increases as the ${\bar{\eta }}$ decreases.

Fig. 14

Superharmonic response amplitude versus $\beta$ for different values of $\alpha$ with ${\xi _0}$ = 0.5, ${\bar{\eta }}$ = 1, $\sigma$ = 0.3, u = 2, ${\Lambda _{1}}$ = 1 and $3\Omega = {\omega _1} + \varepsilon \sigma$

Fig. 15

Superharmonic response amplitude for the first and second modes versus with ${\xi _0}$ = 0.25, $\alpha$ = 0.7, ${\bar{\eta }}$ = 1, u = 2, $\sigma$ = 0.3, ${\Lambda _{2}}$ = 1, ${\Lambda _{1}}$ = $\sqrt{2} /2$

Fig. 16

Superharmonic response amplitude for different values of ${\bar{\eta }}$ with ${\xi _0}$ = $\alpha$ = 0.5, $\beta$ = 0.7, u = 3, ${\Lambda _{1}}$ = 1 and $3\Omega = {\omega _1} + \varepsilon \sigma$

3.4.2 Effect of the flow velocity

The next example is dedicated to assess the effect of u on the response amplitude with ${\xi _0}$ = $\alpha$ = 0.5 and ${\bar{\eta }}$ = ${\Lambda _1}$ = 1. It is observed from Fig. 17 by increasing the flow velocity the peak amplitude increases too. Furthermore, the rate of increase of the peak amplitude for the values u which are near to the critical level is much more. Figure 18 represents the response amplitude versus the excitation amplitude for different values of u. It is observed by increasing the flow velocity the peak amplitude diminishes.

Fig. 17

Superharmonic response amplitude for different values of u with ${\xi _0}$ = $\alpha$ = 0.5, $\beta$ = 0.7, u = 3 and ${\bar{\eta }}$ = ${\Lambda _{1}}$=1 and $3\Omega = {\omega _1} + \varepsilon \sigma$

Fig. 18

Superharmonic response amplitude versus the excitation amplitude for different values of u with ${\xi _0}$ = $\alpha$ =$\sigma$ =0.5, $\beta$ = 0.7, u = 3, ${\bar{\eta }}$ = 2 and $3\Omega = {\omega _1} + \varepsilon \sigma$

3.5 Subharmonic resonance

The effects of the fractional model, the location of the harmonic concentrated force and the flow velocity on subharmonic responses are studied in this subsection.

3.5.1 Effect of fractional model

Fig. 19

Subharmonic response amplitude for different values of $\alpha$ with ${\xi _0}$ = 0.5, $\beta$ = 0.7, u = 3, ${\bar{\eta }}$ = ${\Lambda _{1}}$ = 1 and $\Omega = {3\omega _1} + \varepsilon \sigma$

Fig. 20

Subharmonic response amplitude for the first and second modes with ${\xi _0}$ = 0.25, $\alpha$ = 0.3, u = 3, $\beta$ = 0.7, ${\bar{\eta }}$ = ${\Lambda _{2}}$ = 1 and ${\Lambda _{1}}$ = $\sqrt{2} /2.$

Subharmonic response amplitude with ${\bar{\eta }}$ = 1, u = 3 and $\beta$ = 0.7 is presented in Figs. 19 and 20. In Fig. 19, the effect of $\alpha$ on the subharmonic response amplitude are depicted with ${\Lambda _{1}}$ = 1. As you can see, there are two amplitude for each detuning parameters in subharmonic response. It is observed for fractional model the region where the nontrivial solution exists, has been increased. Figure 20 also shows the response amplitude when the excitation frequency is close to the three times of the first and second natural frequency, $\alpha$ = 0.3, ${\Lambda _1} = \sqrt{2} /2$, $\mathrm{{ }}{\Lambda _2} = 1$ and ${\xi _0} = 0.25$. It is observed when the excitation frequency is close to the three times of the first natural frequency, the region where the nontrivial solution exists, is larger. Figure 21 shows the effects of $\alpha$ on subharmonic response amplitude versus the excitation amplitude with ${\xi _0} = 0.5$, ${\bar{\eta }}$ = 2, $\sigma$ = 4, u = 3 and $\beta$ = 0.7. It can be seen for the larger values of $\alpha$, the region where the nontrivial solution exists, has been decreased. Figure 22 shows the effects of $\beta$ on the response amplitude versus $\beta$ with $\sigma$ = 0.3, u = 2, ${\bar{\eta }}$ = ${\Lambda _1}$ = 1 and $\mathrm{{ }}{\xi _0} =$ 0.5. As you can see, for the fractional model, the region where the nontrivial solution exists, is larger than viscoelastic model. The the response amplitude versus $\beta$ when the excitation frequency is close to the three times of the first and second natural frequency is plotted Fig. 23 with $\sigma$=0.3, u = 2, ${\xi _0}$ = 0.25, $\mathrm{{ }}{\Lambda _1}$ = $\sqrt{2} /2$ and $\mathrm{{ }}{\Lambda _2}$ = ${\bar{\eta }}$ = 1. In Fig. 24 the effect of ${\bar{\eta }}$ on the subharmonic response amplitude is plotted with $\alpha$ = 0.5, ${\xi _0}$ = 0.5, u = 3, $\beta$ = 0.7 and ${\Lambda _{1}}$ = 1. The region for nontrivial solution increases as ${\bar{\eta }}$ decreases. It is also found the upper branch unlike the lower branch changes significantly by changing fractional parameters.

Fig. 21

Subharmonic response amplitude versus the excitation amplitude for different values of $\alpha$ with ${\xi _0}$ = 0.5, ${\bar{\eta }}$ = 2, $\sigma$ = 4, $\beta$= 0.7, u = 3 and $\Omega = {3\omega _1} + \varepsilon \sigma$

Fig. 22

Subharmonic response amplitude versus $\beta$ for different values of $\alpha$ with ${\xi _0}$ = 0.5, u = 2, $\sigma$ = 0.3, ${\bar{\eta }}$ = ${\Lambda _{1}}$=1 and $\Omega = {3\omega _1} + \varepsilon \sigma$

Fig. 23

Subharmonic response amplitude versus $\beta$ with ${\xi _0}$ = 0.25, $\alpha$ = $\sigma$ = 0.3, u = 2, $\beta$ = 0.7, ${\bar{\eta }}$ = ${\Lambda _{2}}$ =1 and ${\Lambda _{1}}$=$\sqrt{2} /2$

Fig. 24

Subharmonic response amplitude for different values of ${\bar{\eta }}$ with ${\xi _0}$ = $\alpha$ =0.5, u = 3, $\beta$ = 0.7, ${\Lambda _{1}}$ = 1 and $\Omega = {3\omega _1} + \varepsilon \sigma$

3.5.2 Effect of the flow velocity

Fig. 25

Subharmonic response amplitude for different values of u with $\eta$ with ${\xi _0}$ = $\alpha$ = 0.5, ${\bar{\eta }}$ = 1, $\beta$ = 0.7, ${\Lambda _{1}}$=1 and $\Omega = {3\omega _1} + \varepsilon \sigma$

The influence of the flow velocity on the subharmonic response amplitude is presented in Fig. 25 with $\alpha$ = 0.5, ${\bar{\eta }}$ = 1, ${\xi _0}$ = 0.5, $\beta$ = 0.7 and ${\Lambda _{1}}$ = 1 . It is obvious by increasing the flow velocity, the region where the nontrivial solution exists, does not change remarkably whereas by decreasing u two responses amplitudes increase. Figure 26 illustrates the subharmonic response amplitude versus the excitation amplitude for different values of the flow velocity, with ${\xi _0}$ = $\alpha$ = 0.5, ${\bar{\eta }}$ = 2, $\beta$ = 0.7 and $\sigma$ = 4. It can be seen by increasing u the region where the nontrivial solution exists, decrees and both upper and lower branches have been changed.

Fig. 26

Subharmonic response amplitude versus the amplitude of excitation for different values of u with ${\xi _0}$ = $\alpha$ = 0.5, ${\bar{\eta }}$ = 2, $\beta$ = 0.7, $\sigma$ = 4 and $\Omega = {3\omega _1} + \varepsilon \sigma$

4 Conclusion

The main effort of this paper is devoted to the nonlinear response analysis of the pipe conveying fluid under primary, superharmonic and subharmonic resonance conditions. The emphasis is on the effects of the fractional derivative order and the retardation time on the nonlinear response. Based on the numerous test cases, the main conclusions obtained are as follows:

Primary resonance

• (i) It is observed, by decreasing the value of the fractional derivative order and retardation time, the peak amplitude will be increased (Fig. 4).

• (ii) It is found, when the excitation frequency is close to the first natural frequency, the response amplitude is much larger than the response amplitude when the excitation frequency is close to the second natural frequency (Fig. 5).

• (iii) With increasing the value of $\beta$, the response amplitude will be decreased and the rate of decreasing in the viscoelastic model is more than the fractional model (Fig. 6).

• (iv) It is shown, by increasing the flow velocity, the peak amplitude will be increased and the rate of increase for the velocities which are close to the critical velocity, is higher (Fig. 10).

Superharmonic resonance

• (i) The results demonstrate, by decreasing the value of the fractional derivative order and the retardation time, the peak amplitude will be increase and shift to the right (Fig. 11).

• (ii) It is found, when the excitation frequency is close to one-third of the second natural frequency, the response amplitude is much larger than the response amplitude when the excitation frequency is close to one-third of the first natural frequency (unlike primary resonance, Fig. 12).

• (iii) With increasing the value of $\beta$, the response amplitude, will be increased and the rate of increase in the fractional model is higher than the viscoelastic model (unlike primary resonance, Fig. 14).

Subharmonic resonance

• (i) It is observed by decreasing the value of the fractional derivative order and the retardation time, the region where the nontrivial solution exists, will be increased (Fig. 19).

• (ii) It is found by changing flow velocity the region where the nontrivial solution exists, does not change remarkably (Fig. 25).

• (iii) The investigation of the response amplitude versus the excitation amplitude for the fractional model shows, with increasing the flow velocity, the region where the nontrivial solution exists and the response amplitudes, will be decreased (Fig. 26).

In total, it can be concluded that the effects of the fractional damping model parameters are more obvious in sub- and superharmonic resonances in comparison with primary resonance. This phenomenon would be beneficial to further development in dynamic control damage detection and health monitoring of the rubber, polymeric and synthetic pipes conveying fluid.