Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

9.1 Introduction

The application of the method of dimensionality reduction to adhesive contacts between elastic bodies is given by the rule of Heß (Eq. 4.1). However, this rule cannot be directly generalized to include contacts between viscoelastic bodies. This can already be seen in the fact that the “separation criterion” from Heß contains the modulus of elasticity. The effective modulus of elasticity of elastomers, however, is dependent on the deformation speed or frequency. Therefore, to be able to transfer the results of Heß [1] to those of viscoelastic media, a better physical understanding of the phenomenon of adhesion is necessary. For this, it is helpful to consider a microscopic picture of an adhesive contact. The fundamentals of this were already described in Chap. 4. At this point, we will generalize these ideas for their application to viscoelastic media .

9.2 Stress Concentration Near the Boundary of an Adhesive Contact

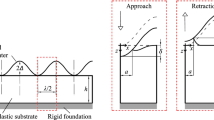
We consider an adhesive contact between a rigid flat indenter and an elastic body (Fig. 9.1). When the indenter is pulled with an upwards-oriented force \( F, \) the following stress distribution develops in the contact area [2]:

$$ \sigma = \sigma_{0} \left( {1 - \left( \frac{r}{a} \right)^{2} } \right)^{ - 1/2} $$
(9.1)

with

$$ \sigma_{0} = \frac{F}{{2\pi a^{2} }}. $$
(9.2)
Fig. 9.1
figure 1

a Adhesive contact of an elastic body with a flat indenter; b Enlarged view of the “tip of the crack” (the area in immediate vicinity to the edge of the contact)

Full size image

At the edge near the tip of the crack, for \( r = a - {\Delta}r, \) the distribution has a singularity of the form

$$ \sigma = \sigma_{0} \sqrt {\frac{a}{{2{\Delta}r}}} . $$
(9.3)

As discussed in Chap. 4 and can be seen in the classical works of Griffith [3] and Prandtl [4], this singularity is essentially the physical cause for the rupture of the adhesive connection between the two bodies. Because the rupture process takes place in a very narrow “process zone” near the tip of the crack, only the form of the singularity is important for the global equilibrium. The stress distribution far from the tip does not play a role. Noteworthy is that the relationship (9.3) does not contain the elastic properties of the medium. Therefore, it is also valid for arbitrary media with a linear rheology.

In the most simple microscopic examination of an adhesive contact, we can think of the bodies as being made of molecules of the characteristic length b. Because of the molecular structure, the singularity (9.3) would not exist in reality, because the distance to the tip cannot be smaller than the size of the molecules. The stress then reaches a high, but finite, maximum on the order of magnitude of

$$ \sigma_{\hbox{max} } \approx \sigma_{0} \sqrt \frac{a}{2b} . $$
(9.4)

The length \( b \) can be interpreted as the size of the “process zone” [5].

The breaking of molecular bonds near the edge of an adhesive contact occurs when certain critical values are exceeded. In the elastic case, it does not matter if we exceed a critical strain, stress, or work, because all three are distinctly related to one another. For the case of elastomers, this is no longer true: For an elastomer, the stress is no longer only a function of strain, but also of the strain rate. Depending on which independent value (stress or strain) assumes a critical value, we obtain different separation criteria. In this chapter, we discuss two criteria, whereby also many other criteria are conceivable. We begin with the case of elastic bodies and later go on to the investigation of viscoelastic bodies.

9.3 Deformation Criterion

Both the stress and the strain obtain their maximum values in the immediate vicinity of the crack tip—roughly put—within one molecular diameter from the crack tip. Thereby, the maximum stress (9.4) leads to a deformation of the material on the order of magnitude of

$$ \varepsilon_{\hbox{max} } \approx \frac{{\sigma_{\hbox{max} } }}{{E^{*} }} = \frac{{\sigma_{0} }}{{E^{*} }}\sqrt \frac{a}{2b} . $$
(9.5)

Let us assume that the molecular contact is lost, when the relative displacement of the “contacting molecules” in the vertical direction reaches a critical value \( b_{c} \). We can then rewrite the approximation (9.5) in the following form:

$$ \varepsilon_{\hbox{max} } \approx \frac{{b_{c} }}{b} \approx \frac{{\sigma_{0} }}{{E^{*} }}\sqrt \frac{a}{2b} . $$
(9.6)

From this, we obtain the critical value of \( \sigma_{0} \):

$$ \sigma_{0} \approx \sqrt 2 E^{*} \frac{{b_{c} }}{{\sqrt {ab} }}. $$
(9.7)

For the adhesion force, we obtain

$$ F_{A} = 2\pi a^{2} \sigma_{0} \approx 2^{3/2} \pi E^{*} b_{c} b^{ - 1/2} a^{3/2} . $$
(9.8)

The maximum vertical displacement of the indenter before separation is given by the equation

$$ u_{A} = \frac{{F_{A} }}{{2aE^{*} }} = 2^{1/2} \pi b_{c} b^{ - 1/2} a^{1/2} . $$
(9.9)

By defining

$$ b^{*} = 2\pi^{2} b_{c}^{2} /b $$
(9.10)

(\( b^{*} \) is the characteristic length on the order of magnitude of the length of a polymer molecule) we bring (9.9) into the form

$$ u_{A} = \sqrt {b^{*} a}. $$
(9.11)

Note that this equation does not contain the modulus of elasticity; therefore, it also valid in the same form for arbitrary media with a linear rheology, as long as the assumed deformation criterion for the crack retains its validity. For elastomers in the case of the “deformation criterion,” the fracture criterion from Heß (4.1) must be replaced by

$$ \Delta \ell_{\hbox{max} } (a) = \sqrt {b^{*} a} . $$
(9.12)

9.4 Stress Criterion

Other criteria are also conceivable. For instance, the contact may be lost when the tip stress (9.4) reaches a critical value \( \sigma_{c} \):

$$ \sigma_{\hbox{max} } \approx \sigma_{0} \sqrt \frac{a}{2b} = \sigma_{c} . $$
(9.13)

Because the relationship (9.4) is universally valid for all media with a linear rheology, we obtain the adhesion force

$$ F_{A} = 2\pi a^{2} \sigma_{0} = 2^{3/2} \pi a^{3/2} b^{1/2} \sigma_{c} . $$
(9.14)

For this criterion, the adhesion force is not dependent on the separation speed. The Heß criterion (4.1) must be replaced in this case with the requirement that the force in the individual springs reaches the critical value

$$ \Delta f_{z,\hbox{max} } = \pi \sigma_{c} \sqrt {2ab} \cdot\Delta x. $$
(9.15)

9.5 Adhesive Contacts Without Initial Stress

In this section, we consider a rigid cylindrical indenter with the diameter L, which is brought into contact with an elastomer without a normal force in a way that the contacting surfaces adhere. Subsequently, a separation force \( F(t) \) is applied. In the one-dimensional system, a flat profile of the length \( L \) is brought into contact with an array of viscoelastic elements, defined according to the rules in Chap. 7. In the elastic case, the normal force \( F \) and the vertical displacement \( u \) are related by the equation

$$ F = LE^{*} u. $$
(9.16)

For incompressible elastomers, as explained in Chap. 7, this relationship must be replaced by the integral relationship

$$ F(t) = 4L\int\limits_{ - \infty }^{t} {G\left( {t - t^{\prime}} \right)} \frac{{{\text{d}}u}}{{{\text{d}}t^{\prime}}}{\text{d}}t^{\prime}. $$
(9.17)

With the help of this equation, we will now discuss the separation process using the deformation criterion. If the deformation criterion is valid, the separation will always occur upon reaching the critical vertical displacement given by (9.12). It is easy to calculate the force exhibited in this state. Let us assume that the speed \( {\text{d}}u/{\text{d}}t \) is zero until the time \( t = 0 \) and at this time, it jumps to \( v_{0} \) and remains constant. The force is then given by the equation

$$ F(t) = 4Lv_{0} \int\limits_{0}^{t} {G\left( {t - t^{\prime}} \right){\text{d}}t^{\prime} = 4Lv_{0} \int\limits_{0}^{t} {G\left( \xi \right){\text{d}}\xi } } $$
(9.18)

and reaches its maximum value at \( t = u_{A} /v_{0} \):

$$ F_{A} = 4Lv_{0} \int\limits_{0}^{{u_{A} /v_{0} }} {G\left( \xi \right){\text{d}}\xi } , $$
(9.19)

where \( u_{A} \) is taken from Eq. (9.11).

We constrict ourselves at this point to the simplest rheology imaginable—that of a linearly viscous fluid. The adhesive contact between media that exhibit a more complicated rheology will be handled in the problems at the end of this chapter. For a linearly viscous medium, Eq. (9.17) can be directly written in the form

$$ F(t) = 4L\eta \frac{{{\text{d}}u}}{{{\text{d}}t}}. $$
(9.20)

For a constant velocity, it is not dependent on time as long as the displacement has not reached its critical value (9.11). Therefore, the adhesion force is

$$ F_{A} = 4L\eta \frac{{{\text{d}}u}}{{{\text{d}}t}}. $$
(9.21)

It is proportional to the diameter of the contact and to the separation speed. This equation is also applicable to pure liquids as long as the capillary effect is neglected. Furthermore, cavitation is not taken into account.

9.6 Problems

Problem 1

Determine the force of separation (without initial stress) of a rigid cylindrical indenter with the diameter \( L \) from a medium that is described by the “standard model” (Fig. 9.2). Use the stress and deformation criteria.

Fig. 9.2
figure 2

A simple model for an elastomer (“standard model”)

Full size image

Solution

  1. (a)

    Stress criterion. If the stress criterion is applicable, the adhesion force is given by Eq. (9.14):

$$ F_{A} = \pi L^{3/2} b^{1/2} \sigma_{c} . $$
(9.22)

It is proportional to \( L^{3/2} \) and is dependent on the critical stress and the size of the process zone, but not on the separation speed. The dependence of the adhesion force on the separation speed is, therefore, an indication that the stress criterion is not valid for a flat indenter.

  1. (b)

    Deformation criterion. The time-dependent shear modulus for this model is [2]

$$ G(t) = G_{1} + G_{2} e^{ - t/\tau } , $$
(9.23)

with \( \tau = \eta /G_{2} \). Insertion into (9.19) results in the adhesion force:

$$ \begin{aligned} F_{A} & = 4Lv_{0} \int\limits_{0}^{{u_{A} /v_{0} }} {\left( {G_{1} + G_{2} e^{ - \xi /\tau } } \right){\text{d}}\xi = 4Lv_{0} \left[ {\frac{{G_{1} u_{A} }}{{v_{0} }} + \tau G_{2} \left( {1 - e^{{ - \frac{{u_{A} }}{{v_{0} \tau }}}} } \right)} \right]} \\ & = 4G_{1} Lu_{A} + 4Lv_{0} \eta \left( {1 - e^{{ - \frac{{u_{A} }}{{v_{0} \tau }}}} } \right). \\ \end{aligned} $$
(9.24)

By taking Eq. (9.11) into account, one can write this equation in the following explicit form:

$$ F_{A} \approx 2^{3/2} LG_{1} \sqrt {b^{*} L} + 4Lv_{0} \tau G_{2} \left( {1 - e^{{ - \frac{{\sqrt {b^{*} L} }}{{2^{1/2} v_{0} \tau }}}} } \right). $$
(9.25)

By introducing

$$ \zeta = \frac{{2^{1/2} v_{0} \tau }}{{\sqrt {b^{*} L} }}, $$
(9.26)

we can write (9.25) in the form

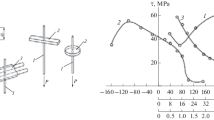
$$ F_{A} \approx 2^{3/2} L^{3/2} b^{*1/2} \left( {G_{1} + G_{2} \zeta \left( {1 - e^{{ - \frac{1}{\zeta }}} } \right)} \right). $$
(9.27)

From this, it is obvious that the separation force is only dependent on the combination of parameters in (9.26). The dependence of the dimensionless force \( f_{A} = F_{A} /\left( {2^{3/2} L^{3/2} b^{*1/2} G_{1} } \right) \) on \( \zeta \) is presented in Fig. 9.3.

Fig. 9.3
figure 3

Dependence of the dimensionless force \( f_{A} = F_{A} /\left( {2^{3/2} L^{3/2} b^{*1/2} G_{1} } \right) \) on the dimensionless separation speed \( \zeta \) for the case of an elastomer, which is described by the standard model, where \( G_{2} /G_{1} = 1{,}000 \) is chosen

Full size image

In the curve of the adhesion force function, three domains can be recognized:

  1. I.

    \( \zeta \ll \frac{{G_{1} }}{{G_{2} }} \). In this case,

    $$ F_{A} \approx 2^{3/2} L^{3/2} b^{*1/2} G_{1} $$
    (9.28)

    is valid. This is the classical result for the adhesion between a rigid cylinder and an elastic medium with the shear modulus \( G_{1} \).

  2. II.

    \( \frac{{G_{1} }}{{G_{2} }} \le \zeta \le 1 \). In this interval,

    $$ F_{A} \approx 4L\eta v_{0} $$
    (9.29)

    is valid, which may be expected, as the system behaves like a linearly viscous fluid here and satisfies Eq. (9.21).

  3. III.

    \( 1 \ll \zeta \). In this domain,

    $$ F_{A} \approx 2^{3/2} L^{3/2} b^{*1/2} \left( {G_{1} + G_{2} } \right) $$
    (9.30)

    is valid. This is the same relation as (9.28), but with a different shear modulus.

Let it be noted that in interval II, the adhesion force is not dependent on the exact microscopic fracture criterion, but only on the viscosity of the medium. The limiting case of a simple viscoelastic body (Kelvin body ) is obtained from the general expression (9.25) by inserting \( G_{2} \to \infty \). The result is

$$ F_{A} \approx 2^{3/2} L^{3/2} b^{*1/2} G_{1} + 4L\eta v_{0} . $$
(9.31)

Because the viscosity exhibits a strong temperature dependence, one may expect that in the intermediate interval of separation speeds, the adhesion force increases with a decrease in temperature.

Problem 2

A rigid cylinder with the diameter \( L \) is pressed into a viscoelastic medium described by the “standard model” (Fig. 9.2) with the normal force \( F_{N} \) and, after a long settling time, pulled away with the speed \( v_{0} \). Determine the adhesion force by using the stress and deformation criteria.

Solution

  1. (a)

    Stress criterion . In using the stress criterion, Eq. (9.22) remains valid: The adhesion force is the same as the case without initial stress.

  2. (b)

    Deformation criterion . During the indentation phase, the material reacts completely elastic after a long settling time, with the shear modulus \( G_{1} \). The indenter presses into the material to a depth of

$$ d_{1} = \frac{{F_{N} }}{{4LG_{1} }}. $$
(9.32)

Instead of Eq. (9.18), a modified equation must be used:

$$ F(t) = - F_{N} + 4Lv_{0} \int\limits_{0}^{t} {G\left( {t - t^{\prime}} \right){\text{d}}t^{\prime} = - F_{N} + 4Lv_{0} \int\limits_{0}^{t} {G\left( \xi \right){\text{d}}\xi } } . $$
(9.33)

\( F(t) \) is a monotonically increasing function in time: The force increases until the fracture criterion (9.12) is reached:

$$ u = - d_{1} + v_{0} t = u_{A} = \sqrt {b^{*} L/2} . $$
(9.34)

From this, the separation time \( \tilde{t} \) can be determined:

$$ \tilde{t} = \frac{{d_{1} + u_{A} }}{{v_{0} }} = \frac{{d_{1} + \sqrt {b^{*} L/2} }}{{v_{0} }}. $$
(9.35)

Consequently, the adhesion force in the general case is

$$ F_{A} = - F_{N} + 4Lv_{0} \int\limits_{0}^{{\frac{{d_{1} + \sqrt {b^{*} L/2} }}{{v_{0} }}}} {G\left( \xi \right){\text{d}}\xi } . $$
(9.36)

Substitution of the time-dependent shear modulus for the standard model (9.23) results in

$$ \begin{aligned} F_{A} & = - F_{N} + 4Lv_{0} \int\limits_{0}^{{\frac{{d_{1} + \sqrt {b^{*} L/2} }}{{v_{0} }}}} {\left( {G_{1} + G_{2} e^{ - \xi /\tau } } \right){\text{d}}\xi } \\ & = 4LG_{1} \sqrt {b^{*} L/2} + 4Lv_{0} \tau G_{02} \left( {1 - e^{{ - \frac{{d_{1} + \sqrt {b^{*} L/2} }}{{v_{0} \tau }}}} } \right). \\ \end{aligned} $$
(9.37)
  1. I.

    If \( v_{0} \tau \ll d_{1} + \sqrt {b^{*} L/2} , \) then

$$ F_{A} \approx 4LG_{1} \sqrt {b^{*} L/2} + 4Lv_{0} \eta $$
(9.38)

and the adhesion force is independent from the indentation force.

  1. II.

    If \( v_{0} \tau \gg d_{1} + \sqrt {b^{*} L/2} , \) then

$$ F_{A} \approx F_{N} \frac{{G_{2} }}{{G_{1} }} + 4L\sqrt {b^{*} L/2} \left( {G_{1} + G_{2} } \right). $$
(9.39)

In this interval, the adhesion force increases linearly with the indentation force. Let it be noted that the boundaries of this interval are dependent on the indentation force itself.

Equation (9.37) can be written in the form

$$ f_{A} \approx 1 + \frac{{G_{2} }}{{G_{1} }}\zeta \left( {1 - e^{{ - \frac{{1 + f_{{}} }}{\zeta }}} } \right), $$
(9.40)

where, in addition to the relation (9.26), we have inserted the dimensionless force \( f_{A} \):

$$ f_{A} = \frac{{F_{A} }}{{2^{3/2} b^{*1/2} L^{3/2} G_{1} }} $$
(9.41)

and the dimensionless initial force \( f \):

$$ f = \frac{{F_{N} }}{{2^{3/2} b^{*1/2} L^{3/2} G_{1} }}. $$
(9.42)

The dependence of (9.40) is presented in Fig. 9.4. While the adhesion force for small separation speeds is not dependent on the indentation force, it can be increased significantly by the indentation force for sufficiently large separation speeds.

Fig. 9.4
figure 4

Dependence of the dimensionless adhesion force on the dimensionless speed for four values of the dimensionless indentation force \( f = 0 ; { 0} . 1 ; { 1; 10} \) and \( G_{2} /G_{1} = 1{,}000 \)

Full size image

Problem 3

A conical indenter (Fig. 9.5) is pressed into a linearly viscous elastomer to a depth of \( d_{0} \) and subsequently pulled up. Using the deformation criterion for the crack, determine the dependence of the contact radius on the indentation depth \( d \).

Fig. 9.5
figure 5

Conical indenter that is pressed into a linearly viscous medium

Full size image

Solution

The form of the cone is described by the equation \( f(r) = \tan \theta \cdot r \). The corresponding scaling factor is \( \kappa_{1} = \pi /2 \), so that the resulting equivalent one-dimensional profile is \( g(x) = \left( {\pi /2} \right)\tan \theta \cdot \left| x \right| \). If the indenter is pressed to a depth of \( d_{0} \) and then pulled out to a depth of \( d \), then the vertical displacement of the foundation at point x is given by

$$ u_{z} (x) = d - (\pi /2)\tan \theta \cdot \left| x \right|. $$
(9.43)

Using the deformation criterion (9.11), we calculate the contact radius \( a \) by requiring that \( u_{z} (a) = - u_{A} \):

$$ d - (\pi /2)\tan \theta \cdot a = - \sqrt {b^{*} a} . $$
(9.44)

Introducing

$$ \tilde{d} = \frac{d}{(\pi /2)\tan \theta } $$
(9.45)

and

$$ \tilde{b} = \frac{{b^{*} }}{{(\pi /2)^{2} \tan^{2} \theta }}, $$
(9.46)

we rewrite Eq. (9.44) in the form

$$ \tilde{d} - a = - \sqrt {\tilde{b}a} . $$
(9.47)

From this, we obtain the contact radius

$$ a = \left( {\tilde{d} + \frac{{\tilde{b}}}{2}} \right) + \sqrt {\tilde{d}\tilde{b} + \left( {\frac{{\tilde{b}}}{2}} \right)^{2} } . $$
(9.48)

Separation occurs at \( \tilde{d} = - \tilde{b}/4 \). Thereby, the contact radius is \( a = \tilde{b}/4 \). Let it be noted that this result is independent from the elastic (or rheological) properties and is valid for a medium of arbitrary rheology (as long as the deformation criterion is valid for the crack).

Problem 4

Discuss the influence of roughness in the case of the contact with a linearly viscous medium (Kelvin body ).

Solution

Assume that the spectrum of the roughness exhibits a cut-off at \( q_{min} \gg 2\pi /L \) (see more in Problem 2 in Chap. 10). We denote the root mean square of the roughness as \( h \). In this case, the contact length is approximately proportional to the normal force

$$ L_{\text{cont}} \approx \frac{{F_{N} }}{Gh}, $$
(9.49)

as long as it remains smaller than the system size \( L, \) at which point it remains constant:

$$ L_{\text{cont}} = L. $$
(9.50)

If the indenter is now pulled off quickly, then the force is given predominantly by the viscous term (9.29):

$$ F_{A} = 4v_{0} \eta L_{\text{cont}} . $$
(9.51)

For subcritical normal forces, the adhesion force is then

$$ F_{A} = F_{N} \frac{{4v_{0} \eta }}{Gh} = F_{N} \frac{{4v_{0} \tau }}{h}, $$
(9.52)

with \( \tau = \eta /G \). For supercritical forces, it is

$$ F_{A} = 4v_{0} \eta L, $$
(9.53)

independently from the indentation force and the roughness. This coincides with the adhesion force of a smooth indenter.