INTRODUCTION

The phenomenon of adhesion is the establishment of energetic bonds between an adhesive (glue) and a substrate (which is glued or coated). When assessing the quality of an adhesive joint, we are able to measure only two parameters—the area of gluing and the force that breaks this gluing. Further, by analogy with materials, the breaking load is referred to the glued area and the resulting value, for example, average tangential stresses \(\bar {\tau }\) = Pb/S is called the “adhesion shear strength” or σtr = Pb/S is the “strength at normal pull-off” or the “transverse strength.” It is then assumed that the stresses are uniformly distributed over the glued area. This is, in fact, the average adhesive strength. In addition, it is known that this value is a strong function of the geometric parameters of the sample and the physical parameters of the experiment (for example, temperature). Figures 1 and 2 show, as examples, the schemes of samples and experimental results of testing these samples for shear by pulling the fiber out from the epoxy matrix (pull out) and connections of “overlap” type [1, 2]. The results are presented as dependences of the above-mentioned ratio of the breaking load to the glued area on the geometric parameters of the sample and temperature. It can be seen from the graphs that these dependences do not allow one to indicate a specific value of the strength of the adhesive bond between the substrate and the adhesive.

Fig. 1.
figure 1

Test samples and experimental dependences of \(\bar {\tau }\) when pulling a fiber (by the pullout method) out from an EDT-10 polymer epoxy matrix on the (1) diameter of the glass fiber, (2) temperature, and (3) gluing length [34].

Full size image
Fig. 2.
figure 2

(a—c) Experimental results of testing joints of plates of “overlap” type for shear: (1) dependence of destructive load P on thickness of glue line hg for the Araldit steel-filled epoxy glue; (2, 3) dependence of average adhesive strength \(\bar {\tau }\) on test temperature for aluminum– epoxy-polyamide glue and aluminum-filled glue EPTs-1 joints, respectively; and (4) dependence of average adhesive strength \(\bar {\tau }\) on gluing length of the glass-epoxy joint (ED-20 epoxy resin and PEPA hardener).

Full size image

The regulation of tests, i.e., the development of standards for sample sizes for some methods, has created the possibility of a relative assessment of the quality of a particular adhesive in interaction with a certain substrate. The informational content of the tests has increased. However, it was not possible to completely solve the problem of assessing the quality of adhesives in this way. First, because not all sizes in the adhesive joint can be regulated. For example, the thickness of the adhesive layer can change from one adhesive to another, even under the same conditions of its formation. Second, and more importantly, in this case, adhesives are evaluated only for one model size, but, in practice, they will be used for gluing parts of various sizes and shapes. In relation to them, judging by the results shown in Figs. 1–3, conclusions drawn from standard tests may turn out to be erroneous.

Fig. 3.
figure 3

Adhesion tests for normal pulloff. Sample and experimental dependences of average strength on (1) radius of contacting surfaces, (2) thickness of adhesive layer, and (3) test temperature.

Full size image

Usually, the physicomechanical analysis of the behavior of solids begins with an experimental study of the simplest case of a homogeneous stress state—created, for example, during tension or shear of a material. Adhesion studies—in particular, adhesion mechanics—always deal with a substantially nonuniform stress distribution over the contact area of ​​the adhesive with the substrate. A convincing example of the distribution of tangential stresses near the gluing boundary is shown in Fig. 4 from [3]. This fact determines the complexity of the problems of adhesion of adhesive mechanics and is the main reason for the significant lag of theory from widely presented (due to practical needs) experimental studies. Thus, one important task that needs to be carried out in the course of adhesion is to determine the strength of the adhesive bond—the true adhesive strength that does not depend on the geometry of the sample—and to determine the intensity of the adhesive interaction (the stiffness of the contact layer). Together, they uniquely characterize the quality of the adhesive bond of a given adhesive–substrate pair.

Fig. 4.
figure 4

Experimental distribution curve at the interface of tangential stresses in a model of three glued glass rods: (1) glass rods; (2) adhesive layer [3]. The tests were carried out by the method of photoelasticity.

Full size image

It should be noted right away that almost all models used for the study of glue (adhesive) joints are micro- or macromodels of composite materials, in the creation of which the role played by adhesion is decisive, although contradictory. For example, adhesion is one reason for the relatively low tightness of products made of reinforced polymers obtained by winding. Therefore, the term “adherent junctions (AJs) will be used here as a more general one. In addition, in contrast to most problems in the theory of elasticity and resistance of materials, in which, according to the principle of Saint-Venant, the edges of models are excluded from consideration, in questions of adhesion mechanics, all problems are largely determined by edge effects—the concentration of stresses [1–4] at the edges.

The question of what adhesion is can be answered as follows. This is a phenomenon or the process of establishing certain bonds with a finite breaking energy between the adhesive (glue, matrix) and the substrate. Let us assume that we can regulate the density of these connections. Let us recall Loschmidt’s number of the number of atoms in a solid, which is about 1022/cm3. Then, for 1 cm2 of the surface, for example, with a bond density of np1 = 1012/cm2, this will mean that approximately one out of every ten atoms of the substrate surface is involved with the opposite adhesive atom. Such a medium will have Young’s modulus E ' along the bonds and shear modulus G*, which characterizes the relationship between shear strain γ in contact plane and the shear stress τ = G*γ. If we use every hundredth atom, then the density of bonds between the adhesive and the substrate will be approximately np1 = 1010/cm2. It is very likely that the actual density of adhesive bonds is much less; i.e., the bonds are rare. Both Young’s modulus E ' and shear modulus G* of the contact layer will, then, also decrease by two orders of magnitude. This is how we can influence the adhesive interaction and its intensity. The magnitude of this interaction can vary in the range of several orders of magnitude. Adhesive interaction is undoubtedly closely related to wetting.

Let us imagine these connections in the form of short, elastic rods with length h*, perpendicular to the surfaces of the substrate and the adhesive. The rods, since they are rare, do not touch each other (Fig. 5). Thus, the binding rods create a certain layer with thickness h* of an anisotropic continuous medium, which can be called a “contact” or “boundary” layer. In such a medium, there are certainly no normal stresses perpendicular to the “side” surface of the rods. The shear modulus of such an anisotropic medium is related to the Young’s modulus along the bonds by the simple relation G* = E*/2.

Fig. 5.
figure 5

Scheme of the contact layer.

Full size image

The theory proposed in [1], which is called “adhesion mechanics,” is based on the concept of the existence of the described contact layer between the adhesive and the substrate. The works devoted to the contact layer method in adhesion mechanics (at first the author called it a boundary layer) began in the Soviet Union in the early 1970s (for example, [11–18]) and are continuing at the present time [1, 2, 6–8, 19, 20]. In Western countries, the first works on the characterization of adhesive contact appeared only in the 1990s [21–26]. It is, basically, a shear spring model like a Winkler base. For example, quite a large number of works by various authors are devoted to the edge effect near the break (end face) of a fiber in a composite (references in [3–5]). However, the role of the adhesive interaction was practically not studied in them, since it was not characterized in any way in these works, and it was assumed to be absolute by default [9, 10]. The latter means that only the fundamental requirements for the continuity of the vectors of displacements and stresses were fulfilled at the boundary; that is, the requirements for maintaining continuity and the fulfillment of Newton’s third law. In this case, solutions are inevitably obtained in which the tangential stresses at the angular points tend to infinity; that is, a so-called “singularity” manifests itself. The use of physically justified strength criteria under these conditions becomes practically impossible. In particular, let us consider a model of numerous and regular prefractures of a fiber in a polymer plate under tension. This is a model of a reinforced polymer (Kargin—Malinsky model). It was tested by the photoelasticity method, calculated by the contact layer method, and explained in the works of the author and his colleagues [14–17] by the extreme distribution of tensile stresses in the fiber near the fiber edge due to the symmetric bending of the composite model. In addition, it was shown in these works that the number of fiber breaks before the destruction of the model as a whole is extremely dependent on the test temperature. A similar study was carried out in Western countries 20 years later in [26] using a spring model at a constant temperature.

As a result of the application of the hypothesis of the anisotropic contact layer described above, a theory has been created [1], which

— is able to calculate substantially nonuniform stress and strain fields in adhesive joints, including stress concentrations;

— is able to satisfy all boundary conditions, in contrast to “strict” solutions, for example, according to the theory of elasticity, when at the corners on surfaces free from loads that are, contrary to the conditions of the problem, infinite, and nonzero values of tangential stresses (singularities) are obtained;

— relies on the achievements of predecessors, being quite noncomplex and allowing simplifications up to one-dimensional problems, the solutions of which are usually obtained in the form of finite formulas without using numerical methods;

— takes into account the technological stresses created by the glue (adhesive) when shrinking or changing the temperature of the model;

— uses physically clear criteria for the destruction of adhesive joints, for example, when the maximum tangential stress reaches a critical value, which was call “the shear strength of the adhesive bond”;

— allows direct comparison of calculations with experimental results, this meaning that the calculation results can be presented in the form of dependences of the average adhesion strength measured in the experiment on various parameters of the model and experiment;

— allows one to enter, along with the adhesive strength, the stiffness parameter of the contact layer, which characterizes the intensity of the adhesive bond and affects the magnitude and nature of stress distribution at the boundary and in all components of the model;

— explains and describes the experimentally discovered phenomenon of synergism of elastic characteristics (Young’s modulus) of thin layers of adhesive and layered structures;

— makes it quite easy to determine the true strength of the adhesive bond and the stiffness of the contact layer from macroexperiments on measuring the average adhesive strength; and

— is applicable to the description of relaxation processes in thin adhesive layers taking into account the stress concentration, for example, using the nonlinear differential coupling equation obtained by G.I. Gurevich [1, 2, 27] as a result of considering the molecular mechanism of deformation of condensed media.

The theoretical results are in qualitative and quantitative agreement with the experimental data.

MAIN PART

This theory is applicable to solving a number of problems of related sciences. In particular, it is involved in solving the problem of sequencing (determining the structure) of a DNA molecule and the interaction of an enzyme with a DNA molecule [1].

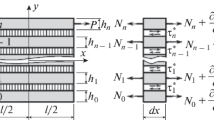
In the contact layer shown in Fig. 5, there is no direct contact of the rods with each other and, therefore, there are no normal stresses σx and σy. Short rods experience shear stresses σzx, σzy, σxy and, naturally, normal stresses σz. Since the rods are short, i.e., h* (the length of the rods or, which is the same thing, the thickness of contact layer k) is small, it can be assumed that, within contact layer k, displacements u or ν are a linear function of the z coordinate (Fig. 6): uk = ak + ckz (k = 0, 1, …, n).

Fig. 6.
figure 6

Scheme of displacements along the x axis of the elements of a layered system. \(h_{k}^{*}\) is the thickness of the contact layer.

Full size image

Figure 7 presents a design diagram of a plane two-dimensional problem corresponding to the simplest model of unidirectionally reinforced plastic. It is a polymer plate, on the major axis of symmetry of which there is a reinforcing element in the form of a fiber or a rod, in particular a glass one. Tensile forces P are applied to the polymer plates along the fiber axis, as shown in the diagram. There are no stresses σx in the contact layer.

Fig. 7.
figure 7

Design scheme of a two-dimensional plane problem. Stresses and forces in the main element of a multilayer plate (two-dimensional problem): (1) reinforcing element or substrate, (2) adhesive layer, and (3) contact layer.

Full size image

In the experiment, this theoretical model corresponded to the Kargin–Malinsky model, which is intended for studying the process of destruction of a reinforcing fiber in a polymer matrix in polarized light using the photoelasticity method. On such a model of unidirectional Kargin–Malinsky plastic, which is a flat standard polymer sample in the form of a so-called “blade” designed for tensile testing, on the longitudinal axis of symmetry of which a reinforcing element in the form of a fiber or rod (here, a glass one) is placed; experiments were carried out on stretching at a constant speed at various temperatures (Fig. 8). The deformation of such samples was observed in polarized light. The tensile strength of such samples in the entire studied temperature range is usually lower than the strength of similar polymer samples without a reinforcing rod. The destruction of the model as a whole is preceded by multiple breaks of the reinforcing element (marked in Fig. 8). Near these breaks, stress concentration zones are observed in polarized light, which contribute to a decrease in the strength of the model samples.

Fig. 8.
figure 8

Diagram of the Kargin–Malinsky model with a fiber on the axis of a polymer plate and fiber breaks during its stretching.

Full size image

Visual observations and filming of the destruction process showed that the sequence of the occurrence of ruptures of the reinforcing element obeys a certain pattern. The first fiber break occurs at a random location. Subsequent breaks, as a rule, occurred at a certain (on average) distance from one of the previous breaks. For example, if the first break occurred in the middle of the fiber length, then the subsequent break occurs to the left or right of this first one at a fairly small distance (about 12–20 fiber diameters). Thereafter, for example, a third break may occur at the same small distance from the second from the side of the still long whole part of the reinforcing fiber. This continues until the final destruction of the sample as a whole occurs.

Fiber breaks that obey the described order (usually from the second to the sixth) in what follows we will conventionally be called “sequential” breaks. About 400 samples were observed in the experiments, and sequential breaks occurred in 80% of cases. It should be noted that sequential ruptures of the reinforcing element during stretching of the model are observed in a certain temperature range, the boundaries of which depends on the polymer used and usually includes the glass-transition temperature of the polymer. For example, for samples based on polyester resin, sequential ruptures are observed in the temperature range from 30 to 70°C, while this range is from 60 to 140°C for epoxy resin. Outside these areas, the order of breaks is random. All these regularities are observed in spite of the fact that the fiber, as is known [1, 34, 35], has a dispersion of strength along its length and, under uniform loading, breaks should have arisen randomly.

However, the dependence of the number of any breaks (sequential and random) preceding the destruction of the entire specimen has an extreme character (Fig. 9). This means that this phenomenon can most likely be explained by a more complex distribution of tensile stresses in the fiber near the place of its rupture and the local excess of stresses should be greater than the dispersion of the fiber strength.

Fig. 9.
figure 9

Temperature dependence of average number of breaks N of the reinforcing element preceding the destruction of the model as a whole. Polyester resin is the adhesive. A glass rod with a diameter of 100 μm is the substrate.

Full size image

To find out the plausibility of this hypothesis, the problem of the stress-strain state of the studied model after the formation of a rupture of the reinforcing fiber in flat two- and one-dimensional formulations was solved by the contact layer method. The scheme of the model, as already mentioned, is shown in Fig. 7. Fiber 1 is considered a rod, and the theory of plates is applied to polymer layers 2. Contact layer 3 is between them.

Only small deformations (ε \( \ll \) 1) characteristic of rigid structural materials are considered. Therefore, the total deformation of the adhesive and the substrate can be represented as the sum of deformations of various physical natures: elastic deformation e related with stresses by Hooke’s law; deformation εq, which is either forced highly elastic deformation ε* that is not reversible in the phase with stresses, or plastic ε0 (i.e., residual or irreversible after stress relief), or temperature εt, or a result of chemical (as a result of the hardening reaction) or physical (for example, during crystallization) shrinkage εс, etc.; or the sum of the deformations involved in the process:

$$\varepsilon = e + {{\varepsilon }_{q}}.$$
(1)

Contact layers are considered as a purely elastic anisotropic medium. For a flat problem, we have:

— equilibrium equations

$$\partial {{\sigma }_{x}}{\text{/}}\partial x + \partial {{\tau }_{{xy}}}{\text{/}}\partial y = 0;\,\,\,\,\partial {{\sigma }_{y}}{\text{/}}\partial y + \partial {{\tau }_{{xy}}}{\text{/}}\partial x = 0;$$
(2)

— Cauchy relations connecting total deformations with displacements of particles of the medium u and ν in the x and y directions,

$${{\varepsilon }_{{xx}}} = \partial u{\text{/}}\partial x;\,\,\,\,{{\varepsilon }_{{yy}}} = \partial \nu {\text{/}}\partial y;\,\,\,\,{{\varepsilon }_{{xy}}} = \partial u{\text{/}}\partial y + \partial \nu {\text{/}}\partial x,$$
(3)

where σx and σy are the normal components of the stress tensor; τxy are shear components (see Figs. 7, 9); εxx and εyy are the components of the strain tensor along the x and y axes; εxy is the shear component of the strain tensor.

Hooke’s law for an orthotropic body, which connects elastic deformations eij in the direction of the elastic anisotropy axes with stresses (for the plane problem ezz = 0), has the form

$$\begin{gathered} {{\sigma }_{x}} = {{E}_{{xx}}}{{\left( {{{e}_{{xx}}} + {{\mu }_{{xy}}}{{e}_{{yy}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{e}_{{xx}}} + {{\mu }_{{xy}}}{{e}_{{yy}}}} \right)} \Delta }} \right. \kern-0em} \Delta }; \hfill \\ {{\sigma }_{y}} = {{E}_{{yy}}}{{\left( {{{e}_{{yy}}} + {{\mu }_{{yx}}}{{e}_{{xx}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{e}_{{yy}}} + {{\mu }_{{yx}}}{{e}_{{xx}}}} \right)} \Delta }} \right. \kern-0em} \Delta }; \hfill \\ {{\tau }_{{xy}}} = {{G}_{{xy}}}{{e}_{{xy}}};\,\,\,\,\Delta = 1 - {{\mu }_{{xy}}}{{\mu }_{{yx}}}, \hfill \\ \end{gathered} $$
(4)

where Exx, Eyy, and Gxy are the Young’s normal moduli and shear modulus of the orthotropic contact layer, while μxy and μyx are the Poisson’s coefficients of the anisotropic contact layer.

For an elastic contact layer, instead of relations (3), we have

$${{e}_{{xx}}} = \partial u{\text{/}}\partial x;\,\,\,\,{{e}_{{yy}}} = \partial \nu {\text{/}}\partial y;\,\,\,\,{{e}_{{xy}}} = \partial u{\text{/}}\partial y + \partial \nu {\text{/}}\partial x.$$
(5)

Since the structure of the contact layer is a “brush” in which the rods are perpendicular to the contact surface and do not touch each other, the stresses σx in it are equal to zero. This means that, in the first equation (4), modulus Exx = 0. This result allows direct integration of equilibrium equations (2). Due to the conservation of continuity at the boundaries y = ±h* of the contact layer, the displacement continuity conditions must be satisfied; i.e., at these boundaries, displacements u and ν of the contact layer and the adjacent plates must be equal to each other. Due to the relatively small transverse dimensions of the model, when solving the problem, one can restrict oneself to the theory of plates or beams. In this case, integrating the system of Eqs. (2)–(5) with the satisfaction of the boundary conditions for the displacements, the following expressions for the stresses and displacements in the contact layer are obtained:

$$\begin{gathered} {{\sigma }_{x}} = 0;\,\,\,\,{{\tau }_{{xy}}} = {{\tau }_{{yx}}} = \tau (x); \\ {{\sigma }_{y}} = - y(d\tau {\text{/}}dx) + (1{\text{/}}h\text{*}){{E}_{{xx}}}\chi ; \\ \nu = (1{\text{/}}2{{E}_{{yy}}})(h \text{*}{^{2}} - {{y}^{2}})(d\tau {\text{/}}dx) + (1{\text{/}}h\text{*})y\chi \\ + \,\,(1{\text{/2}}h\text{*})(h\text{*}{^{2}} - {{y}^{2}})\left( {d\chi {\text{/}}dx - y(d\zeta {\text{/}}dx) + \psi } \right). \\ \end{gathered} $$
(6)

Here, we used the notation for functions of x, representing the half-sums of displacements at the boundaries ±h* of the contact (here, the middle) layer:

$$\begin{gathered} 2\chi = \nu (h\text{*}) - \nu ( - h\text{*});\,\,\,\,2\zeta \nu (h\text{*}) + \nu ( - h\text{*}), \\ 2\lambda = u(h\text{*}) - u( - h\text{*});\,\,\,\,2\psi = u(h\text{*}) + u( - h\text{*}). \\ \end{gathered} $$
(7)

In system of equations (6), all four desired functions u, ν, τxy, and σy, as a result of integration, are expressed in terms of functions τ, ζ, χ, and ψ. This change is made it convenient to apply the well-developed theory of plates. Function λ is expressed in terms of two of these four functions:

$$\begin{gathered} \lambda = (h\text{*}{\kern 1pt} {\text{/}}{{G}_{{xy}}})\tau - (1{\text{/}}3{{E}_{{yy}}})h\text{*} {^{3}}\left( {{{d}^{2}}\tau {\text{/}}d{{x}^{2}}} \right) \\ - \,\,h\text{*}\left( {d\zeta {\text{/}}dx} \right). \\ \end{gathered} $$
(8)

Desired functions τ, ζ, χ, and ψ are determined from the compatibility conditions of deformations of the contact and outer layers and the fulfillment of Newton’s third law. Without going into the details, which can be found, for example, in [2], as a result of the transformations, a system of seven equations is obtained for the seven desired functions χ, λ, ψ, τ, qy1, N1, and N2:

$$\begin{gathered} {{P}_{{y1}}} = - ({{h}_{1}}{\text{/}}2)\left( {{\text{d}}{{P}_{{x1}}}{\text{/d}}x} \right); \\ {{P}_{{x1}}} = - {{D}_{{a1}}}{{{\text{d}}}^{2}}(\psi + \lambda ){\text{/d}}{{x}^{2}}; \\ {{P}_{{x2}}} = {{D}_{{a2}}}\left[ {{{{\text{d}}}^{2}}(\psi - \lambda ){\text{/d}}{{x}^{2}} + {{h}_{2}}{\text{(}}{{{\text{d}}}^{3}}\chi {\text{/d}}{{x}^{3}})} \right]; \\ 2{{B}_{{a2}}}({{{\text{d}}}^{4}}\chi {\text{/d}}{{x}^{4}}) = {{P}_{{y2}}} + 2{{N}_{2}}{\text{(}}{{{\text{d}}}^{2}}\chi {\text{/d}}{{x}^{2}}) \\ - \,\,({{h}_{2}}{\text{/}}2)({\text{d}}{{P}_{{x2}}}{\text{/d}}x); \\ {{N}_{i}} = {{D}_{{ai}}}\left[ {{\text{d(}}\psi \pm \lambda {\text{)/d}}x - {{\varepsilon }_{{qi}}}} \right],\,\,\,\,i = 1,2. \\ \end{gathered} $$
(9)

After simple transformations of system (9), it is possible to obtain a defining equation with respect to desired function χ:

$${{\chi }^{{{\text{VIII}}}}} - \omega {{\chi }^{{{\text{VI}}}}} + {{K}^{2}}{{\chi }^{{{\text{IV}}}}} - K_{M}^{2}\omega {{\chi }^{{{\text{II}}}}} + K_{M}^{2}{{C}_{M}} = 0,$$
(10)

where

$$\begin{gathered} \omega = {{12{{E}_{{yy}}}} \mathord{\left/ {\vphantom {{12{{E}_{{yy}}}} {\left( {h_{3}^{2}{{G}_{{xy}}}} \right)}}} \right. \kern-0em} {\left( {h_{3}^{2}{{G}_{{xy}}}} \right)}};\,\,\,\,K_{M}^{2} = b{{E}_{{yy}}}{\text{/}}({{h}_{3}}{{B}_{{a2}}}); \\ c_{M}^{2} = \left( {12b{{E}_{{yy}}}{\text{/}}h_{3}^{3}} \right)(1{\text{/}}{{D}_{{a1}}} + 1{\text{/}}{{D}_{{a2}}}); \\ {{K}^{2}} = K_{M}^{2}\left[ {1 + 3{{{(1 + {{h}_{2}}{\text{/}}{{h}_{3}})}}^{2}}} \right] + c_{M}^{2}; \\ {{D}_{{ai}}} = {{E}_{i}}{{h}_{i}}b;\,\,\,\,(i = 1,2);\,\,\,\,{{B}_{{a2}}} = {{E}_{2}}bh_{2}^{3}{\text{/}}12. \\ \end{gathered} $$
(11)

The solution to such an equation is sought in the form (taking into account the symmetry with respect to 0y):

$$\chi = \sum\limits_{r = 1}^4 {{{A}_{r}}{\text{ch}}{{s}_{r}}x,} $$
(12)

where sr are the roots of the characteristic equation

$${{s}^{8}} - \omega {{s}^{6}} + {{K}^{2}}{{s}^{4}} - K_{M}^{2}\omega {{s}^{2}} + K_{M}^{2}c_{M}^{2} = 0.$$
(13)

Analysis using Vieta theorem shows that, of the four roots (s2 = w) of Eq. (13), two are real and two are complex conjugate. The approximate expression for real roots is

$$\begin{gathered} s_{1}^{2} \approx {{c_{M}^{2}} \mathord{\left/ {\vphantom {{c_{M}^{2}} \omega }} \right. \kern-0em} \omega } = \left( {b{{G}_{{xy}}}{\text{/}}{{h}_{3}}} \right)\left( {1{\text{/}}{{D}_{{a1}}} + 1{\text{/}}{{D}_{{a2}}}} \right); \\ s_{2}^{2} \approx \omega = {{12{{E}_{{yy}}}} \mathord{\left/ {\vphantom {{12{{E}_{{yy}}}} {\left( {h_{3}^{2}{{G}_{{xy}}}} \right)}}} \right. \kern-0em} {\left( {h_{3}^{2}{{G}_{{xy}}}} \right)}}, \\ \end{gathered} $$
(14)

and that for complex roots is

$$\begin{gathered} s_{{3,4}}^{2} = \alpha \pm i\beta ;\,\,\,\,\alpha \approx \sqrt[4]{{K_{M}^{2}{\text{/}}2 - s_{1}^{2}{\text{/}}4}}; \\ \beta \approx \sqrt[4]{{K_{M}^{2}{\text{/}}2 + s_{1}^{2}{\text{/}}4}}. \\ \end{gathered} $$
(15)

In our case, we can approximately put

$$\alpha \approx \beta \approx \sqrt[4]{{\frac{{6{{E}_{{yy}}}{{E}_{1}}{{h}_{1}}s_{1}^{2}}}{{{{G}_{{xy}}}({{E}_{1}}{{h}_{1}} + {{E}_{2}}{{h}_{2}})h_{2}^{2}}}}};\,\,\,\,s_{{3,4}}^{2} = \alpha (1 \pm i).$$
(16)

The integration constants of coefficients Ar in (15) are determined from the boundary conditions for x = ±l/2:

$$\begin{gathered} {{N}_{1}} = 0;\,\,\,\,{{N}_{2}} = P;\,\,\,\,{{M}_{1}} = {{M}_{2}} = 0;\,\,\,\,{{Q}_{1}} = {{Q}_{2}} = 0; \\ \tau = 0;\,\,\,\,\int\limits_{ - l/2}^{l/2} {{{\sigma }_{y}}{\text{d}}x = 0} ;\,\,\,\,\int\limits_{ - l/2}^{l/2} {\tau {\text{d}}x = 0} . \\ \end{gathered} $$
(17)

Turning to displacements, boundary conditions (17) can be written in the following form:

$$\begin{gathered} {\text{d}}\lambda {\text{/d}}x = {\text{d}}\bar {\lambda }{\text{/d}}x = 1{\text{/}}2( - P{\text{/}}{{D}_{{a2}}} + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q2}}}); \\ {\text{d}}\psi {\text{/d}}x = {\text{d}}\bar {\psi }{\text{/d}}x = 1{\text{/}}2(P{\text{/}}{{D}_{{a2}}} + {{\varepsilon }_{{q1}}} + {{\varepsilon }_{{q2}}});\,\,\,\,\tau = 0. \\ \end{gathered} $$
(18)

Without going into the details of the transformations and solutions, we write out the final formulas:

$$\begin{gathered} \chi (x) = A_{1}^{0}{\text{cosh}}{{s}_{1}}x + A_{2}^{0}{\text{cosh}}{{s}_{2}}x \\ + \,\,2A_{3}^{0}{\text{cosh}}\alpha x{\kern 1pt} \cos {\kern 1pt} \alpha x + 2A_{4}^{0}{\text{sinh}}\alpha x{\kern 1pt} \sin {\kern 1pt} \alpha x. \\ \end{gathered} $$
(19)

Constants \(A_{r}^{0}\) are related to Ar as follows:

$$\begin{gathered} {{A}_{1}} = A_{1}^{0};\,\,\,\,{{A}_{2}} = A_{2}^{0};\,\,\,\,{{A}_{{3,4}}} \pm i{{A}_{4}}; \\ A_{r}^{0} = \frac{{ - 3b({{h}_{2}} + {{h}_{3}})}}{{{{h}_{3}}}}\left( { - \frac{P}{{{{D}_{{a2}}}}} + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q2}}}} \right)({{\phi }_{r}}{\text{/}}\Phi ), \\ \end{gathered} $$
(20)

where

$$\begin{aligned} & {{\phi }_{1}}=1;\,\,\,\,{{\phi }_{2}}=-\frac{{{s}_{2}}}{{{s}_{1}}}\frac{4{{\alpha }^{4}}+s_{1}^{4}\text{sinh}{{\nu }_{1}}}{4{{\alpha }^{4}}+s_{2}^{4}\text{sinh}{{\nu }_{2}}}; \\ & {{\phi }_{3}}=\frac{-\cos {\kern 1pt} \nu \text{cosh}{\kern 1pt} {{\nu }_{1}}}{{{s}_{1}}\left( 4{{\alpha }^{4}}+s_{2}^{4} \right)\text{4}{{\alpha }^{2}}\text{cosh}\nu }\left\{ 4{{\alpha }^{3}}\left( s_{2}^{4}-s_{1}^{4} \right) \right. \\ & \left. +\,\,(1-\tan {\kern 1pt} \nu )\left[ s_{1}^{3}\left( 4{{\alpha }^{4}}+s_{2}^{4} \right)+s_{2}^{3}\left( 4{{\alpha }^{4}}+s_{1}^{4} \right) \right] \right\}; \\ & {{\phi }_{4}}=\frac{\sin {\kern 1pt} \nu \text{cosh}{\kern 1pt} {{\nu }_{1}}}{{{s}_{1}}\left( 4{{\alpha }^{4}}+s_{2}^{4} \right)\text{4}{{\alpha }^{2}}\text{cosh}\nu }\left\{ 4{{\alpha }^{3}}\left( s_{2}^{4}-s_{1}^{4} \right) \right. \\ & \left. +\,\,(1+\text{ctan}{\kern 1pt} \nu )\left[ s_{1}^{3}\left( 4{{\alpha }^{4}}+s_{2}^{4} \right)+s_{2}^{3}\left( 4{{\alpha }^{4}}+s_{1}^{4} \right) \right] \right\}; \\ & \Phi =2\sum\limits_{1}^{4}{{{b}_{r}}\text{cosh}{{\nu }_{r}}}; \\ & 2{{b}_{1}}={{C}_{1}}s_{1}^{6}+{{C}_{2}}s_{1}^{4}+{{C}_{3}};\overrightarrow{\scriptscriptstyle\leftarrow}2{{b}_{1}}={{C}_{1}}s_{2}^{8}+{{C}_{2}}s_{2}^{4}+{{C}_{3}}; \\ & {{b}_{3}}=8{{\alpha }^{6}}{{C}_{1}}{\kern 1pt} \sin {\kern 1pt} \nu -4{{\alpha }^{4}}{{C}_{2}}{\kern 1pt} \cos {\kern 1pt} \nu +{{C}_{3}}{\kern 1pt} \cos {\kern 1pt} \nu ; \\ & {{b}_{4}}=8{{\alpha }^{6}}{{C}_{1}}{\kern 1pt} \cos {\kern 1pt} \nu -4{{\alpha }^{4}}{{C}_{2}}{\kern 1pt} \sin {\kern 1pt} \nu +{{C}_{3}}{\kern 1pt} \sin {\kern 1pt} \nu ; \\ \end{aligned}$$
$$\begin{gathered} {{C}_{1}} = h_{3}^{2}{{B}_{{a2}}}{\text{/}}{{E}_{{yy}}};\,\,\,\,{{C}_{2}} = - 12{{B}_{{a2}}}{\text{/}}{{G}_{{xy}}}; \\ {{C}_{3}} = - 12b{{E}_{{yy}}}{\text{/}}({{h}_{3}}{\text{/}}{{G}_{{xy}}}); \\ {{C}_{4}} = b{{\left( {3h_{2}^{2} + 4h_{3}^{2} + 6{{h}_{2}}{{h}_{3}}} \right)} \mathord{\left/ {\vphantom {{\left( {3h_{2}^{2} + 4h_{3}^{2} + 6{{h}_{2}}{{h}_{3}}} \right)} {{{h}_{3}}}}} \right. \kern-0em} {{{h}_{3}}}}. \\ \end{gathered} $$
(21)

Tangential stresses τ are

$$\begin{gathered} \tau \,\,{\text{ = }}\,\,\frac{{12}}{{{{h}_{3}}\Phi }}\left( { - \frac{P}{{{{D}_{{a2}}}}} + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q2}}}} \right)\left\{ {\left( {{{B}_{{a2}}}s_{1}^{3} + \frac{{b{{E}_{{yy}}}}}{{{{h}_{3}}{{s}_{1}}}}} \right)} \right.{\text{sh}}{{s}_{1}}x \\ + \,\,{{\phi }_{2}}\left( {{{B}_{{a2}}}s_{2}^{3} + \frac{{b{{E}_{{yy}}}}}{{{{h}_{3}}{{s}_{2}}}}} \right){\text{sh}}{{s}_{2}}x + \left( { - 2{{B}_{{a2}}}{{\alpha }^{3}} + \frac{{b{{E}_{{yy}}}}}{{2\alpha {{h}_{3}}}}} \right) \\ \times \,\,\left[ {2{{\phi }_{3}}({\text{tanh}}\alpha x{\kern 1pt} \cos {\kern 1pt} \alpha x + \sin {\kern 1pt} \alpha x)} \right. \\ \left. { + \left. {2\phi {{{_{{_{{}}^{{_{{}}^{{}}}}}}^{{_{{}}^{{}}}}}}_{4}}({\text{tanh}}\alpha x{\kern 1pt} \cos {\kern 1pt} \alpha x - \sin {\kern 1pt} \alpha x)} \right]} \right\}. \\ \end{gathered} $$
(22)

Normal stress σx1 in a reinforcing element (see Fig. 7) is

$$\begin{gathered} {{\sigma }_{{x1}}} = {{N}_{1}}{\text{/(}}b{{h}_{1}}{\text{)}} = {{E}_{1}}{\text{(d}}\lambda {\text{/d}}x \\ + \,\,{\text{d}}\psi {\text{/d}}x - {{\varepsilon }_{{q1}}}) = {{E}_{1}}{\text{(d}}\bar {\lambda }{\text{/d}}x + {\text{d}}\bar {\psi }{\text{/d}}x - {{\varepsilon }_{{q1}}}), \\ \end{gathered} $$
(23)

where

$$\begin{gathered} \frac{{d\bar {\lambda }}}{{dx}} = \frac{1}{{2\Phi }}\left( { - \frac{P}{{{{D}_{{a2}}}}} + {{\varepsilon }_{{q1}}} + {{\varepsilon }_{{q2}}}} \right)\,\,\left[ {{{q}_{1}}{\text{cosh}}{{s}_{1}}x{\kern 1pt} + {{\phi }_{2}}{{g}_{2}}{\text{cosh}}{{s}_{2}}x} \right. \\ \left. { + \,\,{{\phi }_{4}}{{g}_{3}}{\text{cosh}}\alpha {\kern 1pt} x\cos {\kern 1pt} \alpha x + 2({{\phi }_{3}}{{g}_{4}} - {{\phi }_{4}}{{g}_{3}}){\text{sinh}}\alpha {\kern 1pt} x\sin {\kern 1pt} \alpha x} \right]; \\ {{g}_{1}} = 2{{b}_{1}};\,\,\,\,{{g}_{2}} = 2{{b}_{2}};\,\,\,\,{{g}_{3}} = 2{{\alpha }^{2}}({{\alpha }^{4}}{{C}_{1}} - {{C}_{4}}); \\ {{g}_{4}} = {{C}_{3}} - 4{{\alpha }^{4}}{{C}_{2}}; \\ {{{\bar {\psi }}}_{1}} = \frac{{6b}}{{{{h}_{3}}\Phi }}\left( {\frac{1}{{{{D}_{{a2}}}}} - \frac{1}{{{{D}_{{a2}}}}}} \right)\left( { - \frac{P}{{{{D}_{{a2}}}}} + {{\varepsilon }_{{q1}}} + {{\varepsilon }_{{q2}}}} \right) \\ \times \,\,\left\{ {\left( {{{m}_{1}}{\kern 1pt} \cos {\kern 1pt} {{s}_{1}}x + {{q}_{1}}{\text{ch}}{{\nu }_{1}}} \right) + {{\phi }_{2}}\left( {{{m}_{2}}{\kern 1pt} \cos {\kern 1pt} {{s}_{2}}x + {{q}_{2}}{\text{ch}}{{\nu }_{2}}} \right)_{{_{{}}^{{_{{}}^{{}}}}}}^{{_{{}}^{{_{{}}^{{}}}}}}} \right. \\ + \,\,{{\phi }_{3}}\left( {{{m}_{3}}\sin {\kern 1pt} \alpha x{\text{sinh}}\alpha x + {{q}_{3}}{\text{sin}}{\kern 1pt} \nu {\text{cosh}}\nu } \right) \\ - \,\,{{\phi }_{4}}\left( {{{m}_{3}}\cos {\kern 1pt} \alpha x{\text{cosh}}\alpha x + {{q}_{3}}{\text{cos}}{\kern 1pt} \nu {\text{cosh}}\nu } \right) \\ \left. { + \,\,\frac{1}{2}\left( {\frac{P}{{{{D}_{{a2}}}}} + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q2}}}} \right)} \right\}; \\ \end{gathered} $$
$$\begin{gathered} {{q}_{1}} = {{ - b{{E}_{{yy}}}} \mathord{\left/ {\vphantom {{ - b{{E}_{{yy}}}} {\left( {{{h}_{3}}s_{1}^{2}} \right)}}} \right. \kern-0em} {\left( {{{h}_{3}}s_{1}^{2}} \right)}};\,\,\,\,{{m}_{1}} = {{B}_{{a2}}}s_{1}^{2} - {{q}_{1}}; \\ {{q}_{2}} = {{ - b{{E}_{{yy}}}} \mathord{\left/ {\vphantom {{ - b{{E}_{{yy}}}} {\left( {{{h}_{3}}s_{2}^{2}} \right)}}} \right. \kern-0em} {\left( {{{h}_{3}}s_{2}^{2}} \right)}};\,\,\,\,{{m}_{2}} = {{B}_{{a2}}}s_{2}^{2} - {{q}_{2}}; \\ {{q}_{3}} = {{ - b{{E}_{{yy}}}} \mathord{\left/ {\vphantom {{ - b{{E}_{{yy}}}} {\left( {2{{h}_{3}}{{\alpha }^{2}}} \right)}}} \right. \kern-0em} {\left( {2{{h}_{3}}{{\alpha }^{2}}} \right)}};\,\,\,\,{{m}_{3}} = {{B}_{{a2}}}{{\alpha }^{2}} - {{q}_{3}}. \\ \end{gathered} $$
(25)

Finally, σy in the contact layer is

$$\begin{gathered} {{\sigma }_{y}}(x,y) = ({{h}_{1}} + {{h}_{3}}{\text{/}}2 - y)\frac{{{\text{d}}\tau }}{{{\text{d}}x}} - \frac{{2{{E}_{{yy}}}}}{{{{h}_{3}}}}\chi , \\ ({{h}_{1}} \leqslant y \leqslant {{h}_{1}} + {{h}_{3}}). \\ \end{gathered} $$
(26)

Figure 10 shows the distribution curves of the reduced normal stresses \(\sigma _{{x1}}^{*}\) (curve 1) in the reinforcing element and tangential stresses τ* (curve 2) at the boundary. The expressions of these stresses are obtained from (22) and (23) by dividing them by the impact applied to the system, which is the value

$$\begin{gathered} Q = - P + {{D}_{{a2}}}\left( {{{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q2}}}} \right);\,\,\,\,\sigma _{{x1}}^{*} = {{\sigma }_{{x1}}}{\text{/}}Q; \\ \tau \text{*} = \tau {\text{/}}Q. \\ \end{gathered} $$
(27)
Fig. 10.
figure 10

Distribution of normal (1, 1') stresses \(\sigma _{{x1}}^{*}\)(σx1/Q) in the reinforcing element and tangential (2 and 2') stresses τ* (τ/Q) at the fiber–polymer interface. Solid curves are the result of solving a two-dimensional problem: at the left end, both stresses are equal to zero. The dotted line is a one-dimensional problem.

Full size image

In the calculations, the constant of the polyester resin was taken for the polymer plate as E2 = 240 MPa, while, for a reinforcing element (rod) glass, E1 = 72 000 MPa. For the contact layer constants, Eyy = 2400 MPa and Gxy/h3 = 25 000 MPa/mm. The geometrical dimensions of the model are h1 = 0.2 mm, h2 = 4 mm, l = 20, and b = 2.5 mm.

Parameter Gxy/h3 was determined from independent experiments.

Figure 10 shows that the maximum of tensile stresses in the reinforcing element is located closer to the end, and not in the middle of its length, as follows from the solution of the one-dimensional problem (curve 1'), and its value can significantly (by 30–40%) exceed the value of the stress obtained from the one-dimensional problem. If this excess overlaps the dispersion of the fiber strength, then fiber rupture should be expected at the point of maximum σx1. As concerns the experimental model, this means that, after the first, often accidental, fiber break, subsequent breaks can be expected in the vicinity of this first one. An explanation of the limited temperature range in which such a dependence is observed should, apparently, be sought in a change in the physical parameters of the resin and fiber dispersion. The oscillating distribution of tangential stresses near the end (curve 2) is noteworthy, as is the exact satisfaction of boundary conditions τ = 0 at x = ±l/2. All this significantly distinguishes the solution of the two-dimensional problem from the one-dimensional one (curve 2 '). However, the dimensions of the zone of the edge effect of stress concentration in both cases are quite close.

The solution of the considered problem in a one-dimensional formulation is written in the form

$$\begin{gathered} {{\sigma }_{{x1}}} = - {{E}_{1}}\frac{{{{D}_{{a2}}}}}{{{{D}_{{a1}}} + {{D}_{{a2}}}}}\left( { - \frac{P}{{{{D}_{{a2}}}}} + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q2}}}} \right)\left( {1 - \frac{{{\text{cosh}}\alpha x}}{{{\text{cosh}}\nu }}} \right); \\ \tau = - \alpha \frac{{{{D}_{{a2}}}{{D}_{{a2}}}b}}{{{{D}_{{a1}}} + {{D}_{{a2}}}}}\left( { - \frac{P}{{{{D}_{{a2}}}}} + {{\varepsilon }_{{q1}}} - {{\varepsilon }_{{q2}}}} \right)\frac{{{\text{sinh}}\alpha x}}{{{\text{cosh}}\nu }}. \\ \end{gathered} $$
(28)

CONCLUSIONS

B.W. Rosen [5], starting from an analysis of the edge effect in solving a one-dimensional problem, proceeded to consider the process of destruction of unidirectional reinforced plastic. The essence of his approach is as follows. It is known that the strength of a fiber, as well as the strength of a bundle of independent fibers, depends on the base, i.e., on the length of the tested fiber or bundle [1]. At the same time, the strength of a microplastic made from a bundle of such fibers connected into a monolith by a cured resin is practically independent of the base. Applying the solution of the one-dimensional problem and the concept of damage accumulation to the analysis of experimental results on the destruction of microplastics, Rosen came to the conclusion that the strength of microplastics is determined by the strength of the fibers in the bundle over a length equal to the length of the edge-effect zone, i.e., that part of the fiber near its end, which, according to the solution of the one-dimensional problem, is not fully loaded (see Fig. 10, curve 1') and, therefore, is called the “ineffective length.” This concept has found wide acceptance and application. However, it remains unclear how the least loaded (according to the solution of the one-dimensional problem) part of the fiber can determine the strength of the plastic. Apparently, this ambiguity is eliminated as a result of the solution of the two-dimensional problem presented here, because it follows from it (compare curves 2 and 2 ' in Fig. 10) that it is on the length of the edge effect zone, that is, on the “ineffective length,” that tensile stresses in the fiber can reach values ​​that are higher than those obtained from one-dimensional solutions (i.e., far from the fiber end) and, naturally, fiber failure should be expected precisely here.