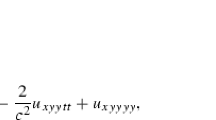Keywords

1 Introduction

Direct numerical simulation (DNS) and large eddy simulation (LES) are two important methods to reveal the mechanism of multiscale problems such as turbulence and aeroacoustics. DNS for multiscale problems requires that the numerical grid should be fine enough to resolve the structure of smallest scales. However, due to the limitation of computational resources, most DNS studies have been carried out with marginal grid resolution. Besides the common problems in DNS of turbulence, there are computational issues that are unique to aeroacoustics (Tam 1995). First, the aerodynamic noise is broadband and the spectrum is fairly wide. Second, the amplitudes of the physical variables of the aerodynamic noise are far smaller than those of the mean flow. Third, the distance from the noise source to the location of interest in aeroacoustic problems is quite long. To ensure that the computed solution is uniformly accurate over such a long propagation distance, the numerical scheme should have minimal numerical dispersion, dissipation, and anisotropy.

The most influential compact schemes for derivatives, interpolation, and filtering were proposed by Lele (1992). Through systematic Fourier analysis, it is shown that these compact schemes have spectral-like resolution for short waves.

In this paper, we propose a new idea to design the compact scheme based on the cell-centered compact scheme of Lele (1992). Instead of using only the values on cell centers, both the values of cell centers and grid nodes are used on the right hand side of compact schemes. Both the accuracy order and the wave resolution property are improved significantly. Numerical tests show that this is an ideal scheme for the DNS for multiscale problems.

2 Central Compact Schemes

In this section, we present the methodology to design central compact schemes (CCS). We start our work from the cell-centered compact scheme (CCCS) proposed by Lele (1992). Then we extend this scheme to a class of higher order schemes with good spectral resolution.

2.1 Lele’s Compact Scheme

Lele (1992) proposed two kinds of central compact schemes. One is a linear CCCS given by

$$ \beta f^{\prime}_{j - 2} \, + \,\alpha f^{\prime}_{j - 1} \, + \,f^{\prime}_{j} \, + \,\alpha f^{\prime}_{j + 1} \, + \,\beta f^{\prime}_{j + 2} = a\frac{{f_{{j + \frac{1}{2}}} \, - \,f_{{j - \frac{1}{2}}} }}{\Updelta x}\, + \,b\frac{{f_{{j + \frac{3}{2}}} \, - \,f_{{j - \frac{3}{2}}} }}{3\Updelta x}\, + \,c\frac{{f_{{j + \frac{5}{2}}} \, - \,f_{{j - \frac{5}{2}}} }}{5\Updelta x} $$
(1)

The other is a cell-noded compact scheme (CNCS) given by

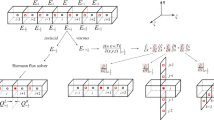
$$ \beta f^{\prime}_{j - 2} \, + \,\alpha f^{\prime}_{j - 1} \, + \,f^{\prime}_{j} \, + \,\alpha f^{\prime}_{j + 1} \, + \,\beta f^{\prime}_{j + 2} = a\frac{{f_{j + 1} \, - \,f_{j - 1} }}{2\Updelta x}\, + \,b\frac{{f_{j + 2} \, - \,f_{j - 2} }}{4\Updelta x}\, + \,c\frac{{f_{j + 3} \, - \,f_{j - 3} }}{6\Updelta x} $$
(2)

The stencil involved in the CCCS and CNCS is shown in Fig. 1. The constraints on the coefficients \( \alpha \), \( \beta \), a, b, and c corresponding to different orders of accuracy can be derived by matching the Taylor series coefficients and these have been listed in Lele (1992).

Fig. 1
figure 1

The stencil of cell-centerd and cell-noded compact schemes

Full size image

2.2 A New Class of Central Compact Schemes

In Lele’s cell-centered compact schemes given by Eq. (1), the stencil contains both the grid point and half grid points. However, only the values at the cell-centers are used to calculate the derivatives at the cell-nodes. If the values at both the cell-nodes and the cell-centers are used, one could get a compact scheme with higher order accuracy and better resolution.

Based on this idea, we design a class of CCS given by the following formula. We use the scheme (3) to compute the values on cell-nodes, and the scheme (4) to compute the values on cell-centers.

$$ \beta f^{\prime}_{j - 2} \, + \,\alpha f^{\prime}_{j - 1} \, + \,f^{\prime}_{j} \, + \,\alpha f^{\prime}_{j + 1} \, + \,\beta f^{\prime}_{j + 2} = a\frac{{f_{{j + \frac{1}{2}}} \, - \,f_{{j - \frac{1}{2}}} }}{\Updelta x}\, + \,b\frac{{f_{j + 1} \, - \,f_{j - 1} }}{2\Updelta x}\, + \,c\frac{{f_{{j + \frac{3}{2}}} \, - \,f_{{j - \frac{3}{2}}} }}{3\Updelta x}\, + \,{d}\frac{{f_{j + 2} \, - \,f_{j - 2} }}{4\Updelta x}\, + \,e\frac{{f_{{j + \frac{5}{2}}} \, - \,f_{{j - \frac{5}{2}}} }}{5\Updelta x} $$
(3)
$$ \beta f^{\prime}_{{j - \frac{5}{2}}} \, + \,\alpha f^{\prime}_{{j - \frac{3}{2}}} \, + \,f^{\prime}_{{j - \frac{1}{2}}} \, + \,\alpha f^{\prime}_{{j + \frac{1}{2}}} \, + \,\beta f^{\prime}_{{j + \frac{3}{2}}} = a\frac{{f_{j} \, - \,f_{j - 1} }}{\Updelta x}\, + \,b\frac{{f_{{j + \frac{1}{2}}} \, - \,f_{{j - \frac{3}{2}}} }}{2\Updelta x}\, + \,c\frac{{f_{j + 1} \, - \,f_{j - 2} }}{3\Updelta x}\, + \,d\frac{{f_{{j + \frac{3}{2}}} \, - \,f_{{j - \frac{5}{2}}} }}{4\Updelta x}\, + \,e\frac{{f_{j + 2} \, - \,f_{j - 3} }}{5\Updelta x} $$
(4)

We note that the cell-centered compact schemes (CCCS) given by Eq. (1) and cell-noded compact schemes (CNCS) given by Eq. (2) of Lele (1992) are both special cases of this class of CCS.

The physical values on cell-centers can be interpolated from the physical values of cell-nodes. In fact, a high order compact interpolation was proposed by Lele (1992), which has the following form:

$$ \beta \hat{f}_{{j - \frac{3}{2}}} \, + \,\alpha \hat{f}_{{j - \frac{1}{2}}} \, + \,\hat{f}_{{j + \frac{1}{2}}} \, + \,\alpha \hat{f}_{{j + \frac{3}{2}}} \, + \,\beta \hat{f}_{{j + \frac{5}{2}}} = \frac{a}{2}\left( {f_{j} \, + \,f_{j + 1} } \right)\, + \,\frac{b}{2}\left( {f_{j - 1} \, + \,f_{j + 2} } \right)\, + \,\frac{c}{2}\left( {f_{j - 2} \, + \,f_{j + 3} } \right) $$
(5)

Taking the Fourier transformation to Eq. (3) and using Euler’s formula, the modified wavenumber of CCS can be obtained. It is:

$$ w^{\prime} = 2\frac{{a\,{ \sin }\left( \frac{w}{2} \right)\, + \,\frac{{b\,{ \sin }\left( w \right)}}{2}\, + \,\frac{{c\,{ \sin }\left( \frac{3w}{2} \right)}}{3}\, + \,\frac{{d\,{ \sin }\left( {2w} \right)}}{4}\, + \,\frac{{e{ \sin }\left( \frac{5w}{2} \right)}}{5}}}{{2\beta \,{ \cos }\left( {2w} \right) + 2\alpha \,{ \cos }\left( w \right)\, + \,1}} $$
(6)

Figure 2 shows the modified wavenumber of CCS, it is clear that the resolutions of CCS are much better than those of CNCS and CCCS.

Fig. 2
figure 2

Modified wavenumber of CCS and comparison with CCCS and CNCS. a tridiagonal schemes; b pentadiagonal schemes; c eighth order tridiagonal CCS and CCCS combined with eighth order compact interpolation; d eighth order tridiagonal CCS and CCCS combined with tenth order compact interpolation

Full size image

3 Numerical Experiments

In this section, we apply eighth order tridiagonal central compact scheme CCS-T8 as an example of CCS to simulate Euler and Navier–Stokes equations. The filter is chosen to be eighth order tridiagonal scheme, the time advancement is a third order TVD Runge–Kutta method.

3.1 Benchmark of Computational Aeroacoustics

We test a benchmark of Computational Aeroacoustics (Hardin et al. 1995). Sponge zones are used to absorb and minimize reflections from the computational boundaries. We take a \( 400 \times 400 \) equally spaced mesh and perform the simulation until t = 600.

Figure 3 contains the distributions of density along y = 0 at typical times and their comparison with the exact solution. No noticeable difference is observed between the numerical results and the exact solution.

Fig. 3
figure 3

The distribution of density along y = 0 and the comparison with the exact solution at typical times of the benchmark of CAA

Full size image

3.2 Three-Dimensional Decaying Isotropic Turbulence

We start with a specified spectrum for the initial velocity field which is divergence free. The normalized temperature and density are simply initialized to unity at all spatial points. The dimensionless parameters are Re = 519 and M = 0.308, yielding the initial turbulent Mach number M t to be 0.3 and the initial Taylor microscale Reynolds number \( \text{Re}_{\lambda } \) to be 72.

The computational domain is \( \left[ {0,2\pi } \right]\, \times \,\left[ {0,2\pi } \right]\, \times \,\left[ {0,2\pi } \right] \). Periodic boundary conditions are used in all boundaries. Figure 4 shows the grid converged results agree well with the numerical result of Samtaney et al. (2001). From this figure, we find that CCS needs 403 grid density to reach grid converged solution, while the smallest grid density to obtain the grid converged results are 643 and 803 for CCCS and CNCS respectively. Again, we find that the resolution of CCS is much better than those of CNCS and CCCS. It is an ideal numerical scheme for DNS of turbulence.

Fig. 4
figure 4

Grid convergence of the turbulent kinetic energy with different schemes

Full size image

4 Conclusions

In this paper, we design a new family of linear compact schemes, named central compact schemes, for the spatial derivatives in the Navier–Stokes equations based on the CCCS proposed by Lele (1992). Compared to other linear compact schemes, CCCS has nice spectral-like resolution, which may be a good method for the computation of multiscale problems. However, previous cell-centered compact schemes have the drawback that not all physical values on the stencil are used, which results in the numerical scheme not reaching its maximum accuracy order. The central compact scheme designed in this paper overcomes the drawbacks mentioned above. First, all physical values on the stencil are used. The schemes could reach the maximum accuracy order.

A systematic comparison with previous compact schemes, including cell-noded compact schemes and the cell-centered compact scheme, is made. The comparison shows the superiority of the central compact scheme over the previous compact schemes in accuracy and resolution. It appears to be an ideal numerical method for the computation of multiscale problems such as turbulence and aeroacoustics.