Compact Schemes for Multiscale Flows with Cell-Centered Finite Difference Method

Abstract

High-order compact interpolation schemes appropriate for multiscale flows are studied within a cell-centered finite difference method (CCFDM) framework where the robustness of high-order schemes on curvilinear grids can be greatly enhanced due to the satisfaction of geometric conservation law. Two types of compact interpolations are mainly developed in this paper for shock-free flows and shock-embedded flows respectively. The present compact schemes are verified to be superior over the explicit counterparts with same orders in terms of the spectral characteristics. Regarding the shock-free flows, low-dissipation low-dispersion properties are achieved by the spectral optimization. Three optimized compact schemes (Opt4, Opt6 and Opt8) are further validated to be attractive for shock-free problems by carrying out benchmarks from computational aeroacoustics workshops and two typical turbulence cases: Tayler–Green vortex and decaying isotropic turbulence. Regarding high-speed flows in the presence of shock waves, the shock-capturing capability is realized by extending the weighting technique to the compact interpolations. The criteria to choose optimally compact nonlinear sub-stencils on a most general compact global stencil are presented. Interestingly, the explicit WENO-type schemes can be reverted within the proposed compact framework. Three nonlinear compact schemes (UI5, CI6 and CI8) on two practical stencils are analyzed and further compared with their explicit counterparts by a series of numerical experiments. The compact ones are superior to explicit ones in resolving rich flow structures as well as discontinuities.

1 Introduction

For flows characterized by a broad range of temporal and spatial scales, such as the broadband turbulence noise involving a broad range of energy-containing turbulent vortices and acoustic waves, the highly accurate numerical methods are in demand to resolve adequate scales of flow structures. Over the past decades, there has been an intensive effort on the development of high-order methods in computational fluid dynamic community, referring the review articles [1,2,3]. Among all, finite difference method (FDM) on structured grid is widely used due to its high efficiency in retaining high-order accuracy for multidimensional problems.

Among the available high-order finite difference schemes, compact schemes [4] possess several superiorities over the explicit counterparts, such as smaller stencils, higher orders of accuracy and spectral-like resolution. The conventional compact schemes are linear and on central stencils without built-in dissipation at all. Hence, additional dissipation mechanism to damp spurious waves is required. One strategy is to use filtering schemes, which has been applied for problems in aeroacoustics [5,6,7] and turbulence [8]. Another alternative is to use upwind-type scheme, including the standard upwind-biased scheme [9, 10] and the upwind scheme on central stencil with optimization strategy [11, 12].

The aforementioned schemes [4,5,6,7,8,9,10,11,12] directly approximate the flux derivatives of convection dominated problems in the finite difference context. Similarly, the compact reconstruction schemes [13,14,15] are developed within the context of finite volume method (FVM) due to its inherent conservative property for non-uniform grids.

However, the above mentioned spectral-like compact schemes [4,5,6,7,8,9,10,11,12,13,14,15] are linear and only suitable for low-speed flows. Regarding the high-speed discontinuous flows in the presence of shock waves, the numerical methods should not only be accurate and free-of-dissipation in smooth region but also be robust to capture shock waves without significant non-physical oscillations [16, 17]. Under such conditions, shock-capturing scheme are needed.

Weighted essentially non-oscillation (WENO) [18] is a typically well-known high-order scheme for shock waves. Yet, the original form of WENO is excessively dissipative for smooth region. Therefore, several attempts to combine the advantages of spectral-like compact schemes with those in WENO schemes are proposed, such as the hybridization techniques [19,20,21] to confine numerical dissipation effectively in shock-embedded region, and the multi-stencil weighting technique according to adaptive reconstruction procedure [22,23,24,25]. The hybridization technique requires a shock sensor to switch between two schemes, which remains a bottleneck. Also, the reverted scheme around discontinuity is explicit. By contrast, the weighting technique yields the reverted scheme still being compact around discontinuity.

For a realistic configuration, implementation of FDMs is carried out in computational space where a body-fitted multiblock structured grid is widely adopted. The coordinate transformation from the Cartesian coordinates in physical space to the curvilinear coordinates in computational space should be carefully treated in order to fulfill the geometric conservation law (GCL) [26] numerically. The conservative WENO reconstructions [18,19,20,21,22,23,24,25] can be carried out in two ways [27]: finite-difference WENO and finite-volume WENO. From the perspective of satisfying GCL condition automatically, finite-volume WENO is preferable due to the conservation property of FVM. Oppositely, finite-difference WENO violates GCL condition because the nonlinear upwind reconstruction is inevitably implemented for the grid metrics. However, from another perspective of computational efficiency for multidimensional problems, the finite-difference WENO is economic due to the essentially dimension-by-dimension decoupling reconstruction procedure, whereas the finite-volume WENO is prohibitively time-consuming because the integration is performed on the Gaussian quadrature points [27, 28]. To sum up, neither the finite-difference WENO nor the finite-volume WENO is satisfactory.

Another high-order shock-capturing scheme in the finite difference context is called weighted compact nonlinear schemes (WCNS) [29] where the WENO interpolations instead of WENO reconstructions are coupled with compact differences to approximate the spatial flux derivatives. WCNS is attractive due to two properties: (1) Efficiency due to dimension-by-dimension decoupling; (2) Satisfaction of GCL condition by the designed symmetric conservative forms of the discretized metrics and Jacobians [30, 31]. Nonomura et al. [32] investigated the performance of finite-difference WENO and finite-difference WCNS in the freestream and vortex preservation properties with curvilinear grids. They found that finite-difference WCNS works well whilst finite-difference WENO cannot. A particular research to ensure the freestream preservation for the finite-difference WENO on curvilinear grids is given by Ref. [33].

A cell-centered finite difference method (CCFDM) [34,35,36] is a cell-centered extension of WCNS for complex curvilinear grids. The corresponding cell-centered symmetric conservative metric method (CCSCMM) is also elaborately designed in Ref. [34] to fulfill the GCL condition in the cell-centered method context. There are three major distinctions between CCFDM [34] and WCNS [29]. Firstly, the flow variables and geometric variables in CCFDM are stored on cell centers and nodes respectively, whereas they are both located on nodes in WCNS. Secondly, the Riemann solver is adopted for multiblock interfaces in CCFDM whilst the characteristic-based interface condition [37] is needed in WCNS. Thirdly, the singular axis with zero metrics is acceptable naturally in CCFDM. Thereby, the present work will be implemented based on CCFDM. All the proposed schemes in this paper can be extended to WCNS-series methods.

From the authors’ perspective, WCNS-series methods and CCFDM are both classified as interpolation-based methods, whilst finite-difference WENO-series methods are classified as reconstruction-based methods. The distinction depends on whether the nonlinear procedure is implemented by reconstruction or interpolation. However, regardless of which one is utilized, the interpolation/reconstruction procedure plays a dominate role in the spectral performance. Nonomura and Fujii [38] also pinpointed the effect of difference schemes of WCNS on the results is marginal. Hence, several recent efforts for WCNS-series schemes are devoted to the interpolations. Considering the spectral-like spectral properties of compact schemes, the linear dissipative compact interpolations [39] and two nonlinear compact interpolations [40, 41] are proposed in recent years.

The objective of this work targets on extending the compact schemes into CCFDM framework comprehensively but from a new perspective different from those in Ref. [39,40,41]. The most general formulations of compact interpolations and their related derivations are given at first. Thereafter, two series of schemes are presented with respect to low-speed smooth flows and high-speed shock-embedded flows for practical purposes. The linear low-dissipation and low-dispersion compact interpolations for low-speed flows are designed according to spectral optimization. The nonlinear compact interpolations for high-speed flows are designed by extending the novel weighting technique [42] to the present compact framework.

The organization of this paper is as follows: in Sect. 2, the Navier–Stokes governing equations and the discretization methodologies are introduced; in Sect. 3, the spectrally optimized linear compact schemes for shock-free problems are discussed where three practical schemes (Opt4/6/8) are particularly analyzed; in Sect. 4, a general method to extend the weighting technique to nonlinear compact schemes is presented, where three schemes (UI5, CI6 and CI8) on two widely used stencils are analyzed; in Sect. 5, a series of benchmark cases are carried out to demonstrate the performance of compact schemes in Sects. 3 and 4; this paper is finally summarized in Sect. 6.

2 Governing Equations and Methodology

2.1 Governing Equations

The non-dimensional Navier–Stokes equations in the Cartesian coordinates (x, y, z) are

$$ \frac{{\partial {\boldsymbol{U}}\left( {\boldsymbol{Q}} \right)}}{\partial t} + \frac{{\partial {\boldsymbol{E}}}}{\partial x}{ + }\frac{{\partial {\boldsymbol{F}}}}{\partial y} + \frac{{\partial {\boldsymbol{G}}}}{\partial z} = \frac{{M_{\infty } }}{Re}\left( {\frac{{\partial {\boldsymbol{E}}_{v} }}{\partial x}{ + }\frac{{\partial {\boldsymbol{F}}_{v} }}{\partial y} + \frac{{\partial {\boldsymbol{G}}_{v} }}{\partial z}} \right) , $$

(1)

where t is time, $M_{\infty }$ is Mach number. $Re$ is Reynolds number. The non-dimensional reference values are in Ref. [34]. The vector of conservative variables U, the inviscid fluxes E, F, G and viscous fluxes ${\boldsymbol{E}}_{v}$, ${\boldsymbol{F}}_{v}$, ${\boldsymbol{G}}_{v}$ are given by

$$ \begin{aligned} {\boldsymbol{U}} & = \left[ {\begin{array}{*{20}c} \rho \\ {\rho u} \\ {\rho v} \\ {\rho w} \\ {\rho e} \\ \end{array} } \right], \, {\boldsymbol{E}} = \left[ \begin{aligned} \rho u \hfill \\ \rho uu + p \hfill \\ \rho uv \hfill \\ \rho uw \hfill \\ (\rho e + p)u \hfill \\ \end{aligned} \right], \, {\boldsymbol{F}} = \left[ \begin{aligned} \rho v \hfill \\ \rho uv \hfill \\ \rho vv + p \hfill \\ \rho wv \hfill \\ (\rho e + p)v \hfill \\ \end{aligned} \right], \, {\boldsymbol{G}} = \left[ \begin{aligned} \rho w \hfill \\ \rho uw \hfill \\ \rho vw \hfill \\ \rho ww + p \hfill \\ (\rho e + p)w \hfill \\ \end{aligned} \right], \\ {\boldsymbol{E}}_{v} & = \left[ \begin{aligned} 0 \hfill \\ \tau_{11} \hfill \\ \tau_{12} \hfill \\ \tau_{13} \hfill \\ \varphi_{1} \hfill \\ \end{aligned} \right], \, {\boldsymbol{F}}_{v} = \left[ \begin{aligned} 0 \hfill \\ \tau_{21} \hfill \\ \tau_{22} \hfill \\ \tau_{23} \hfill \\ \varphi_{2} \hfill \\ \end{aligned} \right], \, {\boldsymbol{G}}_{v} = \left[ \begin{aligned} 0 \hfill \\ \tau_{31} \hfill \\ \tau_{32} \hfill \\ \tau_{33} \hfill \\ \varphi_{3} \hfill \\ \end{aligned} \right] , \end{aligned} $$

(2)

and ${\boldsymbol{Q}} = [\rho ,u,v,w,T]^{T}$ is the vector of primitive variables. $\rho$ is density, (u, v, w) are velocity components, T is temperature. $\rho e = {p \mathord{/ {\vphantom {p {\left( {\gamma - 1} \right)}}} \kern-0pt} {\left( {\gamma - 1} \right)}} + \rho {{\left( {u^{2} + v^{2} + w^{2} } \right)} \mathord{/ {\vphantom {{\left( {u^{2} + v^{2} + w^{2} } \right)} 2}} \kern-0pt} 2}$ is the total energy, and $p = {{\rho T} \mathord{/ {\vphantom {{\rho T} \gamma }} \kern-0pt} \gamma }$ is the non-dimensional static pressure. $\gamma = 1.4$ is the ratio of specific heats. The viscous stress $\tau_{ij}$ and heat flux related terms $\varphi_{i}$ are given by

$$ \begin{aligned} & \tau_{ij} = \mu \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }} - \frac{2}{3}\delta_{ij} \frac{{\partial u_{k} }}{{\partial x_{k} }}} \right),\quad i,j = 1,2,3 , { } \\ & \varphi_{i} = u\tau_{i1} + v\tau_{i2} + w\tau_{i3} + k\frac{\partial T}{{\partial x_{i} }},\quad i = 1,2,3. \\ \end{aligned} $$

(3)

By introducing the following coordinate transformation on stationary grids,

$$ \left\{ \begin{aligned} x = x\left( {\xi , \, \eta , \, \zeta } \right), \hfill \\ y = y\left( {\xi , \, \eta , \, \zeta } \right), \hfill \\ z = z\left( {\xi , \, \eta , \, \zeta } \right), \hfill \\ \end{aligned} \right. \, J = \left| {\begin{array}{*{20}c} {x_{\xi } } & {x_{\eta } } & {x_{\zeta } } \\ {y_{\xi } } & {y_{\eta } } & {y_{\zeta } } \\ {z_{\xi } } & {z_{\eta } } & {z_{\zeta } } \\ \end{array} } \right|, $$

(4)

where $x_{\xi }$ stands for the derivatives ${{\partial x} \mathord{/ {\vphantom {{\partial x} {\partial \xi }}} \kern-0pt} {\partial \xi }}$ and J stands for the Jacobian, the inviscid fluxes in Eq. (1) can be organized in the following form using chain rule,

$$ \begin{aligned} \frac{{\partial {\boldsymbol{E}}}}{\partial x}{ + }\frac{{\partial {\boldsymbol{F}}}}{\partial y} + \frac{{\partial {\boldsymbol{G}}}}{\partial z} = & \frac{{\partial {\boldsymbol{E}}}}{{\partial \xi_{i} }}\frac{{\partial \xi_{i} }}{\partial x} + \frac{{\partial {\boldsymbol{F}}}}{{\partial \xi_{i} }}\frac{{\partial \xi_{i} }}{\partial y} + \frac{{\partial {\boldsymbol{G}}}}{{\partial \xi_{i} }}\frac{{\partial \xi_{i} }}{\partial z} \\ = & \frac{1}{J}\frac{\partial }{{\partial \xi_{i} }}\left( {{\boldsymbol{E}}J\frac{{\partial \xi_{i} }}{\partial x}} \right) - \frac{1}{J}{\boldsymbol{E}}\underbrace {{\frac{\partial }{{\partial \xi_{i} }}\left( {J\frac{{\partial \xi_{i} }}{\partial x}} \right)}}_{{{\boldsymbol{I}}_{x} }} \\ & + \,\frac{1}{J}\frac{\partial }{{\partial \xi_{i} }}\left( {{\boldsymbol{F}}J\frac{{\partial \xi_{i} }}{\partial y}} \right) - \frac{1}{J}{\boldsymbol{F}}\underbrace {{\frac{\partial }{{\partial \xi_{i} }}\left( {J\frac{{\partial \xi_{i} }}{\partial y}} \right)}}_{{{\boldsymbol{I}}_{y} }} \\ & + \,\frac{1}{J}\frac{\partial }{{\partial \xi_{i} }}\left( {{\boldsymbol{G}}J\frac{{\partial \xi_{i} }}{\partial z}} \right) - \frac{1}{J}{\boldsymbol{G}}\underbrace {{\frac{\partial }{{\partial \xi_{i} }}\left( {J\frac{{\partial \xi_{i} }}{\partial z}} \right)}}_{{{\boldsymbol{I}}_{z} }} \\ = & \frac{1}{J}\left( {\frac{{\partial {\tilde{\boldsymbol{E}}}}}{\partial \xi }{ + }\frac{{\partial {\tilde{\boldsymbol{F}}}}}{\partial \eta } + \frac{{\partial {\tilde{\boldsymbol{G}}}}}{\partial \zeta }} \right), \\ \end{aligned} $$

(5)

where $\xi_{i} , \, i = 1,2,3$ represent $\xi$, $\eta$ and $\zeta$ respectively. Equation (5) holds if the following surface conservation law (SCL) [26] is satisfied:

$$ \left\{ \begin{aligned} {\boldsymbol{I}}_{x} = \left( {J\xi_{x} } \right)_{\xi } + \left( {J\eta_{x} } \right)_{\eta } + \left( {J\zeta_{x} } \right)_{\zeta } = 0, \hfill \\ {\boldsymbol{I}}_{y} = \left( {J\xi_{y} } \right)_{\xi } + \left( {J\eta_{y} } \right)_{\eta } + \left( {J\zeta_{y} } \right)_{\zeta } = 0, \hfill \\ {\boldsymbol{I}}_{y} = \left( {J\xi_{z} } \right)_{\xi } + \left( {J\eta_{z} } \right)_{\eta } + \left( {J\zeta_{z} } \right)_{\zeta } = 0. \hfill \\ \end{aligned} \right. $$

(6)

Finally, Eq. (1) under the generalized curvilinear coordinates (ξ, η, ζ) are written as:

$$ \frac{{\partial {\tilde{\boldsymbol{U}}}}}{\partial t} + \frac{{\partial {\tilde{\boldsymbol{E}}}}}{\partial \xi }{ + }\frac{{\partial {\tilde{\boldsymbol{F}}}}}{\partial \eta } + \frac{{\partial {\tilde{\boldsymbol{G}}}}}{\partial \zeta } = \frac{{M_{\infty } }}{Re}\left( {\frac{{\partial {\tilde{\boldsymbol{E}}}_{v} }}{\partial \xi }{ + }\frac{{\partial {\tilde{\boldsymbol{F}}}_{v} }}{\partial \eta } + \frac{{\partial {\tilde{\boldsymbol{G}}}_{v} }}{\partial \zeta }} \right), $$

(7)

where

$$ \begin{aligned} & {\tilde{\boldsymbol{U}}} = J{\boldsymbol{U}}, \\ & {\tilde{\boldsymbol{E}}} = {\boldsymbol{E}}J\xi_{x} + {\boldsymbol{F}}J\xi_{y} + {\boldsymbol{G}}J\xi_{z} ,\quad {\tilde{\boldsymbol{E}}}_{v} = {\boldsymbol{E}}_{v} J\xi_{x} + {\boldsymbol{F}}_{v} J\xi_{y} + {\boldsymbol{G}}_{v} J\xi_{z} , \\ & {\tilde{\boldsymbol{F}}} = {\boldsymbol{E}}J\eta_{x} + {\boldsymbol{F}}J\eta_{y} + {\boldsymbol{G}}J\eta_{z} ,\quad {\tilde{\boldsymbol{F}}}_{v} = {\boldsymbol{E}}_{v} J\eta_{x} + {\boldsymbol{F}}_{v} J\eta_{y} + {\boldsymbol{G}}_{v} J\eta_{z} , \\ & {\tilde{\boldsymbol{G}}} = {\boldsymbol{E}}J\zeta_{x} + {\boldsymbol{F}}J\zeta_{y} + {\boldsymbol{G}}J\zeta_{z} ,\quad {\tilde{\boldsymbol{G}}}_{v} = {\boldsymbol{E}}_{v} J\zeta_{x} + {\boldsymbol{F}}_{v} J\zeta_{y} + {\boldsymbol{G}}_{v} J\zeta_{z} . \\ \end{aligned} $$

(8)

In the following Sects. 2.2 and 2.3, the discretization of spatial flux derivatives in Eq. (7) and the calculations of grid metrics and Jacobian in Eq. (8) will be introduced, respectively. Before proceeding any further, some notations for grid nodes, edges, faces and cells are clarified particularly, involving the locations for flow-dependent variables and geometry-dependent variables. The solution points are located at cell centers: (i, j, k). The grid nodes are denoted by (i ± 1/2, j ± 1/2, k ± 1/2). The fluxes are evaluated on the face centers which are denoted by (i ± 1/2, j, k), (i, j ± 1/2, k) and (i, j, k ± 1/2) according to ξ, η and ζ curvilinear grid lines respectively.

2.2 Cell-Centered Finite Difference Method (CCFDM)

The spatial calculations of flow-dependent variables, involving the inviscid and viscous flux derivatives of Eq. (7), are evaluated in this subsection.

The flux derivative along $\xi$-grid line is taken as illustration. ${\tilde{\boldsymbol{E}^{\prime}}}$ is used to simplify the denotation of ${{\partial {\tilde{\boldsymbol{E}}}} \mathord{/ {\vphantom {{\partial {\tilde{\boldsymbol{E}}}} {\partial \xi }}} \kern-0pt} {\partial \xi }}$ and the operator $\delta_{1}^{\xi } {\tilde{\boldsymbol{E}}}$ is adopted to denote the difference approximation of flux ${\tilde{\boldsymbol{E}^{\prime}}}$. The superscript ξ stands for the $\xi$-curvilinear grid line, and the subscript 1 stands for the face-to-cell difference operator acted on the fluxes. $\delta_{1}^{\xi }$ can be either explicit or implicit operator. The original idea of Refs. [29, 34] is to use 6th-order explicit difference for $\delta_{1}^{\xi }$. In this work, the spectral-like compact difference scheme by Liu et al. [43] is adopted:

$$ \delta_{1}^{\xi } {\tilde{\boldsymbol{E}}}:\left\{ {\begin{array}{*{20}l} {\beta {\tilde{\boldsymbol{E}^{\prime}}}_{i - 2} + \alpha {\tilde{\boldsymbol{E}^{\prime}}}_{i - 1} + {\tilde{\boldsymbol{E}^{\prime}}}_{i} + \alpha {\tilde{\boldsymbol{E}^{\prime}}}_{i + 1} { + }\beta {\tilde{\boldsymbol{E}^{\prime}}}_{i + 2} = a\left( {{\tilde{\boldsymbol{E}}}_{i + 1/2} - {\tilde{\boldsymbol{E}}}_{i - 1/2} } \right) + \frac{b}{2}\left( {{\tilde{\boldsymbol{E}}}_{i + 1} - {\tilde{\boldsymbol{E}}}_{i - 1} } \right)} \hfill \\ {\quad + \,\frac{c}{3}\left( {{\tilde{\boldsymbol{E}}}_{i + 3/2} - {\tilde{\boldsymbol{E}}}_{i - 3/2} } \right) + \frac{d}{4}\left( {{\tilde{\boldsymbol{E}}}_{i + 2} - {\tilde{\boldsymbol{E}}}_{i - 2} } \right) + \frac{e}{5}\left( {{\tilde{\boldsymbol{E}}}_{i + 5/2} - {\tilde{\boldsymbol{E}}}_{i - 5/2} } \right),} \hfill \\ \end{array} } \right. $$

(9)

where the coefficients $\beta$, $\alpha$, $a$, b, c, d and e determining various orders of spatial accuracy are in Ref. [43]. The left-hand side cell-center derivatives are obtained simultaneously by solving Eq. (9) via the Thomas algorithm.

Equation (9) is used for both inviscid and viscous fluxes. On the right-hand side of Eq. (9), ${\tilde{\boldsymbol{E}}}_{i + 1}$ on cell centers is calculated directly from the conservative variables and requires no interpolations. The inviscid and viscous calculations for face-center fluxes at i + 1/2, i + 3/2 etc. are treated differently due to their convection and diffusion properties respectively.

The face-center inviscid fluxes ${\tilde{\boldsymbol{E}}}_{i + 1/2}$ are evaluated by Riemann flux solver:

$$ {\tilde{\boldsymbol{E}}}_{i + 1/2} = {\tilde{\boldsymbol{E}}}(Q_{i + 1/2}^{L} ,Q_{i + 1/2}^{R} ,J\xi_{x,i + 1/2} ,J\xi_{y,i + 1/2} ,J\xi_{z,i + 1/2} ) , $$

(10)

where $Q_{i + 1/2}^{L}$ and $Q_{i + 1/2}^{R}$ are the interpolated left and right primitive variables on face centers. The interpolations for $Q_{i + 1/2}^{{}}$ dominate the spectral property of the whole method [38] and thereby is the main body of this work and is mainly discussed in Sects. 3 and 4.

The viscous fluxes on face centers ${\tilde{\boldsymbol{E}}}_{v,i + 1/2}$ are calculated on the premise that the derivatives of velocity components (u, v, w) and temperature T to Cartesian coordinates (x, y, z) are already obtained on face centers, according to Eq. (3). These derivatives are calculated by the chain rule:

$$ \frac{\partial \phi }{\partial x} = \frac{\partial \phi }{\partial \xi }\frac{\partial \xi }{\partial x}{ + }\frac{\partial \phi }{\partial \eta }\frac{\partial \eta }{\partial x}{ + }\frac{\partial \phi }{\partial \zeta }\frac{\partial \zeta }{\partial x} ,\quad \phi = u,v,w,T. $$

(11)

Taking ${{\partial \phi } \mathord{/ {\vphantom {{\partial \phi } {\partial x}}} \kern-0pt} {\partial x}}$ along the $\xi$-grid line as an illustration, the derivatives of flow variable to curvilinear coordinates $(\phi_{\xi } , \, \phi_{\eta } , \, \phi_{\zeta } )$ and the coordinate transformation metrics $(\xi_{x} , \, \eta_{x} , \, \zeta_{x} )$ on face centers (i + 1/2 etc.) are in demand. The latter aspect is left to Sect. 2.3 and the former aspect is given in details in this section. Since the flow quantities $\phi$ on cell centers (i etc.) are given in advance, the face-center ${{\partial \phi } \mathord{/ {\vphantom {{\partial \phi } {\partial \xi }}} \kern-0pt} {\partial \xi }}$ can be calculated directly via difference scheme Eq. (9) by simply shifting the indices 1/2; besides, the face-center ${{\partial \phi } \mathord{/ {\vphantom {{\partial \phi } {\partial \eta }}} \kern-0pt} {\partial \eta }}$ and ${{\partial \phi } \mathord{/ {\vphantom {{\partial \phi } {\partial \zeta }}} \kern-0pt} {\partial \zeta }}$ are calculated by cell-to-cell difference scheme along $\eta$- and $\zeta$-grid line respectively. The available cell-to-cell difference schemes are in Ref. [4]. Moreover, the additional cell-to-face central interpolations (shown in “Appendix A”) are also in demand for the numerical procedures of ${{\partial \phi } \mathord{/ {\vphantom {{\partial \phi } {\partial \eta }}} \kern-0pt} {\partial \eta }}$ and ${{\partial \phi } \mathord{/ {\vphantom {{\partial \phi } {\partial \zeta }}} \kern-0pt} {\partial \zeta }}$.

For better interpretation of inviscid and viscous spatial discretization of CCFDM, a schematic diagram is depicted in Fig. 1. An important thing necessary to be emphasized is that the order of accuracy for flux derivative Eq. (9) should be consistent with those for Eq. (11).

Fig. 1

A schematic diagram of major procedures of CCFDM: spatial discretization

2.3 Cell-Centered Symmetric Conservative Metric Method (CCSCMM)

The numerical calculations of geometry-dependent variables, including grid metrics and Jacobian in Eq. (8), are evaluated in this subsection. To guarantee the GCL condition (Eq. 6), the symmetric conservative grid metric formulations are calculated by

$$ \begin{aligned} & J\xi_{x} = \frac{1}{2}\left[ {(J\xi_{x} )^{S1} + (J\xi_{x} )^{S2} } \right],\quad J\xi_{y} = \frac{1}{2}\left[ {(J\xi_{y} )^{S1} + (J\xi_{y} )^{S2} } \right] ,\quad J\xi_{z} = \frac{1}{2}\left[ {(J\xi_{z} )^{S1} + (J\xi_{z} )^{S2} } \right], \\ & J\eta_{x} = \frac{1}{2}\left[ {(J\eta_{x} )^{S1} + (J\eta_{x} )^{S2} } \right],\quad J\eta_{y} = \frac{1}{2}\left[ {(J\eta_{y} )^{S1} + (J\eta_{y} )^{S2} } \right],\quad J\eta_{z} = \frac{1}{2}\left[ {(J\eta_{z} )^{S1} + (J\eta_{z} )^{S2} } \right], \\ & J\zeta_{x} = \frac{1}{2}\left[ {(J\zeta_{x} )^{S1} + (J\zeta_{x} )^{S2} } \right],\quad J\zeta_{y} = \frac{1}{2}\left[ {(J\zeta_{y} )^{S1} + (J\zeta_{y} )^{S2} } \right],\quad J\zeta_{z} = \frac{1}{2}\left[ {(J\zeta_{z} )^{S1} + (J\zeta_{z} )^{S2} } \right], \\ \end{aligned} $$

(12)

where

$$ \begin{aligned} & \left( {J\xi_{x} } \right)^{S1} = \left( {y_{\eta } z} \right)_{\zeta } - \left( {y_{\zeta } z} \right)_{\eta } ,\quad \left( {J\xi_{y} } \right)^{S1} = \left( {z_{\eta } x} \right)_{\zeta } - \left( {z_{\zeta } x} \right)_{\eta } ,\quad \left( {J\xi_{z} } \right)^{S1} = \left( {x_{\eta } y} \right)_{\zeta } - \left( {x_{\zeta } y} \right)_{\eta } , \\ & \left( {J\eta_{x} } \right)^{S1} = \left( {y_{\zeta } z} \right)_{\xi } - \left( {y_{\xi } z} \right)_{\zeta } ,\quad \left( {J\eta_{y} } \right)^{S1} = \left( {z_{\zeta } x} \right)_{\xi } - \left( {z_{\xi } x} \right)_{\zeta } ,\quad \left( {J\eta_{z} } \right)^{S1} = \left( {x_{\zeta } y} \right)_{\xi } - \left( {x_{\xi } y} \right)_{\zeta } , \\ & \left( {J\zeta_{x} } \right)^{S1} = \left( {y_{\xi } z} \right)_{\eta } - \left( {y_{\eta } z} \right)_{\xi } ,\quad \left( {J\zeta_{y} } \right)^{S1} = \left( {z_{\xi } x} \right)_{\eta } - \left( {z_{\eta } x} \right)_{\xi } ,\quad \left( {J\zeta_{z} } \right)^{S1} = \left( {x_{\xi } y} \right)_{\eta } - \left( {x_{\eta } y} \right)_{\xi } , \\ \end{aligned} $$

(13)

and

$$ \begin{aligned} & \left( {J\xi_{x} } \right)^{S2} = \left( {yz_{\zeta } } \right)_{\eta } - \left( {yz_{\eta } } \right)_{\zeta } ,\quad \left( {J\xi_{y} } \right)^{S2} = \left( {zx_{\zeta } } \right)_{\eta } - \left( {zx_{\eta } } \right)_{\zeta } ,\quad \left( {J\xi_{z} } \right)^{S2} = \left( {xy_{\zeta } } \right)_{\eta } - \left( {xy_{\eta } } \right)_{\zeta } , \\ & \left( {J\eta_{x} } \right)^{S2} = \left( {yz_{\xi } } \right)_{\zeta } - \left( {yz_{\zeta } } \right)_{\xi } ,\quad \left( {J\eta_{y} } \right)^{S2} = \left( {zx_{\xi } } \right)_{\zeta } - \left( {zx_{\zeta } } \right)_{\xi } ,\quad \left( {J\eta_{z} } \right)^{S2} = \left( {xy_{\xi } } \right)_{\zeta } - \left( {xy_{\zeta } } \right)_{\xi } , \\ & \left( {J\zeta_{x} } \right)^{S2} = \left( {yz_{\eta } } \right)_{\xi } - \left( {yz_{\xi } } \right)_{\eta } ,\quad \left( {J\zeta_{y} } \right)^{S2} = \left( {zx_{\eta } } \right)_{\xi } - \left( {zx_{\xi } } \right)_{\eta } ,\quad \left( {J\zeta_{z} } \right)^{S2} = \left( {xy_{\eta } } \right)_{\xi } - \left( {xy_{\xi } } \right)_{\eta } . \\ \end{aligned} $$

(14)

The surface metrics $\left( {J\xi_{x} } \right)^{S1}$ in Eq. (13) is discretized as illustration:

$$ \left( {J\xi_{x} } \right)^{S1} = \underbrace {{\delta_{2}^{\zeta } (\underbrace {z}_{edge - \eta }\underbrace {{\delta_{3}^{\eta } \underbrace {y}_{node}}}_{edge - \eta })}}_{face - \eta \zeta } - \underbrace {{\delta_{2}^{\eta } (\underbrace {z}_{edge - \zeta }\underbrace {{\delta_{3}^{\zeta } \underbrace {y}_{node}}}_{edge - \zeta })}}_{face - \eta \zeta }, $$

(15)

and the Jacobian J is discretized by

$$ \begin{aligned} J = & \frac{1}{3}\{ \, \underbrace {{\delta_{1}^{\xi } [\underbrace {x}_{face - \eta \zeta }\underbrace {{(J\xi_{x} )}}_{face - \eta \zeta } + \underbrace {y}_{face - \eta \zeta }\underbrace {{(J\xi_{y} )}}_{face - \eta \zeta } + \underbrace {z}_{face - \eta \zeta }\underbrace {{(J\xi_{z} )}}_{face - \eta \zeta }]}}_{cell - \xi \eta \zeta } \\ & + \,\underbrace {{\delta_{1}^{\eta } [\underbrace {x}_{face - \xi \zeta }\underbrace {{(J\eta_{x} )}}_{face - \xi \zeta } + \underbrace {y}_{face - \xi \zeta }\underbrace {{(J\eta_{y} )}}_{face - \xi \zeta } + \underbrace {z}_{face - \xi \zeta }\underbrace {{(J\eta_{z} )}}_{face - \xi \zeta }]}}_{cell - \xi \eta \zeta } \\ & + \,\underbrace {{\delta_{1}^{\zeta } [\underbrace {x}_{face - \xi \eta }\underbrace {{(J\zeta_{x} )}}_{face - \xi \eta } + \underbrace {y}_{face - \xi \eta }\underbrace {{(J\zeta_{y} )}}_{face - \xi \eta } + \underbrace {z}_{face - \xi \eta }\underbrace {{(J\zeta_{z} )}}_{face - \xi \eta }]}}_{cell - \xi \eta \zeta } \, \} . \\ \end{aligned} $$

(16)

Equations (15)–(16) involve three categories of difference operators: face-to-cell difference operator $\delta_{1}$, edge-to-face difference operator $\delta_{2}$ and node-to-edge difference operator $\delta_{3}$. $\delta_{3}$ indicates the coordinate information is transferred from nodes to edge centers; $\delta_{2}$ transmits the information from edge centers to face centers; and $\delta_{1}$ marks the information transferred from face centers to cell centers. In this paper, they are all central linear half-node-to-node difference operators. Apart from these, three categories of interpolation operators are also involved in Eqs. (15)–(16) but not explicitly denoted. They are node-to-edge, edge-to-face and face-to-cell interpolation operators, denoted by $\chi_{3}$, $\chi_{2}$ and $\chi_{1}$ in Eq. (17). And they are all central linear half-node-to-node interpolation schemes, referring to “Appendix A”.

The satisfaction of GCL condition requires the orders of accuracy along each curvilinear coordinate to be consistent, which implies

$$ \begin{aligned} & \delta_{1}^{\xi } = \delta_{2}^{\xi } = \delta_{3}^{\xi } ,\quad \delta_{1}^{\eta } = \delta_{2}^{\eta } = \delta_{3}^{\eta } ,\quad \delta_{1}^{\zeta } = \delta_{2}^{\zeta } = \delta_{3}^{\zeta } , \\ & \chi_{1}^{\xi } = \chi_{2}^{\xi } = \chi_{3}^{\xi } ,\quad \chi_{1}^{\eta } = \chi_{2}^{\eta } = \chi_{3}^{\eta } ,\quad \chi_{1}^{\zeta } = \chi_{2}^{\zeta } = \chi_{3}^{\zeta } . \\ \end{aligned} $$

(17)

More underling insights about Eq. (17) can be found in Ref. [36]. Besides, the face-to-cell difference operator $\delta_{1}^{\xi }$ is exactly equivalent to that denoted by Eq. (9). A schematic diagram is depicted by Fig. 2 to interpret Eqs. (15)–(17).

Fig. 2

A schematic diagram of major procedures of CCSCMM: grid metrics and Jacobian

2.4 Time Integration Method

After the spatial discretization is implemented, Eq. (7) can be written as a system of ordinary differential equations in time:

$$ J\frac{{d{\boldsymbol{U}}}}{dt} = R({\boldsymbol{U}}), $$

(18)

where $R({\boldsymbol{U}})$ is the residual. Eq. (18) is integrated by Runge–Kutta scheme. The procedures to update solution from n to n + 1 pseudo time level are given by:

$$ \left\{ \begin{aligned} {{\boldsymbol{U}}^{(0)}} & = { {\boldsymbol{U}}^{n}}, \\ {{\boldsymbol{U}}^{(1)}} & = { {\boldsymbol{U}}^{(0)}} + {J^n}\Delta tR\left( {{{\boldsymbol{U}}^{(0)}}} \right), \\ {{\boldsymbol{U}}^{(2)}} & = \frac{3}{4}{{\boldsymbol{U}}^{(0)}} + \frac{1}{4}{{\boldsymbol{U}}^{(1)}} + \frac{1}{4} \frac{\Delta t}{J^n} R\left( {{{\boldsymbol{U}}^{(1)}}} \right), \\ {{\boldsymbol{U}}^{(3)}} & = \frac{1}{3}{{\boldsymbol{U}}^{(0)}} + \frac{2}{3}{{\boldsymbol{U}}^{(2)}} + \frac{2}{3} \frac{\Delta t}{J^n} R\left( {{{\boldsymbol{U}}^{(2)}}} \right), \\ {{\boldsymbol{U}}^{n + 1}} & = {{\boldsymbol{U}}^{(3)}}. \end{aligned} \right.$$

(19)

3 Linear Compact Interpolations

Starting from this section, the compact interpolations for $Q_{i + 1/2}^{{}}$ in Eq. (10) are focused. Though the spectral properties of compact schemes are usually superior to the explicit counterparts sharing same orders of accuracy, the standard compact interpolations are not perfect in every aspect. The below analysis is given to pinpoint their advantages and disadvantages. Then the remediation for their disadvantages will be presented in Sects. 3.1 and 3.2.

A general formula of compact interpolation for $Q_{i + 1/2}^{{}}$ is given by

$$ \sum\limits_{n = - K,n \ne 0}^{K} {\beta_{n} Q_{{i + \frac{1}{2} + n}} } + Q_{{i + \frac{1}{2}}} = \sum\limits_{m = - L}^{L + 1} {c_{m} Q_{i + m} } , $$

(20)

where if $\beta_{ - n} = \beta_{n} , \, n = 1 \ldots K$ and $c_{1 - m} = c_{m} , \, m = 1 \ldots L + 1$, (2K + 2L + 2)th-order central compact interpolations are recovered, and if $c_{L + 1} = 0$, (2K + 2L + 1)th-order biased-upwind compact interpolations are obtained. The respective coefficients for tridiagonal (K = 1), pentadiagonal (K = 2) and heptadiagonal (K = 3) interpolations are shown in “Appendix A”. The schemes with asymmetrical left-hand side stencils are excluded due to their poor spectral properties [13], but they are useful for physical boundary interpolations in case that the ghost cells are not available.

Given an initial input $e^{i\omega x}$ for the linear system Eq. (20), the discrepancy between the numerical output and the analytical output is measured by the below transfer function T(k):

$$ T(k) = \frac{{\sum\limits_{m = 1}^{L + 1} {\left( {c_{1 - m} + c_{m} } \right)\cos \frac{(2m - 1)}{2}k} + i\sum\limits_{m = 1}^{L + 1} {\left( {c_{m} - c_{1 - m} } \right)\sin \frac{(2m - 1)}{2}k} }}{{\sum\limits_{n = 1}^{K} {\left( {\beta_{ - n} + \beta_{n} } \right)\cos (nk)} + 1 + i\sum\limits_{n = 1}^{K} {\left( {\beta_{n} - \beta_{ - n} } \right)\sin (nk)} }} , $$

(21)

which is a complex number and $k = \omega \Delta x$ is defined as the wavenumber. The real part $T_{\Re } (k)$ and imaginary part $T_{\Im } (k)$ are associated with dispersion and dissipation errors respectively. Theoretical values for $T_{\Re } (k)$ and $T_{\Im } (k)$ are 1 and 0, indicating no dispersion error and no dissipation error.

The dispersion property $T_{\Re } (k)$ and dissipation property $T_{\Im } (k)$ of tridiagonal, pentadiagonal and heptadiagonal interpolations are compared in Fig. 3. The observations are summarized below:

Fig. 3

Dispersion and dissipation properties of standard compact interpolations in “Appendix A”

• (1) The dispersion property of the upwind scheme is better than that of the central scheme on the same stencil. Similar observation is also given in Ref. [13].

• (2) Regarding the upwind schemes with K fixed, the optimally dispersion property is achieved only when K = L. Providing K > L, excessive dispersion error in high wavenumber range is visible. Providing K < L, increase in L hardly affect the dispersion.

• (3) For upwind schemes with K = L, increase of K and L simultaneously enhance the dispersion and dissipation properties. This is shown by Fig. 3d.

3.1 Spectral Optimization Technique

In Fig. 3, the low-dispersion property of upwind compact schemes is desirable, but the corresponding inherent dissipation is excessive to some extent. On the other hand, either the non-dissipative property of central compact schemes is unsatisfactory. Hence, new compact schemes exhibiting low-dispersion property like that observed in upwind compact schemes and meanwhile possessing a small amount of built-in dissipation to prohibit non-physical spurious oscillations will be proposed in this subsection. And they will be further demonstrated appropriate for problems in aeroacoustics and turbulence in Sect. 5.1.

Technically, the symmetric stencil with asymmetric coefficients is considered:

$$ \sum\limits_{n = - K,n \ne 0}^{K} {\beta_{n} \left( {\xi ,\eta } \right)Q_{{i + \frac{1}{2} + n}} } + Q_{{i + \frac{1}{2}}} = \sum\limits_{m = - L}^{L + 1} {c_{m} \left( {\xi ,\eta } \right)Q_{i + m} } , $$

(22)

where the asymmetry owes to the undetermined coefficients $\beta_{n}$ and $c_{m}$ which are functions of $\xi$ and $\eta$. Depending on the controllable parameters $\xi$ and $\eta$, Eq. (22) can achieve (2K + 2L)th-order accuracy at least and (2K + 2L + 2)th-order accuracy at most.

Defining $\xi = \beta_{1} - \beta_{ - 1}$ and $\eta = \beta_{ - 1} + \beta_{1}$, the analytical transfer function Eq. (21) is rewritten as

$$ T(k) = \frac{{\sum\limits_{m = 1}^{L + 1} {c_{m}^{ + } \left( \eta \right)\cos \frac{(2m - 1)}{2}k} + i\sum\limits_{m = 1}^{L + 1} {c_{m}^{ - } \left( \xi \right)\sin \frac{(2m - 1)}{2}k} }}{{\sum\limits_{n = 1}^{K} {\beta_{n}^{ + } \left( \eta \right)\cos (nk)} + 1 + i\sum\limits_{n = 1}^{K} {\beta_{n}^{ - } \left( \xi \right)\sin (nk)} }} . $$

(23)

The derivative process of Eq. (23) from (21) is shown in “Appendix B”. In Eq. (23), $T(k)$ is also a complex number. Its real part $T_{\Re } (k)$ is related to the dispersion property and its imaginary part $T_{\Im } (k)$ is associated with the dissipation property. A particular case with $\xi = 0$ leads to $T_{\Im } (k) = 0$, indicating Eq. (22) with $\xi = 0$ reverts to be non-dissipative central scheme.

The appropriate ξ and η attaining low-dissipation and low-dispersion properties are specified by the spectral optimization technique. The optimization criteria inspired by the spirit of dispersion-relation-preserving (DRP) [44] are given below:

• (1) The integrated error function considering both dispersive and dissipative errors,

  $$ E = \int_{0}^{{k_{c} }} {\left\{ {\sigma \left| {T_{\Re } (k) - 1} \right| + \left( {1 - \sigma } \right)\left| {T_{\Im } (k) - 0} \right|} \right\}dk} , $$

  (24)

  should reach its minimum value. σ is a weight between 0 and 1. σ = 0.5 is chosen according to Martín et al. [45], which specifies the equal importance of dispersion error and dissipation error. $k_{c} \in \left( {0,\pi } \right]$ is the cut-off wavenumber below which the optimization procedure is focused. $k_{c} = {\pi \mathord{/ {\vphantom {\pi 2}} \kern-0pt} 2}$ is given for the well-known DRP by Tam and Webb [44]; $k_{c} = {{2\pi } \mathord{/ {\vphantom {{2\pi } 3}} \kern-0pt} 3}$ is given for the series of dissipative compact schemes by Deng et al. [39]; $k_{c} = {{4\pi } \mathord{/ {\vphantom {{4\pi } 5}} \kern-0pt} 5}$ is given for the high-order compact filters by Liu et al. [46]; $k_{c} = {{7\pi } \mathord{/ {\vphantom {{7\pi } 8}} \kern-0pt} 8}$ is given for optimized compact difference schemes [12]. Kim and Lee [6] pointed out the range larger than $k_{c} > {{9\pi } \mathord{/ {\vphantom {{9\pi } {10}}} \kern-0pt} {10}}$ should be omitted. Current attempt for k_c involves ${\pi \mathord{/ {\vphantom {\pi 2}} \kern-0pt} 2}$, ${{2\pi } \mathord{/ {\vphantom {{2\pi } 3}} \kern-0pt} 3}$, ${{3\pi } \mathord{/ {\vphantom {{3\pi } 4}} \kern-0pt} 4}$, ${{4\pi } \mathord{/ {\vphantom {{4\pi } 5}} \kern-0pt} 5}$, ${{5\pi } \mathord{/ {\vphantom {{5\pi } 6}} \kern-0pt} 6}$, ${{6\pi } \mathord{/ {\vphantom {{6\pi } 7}} \kern-0pt} 7}$, ${{7\pi } \mathord{/ {\vphantom {{7\pi } 8}} \kern-0pt} 8}$,…. By trials and errors, we take ${{2\pi } \mathord{/ {\vphantom {{2\pi } 3}} \kern-0pt} 3}$,${{ \, 5\pi } \mathord{/ {\vphantom {{ \, 5\pi } 6}} \kern-0pt} 6}$, ${{6\pi } \mathord{/ {\vphantom {{6\pi } 7}} \kern-0pt} 7}$ for Opt4, Opt6 and Opt8 respectively.

• (2) Dispersion error, denoted by $\left| {T_{\Re } (k) - 1} \right|$, should be controlled within an appropriate threshold ε. ε = 1% is adopted by Mullenix and Gaitonde [47] for a 6th-order explicit scheme with six degrees of freedom. ε = 0.5% is adopted by Sun et al. [48] for a 6th-order explicit optimized scheme with eight degrees of freedom. Weirs and Candler [49] pointed out that ε less than 1.5% is acceptable for scheme with six degrees of freedom (like WENO5/6), and ε less than 1% is allowable for scheme with eight degrees of freedom (like WENO7/8). In the present research, 2%, 1% and 0.5% are recommended for Opt4, Opt6 and Opt8 respectively. They are all within the safety limits according to Weirs and Candler [49].

• (3) The amount of dissipation should also be controlled under the condition that no noticeable numerical oscillations be observed in all the benchmark cases in Sect. 5.1. In this paper, they are also controlled to be less than one-third of the built-in dissipation of UI5, UI7 and UI9.

3.2 Three Optimized Linear Interpolations (Opt4, Opt6, Opt8)

For practical purpose, only three tridiagonal compact schemes are discussed in details.

$$ \begin{aligned} \beta_{ - 1} Q_{{i - \frac{1}{2}}} + Q_{{i + \frac{1}{2}}} + \beta_{1} Q_{{i + \frac{3}{2}}} & = c_{ - 3} Q_{i - 3} + c_{ - 2} Q_{i - 2} + c_{ - 1} Q_{i - 1} + c_{0} Q_{i} + c_{1} Q_{i + 1} \\ &\quad + c_{2} Q_{i + 2} + c_{3} Q_{i + 3} + c_{4} Q_{i + 4} , \end{aligned} $$

(25)

where the coefficients relating to ξ and η for different schemes on different stencils (shown in Fig. 4) are listed in Table 1.

Fig. 4

Stencils for the optimized linear interpolations proposed in this paper

Table 1 Coefficients related to ξ and η for linear schemes on stencils A, B and C in Fig. 4

According to Eq. (21) and Table 1, the transfer functions T(k) for each stencil are given by

$$ T\left( k \right)_{{Stencil{\text{ A}}}} = \frac{{\left( {\frac{1}{8}\left( { - 1 + 3\eta } \right)\cos \left( {\frac{3}{2}k} \right) + \frac{1}{8}\left( {9 + 5\eta } \right)\cos \left( {\frac{1}{2}k} \right)} \right) + i\left( {\frac{1}{4}\xi \sin \left( {\frac{3}{2}k} \right) + \frac{5}{4}\xi \sin \left( {\frac{1}{2}k} \right)} \right)}}{{\left( {\eta \cos (k) + 1} \right) + i\left( {\xi \sin (k)} \right)}}. $$

(26)

$$ T\left( k \right)_{{Stencil{\text{ B}}}} = \frac{{\left( {\begin{array}{*{20}l} {\frac{1}{128}\left( {3 - 5\eta } \right)\cos \left( {\frac{5}{2}k} \right) + \frac{1}{128}\left( { - 25 + 63\eta } \right)\cos \left( {\frac{3}{2}k} \right)} \hfill \\ { + \,\frac{5}{64}\left( {15 + 7\eta } \right)\cos \left( {\frac{1}{2}k} \right)} \hfill \\ \end{array} } \right) + i\left( {\begin{array}{*{20}l} { - \frac{1}{64}\xi \sin \left( {\frac{5}{2}k} \right) + \frac{21}{64}\xi \sin \left( {\frac{3}{2}k} \right)} \hfill \\ { + \,\frac{35}{32}\xi \sin \left( {\frac{1}{2}k} \right)} \hfill \\ \end{array} } \right)}}{{\left( {\eta \cos (k) + 1} \right) + i\left( {\xi \sin (k)} \right)}}. $$

(27)

$$ T\left( k \right)_{{Stencil{\text{ C}}}} = \frac{{\left( {\begin{array}{*{20}l} {\frac{1}{1024}\left( { - 5 + 7\eta } \right)\cos \left( {\frac{7}{2}k} \right) + \frac{1}{1024}\left( {49 - 75\eta } \right)\cos \left( {\frac{5}{2}k} \right)} \hfill \\ { + \,\frac{1}{1024}\left( { - 245 + 567\eta } \right)\cos \left( {\frac{3}{2}k} \right) + \frac{1}{1024}\left( {1225 + 525\eta } \right)\cos \left( {\frac{1}{2}k} \right)} \hfill \\ \end{array} } \right) + i\left( {\begin{array}{*{20}l} {\frac{1}{512}\xi \sin \left( {\frac{7}{2}k} \right) - \frac{15}{512}\xi \sin \left( {\frac{5}{2}k} \right)} \hfill \\ { + \,\frac{189}{512}\xi \sin \left( {\frac{3}{2}k} \right) + \frac{525}{512}\xi \sin \left( {\frac{1}{2}k} \right)} \hfill \\ \end{array} } \right)}}{{\left( {\eta \cos (k) + 1} \right) + i\left( {\xi \sin (k)} \right)}}. $$

(28)

According to Eq. (24), the optimized ξ and η for Opt4, Opt6 and Opt8 can be acquired. In Table 2, the chosen ξ and η are listed, where Opt4/6/8 are optimized schemes, UI5/7/9 are compact upwind schemes and CI6/8/10 are compact central schemes sharing same stencils. Figure 5 depicts the spectral properties. Additional dissipative compact schemes (DCS5/7/9) [39] and the widely used upwind explicit schemes (UE5/7/9) are included as references. Figure 5 indicates the optimized schemes exhibit predominant dispersion and dissipation characteristics.

Table 2 Various ξ and η for various linear schemes on stencils A, B and C of Fig. 4

Fig. 5

Dissipation and dispersion properties of linear interpolations in Table 2, as well as (DCS5/7/9) [39] and UE5/7/9. Top: Interpolation schemes; bottom: Interpolation schemes combined with the respective difference schemes

4 Nonlinear Compact Interpolations

For flows with embedded discontinuities, the available shock-capturing strategies are monotonicity preserving limiter [50, 51], hybridization strategy [21] and multi-stencil weighting technique [27, 29]. Due to the generalization and convenience in extending to arbitrarily high-order formulations, the multi-stencil weighting technique [27, 29] will be reconsidered here. In Sect. 4.1, the criteria to choose optimally compact sub-stencils for a given generalized compact global stencil are given. Interestingly, the classical explicit WENO-type schemes with arbitrary orders can be reverted from the proposed framework. For practical purpose, two special cases without loss of generality are analyzed in Sect. 4.2. Moreover, Sect. 4.3 is given to show the implementation of compact interpolations for Euler equations in the projection of characteristic space so as to achieve numerical stability and robustness.

4.1 Extending Weighting Technique for Compact Interpolations

The main idea of weighting technique is to use a convex combination of several lower-order polynomials on the respective sub-stencils via the elaborately nonlinear weights to adaptively approximate the high-order scheme on the global stencil. When the flowfield is smooth, the nonlinear weights approach the linear weights, producing the equivalent effect of adopting the high-order linear scheme. When the flow discontinuity is encountered, the nonlinear weight will approximate zero so that the contribution of corresponding sub-stencil is abandoned. In such way, the high-order accuracy in smooth region and the essentially non-oscillatory property for shocks are both retained. The current work extends the novel nonlinear weights and the smoothness indicators in Ref. [42] to compact interpolations so as to achieve superior low-dissipation low-dispersion properties at smooth regions as well as non-oscillatory property at discontinuities. This subsection mainly focuses on how to choose the optimally compact sub-stencils.

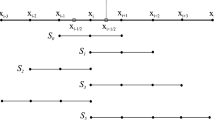
Figure 6 shows the selection of candidate sub-stencils for a compact interpolation where − L to L + 1 cell centers are used to approximate − K + 1/2 to K + 1/2 face centers. The key points are summarized below:

Fig. 6

General analysis of sub-stencils for nonlinear compact interpolations

• (1) On the global stencil, (2K + 2L + 2)th-order accuracy is achieved at most.

• (2) The global stencil is composed of K + L + 2 sub-stencils, on each of which (K + L + 1)th-order accuracy is achieved.

• (3) In Fig. 6, the K + L + 2 sub-stencils are placed successively from left to right. The sub-stencil S_i+1 is composed by discarding the left-hand element in S_i and at the same time picking up the right-hand side degree of freedom outside S_i. Importantly, both cell centers and face centers are regarded as the degrees of freedom.

• (4) The (2K + 2L + 2)th-order linear scheme on the global stencil is exactly the convex combination of (K + L + 1)th-order schemes on K + L + 2 sub-stencils with respective linear weights C_i, i = 1, 2, …, K + L + 2. Specific forms of C_i depend on the desired global accuracy in (1).

• (5) The (2K + 2L + 2)th-order nonlinear scheme on the global stencil is realized by replacing the linear weights C_i, i = 1, 2, …, K + L + 2 with the nonlinear weights $\omega_{i}$, i = 1, 2, …, K + L + 2. Calculations of nonlinear weights refer to Refs. [27, 42].

• (6) In case of K = 0, the explicit WENO-type schemes [27, 29] are reverted, where the arbitrary high-order accuracy is achieved by increasing L.

4.2 Nonlinear Compact Interpolations (UI5, CI6, CI8)

Without loss of generality, two representative cases of Fig. 6 will be analyzed detailly in this subsection, which are (K = 1, L = 1) and (K = 1, L = 2), respectively.

In Fig. 7, four candidate 3rd-order compact schemes on the respective sub-stencils S₁, S₂, S₃ and S₄ along with the linear weights C₁, C₂, C₃ and C₄ are given by

$$ \left\{ {\begin{array}{*{20}l} {S_{1} : \, 3Q_{{i - \frac{1}{2}}} + Q_{{i + \frac{1}{2}}} = Q_{i - 1} + 3Q_{i} } \hfill \\ {S_{2} : \, \frac{1}{3}Q_{{i - \frac{1}{2}}} + Q_{{i + \frac{1}{2}}} = Q_{i} + \frac{1}{3}Q_{i + 1} } \hfill \\ {S_{3} : \, Q_{{i + \frac{1}{2}}} + \frac{1}{3}Q_{{i + \frac{3}{2}}} = \frac{1}{3}Q_{i} + Q_{i + 1} } \hfill \\ {S_{4} : \, Q_{{i + \frac{1}{2}}} + 3Q_{{i + \frac{3}{2}}} = 3Q_{i + 1} + Q_{i + 2} } \hfill \\ \end{array} } \right.,\quad \left\{ {\begin{array}{*{20}l} {C_{1} = \frac{1}{16}\left( { - 1 + 3\eta - 2\xi } \right)} \hfill \\ {C_{2} = - \frac{3}{16}\left( { - 3 + \eta + 2\xi } \right)} \hfill \\ {C_{3} = - \frac{3}{16}\left( { - 3 + \eta - 2\xi } \right)} \hfill \\ {C_{4} = \frac{1}{16}\left( { - 1 + 3\eta + 2\xi } \right)} \hfill \\ \end{array} } \right.. $$

(29)

Fig. 7

Sub-stencils for nonlinear compact interpolations with K = 1 and L = 1

By a convex combination of Eq. (29), the linear scheme on the global stencil (i − 1,…, i + 2) is given by

$$ \begin{aligned} & \underbrace {{\left( {3C_{1} + \frac{1}{3}C_{2} } \right)}}_{{\beta_{ - 1} }}Q_{{i - \frac{1}{2}}} + \underbrace {{\left( {C_{1} + C_{2} + C_{3} + C_{4} } \right)}}_{{\beta_{0} }}Q_{{i + \frac{1}{2}}} + \underbrace {{\left( {\frac{1}{3}C_{3} + 3C_{4} } \right)}}_{{\beta_{1} }}Q_{{i + \frac{3}{2}}} \\ & \quad = \underbrace {{C_{1} }}_{{c_{ - 1} }}Q_{i - 1} + \underbrace {{\left( {3C_{1} + C_{2} + \frac{1}{3}C_{3} } \right)}}_{{c_{0} }}Q_{i} + \underbrace {{\left( {\frac{1}{3}C_{2} + C_{3} + 3C_{4} } \right)}}_{{c_{1} }}Q_{i + 1} + \underbrace {{C_{4} }}_{{c_{2} }}Q_{i + 2} . \\ \end{aligned} $$

(30)

The order of Eq. (30) varies with the adjustment of ξ and η, as is shown in Table 2. If $\left\{ {\xi ,\eta } \right\} = \left\{ {0,{3 \mathord{/ {\vphantom {3 5}} \kern-0pt} 5}} \right\}$, 6th-order central compact scheme (CI6) is attained with

$$ \{ C_{ 1} ,C_{ 2} ,C_{ 3} ,C_{ 4} \} = \{ 1/ 20, 9/ 20, 9/ 20, 1/ 20\} . $$

(31)

If $\left\{ {\xi ,\eta } \right\} = \left\{ { - {2 \mathord{/ {\vphantom {2 5}} \kern-0pt} 5},{3 \mathord{/ {\vphantom {3 5}} \kern-0pt} 5}} \right\}$, 5th-order upwind compact scheme (UI5) is recovered with

$$ \{ C_{ 1} ,C_{ 2} ,C_{ 3} ,C_{ 4} \} = \{ 1/ 10, 3/ 5, 3/ 10,0\} . $$

(32)

The corresponding nonlinear scheme is acquired by replacing the optimally linear weights {C₁, C₂, C₃, C₄} in Eq. (30) with the normalized nonlinear weights {$\omega_{1} ,\omega_{2} ,\omega_{3} ,\omega_{4}$}:

$$ \omega_{k} = \frac{{\alpha_{k} }}{{\sum\nolimits_{k = 1}^{4} {\alpha_{k} } }},\quad k = 1,2,3,4 . $$

(33)

How to compute $\alpha_{k}$ in Eq. (33) has a great impact on the behavior of nonlinear schemes. Providing the standard weighting relation in Ref. [18] is adopted, nonlinear UI5 is acquired.

$$ \alpha_{k} = \frac{{C_{k} }}{{\left( {\varepsilon + IS_{k} } \right)^{2} }},\quad k = 1,2,3,4 , $$

(34)

where the linear weights $C_{k}$ are given by Eq. (32). $\varepsilon = 10^{ - 6}$ is a small constant to prevent division by zero. The smoothness indicators $IS_{1} ,IS_{2} ,IS_{3}$ are in Ref. [18] and $IS_{4} = 0$. Under such circumstance, $C_{4} = 0$, $\alpha_{4} = 0$ and $\omega_{4} = 0$, which implies the downwind sub-stencil S₄ in Fig. 7 does not work, and UI5 (Table 13 in “Appendix A”) is actually used in smooth region.

If the weighting relation in Ref. [42] is adopted, nonlinear CI6 is developed.

$$ \alpha_{k} = C_{k} \left( {C + (\frac{{\tau_{6} }}{{\varepsilon + IS_{k} }})^{q} } \right),\quad k = 1,2,3,4 , $$

(35)

where the linear weights $C_{k}$ are given by Eq. (31). C = 10, q = 1, $\tau_{6} = IS_{4} { - }{{ (IS_{1} + 6IS_{2} + IS_{3} )} \mathord{/ {\vphantom {{ (IS_{1} + 6IS_{2} + IS_{3} )} 8}} \kern-0pt} 8}$, $\varepsilon = 10^{ - 6}$. Details regarding $IS_{1} ,IS_{2} ,IS_{3} ,IS_{4}$ can be found in Ref. [42]. When all the smoothness indicators share equivalent magnitude, the downwind sub-stencil is added and CI6 (Table 11 in “Appendix A”) is actually recovered in smooth region.

Although the explicit sub-stencils for the smoothness indicators $IS_{1} ,IS_{2} ,IS_{3} ,IS_{4}$ are different from the compact sub-stencils for lower-order schemes (Fig. 7), the numerical results in Sect. 5.2 will indicate the high-order accuracy and non-oscillatory property are well preserved. Similar technique is also adopted for CRWENO by Ghosh et al. [22,23,24,25] in their related publications.

On the sub-stencils (S₁, S₂, S₃, S₄, S₅) in Fig. 8, five candidate 4th-order compact interpolations and five corresponding linear weights (C₁, C₂, C₃, C₄, C₅) are given by

$$ \left\{ {\begin{array}{*{20}l} {S_{1} : \, 5Q_{{i - \frac{1}{2}}} + Q_{{i + \frac{1}{2}}} = - \frac{1}{4}Q_{i - 2} + \frac{5}{2}Q_{i - 1} + \frac{15}{4}Q_{i} } \hfill \\ {S_{2} : \, Q_{{i - \frac{1}{2}}} + Q_{{i + \frac{1}{2}}} = \frac{1}{4}Q_{i - 1} + \frac{3}{2}Q_{i} + \frac{1}{4}Q_{i + 1} } \hfill \\ {S_{3} : \, \frac{1}{6}Q_{{i - \frac{1}{2}}} + Q_{{i + \frac{1}{2}}} + \frac{1}{6}Q_{{i + \frac{3}{2}}} = \frac{2}{3}Q_{i} + \frac{2}{3}Q_{i + 1} } \hfill \\ {S_{4} : \, Q_{{i + \frac{1}{2}}} + Q_{{i + \frac{3}{2}}} = \frac{1}{4}Q_{i} + \frac{3}{2}Q_{i + 1} + \frac{1}{4}Q_{i + 2} } \hfill \\ {S_{5} : \, Q_{{i + \frac{1}{2}}} + 5Q_{{i + \frac{3}{2}}} = \frac{15}{4}Q_{i + 1} + \frac{5}{2}Q_{i + 2} - \frac{1}{4}Q_{i + 3} } \hfill \\ \end{array} } \right.,\quad \left\{ {\begin{array}{*{20}l} {C_{1} = \frac{1}{64}\left( { - 3 + 5\eta - 2\xi } \right)} \hfill \\ {C_{2} = \frac{1}{64}\left( {5 + 13\eta - 22\xi } \right)} \hfill \\ {C_{3} = - \frac{3}{16}\left( { - 5 + 3\eta } \right)} \hfill \\ {C_{4} = \frac{1}{64}\left( {5 + 13\eta + 22\xi } \right)} \hfill \\ {C_{5} = \frac{1}{64}\left( { - 3 + 5\eta + 2\xi } \right)} \hfill \\ \end{array} } \right.. $$

(36)

Fig. 8

Sub-stencils for nonlinear compact interpolations with K = 1 and L = 2

By a convex combination of Eq. (36), the linear scheme on the global stencil (i − 2, …, i + 3) is given by

$$ \begin{aligned} & \underbrace {{\left( {5C_{1} + C_{2} + \frac{1}{6}C_{3} } \right)}}_{{\beta_{ - 1} }}Q_{{i - \frac{1}{2}}} + \underbrace {{\left( {C_{1} + C_{2} + C_{3} + C_{4} + C_{5} } \right)}}_{{\beta_{0} }}Q_{{i + \frac{1}{2}}} + \underbrace {{\left( {\frac{1}{6}C_{3} + C_{4} + 5C_{5} } \right)}}_{{\beta_{1} }}Q_{{i + \frac{3}{2}}} \\ & \quad = \underbrace {{ - \frac{1}{4}C_{1} }}_{{c_{ - 2} }}Q_{i - 2} + \underbrace {{\left( {\frac{5}{2}C_{1} + \frac{1}{4}C_{2} } \right)}}_{{c_{ - 1} }}Q_{i - 1} + \underbrace {{\left( {\frac{15}{4}C_{1} + \frac{3}{2}C_{2} + \frac{2}{3}C_{3} + \frac{1}{4}C_{4} } \right)}}_{{c_{0} }}Q_{i} \\ & \quad \quad \, \underbrace {{ - \frac{1}{4}C_{5} }}_{{c_{3} }}Q_{i + 3} + \underbrace {{\left( {\frac{1}{4}C_{4} + \frac{5}{2}C_{5} } \right)}}_{{c_{2} }}Q_{i + 2} + \underbrace {{\left( {\frac{1}{4}C_{2} + \frac{2}{3}C_{3} + \frac{3}{2}C_{4} + \frac{15}{4}C_{5} } \right)}}_{{c_{1} }}Q_{i + 1} . \\ \end{aligned} $$

(37)

If $\left\{ {\xi ,\eta } \right\} = \left\{ {0,{5 \mathord{/ {\vphantom {5 7}} \kern-0pt} 7}} \right\}$, Eq. (37) turns out to be 8th-order central compact scheme (CI8) with

$$ \{ C_{ 1} ,C_{ 2} ,C_{ 3} ,C_{ 4} ,{\text{C}}_{ 5} \} = \{ 1/ 1 1 2, 2 5/ 1 1 2, 1 5/ 2 8, 2 5/ 1 1 2, 1/ 1 1 2\} . $$

(38)

If $\left\{ {\xi ,\eta } \right\} = \left\{ { - {2 \mathord{/ {\vphantom {2 7}} \kern-0pt} 7},{5 \mathord{/ {\vphantom {5 7}} \kern-0pt} 7}} \right\}$, Eq. (37) becomes 7th-order upwind compact scheme (UI7) by

$$ \{ C_{ 1} ,C_{ 2} ,C_{ 3} ,C_{ 4} ,{\text{C}}_{ 5} \} = \{ 1/ 5 6, 9/ 2 8, 1 5/ 2 8, 1/ 8,0\} . $$

(39)

The nonlinear schemes are realized by replacing the linear weights $\left\{ {C_{k} \, ,k = 1,2,3,4,5} \right\}$ in Eq. (37) with the nonlinear weights $\left\{ {\omega_{k} \, ,k = 1,2,3,4,5} \right\}$. If the weighting relation by Jiang and Shu [18] together with Eq. (39) is used to calculate $\omega_{k}$, the nonlinear UI7 is obtained. Yet, to avoid redundancy, UI7 is not detailly studied in Sect. 5.2. The nonlinear CI8 will be validated in details where $\omega_{k}$ is calculated by

$$ \left\{ {\begin{array}{*{20}l} {\omega_{k} = \frac{{\alpha_{k} }}{{\sum\nolimits_{k = 1}^{5} {\alpha_{k} } }}} \hfill \\ {\alpha_{k} = C_{k} \left( {C + (\frac{{\tau_{8} }}{{\varepsilon + IS_{k} }})^{q} } \right)} \hfill \\ \end{array} } \right.,\quad k = 1,2,3,4,5 , $$

(40)

where $C_{k}$ are given by Eq. (38), C = 10, q = 1,$\varepsilon = 10^{ - 6}$, $\tau_{8} = IS_{5} - (IS_{1} + 15IS_{2} + 15IS_{3} { + }IS_{4} ) / 3 2$, details regarding $IS_{1} ,IS_{2} ,IS_{3} ,IS_{4} ,IS_{5}$ can be seen in Ref. [42].

Till now, the nonlinear compact interpolations on stencils shown by Figs. 7 and 8 have been presented. As a brief summary, Table 3 lists all the nonlinear interpolations which will be used for comparison. UI5, CI6 and CI8 are the proposed schemes in this work. UE5, CE6 and CE8 are the corresponding explicit counterparts, where the corresponding sub-stencils can be found in [42].

Table 3 Nonlinear compact interpolations UI5, CI6 and CI8 and nonlinear explicit interpolations UE5, CE6 and CE8, which will be compared in Sect. 5.2

The approximate dispersion relation (ADR) technique [53] is used to analyze the spectral characteristics of nonlinear interpolations in Table 3. Figure 9 shows that compact interpolations outperform their explicit counterparts in dispersion errors and the dissipation of compact schemes is also lower than that of explicit schemes in terms of low to moderate wavenumbers. Also, large amount of dissipation in extremely high wavenumbers is noticed for compact schemes, which is advantageous to suppress non-physical spurious oscillations. Further comparisons by benchmarks will be validated in Sect. 5.2.

Fig. 9

Spectral analysis of nonlinear schemes in Table 3 with approximate dispersion relation technique. Left: Dispersion characteristics; Right: Dissipation characteristics

4.3 Interpolation with Characteristic Variables

For Euler equations, to enhance the robustness of nonlinear schemes for high speed flows in the presence of steep gradients, projecting the interpolated variables ${\boldsymbol{Q}}$ in Eqs. (30) and (37) in the characteristic space is beneficial, though interpolation with primitive variables component by component is simple in implementation and attractive in efficiency. Adopting characteristic variables for interpolations is physically and mathematically reasonable due to the fact that Euler equations behave hyperbolic property along time axis. The solution of Euler equations in projection of the characteristic space can be decomposed into waves, each of which has the corresponding sole eigenvalue and eigenvector.

Considering the Euler equations along $\xi$-curvilinear direction as illustration,

$$ \frac{{\partial {\tilde{\boldsymbol{U}}}}}{\partial t} + \frac{{\partial {\tilde{\boldsymbol{E}}}}}{\partial \xi } = \frac{{\partial {\tilde{\boldsymbol{U}}}}}{\partial t} + {\boldsymbol{A}}\frac{{\partial {\tilde{\boldsymbol{U}}}}}{\partial \xi } = {\boldsymbol{0}} . $$

(41)

where ${\boldsymbol{A}} = {{\partial {\tilde{\boldsymbol{E}}}} \mathord{/ {\vphantom {{\partial {\tilde{\boldsymbol{E}}}} {\partial {\tilde{\boldsymbol{U}}}}}} \kern-0pt} {\partial {\tilde{\boldsymbol{U}}}}}$ is the Jacobian matrix along $\xi$-direction. A can be diagonalized by ${\boldsymbol{A}} = {\boldsymbol{R}^{ - 1}\boldsymbol{\varLambda} \boldsymbol{R}}$ where the diagonal matrix $\boldsymbol{\varLambda}$ is given by $\boldsymbol{\varLambda} = diag(U_{\xi } ,U_{\xi } ,U_{\xi } ,U_{\xi } + c_{\xi } ,U_{\xi } - c_{\xi } )$ and the eigenvectors constituting matrix ${\boldsymbol{R}}$ can be found in Ref. [54]. Substituting ${\boldsymbol{A}} = {\boldsymbol{R}^{ - 1}\boldsymbol{\varLambda} \boldsymbol{R}}$ into Eq. (41), we have

$$ \frac{{\partial {\tilde{\boldsymbol{U}}}}}{\partial t} + {\boldsymbol{R}^{ - 1}\boldsymbol{\varLambda} \boldsymbol{R}}\frac{{\partial {\tilde{\boldsymbol{U}}}}}{\partial \xi } = {\boldsymbol{0}} . $$

(42)

It is important to note that, only on the local stencil surrounding the face-center i + 1/2, ${\boldsymbol{R}}$ is considered as a frozen matrix ${\boldsymbol{R}}_{i + 1/2}$ with Roe’s averaging from left state ${\boldsymbol{Q}}_{i}$ and right state ${\boldsymbol{Q}}_{i + 1}$. The locally characteristic variables ${\tilde{\boldsymbol{C}}}$ are calculated by

$$ {\tilde{\boldsymbol{C}}}_{j} = {\boldsymbol{R}}_{i + 1/2} {\tilde{\boldsymbol{U}}}_{j} ,\quad \, j = \ldots ,i - 1,i,i + 1,i + 2, \ldots . $$

(43)

Substituting Eq. (43) into Eq. (42), the characteristic equations are obtained:

$$ \frac{{\partial {\tilde{\boldsymbol{C}}}}}{\partial t} + \boldsymbol{\varLambda}\frac{{\partial {\tilde{\boldsymbol{C}}}}}{\partial \xi } = {\boldsymbol{0}} . $$

(44)

Equation (44) implies along the local characteristics 3D Euler equations can be decomposed into five advection wave equations, each of which is transported at its propagation wave speed along its propagation direction. The wave speeds correspond to eigenvalues in $\boldsymbol{\varLambda}$, the wave directions correspond to the eigenvectors in ${\boldsymbol{R}}$, and the wave amplitudes correspond to the entries in the column vector ${\tilde{\boldsymbol{C}}}$, respectively.

Implementation of CI6 (Eq. 30) with characteristic variables is illustrated:

$$ {\varvec{\upbeta}}_{ - 1} {\tilde{\boldsymbol{C}}}_{i - 1/2} + {\varvec{\upbeta}}_{0} {\tilde{\boldsymbol{C}}}_{i + 1/2} + {\varvec{\upbeta}}_{1} {\tilde{\boldsymbol{C}}}_{i + 3/2} = {\boldsymbol{c}}_{ - 1} {\tilde{\boldsymbol{C}}}_{i - 1} + {\boldsymbol{c}}_{0} {\tilde{\boldsymbol{C}}}_{i} + {\boldsymbol{c}}_{1} {\tilde{\boldsymbol{C}}}_{i + 1} + {\boldsymbol{c}}_{2} {\tilde{\boldsymbol{C}}}_{i + 2} , $$

(45)

where the coefficient matrices ${\varvec{\upbeta}}_{ - 1}$, ${\varvec{\upbeta}}_{0}$, ${\varvec{\upbeta}}_{1}$, ${\boldsymbol{c}}_{ - 1}$, ${\boldsymbol{c}}_{0}$, ${\boldsymbol{c}}_{1}$, ${\boldsymbol{c}}_{2}$ are

$$ \begin{aligned} {\varvec{\upbeta}}_{k} & = \left[ {\begin{array}{*{20}l} {\beta_{k}^{(1)} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {\beta_{k}^{(2)} } \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {\beta_{k}^{(3)} } \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {\beta_{k}^{(4)} } \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\beta_{k}^{(5)} } \hfill \\ \end{array} } \right],\quad k = - 1,0,1,\quad {\boldsymbol{c}}_{k} = \left[ {\begin{array}{*{20}l} {c_{k}^{(1)} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {c_{k}^{(2)} } \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {c_{k}^{(3)} } \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {c_{k}^{(4)} } \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {c_{k}^{(5)} } \hfill \\ \end{array} } \right],\\ & \quad k = - 1,0,1,2, \end{aligned} $$

(46)

where the subscript k is related to stencils of compact schemes, and the superscript $(j)$ stands for the j-th characteristic wave equation. The diagonal entries $\beta_{k}^{(j)}$ and $c_{k}^{(j)}$ are evaluated via Eqs. (30), (33) and (35) with characteristic variables acquired by Eq. (43) on the local stencil. Substituting Eq. (43) into Eq. (45) yields:

$$ \left[ {\begin{array}{*{20}c} {{\varvec{\upbeta}}_{ - 1} {\boldsymbol{R}}_{i + 1/2} } & {{\varvec{\upbeta}}_{0} {\boldsymbol{R}}_{i + 1/2} } & {{\varvec{\upbeta}}_{1} {\boldsymbol{R}}_{i + 1/2} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {{\tilde{\boldsymbol{U}}}_{i - 1/2} } \\ {{\tilde{\boldsymbol{U}}}_{i + 1/2} } \\ {{\tilde{\boldsymbol{U}}}_{i + 3/2} } \\ \end{array} } \right) = {\boldsymbol{b}}_{i + 1/2} , $$

(47)

where ${\boldsymbol{b}}_{i + 1/2} = {\boldsymbol{c}}_{ - 1} {\tilde{\boldsymbol{C}}}_{i - 1} + {\boldsymbol{c}}_{0} {\tilde{\boldsymbol{C}}}_{i} + {\boldsymbol{c}}_{1} {\tilde{\boldsymbol{C}}}_{i + 1} + {\boldsymbol{c}}_{2} {\tilde{\boldsymbol{C}}}_{i + 2}$. Eq. (47) can be further expanded as:

$$ \begin{aligned} & \left[ {\begin{array}{*{20}l} \ddots \hfill & \ddots \hfill & {} \hfill & {} \hfill & {} \hfill \\ {{\varvec{\upbeta}}_{ - 1,i - 1/2} {\boldsymbol{R}}_{i - 1/2} } \hfill & {{\varvec{\upbeta}}_{0,i - 1/2} {\boldsymbol{R}}_{i - 1/2} } \hfill & {{\varvec{\upbeta}}_{1,i - 1/2} {\boldsymbol{R}}_{i - 1/2} } \hfill & {} \hfill & {} \hfill \\ {} \hfill & {{\varvec{\upbeta}}_{{ - 1,i{ + }1/2}} {\boldsymbol{R}}_{i + 1/2} } \hfill & {{\varvec{\upbeta}}_{{0,i{ + }1/2}} {\boldsymbol{R}}_{i + 1/2} } \hfill & {{\varvec{\upbeta}}_{{1,i{ + }1/2}} {\boldsymbol{R}}_{i + 1/2} } \hfill & {} \hfill \\ {} \hfill & {} \hfill & {{\varvec{\upbeta}}_{ - 1,i + 3/2} {\boldsymbol{R}}_{i + 3/2} } \hfill & {{\varvec{\upbeta}}_{0,i + 3/2} {\boldsymbol{R}}_{i + 3/2} } \hfill & {{\varvec{\upbeta}}_{1,i + 3/2} {\boldsymbol{R}}_{i + 3/2} } \hfill \\ {} \hfill & {} \hfill & {} \hfill & \ddots \hfill & \ddots \hfill \\ \end{array} } \right] \\ &\quad \left( {\begin{array}{*{20}l} \vdots \hfill \\ {{\tilde{\boldsymbol{U}}}_{i - 1/2} } \hfill \\ {{\tilde{\boldsymbol{U}}}_{i + 1/2} } \hfill \\ {{\tilde{\boldsymbol{U}}}_{i + 3/2} } \hfill \\ \vdots \hfill \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} \vdots \hfill \\ {{\boldsymbol{b}}_{i - 1/2} } \hfill \\ {{\boldsymbol{b}}_{i + 1/2} } \hfill \\ {{\boldsymbol{b}}_{i + 3/2} } \hfill \\ \vdots \hfill \\ \end{array} } \right) , \end{aligned} $$

(48)

which is a block-tridiagonal system of equations. The unknown face-center conservative column vector ${\tilde{\boldsymbol{U}}}$ will be obtained simultaneously by solving Eq. (48). Subsequently, the face-center vector of primitive variables ${\boldsymbol{Q}}_{i + 1/2}$ can be obtained from ${\tilde{\boldsymbol{U}}}_{i + 1/2}$ before executing Eq. (10).

Interpolation with characteristics variables is computationally more expensive than the interpolation with primitive variables component by component [21]. The former one requires solving block-tridiagonal systems of equations whereas the latter one requires only solving scalar-tridiagonal systems of equations. Nevertheless, using characteristic-wise variables for interpolation is truly beneficial for robustness and better resolution.

5 Numerical Results

Numerical schemes proposed in Sects. 3 and 4 are validated in Sects. 5.1 and 5.2 separately. “L-” and “N-” are used to distinguish the linear and nonlinear schemes respectively.

5.1 Results for Linear Compact Interpolations

Results with five linear schemes are presented. L-Opt4, L-Opt6 and L-Opt8 are the optimized compact schemes proposed in Sect. 3. L-UE5 and L-UI5 are the standard 5th-order explicit and 5th-order compact schemes for comparisons.

5.1.1 Accuracy and Efficiency

A 2D isentropic vortex is used to demonstrate the accuracy of schemes. The initial velocity, temperature and entropy fluctuations for the vortex located at $\left( {x_{c} ,y_{c} } \right) = \left( {0, \, 0} \right)$ are given as follows:

$$ \begin{aligned} & (\delta u, \, \delta v) = \frac{\beta }{2\pi }e^{{\left( {\frac{{1 - r^{2} }}{2}} \right)}} [ - (y - y_{c} ), \, (x - x_{c} )],\quad \delta T = - \frac{{(\gamma - 1)\beta^{2} }}{{8\gamma \pi^{2} }}e^{{\left( {1 - r^{2} } \right)}} ,\quad \, \rho { = }T^{{\frac{1}{\gamma - 1}}} , \\ & P = \rho T,\quad \, r = \sqrt {(x - x_{c} )^{2} + (y - y_{c} )^{2} } . \\ \end{aligned} $$

The vortex strength β is 1 and the simulations end at t = 12. Two kinds of grids are investigated here: uniform grid and wavy grid [36]. Figure 10 shows that the vortex is well preserved on both Cartesian and wavy grids.

Fig. 10

Density contours of stationary isentropic vortex on two types of grid with 60 × 60 cells. Left: Cartesian grid; Right: Wavy grid

To quantitatively evaluate the numerical errors, six gradually finer grids are studied, containing 60 × 60, 80 × 80, 100 × 100, 120 × 120, 140 × 140 and 160 × 160 cells respectively. The error of density on a specific grid is estimated by

$$ {\text{Error}}(\rho ) = \sqrt {\frac{1}{{N^{2} }}\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\left[ {\rho_{i,j} (t) - \rho_{i,j} (0)} \right]^{2} } } } . $$

We can see from Table 4 and Fig. 11 that the optimal orders of accuracy on both Cartesian and wavy grids are well preserved. Higher-order schemes could yield lower error levels. The errors on Cartesian grid are demonstrated lower than those on wavy grids.

Table 4 Verification of orders of accuracy for linear interpolations on both Cartesian and wavy grids by the isentropic vortex case

Fig. 11

Orders of accuracy for compact linear interpolations on both Cartesian and wavy grids by the isentropic vortex case. The x-axis N denotes the cells along each grid line. Left: Cartesian grid; right: Wavy grid

The computational efficiency of linear schemes is compared in Table 5 by the isentropic vortex case where the simulations end at t = 100 on Cartesian grid with 100 × 100 cells. The time costs of the compact schemes increase by approximate 25% compared to the explicit one (L-UE5), which owes to the tridiagonal systems of equations. Nevertheless, we think it is still worthwhile because the error of L-Opt8 is lower than that of L-UE5 in four orders of magnitude at least.

Table 5 Efficiency comparison among linear interpolations

Furthermore, the performance in preserving the strength of a stronger moving vortex for a long-time duration (t = 100) on the Cartesian grid is investigated in Fig. 12. The standard L-UE5 yields visible dissipation whilst L-UI5 greatly improves the outcome. This enhancement owes to the compact stencil. Further improvement in L-Opt4 is due to the spectral optimization. And the additionally marginal improvement in L-Opt6/8 is due to the increased order of accuracy.

Fig. 12

Density of a moving isentropic vortex with $M_{\infty } = 0.5$ and β = 5 along the x direction on Cartesian grid. Left: 30 × 30 cells; right: 40 × 40 cells

5.1.2 Pulse-Entropy–Vorticity Propagation

This problem [55] describes an acoustic wave, a vorticity wave and an entropy wave propagating in a uniform flow with Mach number 0.5. The initial flowfield are given by

$$ \left\{ {\begin{array}{*{20}l} {p^{\prime} = \varepsilon \exp \left[ { - (\ln 2)\left( {{{\left( {x^{2} + y^{2} } \right)} \mathord{/ {\vphantom {{\left( {x^{2} + y^{2} } \right)} 9}} \kern-0pt} 9}} \right)} \right]} \hfill \\ {\rho^{\prime} = \varepsilon \exp \left[ { - (\ln 2)\left( {{{\left( {x^{2} + y^{2} } \right)} \mathord{/ {\vphantom {{\left( {x^{2} + y^{2} } \right)} 9}} \kern-0pt} 9}} \right)} \right] + 0.1\varepsilon \exp \left[ { - (\ln 2)\left( {{{\left( {(x - 67)^{2} + y^{2} } \right)} \mathord{/ {\vphantom {{\left( {(x - 67)^{2} + y^{2} } \right)} {25}}} \kern-0pt} {25}}} \right)} \right]} \hfill \\ {u^{\prime} = 0.04\varepsilon y\exp \left[ { - (\ln 2)\left( {{{\left( {(x - 67)^{2} + y^{2} } \right)} \mathord{/ {\vphantom {{\left( {(x - 67)^{2} + y^{2} } \right)} {25}}} \kern-0pt} {25}}} \right)} \right]} \hfill \\ {v^{\prime} = - 0.04\varepsilon (x - 67)\exp \left[ { - (\ln 2)\left( {{{\left( {(x - 67)^{2} + y^{2} } \right)} \mathord{/ {\vphantom {{\left( {(x - 67)^{2} + y^{2} } \right)} {25}}} \kern-0pt} {25}}} \right)} \right]} \hfill \\ \end{array} } \right.. $$

where ε = 0.001 is introduced to attenuate the nonlinearity. The outcome is multiplied by 1000 so as to match with analytical results. The computational domain is [− 100, 100] × [− 100, 100] with uniformly spaced grid (Δx = Δy = 2). An additional buffer zone [56] is adopted to prevent the computational zone being contaminated by reflective waves. In Fig. 13, compared with L-UE5, the dissipation error with L-UI5 is reduced but its dispersion error is still visible. Neither does the optimized L-Opt4 remedy its dispersion error. Yet, higher-order L-Opt6 and L-Opt8 give satisfactory remediations and yield solutions closest to the exact solution.

Fig. 13

Density contours (above) and density profiles along the x-axis at y = 0 cross-section (below) of the pulse-entropy–vorticity propagation problem with 100 × 100 cells. Left: T = 30; middle: T = 60; right: T = 100

5.1.3 Scattering of Sound Wave from Multi-Cylinder

This case [57] is to investigate the capability of schemes in capturing waves radiated by complex configurations. A periodic source is added to the energy equation of Eq. (7):

$$ S = \varepsilon \exp \left[ { - 25(\ln 2)\left( {x^{2} + y^{2} } \right)} \right]\sin (8\pi t), $$

where $\varepsilon = 0.001$. Both two and three-cylinder cases are investigated, the grids for which are spaced with Δx ≈ Δy ≈ 0.035 and Δx ≈ Δy ≈ 0.035 respectively. Figure 14 shows the instantaneous pressure perturbation contours and root-mean-square (RMS) pressure contours where the radiated waves are well captured. The quantitative comparisons with the exact solution are shown in Fig. 15. The line obtained by L-UE5 deviates far from the analytical solution whist the line by L-UI5 brings significant enhancement. Moreover, the spectral optimization gives additional improvement, seeing L-Opt4. And the highest-order L-Opt8 yields the best agreement with analytical solution.

Fig. 14

Pressure fluctuation contours. Left: instantaneous contours; right: RMS contours. Top: Two cylinders; bottom: Three cylinders

Fig. 15

Comparison of RMS pressure fluctuations on the surface of cylinders. Left: Two cylinders; right: Three cylinders

5.1.4 Viscous Taylor–Green Vortex Problem

Taylor–Green vortex [58] is a representative benchmark for turbulence. The initial flowfield is given by

$$ \left( \begin{aligned} \rho \hfill \\ u \hfill \\ v \hfill \\ w \hfill \\ p \hfill \\ \end{aligned} \right) = \left( {\begin{array}{*{20}l} {\rho_{0} } \hfill \\ {V_{0} {\text{sin(}}x ) {\text{cos(}}y ) {\text{sin(}}z )} \hfill \\ { - V_{0} {\text{cos(}}x ) {\text{sin(}}y ) {\text{cos(}}z )} \hfill \\ 0 \hfill \\ {P_{0} + \rho_{0} V_{0}^{2} [ {\text{cos(2}}x ) {\text{ + cos(2}}y ) ] [ {\text{cos(2}}z ) { + }2 ] / 1 6} \hfill \\ \end{array} } \right) $$

The computational domain is a [0, 2π] × [0, 2π] × [0, 2π] square box with periodic boundary condition applied. Three different Reynolds number (Re = 100, Re = 400 and Re = 1600) are investigated. All the simulations stop at t = 10. The dissipation rate of kinetic turbulence energy $\kappa$ is plotted to investigate the capability of schemes, which is defined as $\kappa = {{dE_{k} } \mathord{/ {\vphantom {{dE_{k} } {dt}}} \kern-0pt} {dt}}$ where

$$ E_{k} = \frac{1}{{\rho_{0} V_{\varOmega } }}\int_{\varOmega } {\frac{{\rho u_{i} u_{i} }}{2}dV_{\varOmega } } . $$

Figure 16a indicates that except for L-UE5 which exhibits a slight deviation, the compact schemes are all in reasonable agreement with the DNS data [58]. Figure 16b shows, for Re = 400, though the optimized schemes have brought visible improvements, the grid resolution (32 × 32 × 32 cells) is still inadequate to yield satisfactory results. Thereby, a finer grid with 64³ cells is in demand and good agreement with DNS data is shown in Fig. 16e. Figure 16c and f further demonstrate that, compared with L-UE5, L-UI5 only brings limited improvement, and the performance is greatly enhanced by the spectral optimization (L-Opt4/6/8).

Fig. 16

The dissipation rate of kinetic turbulence energy for the viscous Taylor–Green vortex problem

5.1.5 Decaying Isotropic Turbulence Flow

The compressible decaying isotropic turbulence [59] is another classical benchmark to investigate the capability of schemes in handling the evolvement of turbulence statistic quantities. The initial divergence-free velocity flowfield is acquired via inverse Fourier transform of the velocity field in wavenumber domain at a given turbulent spectrum [60]. The initial density and temperature are specified as constants. Two crucial parameters are: the turbulent Mach number given by $M_{t} = {{\sqrt 3 u_{rms} } \mathord{/ {\vphantom {{\sqrt 3 u_{rms} } {\left\langle c \right\rangle }}} \kern-0pt} {\left\langle c \right\rangle }}$ based on the RMS velocity defined as $\, u_{rms} { = }\sqrt {{{\left\langle {u_{i} u_{i} } \right\rangle } \mathord{/ {\vphantom {{\left\langle {u_{i} u_{i} } \right\rangle } 3}} \kern-0pt} 3}} \,$, and the Reynolds number given by $Re_{\lambda } = {{\left\langle \rho \right\rangle u_{rms} \lambda } \mathord{/ {\vphantom {{\left\langle \rho \right\rangle u_{rms} \lambda } {\left\langle \mu \right\rangle }}} \kern-0pt} {\left\langle \mu \right\rangle }}$ based on the Taylor micro-scale length defined as $\lambda^{2} = {{\left\langle {u_{i}^{2} } \right\rangle } \mathord{/ {\vphantom {{\left\langle {u_{i}^{2} } \right\rangle } {\left\langle {({{\partial u_{i} } \mathord{/ {\vphantom {{\partial u_{i} } {\partial x_{i} }}} \kern-0pt} {\partial x_{i} }})^{2} } \right\rangle }}} \kern-0pt} {\left\langle {({{\partial u_{i} } \mathord{/ {\vphantom {{\partial u_{i} } {\partial x_{i} }}} \kern-0pt} {\partial x_{i} }})^{2} } \right\rangle }}$. Here M_t = 0.3 and Re_λ= 72 is chosen. The computation domain is [0, 2π] × [0, 2π] × [0, 2π] with 64 × 64 × 64 cells and the periodic boundary condition is applied. The DNS data from Ref. [59] is adopted for comparison. The time evolvement of the normalized turbulent Mach number M_t/M_t(0), normalized kinetic energy K(t)/K₀ and normalized density ρ/M_t(0)² are shown in Fig. 17a–c respectively, where the time t is normalized by the large eddy turnover time τ = λ₀/u_rms,0. Figure 17a–c indicate, as the numerical dissipation decreases, the agreement with the DNS data becomes more satisfactory. Figure 17d further demonstrates the optimized schemes can resolve rich high wavenumber components whilst L-UE5 and L-UI5 dissipate many broadband contents.

Fig. 17

Results of decaying isotropic turbulence at M_t= 0.3, Re_λ= 72 on grid with 64 × 64 × 64 cells

5.2 Results for Nonlinear Compact Interpolations

In this subsection, the nonlinear compact schemes (N-UI5, N-CI6 and N-CI8) in Sect. 4 are compared with the nonlinear explicit counterparts (N-UE5, N-CE6 and N-CE8).

5.2.1 Freestream Preservation

Freestream preservation [32] refers to a property that on curvilinear grids the given freestream condition on solution points should remain the initial values and is not affected by the geometry discretization. The freestream preservation on curvilinear grids with nonlinear schemes is of crucial importance and a basic inspector for GCL condition.

A highly wavy 2D grid with 60 × 60 cells is chosen where the periodic boundary condition is imposed. The u velocity along x-axis direction is monitored for the error accumulated with time. The results are shown in Fig. 18 and Table 6. It is obvious that, the error accumulated on the wavy grid without the satisfaction of GCL condition is tremendous, whist that with GCL satisfied by CCSCMM could reach machine zero.

Fig. 18

Verification of freestream preservation on a highly wavy grid. a Wavy grid. b Velocity contour where the GCL is violated due to grid metrics calculated by the inversions of coordinate transformation. c Velocity contour where the GCL is satisfied by CCSCMM

Table 6 Error of velocity u on a wavy grid shown by Fig. 18a

5.2.2 Accuracy and Efficiency

The isentropic vortex in Sect. 5.1.1 is also used here to show the orders of accuracy for nonlinear interpolation schemes. Together with Tables 7, 8 and Fig. 19, we can see the optimal orders of accuracy for nonlinear schemes are all well retained on both Cartesian and wavy grids. Also, the compact schemes exhibit lower error level than the explicit counterparts, which is due to the adoption of compact stencils. Moreover, the higher-order schemes could yield lower error level than the lower-order schemes.

Table 7 Verification of orders of accuracy for nonlinear interpolations on Cartesian grids by the isentropic vortex case

Table 8 Verification of orders of accuracy for nonlinear interpolations on wavy grids by the isentropic vortex case

Fig. 19

Orders of accuracy for compact nonlinear interpolations on both Cartesian and wavy grids by the isentropic vortex case. Left: Cartesian grid; right: Wavy grid

The efficiency comparisons of nonlinear interpolations consist of two categories: the primitive variables and characteristic variables, which are shown in Tables 9 and 10 respectively. All the simulations end at t = 100 on grid with 100 × 100 cells.

Table 9 The efficiency comparisons among nonlinear interpolations with primitive variables

Table 10 The efficiency comparisons among nonlinear interpolations with characteristic variables

Table 9 shows the efficiency comparisons among nonlinear interpolations with primitive variables. The extra time consumption of compact schemes, compared with explicit counterparts, results from solving the scalar-tridiagonal systems of equations. Besides, by comparing the costs of N-CI6 and N-UI5 (or N-CE6 and N-UE5), the extra time is due to the downwind sub-stencil and its related smoothness indicator. Since the smoothness indicators for N-CI8 is more complicated than N-CI6, the corresponding time cost increases to some degree.

Table 10 shows the efficiency comparisons among nonlinear interpolations with characteristic variables. Compact schemes are demonstrated to be more costly than the explicit ones. This verifies that solving the block-tridiagonal system of equations is indeed expensive. Yet, this shortcoming is absent for the passive scalar equations, thereby compact schemes are still good alternatives for those scalar equations involving discontinuities. Besides, for subsonic to transonic flows, the interpolation with primitive variables is also viable, trustworthy and computational economic. More advanced technique to improve the computational efficiency is left to our future work.

5.2.3 Sin Wave System

The advection equation $u_{t} + u_{x} = 0$ is solved on the computational domain [0, 3] where the grid is uniformly spaced with Δx = 0.006. The initial condition is given by

$$ u_{0} (x) = \exp ( - 16(x - 0.5)^{2} )\sin (40\pi x). $$

Simulations end at 1.5. Figure 20 shows that N-UE5 damps the amplitude drastically. N-UI5 gives marginally higher amplitude due to the adoption of compact stencil. And N-CI6 yields remarkable improvement than N-UI5. The great reduction of numerical dissipation in N-CI6 is attributed to the introduction of downwind sub-stencil and less-dissipative nonlinear weights. Another interesting observation is the dispersion error produced by N-CI6 is less than that of N-CE6, and this is due to the adoption of compact stencil.

Fig. 20

Results of sin wave system with 500 cells. Left: Global view; right: Local view

5.2.4 Complex Wave System

The advection scalar equation $u_{t} + u_{x} = 0$ is also solved in this case. The initial condition for the propagation of a Gaussian, triangle, square and semi-ellipse waves is given by

$$ u_{0} (x) = \left\{ {\begin{array}{*{20}l} {\left[ {G(x,\beta ,z - \delta ) + 4G(x,\beta ,z) + G(x,\beta ,z + \delta )} \right]/6 ,} \hfill & { \, x \in [ - 0.8, - 0.6],} \hfill \\ {1,} \hfill & {x \in [ - 0. 4, - 0. 2],} \hfill \\ {1 - \left| {10(x - 0.1)} \right|,} \hfill & {x \in [0,0. 2],} \hfill \\ {\left[ {F(x,\alpha ,a - \delta ) + 4F(x,\alpha ,a) + F(x,\alpha ,a + \delta )} \right]/6,} \hfill & {x \in [0. 4,0.6],} \hfill \\ {0,} \hfill & {else,} \hfill \\ \end{array} } \right. $$

where $G(x,\beta ,z){ = }e^{{ - \beta (x - z)^{2} }}$, $F(x,\alpha ,a) = \sqrt {\hbox{max} (1 - \alpha^{2} (x - a)^{2} ,0)}$, $z = - 0.7$, $\beta = {{\log 2} \mathord{/ {\vphantom {{\log 2} {\left( {36\delta^{2} } \right)}}} \kern-0pt} {\left( {36\delta^{2} } \right)}}$, $\delta = 0.005$, a = 0.5, α = 10. The numerical simulations end at $t = 8$. The computational domain is [− 1, 1] containing 100 cells where the periodic boundary condition is applied at $x = \pm 1$.

Figure 21 show the results of different schemes in preserving the original u shape after long time propagation. Local views of Gaussian and square waves by Fig. 21c, d clearly show the compact schemes can yield higher resolution than their explicit counterparts, for instance N-CE6 and N-CI6 (or N-CE8 and N-CI8). Another noticeable finding is the introduction of the downwind sub-stencil to form a central global stencil can bring drastic benefit, shown by comparing N-UI5 with N-CI6. The comparisons of L₂-error of u in Fig. 21b demonstrate the compact schemes produce lower truncation error than the explicit counterparts.

Fig. 21

Results of complex wave system problem with 100 cells

5.2.5 Shu–Osher Problem

The initial condition for Shu–Osher problem is given by

$$ (\rho ,u,p) = \left\{ {\begin{array}{*{20}l} {(3.857143,\,2.629369,\,10.333333) ,} \hfill & { 0\le x < 1,} \hfill \\ {(1 + 0.2\sin \left( {5x} \right),\,0,\,1) ,} \hfill & { 1\le x \le 10.} \hfill \\ \end{array} } \right. $$

The simulations run till t = 1.8 on a uniformly spaced grid with 200 cells. The density plots depicted in Fig. 22 show the amplitudes of entropy wave are dissipated significantly with 5th-order schemes (N-UE5 and N-UI5) whilst dramatic improvements are observed with 6th-order and 8th-order schemes (N-CE6, N-CI6, N-CE8 and N-CI8). Moreover, in comparing the dispersion characteristics of schemes sharing same order of accuracy, the compact schemes are shown less dispersive than the explicit ones, which can be seen by N-CE6 and N-CI6.

Fig. 22

Density plots of Shu–Osher problem with 200 cells. Left: Global view; right: Local view

5.2.6 Lax Problem

The initial condition for Lax problem is

$$ (\rho ,u,p) = \left\{ {\begin{array}{*{20}l} {( 0. 4 4 5,\,0.698,\, 3. 5 2 8),} \hfill & {0 \le x < 0.5,} \hfill \\ {(0.5,\,0,\,0.5710)} \hfill & {0.5 \le x \le 1.} \hfill \\ \end{array} } \right. $$

The simulations end at t = 0.14 on the computational domain with 100 cells. Figure 23 demonstrates that the compact schemes can capture sharper discontinuities than the explicit ones, seeing the comparison between N-UE5 and N-UI5 (or N-CE6 and N-CI6). Moreover, the introduction of downwind sub-stencil brings additional improvement, shown by the comparison between N-CI6 and N-UI5 (or N-CE6 and N-UE5). Furthermore, for higher-order schemes, N-CI8 is evidenced to retain non-oscillatory discontinuity sharply whilst N-CE8 yields non-physical overshoots. This is because the stencil for N-CE8 is larger than that of N-CI8, and larger stencil is more likely to suffer from numerical instabilities. Similar observation is also noticed in Sects. 5.2.7 and 5.2.10.

Fig. 23

Density plots of Lax problem with 100 cells. Left: Global view; right: Local view

5.2.7 Blast Wave Problem

The initial condition for the blast wave problem is given by

$$ (\rho ,u,p) = \left\{ {\begin{array}{*{20}l} {(1,\,0,\,1000),} \hfill & {0 \le x < 0.1,} \hfill \\ {(1,\,0,\,0.01),} \hfill & {0.1 \le x < 0.9,} \hfill \\ {(1,\,0,\,100),} \hfill & {0.9 \le x \le 1.} \hfill \\ \end{array} } \right. $$

The numerical simulations run till t = 0.038 on the grid with 400 cells. The reflective boundary condition is applied at x = 0 and x = 1. It is observed in Fig. 24 that non-physical numerical instabilities are noticed in N-CE8, whereas N-CI8 is more resilient to numerical oscillations.

Fig. 24

Density plots of blast wave problem with 400 cells. Left: Global view; right: Local view

5.2.8 Rayleigh–Taylor Instability Problem

This problem [61] investigates the development of interface instability driven by the gravity of two fluids with different densities. The computational domain is [0, 1/4] × [0, 1] with 125 × 500 cells. The initial condition is given by

$$ (\rho , \, u, \, v, \, p) = \left\{ {\begin{array}{*{20}l} {( 2, \, 0, - 0.025a\cos (8\pi x),{ 2}y + 1),} \hfill & { 0\le y < 0.5,} \hfill \\ {(1, \, 0, - 0.025a\cos (8\pi x), \, y{ + }1.5),} \hfill & { 0. 5\le y \le 1,} \hfill \\ \end{array} } \right. $$

where the sound speed is $a = \sqrt {{{\gamma p} \mathord{/ {\vphantom {{\gamma p} \rho }} \kern-0pt} \rho }}$ with $\gamma = {3 \mathord{/ {\vphantom {3 5}} \kern-0pt} 5}$. Source terms ρ and ${\rho}v$ are added to the momentum equation in y direction and energy equation in Eq. (7) respectively. The top and bottom boundaries are specified as $(\rho ,u,v,p) = (2,0,0,2.5)$ and $(\rho ,u,v,p) = (1,0,0,1)$ respectively. The numerical simulations are conducted till t = 1.95. The density contours, shown by Fig. 25, indicate the compact schemes have better resolution to resolve the complicated flow structures than the explicit counterparts.

Fig. 25

Density contours of Rayleigh–Taylor instability problem with 125 × 500 cells

5.2.9 Double Mach Reflection Problem

This problem [61] describes a right-moving Mach 10 shock which is initially positioned at x = 1/6 and makes an angle 60° with the x-axis. The computational domain is [0, 4] × [0, 1] with 1920 × 480 cells. The bottom boundary from x = 0 to x = 1/6 is assigned as post shock condition and from x = 1/6 to x = 4 is specified as the reflective solid wall. The top boundary condition is specified via the shock wave relation. The pre-shock and post-shock conditions are given by

$$ (\rho ,u,v,p) = \left\{ {\begin{array}{*{20}l} {( 1. 4, \, 0, \, 0,{ 1}),} \hfill & {y < 1.732(x - 0.1667).} \hfill \\ {(8, \, 7.145,{ - 4} . 1 2 5,{ 116} . 8 3 3 3)} \hfill & {} \hfill \\ \end{array} } \right. $$

The simulations end at t = 0.2. The local density contours shown by Fig. 26 demonstrate compact schemes can resolve more fine structures along the slip line than the explicit counterparts.

Fig. 26

Local views of density contours of Double Mach reflective problem with 1920 × 480 cells

5.2.10 Shock–Vortex Interaction Problem

This problem [41, 62] describes the interaction of a stationary shock ($M_{\infty } = 1.2$) at x = 0 with a moving vortex $(M_{v} = 1.0)$ the core of which is located ahead of the shock $(x_{v}, y_{v} = 4, 0)$. The initial condition is given by

$$ \begin{aligned} & \rho = \left( {1 - \frac{\gamma - 1}{2}M_{v}^{2} e^{{1 - r^{2} }} } \right)^{{\frac{1}{\gamma - 1}}} ,\quad p = \frac{1}{\gamma }\left( {1 - \frac{\gamma - 1}{2}M_{v}^{2} e^{{1 - r^{2} }} } \right)^{{\frac{\gamma }{\gamma - 1}}} , \\ & \delta u = - M_{v} e^{{\frac{{1 - r^{2} }}{2}}} \left( {y - y_{v} } \right),\quad \delta v = M_{v} e^{{\frac{{1 - r^{2} }}{2}}} \left( {x - x_{v} } \right), \\ \end{aligned} $$

where $\gamma = 1.4$. The simulations run on a square domain [− 35, 10] × [− 22.5, 22.5] with 600 × 600 cells. Figure 27 depict the pressure fluctuation contours at t = 16 at which the vortex has already passed the shock, been deformed and yielded a quadrupole sound signature with many curved sound waves. The short waves are highly dissipated by N-UE5/N-UI5 but are relatively well captured by N-CE6/N-CI6, which owes to the addition of downwind sub-stencil. N-CE8 creates some high-frequency fake sound waves which is because the stencil is too widen and unable to resist the spurious waves. In contrast, N-CI8 has better resilience to nonphysical oscillations. A quantitative comparison is shown by Fig. 28 where the pressure fluctuation profiles along the dashed line in Fig. 27a are plotted. With no doubting, the profile with N-CE8 largely deviates from the reference data.

Fig. 27

Local views of pressure fluctuation contours of shock–vortex interaction problem at t = 16 with 600 × 600 cells

Fig. 28

Pressure fluctuation profiles of shock–vortex interaction problem at t = 16 along the dashed line in Fig. 27a

5.2.11 Decaying Isotropic Turbulence Flow

The computational setup for this case has been stated clearly in Sect. 5.1.5. The only exception is M_t equals to 0.5. The grid contains 64 × 64 × 64 cells. Figure 29a–d show the time history of normalized density, the time history of turbulent Mach number, the time history of kinetic energy and the energy spectrum at t/τ = 8 respectively. In this case, the improvement due to the adoption of compact stencil is not very obvious, which is illustrated by the comparison between N-CE6 and N-CI6 (N-CE8 and N-CI8). However, 6th-order compact scheme exhibits noticeable enhancement over the 5th-order compact scheme, for instance N-CI6 over N-UI5. This is because the introduction of downwind sub-stencil makes the global stencil to be central which can significantly improve the dissipation characteristics. Furthermore, the comparison between 6th-order and 8th-order schemes indicates the further increase in the order of accuracy hardly brings amazing improvement. Under such condition, refining grid would be a more effective alternative.

Fig. 29

Results of decaying isotropic turbulence at M_t= 0.5, Re_λ= 72 on grid with 64 × 64 × 64 cells

6 Conclusions

For multiscale flows, the presence of a large range of spatial and temporal scales poses challenges for the numerical algorithms. To maximally resolve all the scales, the spectral-like compact interpolations schemes which provide better representation of shorter length scales are extended to a cell-centered finite difference method (CCFDM) in this paper. These schemes are verified with high-order accuracy and validated to be capable of capturing fine structures in complex flows with high resolution. Low-speed flows and high-speed flows are both investigated detailly. The linear compact interpolations in Sect. 3 are for shock-free flows and the nonlinear compact interpolations in Sect. 4 are for shock-embedded flows.

The linear compact interpolations with spectral optimization exhibit superior low-dissipation low-dispersion properties. The detailly analyzed Opt4, Opt6 and Opt8 are validated to be attractive for shock-free problems by carrying out benchmarks from computational aeroacoustics workshops and two typical turbulence cases: Tayler–Green vortex and decaying isotropic turbulence. The greatly reduced error level implies the current optimized linear compact schemes are worthwhile to be attempted for the low-speed realistic complicated configurations.

The nonlinear compact shock-capturing interpolations are realized by extending the novel weighing technique [42] to compact interpolations. The criteria to choose optimally compact sub-stencils for a most general compact global stencil are presented in Sect. 4.1. Within the proposed framework, the explicit WENO-type scheme can be reverted by setting K = 0. For practical purposes, two compact special cases are analyzed: (K = 1, L = 1) and (K = 1, L = 2), leading to the analysis of three nonlinear schemes (UI5, CI6 and CI8). Their orders of accuracy are verified well preserved on both Cartesian and wavy grids. And the approximate dispersion relation (ADR) analysis further demonstrates their superior dispersion and dissipation characteristics compared to the explicit nonlinear counterparts. Finally, the advantages of compact nonlinear schemes over the explicit nonlinear schemes in resolving both the flow discontinuities sharply and rich flow structures are validated by a series of numerical experiments. Additionally, an interesting finding is that the compact scheme is more resilient to suppress the numerical overshoots than the explicit scheme. This is attributed to the adoption of compact sub-stencils. Lastly, interpolation in the projection of characteristic space is indeed more expensive than that with primitive variables due to the requirement of solving a system of block-tridiagonal matrix equations. The advanced technique to improve the computational efficiency of characteristic interpolation is left to our future work.

Appendices

Appendix A: Compact Interpolations

See Tables 11, 12, 13, 14 and 15.

Table 11 Tridiagonal (K = 1) compact central schemes

Table 12 Pentadiagonal (K = 2) compact central schemes

Table 13 Tridiagonal (K = 1) compact upwind schemes

Table 14 Pentadiagonal (K = 2) compact upwind schemes

Table 15 Heptadiagonal (K = 3) compact upwind schemes

Appendix B: Proof of Eq. (23)

Applying Taylor series analysis on Eq. (20) to achieve (2K + 2L)th-order accuracy, the following (2K + 2L) constraints are required:

$$ \begin{aligned} & \underbrace {{ 0^{q} }}_{C} + \underbrace {{\sum\limits_{n = 1}^{K} {n^{q} \left( {\beta_{n} { + }({ - 1})^{q} \beta_{{{ - }n}} } \right)} }}_{A \cdot X} = \underbrace {{\sum\limits_{m = 1}^{L + 1} {\left( {\frac{2m - 1}{ 2}} \right)^{q} \left( {c_{m} { + }({ - 1})^{q} c_{1 - m} } \right)} }}_{B \cdot Y},\\ & \quad q = 0, 1, 2 ,\ldots , 2\left( {K + L} \right) - 1, \end{aligned} $$

(49)

where the column vectors C, X, Y and matrices A, B are

Using block multiplication of matrices, Eq. (49) is written in the following form:

$$ \underbrace {{C_{1} }}_{(K + L) \times 1} + \underbrace {{A_{11} }}_{(K + L) \times K} \, \underbrace {{X_{1} }}_{K \times 1} = \underbrace {{B_{11} }}_{(K + L) \times (L + 1)} \, \underbrace {{Y_{1} }}_{(L + 1) \times 1}. $$

(50)

$$ \underbrace {{C_{2} }}_{(K + L) \times 1} + \underbrace {{A_{22} }}_{(K + L) \times K} \, \underbrace {{X_{2} }}_{K \times 1} = \underbrace {{B_{22} }}_{(K + L) \times (L + 1)} \, \underbrace {{Y_{2} }}_{(L + 1) \times 1}. $$

(51)

There are (K + L) equations but (K + L + 1) unknowns in each equation of Eqs. (50) and (51), which means both Eqs. (50) and (51) are underdetermined. In Eq. (50), the first unknown element in $X_{1}$ is $\beta_{1} { + }\beta_{ - 1}$. Assuming $\beta_{1} { + }\beta_{ - 1} = \eta$, all the entries in $X_{1}$ and $Y_{1}$ are dependent variables of $\eta$. Similarly, in Eq. (51), the first unknown element in $X_{2}$ is $\beta_{1} - \beta_{ - 1}$. Assuming $\beta_{1} - \beta_{ - 1} = \xi$, the other entries in $X_{2}$ and $Y_{2}$ are dependent variables of $\xi$. These yield:

$$ \left\{ {\begin{array}{*{20}l} {c_{1 - m} + c_{m} = c_{m}^{ + } \left( \eta \right),} \hfill & {m = 1, \ldots L + 1,} \hfill \\ {\beta_{ - n} { + }\beta_{n} = \beta_{n}^{ + } \left( \eta \right),} \hfill & {n = 1, \ldots K.} \hfill \\ \end{array} } \right. $$

(52)

$$ \left\{ {\begin{array}{*{20}l} {c_{m} - c_{1 - m} = c_{m}^{ - } \left( \xi \right),} \hfill & {m = 1, \ldots L + 1,} \hfill \\ {\beta_{n} - \beta_{ - n} = \beta_{n}^{ - } \left( \xi \right),} \hfill & {n = 1, \ldots K.} \hfill \\ \end{array} } \right. $$

(53)